
Linear Generalized ElGamal Encryption Scheme
Pascal Lafourcade
1 a
, L
´
eo Robert
1 b
and Demba Sow
2 c
1
Universit
´
e Clermont Auvergne, LIMOS CNRS (UMR 6158), Campus des C
´
ezeaux, Aubi
`
ere, France
2
LACGAA, Universit
´
e Cheikh Anta Diop de Dakar, Senegal
Keywords:
Cryptography, Partial Homomorphic Encryption, Linear Assumption, ElGamal Encryption Scheme.
Abstract:
ElGamal public key encryption scheme has been designed in the 80’s. It is one of the first partial homomorphic
encryption and one of the first IND-CPA probabilistic public key encryption scheme. A linear version has been
recently proposed by Boneh et al. In this paper, we present a linear encryption based on a generalized version
of ElGamal encryption scheme. We prove that our scheme is IND-CPA secure under linear assumption. We
design a generalized ElGamal scheme from the generalized linear. We also run an evaluation of performances
of our scheme. We show that the decryption algorithm is slightly faster than the existing versions.
1 INTRODUCTION
In 2009 in his thesis (Gentry, 2009), G. Grentry pro-
posed the first fully homomorphic encryption scheme.
It was a revolution and it solves an open problem
already stated by Rivest Shamir and Adelman when
they invented RSA in (Rivest et al., 1978). Many ad-
vances have been done and nowadays we have some
efficient implementations like for instance SEAL de-
veloped by Microsoft (SEAL, 2019). However for
some applications like the inversion of a large ma-
trix or multiplications of large matrices fully homo-
morphic encryption schemes can be very slow or pro-
duce large ciphertext or even be inexact. It is why
all partial homomorphic encryptions like RSA (Rivest
et al., 1978), GM (Goldwasser and Micali, 1982),
ElGamal (Elgamal, 1985), Benaloh (Benaloh, 1999;
Fousse et al., 2011), Okamoto-Uchiyama (Okamoto
and Uchiyama, 1998), Naccache-Stern (Naccache
and Stern, 1998), Paillier (Paillier, 1999) or Gal-
braith (Galbraith, 2002), are still widely used. They
can be used to solve such problems in reasonable
among of time like in (Ciucanu et al., 2019).
Many cryptosystems rely on the Diffie-Hellman
decision problem (DDH) (Boneh, 1998; Joux and
Guyen, 2006) assumption, notably the ElGamal en-
cryption scheme and the Cramer-Shoup encryption
scheme (Cramer and Shoup, 1998). In (D. Boneh and
Shacham, 2004b), Boneh et al. introduced the Deci-
a
https://orcid.org/0000-0002-4459-511X
b
https://orcid.org/0000-0002-9638-3143
c
https://orcid.org/0000-0002-1917-2051
sional Linear Assumption (DLA) and a variation of
ElGamal encryption scheme. Our aim is to improve
this linear version of ElGamal encryption scheme us-
ing the same approach proposed in (Sow and Sow,
2011).
Contributions. We propose the following results:
• Most of today’s public key cryptosystems are re-
sistant to various types of attacks and are effec-
tive. Their main role is the protection of commu-
nications so they guarantee the security of the data
exchanged or stored. Thus, it will always be inter-
esting to find a new encryption scheme or to im-
prove a known one. It is in this context that we
propose a linear Generalized ElGamal encryption
scheme. The modifications are about the key gen-
eration which lead to a different encryption and
decryption algorithms. Like linear ElGamal en-
cryption, the linear Generalized ElGamal encryp-
tion scheme is IND-CPA secure under (DLA).
• We also propose the ElGamal and the Generalized
ElGamal schemes from the generalized linear.
• We implement the algorithms and compare their
performances with the original algorithms. Our
performance evaluations show that the decryption
algorithm is faster. We also demonstrate that our
key generation algorithm is slower, but this is not
a problem since this operation is usually done
only once.
372
Lafourcade, P., Robert, L. and Sow, D.
Linear Generalized ElGamal Encryption Scheme.
DOI: 10.5220/0009828703720379
In Proceedings of the 17th International Joint Conference on e-Business and Telecommunications (ICETE 2020) - SECRYPT, pages 372-379
ISBN: 978-989-758-446-6
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Related Works. In 1985, Taher ElGamal (Elgamal,
1985) proposed an encryption and signature scheme
called ElGamal scheme.
In (Hanoymak, 2013), Turgut Hanoymak proves
the security of ElGamal encryption scheme which
is based on the hardness to solve the Computa-
tional Diffie-Hellman (CDH) and Decisional Diffie-
Hellman (DDH) problems.
In (D. Boneh and Shacham, 2004b), Boneh et al.
proposed a linear encryption scheme based on the El-
Gamal encryption scheme. The linear ElGamal en-
cryption scheme is IND-CPA secure under the (DLA).
In (Sow and Sow, 2011), a modified variant of
the ElGamal scheme is presented, and it is called
Generalized ElGamal. As ElGamal’s scheme, the
Generalized ElGamal scheme is based on Decisional
Diffie-Hellman Problem (DDH). In the Generalized
ElGamal scheme, the decryption key size is smaller
than those of ElGamal scheme. Hence the General-
ized ElGamal scheme is more efficient than ElGamal
scheme; since the decryption process is a bit faster.
The encryption mechanism has the same efficiency
than ElGamal encryption mechanism. But, the key
generation algorithm is slower than the key genera-
tion algorithm of ElGamal scheme. However, this is
not a problem since the key generation is done only
once.
Outline of Paper. In Section 2, we present the orig-
inal ElGamal encryption scheme and the Generalized
ElGamal encryption scheme. In Section 3, we present
the Linear assumption, the linear ElGamal encryp-
tion scheme and the ElGamal encryption scheme from
the generalized linear. In Section 4, we propose the
linear Generalized ElGamal encryption scheme and
the Generalized ElGamal encryption scheme from the
generalized linear. In Section 5, we propose a com-
plexity analysis of our scheme. In Section 6.1, we
present the curves showing the average time of the
key generation, encryption and decryption algorithms
of the ElGamal encryption scheme and the General-
ized ElGamal encryption scheme. In Section 6.2, we
also present the curves showing the average time of
the key generation, encryption and decryption algo-
rithms of the Linear ElGamal encryption scheme and
the Linear Generalized ElGamal encryption scheme.
Note that a full version with the security proofs is
available on (Extended Version, ).
2 ElGamal AND GENERALIZED
ElGamal ENCRYPTION
SCHEMES
We recall the ElGamal encryption scheme (Elga-
mal, 1985) and the Generalized ElGamal encryption
scheme (Sow and Sow, 2011).
2.1 The ElGamal Encryption Scheme
Given a computational group scheme G, the ElGamal
public-key encryption is defined as follow (Elgamal,
1985):
Key Generation Algorithm. For the creation of a
public/secret key, Bob should do the following:
1. Select a finite cyclic group G of order d
with generator g.
2. Select a random integer a such that 2 < a < d.
3. Compute h = g
a
in G.
4. The public key is pk = (G,d, g,h) and the
secret key is sk = a.
Encryption Algorithm. To encrypt a message m
for Bob, Alice should do the following:
1. Take pk = (G, d,g,h), the Bob’s public key;
2. Select a random integer r such that
1 < r < d = #G;
3. Compute c
1
= g
r
and c
2
= m · h
r
in G;
4. The ciphertext is c = (c
1
,c
2
).
Decryption Algorithm. To decrypt a ciphertext c,
Bob should do the following:
1. Take sk = a the secret key.
2. Compute m =
c
2
(c
1
)
a
, we note that m ∈ G.
3. The plaintext is m.
Security Proof of ElGamal Encryption. We recall
some theorems, which show the security of ElGamal
encryption scheme under the CDH and DDH assump-
tions. Let GP an algorithm which takes 1
k
and re-
turns the public key pk = (G,d,g,h) of the ElGamal
encryption scheme.
I One-wayness under the CDH Assumption. If
the CDH assumption holds with respect to GP,
then the ElGamal encryption scheme is one-way.
Theorem 2.1. Let adversary A be a probabilis-
tic polynomial-time algorithm against the ElGa-
mal encryption scheme (Elgamal, 1985) in the
OW-CPA sense. Then there is a probabilistic
Linear Generalized ElGamal Encryption Scheme
373

polynomial-time algorithm B against GP solving
the CDH problem such that:
Adv
CDH
GP ,B
(k) = Adv
OW−CPA
Π,A
(k).
I Indistinguishability under the DDH Assump-
tion. If the DDH assumption holds with respect
to G P , then the ElGamal encryption scheme is
indistinguishable under chosen-plaintext attacks,
i.e., it is IND-CPA secure.
Theorem 2.2. Let adversary A be a probabilis-
tic polynomial-time against the ElGamal encryp-
tion scheme in the IND-CPA sense. Then there
is a probabilistic polynomial-time algorithm B
against GP solving the DDH problem such that:
Adv
DDH
GP ,B
(k) =
1
2
· Adv
IND−CPA
Π,A
(k).
I Semantic Security. In (J. Katz, 2008), Katz and
al. prove the semantic security of the ElGamal
encryption scheme.
Theorem 2.3. Under the DDH assumption, El-
Gamal encryption scheme is semantically secure.
2.2 Generalized ElGamal Encryption
Scheme
We give a key generation mechanism and a public key
encryption algorithm (Sow and Sow, 2011), which
can be view as a slight modification of ElGamal’s
schemes (Elgamal, 1985).
Key Generation Algorithm. To create a pair of
public and private key, we do the following:
1. Select a cyclic group G with sufficiently large or-
der d = #G such that G = hgi.
2. Select two random integers r and k sufficiently
large such that 2 < k < d and r of size half the
size of d with d = #G. Compute kd.
3. Compute with euclidean division algorithm, the
pair (s,t) such that kd = rs + t where t = kd
mod s.
4. Compute γ = g
s
and δ = g
t
in G; Note that γ 6= 1
and δ 6= 1.
Then public key is ((γ,δ),G) and the private key is
(r,G).
Encryption Algorithm. To encrypt a message with
the public key ((γ,δ),d,G), we do the following:
1. Select a random integer 2 < α < d = #G such that
α and #G are co-prime.
2. Compute c
1
= γ
α
and λ = δ
α
in G, hence c
1
6= 1
and λ 6= 1.
3. Transform the message m as an element of G and
compute c
2
= λm in G.
The ciphertext is (c
1
,c
2
).
Decryption Algorithm. To decrypt a ciphertext of
the form (c
1
,c
2
) that is encrypted with the public
key ((γ,δ), d,G) and knowing the associate secret key
(r,G), we just need to compute c
r
1
c
2
.
Provable Security of the Generalized ElGamal En-
cryption Scheme.
I One-wayness under the CDH Assumption.
Theorem 2.4. Under the CDH Assumption, the
Generalized ElGamal encryption scheme is One-
Way secure under Chosen Plaintext Attack (OW-
CPA). That is, for a security parameter k, if there
is an attacker A that inverse the Generalized El-
Gamal encryption then we can build an algorithm
B that solves CDH, it means that
Adv
CDH
GP ,B
(k) = Adv
OW−CPA
Π,A
(k).
I Indistinguishability under the DDH Assump-
tion.
Theorem 2.5. Under the DDH Assumption, the
Generalized ElGamal encryption scheme is indis-
tinguishable under Chosen Plaintext Attacks, i.e.,
it is IND-CPA secure. So we have:
Adv
DDH
GP ,B
(k) =
1
2
· Adv
IND−CPA
Π,A
(k),
where A is an attacker of the Generalized ElGa-
mal encryption and k the security parameter.
To justify the performance of Generalized ElGa-
mal encryption scheme described in (Sow and Sow,
2011) with respect to ElGamal encryption scheme,
comparison curves in execution time of the key gen-
eration, encryption and decryption algorithms are per-
formed (see Figure 1, Figure 2 and Figure 3).
3 LINEAR ENCRYPTION
Boneh et al. (D. Boneh and Shacham, 2004b) in-
troduced a decisional assumption, called Linear, in-
tended to take the place of DDH in groups - in partic-
ular, bilinear groups (Joux and Nguyen, 2003) - where
DDH is easy. For this setting, the Linear problem has
desirable properties, as they have shown: it is hard if
DDH is hard, but, at least in generic groups (Shoup,
1997), it remains hard even if DDH is easy. Letting G
be a cyclic multiplicative group of prime order p, and
SECRYPT 2020 - 17th International Conference on Security and Cryptography
374

letting g
1
,g
2
, and g
3
be arbitrary generators of G, we
consider the following problem:
Linear Problem in G: Given g
1
,g
2
,g
3
,g
a
1
,g
b
2
, g
c
3
∈ G
as input, output yes if a+b = c and no otherwise. The
advantage of an algorithm A in deciding the Linear
problem in G is denoted by Adv
linear
A
and it is equal
to:
|Pr[A(g
1
,g
2
,g
3
,g
a
1
,g
b
2
,g
a+b
3
) = yes :
g
1
,g
2
,g
3
R
← G,a, b
R
← Z
p
]
−Pr[A(g
1
,g
2
,g
3
,g
a
1
,g
b
2
,η) = yes :
g
1
,g
2
,g
3
,η
R
← G,a, b
R
← Z
p
]|
with the probability taken over the uniform random
choice of the parameters to A and over the coin tosses
of A. We say that an algorithm A(t, ε)-decides Linear
in G if A runs in time at most t, and Adv
linear
A
is at
least ε.
Definition 3.1. We say that the (t,ε)-Decision Linear
Assumption holds in G if no algorithm (t, ε)-decides
the Decision Linear problem in G.
The Linear problem is well defined in any group
where DDH is well defined. It is mainly used in
bilinear groups like in (Boneh and Franklin, 2003;
D. Boneh and Shacham, 2004a; Paterson, 2005).
3.1 Linear ElGamal Encryption Scheme
Boneh et al proposed a linear encryption scheme
based on the ElGamal encryption scheme. Given a
computational group scheme G, the Linear ElGamal
encryption scheme is defined as follows:
LE.Gg(1
λ
): Choose a random generator g
3
$
← G and
x
1
,x
2
$
← Z
p
, and set g
1
← g
x
−1
1
3
and g
2
← g
x
−1
2
3
. The
public key is pk = (g
1
,g
2
,g
3
) ∈ G
3
; the secret key
is sk = (x
1
,x
2
) ∈ Z
2
p
.
LE.Enc(pk, M): To encrypt a message M ∈ G, parse
pk = (g
1
,g
2
,g
3
) ∈ G
3
, choose random exponents
r
1
,r
2
$
← Z
p
, and set: u
1
← g
r
1
1
and u
2
← g
r
2
2
and
u
3
← Mg
r
1
+r
2
3
. The ciphertext ct = (u
1
,u
2
,u
3
) ∈
G
3
.
LE.Dec(sk, ct): Parse the private key sk as (x
1
,x
2
) ∈
Z
2
p
and the ciphertext ct as (u
1
,u
2
,u
3
) ∈ G
3
and
compute M ← u
3
u
−x
1
1
u
−x
2
2
.
Correctness of Decryption Process. Since u
1
=
g
r
1
1
and u
2
= g
r
2
2
, u
3
= Mg
r
1
+r
2
3
we have:
u
3
/(u
x
1
1
u
x
2
2
) = Mg
r
1
+r
2
3
/((g
r
1
1
)
x
1
(g
r
2
2
)
x
2
)
= (Mg
r
1
+r
2
3
)/(g
r
1
3
g
r
2
3
) = M
Theorem 3.2. Under the Linear Assumption, ElGa-
mal Encryption Scheme is IND-CPA secure (D. Boneh
and Shacham, 2004b).
3.2 ElGamal from Generalized Linear
We define three functions: the setup function, denoted
LE.Gg(), the encryption function, denoted LE.Enc()
and the decryption function, denoted LE.Dec().
We now describe how these functions works.
LE.Gg(1
λ
) : Choose a random generator g
n
$
← G
and x
1
,x
2
,..., x
n−1
$
← Z
p
, and set: g
1
← g
1/x
1
n
,
g
2
← g
1/x
2
n
, . .., g
n−1
← g
1/x
n−1
n
. The public key
is pk = (g
1
,g
2
,..., g
n
) ∈ G
n
; the secret key is
sk = (x
1
,x
2
,..., x
n−1
) ∈ Z
n−1
p
.
LE.Enc(pk, M): To encrypt a message M ∈ G, parse
pk = (g
1
,g
2
,..., g
n
) ∈ G
n
, choose random ex-
ponents r
1
,r
2
,..., r
n−1
$
← Z
p
, and set: u
1
←
g
r
1
1
, u
2
← g
r
2
2
,...u
n
← Mg
r
1
+r
2
+...+r
n−1
n
. the ci-
phertext ct = (u
1
,u
2
,..., u
n
) ∈ G
n
.
LE.Dec(sk, ct): Parse the private key sk as (x
1
,x
2
,
...,x
n−1
) ∈ Z
n−1
p
and the ciphertext ct as (u
1
,u
2
,
...,u
n
) ∈ G
n
) ∈ G
n
and compute :
M ← u
n
/(u
x
1
1
u
x
2
2
...u
x
n−1
n−1
)
4 LINEAR GENERALIZED
ElGamal ENCRYPTION
SCHEME
We present the Linear Generalized ElGamal encryp-
tion scheme, its security and the Generalized ElGamal
encryption scheme from the generalized linear.
4.1 Algorithms
Given a computational group scheme G, the Lin-
ear Generalized ElGamal encryption scheme is com-
posed of the following three functions: the setup func-
tion, denoted LGE.Gg(), the encryption function, de-
noted LGE.Enc() and the decryption function, de-
noted LGE.Dec().
We now describe how these functions works.
LGE.Gg(1
λ
): Choose a random generator g
$
← G
and k
$
← Z
d
, r
$
← Z
d/2
.
Compute (s,t) ∈ Z
2
d
such that s ← b
kd
r
c and t ←
kd mod r and set g
1
← g
r
, g
2
← g
s
, and g
3
← g
t
.
The public key is pk = (g
1
,g
2
,g
3
) ∈ G
3
and the
secret key is sk = (r, s,t) ∈ Z
d/2
× Z
2
d
.
Linear Generalized ElGamal Encryption Scheme
375

LGE.Enc(pk, M): To encrypt a message M ∈ G,
parse pk = (g
1
,g
2
,g
3
) ∈ G
3
, choose random ex-
ponents α
1
,α
2
$
← Z
d
, and set
c
1
← g
α
1
1
and c
2
← g
α
2
2
and c
3
← Mg
α
1
+α
2
3
;
the ciphertext ct = (c
1
,c
2
,c
3
) ∈ G
3
.
LGE.Dec(sk, ct): Parse the private key sk as (r, s,t) ∈
Z
d/2
×Z
2
d
and the ciphertext ct as (c
1
,c
2
,c
3
) ∈ G
3
and compute M ← c
s
1
c
r
2
c
3
.
Before proving the security of our scheme in The-
orem 4.1, we give its correctness.
Correctness of Decryption Process. Since c
1
=
g
α
1
1
, c
2
= g
α
2
2
and c
3
= Mg
α
1
+α
2
3
, we have:
c
s
1
c
r
2
c
3
= g
α
1
s
1
g
α
2
r
2
g
α
1
+α
2
3
M
= Mg
α
1
rs
g
α
2
sr
g
(α
1
+α
2
)t
= Mg
(rs+t)(α
1
+α
2
)
= Mg
kd(α
1
+α
2
)
= M
Theorem 4.1. The Linear Generalized ElGamal En-
cryption Scheme is IND-CPA secure under the Deci-
sional Linear Assumption (DLA).
4.2 Generalized ElGamal from
Generalized Linear
Given a computational group scheme G, the Gener-
alized ElGamal encryption scheme from the general-
ized linear is defined as follows:
LGE.Gg(1
λ
): Choose a random generator g
$
← G
and k, r
i
$
← Z
d
× Z
d/2
, compute (s
i
,t
i
) ∈ Z
2
d
such
that s
i
← b
kd
r
i
c and t
i
← kd mod r
i
, 1 ≤ i ≤
n
3
and
set for 0 ≤ k ≤
n
3
− 1: g
3k+1
← g
r
k+1
, g
3k+2
←
g
s
k+1
and g
3k+3
← g
t
k+1
. The public key is pk =
(g
1
,g
2
,g
3
,..., g
n−2
,g
n−1
,g
n
) ∈ G
n
and the secret
key is sk = (r
i
,s
i
,t
i
) ∈ Z
d/2
× Z
2
d
,1 ≤ i ≤
n
3
.
LGE.Enc(pk, M): . To encrypt a message M ∈
G, parse pk = (g
1
,g
2
,g
3
,..., g
n−2
,g
n−1
,g
n
) ∈ G
n
,
choose random exponents α
1
,α
2
,..., α
n−1
$
← Z
d
,
and set 0 ≤ k ≤
n
3
− 1 : c
3k+1
← g
α
3k+1
3k+1
, c
3k+2
←
g
α
3k+2
3k+2
, c
3k+3
← Mg
α
3k+1
+α
3k+2
3k+3
. The ciphertext ct
is (c
3k+1
,c
3k+2
,c
3k+3
) ∈ G
3
.
LGE.Dec(sk, ct): Parse the private key sk as (r
i
,s
i
,t
i
)
∈ Z
d/2
× Z
2
d
, 1 ≤ i ≤ n/3 and the ciphertext ct as
(c
1
,c
2
,..., c
n
) ∈ G
n
and compute
M ←
n
s
n
∏
k=1
c
s
k+1
3k+1
c
r
k+1
3k+2
c
3k+3
.
Table 1: Comparison of Linear ElGamal and Linear Gen-
eralized ElGamal for each algorithm in terms of computa-
tional cost.
Linear ElGamal Linear General-
ized ElGamal
Size Key secret key ∈ Z
q
,
q = o(G)
secret key ∈ Z
d
,
d = o(G)
Key Gen P = 2, M = 0,
nP = 3, nS = 2
P = 3, M = 1,
nP = 3, nS = 3
Encryption P = 3, M = 1 P = 3, M = 1
Decryption P = 2, M = 2,
I = 2
P = 2, M = 2,
I = 0
5 COMPLEXITY EVALUATION
We present a complexity comparison between the
Linear ElGamal and the Linear Generalized ElGamal
schemes. We give in this section a theoretical com-
plexity where we study the number of computations
needed in each algorithm (key generation, encryption
and decryption). Let us set the following parameters:
• P = power’s number (exponent),
• M = multiplication’s number,
• S = sum’s number,
• I = inverse’s number,
• nP = number of parameters of the public key,
• nS = number of parameters of the private key.
To present the performance of the two encryp-
tion schemes, we study the number of operations per-
formed (according to the parameters described) in the
key generation, encryption and decryption processes.
From the comparative Table 1, we can clearly see
that Linear Generalized ElGamal encryption scheme
is slower at generating keys but is faster for decryp-
tion the exponent used in the decryption algorithm has
a size half of the order of the group. Moreover, we see
that there is no inverse computed (even though this
difference brings only a slight improvement).
6 PERFORMANCE
EVALUATIONS
All our algorithms have been programmed with Sage-
Math (The Sage Developers, 2020). The tests are per-
formed with security parameters of size 32, 64, 128,
512, 1024 bits. Some even go up to 2048 bits. We
start by comparing ElGamal and Generalized ElGa-
SECRYPT 2020 - 17th International Conference on Security and Cryptography
376
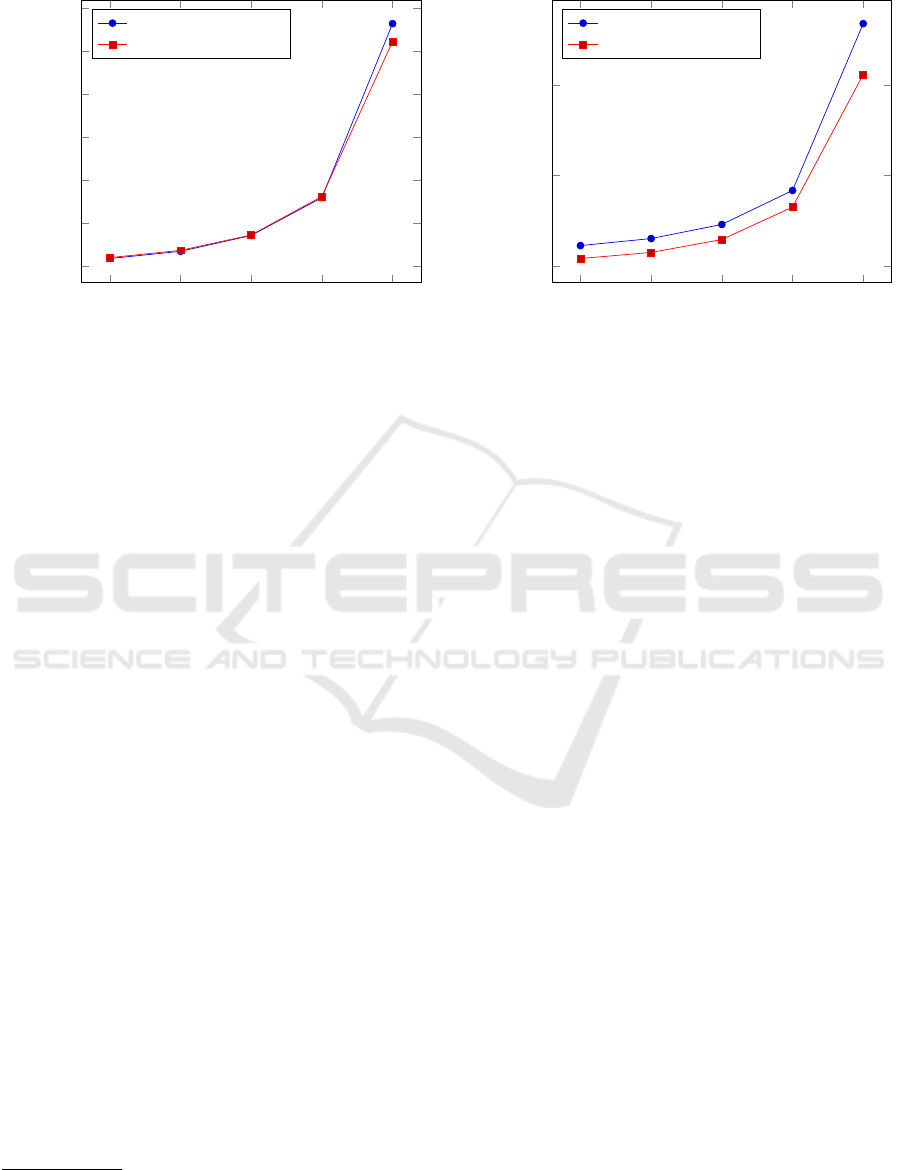
2
5
2
6
2
7
2
8
2
9
0
0.2
0.4
0.6
0.8
1
1.2
·10
−3
Size of security parameter
Time in seconds
Key Generation algorithm, 1000 trials
ElGamal
Generalized ElGamal
Figure 1: Average time of key generation algorithm depend-
ing on the size of security parameter.
mal
1
before comparing Linear ElGamal and Linear
Generalized ElGamal.
6.1 ElGamal and Generalized ElGamal
We present the curves showing the execution time
of the key generation, encryption and decryption al-
gorithms of the ElGamal encryption scheme and the
Generalized ElGamal encryption scheme.
The execution time of those two schemes is car-
ried out under the same conditions in terms of gen-
eration of the values and sizes of the security param-
eters. Indeed, given a size of a security parameter,
there are 1000 trials where new parameters (such as
prime number and messages) are computed for each
trial.
We give a detailed execution time for the key gen-
eration in Figure 1 and 4, the encryption algorithm in
Figure 2 and 5 and the decryption algorithm in Fig-
ure 3 and 6.
Key Generation Algorithms. The curves of Fig-
ure 1 show the execution time of key generation al-
gorithms for the ElGamal encryption scheme and for
Generalized ElGamal encryption scheme. We show
that the two algorithms are similar. When the key size
increases then the Generalized ElGamal is a bit faster.
Encryption Algorithms. The curves of Figure 2
show the execution time of encryption algorithms of
the ElGamal encryption scheme and Generalized El-
Gamal encryption scheme. We observe that the Gen-
1
Surprisingly this performance evaluation has not been
done in (Sow and Sow, 2011).
2
5
2
6
2
7
2
8
2
9
0
0.5
1
·10
−3
Size parameter
Time in seconds
Encryption algorithm, 1000 trials
ElGamal
Generalized ElGamal
Figure 2: Average time of encryption algorithm depending
on the size of security parameter.
eralized ElGamal encryption is always faster that El-
Gamal encryption. Indeed, we observe empirically
that computations of γ
α
and computations of δ
α
for
Generalized ElGamal have the same execution time
than the term h
r
for the standard ElGamal. Yet, the
computations of the term g
r
is slower than the three
others. Thus, the overall execution time of encryption
algorithm for the Generalized scheme is less than the
one for the standard ElGamal.
Decryption Algorithms. The curves given in Fig-
ure 3 show the execution time of decryption algo-
rithms of the ElGamal encryption scheme and Gen-
eralized ElGamal encryption scheme. We can see that
the Generalized ElGamal decryption is always signif-
icantly faster that ElGamal decryption.
6.2 Linear ElGamal and Linear
Generalized ElGamal
We studied the performance of Linear Generalized El-
Gamal encryption scheme with respect to Linear El-
Gamal encryption scheme. We present the execution
time evaluations of the key generation in Figure 4, en-
cryption in Figure 5 and decryption in Figure 6.
Key Generation Algorithms. The curves given in
Figure 4 show the execution time of key generation
algorithms of the Linear ElGamal encryption scheme
and Linear Generalized ElGamal encryption scheme.
We can see that our algorithm for key generation is
clearly slower than the one proposed by Boneh et al. It
is the price to pay in order to have a faster encryption
and decryption algorithms. It is not an issue because
Linear Generalized ElGamal Encryption Scheme
377
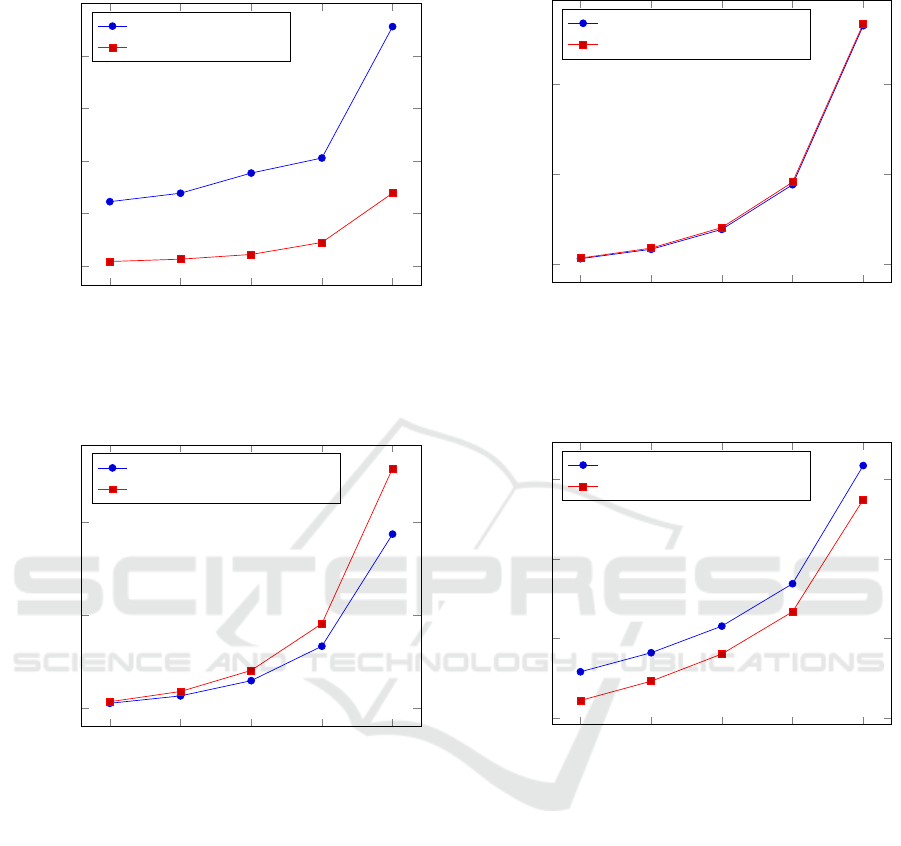
2
5
2
6
2
7
2
8
2
9
0
0.2
0.4
0.6
0.8
1
·10
−3
Size parameter
Time in seconds
Decryption algorithm, 1000 trials
ElGamal
Generalized ElGamal
Figure 3: Average time of decryption algorithm depending
on the size of security parameter.
2
5
2
6
2
7
2
8
2
9
0
1
2
·10
−3
Size of security parameter
Time in seconds
Key Generation algorithm 100 trials
Linear ElGamal
Linear Generalized ElGamal
Figure 4: Average time of key generation algorithm depend-
ing on the size of security parameter.
the key generation is in general done only once while
the encryption and decryption algorithms are more of-
ten used.
Encryption Algorithms. The curves of Figure 5
give the execution time of encryption algorithms of
the Linear ElGamal encryption scheme and Linear
Generalized ElGamal encryption scheme. Accord-
ing to the complexity analysis the timings are similar
since the number of exponentiations are similar. Em-
pirically, we observe that they are similar.
Decryption Algorithms. The curves of Figure 6
represent the execution time of decryption algorithms
of the Linear ElGamal encryption scheme and Linear
2
5
2
6
2
7
2
8
2
9
0
1
2
·10
−3
Size of security parameter
Time in seconds
Encryption algorithm with 100 trials
Linear ElGamal
Linear Generalized ElGamal
Figure 5: Average time of encryption algorithm depending
on the size of security parameter.
2
5
2
6
2
7
2
8
2
9
0
1
2
3
·10
−3
Size of security parameter
Time in seconds
Decryption algorithm, 100 trials
Linear ElGamal
Linear Generalized ElGamal
Figure 6: Average time of decryption algorithm depending
on the size of security parameter.
Generalized ElGamal encryption scheme. We clearly
see that the decryption is faster using our scheme,
which confirms the complexity analysis of the previ-
ous section.
7 CONCLUSION
We have proposed a faster Linear Generalized ElGa-
mal encryption scheme based on the Generalized El-
Gamal encryption scheme. We prove that our linear
scheme is IND-CPA secure under the Linear problem
like the linear encryption scheme based on the ElGa-
mal encryption scheme. It also has a faster encryption
and decryption algorithms.
SECRYPT 2020 - 17th International Conference on Security and Cryptography
378

In the future, we would like to see how our ap-
proach can be applied to improved other schemes.
ACKNOWLEDGEMENT
This study was partially supported by the French
ANR project ANR-18-CE39-0019 (MobiS5).
REFERENCES
Benaloh, J. (1999). Dense probabilistic encryption.
Boneh, D. (1998). The decision diffie-hellman problem.
In In Proceedings of the Third Algorithmic Number
Theory Symposium, volume 1423, pages 48–63.
Boneh, D. and Franklin, M. (2003). Identity-based en-
cryption from the weil pairing. SIAM J. Computing,
32(3):586–615.
Ciucanu, R., Giraud, M., Lafourcade, P., and Ye, L. (2019).
Secure strassen-winograd matrix multiplication with
mapreduce. In Obaidat, M. S. and Samarati, P.,
editors, Proceedings of the 16th International Joint
Conference on e-Business and Telecommunications,
ICETE 2019 - Volume 2: SECRYPT, 2019, pages 220–
227. SciTePress.
Cramer, R. and Shoup, V. (1998). A practical public key
cryptosystem provably secure against adaptive chosen
ciphertext attack. In Proc. of the 18th Annual Interna-
tional Cryptology Conference on Advances in Cryp-
tology, CRYPTO’98.
D. Boneh, B. L. and Shacham, H. (Sept. 2004a). Short
signatures from the weil pairing. J. Cryptology,
17(4):297–319.
D. Boneh, X. B. and Shacham, H. (Aug. 2004b).
Short group signatures. In In M. Franklin, edi-
tor,Proceedings of Crypto 2004, volume 3152, pages
41–55.
Elgamal, T. (1985). A public key cryptosystem and a sig-
nature scheme based on discrete logarithms. IEEE
Transactions on Information Theory, 31(4):469–472.
Extended Version. https://sancy.iut-clermont.uca.fr/
∼
lafourcade/PAPERS/PDF/Secrypt-long2020.pdf.
Fousse, L., Lafourcade, P., and Alnuaimi, M. (2011). Be-
naloh’s Dense Probabilistic Encryption Revisited. In
Progress in Cryptology - AFRICACRYPT 2011 - 4th
Conference on the Theory and Application of Crypto-
graphic Techniques in Africa, volume 6737 of Lecture
Notes in Computer Science, pages 348–362. Springer.
Galbraith, S. D. (2002). Elliptic curve paillier schemes. J.
Cryptol., 15(2):129–138.
Gentry, C. (2009). A Fully Homomorphic Encryption
Scheme. PhD thesis, Stanford, CA, USA.
Goldwasser, S. and Micali, S. (1982). Probabilistic encryp-
tion and how to play mental poker keeping secret all
partial information. In Proceedings of the Fourteenth
Annual ACM Symposium on Theory of Computing,
STOC ’82.
Hanoymak, T. (2013). On provable security of crypto-
graphic schemes. International Journal of Informa-
tion Security Science, 2, No.2.
J. Katz, Y. L. (2008). Introduction to modern cryptography.
CRC PRESS.
Joux, A. and Guyen, K. (2006). Separating decision diffe-
hellman to diffe hellmann in cryptographie groups.
Joux, A. and Nguyen, K. (Sept. 2003). Separating deci-
sion diffie-hellman from computational diffie-hellman
in cryptographic groups. J. Cryptology, 16(4):239–47.
Naccache, D. and Stern, J. (1998). A new public key cryp-
tosystem based on higher residues. In Proceedings of
the 5th ACM Conference on Computer and Commu-
nications Security, CCS ’98, page 59–66, New York,
NY, USA. Association for Computing Machinery.
Okamoto, T. and Uchiyama, S. (1998). A new public-key
cryptosystem as secure as factoring. In Nyberg, K.,
editor, Advances in Cryptology — EUROCRYPT’98,
pages 308–318, Berlin, Heidelberg. Springer Berlin
Heidelberg.
Paillier, P. (1999). Public-key cryptosystems based on com-
posite degree residuosity classes. In Stern, J., editor,
Advances in Cryptology — EUROCRYPT ’99, pages
223–238, Berlin, Heidelberg. Springer Berlin Heidel-
berg.
Paterson, K. (2005). Cryptography from pairings. Cam-
bridge University Press, 317 of London Mathematical
Society Lecture Notes:215–51.
Rivest, R. L., Shamir, A., and Adleman, L. (1978). A
method for obtaining digital signatures and public-key
cryptosystems. Commun. ACM, 21(2):120–126.
SEAL (2019). Microsoft SEAL (release 3.4). https:
//github.com/Microsoft/SEAL. Microsoft Research,
Redmond, WA.
Shoup, V. (May 1997). Lower bounds for discrete log-
arithms and related problems. In In W. Fumy, edi-
tor, Proceedings of Eurocrypt 1997, volume 1233 of
LNCS, pages 256–66.
Sow, D. and Sow, D. (2011). A new variant of el gamal’s en-
cryption and signatures schemes. Journal of Algebra,
Number Theory and Applications, 20(1):21–39.
The Sage Developers (2020). SageMath, the Sage
Mathematics Software System (Version 9.0).
https://www.sagemath.org.
Linear Generalized ElGamal Encryption Scheme
379
