
Wilson Score Kernel Density Estimation for Bernoulli Trials
Lars Carøe Sørensen, Simon Mathiesen, Dirk Kraft and Henrik Gordon Petersen
SDU Robotics, University of Southern Denmark, Campusvej, Odense, Denmark
Keywords:
Iterative Learning, Statistical Function Estimators, Binomial Trials.
Abstract:
We propose a new function estimator, called Wilson Score Kernel Density Estimation, that allows to esti-
mate a mean probability and the surrounding confidence interval for parameterized processes with binomially
distributed outcomes. Our estimator combines the advantages of kernel smoothing, from Kernel Density Esti-
mation, and robustness to low number of samples, from Wilson Score. This allows for more robust and data
efficient estimates compared to the individual use of these two estimators. While our estimator is generally
applicable for processes with binomially distributed outcomes, we will present it in the context of iterative
optimization. Here we first show the advantage of our estimator on a mathematically well defined problem,
and then apply our estimator to an industrial automation process.
1 INTRODUCTION
Optimization of stochastic processes is a common
task in industrial robotics. This includes a wide range
of processes like peg-in-hole and screwing operations,
but also design of feeding solutions as we briefly
touch later in this paper as test case. Such processes
are likely to be influenced by uncertainties, which
need to be handled to achieve a successful execu-
tion. However, many experiments are normally re-
quired to obtain reliable estimates of stochastic func-
tions, and each evaluation is often seen as being ex-
pensive (e.g. costly or time-consuming). Hence, mak-
ing a sampling of the entire parameter space in such
cases is not feasible, since this Naive sampling is
sample-inefficient. The problem becomes even more
severe when the stochastic process is defined in mul-
tiple dimensions with wide parameter ranges, which
results in a large parameter space, and when an eval-
uation of the function is limited to a binary outcome,
which only reveal whether the experiment succeeded
or failed.
One way to approach this problem is by taking
the uncertainty of the function estimate into account
during the optimization of a stochastic function and
thereby obtaining a proper estimate of the unknown
underlying function. This can be done by both cal-
culating statistical estimates on the true mean and the
surrounding confidence interval (e.g., using Normal
Approximation (Ross, 2009)). In addition, Kernel
Density Estimation (H
¨
ardle et al., 2004) can be used
to account for the likely local smoothness in the pa-
rameters of these stochastic problems. As a result,
this makes the selection more effective, since an ex-
periment also expresses information about the neigh-
boring region.
In our previous work (Sørensen et al., 2016), we
have shown that by actively using both the mean es-
timate and the associated uncertainty in an iterative
learning setting, the number of function evaluations
required can be drastically reduced. The purpose of
the iterative learning is to make an effective sampling
of the parameter space. However, each decision on
which part of the parameter space to explore next is in
the beginning being hindered by the sparse amount of
data. Decisions based on little data will often become
unreliable in such situations. The common function
estimators (e.g. Normal Approximation) often require
a significant amount of experiments to obtain a usable
estimate on the true function, which makes them in-
applicable due to sample-ineffectiveness.
As a discrete function estimation, Wilson
Score (Agresti and Coull, 1998) has the property of
making a reasonable estimate when having few sam-
ples compared to Normal Approximation. Moreover,
regression by Kernel Density Estimation (H
¨
ardle
et al., 2004) is a continuous function estimator that
generalizes the outcomes of the function evaluations
to the neighboring region by kernel smoothing. The
novelty of this paper is the derivation of a new statisti-
cal function estimator, which both has the smoothing
property from Kernel Density Estimation and the few
Sørensen, L., Mathiesen, S., Kraft, D. and Petersen, H.
Wilson Score Kernel Density Estimation for Bernoulli Trials.
DOI: 10.5220/0009816503050313
In Proceedings of the 17th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2020), pages 305-313
ISBN: 978-989-758-442-8
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
305

samples correction from Wilson Score while also be-
ing continuous.
The paper is structured as follows: Section 2 starts
by defining the overall goal of the optimization, and
then describing our iterative learning approach. Sec-
tion 3 briefly recaps some methods, namely Normal
Approximation and Kernel Density Estimation, and
discusses in further details why these function estima-
tors are unusable in an iterative setting when having
a limited number of samples. Section 4 includes our
main contribution which is the derivation of the new
function estimator ”Wilson Score Kernel Density Es-
timation” which combines the properties of Wilson
Score and Kernel Density Estimation regression. We
show the advantages of our new function estimator by
applying it on a simple mathematical problem in Sec-
tion 5, but we also use our function estimator in an it-
erative learning setting for optimizing a real industrial
case in Section 6. Finally, we conclude the paper in
Section 7 and then propose future work in Section 8.
2 APPROACH, ASSUMPTIONS
AND CURRENT WORK
The overall goal is to gain the best execution of a
given industrial process based on only binary out-
come (success or failure). This is achieved by op-
timizing the process parameters and thereby finding
the highest probability of success for the process:
x
opt
= argmax
x∈X
(p(x)), (1)
where x is an arbitrary parameter set in a metric pa-
rameter space, X ∈ R, and x
opt
denotes the parameter
set that gives the highest probability of success, p(x).
We assume that the function p(x) is continuous.
What we have to our disposal for performing the
optimization is a manual limitation of the parameter
space to ensure that X is bounded, and the possibility
to perform experiments, i.e. executions of the pro-
cess, with a chosen parameter set. An experiment
with parameter set x can be described as a Bernoulli
trial with (unknown) probability p(x) which generates
an outcome defined as y ∈{0,1}= {f ,s}correspond-
ing to failure and success, respectively. In the itera-
tive learning described below, we perform a sequence
of experiments with different parameter sets, where
the i-th experiment is defined as {x
i
,y
i
}. We assume
that the underlying probability of success for an ex-
periment with parameter set x is independent of when
the experiment is carried out (i.e. independent of the
placement i in the sequence).
2.1 The Iterative Learning Approach
For iterative learning in our setting, an efficient ap-
proach is required to reduce the number of experi-
ments needed for the optimization of the process pa-
rameters. In each iteration a well-considered choice
must be made on which parameter set to investigate
next. In the literature, the choice is realized through
the use of statistical calculations which are based
on all the experiments performed in previous itera-
tions. Hence, each iteration of the learning approach
uses the principles of Bayesian Optimization (Brochu
et al., 2010) which generally is constructed as:
1. Selection: Select the parameter set, x
i
∈ X , for
the next experiment based on the statistical mea-
sures calculated from all the previous experi-
ments, D
i−1
.
2. Experiment: Perform an experiment with the pa-
rameter set x
i
and obtain the outcome y
i
∈ {0, 1}.
3. Save: Save the experiment D
i
= {D
i−1
,{x
i
,y
i
}}.
For Bayesian Optimization, the selection in each
iteration is conducted by maximizing an acquisition
function by x
i
= argmax(acq(x)). There exist a va-
riety of acquisition functions (see e.g. (Brochu et al.,
2010; Sørensen et al., 2016)). Most of the acquisi-
tion functions require estimates of the mean, p(x), and
the variance σ
2
(x) at any x, which must be reliable
for the iterative learning to efficiently select proper
parameter sets. An often used acquisition function
is the Upper Confidence Bound (UCB) (Tesch et al.,
2013), which is defined as ucb(x) = p(x)+κ
p
σ
2
(x),
where κ defines a trade-off between exploration and
exploitation. In the next section, it is explained how
this trade-off can be automatically adjusted by using
the confidence interval.
3 EXISTING STATISTICAL
ESTIMATORS
In this section, we discuss different existing function
estimators for estimating the true mean, p(x), and
variance, σ
2
(x), for any x based on a set of prior ex-
periments D . All the function estimators will for con-
venience be described in terms of the confidence in-
terval, and we therefore introduce the common defi-
nition of the true confidence interval (see e.q. (Ross,
2009)) as:
"
p(x) ±z
q
σ
2
(x)
#
, (2)
where z is defined as the (1 −
α
2
) quantile for a two-
sided interval.
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
306

We start by defining the simple Normal Approxi-
mation (NA), which acts as a basis for Kernel Density
Estimation (KDE). After defining KDE, we then ex-
plain the problem which arises when having a sparse
sampling of the parameter space, X , and how Wilsom
Score (WS) can correct for this problem.
3.1 Normal Approximation
Assume that the parameter space, X , is tesselated into
a finite set of representative points. Consider an arbi-
trary x
i
, and assume that we have performed n
i
exper-
iments with that parameter set. The straightforward
function estimator to use is NA (Ross, 2009). For NA
the true probability, p(x
i
), for a Bernoulli distribution
can be estimated by:
ˆp
na
(x
i
) =
1
n
i
n
i
∑
j=1
y
j
, (3)
where y
j
is the outcome of the j-th experiment in the
i-th point. Moreover, it can be proven that the NA es-
timate converges towards true mean such that ˆp
na
→ p
when n → ∞ (Ross, 2009).
Likewise the variance is defined as:
σ
2
na
(x
i
) =
1
n
i
ˆp
na
(x
i
)(1 − ˆp
na
(x
i
)). (4)
The confidence interval for NA can be obtained by
substituting (3) and (4) into (2).
The problem with NA is that the mean estimate is
very dependent on the individual outcomes for a low
n. This means that a large number of experiments are
typically needed to cover the parameter space and to
obtain reliable statistics. This makes the NA function
estimator ill suited in combination with an iterative
learning method due to effectiveness, since choices
made in the beginning of the iterative process will be
based on unreliable (and potentially wrong) estimates.
Moreover, the probability estimates for neighboring
parameter points will in particular for a relative dense
tessellation be correlated as p(x ) is continuous. An ef-
ficient function estimator needs to exploit this, which
is not the case for NA which is a discrete estimator.
Several approaches utilized smoothing principles
to let the neighboring experiments influence the prob-
ability estimate such as Gaussian Processes (Ras-
mussen and Williams, 2006) or K-nearest neigh-
bors regression (H
¨
ardle et al., 2004). Our previous
work (Laursen et al., 2018) showed how Gaussian
Processes applied to a binomial setting
1
lacks the abil-
ity to properly explore the parameters space. The pa-
per also shows that including the number of samples
1
Formally known as Gaussian Processes Classification.
in the calculation of the confidence interval instead of
only variance improves the performance the acquisi-
tion function when used for iteratively selecting the
next parameter set to explore (see also Section 2.1).
Despite the improved performance, this variations
only mimics the true calculation of the confidence in-
terval in (2) without being theoretically defined. Fur-
thermore, note that the approach used later in this
paper to develop our new function estimator named
WSKDE cannot directly be transferred to Gaussian
Processes Classification due to their derivation. We
will in this paper restrict ourselves to the generic non-
parametric Kernel Density Estimation (KDE) regres-
sion, which previously has been shown to be very
suitable for process optimization (Sørensen et al.,
2016).
3.2 Kernel Density Estimation
The first step in Kernel Density Estimation (KDE) is
to define an estimate of the density of experiments,
f (x), at an arbitrary parameter set, x . This estimate is
in (H
¨
ardle et al., 2004) defined as:
ˆ
f
h
(x) =
1
n
n
∑
i=1
K
h,x
i
(x), (5)
where n is the total number of experiments in the en-
tire parameter space X , and where x
i
is the parameter
set applied in the i-th experiment. Moreover, K
h,x
i
(x)
is the smoothing kernel located in x
i
with a bandwidth
of h.
The estimate of the success probability p(x) by
KDE is defined in (H
¨
ardle et al., 2004) as:
ˆm
h
(x) =
ˆ
f
h,Y
(x)
ˆ
f
h
(x)
=
n
−1
∑
n
i=1
K
h,x
i
(x)y
i
n
−1
∑
n
j=1
K
h,x
j
(x)
, (6)
where
ˆ
f
h,Y
(x) is the estimated density weighted by
the outcome y. Hence, for experiments with a bino-
mial outcome (success or failure),
ˆ
f
h,Y
(x) will sim-
ply be the estimate density of successful experiments.
Accordingly to (H
¨
ardle et al., 2004) the KDE regres-
sion estimate converges towards true mean such that
ˆm
h
(x) → m(x) when h → 0 and nh → ∞.
We can also rewrite (6) as:
ˆm
h
(x) =
1
n
n
∑
i=1
W
h,i
(x)y
i
, (7)
where W
h,i
(x) is referred to as the weighting:
W
h,i
(x) =
K
h,x
i
(x)
n
−1
∑
n
j=1
K
h,x
j
(x)
. (8)
Hence, the confidence interval for KDE regression
can be estimated in (H
¨
ardle et al., 2004) as:
"
ˆm
h
(x) ±z
s
||K||
2
2
ˆ
σ
2
(x)
nh
ˆ
f
h
(x)
#
, (9)
Wilson Score Kernel Density Estimation for Bernoulli Trials
307

where ||K||
2
2
is the squared L
2
norm of an identity ker-
nel (
R
{K(u)}
2
du), and thereby a scalar value only de-
pendent on the chosen kernel type. Additional,
ˆ
σ
2
h
(x)
is the estimated variance which is given in (H
¨
ardle
et al., 2004) as:
ˆ
σ
2
h
(x) =
1
n
n
∑
i=1
W
h,i
(x)(y
i
− ˆm
h
(x))
2
. (10)
Please note that the term under the square root in
(9) differs from the original definition of the confi-
dence interval in (2), since the variance is scaled by
||K||
2
2
/(nh
ˆ
f
h
(x)).
It is important to add, that the KDE regression in
(6) and the confidence interval in (9) estimates both
suffers from a bias and variance error. The bias er-
ror arises from the kernel smoothing and can be elim-
inated by letting h → 0, whereas the variance error
is eliminated by letting nh → ∞. To make the KDE
regression confidence interval in (8) calculable, it is
derived under the assumption that h has been chosen
small enough so that the bias can be neglected. In
Appendix “The Effect of the Bias and Variance Error
in relation to KDE and WSKDE” this assumption and
the effect of the bias is discussed.
3.3 Wilson Score
The aim of our approach is to reduce the number of
samples needed by the iterative learning approach by
focusing on the promising regions of the parameter
space. However, for this approach to obtain good per-
formance, the accuracy of mean estimate and the con-
fidence interval are important. We considered to be-
gin with the NA function estimator. It is well known
that NA needs (as a rule of thumb) at least five ex-
periments leading to each of the two outcomes in or-
der to achieve a robust confidence interval (Brown
et al., 2001). Therefore, for parameter points where
there are very few experiments, NA typically provides
unrealistic confidence intervals. Unfortunately, the
KDE confidence interval estimate in (9) suffer from
the same problem if there are an insufficient amount
of samples in the neighbor region.
To deal with the disadvantages of NA, the Wilson
Score (WS) can be used for estimating on the confi-
dence interval. The estimate of the mean is for WS
defined in (Agresti and Coull, 1998) as:
ˆp
ws
(x
i
) = α
1
ˆp
na
(x
i
) +
1
2n
i
z
2
, (11)
where ˆp
na
(x
i
) is the mean estimated by NA from (3),
n
i
is number of experiments performed in the i-th pa-
rameter point x
i
, and α
1
= 1/(1 + n
−1
i
z
2
).
Moreover, the estimated variance is by WS de-
fined in (Agresti and Coull, 1998) as:
σ
2
ws
(x
i
) = α
1
z
r
1
n
i
ˆp
na
(x
i
)(1 − ˆp
na
(x
i
)) + α
2
, (12)
where α
2
= z
2
/(4n
2
i
).
As for NA, the confidence interval for WS can
be obtained by substituting (11) and (12) into (2).
Studying the WS confidence interval shows that when
n
i
→ 0 then the interval becomes [0;1], or equiva-
lent [0.5 ±0.5], and when n
i
→ ∞ then the WS inter-
val becomes equal to the NA interval including that
ˆp
ws
(x
i
) → ˆp
na
(x
i
) which converges towards the true
mean. By these two properties, WS eliminates the
disadvantage of NA when having a sparse sampling.
However, as for NA, WS is also a discrete function es-
timator opposed to KDE which takes the neighboring
samples into account. In the next section, we present
a novel Wilson Score inspired estimate of the confi-
dence interval for KDE that is more robust than the
classical KDE estimate.
4 WILSON SCORE KERNEL
DENSITY ESTIMATION
Even though Wilson Score (WS) gives a proper func-
tion estimate when having a low number of samples,
it is a discrete function estimator as Normal Approx-
imation (NA), and we therefore want to combine WS
with the smoothing property from regression by Ker-
nel Density Estimation (KDE). To derive our new sta-
tistical KDE confidence interval estimator, we start
with expanding the KDE variance from (10) as:
ˆ
σ
2
h
(x) =
1
n
(β
1
+ β
2
−β
3
) , (13)
which by considering a Bernoulli distribution where
y ∈{0, 1}corresponding to failure and successful out-
comes can be simplified to:
β
1
=
n
∑
i=1
W
h,i
(x)y
2
i
Ber
= n ˆm
h
(x), (14)
β
2
=
n
∑
i=1
W
h,i
(x) ˆm
h
(x)
2
Ber
= n ˆm
h
(x)
2
, (15)
β
3
= 2
n
∑
i=1
W
h,i
(x) ˆm
h
(x)y
i
Ber
= 2n ˆm
h
(x)
2
, (16)
which can be substituted into (13) and simplified to:
ˆ
σ
2
h
(x)
Ber
= ˆm
h
(x)(1 − ˆm
h
(x)). (17)
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
308

This result can be inserted into (9) to obtain the KDE
confidence interval for Bernoulli trials as:
"
ˆm
h
(x) ±z
s
||K||
2
2
nh
ˆ
f
h
(x)
ˆm
h
(x)(1 − ˆm
h
(x))
#
. (18)
Comparing this with the NA estimates from (3)
and (4):
"
ˆp
na
(x
i
) ±z
r
1
n
i
ˆp
na
(x
i
)(1 − ˆp
na
(x
i
))
#
, (19)
allow us to identify the mean and in particular the
KDE sample size at x as:
ˆp
na
(x
i
) = ˆm
h
(x) and n(x) =
nh
||K||
2
2
ˆ
f
h
(x), (20)
where nh/||K||
2
2
scales the estimated sample density
ˆ
f
h
(x) based on the total number of samples, n, and
the chosen bandwidth of the kernel, h.
Hence, the two expressions from (20) can be sub-
stituted into (11) and (12) to obtain the estimated
mean and variance for our new Wilson Score Ker-
nel Density Estimation (WSKDE) function estimator.
The estimated mean is then:
ˆp
wskde
(x) = γ
1
ˆm
h
(x) +
1
2n(x)
z
2
, (21)
where γ
1
= 1/(1 + n(x)
−1
z
2
), and the estimated vari-
ance is:
ˆ
σ
wskde
(x) = γ
1
z
s
1
n(x)
ˆm
h
(x)(1 − ˆm
h
(x)) + γ
2
, (22)
where γ
2
= 1/(4n(x)
2
)z
2
.
The result of the WSKDE derivation in (20) im-
plies that our WSKDE estimate also converges to-
wards the true mean when n → ∞ under the condi-
tions h → 0 and nh → ∞. Moreover, the WSKDE
confidence interval has the same properties as WS by
approaching [ 0.5 ±0.5 ] when n → 0. Note that the
neglection of the bias error for KDE does not effect
the derivation of WSKDE.
In Appendix “Generalization to Multiple
Dimensions” it is briefly explained how the KDE and
WSKDE function estimators can be generalized to
multiple dimensions.
5 EXPERIMENTAL VALIDATION
An experimental validation is conducted to show
the performance difference between the KDE and
WSKDE function estimators. The performance of
KDE or WSKDE is in this experiment defined as how
often their confidence interval includes the underly-
ing function, p(x). We will not compare WSKDE
against NA or WS, since these are discrete estima-
tors. In relation to the iterative learning approach (see
Section 2.1), it is of interest to iteratively conduct ex-
periments so the convergence in performance can be
examined. For our experiment, we use the following
underlying test function:
p
test
(x) = 0.5 (1 + sin(x)) (23)
where x ∈ [0; 2π].
In each test a total of 100 iterations are conducted.
For each iteration an experiment is carried out by
picking a random position x
i
from the uniform dis-
tribution on the interval of x (i.e. [0; 2π]) and picking
a random number r uniformly distributed in the in-
terval [0; 1]. We then define the outcome as y
i
≡ s
if r ≤ f (x
i
) and otherwise y
i
= f , where s and f are
success and failure respectively. The performance of
both KDE and WSKDE is calculated by tessellating
the x-axis into n
tes
= 101 discrete points, and testing
wherever their respective confidence interval encap-
sulates the true function f (x). A confidence of 95% is
used for the intervals which corresponds to z ≈ 1.95.
Hence, the average performance is in the i-th iter-
ation calculated as:
p
avg,i
=
1
n
tes
n
tes
∑
j=1
δ(x
j
), (24)
where δ(x
j
) is 1 if both lcb(x
j
) < f (x
j
) and ucb(x
j
) >
f (x
j
) and otherwise 0. Moreover, x
j
is the j-th tessel-
lation point and lcb(x
j
) and ucb(x
j
) is the lower and
upper bound of the confidence interval of either KDE
or WSKDE (see (9), (21), and (22)).
To illustrate the difference between KDE and
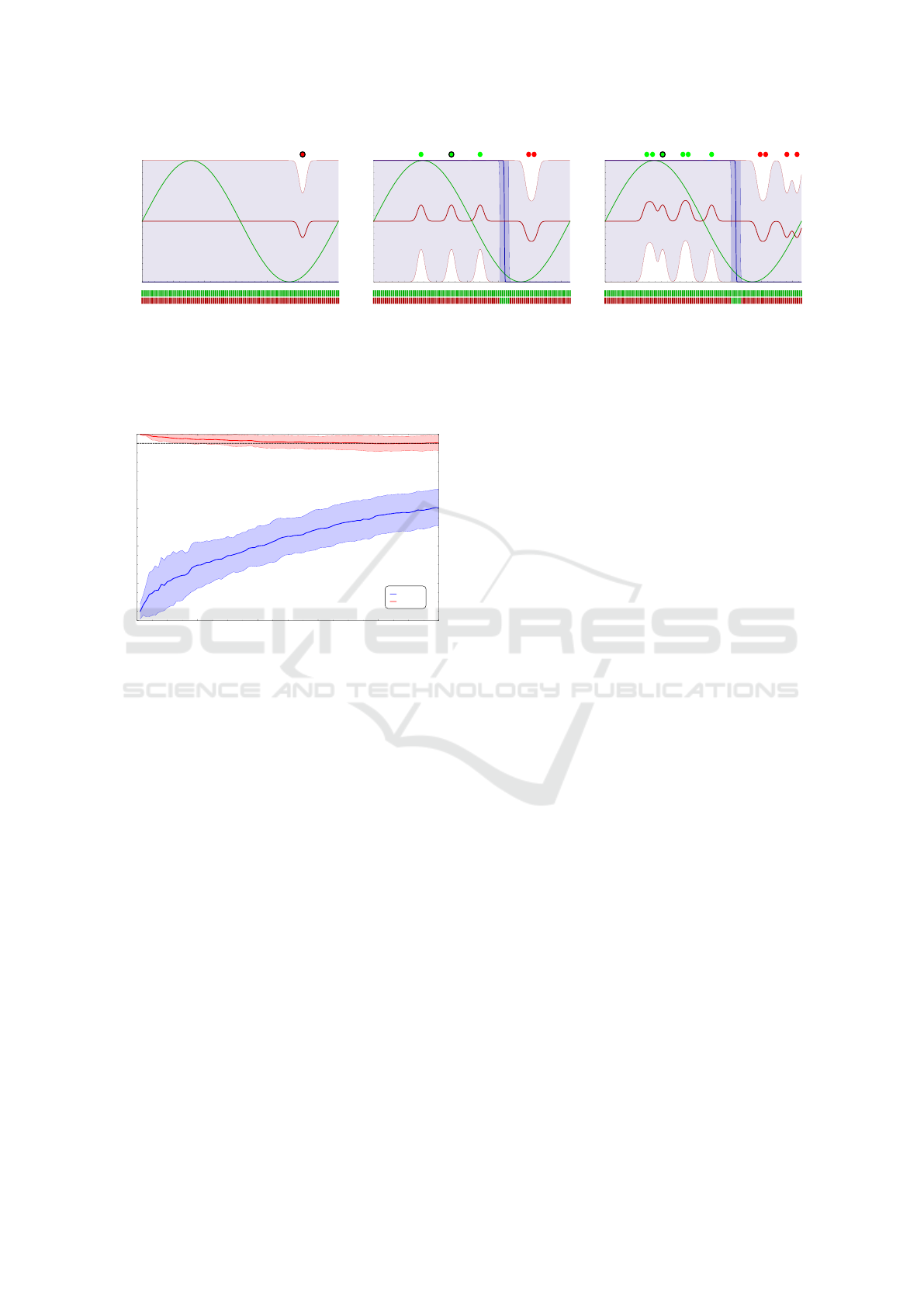
WSKDE, Figure 1 shows three plots of the underly-
ing test function p
test
(x) and the estimated mean and
confidence interval of both the KDE and WSKDE at
different iterations. Also the performance measure
in each of the tessellation points is shown. The fig-
ure clearly shows how KDE (blue curve) struggles
to properly estimate the true function (green curve).
The plots also show how the confidence interval of
WSKDE (red curve) takes advantage of the few sam-
ples correction property of WS by adjusting the es-
timate from [0.5 ± 0.5] towards the true function.
Hence, WSKDE includes the true function signifi-
cantly better than KDE and it is therefore producing
more reliable results when having a sparse sampling
of the parameter space.
To obtain statistics on the results, the procedure
explained above is repeated 50 times and the aver-
age of p
avg,i
is calculated. The results are presented
in Figure 2. It clearly shows that the KDE con-
fidence interval rarely includes the true function in
Wilson Score Kernel Density Estimation for Bernoulli Trials
309
x
Probability
WSKDE
KDE
0 1 2 3 4 5 6
0.0
0.2
0.4
0.6
0.8
1.0
x
Probability
WSKDE
KDE
0 1 2 3 4 5 6
0.0
0.2
0.4
0.6
0.8
1.0
x
Probability
WSKDE
KDE
0 1 2 3 4 5 6
0.0
0.2
0.4
0.6
0.8
1.0
Figure 1: The figure shows a plot of underlying test function p
test
(x) (green curve), the estimated mean and confidence
interval of the KDE (blue curve) and of WSKDE (red curve) for iteration 1, 5, and 10. The two bars below each plot show
the performance of KDE (upper bar) and WSKDE (lower bar) for each of the j tessellation points where green and red
respectively means that confidence interval includes the underlying test function or not. The green and red disks above each
plot represents successful and failed samples. Note the estimated mean and confidence interval KDE in iteration 1 is zero in
the entire parameter space.
KDE
WSKDE
0 20 40 60 80 100
0
20
40
60
80
100
Iterations
Fraction of correct estimates [%]
Figure 2: The figure shows how well the confidence interval
of the KDE (blue) and WSKDE (red) functions estimators
includes the underlying function. The procedure has been
repeated 50 times. Hence, the two solid lines show the per-
centage of how often the confidence interval on average in-
cludes the underlying function, and the hatched area around
the lines represent one standard deviation. The dashed line
shows the 95% performance.
the beginning. KDE gradually improves its perfor-
mance during the iterations, however, it does on av-
erage only reach 60% in iteration 100. Inspecting the
WSKDE result shows that it on average includes 95 %
of the true function, which is also expected since the
function estimators use a 95 % confidence interval.
Note, the WSKDE confidence interval does include
the whole underlying function in the beginning (per-
formance of 100%), which was also expected since
no or only few neighbor samples exist.
6 OPTIMIZATION OF AN
INDUSTRIAL ASSEMBLY CASE
In addition to the experimental validation on the sim-
ple mathematical function in the previous section, we
will in this section apply our iterative learning ap-
proach to a real industrial case. For this test case,
we first carry out the iterative learning process us-
ing dynamic simulations, and then test the best solu-
tion in real-world. We have in previous work (Math-
iesen et al., 2018) shown that our dynamic simulations
align very well with real-world experiments and pro-
duce reliable results. We limit the experiments to the
use of our Wilson Score Kernel Density Estimation
function estimator, since the previous section showed
the problems with the pure Kernel Density Estimation
function estimator. In this section, we first explain the
case, the scenario and which parameters we want to
optimize. We then briefly explain how we select the
sample in each iteration and finally present the results.
6.1 Part Feeding with Vibratory Bowl
Feeders
Vibratory Bowl Feeders (VBFs) is still today an im-
portant part in industrial assembly. The purpose of
the VBFs are to orient parts (which typically come
in bulk) into a desired orientation, so these parts eas-
ily can be handled by subsequent automation system.
VBFs can be used to feed a multitude of parts where
a typical use case is feeding screws. A VBF works by
vibrating parts forward from the bottom of the bowl
along a track on which orienting mechanisms called
traps are located. For our test case we optimize a re-
jection trap for a brass cap (see Figure 3). The pur-
pose of a rejection trap is to reject wrongly oriented
caps for recirculation (position B) and let correctly
oriented caps pass (position A). The figure also shows
the four parameters which control the performance of
the trap and are described in Table 1. These parame-
ters are today tuned manually by human experts, typ-
ically in a trial-and-error process, even though some
guidelines do exist (Boothroyd, 2005).
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
310
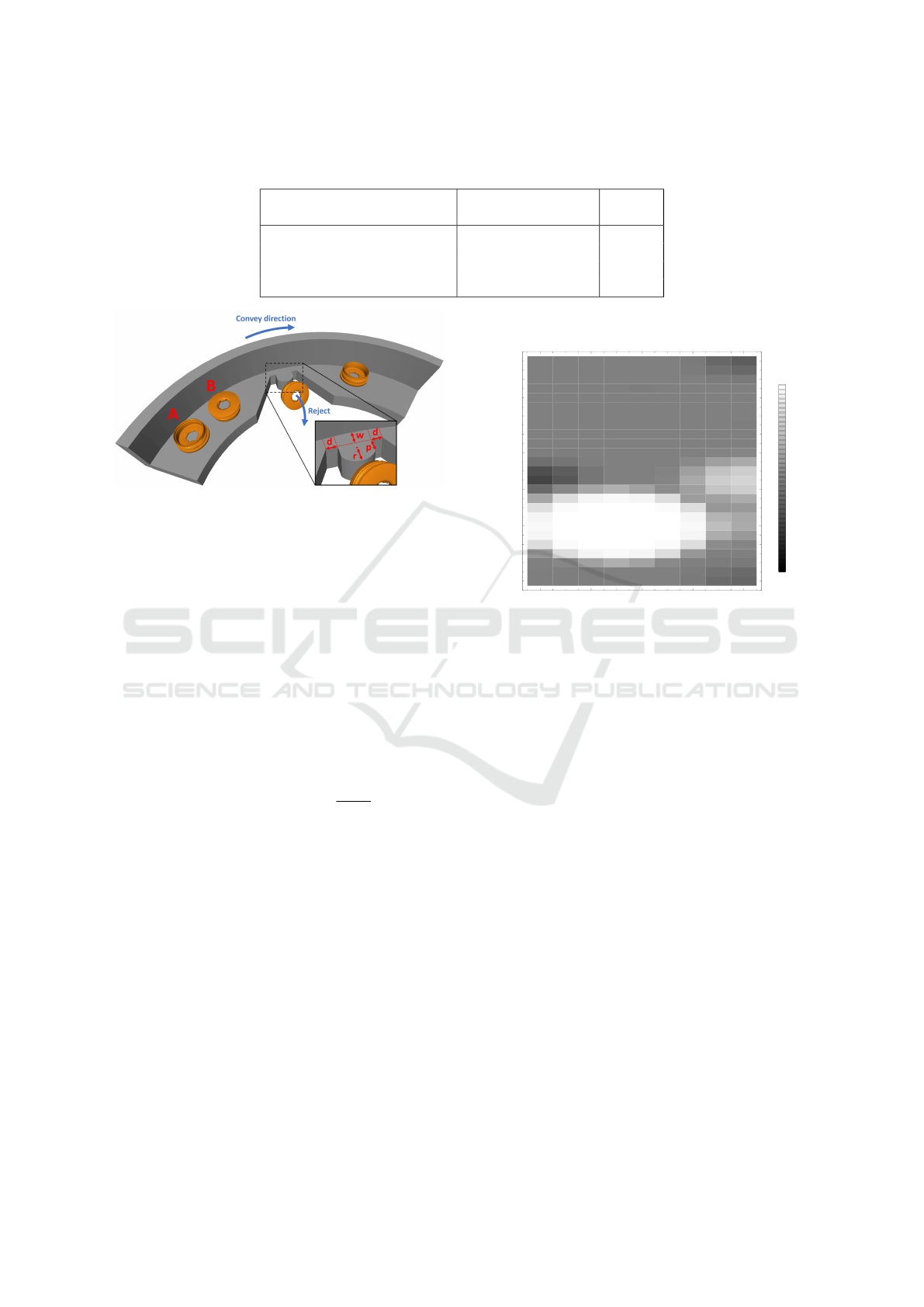
Table 1: The parameters for the chosen rejection trap along with their bounds, discretization. The standard deviation of the
kernel is bandwidth of the kernel, h, which in multiple becomes a bandwidth matrix, H. All values are in millimeters.
Parameters Range Kernel
Name Description Min Max Disc. Std.
w Width of track 0.0 12.0 1.0 1.00
d Distance to cut-out 0.0 8.0 1.0 1.00
r Radius of cut-out 3.0 15.0 0.5 0.25
p Width of protrusion 0.0 11.0 1.0 1.00
Figure 3: The object and rejection trap used in our test case.
The object is a brass cap which can be oriented in one of
two stable poses (A or B). The purpose of the traps is to
reject caps in orientation B and let caps in orientation A
pass. This trap has four parameters which are optimized to
gain the best performance. Rejected parts fall to the bottom
of the bowl and are thereby recirculated.
6.2 Experimental Setup and Choices
We use the iterative learning approach described in
Section 2.1 for optimizing the chosen parameters in
our test case. For the iterative selection of the next
parameter set, we use a refined version of the Up-
per Confidence Bound (UCB) as acquisition function.
Instead of letting κ define the trade-off between ex-
ploration and exploitation, we let the upper bound
of the confidence interval automatically control this
adjustment so acq(x) = p(x) + z
p
σ
2
(x). We name
this acquisition function the Upper Confidence Inter-
val Bound (UCIB). As function estimator we use our
WSKDE (see (20) and (22)) and we utilize a 95% con-
fidence interval which result in z ≈ 1.96.
We choose to discretize the parameter space, X ,
since the selection of the next parameter set then be-
comes as simple as iterating though all sample points
and picking the one with the highest upper confidence
bound (in opposition to finding the maxima in a large
continuous parameter space often consisting of multi-
ple maximums). It also allows for pre-calculating the
kernel mask instead of calculating all the kernel con-
tributions individually. Moreover, we choose a Gaus-
sian kernel with a diagonal kernel matrix consisting of
the standard deviation values shown in Table 1, which
are set to the discretization of parameters to allow for
smoothing. A total of 1500 iterations are conducted.
49.7 49.4 49.7 49.9 50.0 49.8 47.7 42.3 39.6
49.4 49.1 49.6 50.2 50.2 50.0 48.5 44.6 42.3
50.0 53.3 63.2 68.9 63.6 53.9 50.0 48.5 47.7
59.1 86.6 96.2 97.6 96.3 86.8 59.5 50.4 50.0
86.6 98.5 99.7 99.8 99.7 98.6 87.0 55.4 52.4
96.2 99.7 99.9 100.0 99.9 99.7 96.4 67.9 59.9
97.6 99.8 100.0 100.0 100.0 99.8 97.7 74.7 66.8
96.3 99.7 99.9 100.0 99.9 99.7 96.4 70.4 66.0
87.3 98.5 99.7 99.8 99.7 98.6 87.1 59.7 60.0
65.1 87.0 96.2 97.7 96.3 86.8 61.9 63.2 67.6
41.1 53.0 65.5 69.7 63.7 55.1 62.6 76.3 80.2
26.8 34.4 46.5 50.3 50.3 52.4 66.9 80.1 83.1
30.9 36.5 46.3 49.7 50.0 51.4 62.4 76.3 80.1
43.8 46.1 49.1 49.9 50.0 50.3 53.7 62.4 66.9
49.4 49.7 49.9 50.0 50.0 50.0 50.3 51.4 52.3
50.0 50.0 50.0 50.0 50.0 50.0 50.0 50.0 50.0
50.0 50.0 50.0 50.1 50.0 50.0 50.0 49.9 49.8
50.0 50.0 50.0 50.0 50.0 50.0 50.0 49.8 49.7
50.0 50.0 50.0 50.0 50.0 50.0 50.0 49.9 49.8
50.0 50.0 50.0 50.0 50.0 50.0 50.0 50.0 50.0
50.0 50.0 50.0 49.9 49.8 49.9 50.0 50.0 50.0
50.0 50.0 50.0 49.8 49.7 49.8 50.1 50.1 49.9
50.0 50.0 50.0 49.9 49.8 49.9 49.8 48.8 47.7
50.0 50.0 50.0 50.0 50.0 49.9 48.6 44.0 40.7
50.0 50.0 50.0 50.0 50.0 49.8 47.6 40.6 36.2
0 2 4 6 8
4
6
8
10
12
14
Distance to cut-out (d) [mm]
Radius of cut-out (r) [mm]
WSKDE Mean Estimate
Width of track (w=6) and Width of protrusion (p=6) in mm
Mean %
0
20
40
60
80
100
Figure 4: A cross-sectional view of the mean estimated with
WSKDE after 1500 iterations where the parameters w and
p have been fixed. The parameter set with the highest mean
estimate is located at d = 3.0 and r = 6.0 (with w = 6.0 and
p = 6.0).
6.3 Result and Discussion of Test Case
As an example, Figure 4 shows a 2D plot of the pa-
rameter d and r where the parameters w and p both
have been fixed to 6 [mm]. Due to space constraints it
is not possible to show 2D plots of the entire param-
eter space, since we consider four parameters with a
wide range. The result shows that all parameters have
an influence on the trap performance.
For the first 91 iterations, the iterative learning ap-
proach explores the parameter space and obtains both
successes and failures. Hereafter, the iterative learn-
ing finds one parameter set which is exploited for the
majority of the remaining 1409 iterations without any
failures. The reason why the iterative learning keeps
selecting this one parameter set is because the UCIB
is slightly higher than for other parameter sets. More-
over, the UCIB of WSKDE does not get lower if only
successes are obtained, and this parameter set will
therefore be chosen continuous. Only seven time a
different parameter set is selected, but this due to ma-
chine precision and each time iterative learning im-
Wilson Score Kernel Density Estimation for Bernoulli Trials
311

Figure 5: The 3D-printed bowl with the optimized parame-
ters mounted on a VBF drive. The optimized rejection trap
is located in top of the bowl just before the outlet. See Fig-
ure 3 for details on the trap parameters.
mediately returns because a failure is obtained.
After the 1500 iterations, the parameter set with
the highest estimated mean is selected. This param-
eter set has the values of w = 6.0, d = 3.0, r = 6.0,
and p = 6.0 (all values in millimeters), and has a
mean value of 99.97 % and a confidence interval of
[99.95;100.00]% when calculated by the WSKDE
function estimator. The mean is 100% when calcu-
lated by Normal Approximation (see (3)) since only
successes are obtained in this parameter set and only
these are considered by this estimator. The reason
why WSKDE has a slightly lower mean estimate is
because of the few samples correction from Wilson
Score. The many successes in this parameter set lead
to that the few failures close by do not have a signif-
icant impact and the kernel smoothing does therefore
not the cause of this lower mean estimate.
For our real-world test, we 3D-printed a bowl with
the parameters found above which is shown in Fig-
ure 5. The bowl has been tested 200 times for each of
the two stable poses of the brass cap (see Figure 3).
The result shows that all the brass caps starting in sta-
ble pose B were rejected and those starting in stable
pose A all passed the trap. This yields a success rate
of 100%, and with a total of 400 experiments, the re-
sulting design is therefore found to be robust.
7 CONCLUSION
This paper presents a new function estimator denoted
Wilson Score Kernel Density Estimation (WSKDE)
for experiments with binary outcomes. The estimator
has been theoretically derived and has the few sam-
ples correction from Wilson Score and the smooth-
ing property from Kernel Density Estimation regres-
sion. The estimator is especially suited for iterative
learning methods since their sampling strategy often
requires efficient and trustworthy estimators in the be-
ginning of the learning process where decisions are
based on sparse information. The benefit of this es-
timator has been visualized on a mathematically de-
fined problem and shown to work on a real industrial
use case.
8 FUTURE WORK
Future work could both include topics related to the
WSKDE function estimator and the iterative learning
approach. We will below present some of the most
relevant topics for these two subjects.
Categorizing the outcome of an experiment as be-
ing either success or failure is often the most conve-
nient, and sometimes the only possibility, whether ex-
periments are conducted in simulation or real-world.
This makes the presented approach generally appli-
cable. However, further information about the exper-
iment is for some applications available. Therefore,
it would be beneficial to extent the current WSKDE
function estimator for utilizing outcomes in more cat-
egories or even as a continuous value from 0 to 1 rep-
resenting how successful an experiment was.
Other topics worth investigating related the
WSKDE function estimator could be the pros and
cons for using a discrete and continuous parameter
space, but also how the kernel sizes adaptively can
be adjusted. The latter could potentially lower the ef-
fect from smoothing as more samples are taken and
thereby improve the function estimates.
For the iterative learning, a future topic could be to
implement and compare other acquisition functions to
gain other behaviors . This could include studying the
influence of selecting z-score differently than a 95%-
percent confidence interval. Moreover, the iterative
learning is currently terminated after an user-defined
number of iterations. I could be beneficial to expose
other criteria for termination as when the lower con-
fidence bound of one parameters set is above a ac-
ceptable threshold. This would make the termination
criteria more intuitive to choose.
ACKNOWLEDGMENT
This work was supported by Innovation Fund Den-
mark as a part of the project “MADE Digital”.
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
312

REFERENCES
Agresti, A. and Coull, B. A. (1998). Approximate Is Bet-
ter than ”Exact” for Interval Estimation of Binomial
Proportions. The American Statistician.
Boothroyd, G. (2005). Assembly Automation and Product
design. CRC Press, 2nd ed. edition.
Brochu, E., Cora, V. M., and de Freitas, N. (2010). A tuto-
rial on bayesian optimization of expensive cost func-
tions, with application to active user modeling and hi-
erarchical reinforcement learning. CoRR.
Brown, L. D., Cai, T. T., and Dasgupta, A. (2001). Inter-
val estimation for a binomial proportion. Statistical
Science.
H
¨
ardle, W., Werwatz, A., M
¨
uller, M., and Sperlich, S.
(2004). Nonparametric and semiparametric models.
Springer Berlin Heidelberg.
Laursen, J., Sorensen, L., Schultz, U., Ellekilde, L.-P., and
Kraft, D. (2018). Adapting parameterized motions us-
ing iterative learning and online collision detection.
pages 7587–7594.
Mathiesen, S., Sørensen, L. C., Kraft, D., and Ellekilde, L.-
P. (2018). Optimisation of trap design for vibratory
bowl feeders. pages 3467–3474.
Rasmussen, C. and Williams, C. (2006). Gaussian Pro-
cesses for Machine Learning. Adaptive Computation
and Machine Learning. MIT Press, Cambridge, MA,
USA.
Ross, S. M. (2009). Introduction to Probability and Statis-
tics for Engineers and Scientists. Acedemic Press, 4th
edition.
Sørensen, L. C., Buch, J. P., Petersen, H. G., and Kraft, D.
(2016). Online action learning using kernel density
estimation for quick discovery of good parameters for
peg-in-hole insertion. In Proceedings of the 13th In-
ternational Conference on Informatics in Control, Au-
tomation and Robotics.
Tesch, M., Schneider, J. G., and Choset, H. (2013). Ex-
pensive function optimization with stochastic binary
outcomes. In Proceedings of the 30th International
Conference on Machine Learning (ICML).
APPENDIX
The Effect of the Bias and Variance
Error in Relation to KDE and WSKDE
The true confidence interval consists of both a bias
and variance error, however, the bias term has to
be neglected to make confidence interval calculable
(see (9)). The variance term includes f (x) which can
be approximated by
ˆ
f (x), but, unfortunately, the bias
term also includes m
0
(x), m
00
(x) and f
0
(x), which can-
not be approximated properly. Note, the bias and vari-
ance errors can be suppressed by letting h → 0 and
nh → ∞ respectively.
In general, the bias is the vertical difference be-
tween the estimate and the true function and arises
from smoothing effect. This smoothing effect drags
down maxima and pulls up minima of the function
estimate, ˆm(x), compared to m(x). In addition, the
bias is proportional to only m
00
(x) in extrema. Hence,
neglecting the bias error but assuming that m
00
(x)
does not displace the optimum with respect to x, then
ˆx
opt
= x
opt
even though max( ˆm(x)) < max(m(x)).
This assumption requires that important function de-
tails are not smoothed-out and is acceptable when
choosing h appropriately. Furthermore, neglecting the
bias error will offset the confidence interval estimate
compared to the true confidence interval such that the
estimated bounds are raised at minima and lowered at
maxima. For further details see (H
¨
ardle et al., 2004).
Neglecting the KDE regression bias error will also
be reflected in the WSKDE mean and confidence in-
terval estimates, since the KDE regression mean, ˆm
h
,
directly replaces the Normal Approximation mean,
ˆp
na
, as shown in (20). However, the bias error will
be suppressed in sparsely sampled regions due to the
few samples correction of WS (the WS confidence
interval goes towards [0 ; 1] with mean of 0.5 when
n → 0). Regardless the neglection of the KDE regres-
sion bias error, our derivation of WSKDE is still valid
since it is only based on a comparison of the variance
terms of WS and KDE.
Generalization to Multiple Dimensions
The equations of KDE and WSKDE can be general-
ized to multiple dimensions. Hence, the kernel, K,
becomes a multi-dimensional kernel with bandwidth
matrix H, which must be symmetric and positive def-
inite. Whenever the bandwidth, h, is used as a scalar
as in (9) or (20), this becomes the determinant of the
bandwidth matrix |H|. For a multi-normal Gaussian
kernel, ||K||
2
2
is calculated as 1/(2
d
√
π
d
) where d is
the number of dimension, and this constant scalar is
therefore not dependent on the bandwidth of the ker-
nel. Note, the discrete function estimators NA and
WS do not change when going to multiple dimen-
sions, since these are only related to a certain param-
eter set without the influence of experiments made in
neighboring region as when using kernel smoothing.
Wilson Score Kernel Density Estimation for Bernoulli Trials
313
