Backlash Identiﬁcation in Industrial Positioning Systems Aided by a

Mobile Accelerometer Board with Wi-Fi

Mathias Tantau

1 a

, Lars Perner

, Mark Wielitzka

1 b

and Tobias Ortmaier

1 c

Institute of Mechatronic Systems, Leibniz University Hanover, An der Universit

at 2, 30823 Garbsen, Germany

Lenze Automation GmbH, Am Alten Bahnhof 11, D-38122 Braunschweig, Germany

Keywords:

Backlash Identiﬁcation, Accelerometer, Electric Drives, Electric Power Trains.

Abstract:

In electromechanical motion systems performance measures such as positioning accuracy, dynamic stiffness

and control bandwidth are severely limited by backlash. Several control schemes based on backlash com-

pensation or switching control of hybrid systems are known, but many of these approaches require the exact

backlash width as an input parameter. Several existing approaches for backlash identiﬁcation are limited in

accuracy because the load-side velocity is required but it is not directly measurable. In this paper a method

for backlash identiﬁcation tailored to electromechanical motion systems with rotary motor and translationally

moving load is proposed. A mobile sensor board with inertial measurement unit (IMU) is mounted temporar-

ily on the load and serves to acquire the accelerations during the experiment. The connection to the host-PC

is wireless, time synchronisation is not required. It is shown in experiments on a testbed with an adjustable

backlash coupling but otherwise industry-like equipment that high accuracies can be achieved.

1 INTRODUCTION

Electric drives in automation industry are required to

have a high closed-loop bandwidth and a high dy-

namic stiffness in response to external disturbances.

Both is highly limited by backlash between the mo-

tor inertia and the load inertia. Backlash, also called

deadzone, is present in many drive systems, mainly

emerging from gear play.

A number of control metrics have been developed

for systems with backlash (Lagerberg, 2001; Nordin

and Gutman, 2002). Many of them consider the back-

lash gap width explicitly in the design although this

parameter is often unknown and changes over time.

Examples are given in the following paragraph.

An early work on control of systems with back-

lash is the one by Tao and Kokotovic (Tao and Koko-

tovic, 1996). Three different methods of exact lineari-

sation control depending on the availability of angle

sensors at the drive side and/or load side are demon-

strated in (Schoeling and Orlik, 2000). The backlash

width is required in the design. Friedland (Friedland,

1997) developed a load side observer that requires

https://orcid.org/0000-0003-1195-7329

https://orcid.org/0000-0003-0088-6457

https://orcid.org/0000-0003-1644-3685

knowledge of the backlash gap size and the load iner-

tia. A concept based on model predictive control was

developed by Lagerberg and Egardt (Lagerberg and

Egardt, 2005) that requires knowledge of the exact

backlash width. The controller by Nordin and Gut-

man (Nordin and Gutman, 2000) softly switches be-

tween a mode for operation in the backlash gap and

a mode with high gain for operation in contact with

the load. The switching rule requires knowledge of

the backlash width and the stiffness. In (Rostalski

et al., 2007) model predictive control with state ob-

server is proposed for systems with backlash. It is

shown in experiments that uncertainty in the required

model parameters such as the backlash width limits

the performance considerably or respectively leads to

instability. A backlash compensation control scheme

for twin-drive systems with backlash is proposed in

(Itoh, 2008), that requires the backlash width as an

input parameter.

In summary, the explicit consideration of nonlin-

earities like backlash and friction improves perfor-

mance (Marton and Lantos, 2009), but often these

advanced approaches cannot be put into practice be-

cause the required backlash width is not known.

This explains the quest for backlash identiﬁcation

methods that cannot only detect its presence in the

sense of condition monitoring and fault diagnosis, but

576

Tantau, M., Perner, L., Wielitzka, M. and Ortmaier, T.

Backlash Identiﬁcation in Industrial Positioning Systems Aided by a Mobile Accelerometer Board with Wi-Fi.

DOI: 10.5220/0009805305760584

In Proceedings of the 17th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2020), pages 576-584

ISBN: 978-989-758-442-8

can determine the exact value.

Existing works can mainly be divided into min-

imization of simulation model errors, extraction of

features in the measured signals and online state and

parameter observers. The ﬁrst group can further be

divided into time domain approaches and frequency

domain approaches. Examples of the former are

the works of (Ravanbod-Shirazi and Besanc¸on-Voda,

2002; Zemke, 2012; Calvini et al., 2015), where back-

lash and other parameters are identiﬁed by time do-

main output error minimization with for example par-

ticle swarm as an optimizer. A frequency domain ap-

proach is the one presented by (Popp et al., 2019).

Online observers are addressed in the works of Reddy

(Reddy et al., 2019).

Feature-based methods detect the time instances

when the backlash gap is entered and when it is left.

These are also called commutation times (Ravanbod-

Shirazi and Besanc¸on-Voda, 2002) and mainly show

up in the velocity and current signals of the motor, e.g.

(Gebler and Holtz, 1998). The backlash parameter

is obtained by integrating the velocity difference be-

tween motor and load. Details of the load-side veloc-

ity estimation and the detection of commutation times

depend on the availability of sensors and other system

parameters.

In (Marton and Lantos, 2009) it is utilized that the

load stays at rest after a velocity reversal until the

backlash gap is passed, so in this case the load-side

velocity is known (zero). The re-engagement time

is detected in the motor current. Villwock and Pacas

(Villwock and Pacas, 2009) drive a triangular velocity

and detect the commutation instances right after the

maximum velocity peak by analysing the velocity sig-

nal. The load speed is assumed to be constant. Their

technique can be reﬁned by utilizing also the motor

current signal, especially if the load friction is known

(Han et al., 2016). The load deceleration can also

be determined from the commutation times if a sinu-

soidal excitation is used instead of a triangular one

(Specht, 1986) or if a load-side velocity sensor exists

(Ravanbod-Shirazi and Besanc¸on-Voda, 2002). Two

methods based on the assumption of zero load velo-

city in backlash mode are compared in (Zhang et al.,

2018). One of them detects the contact-separation-

contact times via transmission torque mutations, the

other method measures the load-side speed and uses

a describing function to calculate the backlash angle

from the phase lag of the load’s base frequency.

The limitation of most of these methods is that cer-

tain assumptions about the load are made (constant

load-speed, known friction) which are not satisﬁed in

all applications and the true behaviour of the load is

not known if no load-side sensor exists. In real-life

applications it is expectable that the friction is not

negligible and it is not measurable independent of the

motor friction. Gravity is another problem. Load-side

sensors could be installed but only at high costs and

cabling efforts.

This paper aims at backlash identiﬁcation for ro-

tary motors by the help of a mobile, radio controlled

sensor board based on an inertial measurement unit

(IMU). It is attached temporarily to the linearly mov-

ing load and helps to reconstruct the load-side veloc-

ity. The main goal of the presented technique of this

paper is to improve the identiﬁcation accuracy based

on these extra data. Installation effort is minimized

because the sensor board transmits the measurements

via Wi-Fi and it is battery-powered.

2 BACKLASH IDENTIFICATION

This section describes the proposed procedure of

backlash identiﬁcation for an electrical power train

with belt drive as shown in Fig. 1. A controlled servo

motor with angle or angular velocity sensor is con-

nected to a translationally guided load by means of a

belt drive, toothed rack and pinion, or a ball screw.

In the ﬁgure a revolving belt drive is shown. Often,

there is also a gearbox with backlash behind the mo-

tor. The gear ratio is i, the backlash angle is 2α and

the feed constant of the translational element is c

, e.g.

= 2πR for the belt drive with pulley radius R. Such

a conﬁguration is encountered frequently in automa-

tion industry, for example in linear positioning sys-

tems, stacker cranes, rapid prototyping and machine

tools. In contrast to testbeds with free-wheeling load

the belt drive has considerable friction, but as an ad-

vantage the linear acceleration of the load a(t) can be

used as an additional input signal for backlash identi-

ﬁcation.

Servo

drive

Motor with

sensor

Gearbox with

backlash

Translation into

linear motion

Load

Figure 1: Drive train of electromechanical positioning sys-

tem with rotary motor and linearly moving load.

The proposed procedure is developed along Fig. 2.

Although the exact experimental setup is postponed

till Sec. 3 this measurement for 10

◦

serves already

now as a demonstration. It is assumed for now that

gravity has no inﬂuence, i.e. the linear motion is hori-

zontal. Similar to the approach of Villwock (Villwock

and Pacas, 2009) the motor is commanded to acceler-

Backlash Identiﬁcation in Industrial Positioning Systems Aided by a Mobile Accelerometer Board with Wi-Fi

577

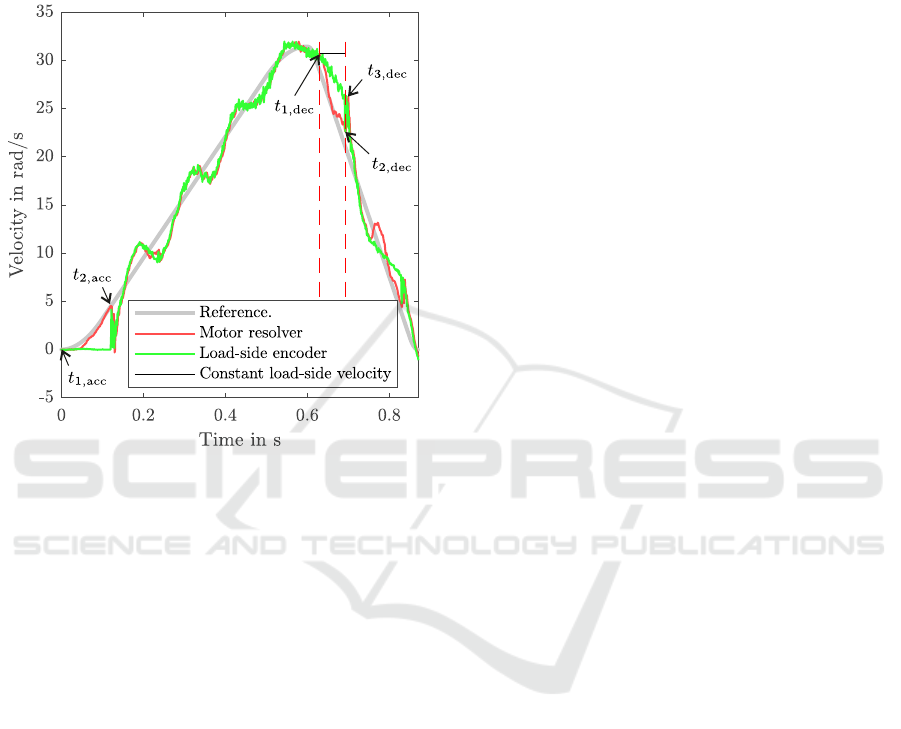
ate up to a certain maximum velocity, followed by a

sharp deceleration, as indicated in grey, Ω

ref

(t). In red

the actual motor speed is shown. In addition, the ve-

locity of the load-side of the backlash element is given

(green line). This signal is measured for visualization

only and it is not used for backlash identiﬁcation.

Figure 2: Velocities of an exemplary experiment with 10

◦

backlash setting without acceleration sensor.

Due to our long-term goal of using the identi-

ﬁed backlash for control design, all measurements are

done with misadjusted control parameters. This leads

to clearly observable oscillations after each backlash

impact. The identiﬁcation algorithm is robust enough

to handle this suboptimal system behaviour.

There are two distinct patterns where the backlash

becomes evident. In the beginning of the acceleration

phase the load remains at rest while the motor accel-

erates already and traverses the backlash gap. This

effect is utilized in (Marton and Lantos, 2009). When

the impact with the load-side occurs, the motor ve-

locity drops instantaneously to a value close to zero

while simultaneously the load is accelerated. The sec-

ond characteristic pattern is observed after the veloc-

ity peak has been passed in the deceleration phase. It

can be seen that the motor decelerates faster than the

load and a clear divergence between the two veloci-

ties occurs. At the other end of the backlash gap the

motor re-engages with the load and is accelerated by

the impact force. This effect is utilized in (Villwock

and Pacas, 2009).

For backlash identiﬁcation both patterns (acceler-

ation and deceleration) can be evaluated as long as the

commutation times can safely be recognized and the

load-side velocity can be approximated (Villwock and

Pacas, 2009):

2α =



Ω

(t) −Ω

(t)dt



. (1)

Ω

and Ω

are the angular velocity of motor and

load, respectively. t

and t

are the commutation times

before and after backlash gap passing. They are re-

placed by the times with index acc and dec for ac-

celeration and deceleration phase, respectively, see

Fig. 2.

For fully automatic backlash identiﬁcation, con-

ditions for detecting the commutation times must be

established. In the acceleration phase t

1,acc

coincides

with t = 0. It is ensured by a slow backward move-

ment preceding the experiment that the backlash el-

ement is actually at the one end, in a deﬁned state

when the shown velocity proﬁle begins. t

2,acc

can be

detected by a sharp drop in the motor velocity. Here,

2,acc

is deﬁned as the time instant in the acceleration

phase when the maximum motor velocity is reached

which is followed by a drop in the velocity of at least

50% of this maximum.

50% is the value expectable for bounce-free but

undamped re-engagement by conservation of momen-

tum if the inertia ratio of motor and load is 1. Usually,

the load inertia exceeds the motor inertia, leading to a

deeper drop and 50 % is a safe setting. On the other

hand, if the load is lighter, backlash identiﬁcation be-

comes less important for control design, because the

control parameters are predominantly determined by

the motor inertia.

In the deceleration phase t

1,dec

is deﬁned as the

time instant corresponding to the maximal motor ve-

locity after the maximum in the reference speed has

been reached (ﬁrst dashed line in Fig. 2). t

2,dec

more difﬁcult to determine automatically. First, the

maximum in Ω

(t) −Ω

ref

(t) is found and marked as

3,dec

. Then, the minimum in the motor velocity be-

tween t

1,dec

and t

3,dec

is detected and associated with

2,dec

(second dashed line). Typically, t

2,dec

and t

3,dec

are close together.

Approximating the load-side velocity in the time

interval of interest in the acceleration phase is trivial

because without gravity the load should be at rest, so

the velocity is zero (Marton and Lantos, 2009). For

the deceleration phase it can be assumed that the load

velocity is constant and identical to Ω

1,dec

) (black

line). While Villwock (Villwock and Pacas, 2009)

achieved good results with this approximation, it was

found that in a real setting with friction in the driven

mechanics a large error is introduced. In Fig. 2 this

error can be quantiﬁed by comparing the surface areas

between the green and black line, resp. between the

ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics

578

red and green line in the time interval marked by the

dashed lines.

Now, the accelerometer comes into the picture.

It is mounted on the translationally moving load and

measures accelerations in three axes. The component

in the direction of motion a(t) serves to obtain the

velocity between the dashed lines from numeric inte-

gration of discrete-time signals:

Ω

L,k+1

Ω

L,k

+ 2πia

. (2)

In this equation ˆ stands for the estimate and T

for the

sampling time. The time at sampling instant k, kT

shortened by the index k.

At kT

= t

1,dec

the velocity could be initialized

to the current motor measurement, but since this

would depend on one single, noisy measurement a

better alternative is to utilize also the common move-

ment of motor and load during the acceleration phase.

The sensor fusion of motor position measurement

and accelerometer measurement could be realized via

Kalman ﬁltering (Shim et al., 1998), or since the cal-

culation is performed ofﬂine Kalman smoothing is

also possible (S

arkk

a, 2013). Here, the acceleration

is simply integrated and the known motor velocity is

used as a feedback:

Ω

L,k+1

= (1 −ε)



Ω

L,k

+ 2πia



+ εΩ

M,k

. (3)

ε is a tuning factor that is adapted manually to adjust

the dynamics of the estimate.

Since the accelerometer outputs the data with a

certain, a priori unknown offset a:

raw,k

= a

+ a, (4)

this offset must be determined and compensated. We

can utilize the fact that right before and after the ex-

periment the velocity is known to be equal and zero:

Ω

2πiT

+ a

+ ···+ a

N−1

+ Na].

(5)

With

Ω

= 0 (5) can be solved for a, which

is then subtracted from a

raw

Another essential preparation step is the synchro-

nisation of signals in time. Since the mobile sensor

for acceleration measurement is started remotely via

a non-realtime connection, the acceleration may have

a time shift. For time synchronisation the cross corre-

lation between the acceleration signals from the two

sensors (motor and accelerometer) is maximized:

lag = arg max

k=∞

∑

k=−∞



2πia

k+m

Ω

M,k+1

−Ω

M,k



. (6)

This way the time lag is determined and the ﬁrst lag

samples of a

are discarded before the above calcula-

tions are carried out.

3 EXERIMENTAL SETUP

For the experimental validation the testbed shown in

Fig. 3 is used. A synchronous motor of the type MCS

12L20 with a rated power of 2.8 kW and a rated torque

of 13.5 Nm is driven by an 9400 servo inverter, both

from Lenze. It is connected to a belt drive of 2.20 m

length by a coupling with adjustable backlash. The

load allows for weight adjustment, but in these ex-

periments a constant load of 11 kg is chosen. On the

load-side of the backlash coupling a rotary multiturn

encoder ’ATD 2B A 4 Y26’ from Baumer Thalheim is

mounted. The resolution of the encoder is 17bits/rev.

Servo inverter and encoder are connected to the main

controller, ’3200 C’ from Lenze via EtherCAT.

Figure 3: Experimental setup.

Figure 4 shows the backlash coupling, which

works similar to the one described in (Villwock,

2007). Ball bearings have been integrated to facili-

tate the alignment. The gap width can be adjusted in

steps: 0

◦

,0.5

◦

,··· ,4.5

◦

,··· ,20

◦

. This range of

adjustable values is comparable to other couplings or

gearboxes with adjustable deadzone (Dagalakis and

Myers, 1985; Schoeling and Orlik, 2000; Merzouki

et al., 2006; Rostalski et al., 2007). In (Merzouki

et al., 2006) the deadzone can even be extended up

to 24

◦

. Industrial gearboxes have a motor-side back-

lash angle in a similar range, typically more for high

transmission ratios (Lenze, 2020).

The mobile sensor is attached to the load with

an ordinary tape. Figure 5 shows a detailed view of

the sensor board. It is based on an Arduino ESP32

NodeMCU from Espressif with dual-core controller

running at 80 MHz and 802.11 b/g/n Wi-Fi function-

ality. The lower PCB has been added to integrate

three SRAM devices ’IS62WVS2568FBLL-20NLI’

with 2 Mb,20 MHz as a data buffer. Also, the MEMS

(micro-electromechanical systems) IMU ’LSM6DS3’

is mounted on the lower PCB. It is conﬁgured to mea-

sure accelerations in three axes with a resolution of

16Bits at ±2g full range, at a nominal noise level of

90µg/

√

Hz.

Backlash Identiﬁcation in Industrial Positioning Systems Aided by a Mobile Accelerometer Board with Wi-Fi

579

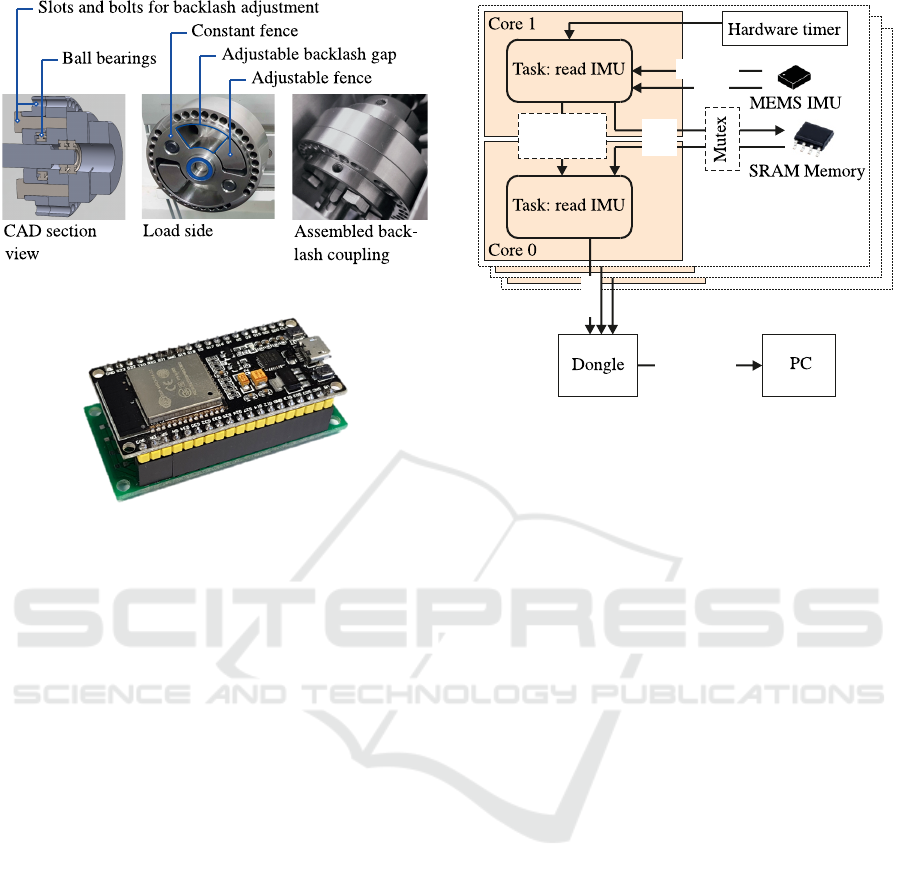
Figure 4: Coupling with adjustable backlash.

Figure 5: Sensor board with MEMS IMU and Wi-Fi data

transmission.

In Fig. 6 the principle of data transmission is

shown. Real-time operating system FreeRTOS

(Amazon Web Services, Inc., 2020) is running on

the sensor board with two tasks, one for reading the

measurements from the IMU and storing them in the

SRAM devices and one for transmitting the data via

Wi-Fi to the receiver. Reading the accelerations from

the sensor can be synchronized with the clock of the

actual measurement, which can be set in steps up

to 1.66 kHz. In this case it is initiated by an inter-

rupt from the sensor. Alternatively, an arbitrary sam-

pling rate can be realized by a hardware timer inter-

rupt. It was found that tolerances of the sensor sam-

pling rate lead to problems in time synchronisation.

For that reason the sensor is conﬁgured to measure at

1.66kHz, while the data are recorded asynchronously

at 1 kHz. This leads to time jitter, but aliasing is pre-

vented by a low-pass ﬁlter at 400 Hz inside the IMU.

Data are transmitted to a receiver board via Wi-Fi

Direct mode, which allows the simultaneous connec-

tion of several sensor boards without a wireless router.

The receiver is also an ESP32, which is connected to

the computer over USB.

4 EXPERIMENTAL RESULTS

In this section experimental results are reported for

backlash identiﬁcation. Firstly, in deceleration phase

Receiver board 3

Receiver board 2

USB/Serial

vSPI

Interrupt

Wi-Fi

hSPI

Receiver board 1

Counting

Semaphore

Figure 6: Schematic of the data transmission from the mo-

bile sensor boards to the PC.

without accelerometer, secondly in acceleration phase

with zero load velocity and thirdly, in deceleration

phase with the mobile sensor unit.

For the identiﬁcation in deceleration phase with-

out accelerometer identiﬁed backlash angles are

shown against those that have been conﬁgured in the

backlash coupling in Fig. 7. Measurements have been

repeated for ﬁve motor orientations spread equally

over one rotation. This procedure ensures that the

identiﬁcation works not only for one particular ori-

entation. In addition, as a reference the backlash val-

ues have been measured by the help of the load-side

encoder (black line). For this experiment the motor-

side part of the backlash coupling was ﬁxed and the

load-side position was rotated slowly by hand, while

the minimum and maximum encoder readings were

recorded.

The fact that the reference measurement is almost

an identity line conﬁrms that the backlash coupling

has been machined accurately, although the actual

width is always approximately 0.5

◦

too low. The

identiﬁcation result is far above the correct value, for

most widths even exceeding 200%. This can be ex-

plained by the error due to neglecting the deceleration

of the load as already shown in Fig. 2.

The result for the acceleration phase is shown in

Fig. 8. These experiments reveal a high accuracy

and repeatability which suggests a clear superiority

of the method. However, it is less robust to sources of

disturbing torques not considered explicitly. For ex-

ample, position-dependent friction could lead to sim-

ilar drops in the velocity causing confusion with the

backlash-induced effect. Also, if due to a slight in-

clination of the linear drive there is a small gravity

ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics

580

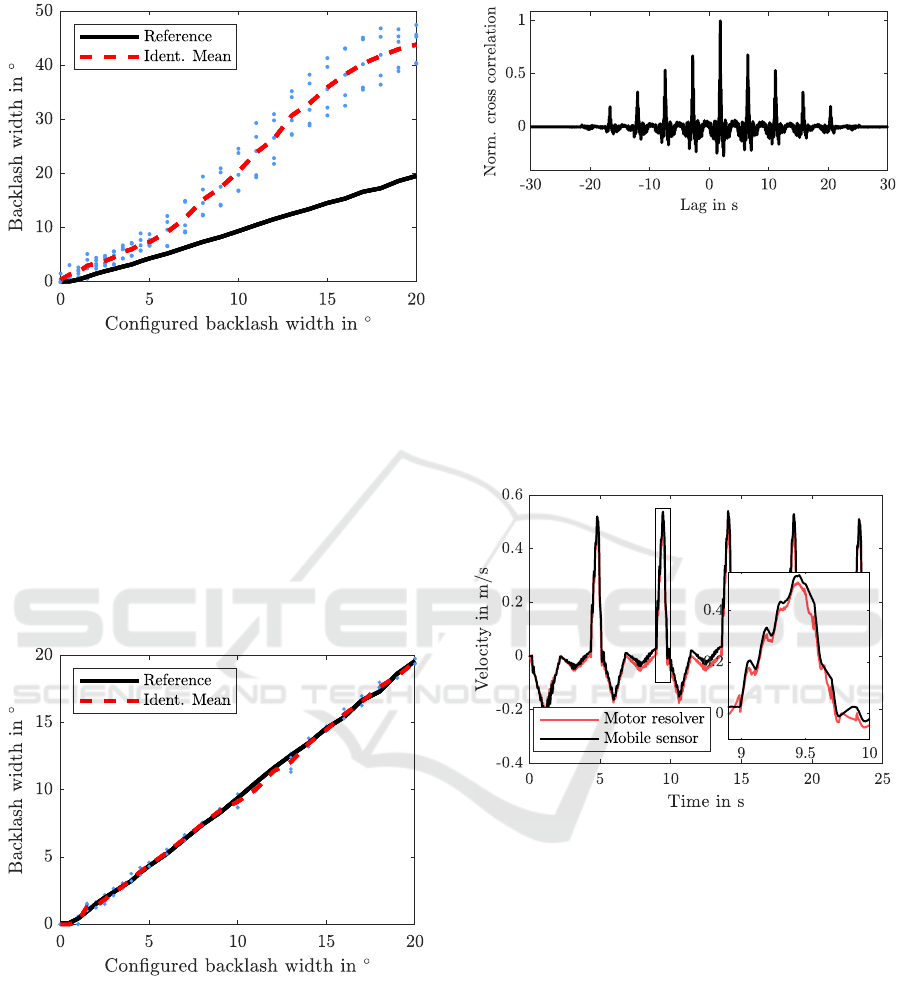
Figure 7: Identiﬁed vs. conﬁgured backlash width when the

load velocity is assumed to be constant and the backlash is

identiﬁed in the deceleration phase.

torque, the load acceleration will depart from zero

during the measurement or the load might leave the

one end of the backlash gap prior to the measurement.

It is expectable that it could even become impossible

to detect t

2,acc

. So, although the results in the acceler-

ation phase are good, it is expectable that this method

is not robust and suffers from similar problems as the

methods cited above that make certain assumptions

about the load-speed.

Figure 8: Identiﬁed vs. conﬁgured backlash width when the

load velocity is assumed to be constant and the backlash is

identiﬁed in the acceleration phase.

In the following, the results with accelerometer

are reported. For an angle of 10

◦

the results of the

time synchronisation step are shown in Fig. 9. In this

ﬁgure as well as in all other experiments a clear max-

imum can be seen and time synchronisation is readily

possible.

After time synchronisation and drift elimination

the velocity could be obtained from the accelerome-

Figure 9: Cross correlation between accelerometer mea-

surement a(t) and numerically differentiated motor velocity

Ω

(t).

ter with only a minor error as shown in Fig 10. Al-

though only the velocities before and after the ﬁve

movements are used for calibration, both graphs are

in good agreement. But this free integration result is

not actually needed and only shown as a veriﬁcation.

Instead the velocity is estimated as explained above

with the result given in Fig. 11.

Figure 10: Velocity obtained from motor encoder

Ω

(t),resp. by integration from the mobile accelerometer.

For the same 10

◦

recording as in Figs. 9 and 10

the velocities of the three different sources are shown.

ε is set to 5%. Apparently, the accelerometer is in

good agreement with the encoder in the deceleration

phase while the backlash gap is traversed.

This impression is conﬁrmed by the other experi-

ments, see Fig. 12. Backlash identiﬁcation is possible

with low variance and high repeatability, albeit less

good than in the acceleration phase, compare Fig. 8.

Some of the results for 1.5

◦

or less are erroneous be-

cause the time t

could not be extracted safely, possi-

bly because the effect of the impact is less pronounced

for small backlash widths. This can be observed in

Fig. 7, too.

Backlash Identiﬁcation in Industrial Positioning Systems Aided by a Mobile Accelerometer Board with Wi-Fi

581

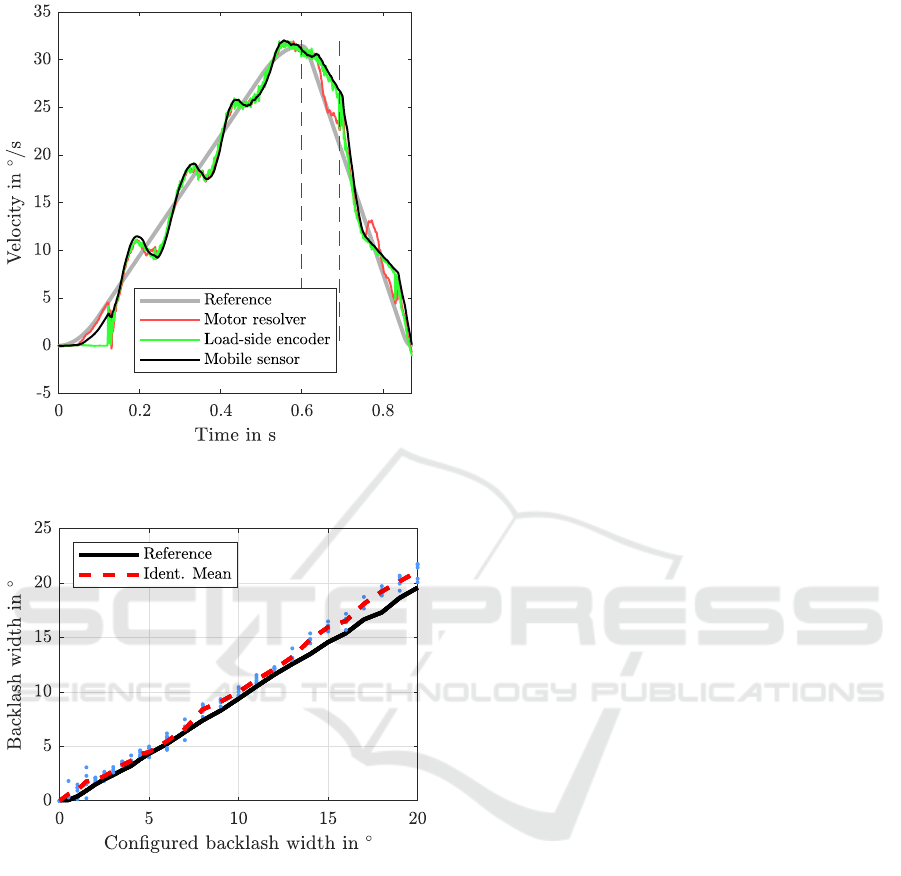
Figure 11: Velocities of an exemplary experiment with 10

◦

backlash setting with acceleration sensor.

Figure 12: Identiﬁed vs. conﬁgured backlash width when

the load velocity is obtained from the accelerometer, decel-

eration phase.

5 DISCUSSION

The presented approach towards backlash identiﬁca-

tion was shown to provide a high accuracy, especially

for high backlash angles. This is remarkable as the ef-

fort and cost of installing the temporary sensor board

at the load is small and it is not necessary to synchro-

nize the different sensors in time. Apparently, the belt

elasticity does not impair the measurements signiﬁ-

cantly. Many applications as listed above could bene-

ﬁt from such a mobile sensor for backlash identiﬁca-

tion. Although not conﬁrmed experimentally, it can

be expected that small disturbances, such as gravity

should not impair the identiﬁcation signiﬁcantly, be-

cause they are detected by the IMU.

Only in the low backlash domain of 1.5

◦

or less

the commutation times could not always be detected

correctly leading to scattering of the results. Fur-

thermore, the experiments have shown that machin-

ing inaccuracies in the backlash coupling lead to an-

gle dependencies and tolerances in the range of 0.5

◦

Therefore, the validation of the methods is also lim-

ited in accuracy and scattering of the measurements

can partly be attributed to machining, not to the iden-

tiﬁcation method. The results could be improved by

averaging several measurements, which was not taken

into account here.

It is astonishing how (Marton and Lantos, 2009)

could achieve identiﬁcation tolerances of only a few

percent for backlash angles of 0.47

◦

, resp. 0.35

◦

. In

(Han et al., 2016), too, accuracies of a few percent are

achieved for 1

◦

. A possible explanation might be the

idealized setup in their experiments contrasting with

the more industry-like setup of our testbed.

It remains to be investigated if the results are

equally good for a real gearbox instead of the back-

lash coupling. Possibly, oil between the teeth and the

interplay of the multiple gear ranges could hinder a

clear detection of the commutation times. Also, if the

transmission ratio is high and accordingly the load ve-

locity is slow, it could become increasingly difﬁcult to

reconstruct the load velocity from the accelerometer

measurement.

Future works should investigate the applicability

of MEMS gyroscopes for purely rotary settings. With

a sensor board like the one used in this work it is pos-

sible to capture also rotating parts with little effort.

6 CONCLUSIONS

In this paper a method for backlash identiﬁcation in

electric drive trains has been proposed. It is tailored

to electromechanical motion systems with rotary mo-

tor and translationally moving load. A mobile sensor

board with IMU is mounted temporarily on the load

and transmits the measured accelerations via Wi-Fi,

thus requiring no cabling. Is was shown in experi-

ments with an adjustable backlash coupling that high

accuracies can be achieved even if the load-side fric-

tion and inertia are unknown, which has so far been a

challenge with series sensor equipment. The testbed

used for the experiments consists of industrial equip-

ment, except for the coupling with adjustable back-

lash. It must still be investigated if similar results

can be achieved with a gearbox instead of the back-

ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics

582

lash coupling. The IMU measurement can be initiated

manually independent of the hardware that controls

the motor, because time synchronisation is possible

based on the recorded signals.

ACKNOWLEDGEMENTS

This work was sponsored by the AiF (Arbeits-

gemeinschaft industrieller Forschungsvereinigungen

Otto von Guericke e.V.) and managed by the FVA

(Forschungsvereinigung Antriebstechnik e.V.) both in

Germany.

REFERENCES

Amazon Web Services, Inc. (2020). FreeRTOS

- real-time operating system for microcontrollers.

https://www.freertos.org/index.html, accesssed: Feb.

2020.

Calvini, M., Carpita, M., Formentini, A., and Marchesoni,

M. (2015). Pso-based self-commissioning of electrical

motor drives. IEEE Transactions on Industrial Elec-

tronics, 62(2):768–776.

Dagalakis, N. G. and Myers, D. R. (1985). Adjustment

of robot joint gear backlash using the robot joint test

excitation technique. The international journal of

robotics research, 4(2):65–79.

Friedland, B. (1997). Feedback control of systems with par-

asitic effects. In Proceedings of the 1997 American

Control Conference (Cat. No. 97CH36041), volume 2,

pages 937–941. IEEE.

Gebler, D. and Holtz, J. (1998). Identiﬁcation and compen-

sation of gear backlash without output position sensor

in high-precision servo systems. In IECON’98. Pro-

ceedings of the 24th Annual Conference of the IEEE

Industrial Electronics Society (Cat. No. 98CH36200),

volume 2, pages 662–666. IEEE.

Han, Y., Liu, C., and Wu, J. (2016). Backlash identiﬁca-

tion for PMSM servo system based on relay feedback.

Nonlinear Dynamics, 84(4):2363–2375.

Itoh, M. (2008). Torsional vibration suppression of a twin-

drive geared system using model-based control. In

2008 10th IEEE International Workshop on Advanced

Motion Control, pages 176–181. IEEE.

Lagerberg, A. (2001). A literature survey on control of au-

tomotive powertrains with backlash. Technical Re-

port R013/2001, Control and Automation Laboratory,

Chalmers University of Technology, G

oteborg, Swe-

den.

Lagerberg, A. and Egardt, B. (2005). Model predictive con-

trol of automotive powertrains with backlash. IFAC

Proceedings Volumes, 38(1):1–6.

Lenze (2020). Product-related documentation. https://

www.lenze.com/en-de/services/knowledge-base/

product-related-documentation/, accesssed: Feb.

2020.

Marton, L. and Lantos, B. (2009). Friction and backlash

measurement and identiﬁcation method for robotic

arms. In 2009 International Conference on Advanced

Robotics, pages 1–6. IEEE.

Merzouki, R., Davila, J. A., Cadiou, J. C., and Fridman, L.

(2006). Backlash phenomenon observation and identi-

ﬁcation. In 2006 American Control Conference, pages

3322–3327. IEEE.

Nordin, M. and Gutman, P.-O. (2000). Nonlinear speed con-

trol of elastic systems with backlash. In Proceedings

of the 39th IEEE Conference on Decision and Control

(Cat. No. 00CH37187), volume 4, pages 4060–4065.

IEEE.

Nordin, M. and Gutman, P.-O. (2002). Controlling mechan-

ical systems with backlash – a survey. Automatica,

38(10):1633–1649.

Popp, E., Tantau, M., Wielitzka, M., Ortmaier, T., and

Giebert, D. (2019). Frequency domain identiﬁcation

and identiﬁability analysis of a nonlinear vehicle driv-

etrain model. In 2019 18th European Control Confer-

ence (ECC), pages 237–242. IEEE.

Ravanbod-Shirazi, L. and Besanc¸on-Voda, A. (2002).

Backlash identiﬁcation: a two step approach. IFAC

Proceedings Volumes, 35(1):85–90.

Reddy, P., Darokar, K., Robinette, D., Shahbakhti, M.,

Blough, J., Ravichandran, M., Farmer, M., and Doer-

ing, J. (2019). Control-oriented modeling of a vehicle

drivetrain for shufﬂe and clunk mitigation. Technical

report, SAE Technical Paper.

Rostalski, P., Besselmann, T., Bari

c, M., Belzen, F. V.,

and Morari, M. (2007). A hybrid approach to mod-

elling, control and state estimation of mechanical sys-

tems with backlash. International Journal of Control,

80(11):1729–1740.

arkk

a, S. (2013). Bayesian ﬁltering and smoothing, vol-

ume 3. Cambridge University Press.

Schoeling, I. and Orlik, B. (2000). Control of a nonlinear

two-mass system with uncertain parameters and un-

known states. In IEEE Industry Applications Confer-

ence (Cat. No. 00CH37129), volume 2, pages 1096–

1103. IEEE.

Shim, H., Kochem, M., and Tomizuka, M. (1998). Use of

accelerometer for precision motion control of linear

motor driven positioning system. In IECON’98. Pro-

ceedings of the 24th Annual Conference of the IEEE

Industrial Electronics Society (Cat. No. 98CH36200),

volume 4, pages 2409–2414. IEEE.

Specht, R. (1986). Ermittlung von Getriebelose und

Getriebereibung bei Robotergelenken mit Gleich-

stromantrieben. VDI-Berichte, (598):71–83.

Tao, G. and Kokotovic, P. V. (1996). Adaptive control of

systems with actuator and sensor nonlinearities. John

Wiley & Sons, Inc.

Villwock, S. (2007). Identiﬁkationsmethoden f

die automatisierte Inbetriebnahme und Zu-

stands

uberwachung elektrischer Antriebe. PhD

thesis, Universit

at Siegen.

Villwock, S. and Pacas, M. (2009). Time-domain iden-

tiﬁcation method for detecting mechanical backlash

Backlash Identiﬁcation in Industrial Positioning Systems Aided by a Mobile Accelerometer Board with Wi-Fi

583

in electrical drives. IEEE Transactions on Industrial

Electronics, 56(2):568–573.

Zemke, S. (2012). Analyse und modellbasierte Regelung

von Ruckelschwingungen im Antriebsstrang von

Kraftfahrzeugen. PhD thesis, Leibniz Universit

Hannover.

Zhang, J., Zhang, H., and Xiao, X. (2018). New iden-

tiﬁcation method for backlash of gear transmission

systems. In 2nd IEEE Advanced Information Man-

agement, Communicates, Electronic and Automation

Control Conference (IMCEC), pages 378–382. IEEE.

ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics

584