A White-Box Encryption Scheme using Physically Unclonable Functions

Sandra Rasoamiaramanana

1,2

, Marine Minier

and Gilles Macario-Rat

Universit

e de Lorraine, CNRS, Inria, LORIA, F-54000 Nancy, France

Orange Labs, Applied Crypto Group, Ch

atillon, France

Keywords:

White-Box Cryptography, Code Lifting Attack, Device Binding, Physically Unclonable Functions.

Abstract:

When a cryptographic algorithm is executed in a potentially hostile environment, techniques of White-Box

Cryptography are used to protect a secret key from a fully-privileged adversary. However, even if the adversary

is not able to extract the secret key from the implementation, they might lift the entire white-box code and

execute it (this is called a code lifting attack). In this work, we introduce an encryption scheme that can be

implemented on an untrusted environment and is still secure even if the white-box code has been lifted. We

base our proposal on a Physically Unclonable Function (PUF) to ensure the execution context of our so-called

PUF-based encryption scheme. This way, the encryption is “locked” by a particular device.

1 INTRODUCTION

White-Box Cryptography (WBC) was ﬁrst introduced

by Chow et al. in

2002

(Chow et al., 2002a; Chow

et al., 2002b) as an obfuscation technique for a cryp-

tographic algorithm. Thus, the purpose of WBC is

to produce an implementation of a cryptographic al-

gorithm which hides the key in the data such that a

fully-privileged adversary which controls the execu-

tion environment of the algorithm and has access to the

implementation cannot extract the key from it. This

statement refers to the key extraction security. How-

ever, Chow et al. also pointed out that in this context,

an adversary might lift the implementation and exe-

cute the algorithm without knowing the key. Thus,

the security of an implementation in the white-box

model brings together the resistance to key extraction

and the resistance to a code lifting attack. Two no-

tions are generally used to capture those security goals:

unbreakability and incompressibility/space-hardness

(Delerabl

ee et al., 2013; Biryukov et al., 2014; Fouque

et al., 2016; Bogdanov et al., 2016). While unbreak-

ability deﬁnes the basic requirement for a white-box

implementation which is to merge the secret key inside

the implementation, space-hardness ensures that an ad-

versary having a portion of the code cannot execute

the algorithm and aims to mitigate code lifting without

preventing it. Following this approach, white-box ded-

icated block ciphers such as SPACE or SPNbox have

been proposed in (Biryukov et al., 2014; Bogdanov

and Isobe, 2015; Bogdanov et al., 2016; Fouque et al.,

2016; Cho et al., 2017). Yet, if the adversary is able to

copy the white-box code, they can take advantage of

the code functionality without any restriction.

In this work, we address this issue and attempt to

avoid code lifting by binding the white-box code to

its environment. The idea is that even if the adversary

lifts the entire white-box code, they will not take ad-

vantage of the code functionality. For that, we make

use of a Physically Unclonable Function (PUF) (Maes,

2012) to reinforce the security against code lifting.

A PUF is a physical system that can be challenged

with a stimuli and which reacts: the so-called response

depends on manufacturing variations which induce a

structural disorder that cannot be cloned or reproduced

exactly. Thanks to such a device-speciﬁc behavior, a

PUF might be used for identiﬁcation, authentication,

and even key generation.

We formalize the concept of PUF in Section 2.

In Section 3, we introduce the notion of PUF-based

encryption scheme as an encryption scheme which

takes three inputs: a secret key, a plaintext and a PUF

response. Thus, the PUF response adds a variability

mechanism to the encryption scheme. First, we formal-

ize the notion of lockability

to guarantee the security

of the scheme when implemented in the white-box

model: lockability states the difﬁculty of executing

a lifted white-box code on a different device. Then,

we instantiate the scheme with the tweakable Even-

Mansour construction of (Cogliati et al., 2015) and

Neologism to deﬁne the possibility to lock a cipher to

an execution environment.

Rasoamiaramanana, S., Minier, M. and Macario-Rat, G.

A White-Box Encryption Scheme using Physically Unclonable Functions.

DOI: 10.5220/0009781002790286

In Proceedings of the 17th International Joint Conference on e-Business and Telecommunications (ICETE 2020) - SECRYPT, pages 279-286

ISBN: 978-989-758-446-6

279

the white-box dedicated block cipher SPNbox-

(Bog-

danov et al., 2016).

2 PHYSICALLY UNCLONABLE

FUNCTIONS

This section gives an overview of the concept of PUF

without being exhaustive. We refer to (Maes, 2012)

for a complete description and analysis.

2.1 Characterization of a Physically

Unclonable Function

A PUF is a physical entity (e.g. an integrated cir-

cuit) that presents random imperfections in its struc-

ture. The imperfections result from the manufactur-

ing process and are expected to be instance speciﬁc

and unclonable. The term PUF also refers to the “ex-

pression” (the challenge-response behavior) of these

random imperfections. To characterize a PUF, the

physical disorder (e.g. a current or a voltage) is gen-

erally measured under a speciﬁc condition (stimuli)

and converted into digital form. Thus, a PUF performs

a probabilistic functional operation: given a certain

input (a stimuli, also called a challenge) it produces

a measurable output (the response). Consequently, a

PUF is seen as a physical realization of a probabilistic

mapping

puf : X → Y

where

is the domain space

called the challenge set and

is an output range called

the response set. The creation of a PUF is expressed

by invoking a manufacturing process on a set of pa-

rameters param. We write

puf ←$ CREATE(param)

signify that a PUF instance is created. The set of all

instances created according to a set of parameters is

called a PUF class and denoted by

. An instance of

can be evaluated on a challenge

x ∈ X

using an eval-

uation procedure EVAL: we write

y ← EVAL(puf,x)

or simply

y ← puf(x)

for the evaluation of

puf

on the

challenge

. The outputs of a PUF instance are gen-

erally noisy, i.e.,

puf

outputs two distinct responses

y, y

when evaluated twice on the same challenge

Thus, a PUF response is considered as a random vari-

able, and information about the distribution of the

PUF responses is obtained through experiment. An

experiment on a PUF class is parametrized by

t,q

and

which are the number of evaluations of one

instance on the same challenge, the number of created

instances, and the number of distinct evaluations on

an instance, respectively. The experiment gives esti-

mated descriptive statistics of the intra-distance

of the instance inter-distance

and of the PUF inter-

distance

. The intra-distance is the distance between

two distinct responses of an instance evaluated on the

same challenge. In the same manner, the instance

inter-distance and the PUF inter-distance characterize

the distance between any two responses

y, y

of an in-

stance puf evaluated on two distinct challenges

x,x

and

the distance between two outputs

y, y

of two distinct

instances puf, puf’ evaluated on the same challenge

, respectively. On the one hand, the intra-distance

property estimates the reproducibility of a PUF out-

put. Thus, low intra-distance ensures that the PUF

outputs are highly reproducible. On the other hand,

the PUF inter-distance estimates the uniqueness of an

instance’s output while the instance inter-distance en-

sures the uniqueness of a response given a challenge.

The intra-distance

should be lower than

and

uniquely distinguish outputs from different instances

and outputs from different challenges. For the rest

of the paper, we denote by dist the distance. Another

property of PUF outputs that should be estimated is

the min-entropy. The min-entropy of a binary string

represents the number of uniform bits and measures

the uncertainty one has on the output. The conditional

min-entropy is more relevant for the distribution of

PUF outputs since an adversary should not deduce

enough information about an unknown output given

many outputs. These properties characterize the out-

put distribution of PUF instances and give an idea of

the reliability of a PUF class. A PUF class may ver-

ify other properties (Maes, 2012). We focus on the

unclonability and unforgeability properties.

2.2 Security Notions

We use the formal deﬁnitions of unforgeability and

unclonability that have been introduced in the paper of

Armknecht et al. (Armknecht et al., 2016).

We denote by

a Probabilistic Polynomial Time

(PPT) adversary. If

is the security parameter then the

running time of

is polynomial in

. Let

ε: N → R

be a negligible function, i.e. for any polynomial func-

tion

p: N → N

there exists

such that

ε(n) < 1/p(n)

for any

n > n

. The following unforgeability game

states the advantage of an adversary

to guess one

output of a PUF without having access to the device.

We assume that the challenger has access to the man-

ufacturing process and thus can invoke the creation

procedure on a set of parameters param. The adver-

sary can only choose a set of parameters to obtain new

instances from an oracle. Thus, they can get instances

of one PUF class or instances of different PUF classes

depending on the chosen set of parameters. We assume

that there exists a recovery procedure that recovers a

noise-free response from noisy ones. Thus, the adver-

sary is only required to guess a noisy response at a

SECRYPT 2020 - 17th International Conference on Security and Cryptography

280

distance not more than δ

from the correct response.

Set Up.

The challenger selects a manufacturing pro-

cess and initial parameters param. The challenger

sends

,param)

to the adversary

and initial-

izes two counters c

Learning. A

adaptively issues two types of oracle

query: a creation query to create a new instance un-

der some chosen parameters and a response query

to get the output of an instance of their choice.

is allowed to issue at most

creation queries and

response queries.

•

When

issues a creation query with

param

the challenger creates

puf

← CREATE(param)

param

= param

and increments

, or creates

puf

← CREATE(param

)

param

6= param

but is a valid creation parameter and increments

. Otherwise the challenger responds ⊥.

•

When

issues a response query with

(b,i,x

)

the challenger sends

i, j

← puf

)

b = 0

and

i 6 c

or sends

i, j

← puf

)

b = 1

and

i 6 c

Otherwise the challenger returns ⊥.

Guess. A outputs (i

∗

The index

∗

denotes the instance chosen by

such

that

∗

is probably the result of the evaluation of

puf

∗

. We denote by EUF-CICA the Existential Un-

forgeability under Chosen Instance and Challenge At-

tack deﬁned as follows.

Deﬁnition 1

(EUF-CICA)

Let

Adv

euf-cica

A,P

(λ,δ

)

be the

advantage of an adversary

playing the unforgeabil-

ity game. We have Adv

euf-cica

A,P

(λ,δ

) =

Pr [dist(y

∗

,puf

∗

)) 6 δ

∗

∈ X \ X

∗

] −

where

puf

∗

is a PUF instance that has been created

by the challenger in the learning phase,

∗

is the set

of challenges that have been issued for the instance

∗

and

B = {y | y

∗

← puf

∗

) and dist(y

∗

,y) 6 δ

}

is the set of outputs

that are at a distance at most

from puf

∗

A PUF provides

,δ

,ε)

-EUF-CICA security

if for any PPT adversary A we have

Adv

euf−cica

A,P

(λ,δ

) > 0

6 ε(λ).

The adversary wins the game if their guess

∗

belongs

to the set

with probability higher than randomly

picking an element of B.

A stronger notion is unclonability which expresses

the hardness of constructing two PUF instances that

show the same input-output behavior. The unclonabil-

ity game is as follows.

Set Up.

The setup phase is the same as in the unforge-

ability game.

Learning. A

issues oracle queries as in the learning

phase of the unforgeability game.

Guess. A outputs (i

∗

,b, j

∗

The output

∗

,b, j

∗

)

is interpreted as follows:

∗

gives

the index of an instance created under the paramater

param. If

b = 0

then

∗

is the index of an instance

created under the parameter

param

; otherwise

∗

the index of an instance created under the parameter

param

. To win,

should exhibit two clones either

from the same class or from two distinct classes. In

other words, the unclonability should garantee that it

is both hard to construct two clones using the same

set of parameters and to ﬁnd a set of parameters that

enables the construction of clones.

We denote by UUC-CICA the Universal Unclon-

ability security deﬁned by the following.

Deﬁnition 2

(UUC-CICA)

Let

Adv

uuc−cica

A,P

(λ,δ

)

the advantage of an adversary

playing the unclon-

ability game. Let

puf

∗

and

puf’

∗

be the PUF instances

which correspond to the output

∗

,b, j

∗

)

. We

have Adv

uuc−cica

A,P

(λ,δ

) =



∀x ∈ X ,dist(puf

∗

(x),puf’

∗

(x)) 6 δ



A PUF provides

,δ

,ε)

-UUC-CICA if for any

PPT adversary A we have Adv

uuc−cica

A,P

(λ,δ

) 6 ε(λ).

3 GENERAL CONSTRUCTION

In the following, we introduce the PUF-based encryp-

tion scheme which is used to deﬁne a PUF-based white-

box encryption scheme when provided with a white-

box compiler.

3.1 PUF-based Encryption Scheme

In the deﬁnition of a PUF-based encryption scheme

below, the encryption and the decryption algorithms

take three arguments, the additional argument being

the PUF output. We denote by

and

the sets of

plaintexts and ciphertexts, respectively.

Deﬁnition 3

(PUF-based Encryption Scheme (PES))

Let

P = {puf : X → Y }

be a PUF class. A PUF-

based encryption scheme consists of polynomial time

algorithms (KGen, EVAL,Enc,Dec) such that

• KGen

is a probabilistic algorithm which outputs a

key: K ←$ KGen(1

• Eval

is a probabilistic algorithm that evaluates a

PUF instance: y ←$ EVAL(puf, x).

• Enc

is a probabilistic algorithm:

C ←$ Enc(K,y,M).

A White-Box Encryption Scheme using Physically Unclonable Functions

281

• Dec

is a deterministic algorithm:

M ←

Dec(K,y,C).

A PUF-based encryption scheme satisﬁes correct-

ness for an instance puf if

∀M ∈ M

and

∀x ∈ X

Pr [Dec(K,y, Enc(K,y, M)) = M

y ← puf(x) ] = 1.

Deﬁnition 4

(White-Box Compiler)

Let

E =

(KGen,Enc,Dec)

be a symmetric encryption scheme.

A white-box compiler for

is a probabilistic algo-

rithm Comp that outputs a white-box program

of the

cipher for a ﬁxed key K.

•

implements

Enc

then

∀M ∈ M

Pr [P(M) = Enc(K, M)] = 1

. We say that

(KGen,Enc,Dec,Comp)

is a white-box encryp-

tion scheme.

•

implements

Dec

then

∀C ∈ C

Pr [P(C) = Dec(K,C)] = 1

. We say that

(KGen,Enc,Dec,Comp)

is a white-box decryp-

tion scheme.

If Comp is a white-box compiler deﬁned for the PES

of Deﬁnition 3, then the white-box program

is such

that, for any

and

P(y, M) = Enc(K,y,M)

in the

case of a white-box encryption scheme and

P(y,C) =

Dec(K,y,C)

for a white-box decryption scheme. The

PES and the white-box compiler form a PUF-based

white-box encryption scheme (PWE).

3.2 Security Models

We consider the white-box setting and state the security

of a PWE. We consider a white-box implementation of

the encryption algorithm, i.e. the program

outputted

by the white-box compiler implements

Enc

for a

ﬁxed key

. The adversary

is divided into two

adversaries

)

such that

is run on

’s output.

is allowed to make at most

creation queries and

response queries while

is allowed to make at

most q decryption queries.

3.2.1 Unbreakability

In the unbreakability game, we only consider the ad-

versary

whose goal is to recover the secret key

We consider the Chosen-Plaintext Attack (CPA) where

the adversary chooses

plaintexts (and the input

)

and encrypts them with the program

and the Chosen-

Ciphertext Attack (CCA) where they are allowed to

query a decryption oracle with

chosen ciphertexts

(and input

) in addition to

chosen-plaintexts. The

advantage of the adversary

in the UBK-ATK secu-

rity game is the probability that

outputs the key

. As in (Delerabl

ee et al., 2013), the white-box en-

cryption scheme is secure in the sense of UBK-ATK

for

ATK ∈ {CPA,CCA}

, if the advantage of any PPT

adversary is negligible.

Moreover, even if full break is not possible, the

adversary can lift the code and encrypt without know-

ing the key. We deﬁne the notion of lockability to

capture the difﬁculty of executing a lifted white-box

code without a PUF instance.

3.2.2 Lockability

We assume that the adversary has access to the white-

box program

. Their goal is to correctly encrypt a

random plaintext given a random challenge

plays

an EUF-CICA or an UUC-CICA game while the attack

model for the adversary A

is either CPA or CCA.

We deﬁne two security notions, depending on the

attack model used against the PUF: either a forging

attack or a cloning attack.

We write LCK-FORGE for the lockability security

under CPA or CCA which is described by the following

security game.

Set Up.

The challenger selects a manufacturing pro-

cess and initial parameters

param

. They generate

K ←$ KGen(1

)

uniformly at random and compile

P ←$ Comp(K)

. They send

,param,P)

to the

adversary and initializes two counters c

Learning 1. A

issues creation queries and response

queries. As in the unforgeability game, the

challenger creates

puf

← CREATE(param)

puf’

← CREATE(param’)

when receiving cre-

ation queries and sends

i, j

← puf

)

i, j

←

puf

) when receiving response queries.

outputs

∗

)

and sends

∗

)

to the chal-

lenger. The challenger evaluates y ← puf

∗

Learning 2. A

chooses

plaintexts and encrypts

them with

and

∗

. In the CCA model,

is-

sues decryption queries with

chosen ciphertexts

and gets M

← Dec(K,y,C

Challenge.

The challenger draws

M ←$ M \ {M

}

uniformly at random, computes

C ← Enc(K,y,M)

and sends M.

Guess. A

outputs C

∗

Deﬁnition 5

(LCK-FORGE)

Let

be a PUF class

with an intra-distance

. Let

be the PUF-based

white-box encryption scheme. Let

Adv

lck−forge

A,E

(λ,δ

)

be the advantage of an adversary playing the

game above. We have

Adv

lck−forge

A,E

(λ,δ

) =

∗

= C : C

∗

← A

,r,P)

r=(i

∗

)←A

,param)

where

de-

notes the decryption oracle in the CCA model. A

PUF-based white-box encryption scheme

provides

SECRYPT 2020 - 17th International Conference on Security and Cryptography

282

,q,ε

)

-LCK-FORGE security if for any PPT ad-

versary A it holds that:

Adv

lck−forge

A,E

(λ,δ

) 6 ε

(λ).

In the above security game, the adversary is required

to output a PUF challenge

∗

for which they can forge

a valid output

∗

for an instance

puf

∗

. The second

learning phase allows the adversary to interact with a

decryption oracle (in the CCA model). If the attack

model for

is the CPA model, then in learning

is only allowed to choose at most

plaintexts and

to encrypt them with

and

∗

. For both models, the

adversary wins if

is able to forge a valid pair

∗

)

for a chosen instance

∗

or if the pair returned by

not valid but A

guesses C.

Remark 1.

In the CCA model,

can compute

←

P(y

∗

)

and send

to the decryption oracle. Thus,

is able to verify if the guess of

is correct. Other-

wise,

is allowed to restart the learning

and makes

a new guess. This way the attack model is adaptive.

However, the total number of queries made by

still bounded by

and

and the total number of

queries made by

is bounded by

. Consequently,

the advantage of the adversary regarding LCK-FORGE

is the same if the model is adaptive or not.

Theorem 1.

If the PUF class

provides

,δ

,ε)

EUF-CICA security then

provides

,q,ε

)

-LCK-

FORGE security with

• ε

: λ 7→



1 −



· ε(λ) +

for CPA.

• ε

: λ 7→



1 −

−q



· ε(λ) +

−q

for CCA.

Proof.

Let

be the event “

Adv

euf−cica

(λ,δ

) > 0

”.

Adv

lck−forge

A,E

(λ,δ

) =

Pr [C

∗

= C

E ] × Pr [E ] + Pr



∗

= C





× Pr





Since

provides

,δ

,ε)

-EUF-CICA security

then

Pr [E ] 6 ε(λ)

and

Pr [C

∗

= C

E ] = 1

. This re-

ﬂects the fact that once the PUF response is guessed

correctly, the adversary inevitably ﬁnds the correct ci-

phertext. Besides,



∗

= C





in the CPA

model and



∗

= C





−q

in the CCA model.

Adv

lck−forge

A,E

(λ,δ

) 6



1 −



· ε(λ) +

under CPA and,

Adv

lck−forge

A,E

(λ,δ

) 6



1 −

− q



· ε(λ) +

− q

under CCA.

The notion of lockability under cloning attack LCK-

CLONE expresses the situation in which we verify the

lockability except if the adversary exhibits two distinct

instances that have the same input-output behavior.

The security game for LCK-CLONE under CPA or CCA

is described as follows:

Set Up. The set up is the same as in LCK-FORGE.

Learning 1.

The learning phase is as in LCK-FORGE.

outputs (i

∗

,b, j

∗

Learning 2. A

chooses

plaintexts and challenges

and encrypts them with

. In the CCA model,

in addition

issues decryption queries with

chosen ciphertexts

and challenges

and gets

← Dec(K,y

) where y

← puf

∗

Challenge.

The challenger picks

M ←$ M \ {M

}

and

x ←$ X \ {x

}

uniformly at random, computes

C ← Enc(K,y,M)

where

y ← puf

∗

(x)

and sends

(M,x).

Guess. A

outputs C

∗

Deﬁnition 6.

Let

be a PUF class with an intra-

distance

. Let

be the PUF-based white-

box encryption scheme. Let

Adv

lck−clone

A,E

(λ,δ

)

be the advantage of an adversary playing the

game above. We have

Adv

lck−clone

A,E

(λ,δ

) =

∗

= C : C

∗

← A

,r,P)

r=(i

∗

,b, j

∗

)←A

,param)

where

denotes

the decryption oracle in the CCA model. A PUF-based

white-box encryption scheme provides

,q,δ

,ε

)

LCK-CLONE security if for any PPT adversary

holds that: Adv

lck−clone

A,E

(λ,δ

) 6 ε

(λ).

Theorem 2.

If the PUF class

provides

,δ

,ε)

UUC-CICA security then the PUF-based white-box

encryption scheme provides

,q,δ

,ε

)

-LCK-

CLONE security with

• ε

: λ 7→



1 −



· ε(λ)

1/(

−q)

for CPA.

• ε

: λ 7→



1 −

−q



· ε(λ)

1/(

−q)

−q

for CCA.

Proof.

Let

be the event “

dist(puf

∗

(x),puf’

∗

(x)) 6

”. Adv

lck−clone

A,E

(λ,δ

) =

Pr [C

∗

= C

E ] × Pr [E ] + Pr



∗

= C





× Pr





Since,

provides

,δ

,ε)

-UUC-CICA security

then

Pr [E ] 6 ε(λ)

1/(

−q)

and

Pr [C

∗

= C

E ] =



∗

= C





in the CPA model and



∗

= C





−q

in the CCA model. Hence,

Adv

lck−clone

A,E

(λ,δ

) 6



1 −



· ε(λ)

(

−q)

A White-Box Encryption Scheme using Physically Unclonable Functions

283

under CPA and,

Adv

lck−clone

A,E

(λ,δ

) 6



1 −

− q



· ε(λ)

(

−q)

− q

, under CCA.

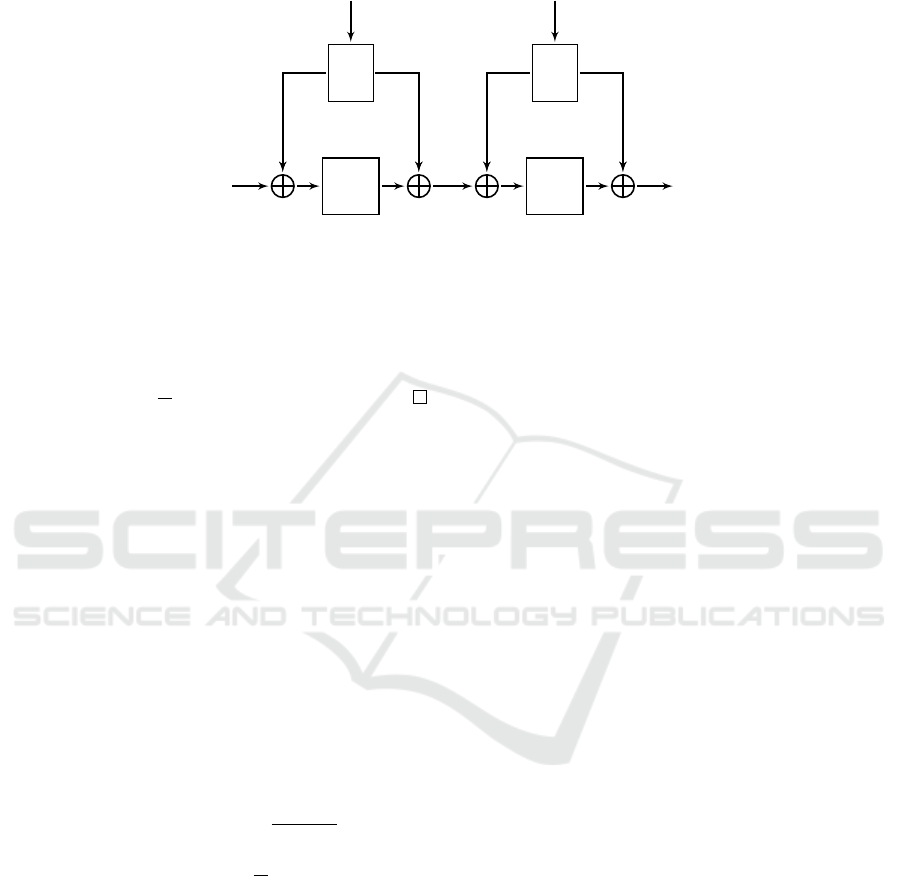
3.3 Construction of a PUF-based Block

Cipher

In this section, we provide one instantiation of the en-

cryption scheme using a tweakable block cipher. A

tweakable block cipher takes three inputs: the plain-

text, the secret key, and a public value called the tweak.

We refer to (Liskov et al., 2002) for more details. Thus,

it matches the Deﬁnition 3 when combined with a PUF

class. We use the

rounds Tweakable Even-Mansour

(

-TEM) of (Cogliati et al., 2015). This construction

applies an almost XOR universal (AXU) hash func-

tion to the tweak value. Since the tweak inputs are

noise-free PUF responses, they are obtained after a

recovery procedure. Thereby, the hash function takes

a noise-free but non-uniform input

and transforms it

to a nearly uniform value xored with the plaintext.

PES with 2 Rounds of TEM.

Let

P = {puf : X →

Y }

be a PUF class. Let

H = {H

: Y → F

}

K∈K

a family of

-uniform and

-AXU hash functions in-

dexed by a set of keys

. Let

Enc : K × Y ×F

→ F

be a

-TEM block cipher (see Figure 1). For any key

K = (K

)

are two hash functions of the

family

and

are two public permutations. For

any PUF response

y ∈ Y

corresponding to a challenge

x ∈ X

, the encryption function is deﬁned, for any plain-

text M ∈ F

, by

Enc(K,y,M) = P

(M ⊕ H

(y)) ⊕ H

(y)

⊕ H

(y)) ⊕ H

(y).

In the same way, the decryption function is deﬁned for

any ciphertext C ∈ F

Dec(K,y,C) = P

−1

(C ⊕ H

(y))

⊕ H

(y) ⊕ H

(y)) ⊕ H

(y).

We denote by

-TEM

(P ) = (F

,Enc,Dec,P )

the constructed PES.

Keyed Hash Functions.

We construct the following

family of keyed hash functions:

Deﬁnition 7.

Let

E : F

× F

→ F

be a block cipher.

Let

H = {H

: (F

)

→ F

}

K∈F

be a family of hash

functions indexed by a set of keys where any hash

function

is deﬁned as follows: for any

x = (x

)

(x) = E

) ⊕ E

)

with

= K ⊗ K

is a mul-

tiplication in the ﬁnite ﬁeld F

Remark 2.

The function

K 7→ K

is a permutation in

, thus E

is a permutation.

We show that the above family of hash functions is

almost uniform and XOR universal.

Deﬁnition 8.

Let

E : F

×: F

→ F

be an

rounds

iterative block cipher and let

be the

-th round

function with a round key

derived from a master key

•

A differential characteristic is a sequence of

r + 1

differences

(∆

,...,∆

)

where

∆

is the difference

between two inputs and

∆

is the output difference.

•

For a key

, the ﬁxed-key differential characteristic

probability

is the probability for a pair of inputs

to follow a given differential characteristic:

= Pr

(X) ⊕ F

(X ⊕∆

) = ∆

,1 6 i 6 r

•

The expected differential characteristic probabil-

ity

is the differential characteristic probability

averaged over all round keys:

π = Pr

X,K

(X) ⊕ F

(X ⊕∆

) = ∆

,1 6 i 6 r

= E

[π

Let

denotes an upper bound on the expected differ-

ential characteristic probability of the block cipher

introduced in Deﬁnition 7.

Theorem 3.

The family of Deﬁnition 7 is

-uniform

and Π-AXU.

Proof.

We ﬁrst prove the XOR universality. Let

x 6=

∈ (F

)

and

b ∈ F

. Without loss of generality,

we assume that

6= x

. Otherwise, interchange the

subscript

with the subscript

in the following. Let

A = {K ∈ F

: H

(x) ⊕ H

) = b}, we have:



(x) ⊕ H

) = b



with



{K,K

: E

) ⊕ E

) = b}



, with

∑

{K : E

) ⊕ E

) = b ⊕ E

) ⊕ E

)}

Since

{K ∈ F

: E

) ⊕ E

⊕ a) = b

6 Π · 2

for any

∈ F

and

K 7→ K

is a bijection then

6 Π · 2

Now, we prove that the family

-uniform.

Let

x ∈ (F

)

and

y ∈ F

. We compute the cardinal-

ity of

A = {K ∈ K : H

(x) = E

) ⊕ E

) = y}

given

x = (x

)

and

. As the probability of pick-

ing randomly a key is equal to 1/2

, it means that the

number of keys verifying properties of

follows a

Poisson distribution with parameter

λ = 1

as it could

SECRYPT 2020 - 17th International Conference on Security and Cryptography

284

y ← puf(x) y ← puf(x)

PUF response PUF response

Figure 1: TEM(P ) construction with 2 rounds and PUF responses as tweak inputs.

be considered as a sum of Bernoulli events with a very

low probability. Thus, it corresponds with the mod-

elling of the law of rare events. For

n = 128

, we obtain

an upper bound equal to 34 for the cardinal of

di-

rectly applying the density of the Poisson law. Thus,

(x) = y] 6

Remark 3

(Estimation of the Probability when

Fixed.)

In the white-box setting, the key

is ﬁxed.

Consequently, we need to estimate the XOR univer-

sality for a ﬁxed key

is an upper bound on

the expected differential characteristic probability of

the block cipher

over all keys. When a key

ﬁxed, we consider the ﬁxed-key differential character-

istic probability

which is the probability that an

input pair

(x,x ⊕ a)

fulﬁlls a differential characteristic

(∆

= a,∆

,...,∆

= b).

Let

N(a,b) =

{x : E

(x) ⊕ E

(x ⊕ a) = b}

, i.e.

N(a,b)

is the number of pairs

(x,x

)

that fulﬁll the

differential characteristic

(∆

= a,∆

,...,∆

= b)

for

a ﬁxed key

. Let

be the probability that all non

trivial characteristics are fulﬁlled by at most

in-

put pairs, i.e.

= Pr

a,b

a6=0

[N(a,b) 6 B]

. According to

(Blondeau et al., 2013):

> 1 −

(n−1)B

(B+1)!

. Hence,

for a ﬁxed key

: if

u 1

then

N(a,b) 6 B

, and

(x) ⊕ E

(x ⊕ a) = b] 6

White-Box Implementation of 2-TEM(P).

We use

the

-bit instantiation of SPNbox (Bogdanov et al.,

2016) as block cipher

. SPNbox-

operates on

t = 16

blocks of

m = 8

bits and applies

R = 10

rounds of the

following transformations:

•

A substitution

γ: F

→ F

applies a S-box

each block as follows:

γ(X) = (S(X

),...,S(X

))

•

A linear transformation

θ: F

→ F

multi-

plies the state

,...,X

)

by a Maximum Dis-

tance Separable matrix as follows:

θ(X) =

,...,X

) · M

where:

= had(0x08,0x16,0x8a,0x01,0x70,

0x8d,0x24,0x76,0xa8,0x91,0xad,0x48,

0x05,0xb5,0xaf,0xf8)

is an Hadamard-Cauchy matrix.

•

A round-dependent transformation

: F

→ F

adds a round-dependent constant to the state as fol-

lows:

(X) = (X

⊕C

,...,X

⊕C

)

for

(r − 1) ·t + i + 1.

For any key

the S-box of the substitution layer is

computed as follows: for any

-bit input

, encrypt

with a small-scale variant of the AES cipher using

as a master key and expanded using the SHAKE

key derivation function. The variant of the AES cipher

is composed of

rounds of the following transfor-

mations: SubBytes, AddRoundKey and MixColumns.

The SubBytes transformation is composed of only one

AES S-box and the Mixcolumns transformation applies

the identity matrix to the state. If the S-box is pre-

computed and implemented by a lookup table then

SPNbox-8 satisﬁes the unbreakability security.

Since

K = (K

)

and

-TEM

(P )

needs four

block cipher calls, the white-box implementation

makes use of four pre-computed S-boxes with

, and K

White-Box Security.

The PWE satisﬁes the UBK-

ATK security, for

ATK ∈ {CPA,CCA}

because of the

unbreakability of SPNbox-

. Regarding the lockabil-

ity security, it is guaranteed by the unforgeability and

unclonability of the PUF instance. Hence, a tight esti-

mation of the security bounds for a speciﬁc PUF class

is necessary to get the security bounds for lockability.

A White-Box Encryption Scheme using Physically Unclonable Functions

285

3.4 Application

Our scheme is designed for exchange of encrypted

data between a trusted server and a client on a mo-

bile device. The server and the client share a secret

key for the encryption: the client is given a white-box

program with a ﬁxed key. In addition, if a secure

PUF exists on the client’s device, it is used to rein-

force the security of the white-box program. Because

of the uniqueness of a PUF instance, an enrollment

phase is needed to “characterize” it. In other words,

the trusted server stores some challenge-response pairs

corresponding to the PUF thanks to an evaluation pro-

gram SECURE.EVAL executed on the client device.

Such an enrollment phase is used for PUF-based au-

thentication. During the enrollment, some helper data

are computed to enable the client to recover the en-

rolled responses from noisy ones. A helper data is

computed by a SECURE.SKETCH procedure and stored

by the server. It is a public side information that en-

ables one to recover a string

from any noisy but

close enough

. Assume that the server sends some

encrypted data to the client and the client needs to

decrypt them. The server randomly picks a pair of

challenge-response and encrypts the data using the

shared key and the PUF response. Then the server

sends the ciphertext together with the challenge and

the helper data to the client. The client evaluates the

PUF instance on the challenge and gets a noisy re-

sponse. Thanks to a recovery procedure REC and the

helper data, the client recovers the correct response

and decrypts the ciphertext. We refer to (Dodis et al.,

2008) for precise deﬁnitions of a secure sketch and a

recovery procedure for noisy data.

REFERENCES

Armknecht, F., Moriyama, D., Sadeghi, A., and Yung, M.

(2016). Towards a uniﬁed security model for physically

unclonable functions. In Topics in Cryptology - CT-

RSA 2016 - The Cryptographers’ Track at the RSA

Conference 2016, volume 9610 of Lecture Notes in

Computer Science, pages 271–287. Springer.

Biryukov, A., Bouillaguet, C., and Khovratovich, D. (2014).

Cryptographic schemes based on the ASASA structure:

Black-box, white-box, and public-key (extended ab-

stract). In Advances in Cryptology - ASIACRYPT 2014

- 20th International Conference on the Theory and

Application of Cryptology and Information Security,

volume 8873 of Lecture Notes in Computer Science,

pages 63–84. Springer.

Blondeau, C., Bogdanov, A., and Leander, G. (2013).

Bounds in shallows and in miseries. In Advances in

Cryptology - CRYPTO 2013 - 33rd Annual Cryptology

Unpredictable and unclonable.

Conference, volume 8042 of Lecture Notes in Com-

puter Science, pages 204–221. Springer.

Bogdanov, A. and Isobe, T. (2015). White-box cryptogra-

phy revisited: Space-hard ciphers. In Proceedings of

the 22nd ACM SIGSAC Conference on Computer and

Communications Security, pages 1058–1069. ACM.

Bogdanov, A., Isobe, T., and Tischhauser, E. (2016). To-

wards practical whitebox cryptography: Optimizing

efﬁciency and space hardness. In Advances in Cryptol-

ogy - ASIACRYPT 2016, Proceedings, Part I, volume

10031 of LNCS, pages 126–158.

Cho, J., Choi, K. Y., Dinur, I., Dunkelman, O., Keller, N.,

Moon, D., and Veidberg, A. (2017). WEM: A new

family of white-box block ciphers based on the even-

mansour construction. In Topics in Cryptology - CT-

RSA 2017 - The Cryptographers’ Track at the RSA

Conference 2017, volume 10159 of Lecture Notes in

Computer Science, pages 293–308. Springer.

Chow, S., Eisen, P. A., Johnson, H., and van Oorschot, P. C.

(2002a). White-box cryptography and an AES imple-

mentation. In Selected Areas in Cryptography - SAC

2002, volume 2595 of Lecture Notes in Computer Sci-

ence, pages 250–270. Springer.

Chow, S., Eisen, P. A., Johnson, H., and van Oorschot, P. C.

(2002b). A white-box DES implementation for DRM

applications. In Security and Privacy in Digital Rights

Management, ACM CCS-9 Workshop, DRM 2002, vol-

ume 2696 of Lecture Notes in Computer Science, pages

1–15. Springer.

Cogliati, B., Lampe, R., and Seurin, Y. (2015). Tweaking

even-mansour ciphers. In Advances in Cryptology -

CRYPTO 2015, volume 9215 of LNCS, pages 189–208.

Springer Berlin Heidelberg.

Delerabl

ee, C., Lepoint, T., Paillier, P., and Rivain, M. (2013).

White-box security notions for symmetric encryption

schemes. In Selected Areas in Cryptography - SAC

2013, volume 8282 of Lecture Notes in Computer Sci-

ence, pages 247–264. Springer.

Dodis, Y., Ostrovsky, R., Reyzin, L., and Smith, A. D. (2008).

Fuzzy extractors: How to generate strong keys from

biometrics and other noisy data. SIAM J. Comput.,

38(1):97–139.

Fouque, P., Karpman, P., Kirchner, P., and Minaud, B. (2016).

Efﬁcient and provable white-box primitives. In Ad-

vances in Cryptology - ASIACRYPT 2016 - Proceed-

ings, Part I, volume 10031 of LNCS, pages 159–188.

Liskov, M. D., Rivest, R. L., and Wagner, D. A. (2002).

Tweakable block ciphers. In Advances in Cryptology -

CRYPTO 2002, 22nd Annual International Cryptology

Conference, volume 2442 of Lecture Notes in Com-

puter Science, pages 31–46. Springer.

Maes, R. (2012). Physically Unclonable Functions: Con-

structions, Properties and Applications. PhD thesis,

Katholieke Universiteit Leuven - Faculty of Engineer-

ing.

SECRYPT 2020 - 17th International Conference on Security and Cryptography

286