FPGA-based McEliece Cryptosystem using Non-linear Convolutional
Codes
Michael Ekonde Sone
College of Technology, University of Buea, Buea, Cameroon
Keywords: McEliece Cryptosystem, Non-linear Convolutional Code, Product Cipher, Generator Matrix, FPGA.
Abstract: The paper reports development of a new version of the McEliece cryptosystem using non-linear convolutional
codes. Cascaded convolutional codes are used to be part of the public key with each stage of the cascade
separated by a product cipher to increase the security level. Cryptanalysis of the new version of the McEliece
cryptosystem is performed using existing attacks of the classical cryptosystem to demonstrate the difficulties
in breaking the new cryptosystem. It is shown that, security levels comparable to the original McEliece
cryptosystem could be obtained by using smaller public key sizes of the new version if multiple stages of the
generator matrix are employed. This aspect makes the new version of the McEliece cryptosystem attractive
in mobile wireless networks since it could be ported onto a single Field Programmable Gate Array (FPGA).
1 INTRODUCTION
The McEliece public key cryptography (PKC) has
received a lot of attention since it is one of the most
attractive options for post-quantum PKC and due to
fewer encryption/ decryption operations compared to
other PKC schemes such as RSA, ECC and ElGamal.
However, low encryption rate and large key size due
to Goppa block codes have motivated major research
efforts targeting the implementation of the McEliece
cryptosystem using alternative codes. Of recent,
convolutional codes have been used as an alternative
in the implementation of the McEliece cryptosystem
(Almeida et al, 2013, 2016 ; Almeida & Napp, 2018;
Moufek & Guenda, 2018; Rosenthal & Smarandache,
1999) . Convolutional codes consider the information
as a whole sequence and better resist decoding attacks
compared to block codes due to the dynamic nature
of the cryptosystem. The output sequence depends on
the current state of the generator matrix, the transition
functions as well as the previous and present input
bits. The major challenge with convolutional coding
remains an efficient decoding method especially with
higher order codes. Decoding methods such as the list
decoding (Zigangirov & Osthoff, 1993), threshold
decoding algorithm (Massey, 1963) and Information
set decoding (Peters, 2010) have been developed. The
most prominent decoding method is the Viterbi
algorithm. The algorithm has the drawback of an
exponential increase in complexity for higher order
codes. Hence, an efficient convolutional
cryptosystem implementation should involve lower
order codes. In (Kumari & Saini, 2016), the authors
presented an efficient method of generating
polynomials for lower order codes using MATLAB
suitable for the Viterbi decoding algorithm.
Existing McEliece cryptosystem implementation
using convolutional codes laid emphasis on basic
ideas and right parameters of convolutional codes
which could be efficient in curbing the attacks of a
classical McEliece cryptosystem (Almeida & Napp,
2018). Aspects such as key size and encryption/
decryption complexity were not addressed.
In this paper, we present the implementation of a
new variant of the McEliece cryptosystem using non-
linear convolutional codes. The number of operations
required to effectively carry out a structural attack or
an information set decoding attack on the new variant
of the McEliece cryptosystem will be used to
establish bounds for the key size. The generator
matrix, G is like the existing convolutional codes used
in the McEliece cryptosystem, the difference in this
new method is that, the generator matrices are
implemented in stages interspaced with product
ciphers. The complexity to decode the ciphertext
increases with the number of stages. Cryptanalysis of
the new version of the McEliece cryptosystem is
performed using existing attacks of the classical
cryptosystem to demonstrate the difficulties in
64
Sone, M.
FPGA-based McEliece Cryptosystem using Non-linear Convolutional Codes.
DOI: 10.5220/0009767000640075
In Proceedings of the 17th International Joint Conference on e-Business and Telecommunications (ICETE 2020) - SECRYPT, pages 64-75
ISBN: 978-989-758-446-6
Copyright
c
 2020 by SCITEPRESS – Science and Technology Publications, Lda. All r ights reserved

breaking the new cryptosystem. In addition, it is
shown that, security levels comparable to the original
McEliece cryptosystem could be obtained by using
smaller public key sizes of the new version if multiple
stages of the same generator matrix are employed.
The aspect of small key sizes makes the new version
of the McEliece cryptosystem attractive in mobile
wireless networks since it could be ported into a
single FPGA. Future research will involve the
application of this novel version of the McEliece
cryptosystem to wireless cooperative networks.
The complete outline of the paper is as follows. In
the next section, a review of non-linear convolutional
cryptosystem is presented (Sone, 2015). The non-
linear convolutional coding is implemented by
inserting product ciphers between conventional
convolutional coding blocks. The classical McEliece
PKC and the new variant of the McEliece PKC based
on the non-linear convolutional codes are presented
in section 3. Section 4 presents the cryptanalysis of
the novel McEliece cryptosystem. The cryptanalysis
is based on assessing the security attacks and the key
size required to curb the attacks. Results and discussion
are presented in section 5. The section presents a
comparative study of the traditional and new variant of
the McEliece cryptosystems with respect to the key
size. Section 6 presents the FPGA implementation of
the new variant of the McEliece cryptosystem. An
overview of wireless networks security attacks is
presented in section 7. Finally, the conclusion and
future work are presented in section 8.
2 NON-LINEAR
CONVOLUTIONAL
CRYPTOSYSTEM
This section reviews the basics of non-linear
convolutional code and the implementation of the
non-linear convolutional encoding/ decoding using
the basic code and product ciphers.
2.1 Non-linear Convolutional Code
Basics
A convolutional code is generated by passing the
information sequence to be transmitted through a
linear finite-state shift register. The shift register
consists of m (k-bit) stages and n linear algebraic
function generators. The n linear algebraic function
generators produce the n output bits for each k-bit
input sequence. Such an encoder produces an (n, k,
m) convolutional code. The function generators are
assembled into a generator matrix (Lathi, 1998). The
generator matrix is specified functionally by using a
set of n vectors, with one vector for each of the n
modulo-2 adders. Each vector has km dimensions and
contains the connections of the encoder to the
modulo-2 adder. For illustrative purposes, a (2, 2, 2)
convolutional code will be used.
The corresponding (2, 2, 2) convolutional encoder is
represented graphically in figure 1.
Figure 1: (2, 2, 2) convolutional encoder.
The elements of the generator matrices of the (2, 2, 2)
convolutional code are given as





















10
11
g ,
00
00
g ,
10
11
g
m,2m,1m,0
(1)
The generator matrix, g
m
can be obtained from the
matrices in (1) and the different states as
































100000
110000
001100
001100
110010
010011
g00
gg0
ggg
g
3
m,0
3
m,1
2
m,0
3
m,2
2
m,1
1
m,0
m
(2)
Coupling of the linear structure in figure 1 onto itself
leads to a cascaded non-linear structure. Meta S-
boxes (or meta substitution) and permutation set are
used to link one linear transducer stage to the next in
the cascade (Sone, 2015). Let the S-box and
permutation set be chosen as shown in table 1.
Table 1: (a) S-box and (b) Permutation set.
(a) (b)
Assuming the initial state for each of the linear
transducer stage to be the first state as shown in figure
1, the initial structure of the cascade using the S-box
and permutation set is as shown in figure 2.
Figure 2: Initial structure of the cascade.
FPGA-based McEliece Cryptosystem using Non-linear Convolutional Codes
65

In figure 2, ‘1’ and ‘2’ at the outputs of the S-box,
indicates the interconnections due to the permutation
set. It is seen in table 1 that, the ‘1’ output from the S-
box is connected to the ‘2’ input of the next stage. The
same applies to the ‘2’ output which is connected to
the ‘1’ input of the next stage.
2.2 Encoding/Decoding using
Non-linear Convolutional Code
The constraint length, L for a (n,k,m) convolutional
code is given as L = k(m-1). The constraint length is
very essential in convolutional encoding since a
Trellis diagram which gives the best encoding
representation populates after L bits. Hence to
encode blocks of n bits, each block must be
terminated by L zeros (0s) before encoding.
For illustrative purposes, a non-linear (4,2,3)
convolutional code will be used to demonstrate
encoding and Viterbi decoding. A possible non-linear
(4,2,3) convolutional code showing mod-2 connect-
ions and the product cipher is shown in figure 3.
Figure 3: 2-stage non-linear (4,2,3) convolutional code.
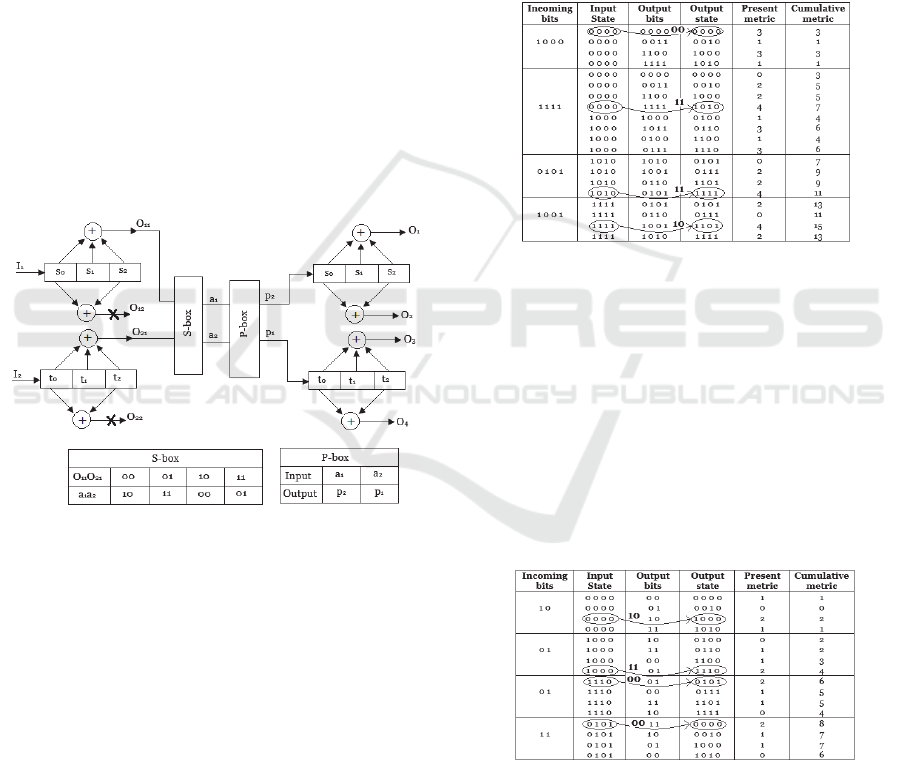
Example: Encode/ Decode the Message M = 10011
 Encoding process
The constraint length, L = k(m-1) = 2(3-1)= 4
Hence 4 zeros will be appended to message M
before encoding. The modified message becomes
M = 10110000
Transition tables for the (4,2,3) convolutional
code shown in the appendix are used to encode the
modified message.
 Using the transition tables, the transmitted
sequence from the 1
st
stage is given as
T
in
= 10 01 01 11
 S-box output is given as S = 00 11 11 01
 P-box output is given as P = 00 11 11 10
 Transmitted sequence into the 2
nd
stage is given
as P = 00 11 11 10
 Using the transition tables, the final transmitted
sequence which is the output bits from the 2
nd
stage is given as T
out
= 0000 1111 0101 1001
 Viterbi decoding process
In performing the Viterbi algorithm, a bit in the
sequence T
out
will be altered. Let the received
sequence be T
R
= 1000 1111 0101 1001 instead of
T
out
= 0000 1111 0101 1001. The Viterbi algorithm
applied to the 2
nd
stage is summarized in table 2.
Table 2: Viterbi algorithm applied to 2
nd
stage of (4,2,3)
code.
The bits above the arrows will constitute the
retrieved sequence from the 2
nd
stage. Hence, the
retrieved sequence is given as, R
1
= 00 11 11 10.
This sequence is fed to the P-box.
 P-box output is given as P1 = 00 11 11 01.
Sequence, P1 is fed to the S-box
 S-box output is given as S1 = 10 01 01 11
Sequence, S1 is fed into the 1
st
stage to retrieve
the final correct message. The Viterbi algorithm
applied to the 1
st
stage is summarized in table 3.
Table 3: Viterbi algorithm applied to 1
st
stage of (4,2,3)
code.
For a good trellis, the final state is the ‘all zero’ state
as seen in the winning path in table 3. The final
received sequence is identical to the original
transmitted message of M = R
final
= 10110000
despite the first bit error. Hence, using the non-
linear convolutional code, the error bit was
identified and corrected.
SECRYPT 2020 - 17th International Conference on Security and Cryptography
66

3 A NEW VARIANT OF THE
MCELIECE CRYPTOSYSTEM
This section explains the implementation of the new
variant of the McEliece cryptosystem using the non-
linear convolutional code in combination with a
scrambled invertible matrix and a permutation matrix.
3.1 The Classical McEliece
Cryptosystem
 Key generation
 Pick a random [n, k, 2t + 1] linear code,
C where n is the number of bits for
codeword; k is the number of message
bits an t is the number of errors the code
can correct
 Compute a k x n generator matrix, G
for C
 Generate a random k x k binary non-
singular (invertible) matrix S
 Generate a random n x n permutation
matrix P
 Compute k x n matrix G = SGP
 Public key is (G, t)
 Private key is (S, G, P, D) where D is the
efficient decoding algorithm
 Encryption
 Message, m  {0, 1}
k
 Random vector, e Є {0, 1}
n
 Ciphertext, c = mG + e
 Decryption
 Ciphertext, c  {0, 1}
n
 Compute CP
-1
= (mS)G + eP
-1
Since (mS)G is a valid codeword for the
chosen linear code and eP
-1
has weight t,
the decoding algorithm, D can be
applied to CP
-1
to obtain c = mS
 Compute m = cS
-1
.
The difficulty of decoding a random encoder, known
to be an NP hard problem underscores the security of
McEliece cryptosystem. This is possible for high
order block codes such as 1024-bit code.
3.2 The New Variant of the McEliece
Cryptosystem
In the new variant of the McEliece cryptosystem
proposed in this research, the key parameters are
follows:
 Public key: (G, t);
 Private key: (S, G, s
box
, p
box
, P, D) where s
box
and p
box
are the additional keys from the
product cipher.
G corresponds to a k x n non-linear convolutional
code that is permutation-equivalent to the chosen
secret key such that P permutes the columns of the
non-linear convolutional code, G and S switches to a
different basis of the same code.
In section 2, aspects of the private key such as the
encoding/ decoding, D; states and transition functions
of generator matrix, G; keys for the product cipher
s
box
, p
box
were presented.
The permutation matrix, P used in this research is
matrix P(D,D
−1
) ∈ 𝔽

developed in (Almeida &
Napp, 2018).
Meanwhile, in classical McEliece cryptosystem,
c = mS is synonymous to scrambling data m to obtain
c where m = cS
-1
is equivalent to descrambling. The
scrambling method will be used for the
implementation of the invertible matrix, S in this
research since it involves shift registers that is easy to
implement in an FPGA.
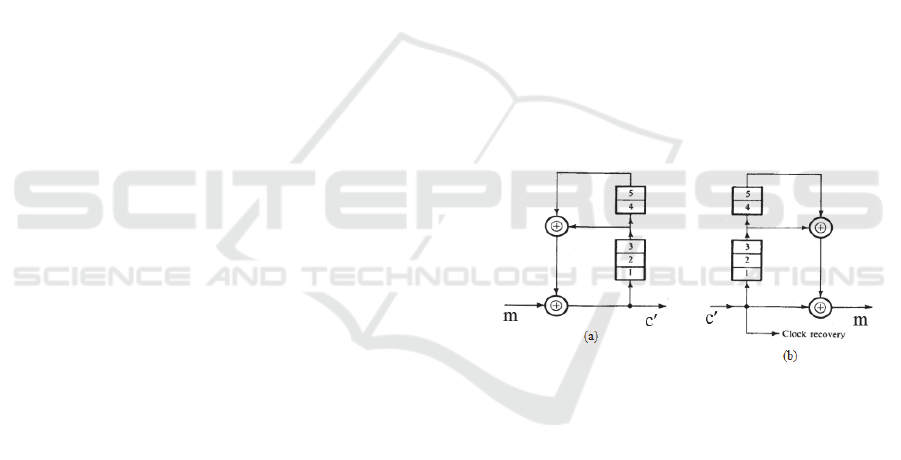
A simple scrambler and descrambler in figure 4
will be used to explain the proposed invertible matrix,
S (Lathi, 1998).
Figure 4: (a) scrambler and (b) descrambler.
The scrambler consists of a feedback shift register
and the matching descrambler has a feedforward shift
register. If m is the input sequence to the scrambler,
then
m  D
3
c  D
5
c = c
where D represents the delay operator, that is D
n
c is
the sequence c delayed by n units. Adding (D
3
 D
5
)
c to both sides of the equation gives
m = c  (D
3
 D
5
) c = [1  (D
3
 D
5
)] c =
(1  F) c
where F = D
3
 D
5
To design the descrambler at the receiver, we start
with c and perform the equation
m = c  F c = c  (D
3
 D
5
) c
FPGA-based McEliece Cryptosystem using Non-linear Convolutional Codes
67

Let message, m = 1010101 be fed into the
scrambler.
Initially c = m, and the sequence m enters the
register and is returned as (D
3
 D
5
)m = Fm through
the feedback path. This new sequence Fm enters the
register and is returned as F
2
m, and so on. Hence
c = m  Fm  F
2
m  F
3
m  . . .
Recognizing that
F = D
3
 D
5
we have
F
2
= (D
3
 D
5
) (D
3
 D
5
) = D
6
 D
10
 D
8

D
8
= D
6
 D
10
Since D
8
 D
8
= 0
Similarly,
F
3
= (D
6
 D
10
) (D
3
 D
5
) = D
9
 D
11
 D
13

D
15
and so on.
Hence
c = (1  D
3
 D
5
 D
6
 D
9
 D
10
 D
11

D
13
 D
15
 . . .)m
Because D
n
m is simply the sequence m delayed by n
bits, various terms in the preceding equation
correspond to the following sequences:
m = 1 0 1 0 1 0 1
D
3
m = 0 0 0 1 0 1 0 1 0 1
D
5
m = 0 0 0 0 0 1 0 1 0 1 0 1
D
6
m = 0 0 0 0 0 0 1 0 1 0 1 0 1
D
9
m = 0 0 0 0 0 0 0 0 0 1 0 1 0 1
c = 1 0 1 1 1 0 0
It is worth noting that, the string c is calculated
vertically using mod-2 arithmetic and input sequence,
m has 7 digits hence only 7 digits of the scrambler
output are retained.
When sequence c is applied to the input of the
descrambler, the output is the original sequence, m
m = (1  D
3
 D
5
) c
c = 1 0 1 1 1 0 0
D
3
c = 0 0 0 1 0 1 1 1 0 0
D
5
c = 0 0 0 0 0 1 0 1 1 1 0 0
mod-2 arithmetic gives the 7-bit sequence 1010101
which is identical to the input sequence m = 1010101
Based on the afore-mentioned analysis, a k x k
invertible matrix, S and the scrambled message c
could be deduced from a k-bit message fed into the
scrambler as follows:
 Each row of the k x k matrix, S contains
elements of the shifted message, m deduced
from the scrambler
 Each bit of the scrambled message, c is
computed from the sum of each column of
the k x k matrix.
Hence the k x k matrix, S of the scrambler in figure 4
is given as
(3)
Similarly, for the descrambler, the matrix S
-1
and the
original message, m are obtained as follows:
 Each row of the matrix, S
-1
contains
elements of the shifted scrambled message,
c deduced from the descrambler
 Each bit of the message, m is computed from
the sum of each column of the matrix, S
-1
Hence the matrix, S
-1
of the descrambler in figure 4 is
given as
(4)
4 CRYPTANALYSIS
The security of the cryptosystem is based on two
computationally hard problems namely, exhaustive
search of the key space and maximum-likelihood
decoding (syndrome decoding). Therefore, the two
types of attacks, which are principally structural and
decoding, will be the basis of the cryptanalysis of the
new variant of the McEliece cryptosystem. In this
section, cryptanalysis will explore the additional
security due to the non-linear convolutional
cryptosystem and not the entire new variant which
involves also the invertible matrix, S and the
permutation matrix, P. Hence, the cryptanalysis will
establish baseline values for the key sizes for the new
variant of the McEliece cryptosystem.
4.1 Structural Attack
Structural attacks against the McEliece cryptosystem
involve recovering of the secret key from the public
key, G in order to determine an equivalent code from
c generated by G. It is worth noting that, in classical
convolutional codes, G is a generator matrix
SECRYPT 2020 - 17th International Conference on Security and Cryptography
68

characterised by the states of the mod-2 adders and
the transition functions, whereas in the new variant of
the McEliece cryptosystem, G is a generator matrix
that is coupled to the product cipher. Hence, in
addition to the states and transition functions of the
generator matrix, the combinations in the S-boxes and
P-boxes must be considered.
Therefore, a successful structural attack on the
new variant of the McEliece cryptosystem should
require a minimum number of plaintext – ciphertext
pairs in order to reveal the following parameters:
 States and transition functions of the
generator matrix;
 Bit shuffling and permutation combinations
of the S-box and P-box.
4.1.1 States and Transition Functions
Generally, a (k, k, m) convolutional transducer with q
states and having p blocks of input vector, u, will have
the generator matrix given as (Biggs, 2008)
(5)
Gaussian elimination attack could be effectively
mounted on the generator matrix to reveal all the
states of the cryptosystem (Biggs, 2008). The attack
is based on forming simultaneous equations using a
(k, k, m) convolutional code function, t given by
t(u) = u * g
ixj
(6)
where u is a row vector of message bits and g
ixj
is a
generator matrix. To illustrate the principle involved
in this attack, the (2, 2, 2) cryptosystem in section 2.1
with three states will be used. This simple
cryptosystem has a readable generator matrix and the
analysis will be extended to a general case of a (k, k,
m) cryptosystem with q states.
Consider the (2, 2, 2) cryptosystem with three
states as follows:





















10
11
g ,
00
00
g ,
10
11
g
0
2
0
1
0
0





















11
11
g ,
00
00
g ,
10
11
g
1
2
1
1
1
0





















11
01
g ,
00
00
g ,
10
11
g
2
2
2
1
2
0
and a proposed transition function, f given in table 4.
Table 4: Transition table for (2, 2, 2) cryptosystem.
With respect to the (2, 2, 2) cryptosystem, using p =
5 blocks of input, the generation matrix becomes

















4
0
4
1
3
0
4
2
3
1
2
0
3
2
2
1
1
0
2
2
1
1
0
0
10
g
gg
ggg
ggg
ggg
(u)g
(7)
The intruder will have to determine 48 unknown
matrix elements in the matrix
(u)g
'
10
. The unknown
generator matrix is given as
(8)
Let (u
1
, v
1
) =

 


1 0 0 1 1 0 0 0 1 0 , 0 0 1 1 1 1 0 0 1 0
be plaintext – ciphertext pair equivalent to 5 blocks
of 2-bit input. By applying Gaussian elimination
attack (Sone, 2015) to the unknown matrix in (7) the
intruder obtains the following matrix

































10
11
0010
0011
110010
010011
110010
110011
110010
010011
(u)g
'
10
(9)
Close examination of
(u)g
'
10
in (9) shows that
(u)g
'
10
contains two distinct states. One of the states
is given by columns 5 and 6 (or equivalently by
columns 9 and 10) and the other state is given by
columns 7 and 8. The third state could be found by
using another plaintext-ciphertext pair. Let (u
2
, v
2
) =
FPGA-based McEliece Cryptosystem using Non-linear Convolutional Codes
69

  
1 0 0 1 0 0 1 0 0 1 , 0 0 1 0 1 0 1 0 1 1
be a second
plaintext-ciphertext pair used by the attacker.
Applying Gaussian elimination attack, the unknown
matrix becomes

































10
11
0010
0011
100010
110011
110010
110011
110010
010011
(u)g
'
10
(10)
(u)g
'
10
in (10) reveals the last state of the
cryptosystem in columns 9 and 10, namely


























10
11
,
00
00
,
10
11
Thus, by using two plaintext-ciphertext pairs, the
states of the cryptosystem are found, and the
cryptosystem is partially broken since the remaining
private keys, namely the transition functions and keys
used in product cipher also need to be unveiled.
Let the state


























11
01
,
00
00
,
10
11
be denoted as i
1
, the state


























11
11
,
00
00
,
10
11
be denoted as i
2
and the state


























10
11
,
00
00
,
10
11
as i
3
.
In a convolutional cryptosystem, the private
parameter f compares the present state and the input
in order to output the next state of the cryptosystem.
In the generator matrix,
(u)g
'
10
in (9) the transitions
are i
1
 i
2
 i
1
and the input vector has u
1
[5, 6] = [1
1]. Using (7),
11
'
101
v )(ug u 
, this implies
f
1
(i
1
, u
1
[5, 6] ) = f
1
(i
1
, [1 1] ) = i
2
(11)
where
8] [7, g i
'
102

. Also
f
2
(i
2
, u
1
[7, 8] ) = f
2
(i
2
, [1 1] ) = i
1
(12)
where
10] [9, g i
'
101

Similarly, the transition of
(u)g
'
10
in (8) are i
1
 i
2
 i
3
and
22
'
102
v )(ug u 
.
Using u
2
[5, 6] = [0 1], this will generate columns 7
and 8 from columns 5 and 6 in the generator matrix
(u)g
'
10
, that is
f
3
(i
1
, [0 1] ) = i
2
(13)
and
f
4
(i
2
, [0 1] ) = i
3
(14)
Hence using ten plaintext – ciphertext pairs, all the
states of the cryptosystem are revealed and four
functions f
1
, f
2
, f
3
, f
4
out of the twelve values of the
private parameter f are revealed. However, by using
additional twenty plaintext-ciphertext pairs, the
remaining eight values of the private parameter f are
revealed. Hence at least thirty plaintext-ciphertext
pairs are required for all values of parameter f and
states to be revealed.
Generally, for a (k, k, m) cryptosystem with q
states and p blocks of message bits, each matrix g
kp
(u)
reveals at most p – k – 1 values of f. Since there will
be (q . 2
k
) values of f, where q is the number of states,
the minimum number of plaintext-ciphertext pairs (u,
v) required to reveal all values of private parameter f
and the states is given as
N
1
=
1 - k - p
k
2 . q
(15)
Hence, total number of plaintext-ciphertext pairs
required,
N
T1
= kpN
1
(16)
For the (2,2,2) convolutional code
N
1
= 3x2
2
/ (5 – 2- 1) = 3 and N
T1
= 2x5x3 = 30 pairs
Therefore, for a successful structural attack for a
classical convolutional code, G the total number of
representation code which the attacker has to compare
to ciphertext c
 generated by G has to be N
T1
for an
(n,k,m) code with q states.
4.1.2 Shuffling Boxes and Permutation Sets
To analyse all the permutations, the minimum
number of plaintext – ciphertext pairs required for an
(n,k,m) code with p blocks of k-bit input is
N
2
= pk! (17)
In addition, to analyse all the different 2-bit
combinations in the s-boxes, the minimum number of
plaintext – ciphertext pairs is given as
N
3
= 2
2k
(18)
SECRYPT 2020 - 17th International Conference on Security and Cryptography
70

Hence, for a successful structural attack for either
 one stage or
 multiple stages with the same generator
matrix and product cipher
of the new non-linear convolutional code, G the
total number of representation code which the
attacker must compare to ciphertext c
 generated by
G
 has to be N
T
for an (n,k,m) code with q states and
is given as
𝑁

𝑝𝑘! .2

.
.


(19)
For µ stages of the new variant of the McEliece
cryptosystem using stages with different
configuration, the total number of representation code
which the attacker has to compare to ciphertext c

generated by G
 has to be N
Total
for an (n,k,m) code
with q states and is given as
𝑁

 𝑝𝑘! .2

.
.




(20)
4.2 Decoding Attack
A decoding attack consists of decoding the
intercepted ciphertext. The cost of the attack depends
on the parameters of c
 namely, length, dimension and
error-correcting capability since the underlying code
and c are equivalent.
If a message of length n bits is received, then the
possible number of codewords are 2
n
.
For an (n,k,m) convolutional code, only 2
kL
codewords are valid of the possible 2
n
. The Viterbi
algorithm applies the maximum-likelihood principles
to limit the comparison to 2
kL
surviving paths instead
of checking all the paths where L = constraint length
= k(m-1) .
For µ stages of the new variant of the McEliece
cryptosystem using non-linear convolutional codes,
the total number of operations the attacker must
perform in order to decode the ciphertext has to be
N
Tot
for an (n,k,m) code with q states and is given as
𝑁



𝑝𝑘! .2

. 2



(21)
Note that, in establishing (21) the product cipher
was used in conjunction with the Viterbi algorithm.
5 RESULTS AND DISCUSSION
There are several ways to attack the McEliece
cryptosystem. In this section, we shall analyse the
structural and decoding attacks using appropriate
convolutional codes and compare the results to the
baseline parameters of the original McEliece
cryptosystem.
Original parameters n=1024, k =524, t=50,
suggested by McEliece in (McEliece, 1978) are now
considered insecure, as they only offer approximately
50-bit security (Bernstein et al, 2011). There is no
clear consensus on recommended parameters for
MECS for various typical security levels. There have
been various theoretical articles suggesting and
analysing security of MECS parameters (McEliece,
1978; Bernstein et al, 2011; Biswas & Sendrier, 2008;
Eisenbarth et al, 2009).
In this research, we shall consider the baseline
parameters n=1024, k =524, t=50 as the basis for
comparison with the new variant of the McEliece
cryptosystem. It is worth noting that, the expressions
deduced in section 4 are baseline number of
operations required for the structural and decoding
attacks since only the non-linear convolutional code,
G was considered instead of the entire public key G

= SGP.
5.1 Appropriate Polynomials
There are many choices for polynomials for any m
order code where m is the number of registers for an
(n,k,m) code. The polynomials do not all result in
output sequences that have good error protection
properties. Petersen and Weldonís book contain a
complete list of these polynomials (Peterson &
Weldon, 1972) and good polynomials are found from
this list usually by computer simulation/MATLAB
(Arasteh, 2006). There is no known constructive way
for selection of generator polynomials, however a
convolutional code can be analysed to find its
distance properties. A good convolutional code has
large free hamming distance (Kumari & Saini, 2016).
Existing works on McEliece cryptosystem based
on convolutional codes used high order convolutional
codes such as (305,150,4), (570,421,3) and
(284,71,5) (Moufek & Guenda, 2015). Such high
order codes are difficult to implement in hardware
and the decoding process is quite cumbersome.
Hence, low order codes developed in (Kumari &
Saini, 2016) will be adopted.
5.2 Structural Attacks
In the general case, the structural attack quickly
becomes infeasible for any reasonable choice of
parameters for the Goppa code (Loidreau & Sendrier,
2001). For the original McEliece parameters with
codeword, n = 1024, message bits, k = 512 and error-
FPGA-based McEliece Cryptosystem using Non-linear Convolutional Codes
71

Table 5: Total number of corresponding representation code, N
Total
.
(n,k,m)
convolutional
code
Octal value of
generator matrices
Error-correcting
capability, t
N
Total
p
=10;
µ
=15
p
=20;
µ
=10
p
=15;
µ
=10
(3,1,3)
6,5,7
10 errors
2
367
2
637
2
429
3,4,7
7,6,5
20 errors
5,7,2
(3,1,4)
17,15,3
20 errors 2
382
2
647
2
439
16,13,15
Table 6: Total number of corresponding representation code, N
Tot
.
(n,k,m)
convolutional
code
Octal value of
generator
matrices
Error-
correcting
capability, t
N
Total
p
=5;
µ
=6
p
=10;
µ
=2
p
=8;
µ
=4
(3,1,3)
6,5,7
10 errors
2
64
2
51
2
75
3,4,7
7,6,5
20 errors
5,7,2
(3,1,4)
17,15,3
20 errors 2
70
2
53
2
80
16,13,15
correcting capability, t = 50, this mounts up to
roughly 2
461
total number of representation code
which the attacker has to compare to ciphertext c

generated by G
 (Loidreau & Sendrier, 2001). Using
low order codes developed in (Kumari & Saini,
2016), (20) is used to compute N
Total
deduced in
section 4.1 and results compared to 2
461
obtained
using the original McEliece cryptosystem. The results
for the best generator polynomials in terms of
performance for code rate 1/3 are summarized in table
5 for appropriate number of blocks, p, number of
states, q = 2
m
and number of stages, µ in the non-
linear cascaded encoder. Appropriate values for p, q
and μ which give N
Total
comparable to 2
461
are used.
Hence, using low order codes there is the
possibility of attaining high security levels
comparable to the original 1024-bit McEliece
cryptosystem if appropriate values of the number of
states of the non-linear convolutional code and
number of blocks for k-bit input are chosen as shown
in table 5. As mentioned earlier, the values displayed
in table 5 are baseline number of operations required
for the structural attack since only the non-linear
convolutional code, G was considered instead of the
entire public key G
 = SGP. Hence, higher values of
N
Total
compared to those displayed in table 5 could be
obtained using G
 for the same values of p, q and µ.
5.3 Decoding Attacks
A decoding attack consists of decoding the
intercepted ciphertext. Since the underlying code and
c
 are equivalent, they have the same error-correcting
capability. Thus, the cost of the attack depends only
on the parameters of c
– its length, dimension and
error-correcting capability. When the length is n =
1024, the dimension is k = 524 and the error-
correcting capability is t = 50, decoding one word
requires 2
64
binary operations (Loidreau, 2000).
Similarly, using low order codes, (21) is used to
compute N
Tot
deduced in section 4.2 and results
compared to 2
64
obtained using the original McEliece
cryptosystem. The results are summarized in table 6
for appropriate number of blocks, p, number of states,
q = 2
m
and number of stages, µ in the non-linear
cascaded encoder.
Hence, using low order codes there is the
possibility of attaining high security levels with N
Tot
≥ 2
64
for the new variant of the McEliece
cryptosystem based on the non-linear convolutional
code as shown in table 6.
SECRYPT 2020 - 17th International Conference on Security and Cryptography
72

6 FPGA IMPLEMENTATION
A good overview of the existing hardware
implementations of the McEliece cryptosystem can
be found in (Repka & Cayrel, 2014). Most of the
implementations require external memory for both
the public and private key structures. In (Shoufan et
al, 2009), the authors implemented a MECS with n =
2048, t = 50 in a Virtex 5 FPGA using 84% of slices
and 50% of BRAMs (2700 Kb).
The implementation of the new variant of the
McEliece cryptosystem is ported onto a Virtex 4
FPGA and the architecture has the following features:
 An instantiated encryption package;
 An instantiated decryption package;
 A finite state machine;
 An instantiated look-up table used in the
Viterbi decoding process.
An important aspect in FPGA-based MECS is to
obtain synthesizable architectures from the multi-
dimensional arrays, that is, arrays with more than one
index such as matrices. Multi–dimensional arrays are
not allowed for hardware synthesis. One way around
this, is to declare two one–dimensional array types.
This approach is easier to use and more representative
of actual hardware. The VHDL code used in this
research to declare the two one–dimensional array
types for 256x256 matrix is shown in figure 5.
Figure 5: VHDL code for synthesizable 256 x 256 matrix.
The device utilization summary for a (3,1,3) non-
linear convolutional code MECS for number of
blocks, p = 15 and number of stages, µ = 10 is as
follows:
- Number of slices: 66816 out of 89088 75%
- Number of slice Flip flops: 124720 out of 178176
70%
7 WIRELESS NETWORKS
SECURITY ATTACKS
Threats that violate the security criteria of wireless
networks are generally called security attacks. The
main attacks are impersonation, eavesdropping,
Denial of Service and Sensing (DoSS), sybil, node
capture, selective forwarding, and various routing
attacks. Some of these attacks which are related to the
confidentiality property of secure communication
could be circumvented using the new variant of the
McEliece cryptosystem. McEliece based digital
signature scheme when implemented using the new
variant, could be used to curb other security attacks
which are related to authentication of the wireless
network nodes. It is widely believed that, code-based
cryptosystem do not allow practical digital signatures.
However, McEliece based digital signature scheme
has been proposed in (Courtois et al, 2001). Future
research work will implement a McEliece based
digital signature scheme using the new variant in
order to curb the above-mentioned attacks in wireless
cooperative networks.
8 CONCLUSION
In this paper, a new variant of the McEliece
cryptosystem using non-linear convolutional codes is
proposed. The rationale in designing the new variant
is to establish key sizes which could enable
implementation of the McEliece cryptosystem in a
single FPGA device with ultimate application in
mobile wireless communication. The new variant of
the McEliece cryptosystem is implemented using
non-linear convolutional codes, a scrambled matrix
and a permutation matrix. The non-linear
convolutional code is a combination of the
conventional convolutional code and product ciphers.
The baseline key sizes used in the implementation
depends on the number of blocks of the k-bit input,
the number of stages in the n-cascaded non-linear
convolutional cryptosystem and the number of states
in the generator matrices. The results of this research
show that, small key sizes used to establish the
matrices in the McEliece cryptosystem could be
attained for 15 blocks of k-bit input and 10 stages of
cascaded convolutional codes to prevent structural
attacks and 5 blocks of k-bit input and 6 stages of
convolutional codes to prevent decoding attacks. The
entire scheme was implemented in a Virtex-4 FPGA
to circumvent the key management drawback
associated with the additional keys due to the product
ciphers.
Future research will focus on two fundamental
problem areas that must be addressed if wireless
networks such as cooperative networks are to have
security comparable to traditional networks. These
areas are:
FPGA-based McEliece Cryptosystem using Non-linear Convolutional Codes
73

 Trust establishment, key management and
membership;
 Network availability and routing security
The new variant of the McEliece cryptosystem will
be used to explore these problem areas by
implementing efficient encryption and authentication
schemes. The implementation will consider the
specificities of wireless cooperative networks such as,
limited energy; limited memory; transient
connectivity and availability; shared physical
medium amongst others.
REFERENCES
Almeida, P., Napp, D., Pinto, R., 2013. A new class of
superregular matrices and MDP convolutional codes. In
Linear Algebra and its Applications 439 (7), 2145–
2157.
Almeida, P., Napp, D., Pinto, R., 2016. Superregular
matrices and applications to convolutional codes. In
Linear Algebra and its Applications 499, 1–25.
Almeida, P., Napp, A.D., 2018. A new class of
convolutional codes and its use in the McEliece
Cryptosystem. In ArXiv, vol. 1804.08955
Moufek, H., Guenda, K., 2018. A new variant of the
mceliece cryptosystem based on the smith form of
convolutional codes. In Cryptologia 42 (3), 227–239.
Rosenthal, J., Smarandache, R., 1999. Maximum distance
separable convolutional codes. In Appl. Algebra Engrg.
Comm. Comput. 10 (1), 15–32.
Zigangirov, K., Osthoff, H., 1993. Analysis of global list
decoding for convolutional codes. In European
Transactions on Telecommunications 4 (2), 165–173.
Massey, J., 1963. Threshold decoding. MIT Press,
Cambridge, Massachusetts.
Peters, C., 2010. Information-set decoding for linear codes
over f q. In: Sendrier, N. (Ed.), Post-Quantum
Cryptography. Springer Berlin Heidelberg, Berlin,
Heidelberg, pp. 81–94.
Kumari, D., Saini, M. L., 2016. Design and Performance
Analysis of Convolutional Encoder and Viterbi
Decoder for Various Generator Polynomials. In Int.
Journal of Engineering Research and Applications. Vol.
6, Issue 5, (Part - 2) May 2016, pp.67-71
Sone, M.E., 2015. Efficient Key Management Scheme To
Enhance Security-Throughput Trade-Off Performance
In Wireless Networks. In Proc. Science and Information
Conference (SAI), London, UK, July 28-30 2015, pp.
1249 – 1256
Lathi, B. P., 1998. Modern Digital and Analog
Communication Systems. 3
rd
edition. Oxford
University Press
Biggs, N. L., 2008. Codes: An Introduction to Information
Communication and Cryptography. Springer – Verlag
Berlekamp, E. R., 1974. Key papers in the Development of
Coding Theory. In IEEE Press, New York.
P. Loidreau, P., Sendrier, N., 2001. Weak keys in the
McEliece public-key cryptosystem. In IEEE
Transactions on Information Theory, 47(3):1207–1211.
Loidreau, P., 2000. Strengthening McEliece Cryptosystem.
Springer-Verlag Berlin Heidelberg.
McEliece, R. J., 1978. A public-key cryptosystem based on
algebraic coding theory. In DSN Progress Report 42,
114–116.
Bernstein, D. J., Lange, T., PETERS, C., 2011. Smaller
decoding exponents: Ball-collision decoding, in:
Advances in Cryptology. In CRYPTO ’11, 31st Annual
Cryptology Conf., Santa Barbara, CA, USA, 2011, (P.
Rogaway, ed.), Lecture Notes in Comput. Sci., Vol.
6841, Springer, Berlin, pp. 743–760.
Bernstein, D. J., Lange, T., Peters, C., 2008. Attacking and
defending the McEliece cryptosystem, in: Post-
Quantum Cryptography. In 2nd Internat. Workshop -
PQCrypto ’08 (J. Buchmann et al., eds.), Cincinnati,
OH, USA, 2008, Lecture Notes in Comput. Sci., Vol.
5299, Springer, Berlin, pp. 31–46.
Biswas, B., Sendrier, N., 2008. McEliece cryptosystem
implementation: theory and practice, in: Post-Quantum
Cryptography. In 2nd Internat. Workshop—PQCrypto
’08, Cincinnati, OH, USA, 2008 (J. Buchmann et al.,
eds.), Lecture Notes in Comput. Sci., Vol. 5299,
Springer, Berlin, pp. 47–62.
Eisenbarth, T., G¨Uneysu, T., Heyse, S., Paar, C., 2009.
McEliece for embedded devices. In Cryptographic
Hardware and Embedded Systems—CHES ’09, 11th
Internat. Workshop Lausanne, Switzerland, 2009 (Ch.
Clavier et al., eds.), Lecture Notes in Comput. Sci., Vol.
5747, Springer, Berlin, 2009, pp. 49–64.
W.W. Peterson, W. W., Weldon, Jr., E. J., 1972. Error
Correcting Codes. 2nd Edition Cambridge, MA: The
MIT Press.
Arasteh, D., 2006. Teaching Convolutional Coding using
MATLAB in Communication Systems Course. In
Proceedings of the 2006 ASEE Gulf-Southwest Annual
Conference Southern University and A & M College.
Moufek, H., Guenda, K., 2015. McEliece Cryptosystem
Based on Punctured Convolutional Codes and the
Pseudo-Random Generators. In ACM Communications
in Computer Algebra, vol. 49, No.1,
Repka, M., Cayrel, P. L., 2014. Cryptography based on
error correcting codes: a survey. In Multidisciplinary
Perspectives in Cryptology and Information Security,
IGI Global, pp. 133–156.
Shoufan, A., Wink, T., Molter, H. G., Huss, S. A., Strenzke,
F., 2009. A novel processor architecture for McEliece
cryptosystem and FPGA platforms. In
ApplicationSpecific Systems, Architectures and
Processors—ASAP ’09, 20th IEEE Internat. Conf.,
Boston, MA, IEEE, pp. 98–105.
Courtois, N., Finiasz, M., and Sendrier, N., 2001. How to
achieve a McEliece-based digital signature scheme. In
ASIACRYPT 2001, Springer-Verlag, 2001, pp. 157-
174
SECRYPT 2020 - 17th International Conference on Security and Cryptography
74

APPENDIX
Transition Tables
FPGA-based McEliece Cryptosystem using Non-linear Convolutional Codes
75