Last Mile Delivery with Lockers: Formulation and Heuristic

Willian Jorge Pereira Oliveira

and Andr

e Gustavo dos Santos

Universidade Federal de Vic¸osa, Vic¸osa, Brazil

Keywords:

Combinatorial Optimization, Vehicle Routing, Facility Location, Location Routing Problem, Last Mile

Delivery.

Abstract:

The creation of efﬁcient routes is essential for different areas having several practical applications mainly in

the transport of goods. With the growth of e-commerce and consequently the increase in demand for delivery

to end users, minimizing costs in the delivery process has gained more importance, especially the last mile

stage. It is in this context that the use of lockers emerges to optimize last mile deliveries. Lockers have

compartments of different sizes, with self-service interface and they can be positioned in supermarkets, parks

and other areas that are of interest to customers. The problem addressed in this work is to determine the

positioning of the lockers and the necessary routes to supply them and to serve the remaining customers. We

present a mathematical model to deﬁne the problem, but due to the complexity of the problem obtaining a

solution can be very expensive and require a lot of computational effort, therefore we present a heuristic,

based on Variable Neighborhood Descent (VND), using a greedy construct inspired by the Clark & Wright

savings method. By comparing the results of the heuristic with the Gurobi optimizer, we conclude that the

heuristic is capable of obtaining competitive solutions in less time than the exact methods.

1 INTRODUCTION

The creation of routes and facilities allocation have

been the focus of studies for a long time due to its

applicability in different areas. Several characteris-

tics can be explored in these problems, such as the

homogeneity of the vehicle ﬂeet to be used, deliv-

ery time constraints, among others. The growth of

e-commerce in recent years and, consequently, the de-

mand for delivery to customers, turned the efﬁcient

routes planning an increasingly important problem.

Due to the worldwide urbanization trend, trafﬁc prob-

lems have increased. There are several challenges

to deal with the delivery of goods, among them the

last mile problems have gained more attention, mainly

due to the trafﬁc of large centers.

The last mile step consists of distributing products

from the distribution center to ﬁnal consumers. This

step may have different characteristics from the rest

of the delivery process and that is why it is necessary

to study it separately.

The problem addressed in this work assumes the

inclusion of lockers as an alternative to reduce costs

in last mile deliveries. Lockers are kiosks with com-

partments accessed by self-service interface that can

https://orcid.org/0000-0002-6377-0809

be used to store the goods of customers until they can

collect them, reducing completely the fail to deliver-

ing caused by the absence of the customer. The model

proposed deﬁnes the problem mathematically and a

heuristic is suggested to obtain satisfactory solutions

to the problem. In the next section we detail the use of

lockers with real-world examples and related works in

the literature.

2 THE PROBLEM AND ITS

IMPORTANCE

There are several challenges in last mile deliveries.

Among them, we can highlight the increasing in con-

gestion in large centers, the increasing in pollution,

the demand of the consumer in relation to services,

in addition to restrictions, such as the time window

available for delivery. The use of lockers has been

shown as an alternative to deal with such challenges

due to the ﬂexibility of the collection and supply

schedule. The use of several shifts of the same vehi-

cle can help to reduce the size of the ﬂeet. Song et al.

(2009) shows that the use of lockers generates savings

in the last mile stage, mainly due to the repeated de-

liveries that need to be made when the consumer is

460

Oliveira, W. and Santos, A.

Last Mile Delivery with Lockers: Formulation and Heuristic.

DOI: 10.5220/0009580004600467

In Proceedings of the 22nd International Conference on Enterprise Information Systems (ICEIS 2020) - Volume 1, pages 460-467

ISBN: 978-989-758-423-7

not at the address to receive your order.

Lockers are collection points, where goods are

available for a certain period of time and users can

collect them on an appropriate time. User interaction

with the locker is done through a self-service interface

that requires user authentication to ensure the security

of orders.

Lockers can be located anywhere that facilitates

their access, such as shopping malls, restaurants, gas

stations and also in residential areas as long as there

is demand from customers.

The installation of the locker in places that have

parking, toilets, among other facilities, helps in pop-

ularizing the locker. It can also bring advantages to

existing businesses close to the locker, as the circula-

tion of customers can generate consumption and con-

sequently proﬁt for traders.

The location is the most important and chal-

lenging feature of the implementation of the self-

collection, because, in addition to the investment in

the construction of the locker, it is essential for its

popularization. In this work, we consider that each

locker has a coverage distance, that is, we consider

that users with addresses in the coverage area would

accept that their orders were delivered to the locker.

Wang et al. (2017) highlight the closure of sev-

eral lockers in Singapore between 2015 and 2017, the

main indication being that the location of the lock-

ers did not favor its popularization. The Locker Al-

liance (LA) was proposed by the government of Sin-

gapore in 2019 and consists of a network of lockers

distributed across residential areas and metro stations

to help to optimize last mile delivery. Lyu and Teo

(2019) propose methods to deﬁne the location of the

network lockers and the demand to be aimed at them.

In door-to-door delivery, it is necessary to con-

sider additional time for interaction with the con-

sumer and the possibility that the consumer is not

available to receive his goods. Building lockers, we

can reduce operating costs due to the condensation of

several deliveries at the same point, reducing the dis-

tance covered, eliminating the interaction time with

the consumer and consequently reducing the delivery

time. The supply of the lockers can also be done at pe-

riods with less trafﬁc, using the same vehicle for dif-

ferent work shifts. With the decrease in delivery ve-

hicles circulating during heavy trafﬁc hours, we have

a small reduction in the emission of gases harmful to

the environment (Edwards et al., 2009).

In this work, the objective is to determine which

lockers will be built, the routes to supply them and the

routes to meet the demand of customers who have not

been allocated to lockers.

We can consider this problem as a variation of the

location-routing problem since it is necessary to de-

termine the location of the lockers and create routes

to meet the demands. Customers’ demands can be

met in two different ways: by door-to-door delivery

or through the collection from lockers. Given a set

of potential locations for building lockers and a set of

customers with their respective demands, it is neces-

sary to create two groups of routes: the delivery routes

and supply routes, and the associations between cus-

tomers and lockers. The built-in lockers must also be

served through supply routes.

2.1 RELATED WORKS

The last mile problem with the use of lockers is dis-

cussed by Wen and Li (2016). The paper presents

a model using lockers in vehicle routing, consider-

ing relevant aspects such as CO

emission, customer

time window and congestion. Actual data from Ming-

guangcun in Beijing is used to apply the proposed

model. In this case study, it was possible to conclude

that the use of lockers contributes to a better solution,

because, relaxes the restriction of time window and

reduces trafﬁc congestion.

Faugere and Montreuil (2016) analyzed the busi-

ness model of twelve companies using lockers and/or

access points in order to identify different characteris-

tics in their services. The data were obtained through

the companies’ websites and online press. The enti-

ties involved in the process, and the impacts generated

by them, are observed: customers, salespeople, deliv-

ery personnel, cities, and the environment. The re-

sults consist of the classiﬁcation of the business mod-

els used by the companies and their general charac-

teristics.

Through the observed points, it was possible to

conclude that the use of lockers generates a decrease

in the delivery time. However, it is a good solution

only if they are conveniently located for customers.

For logistics providers, they may have a reduced ﬂeet

since delivery points are condensed in the lockers,

also eliminating multiple trips due to the absence of

the customer at the time of delivery. For sellers, the

price of deliveries is expected to be reduced in the

long term. Finally, reducing gas emissions and con-

gestion is an advantageous consequence for cities and

the environment.

Veenstra et al. (2018) proposed to integrate the fa-

cility location problem with the vehicle routing prob-

lem and lockers service. This integrated problem was

applied to the delivery of medicines in the Nether-

lands. This problem differs from other classic prob-

lems due to the possibility of serving a customer in

two ways, through the locker or with door-to-door

Last Mile Delivery with Lockers: Formulation and Heuristic

461

service. A mathematical model and a heuristic are

deﬁned to solve the problem. The objective is to min-

imize total costs, considering the routes and the cost

of opening the lockers. Computational tests were per-

formed with two sets of instances: random and based

on real data. The branch-and-bound method was ap-

plied to the proposed mathematical model, obtaining

results for instances with 100 patients and 50 poten-

tial lockers with a time limit of 7200 seconds. The

proposed heuristic achieves solutions that surpass the

optimization software, CPLEX, with only a fraction

of the time (4.18% better for the set of random in-

stances and 3.64% better for the instances based on

real data). The heuristic proved to be consistent in

obtaining the same results considering 10 executions

for each instance.

Wang et al. (2017) discussed relevant questions

about the use of lockers. The paper uses Singapore’s

case as an example, where the lockers from POPSta-

tion, a leader in this market, are positioned at 2500m

from each other. From 2015 to 2017 it was observed

that several lockers were closed permanently. Ac-

cording to the authors, the location of the lockers is

crucial for its popularization, so they must be posi-

tioned in an attractive way for the customer. The com-

petition between various companies and their lock-

ers should also be considered. The article also con-

tributed to the literature because it was the ﬁrst work

related to lockers and your positions, which is based

on real and public data. Real distances between loca-

tions were also used instead of the Euclidean distance,

commonly used in the literature.

Huang et al. (2019) present the problem of vehicle

routing using electric cars and stations. The stations

can be of three types, the ﬁrst one, only to recharge

cars used on delivery of goods, the second one, only

to store goods of customers, such as locker, the third

one, a hybrid station, which can be used for both pur-

poses. In the work, two integer programming models

are proposed: in the ﬁrst one, the routes for supply-

ing the lockers and the routes for customer deliveries

are separated; in the second one, a hybrid route is al-

lowed. A hybrid heuristic is proposed which, com-

pared to CPLEX, presents good results efﬁciently and

effectively. The results obtained show that the use

of lockers combined with door-to-door deliveries can

help to reduce the cost of deliveries.

Relevant reasons are presented for calculating the

routes separately. Firstly, it is not possible to measure

the time that would be spent on each customer. There-

fore, on a hybrid route, if a delivery to a customer is

delayed, one is forced to delay the delivery to a locker,

which will affect multiple users. Second, the hours of

interest for deliveries are different: lockers may be lo-

cated at points with congestion during business hours,

so it is interesting to deliver at less busy times, while

for door-to-door delivery, deliveries are usually dur-

ing business hours. Third, the required skills of the

driver are different depending on the type of delivery

he/she will make: for door-to-door deliveries, the de-

livery person must have interpersonal skills while for

the supply to lockers the driver must have availability

in times less conventional.

In this paper, a variation is also proposed that al-

lows for more work shifts. The same vehicle can be

used during the day for door-to-door deliveries and,

at night, for supplying lockers. In this variation, the

vehicle may have more than one route associated with

it and the ﬁxed cost of the vehicle is considered only

once. In all of the proposed models, the objective is to

minimize the total costs including expenses with the

construction of the stations and the ﬁxed costs of the

vehicles, considered heterogeneous. We do not con-

sider the construction costs, as lockers are built only

once and used for years. Considering these costs on

a daily delivery would highly overestimate the cost.

The instances used to test the methods were created

by the authors by combining several instances of the

literature. They consider electrical vehicles but char-

acteristics about charging electric cars at stations are

not considered, such as charging waiting time, the

possibility of changing batteries or charging queue.

As part of The Federated Lockers and Collection

Points program, the government of Singapore has pro-

posed the creation of the Locker Alliance (LA) which

consists of a network of lockers to complement exist-

ing lockers and to improve the performance of deliv-

eries to consumers. Lyu and Teo (2019) aim to deter-

mine the best design of the locker network in order to

increase its coverage and use. With the increasing in

coverage, it is expected that the concentration of ex-

isting deliveries in the central business district (CBD)

would be reduced by 7.5% due to the possibility of

collecting items in locations away from the CBD.

Unlike the current work, the solutions obtained by

them are evaluated on the perspective of the attrac-

tiveness of the use of lockers, that is, the objective

is to optimize the location of the lockers so that the

volume of users who choose this type of delivery is

maximized. The data collected in the study are from

a time when LA did not exist, and therefore, the work

takes into account that after the implementation of the

network, certain changes will occur in the choice of

users. Using real data, a model was developed and

calibrated to calculate whether the user would be sub-

ject to using the locker, thus, it was possible to mea-

sure the effectiveness of the network design concern-

ing the popularity of locker. The supply and delivery

ICEIS 2020 - 22nd International Conference on Enterprise Information Systems

462

routes of users who have not opted for the locker are

not addressed in their work.

3 INTEGER PROGRAMMING

FORMULATION

We propose here an Integer Linear Programming for-

mulation to formally deﬁne the problem.

As input we have the location of the depot, the

customers and the candidate positions for lockers. We

consider a complete graph, i.e., we know the distance

between any pair of locations.

As output we have the the lockers chosen to be

used, which customers are associated to each of those

lockers, and the routes to delivery items to the lockers

and to the customers not served by any locker. All

the output is represented by binary variables, but we

use also integer variable to keep track of the load in

each vehicle, as a way to guarantee that the capacity

of lockers and vehicles are satisﬁed and also avoid

isolated sub-tours along the routes.

3.1 Input and Decision Variables

The parameters and the decision variables of the pro-

posed model are presented below.

dep: depot

I: set of customers

: set of nodes, I

= {dep} ∪ I

J: set of candidate location for lockers

: set of nodes, J

= {dep} ∪ J

n: number of customers, n = |I|

m: number of locker candidate locations, m = |J|

: demand of customer i

Q: capacity of vehicles for door-to-door delivery

QL: capacity of vehicles that supply lockers

capacity of locker j

i j

: binary, 1 if arc (i, j ) used, i, j ∈ I

, 0 otherwise

i j

: binary, 1 if arc (i, j) used, i, j ∈ J

, 0 other-

wise

i j

: integer, ﬂow on arc (i, j) on customers’ route

f L

i j

: integer, ﬂow on arc (i, j) on lockers’ route

: binary, 1 if customer i is served by a locker, 0

otherwise

i j

: binary, 1 if i is served by locker j, 0 otherwise

: binary, 1 if locker j is used, 0 otherwise

i j

: distance between nodes i and j, i, j ∈ I

i j

: distance between nodes i and j, i, j ∈ J

dIJ

i j

: distance between customer i and locker j

: cover distance of locker j

3.2 Objective Function

The objective function is deﬁned below.

min

∑

i∈I

∑

j∈I

i j

∗ dI

i j

+ (

∑

i∈J

∑

i∈J

i j

∗ dJ

i j

) ∗ 0.8 (1)

The aim is to minimize the total cost of the routes.

We consider the cost proportional to the distance, then

the cost of the customers’ routes is simply the sum of

the distances of the arcs used (ﬁrst term of (1)). For

the lockers supply routes (second term), we consider

the cost as 80% of the normal cost, as these routes are

favourable due to several conditions: higher ﬂexibil-

ity in the period of attendance; no temporary absent

and no need to return,, which may happen in the cus-

tomers’ route; possibility of night attendance, in pe-

riod of no trafﬁc congestion; possibility to reuse the

same vehicle used in normal routes during the day, so

as to reduce ﬁxed costs of vehicles.

3.3 Constraints

(

∑

j∈I

i j

) + l

= 1, ∀i ∈ I (2)

(

∑

j∈I

) + l

= 1, ∀i ∈ I (3)

∑

i∈I

i,dep

∑

i∈I

dep,i

(4)

(

∑

j∈I

) − (

∑

j∈I

i j

) + (l

∗ q

) = q

, ∀i ∈ I (5)

i j

≤ Q ∗ x

i j

, ∀i, j ∈ I

(6)

∑

i∈I

i j

∗ q

≤ qL

, ∀ j ∈ J (7)

∑

j∈J

i j

= l

, ∀i ∈ I (8)

i j

∗ dIJ

i j

≤ r

, ∀i ∈ I, j ∈ J (9)

i j

≤ c

, ∀i ∈ I, j ∈ J (10)

∑

i∈J

= c

, ∀ j ∈ J (11)

∑

i∈J

i j

= c

, ∀ j ∈ J (12)

∑

j∈J

j,dep

∑

j∈J

dep, j

(13)

f L

i j

≤ QL ∗ xL

i j

, ∀i, j ∈ J

(14)

∑

i∈J

f L

i j

−

∑

i∈J

f L

∑

k∈I

k j

∗ q

, ∀ j ∈ J (15)

Last Mile Delivery with Lockers: Formulation and Heuristic

463

i j

∈ {0, 1}, ∀i, j ∈ I

(16)

i j

∈ {0, 1}, ∀i, j ∈ J

(17)

i j

≥ 0, ∀i, j ∈ I

(18)

f L

i j

≥ 0, ∀i, j ∈ J

(19)

∈ {0, 1}, ∀i ∈ I (20)

∈ {0, 1}, ∀i ∈ I, j ∈ J (21)

∈ {0, 1}, ∀ j ∈ J (22)

Routes are modeled using ﬂow variables to con-

trol nodes demand service and avoid sub-tours. There

are two set of routes, one set for in-door service (con-

straints (2)- (6)) and one set for lockers supply (con-

straints (11)- (15)). The remaining constraints (7)-

(10) deﬁne the assignment of customers to lockers

and, ﬁnally, (16)-(22) the range of variables.

Constraint (2) and (3) deﬁne that must be a chosen

arc leaving and respectively reaching each customer

or else the customer must be served by a locker. To-

gether, they deﬁne that each customer must be served

by a locker or by exactly one in-door route.

Constraint (4) balance the number of arcs leaving

and reaching the depot, so that every route starting at

the depot must come back to it. Notice that, although

a customer may not be served by more than one route,

the depot may be in as many routes as needed.

The demand of each customer is guaranteed by

constraint (5), either by the ﬂow of a route or by as-

signing it to a locker. The following two constraints

establish that the capacity of vehicles may not be ex-

ceeded in any point of the route neither the capacity

of a locker may be surpassed.

Constraints (8)-(10) assure that a customer may be

assigned only to lockers nearby (within their covering

distance) and at most to one locker. If customer i is

assigned to a locker j, the corresponding variables l

(customer served by locker) and c

(locker used) are

set to 1.

Constraints (11)-(15) control the routes to serve

lockers in the same way constraints (2)- (6) control

the door-to-door routes. Particularly, (11) and (12)

deﬁne that, if a locker is used, it must be served by

a route (arc arriving and leaving the node); (13) bal-

ances the number of arcs leaving and reaching the de-

pot (the number of routes to supply lockers); (14) as-

sure that the capacity of the vehicle is respected and

(15) that when visiting a locker the demand of all cus-

tomers assigned to it must be unload there.

Finally, constraints (16)-(22) deﬁne the domain of

the decision variables.

4 VND

As detailed later in the experiments, optimal solutions

using the proposed formulation are reached only for

small instances, with up to 75 customers. Heuristic

method is needed to handle larger instances.

The proposed heuristic follows the standard Vari-

able Neighborhood Descent (VND) metaheuristic as

proposed by Mladenovi

c and Hansen (1997), using a

local search with three neighborhood. To provide an

initial solution, a random greedy constructive method

was used. The construction is followed by a local

search and the two steps are performed 200 times, af-

ter which the best solution found is returned.

A solution consists of two parts, a set of routes and

a set of assimilations. Each route can be of delivery

or supply. Both are represented by a vector of identi-

ﬁers, of customers or lockers. Where n is the number

of lockers, the assimilations consist of n lines, starts

with locker identiﬁer followed by the customers as-

similates to each locker.

An initial solution is generated by a greedy ran-

domized solution: a subset of candidate lockers is

chosen at random, and the customers within the cover-

age distance of these lockers are sorted by distance to

the depot. The further away the customer the sooner

it is associated to a locker.

Customers may end up not associated to any

locker, some because they are not within the coverage

radius of any locker and others because when they are

considered the possible lockers cannot serve their de-

mand anymore due to previously assignments. Routes

are built to serve those customers using the Clare and

Wright saving heuristic (Clarke and Wright, 1964),

satisfying vehicle capacities. The lockers are served

by separated routes, created with the same method.

The routes of the constructed solution is then im-

proved by a local search using three different neigh-

borhoods: 2-swap, 2-opt and exchange. They are used

sequentially, as in the VND metaheuristic.

The 2-swap neighborhood consists in swapping

two customers inside a route. A best improvement

strategy is used in this stage: the best swap is chosen

and performed until there is no possible improvement.

For the 2-opt neighborhood, two nodes are ran-

domly chosen and the visit sequence between those

nodes is reversed. Successive improvements are made

until a stop criteria is reached. We used as stop con-

dition 500 iteration without improvement.

The third and last neighborhood is the exchange.

For each node a, the nearest node b in a different route

is determined. If moving node a to the route of b just

before or after b improves the cost, it is considered for

exchange. Then, the best improvement is made. The

ICEIS 2020 - 22nd International Conference on Enterprise Information Systems

464

process continues until no improvement can be made.

The algorithm of VND-based heuristic can be

seen below:

for(int i=0;i<ITERATIONS;i++){

s = constructiveMethod();

int k = 1;

while(k<3){

s’ = bestOfNeighborhood(k);

if (f(s’) < f(s)){

s = s’;

k = 0;

}else{

k++;

}

if (f(s) < f(s*)){

s* = s;

}

return s*;

5 INSTANCES

We adapt a set of classic instances from the Vehicle

Routing Problem (VRP) (Rochat and Taillard, 1995).

We chose 8 instances, with 75, 100 and 150 cus-

tomers, and adapt them by inserting 10 candidates for

lockers. The position of these candidates were manu-

ally chosen in areas with many customers. The capac-

ity of each locker was deﬁned randomly in the range

of 10 to 20 times the average of customers demand,

so a locker may serve around 10 to 20 customers.

Table 1 lists some characteristics of each instance:

the number of customers (n) and the capacity of the

vehicles (Q). We do not impose a limit on the ca-

pacity of the vehicles that supply lockers (QL), as the

capacity of lockers in the instances used already limit

a reasonable capacity.

Table 1: Instances.

ID #Customers #Vehicle Capacity

c tai75a 75 1445

c tai75b 75 1679

c tai75c 75 1122

c tai75d 75 1699

c tai100a 100 1409

c tai100b 100 1842

c tai100c 100 2043

c tai150a 150 1544

6 RESULTS

The machine used was an i5-7400 CPU @ 3.00GHz

with 8GB RAM. The Integer Linear Programming

(ILP) model was implemented in Julia, using JuMP

as modelling language, and run on Gurobi solver, with

time limit of 1 hour. The heuristic was implemented

in C++ and run 3 times for each instance. The average

value is reported for analysis.

The results of the ILP model are reported in Table

2: solution value, runtime and the linear gap reported

by Gurobi. Optimal results were found for only 3 in-

stances, among those with less customers. However,

the difﬁcult is not related only to the number of cus-

tomers. Instance c tai75a has the same number of

customers and lockers but the optimal solution was

not guaranteed in the time available, ﬁnishing with a

gap of 3.6%. This may be due to the relative loca-

tion of lockers and customers. For example, a cus-

tomer may be located in an area covered by two or

more lockers, so may be served by any of them either

by a door-to-door route. The higher the alternatives

the greater the solution space, which may increase the

running time to reach an optimal solution.

Table 2: Results of the ILP formulation.

Instance Solution Runtime gap

c tai75a 803.613 3600 3.63

c tai75b 537.113 25 -

c tai75c 804.118 194 -

c tai75d 420.707 55 -

c tai100a 971.408 3600 3.13

c tai100b 982.592 3600 4.93

c tai100c 870.561 3600 2.59

c tai150a 1097.150 3600 16.01

Table 3 show the results of the proposed heuris-

tic. Column gap

ILP

represents the percentual differ-

ence between the solution of the heuristic and the one

reached by the ILP in 1 hour. One may notice that

the heuristic found the same result for 4 instances.

Column gap

show the percentual difference to the

lowew bound found the ILP model, which is the best

known still possible result. Besides the two optimal

solutions, for three other the gap was less than 4%.

The time to reach the optimal solution is substan-

tially less in comparison to the ILP model, and for the

others the gap was less than 5%.

In Figure 1 we can see the comparison between

the lower bound and the two approaches proposed

in this work. The results obtained by ILP and VND

are close for most instances, increasing for larger in-

stances, however, as previously mentioned, the time

spent by VND to obtain solutions is signiﬁcantly less.

Last Mile Delivery with Lockers: Formulation and Heuristic

465

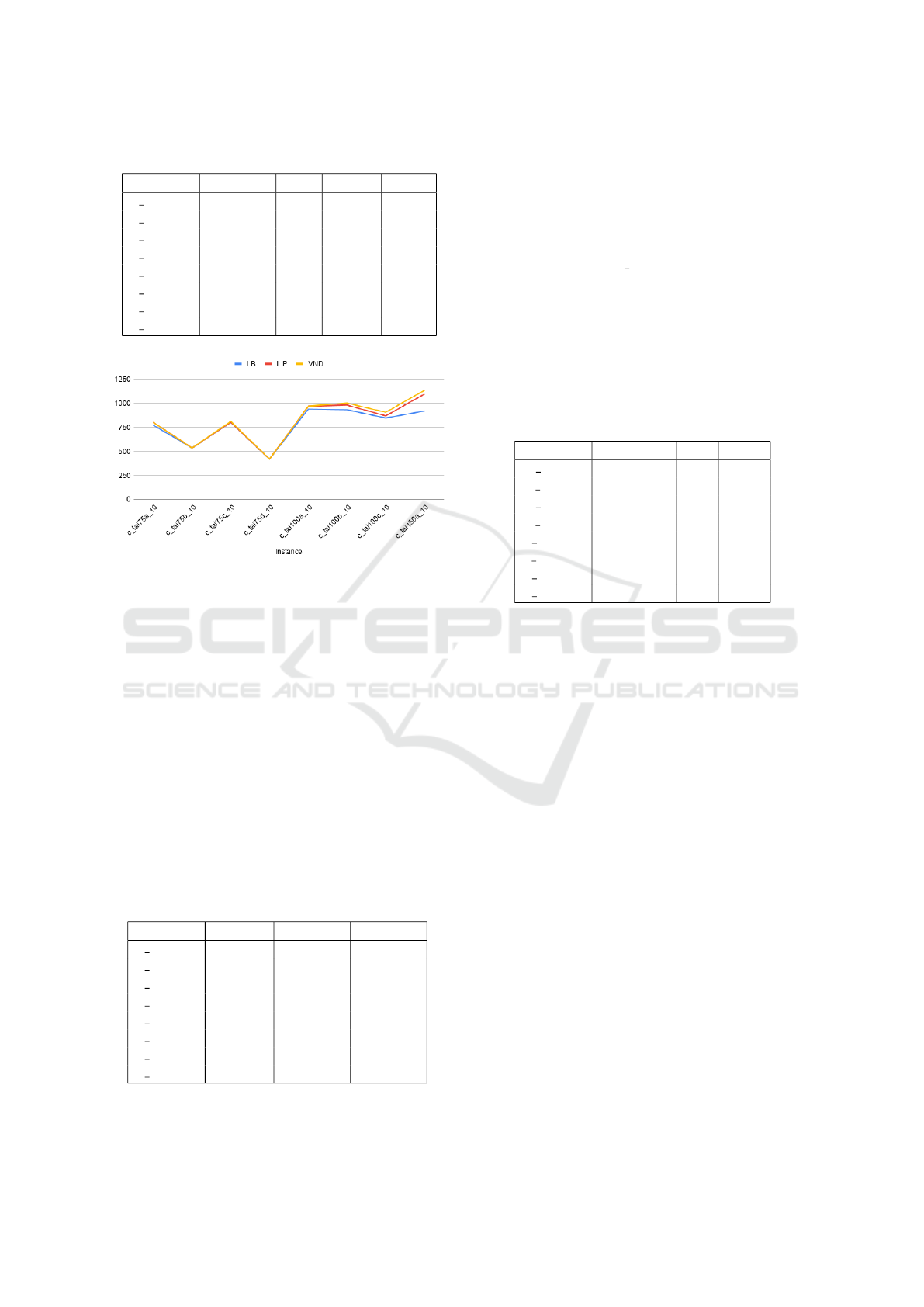
Table 3: Results of the heuristic.

Instance VND time gap

ILP

gap

c tai75a 803.613 9 - 3.63

c tai75b 537.113 6 - -

c tai75c 813.119 9 1.11 1.11

c tai75d 420.707 6 - -

c tai100a 971.408 22 - 3.13

c tai100b 1002.820 19 2.02 6.85

c tai100c 908.177 17 4.14 6.62

c tai150a 1136.280 54 3.44 18.91

Figure 1: Comparison of the Lower Bound reported by

CPLEX and the feasible solutions from ILP and VND for

each instance.

The instances used in this work, proposed by

Rochat and Taillard (1995), are commonly used for

the VRP and some of its variations. Table 4 show

on column VRP the best known results for the clas-

sic VRP, which may be used to study and foresee

the saving that the use of lockers can bring. Solu-

tions using lockers save in average 52% of the trans-

portation costs. The real saving is not that amount,

of course, because we are considering that routes to

supply locker are 20% cheaper and we are not consid-

ering the costs of building and maintaining the lock-

ers. However, the saving is clear, as the ﬁxed costs of

locker are spread over years and the costs of the table

are a daily cost.

Table 4: Impact of the use of lockers.

Instance VRP ILP VND

c tai75a 1618.36 803.613 803.613

c tai75b 1344.64 537.113 537.113

c tai75c 1291.01 804.118 813.119

c tai75d 1365.42 420.707 420.707

c tai100a 2041.34 971.408 971.408

c tai100b 1940.61 982.592 1002.820

c tai100c 1406.21 870.561 908.177

c tai150a 3055.23 1097.150 1136.280

Table 5 shows, for each instance, the number of

customers that are served by lockers in the best so-

lution found by each method. One might intuitively

think that the optimal solution would include the max-

imum possible number of customers to lockers. How-

ever, this is not always the case, as shown by the re-

sults for the instance c tai100c: the heuristic solu-

tion is 4% costly, despite having more customers as-

sociated to lockers. This happens because, in some

scenarios, the cost to visit a locker may be higher

than the cost to include the costumers associated to

it in other route. Hence, even disregarding installa-

tion costs, lockers should not be build deliberately, as

there would be still supply costs.

Table 5: Customers served by lockers.

Instance Customers ILP VND

c tai75a 75 62 62

c tai75b 75 69 69

c tai75c 75 58 57

c tai75d 75 72 72

c tai100a 100 82 82

c tai100b 100 83 83

c tai100c 100 59 61

c tai150a 150 125 121

7 CONCLUSION

Due to the increasing popularity of e-commerce the

last mile step in the delivery of goods has become

more important and relevant in the delivery planning.

The use of lockers has gained attention as an alterna-

tive to reduce costs, to optimize the delivery time and

is also beneﬁcial to the environment, as it contribute

to reduce gas emission.

In this work we study methods for a vehicle rout-

ing combined with a facility problem for delivering

goods using lockers. To deﬁne and solve the prob-

lem we propose an integer linear programming model,

implemented and solved by Gurobi. Due to the com-

plexity of the formulation, a heuristic is also proposed

to handle larger instances. The heuristic is based on

the VND metaheuristic and uses 3 neighborhoods to

improve a greedy initial solution.

Experimental tests were made with 8 cases

adapted from VRP classical instances. The ILP for-

mulation found the optimal solution for three in-

stances and a linear gap below 5% for other four in-

stances within 1 hour of execution time. The heuristic

found solutions close to the ones found by the ILP for

most of the instances in few seconds.

ICEIS 2020 - 22nd International Conference on Enterprise Information Systems

466

We show the impact of the use of the lockers and

as future works we plan to incorporate time windows

and trafﬁc conditions, as the problem in the real con-

text has such characteristics. We also plan to improve

the heuristic by adding more neighborhoods and use

good solutions to instead of creating new random so-

lutions on each iteration.

ACKNOWLEDGEMENTS

The authors thank Coordenac¸

ao de Aperfeic¸oamento

de Pessoal de N

ıvel Superior (CAPES) and Fundac¸

de Amparo

a Pesquisa do Estado de Minas Gerais

(FAPEMIG) for the ﬁnancial support of this project.

REFERENCES

Clarke, G. and Wright, J. W. (1964). Scheduling of vehicles

from a central depot to a number of delivery points.

Operations research, 12(4):568–581.

Edwards, J., McKinnon, A., Cherrett, T., McLeod, F., and

Song, L. (2009). The impact of failed home deliveries

on carbon emissions: Are collection/delivery points

environmentally-friendly alternatives. In 14th Annual

Logistics Research Network Conference, page M117.

Citeseer.

Faugere, L. and Montreuil, B. (2016). Hyperconnected city

logistics: Smart lockers terminals & last mile deliv-

ery networks. In Proceedings of the 3rd International

Physical Internet Conference, Atlanta, GA, USA, vol-

ume 29.

Huang, Z., Huang, W., and Guo, F. (2019). Integrated sus-

tainable planning of self-pickup and door-to-door de-

livery service with multi-type stations. Computers &

Industrial Engineering.

Lyu, G. and Teo, C.-P. (2019). Last mile innovation: The

case of the locker alliance network. Available at SSRN

3471166.

Mladenovi

c, N. and Hansen, P. (1997). Variable neigh-

borhood search. Computers & operations research,

24(11):1097–1100.

Rochat, Y. and Taillard,

E. D. (1995). Probabilistic diversi-

ﬁcation and intensiﬁcation in local search for vehicle

routing. Journal of heuristics, 1(1):147–167.

Song, L., Cherrett, T., McLeod, F., and Guan, W. (2009).

Addressing the last mile problem: transport impacts

of collection and delivery points. Transportation Re-

search Record, 2097(1):9–18.

Veenstra, M., Roodbergen, K. J., Coelho, L. C., and Zhu,

S. X. (2018). A simultaneous facility location and ve-

hicle routing problem arising in health care logistics

in the netherlands. European Journal of Operational

Research, 268(2):703–715.

Wang, Y., Ong, T., Lee, L. H., and Chew, E. P. (2017).

Capacitated competitive facility location problem of

self-collection lockers by using public big data. In

2017 13th IEEE Conference on Automation Science

and Engineering (CASE), pages 1344–1344. IEEE.

Wen, J. and Li, Y. (2016). Vehicle routing optimization

of urban distribution with self-pick-up lockers. In

2016 International Conference on Logistics, Infor-

matics and Service Sciences (LISS), pages 1–6. IEEE.

Last Mile Delivery with Lockers: Formulation and Heuristic

467