Radial Basis Function Neural Network Receiver Trained by Kalman

Filter Including Evolutionary Techniques

Pedro Henrique Gouvêa Coelho, J. F. M. Do Amaral and A. C. S. Tome

State Univ. of Rio de Janeiro, FEN/DETEL, R. S. Francisco Xavier, 524/Sala 5001E, Maracanã, RJ, 20550-900, Brazil

Keywords: Neural Networks, Artificial Intelligence Applications, Channel Equalization, Wireless Systems.

Abstract: Artificial Neural Networks have been broadly used in several domains of engineering and typical

applications involving signal processing. In this paper a channel equalizer using radial basis function neural

networks is proposed, on symbol by symbol basis. The radial basis function neural network is trained by an

extended Kalman filter including evolutionary techniques. The key motivation for the equalizer application

is the neural network capability to establish complex decision regions that are important for estimating the

transmitted symbols appropriately. The neural network training process using evolutionary techniques

including an extended Kalman filter enables a fast training for the radio basis function neural network.

Simulation results are included comparing the proposed method with traditional ones indicating the

suitability of the application.

1 INTRODUCTION

Channel equalization is intended to mitigate the

effects of the transmitted media on the transmitted

symbol sequence, known as the inter-symbol

interference (ISI). Adaptive equalizers are essential

in these communications systems to achieve reliable

data transmission. Usually two approaches are used:

sequence estimation equalizers and the symbol

decision equalizers. The optimal sequence

estimation is yielded by MLSE (Maximum

Likelihood Sequence Estimation) (Chen et. al.,

1995), (Gibson and Cowan, 1989) implemented by

the Viterbi algorithm. It is optimal for detecting the

full transmitted sequence. High complexity in

connection with the MLSE are however usually

unacceptable in many typical communication

systems. Most of the practical equalizers therefore

employ a structure of making decision symbol by

symbol. Symbol decision equalizers can still be

classified into two categories according to whether

they estimate a channel model explicitly. One is the

direct-modelling equalizer which is not widely used

once the knowledge of the channel model is needed.

The other category is the indirect modelling

equalizer that does not require the knowledge of the

channel model. In this category, we mention among

others, the linear transverse adaptive equalizers that

are required in these communications systems to

obtain reliable data transmission. Among the effects

of wireless channels is delay dispersion, due to Multi

Path Components (MPCs) having different runtimes

from the transmitter (TX) to the receiver (RX).

Delay dispersion causes ISI, which can largely

degrade the transmission of digital signals. It is

worth mention that even a delay spread that is

smaller than the symbol duration can cause a

significant Bit Error Rate (BER) degradation. If the

delay spread becomes comparable with or larger

than the symbol duration, as occurs often in third

and fourth generation cellular systems, then the BER

turns unacceptably large if no compensation are

performed. Also when a signal is transmitted

through wireless medium then due to multipath

effect there is fluctuation in signal amplitude, phase,

and time delay. This effect is often known as fading

(Proakis, 2001). The use of coding and diversity can

decrease, but not fully eliminate, errors due to ISI.

However, delay dispersion can also be a positive

effect. Since fading of the distinct MPCs is

statistically independent, resolvable MPCs can be

modeled as diversity paths. So, delay dispersion

allows the possibility of delay diversity, if the RX

can extract, and exploit, the resolvable MPCs.

Equalizers can be interpreted as devices that work

both ways - they decrease or eliminate ISI, and

simultaneously exploit the delay diversity inherent

626

Coelho, P., M. Do Amaral, J. and Tome, A.

Radial Basis Function Neural Network Receiver Trained by Kalman Filter Including Evolutionary Techniques.

DOI: 10.5220/0009565806260631

In Proceedings of the 22nd International Conference on Enterprise Information Systems (ICEIS 2020) - Volume 1, pages 626-631

ISBN: 978-989-758-423-7

in the channel. The principle of an equalizer can be

analyzed either in the time or frequency domain. In

the present work the time-domain method is taken

which is feasible in most of the applications.

Usually, the channel response may not be known at

startup. Besides, the channel may be time-varying,

so an adaptive structure of the equalizer is essential.

One can identify distinct modes of adaptation:

• A training signal aided adaptation;

• Decision directed adaptation - An error signal

defined by comparing input and output of the

decision device;

• Blind adaptation: Signal properties aided

adaptation instead of making use an error signal;

A training signal is considered in this article for

the equalizer adaptation. It should be stressed that,

digital communication systems typically operate on

time varying dispersive channels which usually

employ a signaling format in such way that user data

are set up in blocks preceded by a known training

sequence. That training sequence at the beginning of

each block is used to estimate channel or train an

adaptive equalizer. Depending on the rate at which

the channel changes with time, there may not be a

need to further track the channel variations during

the user data sequence. The present article proposes

a channel equalizer for wireless channels using

Radial Basis Function (RBF) neural networks

including evolutionary techniques on a symbol by

symbol decision basis. Their use was spread by

(Moody and Darken, 1989), and has proven to be

useful neural network architecture. The major

difference between RBF networks and back

propagation networks is the behavior of the single

hidden layer. Rather than using the sigmoidal or S-

shaped activation function as in back propagation,

the hidden units in RBF networks use a Gaussian or

some other basis kernel function. Each hidden unit

acts as a locally tuned processor that computes a

score for the match between the input vector and its

connection weights or centers. In effect, the basis

units are highly specialized pattern detectors. The

weights connecting the basis units to the outputs are

used to take linear combinations of the hidden units

to product the final classification or output. The RBF

equalizer classifies the received signal according to

the class of the center closest to the received vector

(Assaf et al, 2005), (Burse et al, 2010). The output

of the RBF equalizer offers an attractive alternative

to the Multi-Layer Perceptron (MLP) type of Neural

Network for channel equalization problems because

the structure of the RBF network has a close

relationship to Bayesian methods for channel

equalization and interference exclusion. RBF

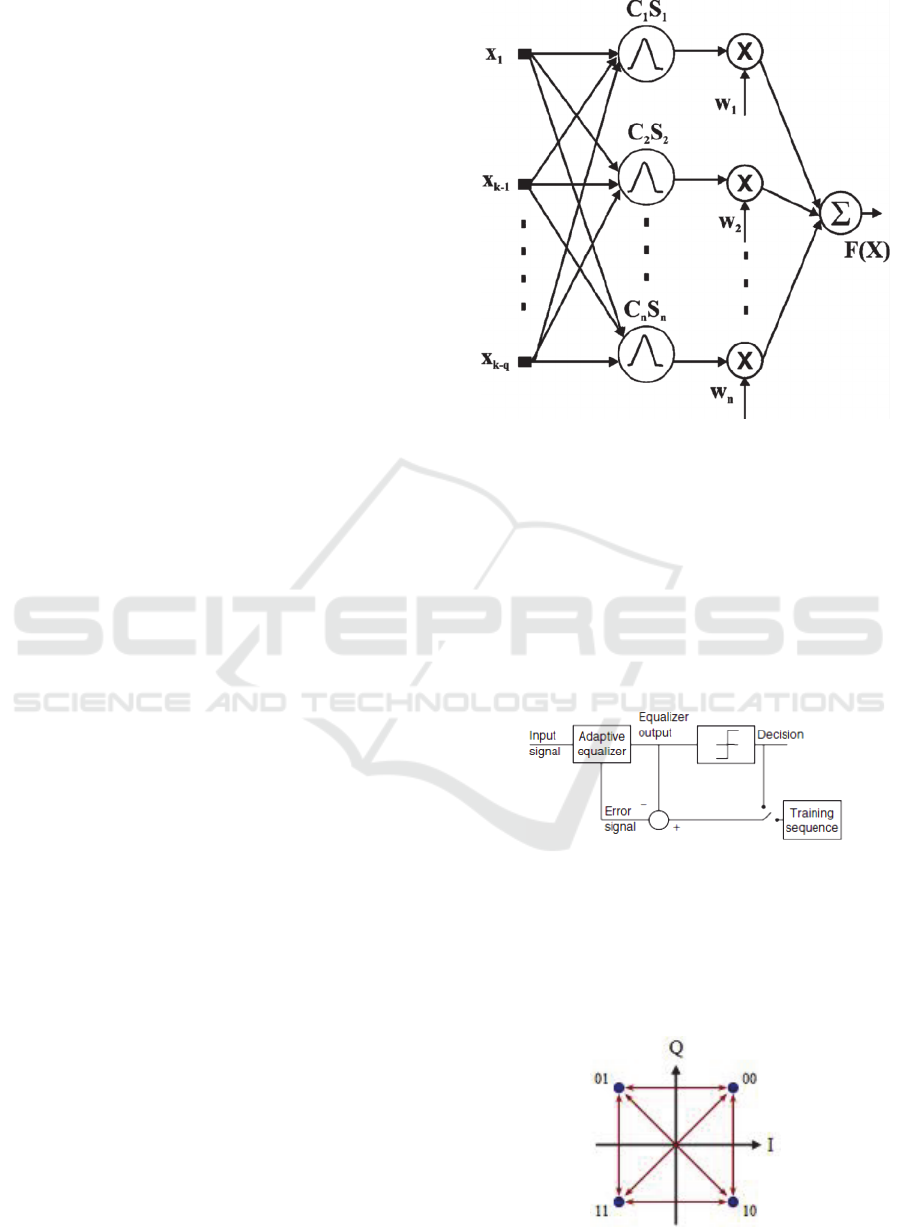
networks comprise three layers: the input layer, the

hidden layer with the RBF nonlinearity, and a linear

output layer, as shown in Fig. 1(Burse et al, 2010).

This paper is divided into four sections. Section 2

does a brief discussion of RBF artificial neural

networks. Section 3 presents the RBF neural net

equalizer and case studies and section 4 ends the

paper with conclusions.

2 RBF NEURAL NETS

RBF neural networks are a very popular architecture

only surpassed by feedforward neural networks.

Denoting the input (vector) as x and the output as

y(x) (scalar), the architecture of a RBF neural

network is given by





















||)(||

expy(x)



(1)

using Gaussian function as basis functions. Observe

that, c

are called centers and  is called the width.

There are M basis functions centered at c

, and w

are named weights.

RBF neural networks are very popular for function

approximation, curve fitting, time series prediction,

control and classification problems. The radial basis

function network differs from other neural networks,

showing many distinctive features. Due to their

universal approximation, more concise topology and

quicker learning speed, RBF networks have attracted

considerable attention and they have been widely

used in many science and engineering fields (Oyang

et al., 2005), (Fu et al., 2005), (Devaraj et al., 2002),

(Du et al., 2008), (Han et al., 2004). The

determination of the number of neurons in the

hidden layer in RBF networks is somewhat

important because it affects the network complexity

and the generalizing capability of the network. In

case the number of the neurons in the hidden layer is

insufficient, the RBF network cannot learn the data

adequately. On the other hand, if the number of

neurons is too high, poor generalization or an

overlearning situation may take place (Liu et al.,

2004). The position of the centers in the hidden layer

also influences the network performance

significantly (Simon, 2002), so determination of the

optimal locations of centers is an important job.

Each neuron has an activation function in the hidden

layer. The Gaussian function, which has a spread

parameter that controls the behavior of the function,

Radial Basis Function Neural Network Receiver Trained by Kalman Filter Including Evolutionary Techniques

627

is the most preferred activation function. The

training method of RBF networks also includes the

optimization of spread parameters of each neuron.

Later on, the weights between the hidden layer and

the output layer must be selected suitably. Finally,

the bias values which are added with each output are

determined in the RBF network training procedure.

In the literature, several algorithms were proposed

for training RBF networks, such as the gradient

descent (GD) algorithm (Karayiannis, 1999) and

Extended Kalman filtering (EKF) (Simon, 2002).

Several global optimization methods have been used

for training RBF networks for different science and

engineering problems such as genetic algorithms

(GA) (Barreto et al., 2002), the particle swarm

optimization (PSO) algorithm (Liu et al., 2004), the

artificial immune system (AIS) algorithm (De Castro

et al., 2001) and the differential evolution (DE)

algorithm (Yu et al., 2006). The Artificial Bee

Colony (ABC) algorithm is a population based

evolutional optimization algorithm that can be used

to various types of problems. The ABC algorithm

has been used for training feed forward multi-layer

perceptron neural networks by using test problems

such as XOR, 3-bit parity and 4-bit encoder/decoder

problems (Karaboga et al., 2007). Due to the need of

fast convergence, EKF training was chosen for the

RBF equalizer reported in this paper including

evolutionary techniques briefly depicted in the next

section. Details on the training process can be found

in (Simon, 2002).

3 RBF EQUALIZATION DEVICE

Radial Basis Function Neural Networks have been

used for channel equalization purposes (Lee et al.,

1999), (Gan et al., 1999), (Kumar et al. 2000), (Xie

and Leung, 2005). Typically, such networks have

three layers: the input layer, the hidden layer with

the RBF nonlinearity, and a linear output layer, as

shown in Fig. 1 (Burse et al., 2010). Simulations

carried out on time-varying channels using a

Rayleigh fading channel model to compare the

performance of RBF with an adaptive maximum

likelihood sequence estimator (MLSE) show that the

RBF equalizer produces superior performance with

less computational complexity (Mulgrew, 1996).

Several techniques have been developed in literature

to solve the problem of blind equalization using

RBF (Tan et al., 2001), (Uncini et al., 2003) and

others. RBF equalizers require less computing

demands than other equalizers (Burse et al., 2010).

Figure 1: RBF neural network (from Burse et al., 2010).

A comprehensive review on channel equalization

can be found in (Qhreshi, 1985). A recent review on

Neural Equalizers can be found in (Burse et al.,

2010). The equalization scheme can be seen in Fig. 2

(taken from (Molisch, 2011)). The adaptive

equalizer in the figure is the RBF Neural equalizer

trained by EKF according to (Simon, 2002)

including evolutionary techniques. The considered

channel uses the Rayleigh model (Molisch, 2011)

using QPSK modulation.

Figure 2: Equalization procedure (from Molisch, 2011).

The QPSK ideal constellation symbols are shown in

figure 3. In other words when the communications

channel is ideal, there is no distortion or noise so

that the symbols are always received with no error.

For a real channel the received symbols will show

some dispersion as shown in figure 4.

Figure 3: QPSK ideal constellation.

ICEIS 2020 - 22nd International Conference on Enterprise Information Systems

628

Figure 4: QPSK real scenario constellation.

The evolutionary techniques used in connection to

extended Kalman filtering training of the RBF

equalizer take into account the differential

evolutionary (DE) approach (Brownlee, 2011).

(Souza et al., 2007) used it in a Kalman filter trained

RBF arrangement for forecasting the soybean price.

The DE technique basically involved the estimation

of the main diagonal of matrices P, Q and R that are

respectfully the filter error covariance matrix, the

system noise covariance matrix and the observation

noise covariance matrix. The fitness function for the

DE technique is the multiple correlation coefficient

which measures the fitness of the model with

measured data. A value close to 1 indicates the

model is adequate (Brownee, 2011). Several

simulations were carried out for realistic channel

characteristics. Two case studies were considered.

For the first case study, a flat fading channel was

considered. Flat fading channels have amplitude

varying channel characteristics and are narrowband

(Molisch, 2011). A transmission of an image was

considered in both case studies. The transmitted

image is depicted in figure 5.

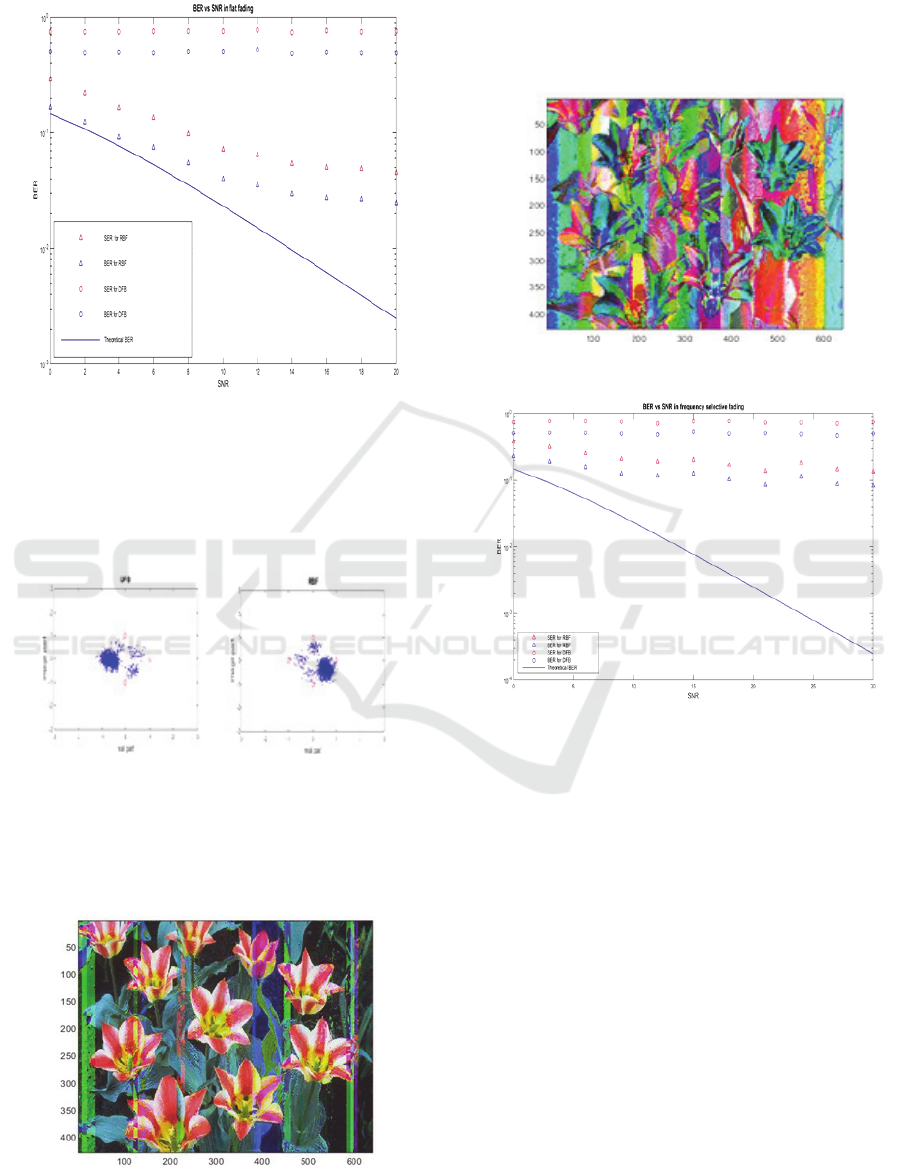
Figure 5: Original transmitted image in case studies.

The simulations also made possible to plot results

for comparing the performance in terms of Bit Error

Rate (BER) against Signal to Noise Ratio (SNR) and

Symbol Error Rate (SER) against SNR. The

received image for the RBF equalizer and the

Decision Feedback Equalizer (DFB) which is a quite

popular traditional equalizer is shown in figures 6

and 7. The simulated RBF equalizer produced an

average correlation coefficient of 0.993 with

standard deviation of 0.085 and used 7 Gaussian

functions in the hidden layer. The computational

complexity of the DFB was chosen to be comparable

to the RBF equalizer.

Figure 6: RBF received image for flat fading.

Figure 7: DFB received image for flat fading.

In a qualitative way, one can see that the RBF

equalizes better. For a quantitative description figure

8 shows the BER x SNR and SER x SNR for the two

equalizers. The theoretical curve is also shown for

comparative purposes. One can see that the RBF

equalizer performs better as the images of the

received figures indicated. It can be also seen that

for low SNRs the performance of the RBF equalizer

is very close the theoretical performance. As SNR

values increase the equalizer begins to get away

from the theoretical model. Figure 9 shows a

constellation diagram for the equalizers in case study

1, and it can be seen a cluster formation around the

original symbols for both equalizers, indicating that

errors might occur in the receiver output. The

constellation diagram is a qualitative way of

comparing the performance of received symbols and

complements the information given by the curves

BER x SNR. Usually are made available in displays

Radial Basis Function Neural Network Receiver Trained by Kalman Filter Including Evolutionary Techniques

629

of measurements instruments for maintenance

purposes.

Figure 8: BER x SNR for case study 1.

Figure 9 shows a constellation diagram for the

equalizers in case study 1, and it can be seen a

cluster formation around the original symbols for

both equalizers, indicating that errors might occur in

the receiver output.

Figure 9: Constellation diagram for case study 1.

In case study 2, a frequency selective fading was

considered which is a more severe type of fading

(Moslisch, 2010). Figures 10 and 11 show the

received images corresponding to RFB and DFB

Figure 10: RBF received image for case study 2.

equalizers. One can see a more intensive degradation

in the image for both equalizers, although the DFB

is still worse. The performance curves are depicted

in figure 12 which shows clearly the degradation in

performance for both equalizers as far as frequency

selective fading is concerned.

Figure 11: DFB received image for case study 2.

Figure 12: BER x SNR for case study 2.

4 CONCLUSIONS

This paper proposed a radial basis function (RBF)

equalizer trained by an extended Kalman filter

(EKF) using DE techniques. The advantages of

using a Kalman filter for training the RBF neural

equalizer are that it provides the same performance

as gradient descent training, but with much less of

the computational effort. Moreover if the decoupled

Kalman filter is used in connection with DE

techniques, the same performance is guaranteed with

further decrease on the computational effort for large

computational demand problems. The equalizer was

tested and two case studies were carried out where

its performance was compared with the popular

Decision feedback equalizer and the results

indicated the proposed equalizer performed better.

For future work the authors intend to consider

ICEIS 2020 - 22nd International Conference on Enterprise Information Systems

630

hybrid solutions involving the RBF and other

equalizer architectures as far as the tracking of time-

variations is concerned. In this respect the use of

deep learning techniques might be an attractive way

of achieving such a purpose.

REFERENCES

Proakis, J. G., 2001. Digital Communications. Fourth

Edition, McGraw-Hill.

Moody, J. E. and Darken, J. E., 1989. Fast Learning in

Networks of Locally-tuned Processing Units. Neural

Computation 1, 281-294.

Chen, S. et. al., 1995.Adaptive Bayesian Decision Feedback

Equalizer for Dispersive Mobile Radio Channels, IEEE

Trans. Communications, Vol. 43, No. 5, pp 1937-1946.

Gibson G. J., and Cowan, C. F. N., 1989. Applications of

Multilayer Perceptron as Adaptive Channel equalizers,

In Proc. IEEE Internat. Conf. Acoust. Speech Signal

Process., Glasgow, Scotland, 23-26 May, pp 1183-

1186.

Burse K., Yadav R. N., and Shrivastava S. C., 2010.

Channel Equalization Using Neural Networks: A

Review. IEEE Transactions on Systems, Man, and

Cybernetics, Part C: Applications and Reviews, Vol. 40,

No. 3.

Assaf, R., El Assad, S., Harkouss, Y., 2005. Adaptive

equalization for digital channels RBF neural network. In

The European Conference on Wireless Technology, pp.

347-350.

Lee J., Beach C., and Tepedelenlioglu N., 1999. A practical

radial basis function equalizer. IEEE Trans. Neural

Netw., vol. 10, no. 2, pp. 450–455.

Gan Q., Saratchandran P., Sundararajan N., and

Subramaniam K. R., 1999. A complex valued RBF

network for equalization of fast time varying channels.

IEEE Trans. Neural Netw., vol. 10, no. 4, pp. 958–960.

Kumar C. P., Saratchandran P., and Sundararajan N., 2000.

Nonlinear channel equalization using minimal radial

basis function neural networks. Proc. Inst. Electr. Eng.

Vis., Image, Signal Process., vol. 147, no. 5, pp. 428–

435.

Xie N. and Leung H., 2005. Blind equalization using a

predictive radial basis function neural network. IEEE

Trans. Neural Netw., vol. 16, no. 3,pp. 709–720.

Tan Y., Wang J., and. Zurada J. M, 2001. Nonlinear blind

source separation using a radial basis function network.

IEEE Trans. Neural Netw., vol. 12,no. 1, pp. 124–134.

Uncini A. and Piazza F., 2003. Blind signal processing by

complex domain adaptive spline neural networks. IEEE

Trans. Neural Netw., vol. 14,no. 2, pp. 399–412.

Oyang, Y.J., Hwang, S.C., Ou, Y.Y., Chen, C.Y., Chen,

Z.W., 2005. Data classification with radial basis

function networks based on a novel kernel density

estimation algorithm. IEEE Trans. Neural Netw., 16,

225–236.

Fu, X., Wang, L., 2003. Data dimensionality reduction with

application to simplifying rbf network structure and

improving classification performance. IEEE Trans. Syst.

Man Cybern. Part B, 33, 399–409..

Devaraj, D., Yegnanarayana, B., Ramar, K., 2002. Radial

basis function networks for fast contingency ranking.

Electric. Power Energy Syst., 24, 387–395.

Mulgrew, B., 1996. Applying Radial Basis Functions. IEEE

Signal Processing Magazine, vol. 13, pp. 50-65.

Du, J.X., Zhai, C.M., 2008. A Hybrid Learning Algorithm

Combined With Generalized RLS Approach For Radial

Basis Function Neural Networks. Appl. Math. Comput.,

208, 908–915.

Singh D. K., Shara, D., Zadgaonkar, A. S., Raman,

C.V.,2014. Power System Harmonic Anallysis Due To

Single Phase Welding Machine Using Radial Basis

Function Neural Network. International Journal of

Electrical Engineering and Technology (IJEET),

Volume 5, Issue 4, April, pp. 84-95.

Han, M., Xi, J., 2004. Efficient clustering of radial basis

perceptron neural network for pattern recognition.

Pattern Recognit, 37, 2059–2067.

Liu, Y., Zheng, Q.; Shi, Z., Chen, J., 2004. Training radial

basis function networks with particle swarms. Lect.

Note. Comput. Sci., 3173, 317–322.

Simon, D., 2002. Training radial basis neural networks with

the extended Kalman filter. Neurocomputing, 48, 455–

475.

Karayiannis, N.B., 1999. Reformulated radial basis neural

networks trained by gradient descent. IEEE Trans.

Neural Netw., 3, 2230–2235.

Barreto, A.M.S., Barbosa, H.J.C., Ebecken, N.F.F., 2002.

Growing Compact RBF Networks Using a Genetic

Algorithm. In Proceedings of the 7th Brazilian

Symposium on Neural Networks, Recife, Brazil, pp. 61–

66.

De Castro, L.N., Von Zuben, F.J., 2001. An Immunological

Approach to Initialize Centers of Radial Basis Function

Neural Networks. In Proceedings of Brazilian

Conference on Neural Networks, Rio de Janeiro, Brazil,

pp. 79–84.

Yu, B., He, X., 2006.Training Radial Basis Function

Networks with Differential Evolution. In Proceedings of

IEEE International Conference on Granular

Computing, Atlanta, GA, USA, pp. 369–372.

Karaboga, D., Akay, B., 2007. Artificial Bee Colony (ABC)

Algorithm on Training Artificial Neural Networks. In

Proceedings of 15th IEEE Signal Processing and

Communications Applications, Eskisehir, Turkey.

Qureshi, S.,1985. Adaptive equalization. Proceedings of

The IEEE - PIEEE, vol.73, no. 9, pp. 1349-1387.

Molisch,A. S., 2011. Wireless Communications.Second

Edition. John Wiley & Sons.

Souza, R. C. T. and Coelho, L. S., 2007. RBF Neural

Network With Kalman Filter Based Training and

Differential Evolution Applied to Soybean Price

Forecast. In Proceedings of the 8th Brazilian Neural

Networks Conference, pp. 1-6.

Brownlee, J., 2011. Clever Algorithms. Nature-Inspired

Programming Recipes, LuLu.

Radial Basis Function Neural Network Receiver Trained by Kalman Filter Including Evolutionary Techniques

631