An Improvement of Genetic Algorithm based on Dynamic Operators

Rates Controlled by the Population Performance

Beatriz Flamia Azevedo

1,3 a

, Ana I. Pereira

1,2 b

and Glaucia Maria Bressan

3 c

Research Centre in Digitalization and Intelligent Robotics (CeDRI), Instituto Polit

ecnico de Braganc¸a, Braganc¸a, Portugal

Algoritmi Research Centre, University of Minho, Campus de Gualtar, Braga, Portugal

Federal University of Technology - Paran

a, Corn

elio Proc

opio, Paran

a, Brazil

Keywords:

Genetic Algorithm, Genetic Operators, Dynamic Rates, Hybrid Approach.

Abstract:

This work presents a hybrid approach of genetic algorithm with dynamic operators rates that adapt to the

phases of the evolutionary process. The operator’s rates are controlled by the amplitude variation and standard

deviation of the objective function. Besides, a new stopping criterion is presented to be used in conjunction

with the proposed algorithm. The developed approach is tested with six optimization benchmark functions

from the literature. The results are compared to the genetic algorithm with constant rates in terms of the

number of function evaluations, the number of iterations, execution time and optimum solution analysis.

1 INTRODUCTION

Optimization is a mathematics ﬁeld that studies the

identiﬁcation of functions’ extreme points, either

maximal or minimal. In the last decade, the use of

optimization methods has become an essential tool

for management, decision making, as well as improv-

ing and developing technologies as it allows gaining

competitive advantages (Mitchell, 1998; Haupt and

Haupt, 2004).

Inspired by Darwin natural selection theory, op-

timization techniques had considerable progress in

the area of population algorithms. J. H. Holland

(Holland, 1992) and his collaborators tightly studied

the natural optimization mechanisms and mathemati-

cally formalized the natural process of evolution and

adaptation of living beings. These researchers devel-

oped artiﬁcial systems inspired in natural optimiza-

tion mechanisms (Mitchell, 1998), that can be used

to solve real optimization problems that arise from

industrial ﬁelds. Genetic Algorithms (GA) are the

most famous example of this methodology and they

are used in wide ﬁelds, such as image processing,

pattern recognition, ﬁnancial analysis, industrial opti-

mization, etc (Ghaheri et al., 2015; Haupt and Haupt,

2004; Xu et al., 2018).

https://orcid.org/0000-0002-8527-7409

https://orcid.org/0000-0003-3803-2043

https://orcid.org/0000-0001-6996-3129

The several applications of GA led to numerous

computational implementations and algorithm varia-

tions. Many works propose strategies to improve the

GA and consequently the optimization problem solu-

tion. However, in most works, these improvements

are restricted to speciﬁc applications that cannot be

extended to optimization problems in general.

Knowing that GA performance depends on the op-

timization problem, this work consists of exploring

strategies to automatically adapt the GA to the op-

timization problem and proposes a variation of the

Genetic Algorithm to be used in general optimization

problems.

The traditional version of GA uses constant val-

ues in the genetic operator’s rates for the evolution-

ary process. In this paper is presented a dynamic GA

that considers three phases, where different operators

rates are used and they are dynamically controlled by

the amplitude and standard deviation of the objective

function. Besides this, a new stopping criterion is pro-

posed that depends on the algorithm behavior in the

last phase. This approach is tested by six optimiza-

tion test function and the results are compared with

the Genetic Algorithm with constant rates.

This paper is organized as follows: in Section 2,

GA concepts are introduced, highlighting the behav-

ior of the genetic operators. In Section 3 some stud-

ies and variations of GA are presented. In Section 4

the dynamic GA proposed in this work is described,

388

Azevedo, B., Pereira, A. and Bressan, G.

An Improvement of Genetic Algorithm based on Dynamic Operators Rates Controlled by the Population Performance.

DOI: 10.5220/0009385403880394

In Proceedings of the 9th International Conference on Operations Research and Enterprise Systems (ICORES 2020), pages 388-394

ISBN: 978-989-758-396-4; ISSN: 2184-4372

while the numerical results are presented in Section 5.

Finally, the conclusion and future work proposed are

presented in Section 6.

2 GENETIC ALGORITHM

The Genetic Algorithm is composed of a set of in-

dividuals, usually named as chromosomes, that are

considered solutions for the optimization problem.

This set of individuals is known as the population,

and they have a ﬁxed number of individuals in each

generation (iteration). The population is represented

by N

pop

individuals distributed in the feasible region,

which is the space where each variable can have val-

ues (Sivanandam and Deepa, 2008).

Thereby, the basic idea of GA is to create an initial

population P

of feasible solutions, to evaluate each

individual using the objective function and to select

some individuals to deﬁne the optimum subset of in-

dividuals N

keep

, and to modify them by the crossover

and mutation operators, in order to create new indi-

viduals (offspring).

The value provided by the objective function de-

ﬁnes how adapted an individual is to solve the opti-

mization problem. The most adapted individuals have

a greater chance of surviving for the next generation,

while the less adapted are eliminated; similar to what

is proposed by Darwin’s theory. This is an iterative

process in which at the end of each iteration all in-

dividuals are evaluated and ordered according to the

objective function value until a stopping criterion be

achieved (Haupt and Haupt, 2004; Sivanandam and

Deepa, 2008).

Some genetic algorithms variants are combined

with a local search method to present the global so-

lution with better precision. These algorithms are

considered hybrid genetic algorithms. In this work,

the Nelder Mead method (Nelder and Mead, 1965) is

used to improve the solution precision. The Hybrid

Genetic Algorithm is represented in the Algorithm 1.

A Genetic Algorithm depends substantially on the

efﬁciency of genetic operators. These operators are

responsible for new individuals creation, diversiﬁ-

cation and maintenance of adaptation characteristics

acquired in previous generations (Sivanandam and

Deepa, 2008). The most useful operators are the se-

lection, crossover and mutation which are used in this

work and described below.

The selection operator selects elements of the cur-

rent population in order to produce more individuals

(offspring). It has the mission to guide the algorithm

for promising areas, where the probability to ﬁnd

the optimum solution is higher (Pham and Karaboga,

Algorithm 1 : Hybrid Genetic Algorithm with Constant

Rates Operators.

Generates a randomly population of individuals,

, with dimension N

pop

Set k = 0.

Set the operators rates.

while stopping criterion is not met do

Set k = k +1.

= Apply selection procedure in N

pop

= Apply crossover procedure in N

keep

000

= Apply mutation procedure in N

keep

k+1

= N

pop

best individuals of {P

∪ P

∪

000

Apply the local search method in the best solution

obtained by genetic algorithm.

2000; Sivanandam and Deepa, 2008). This procedure

is based on the survival probability that depends on

the objective function value for each individual.

The crossover operator is used to create new in-

dividuals from surviving individuals selected through

the selection operator. The crossover procedure is re-

sponsible for recombining the individuals characteris-

tic during the reproduction process, with this process

it is possible for the offspring to inherit characteristics

of previous generations (Pham and Karaboga, 2000;

Sivanandam and Deepa, 2008).

The mutation operator is responsible for diversify-

ing the existing population allowing the search for the

solution in promising areas and avoiding premature

convergence in local points. This process helps the al-

gorithm to escape from local optimum points because

it slightly modiﬁes the search direction and introduces

new genetic structures in the population (Pham and

Karaboga, 2000; Sivanandam and Deepa, 2008).

Each genetic operator has a speciﬁc rate that de-

termined how many individuals will be used and gen-

erated in each genetic procedure. In the traditional

GA the rates are constant values for all evolutionary

process. However, there is not a consensus in the lit-

erature about which value should be used on each op-

erator. On the other hand, many works in literature

assert the intuitive idea that crossover and mutation

rates should not be constant throughout the evolution-

ary process (Vannucci and Colla, 2015), but should

rather vary in the different phases of the search. Once

again there is no consensus on the values of the rates

and how to calculated them. For these reasons the de-

termination of operators rates is normally deﬁned by

individual problem analysis or they are calculated by

means of trial-and-error (Lin et al., 2003).

An Improvement of Genetic Algorithm based on Dynamic Operators Rates Controlled by the Population Performance

389

3 RELATED WORKS

Several versions of genetic operators are described in

the literature and many studies have been done to im-

prove these operators’ performance, see for example

ano

ıkov

a et al., 2017; Xu et al., 2018; Das and

Pratihar, 2019). The problem of operator rates calcu-

lation is considered a challenging problem in the liter-

ature either for constant rates or dynamic approaches.

The optimal rates setting is likely to vary for differ-

ent problems (Pham and Karaboga, 2000), but it is a

time consuming task. For these reasons, some studies

focused on determining good control rates values for

the genetic operators.

For constants rates and binary individuals rep-

resentation, (De Jong, 1975) recommends a range

of [50,100] individuals in the population size, 60%

for crossover rate and 0.1% for mutation rate. The

(Schaffer et al., 1989) suggests a range of [20-30] in-

dividuals in the population, [75% - 95%] for crossover

rate and [0.5% - 1%] for mutation rate, while (Grefen-

stette, 1986) uses a population of 30 individual, 95%

for crossover and 1% for mutation. As it is possi-

ble to see, these ranges have large variations, being

inconclusive and strongly dependent on the research

knowledge and the problem variations.

On the other hand, some studies concentrate ef-

forts on adapting the control parameters during the

optimization process. These techniques involve ad-

justing the operators’ rates according to problems

characteristic as the search process, the trend of the

ﬁtness, stability (Vannucci and Colla, 2015), ﬁtness

value (Priya and Sivaraj, 2017; Pham and Karaboga,

2000), or based on experiments and domain expert

opinions (Li et al., 2006).

In order to adjust the mutation and crossover rates,

(Vannucci and Colla, 2015) uses a fuzzy inference

system to control the operators’ variation. Accord-

ing to the authors, this method also accelerates the at-

tainment of the optimal solution and avoid premature

stopping in a local optimum through a synergic effect

of mutation and crossover.

Another approach is presented in (Xu et al., 2018),

which uses the GA method to solve the traveling

salesman problem optimizing the mutation charac-

ters. In this case, a random cross mapping method and

a dynamic mutation probability are used to improve

the algorithm. In the approach, the crossover op-

eration varies according to the randomly determined

crossover point and the mutation rate is dynamically

changed according to population stability.

In (Das and Pratihar, 2019) the crossover operator

guided by the prior knowledge about the most promis-

ing areas in the search region is presented. In this

approach four parameters are deﬁned to control the

crossover operator: crossover probability, variable-

wise crossover probability, multiplying factor, direc-

tional probability. It was noted the use of the direc-

tional information helps the algorithm to search in

more potential regions of the variable space.

In (Whitley and Hanson, 1989) is proposed an

adaptive mutation through monitoring the homogene-

ity of the solution population by measuring the Ham-

ming distance between the parents’ individuals during

the reproduction. Thereby, the more similar the par-

ents, the higher mutation probability.

In study of (Fogarty, 1989) adopts the same mu-

tation probability for all parts of an individual and

then decreased to a constant level after a given num-

ber of generations. Another strategy is presented in

(Pham and Karaboga, 2000), upper and lower limits

are chosen for the mutation rate and within those lim-

its the mutation rate is calculated for each individual,

according to the objective function value.

According to (Pham and Karaboga, 2000) in the

ﬁrst 50 generations there are few good solutions in

the population, so in the initial stage high mutation

rate is preferable to accelerate the search. In contrast,

(Shimodaira, 1996) supports high mutation rates at

the end of the process, in order to come out from lo-

cal optima where the algorithm can be stuck. For the

references presented is possible to verify that there is

no consensus on the values of the rates. For this rea-

son, in this work the rates are dynamically established

by the analysis of population performance throughout

the evolutionary process.

4 DYNAMIC GENETIC

ALGORITHM

This study presents a dynamic Genetic Algorithm

with continuous variable individual representation

that is initially randomly generated (Haupt and Haupt,

2004). Through analysis of the GA behavior, it was

noted that the objective function standard deviation

of the beginning evolutionary process is higher, as ex-

pected because the generation of the initial population

is random. For this reason, the individuals are very

dispersed in the search region. For the same reason,

in the ﬁrst iterations, the population amplitude is also

very higher. As the search process evolves, the popu-

lation tends to concentrate in speciﬁc feasible regions,

in which the chance to ﬁnd the optimum solution is

higher (promising regions). This causes a decrease in

the standard deviation and amplitude of the objective

function value. At the end of the evolutionary pro-

cess, both amplitude and standard deviation tend to

ND2A 2020 - Special Session on Nonlinear Data Analysis and Applications

390

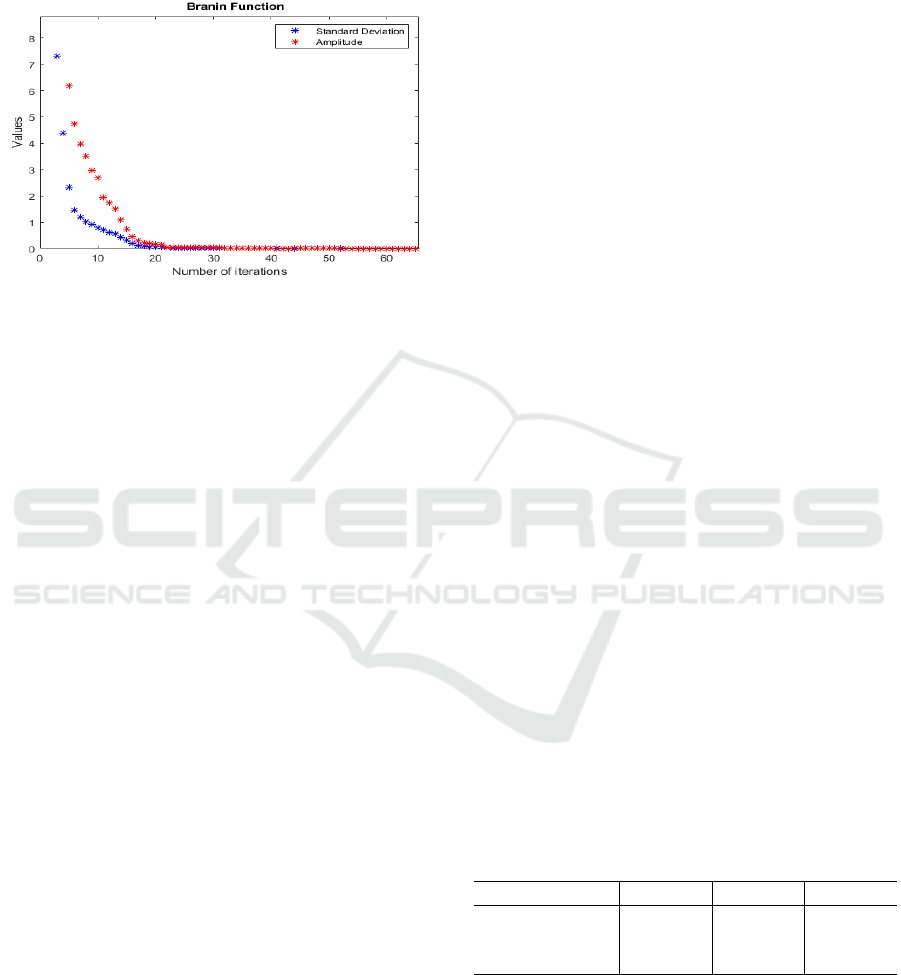
zero, due to the population convergence to the opti-

mum solution point. An example of this behavior is

presented in Figure 1, for the Branin function, consi-

dering an approximation in the initial interactions.

Figure 1: Standard deviation and amplitude of Branin func-

tion.

In this work the individuals are randomly selected

for the crossover and mutation procedures. The two-

point crossover and continue mutation procedures are

used, similar as in (Bento et al., 2013). The rates

variations are controlled by the amplitude and the

standard deviation of each generation and the ampli-

tude differences between successive populations. Be-

sides, a new stopping criterion is also proposed to be

used in conjunction with the traditional ones.

The results of the proposed algorithm are com-

pared with the executions of a hybrid Genetic Algo-

rithm presented in (Bento et al., 2013), considering

the Nelder Mead method, as local search. In (Bento

et al., 2013) the continuous representation is used, and

the follow constants rates are suggested: population

size equal 100 individuals, 0.5 × N

pop

individuals in

selection procedure and 0.25 × N

pop

individuals for

crossover and mutation procedures.

4.1 Determination and Control of the

Operators Rates

By the algorithm analysis is easy to note that the al-

gorithm has different properties throughout the evolu-

tionary process. For this reason, three different phases

were identiﬁed according to the amplitude and stan-

dard deviation patterns observed in the algorithm and

by literature review and described in the following

condition

| f (x

) − f (x

pop

)| ≤ ε ∧ s

≤ ε,

where f (x

) and f (x

pop

) are the best and the worst

objective values in the current population, s

is the

standard deviation of the current population and ε ∈

{ε

, e

}. The three search phases are described in de-

tail as follows.

• Phase 1 - Initial: in this phase the population

amplitude and standard deviation are higher and

there are few good solutions in the population.

For these reasons, higher rates are considered to

accelerate the search. This phase initiates when

the algorithm starts and stops when the population

standard deviation and amplitude be smaller than

, and a condition of k

iterations be exceeded.

• Phase 2 - Development: the Development phase

starts immediately after Phase 1 and ends when

the population amplitude and standard deviation

are smaller than ε

and exceed at least k

itera-

tions. The condition of k

iteration was deﬁned

to avoid the algorithm remain too short time at

this phase, because depending on the problem the

value is quickly reached and consequently the

possible solutions are not so well explored. In this

second phase the operator parameters should not

be so higher as in the initial phase because the

search is concentrated in the promising areas ob-

tained in the ﬁrst phase. At the end of this phase

the algorithm has already found the optimum re-

gion, but needs to reﬁne the optimum solution.

• Phase 3 - Reﬁnement: this phase has the aim to

reﬁne the solution. The amplitude and standard

deviation are small, that is possible to conclude

that the optimum solution is very close to being

achieved. The rates used in this phase are smaller

than in the other phases because few modiﬁca-

tions are needed. This phase starts immediately

after Phase 2, and continues until a stopping

criterion be achieved.

This work not established constants parameters in

the different phases. Thus, an initial value for each

operator rate is determined in the beginning of each

phase as presented in Table 1.

Table 1: Initial operator rates for each phase.

Genetic Operator Phase 1 Phase 2 Phase 3

Selection 0.7 × N

pop

0.6 × N

pop

0.5 × N

pop

Crossover 0.5 × N

pop

0.4 × N

pop

0.3 × N

pop

Mutation 0.4 × N

pop

0.3 × N

pop

0.2 × N

pop

In the second and third phases, the rate values can

vary 10% considering the initial value. This decision

is based on the amplitude difference between succes-

sive populations. Thereby, if the amplitude difference

between k and k − 1 iterations is smaller than ε

ph2

in the second phase, or smaller than ε

ph3

in the third

phase, the rates increase 1%, otherwise decrease 1%.

An Improvement of Genetic Algorithm based on Dynamic Operators Rates Controlled by the Population Performance

391

This strategy is designed to stimulate small modiﬁ-

cations in the algorithm search and prevent it from

getting stuck at local points. The codiﬁcation of the

proposed algorithm is shown in the algorithm 2.

Algorithm 2: Hybrid Genetic Algorithm with Dynamic Op-

erators Rates.

Generates a randomly population of individuals,

, with dimension N

pop

Set k = 0.

while stopping criterion is not met do

Set k = k +1.

Identify the Phase and update the operator rates

if necessary

= Apply selection procedure in N

pop

= Apply crossover procedure in N

keep

000

= Apply mutation procedure in N

keep

k+1

= N

pop

best individuals of {P

∪ P

∪

000

Apply the local search method in the best solution

obtained by genetic algorithm.

4.2 Stopping Criterion

In the third phase, the algorithm is very close to the

optimum solution and few modiﬁcations are done at

each iteration in order to preserve the good results al-

ready found. For this reason, it not useful to waste ex-

ceeding time in this phase. In this sense, the following

criterion is proposed that can be used in conjunction

with the other criterion already used, as the maximum

number of generation, time limit, number of function

evaluation, minimum error, etc.

This proposed stopping criterion consists of ana-

lyzing the population evolution in the Phase 3. There-

fore, if the standard deviation and amplitude differ-

ences are smaller than 10

−10

in a N

pop

× n in succes-

sive iterations, the algorithm stops. With this strategy,

the stopping criterion adapts to different optimization

problems.

5 NUMERICAL RESULTS

The dynamic Genetic Algorithm variant and the stop-

ping criterion proposed in this study are validated us-

ing six benchmark functions deﬁned in the literature:

Branin function (dimension 2), Easom function (di-

mension 2), Ackley Function (dimension 3), Rosen-

brock function (dimension 3), Sum Squares function

(dimension 4) and Levy function (dimension 5) (Gra-

macy and Lee, 2012; Jamil and Yang, 2013; Sur-

janovic and Bingham, ).

These benchmark functions have several proper-

ties that can be truly useful to test the algorithm per-

formance in an unbiased way (Jamil and Yang, 2013).

Besides, the results are compared with the Genetic Al-

gorithm with constant rates proposed in (Bento et al.,

2013).

The numerical results were obtained using a In-

tel(R) Core (TM) i3 CPU M920 @2.67GHz with 6

GB of RAM. It was considered the following parame-

ters k

= 50, ε

= 1, k

= 150, ε

= 10

−3

, ε

ph2

= 10

−3

ph3

= 10

−6

, N

pop

= 100 individuals at each genera-

tion, and each problem was executed 100 times, since

the Genetic Algorithm is a stochastic method.

The average of the objective function value, f

∗

the number of iterations needed, k, the number of

function evaluation f un.eval and the time needed in

seconds, T, are presented in the Tables 2 and 3 for the

Genetic Algorithm with constants rates and dynamic

rates, respectively.

Table 2: GA with constant rates algorithm results.

Function f ∗ k f un.eval T

Branin 3.9789 × 10

−1

1040 54131 2.18

Easom −9.9900 × 10

−1

1080 56191 2.29

Ackley 1.5100 × 10

−4

2765 143848 5.88

Rosenbrock 1.5120 × 10

−9

5404 281145 11.28

S. Squares 1.7937 × 10

−6

1526 79397 3.31

Levy 4.6310 × 10

−10

872 45499 2.34

Table 3: GA with dynamic rates algorithm results.

Function f ∗ k f un.eval T

Branin 3.9789 × 10

−1

410 36439 1.36

Easom −9.9900 × 10

−1

415 36789 1.39

Ackley 1.0500 × 10

−4

881 75030 2.80

Rosenbrock 1.5945 × 10

−9

1936 161748 5.88

S. Squares 2.1476 × 10

−6

803 68618 2.59

Levy 4.5925 × 10

−10

448 39389 1.87

Analyzing Tables 2 and 3 is possible to conclude

that the optimum solution obtained by both algo-

rithms is very similar. However, the performance of

the GA with dynamic rates is higher because the opti-

mum solution for all problems tested was found using

fewer iterations, function evaluations in a short time

than the Genetic Algorithm with constant rates.

In order to compare the accuracy of the proposed

approach, the Euclidean distance was evaluated and

compared between the results obtained and the opti-

mum solution presented in the literature (Literature).

Table 4 presents the numerical results.

It is possible to observe in Table 4 that the op-

timum solution obtained by both algorithms is very

ND2A 2020 - Special Session on Nonlinear Data Analysis and Applications

392

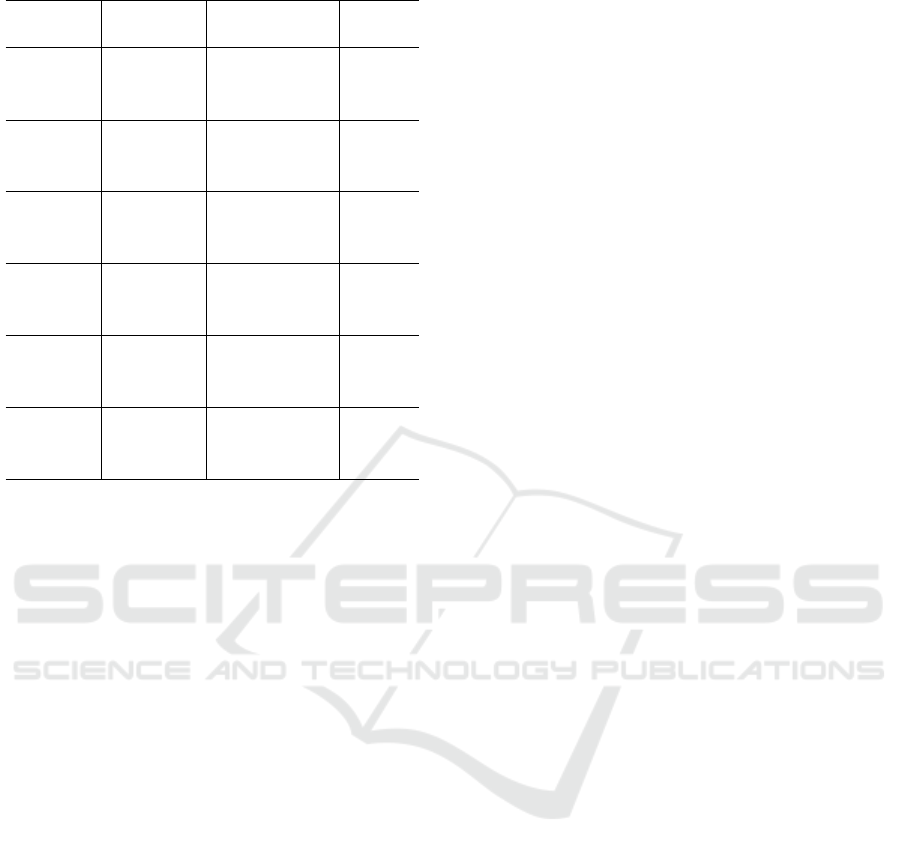
Table 4: Average of euclidean distances comparison.

Function Method

Optimum

Solution

Euclidean

Distance

Branin

Literature 3.9789 × 10

−1

Constant rates 3.9789 × 10

−1

1 × 10

−3

Dynamic rates 3.9789 × 10

−1

1 × 10

−3

Easom

Literature -1 0

Constant rates−9.9900 × 10

−1

3 × 10

−2

Dynamic rates−9.9900 × 10

−1

3 × 10

−2

Ackley

Literature 0 0

Constant rates 1.5100 × 10

−4

3 × 10

−4

Dynamic rates 1.0500 × 10

−4

2 × 10

−4

Rosenbrock

Literature 0 0

Constant rates 1.5120 × 10

−9

3 × 10

−5

Dynamic rates 1.5945 × 10

−9

3 × 10

−5

S. Squares

Literature 0 0

Constant rates 1.7937 × 10

−6

9 × 10

−4

Dynamic rates 2.1476 × 10

−6

8 × 10

−4

Levy

Literature 0 0

Constant rates 4.6310 × 10

−10

5 × 10

−5

Dynamic rates 4.5925 × 10

−10

5 × 10

−5

close to the optimum solution presented in the litera-

ture, which proves the efﬁciency of the proposed ap-

proach.

6 CONCLUSION AND FUTURE

WORK

This work presents a new variation of hybrid Ge-

netic Algorithm considering dynamic operators rates.

The obtained results were very satisfactory since

the Genetic Algorithm combined with dynamic rates

demonstrated excellent ability to found the optimal

solution and when compared to the Genetic Algo-

rithm with constant rates, the approach stands out

since it requires less computational effort. Since it

was used benchmark functions with different proper-

ties, the Genetic Algorithm with dynamic rates can be

applied to different optimization problems. As future

work, it is intended to use machine learning, as Fuzzy

Systems and Artiﬁcial Neural Networks, to identify

patterns in the Genetic Algorithm and use this infor-

mation to improve the dynamic rates.

ACKNOWLEDGEMENTS

This work has been supported by FCT — Fundac¸

para a Ci

encia e Tecnologia within the Project Scope:

UIDB/5757/2020.

REFERENCES

Bento, D., Pinho, D., Pereira, A. I., and Lima, R. (2013).

Genetic algorithm and particle swarm optimization

combined with powell method. In 11th International

Conference of Numerical Analysis and Applied Math-

ematics, volume 1558, pages 578–581. ICNAAM

2013.

Das, A. K. and Pratihar, D. K. (2019). A directional

crossover (dx) operator for real parameter optimiza-

tion using genetic algorithm. Applied Intelligence,

49:1841––1865.

De Jong, K. A. (1975). An analysis of the behavior of a

class of genetic adaptive systems. PhD thesis, Univer-

stity of Michigan, Ann Arbor, Michigan.

Fogarty, T. C. (1989). Varying the probability of mutation in

the genetic algorithm. In Proceedings of the Third In-

ternational Conference on Genetic Algorithms, pages

104–109, San Francisco, CA, USA. Morgan Kauf-

mann Publishers Inc.

Ghaheri, A., Shoar, S., Naderan, M., and Hoseini, S. S.

(2015). The applications of genetic algorithms in

medicine. Oman Medical Journal, 30(6):406–416.

Gramacy, R. B. and Lee, H. K. (2012). Cases for the

nugget in modeling computer experiments. Statistics

and Computing, 22(3):713–722.

Grefenstette, J. (1986). Optimization of control parameters

for genetic algorithms. IEEE Trans. Syst. Man Cy-

bern., 16(1):122–128.

Haupt, R. and Haupt, S. E. (2004). Practical Genetic Algo-

rithms. John Wiley & Sons, 2 edition.

Holland, J. H. (1992). Adaptation in natural and artiﬁcial

systems: an introductory analysis with applications to

biology, control, and artiﬁcial intelligence. University

of Michigan Press, Cambridge, MA, USA.

Jamil, M. and Yang, X. (2013). A literature survey of bench-

mark functions for global optimization problems. In-

ternational Journal of Mathematical Modelling and

Numerical Optimisation, 4(2):150–194.

ano

ıkov

a, L., Herda, M., and Haviar, M. (2017). Hybrid

genetic algorithms with selective crossover for the ca-

pacitated p-median problem. Central European Jour-

nal of Operations Research, 25(1):651–664.

Li, Q., Tong, X., Xie, S., and Liu, G. (2006). An im-

proved adaptive algorithm for controlling the proba-

bilities of crossover and mutation based on a fuzzy

control strategy. In Sixth International Conference on

Hybrid Intelligent Systems (HIS’06), Rio de Janeiro,

Brazil. IEEE.

Lin, W., Lee, W., and Hong, T. (2003). Adapting crossover

and mutation rates in genetic algorithms. Journal

of Information Science and Engineering, 19(5):889–

903.

Mitchell, M. (1998). An Introduction to Genetic Algo-

rithms. MIT Press, Cambridge, MA, USA, 1 edition.

Nelder, J. A. and Mead, R. (1965). A simplex method

for function minimization. The Computer Journal,

7(4):308–313.

An Improvement of Genetic Algorithm based on Dynamic Operators Rates Controlled by the Population Performance

393

Pham, D. and Karaboga, D. (2000). Intelligent optimisa-

tion techniques: genetic algorithms, tabu search, sim-

ulated annealing and neural networks. Springer, 1

edition.

Priya, R. D. and Sivaraj, R. (2017). Dynamic ge-

netic algorithm-based feature selection and incom-

plete value imputation for microarray classiﬁcation.

Current Science, 112(1):126–131.

Schaffer, J. D., Caruana, R. A., Eshelman, L. J., and Das, R.

(1989). A study of control parameters affecting online

performance of genetic algorithms for function opti-

mization. In Proceedings of the Third International

Conference on Genetic Algorithms, pages 51–60, San

Francisco, CA, USA. Morgan Kaufmann Publishers

Inc.

Shimodaira, H. (1996). A new genetic algorithm using

large mutation rates and population-elitist selection

(galme). In Proceedings of the 8th International Con-

ference on Tools with Artiﬁcial Intelligence, ICTAI

’96, pages 25–32, Washington, DC, USA. IEEE Com-

puter Society.

Sivanandam, S. N. and Deepa, S. N. (2008). Introduction to

Genetic Algorithms. Springer, 1 edition.

Surjanovic, S. and Bingham, D. Virtual library of simula-

tion experiments: Test function and datasets.

Vannucci, M. and Colla, V. (2015). Fuzzy adaptation of

crossover and mutation rates in genetic algorithms

based on population performance. Journal of Intel-

ligent & Fuzzy Systems, 28(4):1805–1818.

Whitley, D. and Hanson, T. (1989). Optimizing neural net-

works using faster, more accurate genetic search. In

Proceedings of the Third International Conference on

Genetic Algorithms, pages 391–396, San Francisco,

CA, USA. Morgan Kaufmann Publishers Inc.

Xu, J., Pei, L., and Zhu, R. (2018). Application of a ge-

netic algorithm with random crossover and dynamic

mutation on the travelling salesman problem. Proce-

dia Comput. Sci., 131:937–945.

ND2A 2020 - Special Session on Nonlinear Data Analysis and Applications

394