Activation Adaptation in Neural Networks

Farnoush Farhadi

, Vahid Partovi Nia

1,2 a

and Andrea Lodi

1 b

Polytechnique Montreal,2900 Edouard Montpetit Blvd, Montreal, Quebec H3T 1J4, Canada

Huawei Noah’s Ark Lab, Montreal Research Centre, 7101 Park Avenue, Quebec H3N 1X9, Canada

Keywords:

Activation Function, Convolution, Neural Networks.

Abstract:

Many neural network architectures rely on the choice of the activation function for each hidden layer. Given

the activation function, the neural network is trained over the bias and the weight parameters. The bias catches

the center of the activation, and the weights capture the scale. Here we propose to train the network over a

shape parameter as well. This view allows each neuron to tune its own activation function and adapt the neuron

curvature towards a better prediction. This modiﬁcation only adds one further equation to the back-propagation

for each neuron. Re-formalizing activation functions as a comulative distribution function (cdf) generalizes

the class of activation function extensively. We propose to generalizing towards extensive class of activation

functions and study: i) skewness and ii) smoothness of activation functions. Here we introduce adaptive

Gumbel activation function as a bridge between assymmetric Gumbel and symmetric sigmoid. A similar

approach is used to invent a smooth version of ReLU. Our comparison with common activation functions

suggests different data representation especially in early neural network layers. This adaptation also provides

prediction improvement.

1 INTRODUCTION

Neural networks achieved considerable success in im-

age, speech, and text classiﬁcation. In many neural

networks only bias and weight parameters are learned

to ﬁt the data, while the activation function of each

neuron is pre-speciﬁed to sigmoid, hyperbolic tan-

gent, ReLU, etc. From a theoretical standpoint, a

neural network reasonably wide and deep, approx-

imates an arbitrarily complex function independent

of the chosen activation function, see (Hornik et al.,

1989) and (Cho and Saul, 2010). However, in prac-

tice, the prediction performance and the learned rep-

resentation depends on hyperparameters such as net-

work architecture, number of layers, regularization

function, batch size, initialization, activation function,

etc. Despite large studies on network hyperparam-

eter tuning, there have been few studies on how to

choose an appropriate activation function. The choice

of activation function changes learning representation

and also affects the network performance (Agostinelli

et al., 2014). We propose let data estimate the activa-

tion function during training by developing a ﬂexible

activation function. We demonstrate how to formalize

https://orcid.org/0000-0001-6673-4224

https://orcid.org/0000-0002-5101-095X

this such activations and show how to embed it in the

back-propagation.

Developing an adaptive activation function helps

fast training of deep neural networks, and has at-

tracted attention, see for instance (Zhang and Wood-

land, 2015), (Agostinelli et al., 2014), (Agostinelli

et al., 2014), (Jarrett et al., 2009), (Glorot et al.,

2011), (Goodfellow et al., 2013), (Springenberg and

Riedmiller, 2013) and recently (Dushkoff and Ptucha,

2016), (Hou et al., 2016), (Hendrycks and Gimpel,

2016), (Hou et al., 2017) and (Klambauer et al.,

2017). Here, we introduce adaptive activation func-

tions by combining two main tools: i) looking at acti-

vation as a cumulative distribution function (cdf) and

ii) making an adaptive version by equipping a distri-

bution with a shape parameter. The shape parameter

is continuous, so that an update equation can be added

in back-propagation. Here, we focus on the simple

architecture of LeNet5, but this idea can be used to

equip more complex and deep architectures with ﬂex-

ible activations (Ramachandran et al., 2018).

There has been a surge of work in modifying the

ReLU. Leaky ReLU is one of the most famous modiﬁ-

cations that gives a slight negative slope on a negative

argument (Maas et al., 2013). Another modiﬁcation

called ELU (Clevert et al., 2015) attempts exponen-

Farhadi, F., Nia, V. and Lodi, A.

Activation Adaptation in Neural Networks.

DOI: 10.5220/0009175102490257

In Proceedings of the 9th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2020), pages 249-257

ISBN: 978-989-758-397-1; ISSN: 2184-4313

249

tial decrease of the slope from a predeﬁned value to

zero. Taking a mixture approach, (Qian et al., 2018)

proposed a mixed function of leaky ReLU (Maas

et al., 2013) and ELU (Clevert et al., 2015) as an

adaptive function, that could be learned in a data-

driven way unlike SeLU (Klambauer et al., 2017). In-

spired by (Agostinelli et al., 2014), (Zhang and Wood-

land, 2015) (Qian et al., 2018) and (Klambauer et al.,

2017), we study the effect of i) the asymmetry and ii)

the smoothness of activation function. Our approach

can build recntly proposed modiﬁcations for quan-

tized training such as SignSWISH of (Darabi et al.,

2019) and foothill of (Belbahri et al., 2019). The

ﬁrst study is performed by introducing an adaptive

asymmetric Gumbel activation that changes its shape

towards the symmetric sigmoid function. The sec-

ond study is achieved by equipping the ReLU func-

tion with a smoothness parameter which generalizes

the existing adaptive activations through distribution

functions. In both cases, we tune the shape parameter

for each neuron independently by adding an updating

equation to back-propagation.

The performance of two fully-connected neural

networks and a convolutional network are compared

on simulated data, MNIST benchmark, and Movie re-

view sentiment data. As an application, we use the

classical LeNet5 architecture (Kim, 2014) to classify

the users’ intention using URLs they navigated on

their browser.

2 ADAPTIVE ACTIVATIONS

We recommend to perceive the activation function as

a cumulative distribution function bounded on [0, 1].

Common activation functions are bounded, but not

necessarily to [0, 1] like hyperbolic tangent. A lo-

cation and scale transformation is sufﬁcient to trans-

form their range if necessary. However, still widely-

used activations such as ReLU or leaky ReLU are un-

bounded. One may decompose unbounded activation

functions into two components: i) a bounded compo-

nent and ii) an unbounded component, and only adapt

the bounded ingredient through a continuous cumula-

tive distribution function.

2.1 Adaptive Gumbel

One of the common activation functions is the sig-

moid function that maps a real value to [0, 1] similar

to cumulative distribution functions. Although sig-

moid is rarely used in convolution layers, still it is

widely used in softmax layer and attention type mod-

els that revolutionized in natural language processing

(Vaswani et al., 2017). More precisely, the sigmoid

function is the cumulative distribution function of the

symmetric and bell-shaped logistic distribution. An

asymmetric activation can be developed using a cu-

mulative distribution function of a skewed distribu-

tion like Gumbel, for example. Gumbel distribution is

the asymptotic distribution of extreme values such as

minimum or maximum (Coles et al., 2001). A shape

parameter that pushes a sigmoid distribution function

away from the logistic and more towards a Gumbel

distribution deﬁnes a sort of a shape parameter. Our

proposed adaptive Gumbel activation is

(x) = 1 − {1 + αexp(x)}

−

α ∈ IR

, x ∈ IR.

(1)

The above form is inspired by Box-Cox transfor-

mation (Box and Cox, 1964) for binary regression.

The simplest form of neural network with no hidden

layer is a binary regression in which (1) generalizes

logistic regression towards complementary log-log re-

gression by tuning α ∈ (0, 1], see Figure 1 (left panel).

The Gumbel cumulative distribution function arises in

the limit while α → 0. The foothill function of (Bel-

bahri et al., 2019) and SignSwish function of (Darabi

et al., 2019) can be re-formalized in this context.

2.2 Adaptive ReLU

The ReLU activation function

σ(x) = max(0, x)

is unbounded, unlike the sigmoid or hyperbolic tan-

gent. One may re-write the ReLU activation as

σ(x) = x∆(x),

where ∆(x) is the cumulative distribution function of

a degenerate distribution. The function ∆(x) is also

known as Heaviside function and coincides with the

integral of the Dirac delta function. We propose to

replace ∆(x) with a smooth cumulative distribution

function ∆

(x) such as the exponential cumulative

distribution function

∆

(x) = (1 − e

−αx

{x>0}

(x),

(x) = x∆

(x), α ∈ IR

, x ∈ IR, (2)

where I

(x) is the indicator function on set A.

In (2) we recommend to equip the degenerate dis-

tribution ∆(x) with a smoothing parameter α. Any

continuous random variable with a scale parameter

is a convenient choice for ∆

(x). A random vari-

able with inﬁnitesimal scale behaves like a degener-

ate distribution, so ∆(x) is retrieved when the scale

tends to zero, or equivalently α → ∞. The general-

ized ReLU (2) coincides with the SWISH activation

ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods

250

−10 −5 0 5 10

−0.5 0.0 0.5 1.0

Adaptive Gumbel

α=1

α=2

α=5

−1.0 −0.5 0.0 0.5 1.0

−0.5 0.0 0.5 1.0

Adaptive Relu

Figure 1: Adaptive Gumbel activation (left panel) and adap-

tive ReLu activation (right panel) for α = 1, 2, 5.

function (Ramachandran et al., 2018) if ∆

(x) is the

logistic cumulative distribution function

∆

(x) = (1 + e

−αx

)

−1

. (3)

The SiLU (Elfwing et al., 2018) is a special case of

(3) while α = 1.

One may show that the proposed parameterization

preserves model identiﬁability in simple Bernoulli re-

gression model.

Theorem 1. a binary regression with the adaptive ac-

tivation (1) is identiﬁable.

See Appendix for the proof.

3 BACK-PROPAGATION

Deﬁne the vector of linear predictors of layer l as

= [η

, . . . , η

]

where

= w

+ w

, i = 1, . . . , n,

and the lth hidden layer output h

= σ(η

), in which

= w

+ w

l−1

Traditionally, σ(x) is sigmoid or ReLU activation.

The adapted back-propagation uses the conventional

back-propagation, but each neuron carries its own ac-

tivation function σ

(x). The adaptation parameter α

for each neuron is trained along with bias and weights

, w]

Suppose the vector of parameters for a neuron in

layer l is θ

= [α

, w

] and the network is trained

using loss function L(.).

In practice, L(.) is the entropy loss for classiﬁ-

cation, and the squared error loss for regression, pe-

nalized with an L

norm

∑

or an L

norm

∑

|θ

upon convenience. The updating back-propagation

rule, given a learning rate γ > 0, for a neuron in layer

l is

← w

− γ

∂L

∂w

, (4)

← w

− γ

∂L

∂w

, (5)

← α

− γ

∂L

∂α

, (6)

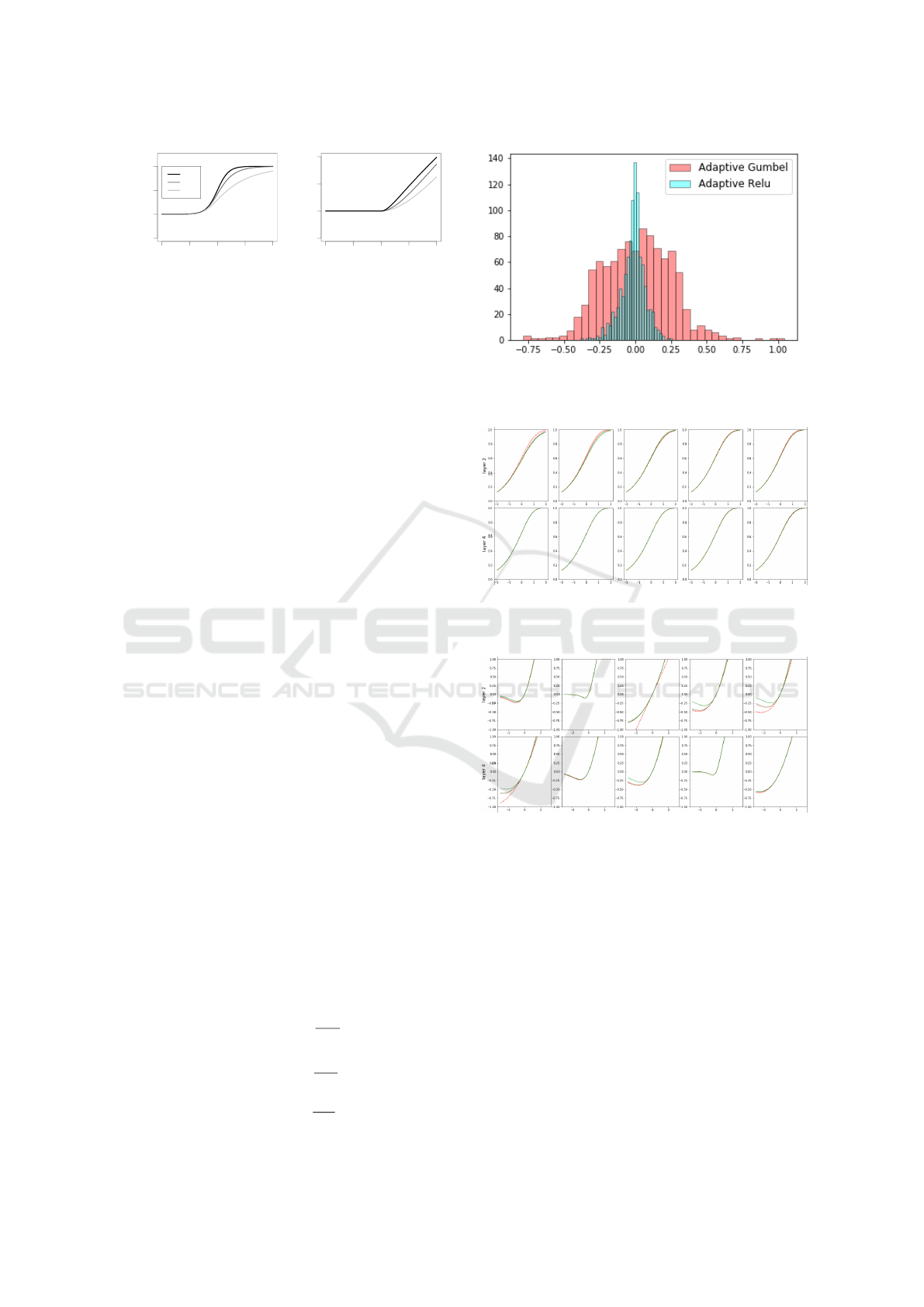
Figure 2: Histogram of ﬁtted α for Adaptive ReLu (blue)

and Adaptive Gumbel (red) activation functions for simu-

lated data with one hidden layer.

Figure 3: Fitted adaptive Gumbel activations on layer 2 and

layer 4 of an eight hidden layer network. Adapted activa-

tions vary more often in earlier layers, see also Figure 4.

Figure 4: Fitted adaptive ReLU activations on layer 2 and

layer 4 of an eight hidden layer network. Adapted activa-

tions vary more often in earlier layers, see also Figure 3.

where (4) updates the bias, (5) updates the weights,

and (6) adapts the activation function. Note that one

may choose different learning rates for each equation.

We recommend to reparametrize (6) with e

in nu-

merical computations to enforce α > 0.

4 BENCHMARKS

Here, we compare the adaptive modiﬁcation in three

datasets. One dataset is a simulated fully-connected

network in Section 4.1, where the true activation func-

Activation Adaptation in Neural Networks

251

tion and true labels are known. Furthermore, we eval-

uate activation adaptation on convolutional models on

the MNIST image data in Section 4.2, and on Movie

Review text data in Section 4.3.

4.1 Simulated Data

Our objective in this experiment is to understand how

the choice of activation function affects the perfor-

mance of the network. We simulated data from two

fully-connected neural networks: i) a network with

only 1 hidden layer, and ii) with 8 hidden layers, each

layer with 10 neurons. Activation functions are ﬁxed

to ReLU and sigmoid in data simulation setup. Ac-

cording to works in (LeCun et al., 1998b) and recently

in (Krizhevsky et al., 2012) and (Glorot and Bengio,

2010), several weight initialization and different com-

bination of number of input and output units in weight

initialization formulation along with different type of

activation functions could be employed in deep neu-

ral networks. In this paper, biases were initialized

from N (0, 0.5) in simulated models and biases in ﬁt-

ted models are initialized by formulation suggested in

(LeCun et al., 1998b). The original weights in simu-

lated models were initialized from a mixture of two

normals N

(1, 0.5) and N

(−1, 0.5) with an equal

proportion and weights in ﬁtted models initialized by

(LeCun et al., 1998b) settings.

The simulated data set includes 10

000 examples

of 10 features with a binary output. In each conﬁg-

uration, we have a fully-connected network with 10

neurons at each layer is trained with a ﬁxed learning

rate γ = .01, regularization parameters L

= .001 and

= .001, batch size = 20, and number of epochs =

2000 for both simulated and ﬁtted models. The learn-

ing rate, L

and L

regularization constants are tuned

using 5-fold cross-validation. The average results are

reported from a 5-fold cross validation as well.

The results summarized in Table 1 show that,

overall, adaptive Gumbel outperforms sigmoid.

Adaptive ReLU competes closely with ReLU in shal-

low networks, and slightly outperforms ReLU in

deeper networks. Figure 2 conﬁrms adaptive Gum-

bel and adaptive ReLU have different training range

for α. Figure 3 and Figure 4 depicts the learned acti-

vations in an eight hidden layer fully connected net-

work. Early layers have more variable learned activa-

tions, and often the last layers do not change much.

The deeper layers are more difﬁcult to learn.

We run several models with different number of

fully connected hidden layers from 1 to 8 including 1,

2, 4 and 8 layers. In Table 1, we aimed at studying the

effect of varying activation functions on the accuracy

of the predictions produced by the ﬁtted model com-

Table 1: Prediction accuracy for data simulated with sig-

moid (Sig), adaptive Gumbel (AGumb), ReLU and adaptive

ReLU (AReLU) in networks with 1 and 8 hidden layers.

The maximum standard error is 0.22.

simulated ﬁtted network

layers Sig AGumb ReLU AReLU

Sig 95.8 97.5 97.8 97.7

ReLU 96.1 97.4 98.2 98

Sig 83.7 83.8 81.8 81.9

ReLU 57.3 88.2 89.3 89.9

Figure 5: The LeNet5 architecture. Two convolutional lay-

ers, each layer followed by a max polling, and eventually a

fully-connected layer on top.

pared to its original counterpart when they have the

same number of hidden layers, same number of neu-

rons at each layer. Our goal was to understand how

accurately ﬁtted model could predict the class labels

at the end of training step while we increase the num-

ber of hidden layers from 1 (as a simple fully con-

nected multi-layer perceptron) to a very deeper one

with 8 hidden layers. In this paper we only present

the results for 1 and 8 hidden layers due to page limits.

For models with less layers, ﬁtting models with ReLU

or adaptive ReLU almost outperforms the other acti-

vation functions. For deeper models, ﬁtting models

with the adaptive Gumbel also exhibits a good perfor-

mance in competition with ReLU and adaptive ReLU.

As seen in this table, as the number of hidden lay-

ers increases, an expected drop in the performance

of all ﬁtted models is observed. Hence, it is evident

that there is no question to continue for deeper fully-

connected layers.

4.2 MNIST Data

Here we evaluate the performance of adapting acti-

vation on convolutional neural networks using hand-

written digits grayscale image data. Our convolu-

tional architecture is the classical LeNet5 (LeCun

et al., 1998a), but with adaptive activations. The orig-

inal LeNet5 use a modiﬁed hyperbolic tangent activa-

tion, but the ReLU activation is often used which pro-

vides a superior classiﬁcation accuracy. The LeNet5

architecture contains two convolutional layers, each

convolutional layer followed by a max-pooling layer.

A single fully-connected hidden layer is put on top

ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods

252

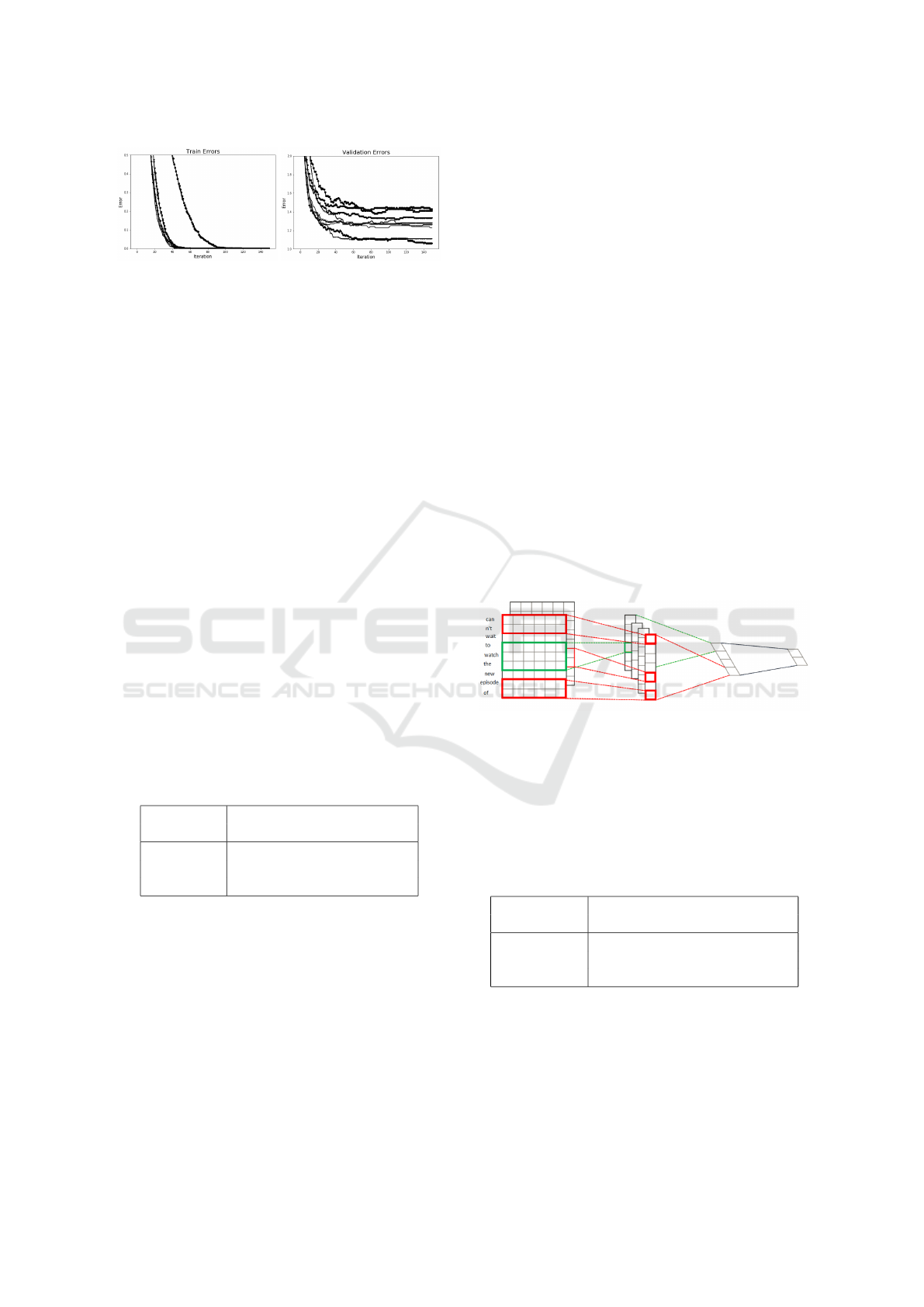
Figure 6: Training and validation error curves of different

adaptive models on MNIST data.

with 1000 neurons, see Figure 5.

Motivated from Section 4.1, we only keep ReLU

as the strong competitor, because adaptive Gumbel

always outperforms sigmoid. The network param-

eters are trained with batch normalization, learning

rate γ = 0.01, batch size 100, and iterated 150 epochs.

Figure 8 (left panel) shows are adaptive models con-

verge. Prediction accuracy is summarized in Table 2.

The best performance appears for adaptive Gumbel on

convolutional layer, closely followed by ReLU. Hy-

per parameters including learning rate for CNN mod-

els are chosen according to the primary settings of

LeNet5 implementation developed by Theano devel-

opment team. We select ﬁxed hyper parameters in

all CNN models to study the effect of changing acti-

vation functions on ﬁnal performance. The accuracy

of each model is reported by running the correspond-

ing algorithm on standard test set provided in MNIST

data.

Table 2: Convolutional architecture of LeNet5 on MNIST

data. The activations in the rows represent the activation

functions of convolutional layers, while the columns repre-

sent activations of fully-connected layers for ReLU, adap-

tive ReLU (AReLU), and adaptive Gumbel (AGumb) acti-

vations. The sigmoid activation is not reported as it was

beaten always by the other techniques. The accuracy is

computed over the standard test set.

Conv layer fully-connect layer

ReLU AReLU AGumb

ReLU 99.1 98.7 99.1

AReLU 98.8 98.9 98.9

AGumb 98.7 98.8 98.9

4.3 Movie Review Data

This time we try convolutional architecture on text

data over pre-trained word vectors. The data consists

of 2000 movie reviews, 1000 positive and 1000 nega-

tive (Pang and Lee, 2004).

These word vectors use the word2vec (Mikolov

et al., 2013) trained on 100 billion words of Google

News to embed a word in a vector of dimension

300. Word2vec transforms each word into a vector

such that the words semantics is preserved. A CNN

model with pre-trained word2vec vectors called static

in (Kim, 2014), is used in our experiments. In this

variant, the static CNN we use involves two convolu-

tional layers each of them followed by a max-pooling

layer and a fully-connected layer at the end. The

fully-connected network includes one hidden layer

with 100 neurons and a softmax output layer for bi-

nary text classiﬁcation. The hyper parameters in all

models are same including learning rate γ = 0.05, im-

age dimensions (img-w) = 300, ﬁlter sizes = [3, 4, 5],

each have 100 feature maps, batch size = 50, dropout

= 0.5, number of hidden layers = 1, number of neu-

ron = 100 and number of epochs = 50. For consis-

tency, same data, pre-processing and hyper-parameter

settings are used as reported in (Kim, 2014). Unlike

MNIST data, the Movie Review dataset does not have

a standard test set. So, we report the average accuracy

over 5-fold cross-validation in Table 3.

Again adaptive activation provides a better predic-

tion accuracy. Figure 8 (right panel) suggests that for

Movie review data is more difﬁcult to converge com-

pared to MNIST. We suspect this happens, because i)

text data carry less information compared to image,

ii) embedding may mas some information that exists

in the text.

Figure 7: Movie comments are embedded into a vector.

Then a CNN model classiﬁes the text to a ”positive review”

or ”negative review”.

Table 3: Convolutional architecture of LeNet5 on Movie

review data. The activations in the rows represent the acti-

vation functions of convolutional layers, while the columns

represent activations of fully-connected layers for ReLU,

adaptive ReLU (AReLU), and adaptive (AGumb) Gumbel

activations. The maximum standard error estimated using

5-fold cross-validation is 0.17.

Conv layer Fully-connect layer

ReLU AReLU AGumb

ReLU 79.1 79.1 78.9

AReLU 78.9 78.5 79.3

AGumbel 52.3 77.4 78.7

Accordingly, our empirical results show that us-

ing adaptive Gumbel, as the activation function, in

fully-connected layer is a good choice. Moreover,

adaptive ReLU works when it is applied in convolu-

tional layers. A comparison between the best results

of our experiments (reported from 5-fold crossvalida-

tion) and the state-of-the-art results by (Kim, 2014)

Activation Adaptation in Neural Networks

253

Figure 8: Training and validation error curves of different

adaptive models on Movie review data.

on the same version of Movie Review data shows that

our adaptive activation functions perform fairly good

and are match on Movie Review data in terms of ac-

curacy. Applying those adaptive activation functions

with ﬁne-tuning the hyper parameters may result in

further improvement.

5 APPLICATION

The sequence of URL clicks are gathered to study

user intentions by an international tech company. The

dataset is private and is extracted from a survey, while

anonymous visitors visited a commercial website over

a period of three months and their action is recorded

at the end of the session. In those surveys, visitors

are typically asked to tell their purpose of visit from

the “browse-search product”, “complete transaction-

purchase”, “get order-technical support” or “other”,

so treated as a four-class problem. The study aims

at exploring the relationship between user behavioral

data (which includes URL sequences as features).

The stated purpose of the visit provided in the survey

after the end of sessions. The data consist of approxi-

mately 13500 user sessions and each record is limited

to maximum of 50 page visits. The goal is to con-

struct a model that predicts visitors’ intention based

on URL sequence they navigated from page to page.

The application on user intention prediction are

just about to make their early steps, see (Liu et al.,

2015), (Vieira, 2015), (Korpusik et al., 2016), (Lo

et al., 2016), and (Hashemi et al., 2016). Our ap-

proach in this work is to use neural networks in two

steps; like in the Movie review data of Section 4.3, by

i) embedding a URL into representative vectors and

ii) using these representations as features to a neu-

ral network to predict the user intention. We treat

each URL as a sentence, where each word of this

sentence is separated by “/”. A similar approach is

used in text classiﬁcation, sentiment analysis (Kim,

2014), semantic parsing (Yih et al., 2014) and sen-

tence modeling, see (Kalchbrenner et al., 2014) and

(Kim, 2014). Again we applied LeNet5 architecture

with adaptive activation. We report precision and re-

call, because different methods compete very closely

in terms of accuracy.

The results summarized in Table 4 show that adap-

tive Gumbel performs slightly better, while ReLU and

adaptive ReLU closely compete with each other.

Table 4: Running LeNet5 convolutional model with ReLU,

adaptive ReLU (AReLU), and adaptive Gumbel (AGumb)

activations on URL data. Different activations performed

almost identical in terms of accuracy, so only the prescition

(P), and the recall (R) are reported.

Conv layer Fully-connect layer

ReLU AReLU AGumb

P R P R P R

ReLU 68.0 68.0 68.1 67.9 68.0 67.8

AReLU 68.1 67.9 68.0 68.0 67.9 67.9

AGumb 68.1 68.3 68.2 68.1 68.1 68.3

5.1 Conclusion

We proposed a general method to adapt activation

functions by looking at the activation function as a

cumulative distribution function. This view is useful

to adapt a bounded activation such as sigmoid or hy-

perbolic tangent commonly used in recurrent neural

networks and attention models. It is well-known in

deep neural networks with bounded activations suf-

fer from vanishing gradient. Therefore, a method-

ology for adapting unbounded activations is as im-

portant. We recommended to decompose ReLU into

an unbounded component and a bounded component.

Therefore, the cumulative distribution function idea

can be re-used to adapt the bounded counterpart.

In fully-connected networks adapting activation

helps prediction most of the time. According to our

experiments adapting activation helps prediction ac-

curacy often, even in complex architectures. How-

ever, adaptive Gumbel mostly outperforms other acti-

vations in convolutional architectures.

We designed a series of experiments to understand

how our proposed activation functions affect on the

prediction of the ﬁtted models using a simulated data.

The results of this experiment show that using adap-

tive activation functions in ﬁtting models for predic-

tion approximation is superior compared to standard

functions in terms of accuracy regardless of network

size and activation functions used in original model.

In the next step, we aim at evaluating the performance

of the typical convolutional neural network (CNN)

models using our proposed activation functions on

image and text data. Accordingly, we design a series

of experiments on MNIST as a widely-used image

benchmark to understand how accurate the adaptive

activation functions in LeNet5 CNN models classify

the hand-written digit images compared to standard

activation functions. Compared to standard sigmoid,

ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods

254

applying adaptive Gumbel in fully-connected layer of

the CNN models are recommended. Generally, CNN

models using proposed activation functions improves

prediction and convergence speed compared to mod-

els that work exclusively with standard functions.

A series of experiments using CNN models

trained on a top of word2vec text data is performed

to evaluate the performance of the proposed activa-

tion functions in a sentiment analysis application on

Movie Review benchmark. Our empirical results im-

ply that using adaptive Gumbel as activation functions

in fully-connected layer and adaptive ReLU in con-

volutional layers are strongly recommended. These

observations are consistent with the ﬁndings were no-

ticed in experiments on MNIST data. Also, a com-

parison between our best observations and the state-

of-the-art results in (Kim, 2014) indicates that our re-

ported accuracy using adaptive activation functions

reproduces their accuracy. We believe that applying

more ﬁne-tuning hyper parameters and using other

complex variants of CNN models accompanied with

our proposed activation functions could improve the

existing results. To recap, our experiments on two

well-known image and text benchmarks imply that by

virtue of using adaptive-activation functions in CNN

models, we can improve the performance of the deep

networks in terms of accuracy and convergence.

Learning the adaptation parameter is feasible by

adding only one equation to back-propagation. Com-

putationally, letting neurons of a layer choose their

own activation function, in this framework, is equiv-

alent to adding a neuron to a layer. This minor extra

computation changes the network ﬂexibility consider-

ably, especially in shallow architectures. We focused

only on the classic LeNet5 architecture, but there is a

potential of exploring this methodology with a wide

variety of distribution functions for portable architec-

tures such as MobileNets (Howard et al., 2017), Pro-

jectionNets (Ravi, 2017), SqueezeNets (Iandola et al.,

2016), QuickNets (Ghosh, 2017), etc. It also has

a potential to generalize modiﬁed quantized training

(Hubara et al., 2018) and (Partovi Nia and Belbahri,

2018).

REFERENCES

Agostinelli, F., Hoffman, M., Sadowski, P., and Baldi, P.

(2014). Learning activation functions to improve deep

neural networks. arXiv preprint arXiv:1412.6830.

Belbahri, M., Sari, E., Darabi, S., and Partovi Nia, V.

(2019). Foothill: A quasiconvex regularization for

edge computing of deep neural networks. In Interna-

tional Conference on Image Analysis and Recognition,

pages 3–14.

Box, G. E. and Cox, D. R. (1964). An analysis of trans-

formations. Journal of the Royal Statistical Society.

Series B (Methodological), pages 211–252.

Cho, Y. and Saul, L. K. (2010). Large-margin classiﬁca-

tion in inﬁnite neural networks. Neural Computation,

22(10):2678–2697.

Clevert, D.-A., Unterthiner, T., and Hochreiter, S.

(2015). Fast and accurate deep network learning

by exponential linear units (elus). arXiv preprint

arXiv:1511.07289.

Coles, S., Bawa, J., Trenner, L., and Dorazio, P. (2001). An

introduction to statistical modeling of extreme values.

Springer.

Darabi, S., Belbahri, M., Courbariaux, M., and Partovi

Nia, V. (2019). Regularized binary network training.

In Neural Information Processing Systems, Workshop

on Energy Efﬁcient Machine Learning and Cognitive

Computing.

Dushkoff, M. and Ptucha, R. (2016). Adaptive activa-

tion functions for deep networks. Electronic Imaging,

2016(19):1–5.

Elfwing, S., Uchibe, E., and Doya, K. (2018). Sigmoid-

weighted linear units for neural network function ap-

proximation in reinforcement learning. Neural Net-

works.

Ghosh, T. (2017). Quicknet: Maximizing efﬁciency

and efﬁcacy in deep architectures. arXiv preprint

arXiv:1701.02291.

Glorot, X. and Bengio, Y. (2010). Understanding the dif-

ﬁculty of training deep feedforward neural networks.

In Proceedings of the Thirteenth International Con-

ference on Artiﬁcial Intelligence and Statistics, pages

249–256.

Glorot, X., Bordes, A., and Bengio, Y. (2011). Deep sparse

rectiﬁer neural networks. In Proceedings of the Four-

teenth International Conference on Artiﬁcial Intelli-

gence and Statistics, pages 315–323.

Goodfellow, I. J., Warde-Farley, D., Mirza, M., Courville,

A., and Bengio, Y. (2013). Maxout networks. arXiv

preprint arXiv:1302.4389.

Hashemi, H. B., Asiaee, A., and Kraft, R. (2016). Query

intent detection using convolutional neural networks.

In International Conference on Web Search and Data

Mining, Workshop on Query Understanding.

Hendrycks, D. and Gimpel, K. (2016). Gaussian error linear

units (gelus). arXiv preprint arXiv:1606.08415.

Hornik, K., Stinchcombe, M., and White, H. (1989). Multi-

layer feedforward networks are universal approxima-

tors. Neural networks, 2(5):359–366.

Hou, L., Samaras, D., Kurc, T., Gao, Y., and Saltz, J. (2017).

Convnets with smooth adaptive activation functions

for regression. In Artiﬁcial Intelligence and Statistics,

pages 430–439.

Hou, L., Samaras, D., Kurc, T. M., Gao, Y., and Saltz,

J. H. (2016). Neural networks with smooth adap-

tive activation functions for regression. arXiv preprint

arXiv:1608.06557.

Howard, A. G., Zhu, M., Chen, B., Kalenichenko, D.,

Wang, W., Weyand, T., Andreetto, M., and Adam,

Activation Adaptation in Neural Networks

255

H. (2017). Mobilenets: Efﬁcient convolutional neu-

ral networks for mobile vision applications. arXiv

preprint arXiv:1704.04861.

Huang, G.-H. (2005). Model identiﬁability. Wiley StatsRef:

Statistics Reference Online.

Hubara, I., Courbariaux, M., Soudry, D., El-Yaniv, R., and

Bengio, Y. (2018). Quantized neural networks: Train-

ing neural networks with low precision weights and

activations. The Journal of Machine Learning Re-

search, 18(187):1–30.

Iandola, F. N., Han, S., Moskewicz, M. W., Ashraf, K.,

Dally, W. J., and Keutzer, K. (2016). Squeezenet:

Alexnet-level accuracy with 50x fewer parame-

ters and¡ 0.5 mb model size. arXiv preprint

arXiv:1602.07360.

Jarrett, K., Kavukcuoglu, K., LeCun, Y., et al. (2009). What

is the best multi-stage architecture for object recogni-

tion? In Computer Vision, 2009 IEEE 12th Interna-

tional Conference on, pages 2146–2153. IEEE.

Kalchbrenner, N., Grefenstette, E., and Blunsom, P. (2014).

A convolutional neural network for modelling sen-

tences. arXiv preprint arXiv:1404.2188.

Kim, Y. (2014). Convolutional neural networks for sentence

classiﬁcation. arXiv preprint arXiv:1408.5882.

Klambauer, G., Unterthiner, T., Mayr, A., and Hochre-

iter, S. (2017). Self-normalizing neural networks. In

Advances in neural information processing systems,

pages 971–980.

Korpusik, M., Sakaki, S., Chen, F., and Chen, Y.-Y. (2016).

Recurrent neural networks for customer purchase pre-

diction on twitter. In CBRecSys@ RecSys, pages 47–

50.

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Im-

agenet classiﬁcation with deep convolutional neural

networks. In Advances in Neural Information Pro-

cessing Systems, pages 1097–1105.

LeCun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998a).

Gradient-based learning applied to document recogni-

tion. Proceedings of the IEEE, 86(11):2278–2324.

LeCun, Y., Bottou, L., Orr, G. B., and M

uller, K.-R.

(1998b). Efﬁcient backprop. In Neural networks:

Tricks of the Trade, pages 9–50. Springer.

Liu, Q., Yu, F., Wu, S., and Wang, L. (2015). A convolu-

tional click prediction model. In Proceedings of the

24th ACM International on Conference on Informa-

tion and Knowledge Management, pages 1743–1746.

ACM.

Lo, C., Frankowski, D., and Leskovec, J. (2016). Under-

standing behaviors that lead to purchasing: A case

study of pinterest. In KDD, pages 531–540.

Maas, A. L., Hannun, A. Y., and Ng, A. Y. (2013). Rec-

tiﬁer nonlinearities improve neural network acoustic

models. In Proc. ICML, volume 30.

Mikolov, T., Sutskever, I., Chen, K., Corrado, G. S., and

Dean, J. (2013). Distributed representations of words

and phrases and their compositionality. In Advances in

neural information processing systems, pages 3111–

3119.

Pang, B. and Lee, L. (2004). A sentimental education:

Sentiment analysis using subjectivity summarization

based on minimum cuts. In Proceedings of the 42nd

annual meeting on Association for Computational

Linguistics, page 271. Association for Computational

Linguistics.

Partovi Nia, V. and Belbahri, M. (2018). Binary quan-

tizer. Journal of Computational Vision and Imaging

Systems, 4(1):3–3.

Qian, S., Liu, H., Liu, C., Wu, S., and San Wong, H. (2018).

Adaptive activation functions in convolutional neural

networks. Neurocomputing, 272:204–212.

Ramachandran, P., Zoph, B., and Le, Q. V. (2018). Search-

ing for activation functions.

Ravi, S. (2017). Projectionnet: Learning efﬁcient on-

device deep networks using neural projections. arXiv

preprint arXiv:1708.00630.

Springenberg, J. T. and Riedmiller, M. (2013). Improving

deep neural networks with probabilistic maxout units.

arXiv preprint arXiv:1312.6116.

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones,

L., Gomez, A. N., Kaiser, Ł., and Polosukhin, I.

(2017). Attention is all you need. In Advances in

neural information processing systems, pages 5998–

6008.

Vieira, A. (2015). Predicting online user behaviour

using deep learning algorithms. arXiv preprint

arXiv:1511.06247.

Yih, S. W.-t., He, X., and Meek, C. (2014). Semantic pars-

ing for single-relation question answering.

Zhang, C. and Woodland, P. C. (2015). Parameterised

sigmoid and relu hidden activation functions for dnn

acoustic modelling. In Sixteenth Annual Conference

of the International Speech Communication Associa-

tion.

APPENDIX

Proof of Theorem 1. Suppose the Bernoulli distribu-

tion

p(y

) = π

(1 − π

)

(1−y

)

, y

= {0, 1},

where π

is a function of parameters ω = (η, α) where

η is the linear predictor, and α is the activation shape

= σ

(η) (7)

Therefore, to ensure distinct probability distributions

are indexed by α on a continuum of α > 0, the identi-

ﬁability of σ

(x) must be studied, i.e. distinct values

of parameter α lead to distinct activation functions.

Formally,

α 6= α

↔ ∃x ∈ IR s.t. σ

(x) 6= σ

(x). (8)

Equivalently

(x) = σ

(x) ↔ α = α

(9)

ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods

256

which falls on σ

(x) identiﬁability deﬁnition (Huang,

2005). Take σ

(x) in equation (1) that deﬁnes adap-

tive Gumbel

(x) = σ

(x),

{1 + α exp(x)}

= {1 + α

exp(x)}

Given 1 + αexp(x) > 0

log{1 + α exp(x)} =

log{1 + α

exp(x)}.

Let z = exp(x) and f

(α) = log(1 + αz) which has

derivative of arbitrary order. Take the Taylor expan-

sion of log(1 + αz)

(

∞

∑

n=0

(n)

(0)α

)

(

∞

∑

n=0

(n)

(0)α

)

The latter equation holds for all z if and only if all cor-

responding polynomial coefﬁcients are equal. Equiv-

alently,

α = α

. (10)

Activation Adaptation in Neural Networks

257