Coalitional Power Indices Applied to Voting Systems
Xavier Molinero
1
and Joan Blasco
2
1
Mathematics Department, Universitat Polit
`
ecnica de Catalunya·BarcelonTech,
Barcelona Graduate School of Mathematics, Spain
2
Barcelona School of Informatics, Universitat Polit
`
ecnica de Catalunya BarcelonTech, Spain
Keywords:
Simple Games, Coalitional Power Indices, Voting Systems.
Abstract:
We describe voting mechanisms to study voting systems. The classical power indices applied to simple games
just consider parties, players or voters. Here, we also consider games with a priori unions, i.e., coalitions
among parties, players or voters. We measure the power of each party, player or voter when there are coali-
tions among them. In particular, we study real situations of voting systems using extended Shapley–Shubik
and Banzhaf indices, the so-called coalitional power indices. We also introduce a dynamic programming to
compute them.
1 INTRODUCTION
Classical cooperative games provide mathematical
tools useful to study situations of conflict of inter-
est and cooperation arising from the real world. A
field where cooperative games have been frequently
applied is political science. By using simple games,
collective decision–making mechanisms ruled by vot-
ing have often been described and analyzed (Carreras,
2004). The value theory (one of the main streams of
the cooperative game theory) has given rise, by re-
stricting it to simple games, to a “power index the-
ory”. The most conspicuous representatives of this
line of research are the Shapley–Shubik (Shapley and
Shubik, 1954) and the Banzhaf-Coleman (Penrose,
1946; Banzhaf III, 1964; Coleman, 1971; Owen,
1975; Moshe’Machover Dan, 1998) power indices. A
survey about power indices can be found in (Freixas,
2010).
However, it seems that this framework does not
suffice to analyze all aspects of voting. Following
early initial papers by Lucas and Thrall (Thrall and
Lucas, 1963) and Myerson (Myerson, 1977) who,
respectively, generalized cooperative games in char-
acteristic function form to “games in partition func-
tion form” and extended the Shapley value (Shap-
ley, 1953) to this new class of games, Bolger (Bol-
ger, 1983) used a Banzhaf–type power index for the
so–called “multicandidate voting games”. Bolger
(Bolger, 1993) also defined and axiomatically char-
acterized a new extension of the Shapley value rela-
tively to each alternative. We agree that this relativity
is an essential feature of any evaluation of games with
alternatives.
In classical simple games it is implicitly assumed
that players can join them to form coalitions or strate-
gies (Holler and Owen, 2013; Carreras and Owen,
1988; Owen, 1977a; Fagen, 1963). The goal of this
paper is to show the wide possibilities of games with
coalitions among players to represent real voting sys-
tems. We consider real situations and we study the ex-
act role of each player. The analysis is done with the
classical Shapley–Shubik and Banzhaf power indices
with coalitions. Note that some definitions and con-
cepts have been gotten from previous works as (Car-
reras and Maga
˜
na, 2008; Nieto, 1996), among others.
2 CLASSICAL COALITIONAL
POWER INDICES FOR SIMPLE
GAMES
This section considers Shapley-Shubik and Banzhaf
power indices, as well as coalitional Shapley-Shubik
and Banzhaf power indices. Next we introduce some
references and definitions related with them.
Simple games can be viewed as models of voting
systems in which a single alternative, such as a bill or
an amendment, is pitted against the status quo.
Definition 1 ((Freixas and Molinero, 2009)). A sim-
ple game is a pair (N,v) in which N = {1,2,...,n} and
v(S) = 1 or 0, where S in a subset of N, that satisfies:
372
Molinero, X. and Blasco, J.
Coalitional Power Indices Applied to Voting Systems.
DOI: 10.5220/0009166803720376
In Proceedings of the 9th International Conference on Operations Research and Enterprise Systems (ICORES 2020), pages 372-376
ISBN: 978-989-758-396-4; ISSN: 2184-4372
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

(1) v(N) = 1, (2) v(
/
0) = 0 and (3) the monotonicity
property: v(s) = 1 and S ⊆ T ⊆ N implies v(T ) = 1 .
So far, a coalition has represented a set of agents
that worked on its own. In a coalition structure (CS),
the different coalitions are intended to work indepen-
dently of each other. We can also interpret a coali-
tion to represent a group of agent that is more likely
to work together within a larger group of agents (be-
cause of personal or political affinities).The members
of a coalition do not mind working with other agents,
but they want to be together and negotiate their payoff
together, which may improve their bargaining power.
This is the idea used in games with a priori unions.
Formally, a game with a priori unions is similar to a
game with CS: it consists of a triplet (N, v, B ) where
(N,v) is a simple game
1
and B = {B
1
,B
2
,...,B
m
} is a
CS defined over the set of players, N.
Based on Shapley’s value, Owen characterizes ax-
iomatically a new value, now known as Owen’s coali-
tional value or simply coalitional value, which reflects
the different possibilities of each player depending on
the subset of the coalition structure to which he be-
longs. In the development of this idea, the possibility
that the different blocks of the coalition structure co-
operate with each other is not excluded. On the con-
trary, it is considered that each block chooses a rep-
resentative, k for the B
k
block, and these are the ones
that negotiate (play). If M = {1,2,...,m} is the set
formed by the representatives of the blocks of B, then
the coalitional value of a player i ∈ B
k
is:
Definition 2 ((Owen, 1977b)). The Owen’s coali-
tional value is
φ
i
[v;B] =
∑
S⊆B
k
∑
T ⊆M
(t − 1)!(m −t)!
m!
·
(s − 1)!(b
k
− s)!
b
k
!
·
[v
S
(T ) − v
S
(T \ {i})]
(1)
where t = |T |, m = |M|, s = |S| and b
k
= |B
k
|.
Later, Owen also defined the corresponding coali-
tional value for Banzhaf power index as follows.
Definition 3 ((Owen, 1981)). The Banzhaf-Owen’s
coalitional value is
ψ
i
[v;B] =
∑
S⊆B
k
∑
T ⊆M
1
2
m−1
·
1
2
b
k
−1
·
[v
S
(T ) − v
S
(T \ {i})]
(2)
where t = |T |, m = |M|, s = |S| and b
k
= |B
k
|.
Note that Owen’s coalitional and Banzhaf-Owen’s
coalitional power indices are also called coalitional
Shapley-Shubik and coalitional Banzhaf power in-
dices, respectively.
1
Note that it also works for cooperative games (see (Tay-
lor and Zwicker, 1999)).
3 THE IMPLEMENTATION OF
CLASSICAL COALITIONAL
POWER INDICES
Using all the information from the previous section,
Formulas 1 and 2, we have done a program that
computes coalitional Shapley-Shubik and coalitional
Banzhaf power indexes.
The basic case for this formula is when every
party is in a coalition by itself, i.e., B
k
= {k} for
1 ≤ k ≤ n = m. Then, the formula is the same as the
one for simple games without coalitions. The algo-
rithm uses backtracking to get the 2
b
k
+m−2
different
combinations. The function will have b
k
+ m − 2 lev-
els but this time the options are between getting that
player or ignoring it.
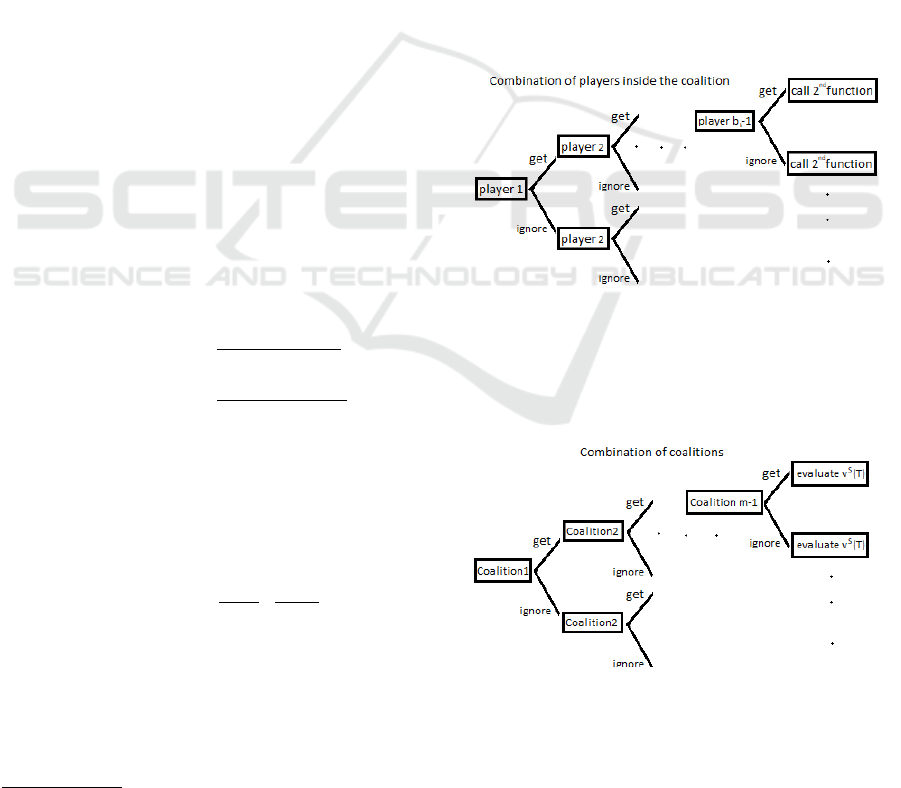
We divided our function in two parts.
The first one chooses all combinations with b
k
players inside the coalition B
k
in which our player i
belongs to, i.e., i ∈ B
k
. See Figure 1.
Figure 1: Combinations of players inside of B
k
.
Afterwards, we call the 2
nd
function. This function
considers all combinations with m indices inside M
including the index j ∈ M which our player i belongs
to, i.e., i ∈ B
j
. See Figure 2.
Figure 2: Combinations of indices inside of M.
3.1 Dynamic Programming
In this section we just consider the so-called weighted
majority games, a subclass of simple games defined as
follows.
Coalitional Power Indices Applied to Voting Systems
373

Definition 4 ((Freixas and Molinero, 2009)).
A weighted majority game is a simple game
(N,v), where there exists a representation
(q,w = {w
1
,...,w
n
}) such that v(S) = 1 if and
only if w(S) ≥ q, where w(S) =
∑
i∈S
w
i
.
There is an algorithm that uses dynamic program-
ming to calculate the Shapley-Shubik and Banzhaf in-
dices, for weighted majority games, with a time com-
plexity of O(n
2
q) and space requirement of O(nq) for
a defined quota q (Lucas, 1983; Brams and Affuso,
1976).
We extended the previous dynamic algorithm in-
troduced for simple games (Lucas, 1983; Brams and
Affuso, 1976) to one that can use coalitions.
Our first step in our algorithm is to reshape our n
players divided in m coalitions into n
0
players that will
serve as our input.
Those n
0
players will be composed for the b
k
− 1
players in our coalition and the m − 1 coalitions that
we will transform into players c
i
with the weight of
the whole coalition.
N
0
= {p
1
,..., p
b
k
−1
} ∪ {c
1
,...,c
m−1
} (3)
In which:
p(S) = |V|,V ⊆ S, ∀x ∈ V,x ∈ B
k
(4)
Then we will make a partition of N
0
players into sub-
sets N
0
1
,N
0
2
,...,N
0
z
satisfying that:
1. N
0
1
∪ N
0
2
∪ ... ∪ N
0
z
= N
0
,N
0
x
∩ N
0
y
=
/
0(x 6= y),
2. For all x,y : 1 ≤ x < y ≤ z, ∀i ∈ N
0
x
, ∀ j ∈ N
0
y
, w
i
>
w
j
,
3. For all x : 1 ≤ x ≤ z, ∀i, j ∈ N
0
x
,w
i
= w
j
.
For every player i, ˆc
i
(w,t, s, x) denotes the number
#{S ⊆ N
0
− {i} : w(S) = w,|S| = t, p(S) = s,
S ∩ N
0
x
6=
/
0,S ∩ N
0
x+1
= ... = S ∩ N
0
z
=
/
0}.
and, for every player i, c
i
(w,t, x) denotes the number
#{S ⊆ N
0
− {i} : w(S) = w,|S| = t,S ∩ N
0
x
6=
/
0,
S ∩ N
0
x+1
= ... = S ∩ N
0
z
=
/
0}.
Then the Owen (φ) and Banzhaf-Owen (ψ) coalitional
power indices of the player i ∈ N
y
are described as
follows,
φ
i
[v;B] =
n
0
−1
∑
t=1
q−1
∑
w=q−w
i
z
∑
x=1
b
k
∑
s=1
(t−s)!(m−(t−s)−1)!
m!
·
s!(b
k
−s−1)
b
k
!
·
ˆc
i
(w,t, s, x),
and
ψ
i
[v;B] =
1
2
m−1
·
1
2
b
k
−1
·
n−1
∑
t=1
q−1
∑
w=q−w
i
z
∑
x=1
c
i
(w,t, x),
respectively.
Note that v( j) is the number of combinations get-
ting j elements from the s
0
elements, times, the com-
binations getting y − j elements from y
0
− s
0
.
Then we can get an algorithm with time complex-
ity of O((n
0
b
k
)
2
q) and space requirement of O(n
0
q).
This algorithm improves the time to calculate our
index when the number of players grows but it be-
comes slower when the quota is too big. To reduce
the quota we can try to apply Greatest Common Divi-
sor to the weight of our players and the quota.
Nevertheless the biggest parliament in the world is
China’s National People’s Congress with 2890 seats
in which the biggest party controls the 71.1% of the
seats. This parliament is followed by the UK Upper
House with 793 and the European Parliament with
751 seats. So, in the worst case scenario where China
needs a quota of 75% and there will be n players in
B
k
our algorithm will have a time cost of O(1987n
3
).
That means it will start to be faster than the exponen-
tial version for n > 24. See Figure 3.
Figure 3: Complexity of the standard (O(2
n
)) and the dy-
namic programming (O(1987n
3
)) algorithms.
For the parliament of the UK Upper House, the aver-
age parliament has 300 seats, with a quota of 75% and
half of the players in the coalition, our algorithm will
have a time cost of O(100n
3
). So our algorithm will
act faster than the exponential version for n > 19 .See
Figure 4.
Figure 4: Complexity of the standard (O(2
n
)) and the dy-
namic programming (O(100n
3
)) algorithms.
ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems
374

4 REAL VOTING SYSTEMS
To success a game (the approval or defeat of a mo-
tion), a number of players need to agree in the same
decision to reach a certain quorum amount of votes.
Here we mention three different scenarios.
• Voting a motion that requires a qualified majority
of 2/3 of the players. This kind of motion is nec-
essary to reform the constitution in the Spanish
parliament.
• Voting a motion that requires an absolute majority
of 1/2 of the players. This motion is used for a
censure motion in the Spanish parliament.
• Voting a motion that requires a relative majority,
i..e, more votes for the motion than against it. This
is the most common form of voting and the one
in which abstention plays a different role than in
the other two cases because we do not take into
account abstention votes, i.e., we just compare the
votes in favour with the votes against.
We study now two different voting rules: Catalan Par-
liament 2019 and German Parliament 2019,
4.0.1 Catalan Parliament 2019
φ
i
[v
q
,B] is the coalitional Owen’s power index for the
player i, with quota q and structure of coalitions
B = {{JUNT SxCAT,ERC},{C
0
s},{PSC},
{EnComu},{CUP},{PP}} ,
see Table 1, and
B = {{JUNT SxCAT,ERC,CU P},{C
0
s},{PSC},
{EnComu},{PP}} ,
see Table 2.
Table 1: Power distribution in the Catalan Parliament 2019
using coalitions B
1
= {JUNT SxCAT,ERC}.
party weight %weight φ
i
[v
2/3
,B ] φ
i
[v
1/2
,B ]
C’s 36 26.66% 21.6667 6.6667
JUNTSxCAT 34 25.19% 31.6667 33.3333
ERC 32 23.70% 38.3333 33.3333
PSC 17 12.59% 10 6.6667
EnComu 8 5.92% 5 6.6667
CUP 4 2.96% 1.6667 6.6667
PP 4 2.96% 1.6667 6.6667
In the government in catalonia 2019 it was a coalition
between JUNTSxCAT and ERC (Table 1), but if
CUP, which had similar political interest, was added
to the coalition they will have a complete majority.
Table 2: Power distribution in the Catalan Parliament 2019
using coalitions B
1
= {JUNT SxCAT,ERC,CUP}.
party weight %weight φ
i
[v
2/3
,B ] φ
i
[v
1/2
,B ]
C’s 36 26.66% 20 0
JUNTSxCAT 34 25.19% 31.6667 43.3333
ERC 32 23.70% 38.3333 43.3333
PSC 17 12.59% 11.6667 0
EnComu 8 5.92% 3.3333 0
CUP 4 2.96% 2.5 13.3333
PP 4 2.96% 3.3333 0
4.0.2 German Parliament 2019
ψ
i
[v
q
,B] denotes the coalitional Banzhaf-Owen’s
power index for the player i, with quota q and struc-
ture of coalitions B . Tables 3 and 4 analyze the Ger-
man parliament 2019 using the Banzhaf-Owen coali-
tional value for B without coalitions and
B = {{CDU, SPD,CSU },{A f D}, {FDP},
{DIELINKE},{GR
¨
UNE}} ,
which is the current coalition in the government, re-
spectively.
Table 3: Power distribution in the German Parliament (Bun-
destag) 2019 without coalitions.
party weight %weight ψ
i
[v
2/3
,B ] ψ
i
[v
1/2
,B ]
CDU 200 28.21% 30.4348 29.0323
SPD 153 21.58% 21.7391 19.3548
AfD 94 13.26% 13.0435 16.129
FDP 80 11.28% 10.7696 9.6774
DIE LINKE 69 9.73% 8.6956 9.6774
GR
¨
UNE 67 9.45% 8.6956 9.6774
CSU 46 6.49% 6.5217 6.4516
Table 4: Power distribution in the German Parliament (Bun-
destag) 2019 using coalitions B
1
= {CDU,SPD,CSU}.
party weight %weight ψ
i
[v
2/3
,B ] ψ
i
[v
1/2
,B ]
CDU 200 28.21% 32.5581 52.9412
SPD 153 21.58% 23.2558 35.2941
AfD 94 13.26% 13.9535 0
FDP 80 11.28% 13.9535 0
DIE LINKE 69 9.73% 4.6512 0
GR
¨
UNE 67 9.45% 4.6512 0
CSU 46 6.49% 6.9767 11.7647
Note that if we take into account the coalition that
forms the government, the power of each party
changes a lot, specially if that coalition has absolute
majority.
5 CONCLUSIONS AND FUTURE
WORK
We have computed some specific measures to es-
tablish the power that each party in a parliament
Coalitional Power Indices Applied to Voting Systems
375

holds, taking special attention when coalitions ap-
pears. In this vein, we have implemented the exten-
sion of Shapley-Shubik and Banzhaf power indices
with coalitions. We have also studied more real vot-
ing systems in deep.
For our future work we are also planning on ex-
tending the considered definitions and algorithms. It
could express multiple alternatives (as abstention) be-
tween input options, voting likeness (two parties with
opposed ideologies are less likely to vote the same),
and try to put both concepts together.
We also plan to improve the complexity of our
algorithm (by the way, all of them are NP-Hard) us-
ing approximation methods for computing power in-
dices (Fatima et al., 2012; Bachrach et al., 2010) and
another methods (Alonso-Meijide and Bowles, 2005).
ACKNOWLEDGEMENTS
X. Molinero has been partially supported by funds
from the Spanish Ministry of Economy and Com-
petitiveness (MINECO) and the European Union
(FEDER funds) under grants MTM2015-66818-P
(VOTA-COOP) and MDM-2014-044 (BGSMath).
REFERENCES
Alonso-Meijide, J. M. and Bowles, C. (2005). Generat-
ing functions for coalitional power indices: An ap-
plication to the imf. Annals of Operations Research,
137(1):21–44.
Bachrach, Y., Markakis, E., Resnick, E., Procaccia, A. D.,
Rosenschein, J. S., and Saberi, A. (2010). Approxi-
mating power indices: theoretical and empirical anal-
ysis. Autonomous Agents and Multi-Agent Systems,
20(2):105–122.
Banzhaf III, J. F. (1964). Weighted voting doesn’t work: A
mathematical analysis. Rutgers L. Rev., 19:317.
Bolger, E. M. (1983). The banzhaf index for multicandi-
date presidential elections. SIAM Journal on Alge-
braic Discrete Methods, 4(4):442–458.
Bolger, E. M. (1993). A value for games withn players andr
alternatives. International Journal of Game Theory,
22(4):319–334.
Brams, S. J. and Affuso, P. J. (1976). Power and size: A
new paradox. Theory and Decision, 7(1-2):29–56.
Carreras, F. (2004). α-Decisiveness in Simple Games, pages
77–91. Springer US, Boston, MA.
Carreras, F. and Maga
˜
na, A. (2008). The shapley–shubik
index for simple games with multiple alternatives. An-
nals of Operations Research, 158(1):81–97.
Carreras, F. and Owen, G. (1988). Evaluation of the cat-
alonian parliament, 1980–1984. Mathematical Social
Sciences, 15(1):87 – 92.
Coleman, J. S. (1971). Control of collectivities and the
power of a collectivity to act. Social choice, pages
269–300.
Fagen, R. R. (1963). The theory of political coalitions.
American Political Science Review, 57(2):446–447.
Fatima, S., Wooldridge, M., and Jennings, N. R. (2012).
A heuristic approximation method for the banzhaf in-
dex for voting games. Multiagent and Grid Systems,
8(3):257–274.
Freixas, J. (2010). Power indices. Wiley Encyclopedia of
Operations Research and Management Science.
Freixas, J. and Molinero, X. (2009). Simple games and
weighted games: A theoretical and computational
viewpoint. Discrete Appl. Math., 157(7):1496–1508.
Holler, M. J. and Owen, G. (2013). Power Indices and
Coalition Formation. Springer US, Boston, MA.
Lucas, W. F. (1983). Measuring power in weighted voting
systems. In Political and related models, pages 183–
238. Springer.
Moshe’Machover Dan, S. F. (1998). The measurement of
voting power: theory and practice, problems and para-
doxes.
Myerson, R. B. (1977). Values of games in partition func-
tion form. International Journal of Game Theory,
6(1):23–31.
Nieto, A. M. (1996). Formaci
´
on de coaliciones en los jue-
gos cooperativos y juegos con m
´
ultiples alternativas.
PhD thesis, Universitat Polit
`
ecnica de Catalunya.
Owen, G. (1975). Multilinear extensions and the banzhaf
value. Naval research logistics quarterly, 22(4):741–
750.
Owen, G. (1977a). Values of games with a priori unions.
In Henn, R. and Moeschlin, O., editors, Mathematical
Economics and Game Theory, pages 76–88, Berlin,
Heidelberg. Springer Berlin Heidelberg.
Owen, G. (1977b). Values of games with a priori unions.
In Mathematical economics and game theory, pages
76–88. Springer.
Owen, G. (1981). Modification of the banzhaf-coleman in-
dex for games with a priori unions. In Power, voting,
and voting power, pages 232–238. Springer.
Penrose, L. S. (1946). The elementary statistics of major-
ity voting. Journal of the Royal Statistical Society,
109(1):53–57.
Shapley, L. S. (1953). A value for n-person games. Contri-
butions to the Theory of Games, 2(28):307–317.
Shapley, L. S. and Shubik, M. (1954). A method for evalu-
ating the distribution of power in a committee system.
American political science review, 48(3):787–792.
Taylor, A. and Zwicker, W. (1999). Simple games: Desir-
ability relations, trading, pseudoweightings. Prince-
ton University Press, Princeton, NJ.
Thrall, R. M. and Lucas, W. F. (1963). N-person games
in partition function form. Naval Research Logistics
Quarterly, 10(1):281–298.
ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems
376