
Secure Multi-agent Planning via Sharemind
Radek Bumb
´
alek, Michal
ˇ
Stolba and Anton
´
ın Komenda
Department of Computer Science, Czech Technical University in Prague,
Karlovo n
´
am
ˇ
est
´
ı 13, 121 35, Prague, Czech Republic
Keywords:
Multi-agent Planning, Secure Multiparty Computation, Privacy-preserving Planning.
Abstract:
Classical planning provides models and algorithms for solving problems of finding a sequence of actions
that transforms the initial state of the world into a state of the world with the desired properties. In classical
planning, we assume that the solution plan entails all actors in the world and thus it can be computed centrally.
In multi-agent planning, this assumption is dropped in favor of situations where there is multitude of actors
with individual capabilities, goals, and objectives, called agents. In this work, we propose a novel technique for
multi-agent planning which combines a state-of-the-art planner called Planning State Machine (PSM) Planner
with a framework for mutli-party secure computation, Sharemind. This allows the agents to find a cooperative
plan while preventing the leakage of private information in a practical and scalable way.
1 INTRODUCTION
Automated (classical) planning is a long-studied tech-
nique of Artificial Intelligence allowing for efficient
solution of complex combinatorial problems. The plan-
ning problem consists of a logical description of the
world, the actions or operators which can be used to
modify the world and a set of conditions which are
desirable to hold in the goal world state. The task is
to find a plan, that is, a sequence of actions, which
modifies the initial world state into a world state which
fulfills the goal conditions. The most common plan-
ning paradigms are heuristic state space search and
plan space search. Both techniques are based on in-
telligent exploration of the combinatorially expanding
space of reachable world states (in the first case) and
possible partial plans (in the second case).
In modern real-world large-scale personal, corpo-
rate or military applications, the whole environment
is often not under control of one entity. An com-
plex interplay of more or less cooperative entities is
often present. Such entities may need to cooperate
in the plan synthesis, while still wanting to protect
the privacy of their input data and internal processes.
Multi-agent and privacy-preserving multi-agent plan-
ning allow the definition of factors of the global plan-
ning problem private to the respective entities (i.e.,
agents) in order to improve the efficiency of plan-
ning and/or to maintain the privacy of the informa-
tion. Similarly to classical planning, the most preva-
lent planning paradigms in multi-agent planning are
multi-agent (distributed) variants of state-space and
plans-space search.
In (To
ˇ
zi
ˇ
cka et al., 2017), the authors have shown
that it is not possible for a multi-agent planner based
on either of the planning paradigms mentioned above
to be strong privacy-preserving. A strong privacy-
preserving planner is a multi-agent planner such that
after the execution of the planning process, none of
the agents learn any private information they could
not have learned from the planning problem input and
the public part of the solution plan. Nevertheless, the
authors have proposed a theoretical strong-privacy pre-
serving planner (albeit not complete) based on an ex-
isting multi-agent planner, the Planning State Machine
(PSM) Planner.
In this work, we utilize a Secure Mutliparty Com-
putation framework Sharemind (Bogdanov et al., 2008;
Bogdanov, 2013) to implement the most crucial part
of the PSM planner and thus draw nearer to a prov-
ably and truly strong privacy-preserving planner. We
leave less important aspects of the planner for future
work, thus we cannot claim full strong privacy preser-
vation yet. We have thoroughly evaluated the new
PSM planner variant and we have shown that it is still
competitive in terms of planning performance while
bringing the aspect of secure computation.
852
Bumbálek, R., Štolba, M. and Komenda, A.
Secure Multi-agent Planning via Sharemind.
DOI: 10.5220/0009147908520859
In Proceedings of the 12th International Conference on Agents and Artificial Intelligence (ICAART 2020) - Volume 2, pages 852-859
ISBN: 978-989-758-395-7; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 MULTI-AGENT PLANNING
In this section, we present the formalism used through-
out the paper. First of all, we define a general (that
is single-agent) planning task in the form of Multi-
Valued Planning Task (MPT). The MPT is a tuple
Π =
V , O, s
I
, s
where
V
is a finite set of finite-domain variables,
O
is
a finite set of operators,
s
I
is the initial state, and
s
is
the goal condition. An operator
o
from the finite set
O
has a precondition
pre(o)
and effect
eff(o)
which
are both partial variable assignments. An operator
o
is applicable in a state
s
if
pre(o)
is consistent with
s
. Application of operator
o
in a state
s
results in a
state
s
0
such that all variables in
eff(o)
are assigned to
the values in
eff(o)
and all other variables retain the
values from
s
, formally
s
0
= o ◦ s
. A solution to MPT
Π
is a sequence
π = (o
1
, ..., o
k
)
of operators from
O
(a plan), such that
o
1
is applicable in
s
I
= s
0
, for each
1 ≤ l ≤ k
,
o
l
is applicable in
s
l−1
and
s
l
= o
l
◦s
l−1
and
s
k
is a goal state (i.e., s
is consistent with s
k
).
Similarly as MA-STRIPS (Brafman and Domshlak,
2008) is an extension of STRIPS (Fikes and Nilsson,
1971) towards privacy and multi-agent planning, MA-
MPT is a multi-agent extension of the Multi-Valued
Planning Task. For
n
agents, the MA-MPT problem
M = {Π
i
}
n
i=1
consists of a set of
n
MPTs. Each MPT
for an agent α
i
∈ A is a tuple
Π
i
=
D
V
i
= V
pub
∪ V
priv
i
, O
i
= O
pub
i
∪ O
priv
i
, s
Bi
I
, s
Bi
E
where
V
priv
i
is a set of private variables,
V
pub
is a set
of public variables shared among all agents
V
pub
∩
V
priv
i
=
/
0
and for each
i 6= j
,
V
priv
i
∩ V
priv
j
=
/
0
and
O
i
∩ O
j
=
/
0
. All variables in
V
pub
and all values in
their respective domain are public, that is known to all
agents. All variables in
V
priv
i
and all values in their
respective domains are private to agent
α
i
which is the
only agent aware of such
V
and allowed to modify its
value.
The set
O
i
of operators of agent
α
i
consists of pri-
vate and public operators such that
O
pub
i
∩ O
priv
i
=
/
0
.
The precondition
pre(o)
and effect
eff(o)
of private op-
erators
o ∈ O
priv
i
, are partial assignments over
V
priv
i
,
whereas in the case of public operators
o ∈ O
pub
i
the
assignment is over
V
i
and either
pre(o)
or
eff(o)
as-
signs a value to at least one public variable from
V
pub
.
Because
V
pub
is shared, public operators can influence
(or be influenced by) other agents.
The global problem is the actual problem the
agents are solving. We define a global problem (MPT)
as a union of the agent problems, that is
Π
G
=
*
[
i∈1..n
V
i
,
[
i∈1..n
O
i
, s
I
, s
+
An
i
-projected problem is a complete view of agent
α
i
on the global problem
Π
G
. The
i
-projected problem
of agent
α
i
contains
i
-projections of all operators of all
agents. Formally, an
i
-projection
o
i
of
o ∈ O
i
is
o
. For
a public operator
o
0
∈ O
pub
j
of some agent
α
j
s.t.
j 6= i
,
an
i
-projected operator
o
0i
is
o
0
with precondition and
effect restricted to the variables of
V
i
, that is
pre(o
0i
)
is a partial variable assignment over
V
i
consistent
with
pre(o
0
)
(
eff(o
0
)
treated analogously). The set of
i
-projected operators is
O
i
and an
i
-projected problem
is
Π
i
. The set of all
i
-projected problems is then
M
= {Π
i
}
n
i=1
.
A public plan
π
B
j
is
i
-extensible, if by adding pri-
vate operators from
O
priv
i
to
π
B
j
and replacing all projec-
tions
o
B
s.t.
o ∈ O
pub
i
by
o
, we obtain a local solution
to
Π
i
. According to (To
ˇ
zi
ˇ
cka et al., 2016), a public
plan which is i-extensible by all i ∈ 1, ..., n is a global
solution to
M
and can be extended by all agents to
form {π
i
}
n
i=1
.
3 PRIVACY-PRESERVING
MULTI-AGENT PLANNING
The Privacy-Preserving Multi-Agent Planning (PP-
MAP) is based on concepts from the field of Secure
Multiparty Computation and their application to MAP,
as described in the following sections.
3.1 Secure-multiparty Computation
Secure multiparty computation (MPC) (Yao, 1986) is
a subfield of cryptography, which studies computing
a function
f
by a set of
n
parties
p
1
, . . . , p
n
such that
each
p
i
knows part of the input of
f
. The goal of MPC
is to compute
f
in a way that no party
p
i
learns more
information about the inputs of other parties than what
can be learned from the output of
f
. Clearly, PP-MAP
is an instance of MPC, where the respective problems
of the agents are the inputs and the global plan is the
desired output.
In an ideal world, assuming secure communication
channels, a trusted third-party could receive the inputs
from the parties, perform the needed computation, and
return the solutions to the respective parties. Secure
MPC studies whether and how such computations can
be done in the real world without the trusted third-
party, and alternatively how much private information
leaks in comparison to the ideal execution (recently
applied to PP-MAP in (
ˇ
Stolba et al., 2019)). In some
cases, the trusted third-party can be replaced by a rela-
tively small number (e.g., three) computation agents
which can be trusted not to collude as each of them is
Secure Multi-agent Planning via Sharemind
853

controlled by a different party. Such approach is taken
by some real-world secure MPC solutions, such as
Sharemind (Bogdanov et al., 2008) used in this work.
In MPC, assumptions are typically placed on the
participating parties (agents in our case) and their com-
munication and computation capabilities. The assump-
tions we consider in ths work are the following: (i)
There is no trusted third-party. (ii) The planning agents
are semi-honest (or honest but curious). (iii) The
computation power of the agents is either unbounded
(information-theoretic security), or polynomial-time
bounded (computational security).
The assumption of semi-honest agents means, as
opposed to malicious agents, that every agent follows
the rules of the computation protocol based on its in-
put data, but after the computation is finished, it is
allowed to use any information it has received during
the protocol to compromise the privacy. The com-
putation power of the agents (which can be used to
infer additional knowledge from the executed proto-
col) is typically seen either as unbounded, in which
case we are talking about information-theoretic secu-
rity, or polynomial-time bounded, which is the case of
computational security.
When applied to PP-MAP, the notion of
polynomial-time bounded adversary may seem some-
what less suitable, as the planning itself is not polyno-
mial (but PSPACE-complete (Bylander, 1994)). Nev-
ertheless, the computation power of the agents is still
polynomial, thus allowing to solve either polynomial
instances or small instances. For such instances of
planning problems which can be practically solved, the
cryptographic assumptions (such as that the factoring
of large integers is hard), for which the polynomial-
time bound is typically used are still valid.
There are basically two approaches to multi-agent
planning based on the MPC techniques. The first ap-
proach is to encode planning in some general MPC
technique such as cryptographic circuits (Yao, 1986).
For example, the cryptographic circuits encode the
whole computation of a function into a boolean or al-
gebraic circuit, which can be then securely evaluated
using some of the existing secure protocols. The prob-
lem related to MAP is, that the worst-case scenario
has to be encoded, that is, the complete exploration of
the search space, which itself is exponential in the size
of the MAP input (e.g., MA-STRIPS). Therefore, it is
not clear how exactly PP-MAP would be encoded in
such general model, whether it is even feasible, and
what the overhead of such encoding would be.
The second approach is to devise a specific PP-
MAP algorithm based on MPC primitives, such as
private set intersection (Li and Wu, 2007). There is
a number of solutions for a related problem, shortest
path in a graph (Brickell and Shmatikov, 2005). Such
techniques solve the shortest path problem for an ex-
plicit graph, typically represented by a matrix. In clas-
sical planning and subsequently in MAP, the explicit
graph (that is, the transition system) is exponential in
the problem size, which, for practical problem sizes,
makes it impossible to use such explicit (e.g., matrix)
representation. So far, the only published (theoreti-
cal) MAP planner using MPC primitives is (To
ˇ
zi
ˇ
cka
et al., 2017) which uses the secure set intersection as
part of the planning process. In this work we imple-
ment the theoretical concept by implementing the set
intersection using the Sharemind framework.
3.2 Weak and Strong Privacy
In the MAP and PP-MAP literature, the concept of
privacy has been mostly reduced to the idea of weak
privacy, as stated in (Nissim and Brafman, 2014). Here,
we rephrase the (informal) definition:
We say that an algorithm is weak privacy-
preserving if, during the whole run of the al-
gorithm, the agent does not communicate (un-
encrypted) private parts of the states, private
actions and private parts of the public actions.
In other words, the agent openly communicates
only the information in M
= {Π
i
}
n
i=1
.
Obviously, the weak privacy does not give any guar-
antees on privacy whatsoever, as the adversary may
deduce private knowledge from the communicated
public information. Nevertheless, not all weak privacy-
preserving algorithms are equal in the amount of pri-
vacy leaked as shown in (
ˇ
Stolba et al., 2019).
In (Nissim and Brafman, 2014), the authors define
also strong privacy, which is in accordance with the
cryptographic and secure MPC model. Here we infor-
mally rephrase the definition of Nissim&Brafman:
A strong privacy-preserving algorithm is such
a distributed algorithm that no agent
α
i
can
deduce an isomorphic (that is differing only in
renaming) model of a private variable, a private
operator and its cost, or private precondition
and effect of a public operator belonging to
some other agent
α
j
, beyond what can be de-
duced from the public input (M
= {Π
i
}
n
i=1
)
and the public output (projection of the solu-
tion plan π
B
).
A more precise formal definition can be stated based
on the definition of privacy in secure MPC, where
privacy is typically defined with respect to the ideal
world in which a trusted third party exists.
Definition 1.
(Strong privacy MPC) Let
p
1
, ..., p
n
be
n
parties computing an algorithm
P
which takes
n
pri-
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
854

vate inputs
in
1
, ..., in
n
respective to the parties, and pro-
duces
n
private outputs
out
1
, ..., out
n
respective to the
parties. Let
T
be a trusted third-party. An algorithm
P
is strong privacy-preserving if the parties
p
1
, ..., p
n
do
not learn more information from executing
P
without
the third-party (in a distributed way), than by sending
their respective private inputs
in
i
via a secure channel
to
T
and receiving their respective outputs
out
i
via a
secure channel.
Formally, the definition is bound to the existence
of a simulator which, based solely on the input and
output of a party
i
, can simulate the execution of the
protocol so that the simulated execution (its distribu-
tion, in the probabilistic case) is indistinguishable from
the execution of the protocol by the party
i
. See (Gol-
dreich, 2009) for detailed formal definitions. Now we
rephrase the definition in the context of MAP, where
the difference is that there is a public part of the input
and also a public part of the output.
Definition 2.
(Strong privacy MAP) Let
M =
{Π
i
}
n
i=1
be a MAP problem for a set
A
of
n
agents. Let
T
be a trusted third-party. A MAP planner
P
is strong
privacy preserving, if the agents
α
1
, ..., α
n
do not learn
more information from solving
M
with
P
without the
third-party (in a distributed way), than by sending their
respective agent planning problems
Π
i
via a secure
channel to
T
and receiving the
i
-projections
π
Bi
of the
global plan via a secure channel.
The Definition 2 is compatible with the definition
of Nissim&Brafman published in (Nissim and Braf-
man, 2014; Brafman, 2015).
4 ONE-SHOT SECURE PSM
PLANNER
In this section, we describe the main contributions of
this work. We start by describing the PSM planner,
its variants, and the necessary modifications we made.
Then, we describe the implementation of set intersec-
tion in Sharemind and its use in the novel One-Shot
Secure PSM Planner.
4.1 PSM Planner
The PSM was originally introduced in (To
ˇ
zi
ˇ
cka et al.,
2016) together with the Planning State Machine (PSM)
data structure it is based on. The PSM structure is used
to compactly represent a (possibly infinite) set of plans.
In this work we somewhat simplify the planner to use
only sets of plans and set intersection. The main idea
of the PSM Planner is the following generate and test
planning paradigm:
1.
For each agent, generate a set
S
i
of solutions of
Π
i
consisting of valid plans for agent i.
2.
For each agent, construct a set
S
B
i
= {π
B
|π ∈ S}
of projected plans.
3.
Construct an intersection
S
B
=
T
i∈A
S
B
i
of all pro-
jected plans.
4.
Based on (To
ˇ
zi
ˇ
cka et al., 2016) any plan
π
B
∈ S
B
is publicly extensible and thus is a solution to the
global planning problem M .
Based on instantiations of the above steps, multiple
variants of the planner can be constructed as proposed
in (To
ˇ
zi
ˇ
cka et al., 2017):
One-Shot-PSM Planner:
generates a proper random
subset of all solutions in Step 1. and terminates in
Step 3, even if a solution is not found (incomplete).
Iterative-PSM Planner: repeats steps 1.-3. until the
intersection
S
B
=
T
i∈A
S
B
i
is nonempty, or all
agents have generated all possible solutions, in
which case if the intersection is empty, there is no
global solution. In each iteration of Step 1., new
plans are added systematically (e.g., ordered by
length).
Full-PSM Planner:
each agent first generates all pos-
sible solutions in Step 1 (might not terminate due
to infinite number of possible solutions). If the
problem has a global solution, all solutions are
found in the first iteration of Step 4.
By using a secure set intersection (e.g., PSI (Li and
Wu, 2007)), both One-Shot-PSM and Full-PSM can
be made strong privacy preserving in the information-
theoretic sense (without any assumptions), although
Full-PSM would not terminate in the presence of infi-
nite number of plans (i.e., including loops). Another
promising feature of the One-Shot-PSM planner is
that there is a trade-off between completeness and ef-
ficiency, which can be exploited. The more plans are
generated, the more time it takes, but also the higher
is the chance of success in the one shot secure set
intersection.
The original Iterative-PSM planner starts with the
preparation of a problem and a domain. The prepro-
cessing phase does not only prepare data for the plan-
ner but also contains a distributed relaxed reachability
analysis algorithm (
ˇ
Stolba and Komenda, 2013) and
sets initial landmarks. Landmarks are used to guide
the plan generation process towards the solution as the
planner is trying to primarily use landmark actions in
the generated solutions. Preprocessing does not share
private actions and facts directly. However, there is
a possibility of privacy information leakage because
of public fact sharing during relaxed planning. Deter-
mining the amount of information leaked is beyond
Secure Multi-agent Planning via Sharemind
855
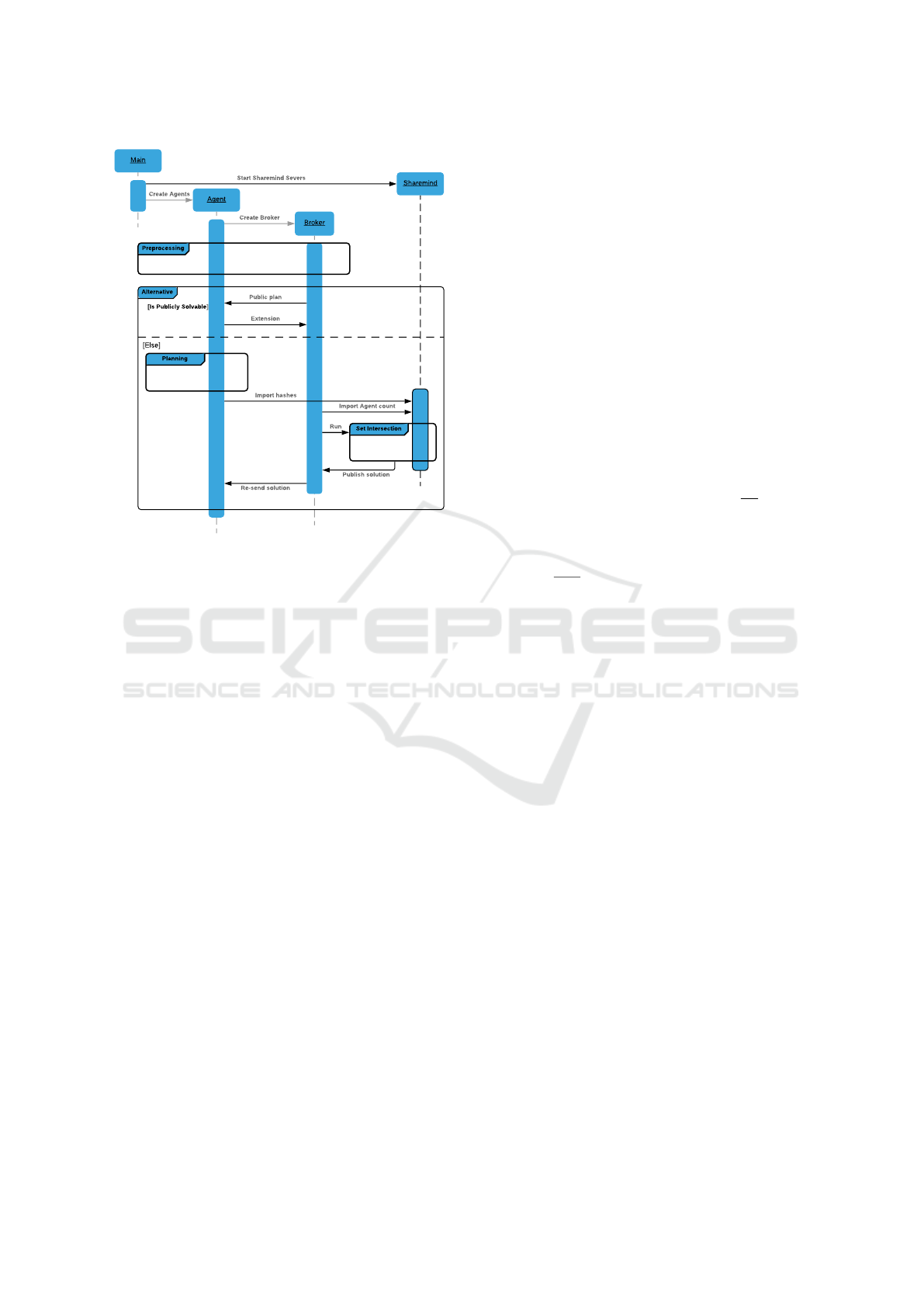
Figure 1: One-shot PSM Planner UML diagram.
this work, see e.g. (
ˇ
Stolba et al., 2019). We leave the
relaxed reachability in place for this work and post-
pone its replacement or secure re-implementation for
future work. This means that the presented planner
is not fully strong privacy-preserving, but neverthe-
less serves as a valuable stepping stone towards this
ultimate goal.
4.2 One-Shot PSM Planner
Let us now describe the modifications necessary to im-
plement the One-Shot PSM Planner which is then com-
bined with the Sharemind Secure MPC framework to
obtain the Secure One-Shot PSM Planner. As already
mentioned before, the initial preprocessing remains
unchanged in the current version of the planner (see
Figure 1). Because the preprocessing is not changed,
in some cases planner solves the problem even without
even calling the One-Shot algorithm. After grounding
One-Shot agents call Fast-downward in a loop. Each
call returns several plans which are saved for future
use. When the time limit expires, all Fast-downward
threads are killed. Agents then make public projec-
tions of plans they have found. Different plans may
share the same public projection. These duplicates are
removed, keeping the plan with the shortest private
part.
To justify the next step, we first need to explain how
the Sharemind framework processes input. Sharemind
itself does not have a simple input, the language se-
creC 2 does not allow scripts to be run with additional
arguments. Sharemind was implemented for opera-
tions over databases, therefore we need to convert the
generated plans into a database. The iterative algo-
rithm makes use of knowledge of how similar plans
are. Based on similarity and usage of public actions,
landmarks are set. However, in the One-Shot algo-
rithm, only one comparison is made. Any additional
information could not be used anyway. Therefore we
only need a simple comparison, whether the plans are
the same, or not. Therefore we can use encryption over
the whole plans. We decided for hashing our public
projections with SHA256. Because public plans are
strings of variable lengths usually much longer than
is a hash size, it is possible that different plans would
be encrypted with the same hash. However, it is ex-
tremely improbable. In test situations we usually have
2-8 agents, each generating roughly 30-100 original
public projections. Counting the probability leads to
the so-called birthday problem. Rough estimation via
Taylors polynomial leads to
p(n, d) ≈ 1−e
−n
2
2d
. Where
d
is the size of hash
d = 2256
and
n
is the number of
plans. Even if we use a ridiculously huge estimation
such as
n = 10
10
we still obtain the probability of col-
lision
1 − e
−10
20
2
257
= 4.31 × 10
−68
. Hashed plans are
then saved into the table database as sets of four 64bit
Longs. Hashes are much easier to compare than sets
of strings of variable length. Also hashing increase
security in case of eavesdropping on the input or the
output of the Sharemind script. The table database
is created via Sharemind CSV importer. Each agent
creates a CSV file containing hashes and XML file
with a description of tables to be imported. Then they
call the import command. The broker also creates
CSV and XML files with simple information about
the number of agents for the Sharemind script. Name
conventions are based on the numbering of agents,
therefore knowledge of their count is crucial. After
all the agents imported their hashed plans, the broker
calls set intersection script. The script returns a hash
of a common plan if there is at least one. The broker
then resends it back to agents so every agent could
reconstruct the original plan based on the hash and
create an output.
4.3 Plan Intersection via Sharemind
Sharemind is operated via built-in commands and cre-
ated scripts. These scripts as already mentioned are
written in the secreC 2 language. This language is
rather limited and resembles the C language. The spe-
cific part of this language is privacy types, which are
annotated with a privacy domain. Private variables are
being treated in a very specific way. Each variable is
divided into three parts, one for each of the Sharemind
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
856

servers. Every operation over these variables is done
in means of multi-party computation. Declassification
can be done only by a declassify expression.
We compute a set intersection by a simple compar-
ison each element of a set A with each element of a
set B. The set created by comparison of two previous
sets is then used for comparing with the next set until
the complete intersection is made. Function setInter-
section makes an intersection of given arguments, by
comparing each member of the first argument, with
each member of the second argument. Because of the
encryption, we can not directly declare whether two
numbers are equal. However, we can apply basic arith-
metic operations such as subtraction and retype the
variable from a number to a boolean. By a subtraction
and retyping it is guaranteed that the declassification
of the variable will not expose original values. The
output of the script is the first hashed plan in the re-
sultant set or an empty set in case the algorithm will
end with an empty intersection. The output is read by
the broker and resent to agents. In case of an empty
intersection, the broker terminates the program.
5 EVALUATION
The evaluation consists of two main parts, testing of
the planner itself and testing of the sharemind set in-
tersection algorithm. Because of the character of the
One-Shot algorithm, we can not easily compare its
planning speed, because it will always use the maxi-
mum time given for planning. However, we can ob-
serve efficiency with changing time. Also, we want to
measure a time consumption of the sharemind set inter-
section script. We need to account this time when we
start our planner in order to assure that the algorithm
will finish before the time limit.
5.1 Planner Evaluation
For the planner evaluation we use the benchmarks and
restrictions of the CoDMAP Competition (Komenda
et al., 2016). Our main concern is the number of prob-
lems solved (coverage) in the given time limit, which
is 30 minutes. The Sharemind framework supposed
to run on three independent servers to assure privacy
preservation. In our testing scenarios, we emulate
such environment in the virtualization tool VirtualBox.
VirtualBox allows us to strictly set properties of the
virtual machine. We used settings from CoDMAP,
which allows 4 thread processor and 8GB of RAM.
Table 2, column “Pre.” shows the domains where
a public plan solution was found by the reachability
analysis and the One-Shot algorithm itself was not
Table 1: Problems solved by One-shot algorithm.
Elevators Rovers Satellites
100 300 1740 100 300 1740 100 300 1740
1 ok ok ok ok ok ok ok ok ok
2 x x x ok ok ok ok ok ok
3 x x x ok ok ok ok ok ok
4 x x x ok ok ok ok ok ok
5 x x x ok ok ok ok ok ok
6 x x x ok ok ok ok ok ok
7 x x x ok ok ok ok ok ok
8 x x x ok ok ok ok ok ok
9 x x x x ok ok x x x
10 x x x x x ok ok ok ok
11 x x x x x x ok ok ok
12 x x x x ok ok x x x
13 x x x x x x ok ok ok
14 x x x x x x x x x
15 x x x x x x x x x
16 x x x x x ok x x x
17 x x x x x x x x x
18 x x x x x x x x x
19 x x x x x x x x x
20 x x x x x x x x x
started. The One-Shot algorithm was applied in the
following domains: Elevators, Rovers, Satellites, and
Zenotravel (where it does not solve any problems).
We tested the algorithm with three settings, giving the
planning part 100, 300 and 1740 seconds. We assume
one-minute time reserve for the preprocessing and the
set intersection. Even though the planner did not solve
even half of the problems, the efficiency has to be
put in the context by comparing it with the original
planner. Virtualization and running all agents on a
single device may lower efficiency significantly when
compared with the results of the CoDMAP competi-
tion. Therefore we tested the iterative algorithm as
well, the comparison is shown in Table 2. We can see
that in some domains (Elevators, Zenotravel) our so-
lution offers unconvincing results. However, domains
such as Rovers and Satellites were solved successfully.
In some domains, the planner succeeded even with a
small amount of planning time, but efficiency boost
with a long time is rather limited. This is caused by
the rapidly growing state space during a search.
5.2 Evaluation of the Set Intersection
Algorithm
We generated sets of hashes to simulate problems
that the Sharemind script will be solving. Because
of the character of used data (hashes), artificially man-
ufactured sets are indistinguishable from the original.
Secure Multi-agent Planning via Sharemind
857
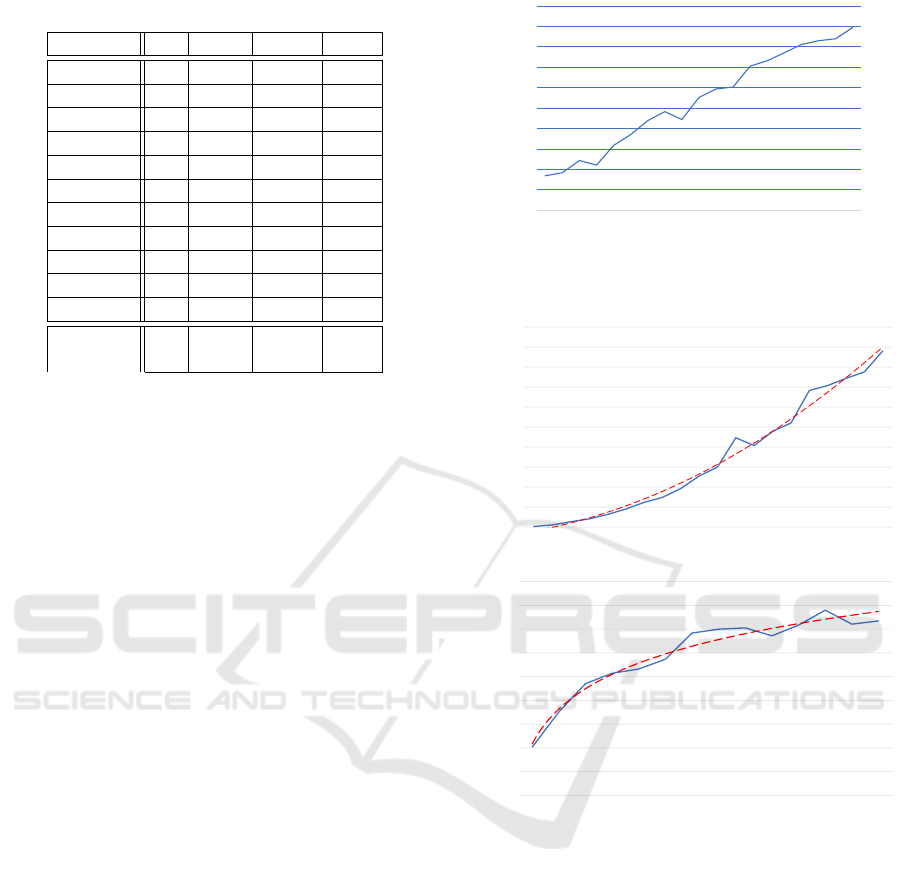
Table 2: Comparison of One-Shot and iterative PSM.
Domain Pre. Iterative One Shot Total
Blocksworld 20 20 20 20
Depot 17 17 17 20
Driverlog 20 20 20 20
Elevators - 12 1 20
Logistics 20 20 20 20
Rovers - 14 12 20
Satellites - 11 11 20
Sokoban 17 17 17 20
Taxi 20 20 20 20
Woodworking 20 20 20 20
Zenotravel - 8 0 20
∑
179 158 220
(81.4%) (71.8%) (100%)
Therefore we can faithfully imitate real problems in
a controlled environment. We can control nature of
the problem by 3 main attributes: (i) Sizes of sets, (ii)
Number of sets, and (iii) Similarity rate. The similarity
rate defines a percentage loss of plans in each intersec-
tion iteration. For example, with 3 sets of size 100 and
the similarity rate 50%, each iteration eliminates 50%
of plans. After 1 iteration (comparing the first 2 sets)
only 50 plans remain. After the second iteration (the
result of the first iteration intersected with the third
set) only 25 plans remain. We assume 5 sets, because
of the average number of agents. We also assume each
set holding 200 members. Higher set sizes allow us
to better observe similarity rate impact, because with
a lower number of members in each set, low similar-
ity rate would cause intersection to contain only one
member in a small number of iterations.
We can see in Figure 2 that the growth is unstable.
This is caused by the random shuffling of set members.
In some occasions, sets intersect very fast with a com-
parison of the only the first couple of members. The
role of chance is more noticeable when a difference
between member count of sets is higher. This differ-
ence lowers with higher similarity rate. For example,
with similarity rate 1.0, member count of each set 75,
we com- pare 5 identical sets in 4 iterations. When
all set members are present in both sets, we always
make 75 comparisons per iteration, 1560 comparisons
in Sharemind experiments total, with no difference
between shuffled and unshuffled sets. But with a low
similarity rate such as 0.2, we compare 75 with 75
members only in the first iteration. In the second itera-
tion, we will compare only 15 members with 75 and
in the third only 3 members of the intersection with 75
members of the fourth set. Based on shuffle, we can
make between 6 (1 + 2 + 3) and 222 (73 + 74 + 75)
comparisons.
Next, we examined time complexity grow with an
100
120
140
160
180
200
220
240
260
280
300
0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0.55 0.6 0.65 0.7 0.75 0.8 0.85 0.9 0.95 1
Time
[seconds]
Similarity rate
Figure 2: Sharemind script time complexity based on simi-
larity of sets.
0
100
200
300
400
500
600
700
800
900
1000
20
40
60
80
100
120
140
160
180
200
220
240
260
280
300
320
340
360
380
400
Time [seconds]
Set size
0
50
100
150
200
250
300
350
400
450
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Time
[seconds]
Number of Sets
Figure 3: Sharemind script time complexity based on set
size (top blue) and number of sets (bottom blue), includ-
ing polynomial and logarithmic approximation respectively
(red).
increase of set sizes. We were always comparing 5
sets and a similarity rate of 75%. We use a higher
similarity rate in order to lower the impact of the ran-
dom plan shuffle. The intersection of n sets with m
members is done by comparing their m x m members
n times which leads to O(m 2 ), as observed from the
experiment in Figure 3 (top). Lastly, we observe time
complexity with the growing number of sets. We used
to set size 200 and 75% similarity rate. As we can
see, even with a high amount of agents, time complex-
ity grows slowly, because intersection will get very
small after a couple of iterations as seen in Figure 3
(bottom).
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
858

6 CONCLUSION AND FUTURE
WORK
In this work, we have pioneered the use of Secure
Multiparty Computation primitives and tools repre-
sented by the Sharemind framework on the problem
of Privacy-Preserving Multi-Agent Planning. We have
implemented concepts so far described only in theory
and shown that they are competitive in terms of plan-
ning performance and valuable in therms of privacy
preservation. We have not succeeded in implementing
a full general strong privacy-preserving planner, but
the presented work is a crucial stepping stone towards
such ultimate goal. To reach that goal, the main future
work lies in either eliminating or, better, replacing the
relaxed reachability analysis step with its secure vari-
ant. A future work in terms of improving the planner’s
performance is to use the full PSM structures in the
planner and implement their intersection inside the
Sharemind framework.
ACKNOWLEDGEMENTS
This research was supported by the Czech Science
Foundation (grant no. 18-24965Y).
REFERENCES
Bogdanov, D. (2013). Sharemind: programmable secure
computations with practical applications. PhD thesis.
Bogdanov, D., Laur, S., and Willemson, J. (2008). Share-
mind: A framework for fast privacy-preserving com-
putations. In Proceedings of the European Symposium
on Research in Computer Security, pages 192–206.
Springer.
Brafman, R. I. (2015). A privacy preserving algorithm for
multi-agent planning and search. In Proceedings of
the Twenty-Fourth International Joint Conference on
Artificial Intelligence, (IJCAI’15), pages 1530–1536.
Brafman, R. I. and Domshlak, C. (2008). From one to many:
Planning for loosely coupled multi-agent systems.
In Proceedings of the 18th International Conference
on Automated Planning and Scheduling (ICAPS’08),
pages 28–35.
Brickell, J. and Shmatikov, V. (2005). Privacy-preserving
graph algorithms in the semi-honest model. In Proceed-
ings of the International Conference on the Theory and
Application of Cryptology and Information Security,
pages 236–252. Springer.
Bylander, T. (1994). The computational complexity of propo-
sitional STRIPS planning. Artificial Intelligence, 69(1-
2):165–204.
Fikes, R. and Nilsson, N. (1971). STRIPS: A new approach
to the application of theorem proving to problem solv-
ing. In Proceedings of the 2nd International Joint
Conference on Artificial Intelligence (IJCAI’71), pages
608–620.
Goldreich, O. (2009). Foundations of cryptography: volume
2, basic applications. Cambridge university press.
Komenda, A., Stolba, M., and Kovacs, D. L. (2016). The
international competition of distributed and multiagent
planners (CoDMAP). AI Magazine, 37(3):109–115.
Li, R. and Wu, C. (2007). An unconditionally secure pro-
tocol for multi-party set intersection. In Proceedings
of Applied Cryptography and Network Security, pages
226–236. Springer.
Nissim, R. and Brafman, R. I. (2014). Distributed heuristic
forward search for multi-agent planning. Journal of
Artificial Intelligence Research, 51:293–332.
ˇ
Stolba, M., Fi
ˇ
ser, D., and Komenda, A. (2019). Privacy leak-
age of search-based multi-agent planning algorithms.
In Proceedings of the International Conference on Au-
tomated Planning and Scheduling, volume 29, pages
482–490.
ˇ
Stolba, M. and Komenda, A. (2013). Fast-forward heuris-
tic for multiagent planning. In Proceedings of the 1st
ICAPS Workshop on Distributed and Multi-Agent Plan-
ning (DMAP’13), pages 75–83.
To
ˇ
zi
ˇ
cka, J., Jakubuv, J., Komenda, A., and Pechou
ˇ
cek,
M. (2016). Privacy-concerned multiagent planning.
Knowledge Information Systems, 48(3):581–618.
To
ˇ
zi
ˇ
cka, J.,
ˇ
Stolba, M., and Komenda, A. (2017). The limits
of strong privacy preserving multi-agent planning. In
Proceedings of the 27th International Conference on
Automated Planning and Scheduling (ICAPS’17).
Yao, A. (1986). How to generate and exchange secrets. In
Proceedings of the Foundations of Computer Science,
1986., 27th Annual Symposium on, pages 162–167.
IEEE.
Secure Multi-agent Planning via Sharemind
859
