
Dynamic Mode Decomposition via Dictionary Learning for Foreground
Modeling in Videos
Israr Ul Haq
1
, Keisuke Fujii
1,2
and Yoshinobu Kawahara
1,3
1
Center for Advanced Intelligence Project, RIKEN, Japan
2
Graduate School of Informatics, Nagoya University, Japan
3
Institute of Mathematics for Industry, Kyushu University, Fukuoka, Japan
Keywords:
Dynamic Mode Decomposition, Nonlinear Dynamical System, Dictionary Learning, Object Extraction,
Background Modeling, Foreground Modeling.
Abstract:
Accurate extraction of foregrounds in videos is one of the challenging problems in computer vision. In this
study, we propose dynamic mode decomposition via dictionary learning (dl-DMD), which is applied to extract
moving objects by separating the sequence of video frames into foreground and background information with
a dictionary learned using block patches on the video frames. Dynamic mode decomposition (DMD) decom-
poses spatiotemporal data into spatial modes, each of whose temporal behavior is characterized by a single
frequency and growth/decay rate and is applicable to split a video into foregrounds and the background when
applying it to a video. And, in dl-DMD, DMD is applied on coefficient matrices estimated over a learned
dictionary, which enables accurate estimation of dynamical information in videos. Due to this scheme, dl-
DMD can analyze the dynamics of respective regions in a video based on estimated amplitudes and temporal
evolution over patches. The results on synthetic data exhibit that dl-DMD outperforms the standard DMD and
compressed DMD (cDMD) based methods. Also, the results of an empirical performance evaluation in the
case of foreground extraction from videos using publicly available dataset demonstrates the effectiveness of
the proposed dl-DMD algorithm and achieves a performance that is comparable to that of the state-of-the-art
techniques in foreground extraction tasks.
1 INTRODUCTION
One of the fundamental computer vision objectives is
to extract accurate dynamic information from video
sequences. The basic application can be the sepa-
ration of foreground and background information in
videos. This is still considered to be a challenging
task in practice because the true background is of-
ten difficult to estimate. To address this issue, vari-
ous methods have been proposed over the last decade.
For detailed overview of some of the traditional and
state-of-the-art methods, we recommend (Bouwmans
et al., 2017; Sobral and Vacavant, 2014). One of
the most extensively used frameworks to separate a
video into foreground and background information is
decomposing the video frames into a low-rank ma-
trix (background) and a sparse matrix (foreground)
by principal component analysis (PCA) (Oliver et al.,
1999). Variants of this method, such as robust prin-
cipal component analysis (RPCA), are further dis-
cussed in (Cand
`
es et al., 2011). The decomposition
of a matrix into low-rank and sparse matrices can
be alternatively solved by dynamic mode decomposi-
tion (DMD), which accurately separates a matrix into
the stationary background and foreground motions
by differentiating between the near-zero frequency
modes and the remaining non-zero frequency modes
(Kutz and Fu, 2015). However, there are some limita-
tions in the standard DMD method that often causes
inaccurate extraction of dynamics from the video. In
standard DMD method, image sequences ordered in
time as column vectors are considered as input, such
arrangement of image sequences is unable to extract
complex dynamics in videos. Also a modified version
of standard DMD; compressed DMD (cDMD) have
been proposed in (Erichson et al., 2016). The com-
pressed DMD achieves almost the same results as the
standard DMD method but at low computation cost.
In this study, we advocate the use of DMD via
dictionary learning (dl-DMD) for accurate extraction
of dynamics in videos. For this purpose, a dictio-
nary is learned using random patches of input image
476
Haq, I., Fujii, K. and Kawahara, Y.
Dynamic Mode Decomposition via Dictionary Learning for Foreground Modeling in Videos.
DOI: 10.5220/0009144604760483
In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 5: VISAPP, pages
476-483
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

sequences for better approximation of the input sig-
nals. Then coefficient matrices are obtained over this
learned dictionary those contain the better represen-
tation of underlying dynamics in videos which results
in a sharp extraction of foreground structures from the
background than standard DMD and cDMD.
The remainder of this study can be organized as
follows. First, we provide an overview of the dynamic
mode decomposition in Section 2. Then in Section 3,
we describe a problem formulation and procedure to
perform dl-DMD. Experiments are presented in Sec-
tion 4 along with performance evaluations. Finally,
Section 5 summarizes and concludes the study.
2 DYNAMIC MODE
DECOMPOSITION
DMD spatiotemporally decomposes the sequential
data via data-driven realization of the spectral decom-
position of the Koopman operator (Koopman, 1931).
Spectral analysis of the Koopman operator lifts the
analysis of nonlinear dynamical systems to those of
linear systems in function spaces. Further, we briefly
review the underlying theory.
Consider a (possibly nonlinear) dynamical sys-
tem:
x
x
x
t+1
= f
f
f (x
x
x
t
), x
x
x ∈ M ,
where f
f
f
:
M → M , M is the state space, and t is the
time index. In this system, the Koopman operator K
for ∀x
x
x ∈ M can be defined as follows:
K g(x
x
x) = g( f
f
f (x
x
x)),
where g
:
M → C (∈ F ) denotes an observable in
function space F . By definition, K is a linear op-
erator in F . Assume that there exists a subspace of
F invariant to K , which can be denoted by G ⊂ F .
Additionally, assume that G is finite-dimensional and
that a set of observables {g
1
,... ,g
n
} that span over G
are observed to exist. If g
g
g = [g
1
,. .. ,g
n
]
>
:
M → C
n
,
the one-step evolution of g
g
g for ∀x
x
x ∈ M can be ex-
pressed as follows:
K
K
Kg
g
g(x
x
x) = g
g
g( f
f
f (x
x
x)),
where the finite dimensional K
K
K is the restriction of
K to G. An eigenfunction of K
K
K can be expressed as
ϕ
ϕ
ϕ
:
M → C
n
, and the corresponding eigenvalue can
be expressed as λ ∈ C, i.e., K
K
Kϕ
ϕ
ϕ(x
x
x) = λϕ
ϕ
ϕ(x
x
x). If all
eigenvalues are distinct, any value of g
g
g can be ex-
pressed as follows:
g
g
g(x
x
x) =
∑
n
i=1
ϕ
ϕ
ϕ(x
x
x)ξ
i
with some coefficients ξ
i
. Thus, we obtain
Algorithm 1 : Dynamic Mode Decomposition (Schmid,
2010).
Require: Y
Y
Y
1
and Y
Y
Y
2
defined in Eq. (1)
Ensure: Dynamic modes Φ
Φ
Φ and eigenvalues ∆
∆
∆
1: U
U
U
r
,S
S
S
r
,V
V
V
r
← compact SVD of Y
Y
Y
1
.
2:
˜
A
A
A ← U
U
U
∗
r
Y
Y
Y
2
V
V
V
r
S
S
S
−1
r
.
3:
˜
W
W
W ,∆
∆
∆ ← eigenvectors and eigenvalues of
˜
A
A
A.
4: Φ
Φ
Φ ← Y
Y
Y
2
V
V
V
r
S
S
S
−1
r
˜
W
W
W
r
5: return: Φ
Φ
Φ,∆
∆
∆;
Algorithm 2: Compressed Dynamic Mode Decomposition.
Require: Video frames Y
Y
Y
1
,Y
Y
Y
2
1: R
R
R = rand(p
c
,m) Generate sensing matrix
2: Y
Y
Y
c
= R
R
R*Y
Y
Y
1
, Y
Y
Y
0
c
=R
R
R*Y
Y
Y
2
Compress input matrix
3: U
U
U,S
S
S,V
V
V = svd(Y
Y
Y
c
) SVD
4: A
A
A = U
U
U * Y
Y
Y
0
c
*V
V
V *S
S
S
−1
Least squares fit
5: W
W
W ,∆
∆
∆ = eig(A
A
A) Eigenvalue decomposition
6: Φ
Φ
Φ
c
= Y
Y
Y
2
∗V
V
V ∗ S
S
S
−1
∗W
W
W Compute DMD modes
7: b
b
b = lstsq(Φ
Φ
Φ,Y
Y
Y
1
) Compute amplitudes by least
square method
g
g
g(x
x
x
t
) =
∑
n
i=1
λ
t
i
c
c
c
i
, c
c
c
i
= ϕ
ϕ
ϕ
i
(x
x
x
0
)ξ
i
,
where g
g
g is decomposed into modes {c
c
c
i
}, and the mod-
ulus and argument of λ
i
express the decay rate and
frequency of c
c
c
i
, respectively. Differing from classical
modal decomposition of linear systems, this decom-
position can be applied to nonlinear systems. DMD
computes such decomposition using the numerical
data. Assume the following data matrices of sizes
C
n×T
:
Y
Y
Y
1
= [g
g
g(x
x
x
0
),. ..,g
g
g(x
x
x
T −1
)],
Y
Y
Y
2
= [g
g
g(x
x
x
1
),. ..,g
g
g(x
x
x
T
)].
(1)
Then, the most popular variant of the DMD al-
gorithm is described in Algorithm 1. In compressed
DMD (cDMD) method, data matrices are first com-
pressed by a random sensing matrix and then modes
are reconstructed using the original data matrix. The
algorithm is further summarized in Algorithm 2.
3 PROPOSED METHOD
We propose dl-DMD by extending DMD to employ
the dictionary atoms that have been learned using ran-
dom patches in video frames. The dictionary learning
step allows the reconstruction of input video frames
using a small subset of dictionary atoms. Then, DMD
is performed over the coefficient matrices those are
obtained over the dictionary atoms (explained in sub-
section. 3.2) which contain the better representation
of underlying dynamics of input video and expected
Dynamic Mode Decomposition via Dictionary Learning for Foreground Modeling in Videos
477

Figure 1: Illustration of dl-DMD for back-
ground/foreground separation in videos.
Algorithm 3: dl-DMD for foreground extraction in videos.
Require: Video frames V, patch size d, dictionary
atoms k.
1: Learn a dictionary D as in Eq. (2).
2: Calculate the coefficient matrices B
1
and B
2
as in
Eqs. (3) and (4), respectively.
3: Perform DMD over coefficient matrices B
1
and
B
2
(subsection 3.3).
4: Threshold zero-frequency modes based on the
eigenvalues obtained by Step 3.
5: Reconstruct foregrounds from the approximated
coefficient matrix and dictionary as in Eq. (9).
to cause accurate foreground/background separation
based on the obtained eigenvalues and spatial modes
(explained in subsection 3.3). However, in stan-
dard DMD and cDMD methods, DMD is directly
applied over spatiotemporal matrices those are built
from input frames of a video due to which it be-
comes difficult to extract dynamics and seperate fore-
ground/background information. The overall proce-
dure of dl-DMD is summarized in Algorithm 3, and
the proposed method is further illustrated in Figure 1.
The details of the main steps are described as follows:
3.1 Dictionary Learning
First, in case of a given video frames V ∈ R
n
1
×n
2
×T
,
each frame {v
1
,v
2
,. .. ,v
T
} is converted to a set of
overlapping patches, and l patches from the entire set
are selected randomly to train a dictionary D ∈ R
d×k
,
where d is the size of a patch and k is the number of
atoms or elements in the dictionary. The dictionary
can be learned by optimizing the coefficient matrix
Z ∈ R
k×l
and the dictionary in an iterative manner.
The dictionary and coefficient matrix are estimated to
give a representation to approximate X ∈ R
d×l
, which
contains the randomly selected patches {x
j
}
l
j=1
in the
columns (Aharon et al., 2006). This can be performed
by solving the following minimization problem:
min
D,Z
kX − DZk
2
F
subject to ∀
i
,||z
z
z
i
||
0
≤ T
0
,
(2)
where the coefficient matrix Z = {z
z
z
1
,. .. ,z
z
z
l
} contains
coefficients that represent each patch and T
0
is the
maximum number of non-zero coefficients that can
be used to represent each patch.
3.2 Coefficient Matrix Estimation
The coefficient matrices B
1
=
{
˜
β
β
β
1
i,1
,
˜
β
β
β
1
i,2
,. .. ,
˜
β
β
β
1
i,(T −1)
}
P
i=1
and B
2
= {
˜
β
β
β
2
i,1
,
˜
β
β
β
2
i,2
,. .. ,
˜
β
β
β
2
i,(T −1)
}
P
i=1
of sizes R
K×(T −1)
are learned
over the trained dictionary to approximate the patches
of image sequences Q
1
= {q
q
q
i,1
,q
q
q
i,2
,. .. ,q
q
q
i,(T −1)
}
P
i=1
and Q
2
= {q
q
q
i,2
,q
q
q
i,3
,. .. ,q
q
q
i,T
}
P
i=1
of sizes R
N×(T −1)
.
Here, {·}
P
i=1
is the vectorized column with the total
number of overlapping patches, P; further, N and
K represent the total number of rows in the aligned
frames and coefficient matrices, respectively. The
patches along all the aligned frames are represented
as Q = {q
q
q
i, j
}
P
i=1
∈ R
N×T
for j = 1,...,T , and
those approximations can be obtained by solving the
following minimization problems:
˜
β
β
β
1
i, j
= arg min
β
β
β
1
i, j
kq
q
q
i, j
− Dβ
β
β
1
i, j
k
2
+ λ
1
kβ
β
β
1
i, j
k
1
(i = 1, 2,. .. ,P, j = 1,2, .. ., T − 1),
(3)
˜
β
β
β
2
i, j
= arg min
β
β
β
2
i,( j−1)
kq
q
q
i, j
− Dβ
β
β
2
i,( j−1)
k
2
+ λ
2
kβ
β
β
2
i,( j−1)
k
1
(i = 1, 2,. .. ,P, j = 2,. .. ,T ),
(4)
where λ
1
and λ
2
in Eqs. (3) and (4) denote the reg-
ularization parameters to control the sparsity in the
coefficient matrices B
1
and B
2
, respectively.
3.3 Dynamic Mode Decomposition
The dynamic modes are computed by applying Algo-
rithm 1 to the coefficient matrices B
1
and B
2
. A set
of dynamic modes Φ
Φ
Φ
:
= {φ
φ
φ
1
,. .. ,φ
φ
φ
r
} and the corre-
sponding eigenvalues ∆
∆
∆
:
= {Λ
1
,. .. ,Λ
r
} are obtained,
those represent the spatial and frequency informa-
tion of the video. Here, r is the number of adopted
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
478

eigenvectors. These modes represent the slowly vary-
ing or rapidly moving objects at time points t ∈
{0,1, 2. .. ,T − 1} in the video frames with associated
continuous-time frequencies and can be expressed as
follows:
ω
ω
ω
j
=
log(Λ
j
)
∆t
. (5)
Further, the approximated video frames for low- and
high-frequency modes at any time point can be recon-
structed as
˜
B(t) ≈
r
∑
j=1
φ
φ
φ
j
exp(ω
ω
ω
j
t)α
α
α
j
= Φ
Φ
Φexp(Ω
Ω
Ωt)α
α
α, (6)
where φ
φ
φ
j
is a column vector of the i-th dynamic mode
that contains the spatial structure information and α
α
α
j
is the initial amplitude of the corresponding DMD
mode. The vector of the initial amplitudes α
α
α can
be obtained by taking the initial video frame at time
t = 0, which reduces Eq. (6) to {
˜
β
β
β
1
i,1
}
P
i=1
= Φ
Φ
Φα
α
α. Note
that the matrix of eigenvectors is not square; thus, the
initial amplitudes can be observed using the following
pseudoinverse process:
α
α
α = Φ
Φ
Φ
†
{
˜
β
β
β
1
i,1
}
P
i=1
. (7)
3.4 Foreground/Background Separation
The key principle to separate the video frames into
foregrounds and the background is the thresholding
of low frequency modes based on the corresponding
eigenvalues. Generally, the portion that represents the
background is constant among the frames and satis-
fies |ω
ω
ω
p
| ≈ 0, where p ∈ {1,2,..., r}. Typically, a
single mode represents the background, which is lo-
cated near the origin in the complex space, whereas
|ω
ω
ω
j
|,∀ j 6= p are the eigenvalues that represent the
foreground structures bounding away from the origin.
Therefore, the reconstructed video frames can be sep-
arated into the background and foreground structures
as follows:
˜
B = φ
φ
φ
p
exp(ω
ω
ω
p
t)α
α
α
p
| {z }
Background
+
∑
j6=p
φ
φ
φ
j
exp(ω
ω
ω
j
t)α
α
α
j
| {z }
Foreground
, (8)
where
˜
B = {
˜
β
β
β
i,1
,
˜
β
β
β
i,2
,. .. ,
˜
β
β
β
1
i,T
}
P
i=1
is the reconstructed
coefficient matrix and t = {0,. .. ,T − 1} is the time
indices up to (T − 1) frames. Note that the initial
amplitude α
α
α
p
= φ
φ
φ
†
p
{
˜
β
β
β
1
i,1
}
P
i=1
of the stationary back-
ground is constant for all the future time points,
whereas α
α
α
j
= φ
φ
φ
†
j
{
˜
β
β
β
1
i,1
}
P
i=1
,∀ j 6= p are the initial am-
plitudes of varying foreground structures. However,
full flattened approximated video sequences are re-
constructed with a learned dictionary (in subsection
3.1) by the following equation:
{
˜
q
q
q
i, j
}
P,T
i=1, j=1
= D{
˜
β
β
β
i, j
}
P,T
i=1, j=1
(9)
Foregrounds and background separation in a video
is illustrated in Figure 2, that depicts the continu-
ous time eigenvalues and temporal evolution of am-
plitudes (Erichson et al., 2016). Subplot (a) shows a
set of video frames of a moving boat
1
. It can be ob-
served that the boat is absent during the initial and
last frames, whereas the middle frame exhibits a full
moving boat. The representation of these frames into
modes that describe dynamics by applying dl-DMD
provides an interesting insight related to the moving
objects in the foreground, which can be achieved by
factorizing these frames into spatial modes, ampli-
tudes, and temporal evolutions. Subplot (b) exhibits
the different eigenvalues that are based on the infor-
mation present in the frames. The background is usu-
ally static in videos, which corresponds to the zero
eigenvalue that is located near the origin, whereas
the eigenvalues that are located away from the ori-
gin confirm the presence of other dynamics. Further,
subplot(c) depicts the amplitude evolution and dic-
tates that the zero-frequency mode which is constant
over time, is the background, and that the remain-
ing modes, which correspond to different frequen-
cies, depict the foreground structures. Additionally,
we note that the amplitude that describes the moving
boat is negative in the initial frames and begins to in-
crease, eventually reaching its maximum at a frame
index of 40 when the boat is almost at the center of
the video, capturing majority of the foreground infor-
mation. The amplitude begins to decrease when the
boat moves away from the center. The remaining am-
plitudes with different frequencies describe the other
dynamics of the moving objects in the video.
4 EXPERIMENTAL RESULTS
We empirically investigated the performance of the
proposed dl-DMD using synthetic data (Section 4.1)
and a real video dataset, i.e., BMC (Section 4.2).
For the synthetic data, we compared our proposed dl-
DMD method with standard DMD and compressed
DMD because the comparative results of other algo-
rithms can be found in (Takeishi et al., 2017).
1
http://changedetection.net/
Dynamic Mode Decomposition via Dictionary Learning for Foreground Modeling in Videos
479
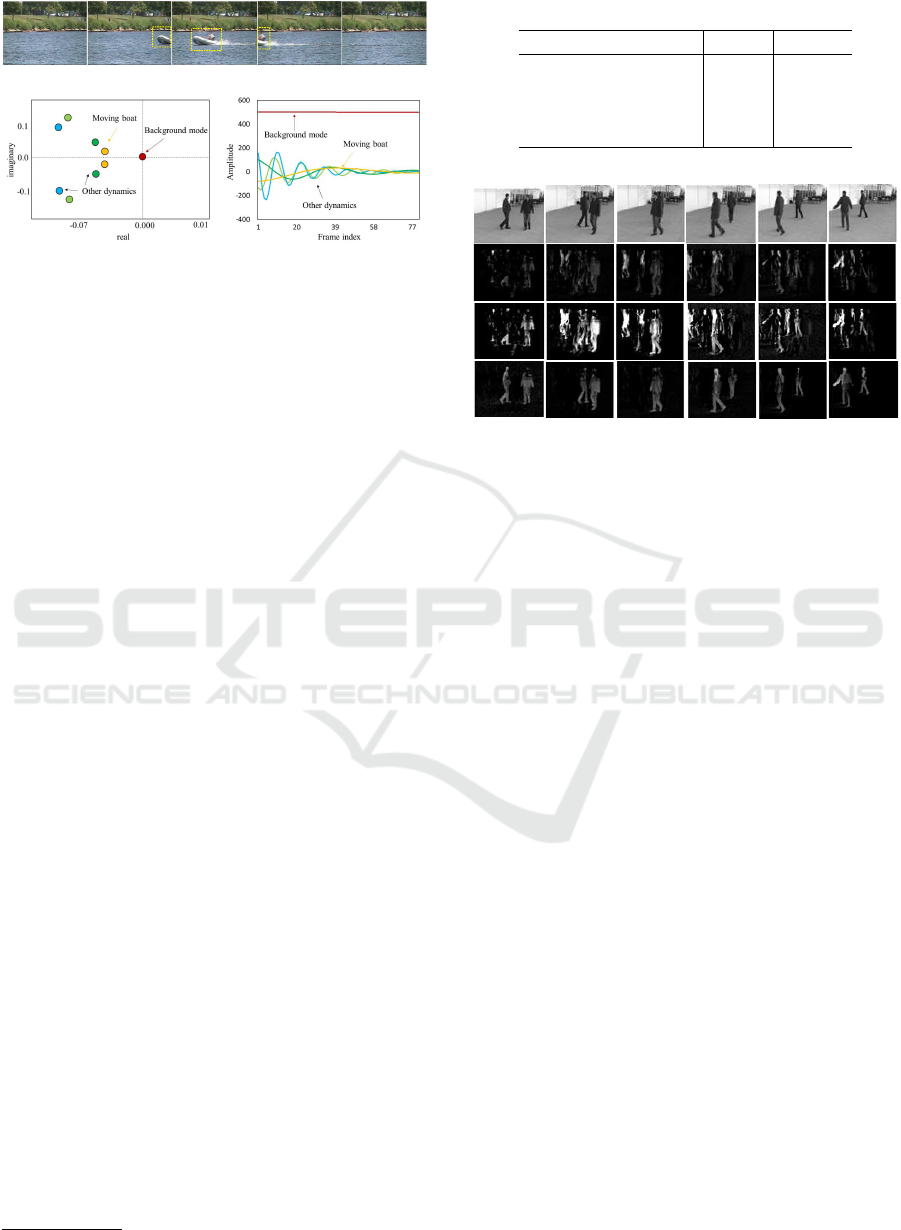
(a)
(b)
(c)
Figure 2: Splitting foreground and the background
(Changedetection.net (Goyette et al., 2012) video sequence
“boats”) . (a) five frames of a moving boat. (b) the near
zero eigenvalue corresponds to the background and rest to
other dynamics. (c) temporal evolutions of amplitudes.
4.1 Synthetic Data
We quantitatively evaluated the performance using
the synthetic data that were generated as follows.
First, a sequence of noisy images {s
t
∈ R
128×128
} was
generated using the following equation:
s
t
= e
t
1
p
1
+ e
t
2
p
2
+ N
t
, (10)
where p
1
, p
2
∈ R
128×128
and N
t
is the zero-mean
Gaussian noise with standard deviation σ = {0.3} for
t = 0,1, .. ., 15. The dynamic modes of the noise-
free image sequences are p
1
and p
2
, where e
1
= 0.99
and e2 = 0.9, are the corresponding eigenvalues, re-
spectively. The standard DMD, cDMD and dl-DMD
methods were applied on these noisy sequence of im-
ages. The comparison of these methods demonstrates
that the dl-DMD can approximate the underlying dy-
namics more accurately by estimating the true eigen-
values (e
1
,e
2
) even in the presence of noise compared
to the standard DMD and cDMD. Table. 1 shows the
estimated eignevalues by standard, compressed and
dl-DMD method.
To demonstrate the effectiveness of the proposed
method visually, another experiment is performed
on a video of SBMnet
2
dataset, where people are
strolling in a terrace with no original background pro-
vided in the dataset. To visualize the foreground
structures extracted by the dl-DMD, standard and
cDMD methods we chose 200 consecutive frames
from the video and then applied all those three meth-
ods. Figure 3 (first row) shows every 20th frame
of first 100 frames of a video. Second row shows
the foregrounds extracted by standard DMD method.
Third and fourth rows show the foregrounds extracted
by the compressed DMD and the proposed method,
2
http://scenebackgroundmodeling.net/
Table 1: Estimated and the ground-truth eigenvalues.
e
1
e
2
Ground truth 0.99 0.9
Standard DMD 0.994 0.8319
Compressed DMD 0.994 0.8348
dl-DMD (proposed) 0.991 0.90
Figure 3: First-row: original video frames of moving peo-
ple; second-row: extracted foregrounds with standard DMD
method; Third-row: extracted foregrounds with compressed
DMD; Last-row: extracted foregrounds with dl-DMD (Pro-
posed).
respectively. It can be visualized that dl-DMD can
extract the foreground dynamics more accurately than
standard and cDMD methods. Note that, for this ex-
periment size of sensing matrix in cDMD was set to
p
c
= (n1 ∗ n2)/2 (see Algorithm 2), since too much
compression will result in loss of spatial information.
Parameters Selection: The parameters of dl-DMD
were tuned manually for best results and set to T
0
=
16, λ
1
,λ
2
= 10
−3
, dictionary size = 64 × 128, patch
size 8 ×8 with overlapping factor 1. A dictionary with
more number of dictionary atoms minimize the recon-
struction error after applying the DMD at the cost of
high computation time, whereas a dictionary with few
atoms holds less information that in result increases
the reconstruction error. Figure. 4 shows the decrease
in reconstruction error by increasing the size of dictio-
nary atoms. Another important parameter is the patch
size, the relation between the patch size and the mean
reconstruction error (between the DMD reconstructed
output and input video) is shown in Table. 2. This
relation shows that for a fixed number of dictionary
atoms, increasing the patch size results in increasing
the reconstruction error. Figure. 5 shows some of the
learned dictionaries on BMC dataset.
4.2 Real Video Dataset
We further measured the quantitative performance of
our proposed method on the publicly available BMC
dataset (Vacavant et al., 2012; Sobral and Vacavant,
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
480
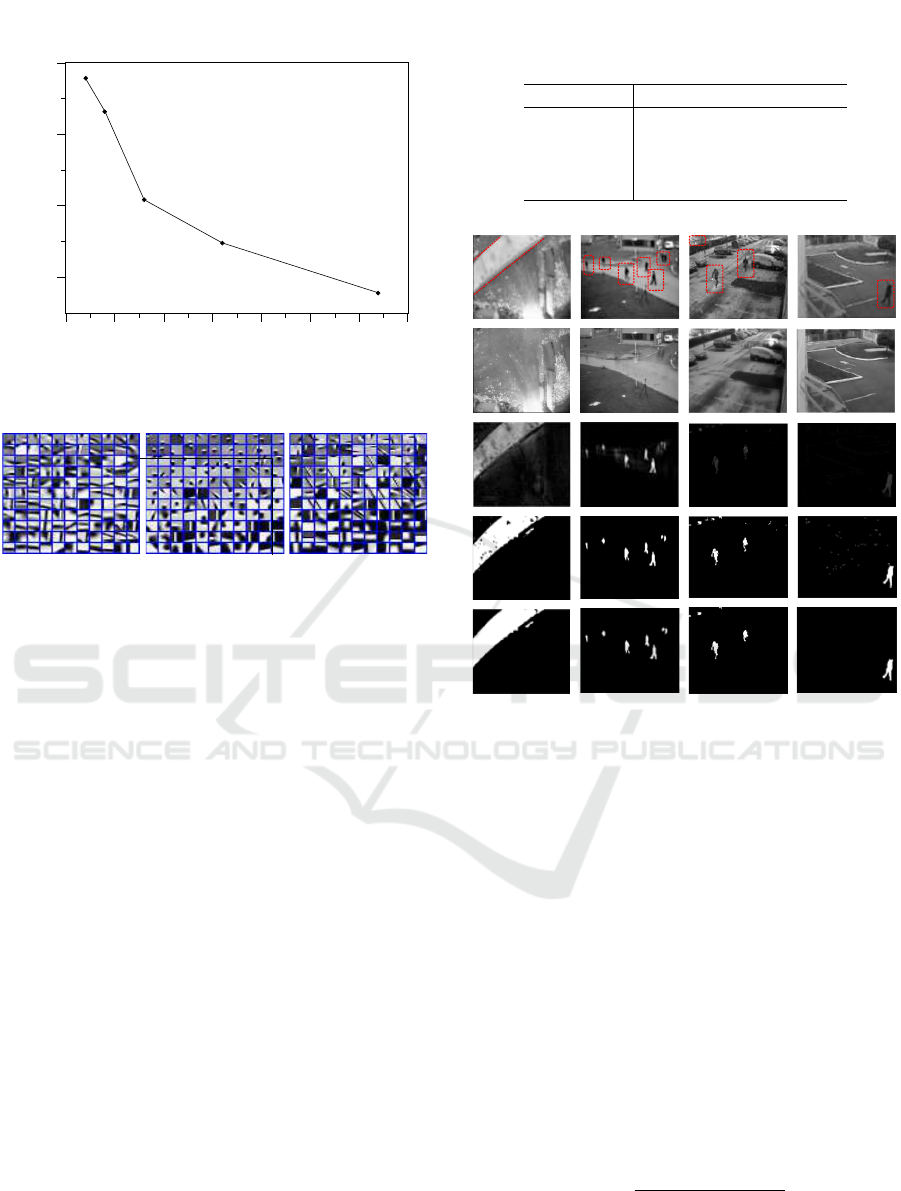
Reconstruction Error
0.04
0.06
0.08
0.1
Number of Dictionary elements
0 20 40 60 80 100 120 140
Figure 4: Reconstruction error decreases with increasing
dictionary atoms.
Figure 5: Trained dictionaries on BMC dataset of first three
videos; (001) Boring parking, (002) Big trucks and (003)
Wandering students.
2014). This dataset is a benchmark for background
modeling of various outdoor surveillance scenarios,
such as raining or snowing at different time inter-
vals, illumination changes or snowing at different
time intervals, illumination changes relative to out-
door lighting conditions, long duration of motionless
foreground objects, and dynamic backgrounds (e.g.,
moving clouds or trees).
Some of the foreground extraction results of BMC
videos (002), (003), (005) and (009) are shown in Fig-
ure 6 and evaluation results for all the nine videos
on this dataset are presented in Table. 3 (Erichson
et al., 2016). For pre-processing we cropped 200
consecutive frames of each video, and more than one
background is estimated for those videos where back-
ground changes with time as in videos (001), (005)
and (008).
These results indicate some of the strengths and lim-
itations of the proposed method. Note that the pro-
posed method is presented as a batch algorithm ap-
plied to a set of consecutive frames. Thus, any
changes that occur later in time are difficult to de-
tect, such as the sleeping foreground in video (001),
when the cars are parked for a long period of time;
this reduces the F-measure value. Another factor
that reduces the F-measure value is the presence of
non-periodic backgrounds, such as snow and moving
clouds, which prominently appear in videos (005) and
(008), respectively. However, in case of videos with
Table 2: Relation b/w patch size and reconstruction error.
Patch size Reconstruction error
4 × 4 0.0326
8 × 8 0.0369
12 ×12 0.0373
16 × 16 0.0411
Figure 6: Foreground extraction corresponding to BMC
videos: 002, 003, 005 and 009. The top row shows a sin-
gle frame of each video. The second row shows the esti-
mated backgrounds. The third row shows the difference be-
tween the original frames and backgrounds reconstructed.
The fourth row shows the thresholded frames, and the fifth
row shows the extracted foregrounds after applying mor-
phological operations (closing and dilation to fill holes).
little variation in the background, high F-measure
values were obtained. The recall, precision, and F-
measure metrics were calculated to evaluate the real
videos.
Recall: It measures the ability to accurately detect the
foreground pixels which belong to the foreground.
Precision: It measures the number of accurately de-
tected foreground pixels which are actually correct.
F-measure: It is the harmonic mean of recall and pre-
cision that provides an average value when the values
are close, and calculated as
F = 2.
Precision × Recall
Precision + Recall
, (11)
dl-DMD achieves high F-measure values in videos
(003), (004) and (009) because the backgrounds of
these videos are almost static for the entire duration
and in video (002) background is static at different in-
Dynamic Mode Decomposition via Dictionary Learning for Foreground Modeling in Videos
481
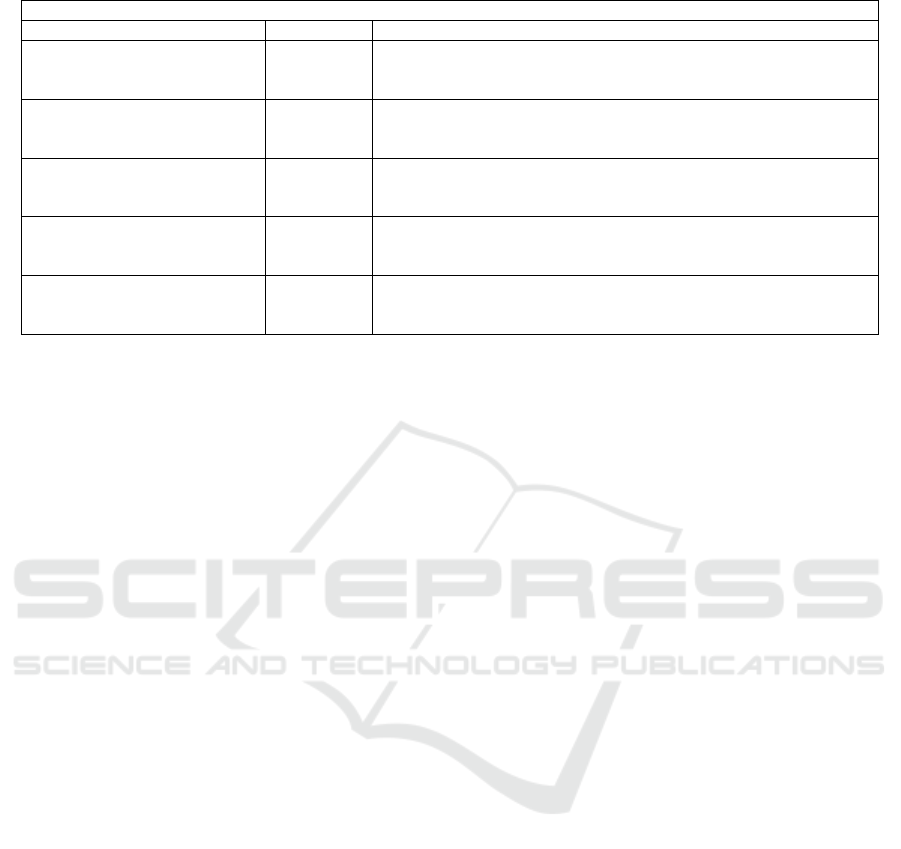
Table 3: Evaluation results (BMC dataset).
Measure BMC videos
001 002 003 004 005 006 007 008 009
Recall 0.800 0.689 0.840 0.872 0.861 0.823 0.658 0.589 0.690
RSL De La Torre Precision 0.732 0.808 0.804 0.585 0.598 0.713 0.636 0.526 0.625
(De La Torre and Black, 2003) F-Measure 0.765 0.744 0.821 0.700 0.706 0.764 0.647 0.556 0.656
Recall 0.693 0.535 0.784 0.721 0.643 0.656 0.449 0.621 0.701
LSADM Goldfarb Precision 0.511 0.724 0.802 0.729 0.475 0.655 0.693 0.633 0.809
et al.(Goldfarb et al., 2013) F-Measure 0.591 0.618 0.793 0.725 0.549 0.656 0.551 0.627 0.752
Recall 0.684 0.552 0.761 0.709 0.621 0.670 0.465 0.598 0.700
GoDec Zhou and Tao Precision 0.444 0.682 0.808 0.728 0.462 0.636 0.626 0.601 0.747
(Zhou and Tao, 2011) F-Measure 0.544 0.611 0.784 0.718 0.533 0.653 0.536 0.600 0.723
Recall 0.552 0.697 0.778 0.693 0.611 0.700 0.720 0.515 0.566
Erichson Precision 0.581 0.675 0.773 0.770 0.541 0.602 0.823 0.510 0.574
et al.(Erichson et al., 2016) F-Measure 0.566 0.686 0.776 0.730 0.574 0.647 0.768 0.512 0.570
Recall 0.584 0.732 0.806 0.882 0.493 0.608 0.565 0.456 0.713
dl-DMD (proposed) Precision 0.587 0.784 0.931 0.624 0.591 0.605 0.660 0.552 0.811
F-Measure 0.586 0.757 0.864 0.731 0.537 0.607 0.608 0.500 0.758
tervals of time. dl-DMD can extract small and large
moving foreground objects, such as a running rabbit
in video (004) and the big moving trucks with illumi-
nation changes in video (002), respectively; addition-
ally, the competitive F-measure values were obtained.
5 CONCLUSIONS
We proposed dl-DMD for accurate foreground extrac-
tion in videos. In dl-DMD, DMD is performed on
coefficient matrices estimated over a dictionary that
is learned on the randomly selected patches from the
video frames. The experiments on synthetic data re-
veals that the use of dictionary with DMD can extract
complex dynamics in time series data more accurately
than standard DMD and cDMD methods. Also, ex-
periments on real video dataset demonstrates that our
proposed method can extract foreground and back-
ground information in videos with comparable per-
formance to other methods.
ACKNOWLEDGEMENTS
This work was supported by JSPS KAKENHI (Grant
Number JP18H03287) and JST CREST (Grant Num-
ber JPMJCR1913).
REFERENCES
Aharon, M., Elad, M., and Bruckstein, A. (2006). rmk-svd:
An algorithm for designing overcomplete dictionaries
for sparse representation. IEEE Transactions on Sig-
nal Processing, 54(11):4311–4322.
Bouwmans, T., Sobral, and Javed, S. (2017). Decompo-
sition into low-rank plus additive matrices for back-
ground/foreground separation. Computer Science Re-
view, 23:1–71.
Cand
`
es, E. J., Li, X., Ma, Y., and Wright, J. (2011). Robust
principal component analysis? Journal of the ACM
(JACM), 58(3):11.
De La Torre, F. and Black, M. J. (2003). A framework
for robust subspace learning. International Journal
of Computer Vision, 54(1-3):117–142.
Erichson, N. B., Brunton, S. L., and Kutz, J. N. (2016).
Compressed dynamic mode decomposition for back-
ground modeling. Journal of Real-Time Image Pro-
cessing, pages 1–14.
Goldfarb, D., Ma, S., and Scheinberg, K. (2013). Fast alter-
nating linearization methods for minimizing the sum
of two convex functions. Mathematical Programming,
141(1-2):349–382.
Goyette, N., Jodoin, P.-M., Porikli, F., Konrad, J., and Ish-
war, P. (2012). Changedetection. net: A new change
detection benchmark dataset. In CVPRW, 2012 IEEE
Computer Society Conference on, pages 1–8. IEEE.
Koopman, B. (1931). Hamiltonian systems and transfor-
mation in Hilbert space. Proceedings of the National
Academy of Sciences USA, 17(5):315–318.
Kutz, J. N. and Fu (2015). Multi-resolution dynamic mode
decomposition for foreground/background separation
and object tracking. In 2015 IEEE (ICCVW), pages
921–929. IEEE.
Oliver, N., Rosario, B., and Pentland, A. (1999). A bayesian
computer vision system for modeling human interac-
tions. In ICVS, pages 255–272. Springer.
Schmid, P. J. (2010). Dynamic mode decomposition of nu-
merical and experimental data. Journal of fluid me-
chanics, 656:5–28.
Sobral, A. and Vacavant, A. (2014). A comprehensive re-
view of background subtraction algorithms evaluated
with synthetic and real videos. Computer Vision and
Image Understanding, 122:4–21.
Takeishi, N., Kawahara, Y., and Yairi, T. (2017). Sparse
non-negative dynamic mode decomposition. In 2017
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
482

IEEE Int. Conf. on Image Process. (ICIP’17), pages
2682–2686.
Vacavant, A., Chateau, T., Wilhelm, A., and Lequi
`
evre,
L. (2012). A benchmark dataset for outdoor fore-
ground/background extraction. In Asian Conference
on Computer Vision, pages 291–300. Springer.
Zhou, T. and Tao, D. (2011). Godec: Randomized low-
rank & sparse matrix decomposition in noisy case. In
ICML. Omnipress.
Dynamic Mode Decomposition via Dictionary Learning for Foreground Modeling in Videos
483
