
RBF Neural Network based Trajectory Control and Impedance Control
of a Upper Limb Tele-rehabilitation Process
Ting Wang
1 a
and Yanfeng Pu
2 b
1
School of Instrument Science and Engineering, Southeast University, 2, Sipailou, Xuanwu District, Southeast University,
210096, Nanjing, China
2
Nanjing Customs District P. R. China, 360, Longpanzhong Road, Qinhuai District, Nanjing, China
Keywords:
Impedance Control, Upper Limb, Tele-rehabilitation.
Abstract:
In the passive tele-rehabilitation process, the safety is the most important thing for patients avoiding the sec-
ondary damage of the impaired upper limb. Aiming at adjusting the appropriated contact force in time during
the training exercises, an adaptive impedance control is proposed for the slave side. At the same time, the
trajectory control based on the Hamilton-Jacobi-Inequality theory and the RBF Neural network is performed
for the master manipulator operated by therapists. The stability is analyzed and numerical simulations show
the efficiencies and high performances of the proposed method.
1 INTRODUCTION
Recently, researchers publish their study in the New
England Journal of Medicine (NEJM) based on the
GBD data in 2016 (GBDStrokeCollaborators, 2018),
which calculates the lifetime stroke risk in various
countries and regions from 1990 to 2016. Results
demonstrate that the risk of the lifetime stroke in
adults aged 25 increases by 8.9% to 24.9% in the
past 26 years. What is more, the overall risk of
the lifetime stroke in China and Chinese men both
reach 40%. Scientists continue to point out that the
number of stroke in China accounts for the first rank
in the world (GBDStrokeCollaborators, 2019)(Gore-
lick, 2019). After the participation of the Chinese re-
searchers, the latest research evidence and the specific
information in the field of stroke prevention and treat-
ment in China are published in(S Wu, 2019). It re-
veals that the incidence of stroke in China is promoted
in the past 20 years. The prevention and treatment of
stroke in China is not balanced among regions. The
risk factors of stroke are higher in the countryside
than in the city (Brainin, 2019). With the continu-
ous improvement of the stroke treatment in China in
recent years, the mortality of stroke patients are not
enhanced significantly in the past 20 years. However,
the incidence of stroke is still rising. That is, the bur-
a
https://orcid.org/0000-0001-7414-5390
b
https://orcid.org/0000-0003-0857-9048
den of the stroke is still heavy. In recent 10 years,
the prevalence of stroke among urban and rural resi-
dents has a stable trend, while the prevalence in rural
areas has increased significantly (Z Li, 2019). Since
the China has the vast territory, many rural stroke pa-
tients live far away from the city, so that it is more
difficult for them to go to hospital for rehabilitation
treatment than urban residents. Therefore, the tele-
rehabilitation training is a good way to solve the prob-
lem. In the meantime, it may decrease the cost of ex-
pensive therapies, and it also raise the efficiency of
the medical therapists.
The upper limb tele-rehabilitation refers that a
therapist operates a rehabilitative manipulator in the
master side, while another rehabilitation manipulator
simultaneously assists patients in the slave side so as
to achieve training exercises in the remote place. Via
the internet vision and the communication on both
sides, the therapist may connivently guide and adjust
the patient’s training exercises. Since it is an inter-
esting and a new active issue, many researchers de-
vote various study for the purpose of spreading the
tele-rehabilitation mode rehabilitation to remote pas-
sive therapists. On the basis of the wave variable the-
orem, Mendoza and his colleagues present a novel
bilateral tele-rehabilitation method in (M Mendoza,
2016). In the tele-rehabilitation system, the motion-
based adaptive impedance control is exerted on both
the master and slave robot manipulators for robot as-
sisted passive rehabilitation. Thinking of the time de-
Wang, T. and Pu, Y.
RBF Neural Network based Trajectory Control and Impedance Control of a Upper Limb Tele-rehabilitation Process.
DOI: 10.5220/0009143401090116
In Proceedings of the 17th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2020), pages 109-116
ISBN: 978-989-758-442-8
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
109
lay, the stability of the tele-rehabilitation system is
analyzed. Numerical simulations are performed and
results demonstrate that the proposed method may
ensure the stable humanrobot interaction as well as
compensate the position drift. The paper developed a
novel control method based on the estimation of the
forces on both the master and slave robots so as to re-
place the expensive force sensor (F Azimifar, 2017).
The stability is analyzed with the consideration of the
time delay. The proposed method is verified by posi-
tion tracking experiments. In order to enhance the pa-
tienttherapist interaction, Mojtaba and his colleagues
introduce a adaptive bilateral impedance controller
for the upper limb tele-rehabilitation training process
(M Sharifi, 2017). The proposed method is verified
by experiments on a nonlinear multi-DOF manipula-
tors. Thus, they continue to study the impedance con-
trol of robot assisted tele-operation process (M Shar-
ifi, 2018). They tune an adaptive law with bilat-
eral impedance control for the purpose of changing
impedance model parameters during the tele-surgery
of a beating heart. The advantage of their proposed
method is that it avoids affording expensive force sen-
sor’s device as well estimating the heart’s motion. Af-
ter the discuss of the stability, experimental results
demonstrate that the proposed bilateral impedance
control may increase the safety of patients and com-
pensate the motion of the beating heart.
In this paper, we focus on the bilateral impedance
control for the upper limb tele-rehabilitation training
process so as to achieve the protection of the safety of
impaired patients. Simultaneously, a trajectory con-
troller is proposed also on the basis of the Hamilton-
Jacobi-Inequality (HIJ) theory and the RBF Neural
network to ensure the normal training exercises. The
therapist may change the motion through regulating
parameters of the impedance model from the contact
force in the slave side. Rest of the paper is organized
as follows. The dynamic model and the impedance
model is introduced in section 2. Section 3 explains
the trajectory control and the impedance control in the
master side and the adaptive neural fuzzy impedance
control in the slave side. Numerical simulations are
demonstrated in section 4. Some conclusions are
given in the conclusion part.
2 THE DYNAMIC MODEL AND
THE IMPEDANCE MODEL OF
THE TELE-REHABILITATION
SYSTEM
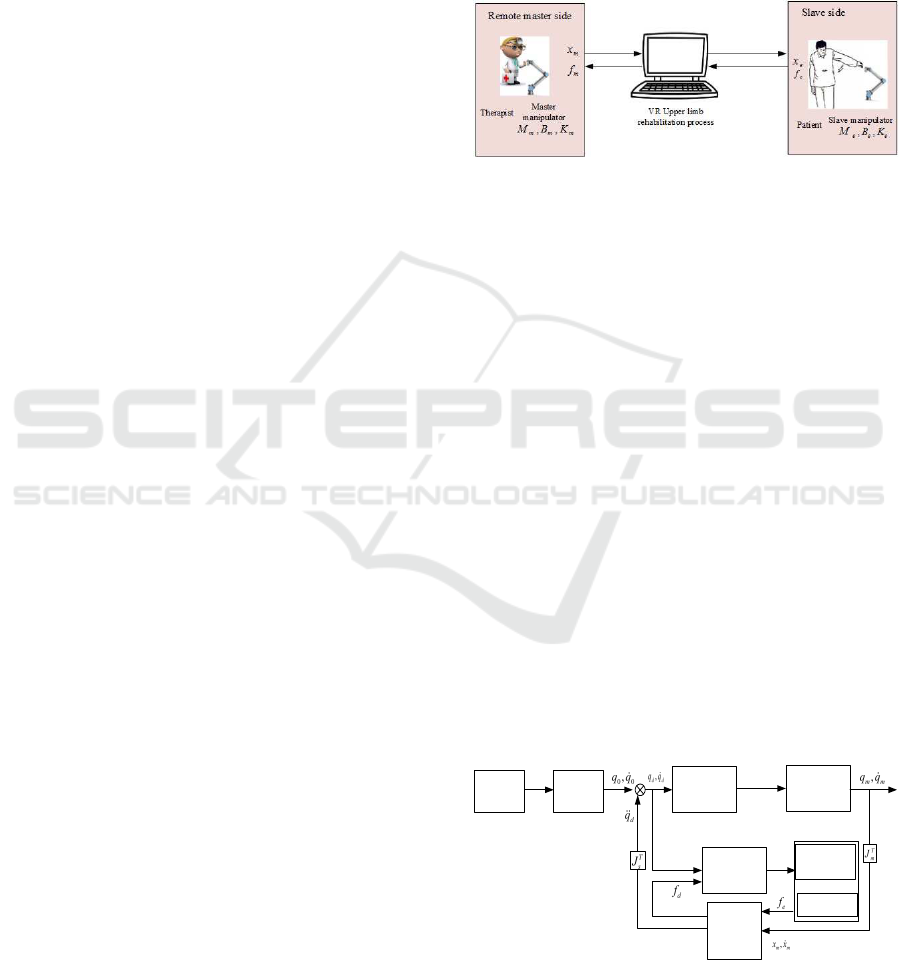
The upper limb tele-rehabilitation process may be de-
scribed in the following picture as shown in Figure.1.
Figure 1: The upper limb tele-rehabilitation process.
The integral system may be regarded as a bilateral
tele-operation system involving (1)the therapist and
the master manipulator in the master side, (2) the pa-
tient and the slave manipulator in the slave side and
(3) a VR screen which exhibits the training process
by the internet. At the beginning of our study, the
time delay is simplified to zero in this paper although
it cannot be ignored in the reality. Therefore, the up-
per limb tele-rehabilitation system can be separated
into two subsystems as shown in Figure. 2. The first
subsystem is the master trajectory control loop. As
the therapist designs the desired training exercises tra-
jectory, the master manipulator tracks it by the mas-
ter trajectory control. In the initial training exercises,
the slave manipulator follows the master manipulator
to push the upper limb of the patient. Since patients
have different degree of disability, they can bear dif-
ferent contact forces. The second subsystem is the
slave impedance control. With the changes of the con-
tact forces, the desired trajectory is adjusted through
the slave impedance control. In fact, the role of the
slave impedance control is a forward feedback using
to modify the training exercises trajectory depending
on the affordable conditions of patients.
Master
Manipulator
Therapist
Master
Trajectory
control
Path
planning
Slave
Manipulator
Environment
Slave
Trajectory
control
Slave
Impedance
Control
Figure 2: The composition of the tele-rehabilitation system.
Assuming that both the master and the slave take
the n DOF manipulator system, the dynamic model is
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
110

expressed as follows.
M
i
(q
i
(t)) ¨q
i
(t)+C
i
(q
m
(t), ˙q
i
(t)) ˙q
i
(t)+G
i
(q
i
)+∆(q
i
, ˙q
i
)+d
i
(t) = T
i
(t)
(1)
where M
i
∈ R
m×n
,C
i
∈ R
m×n
, G
i
∈ R
m×n
, i = m, s
stand for the inertial items, the Coriolis and centrifu-
gal effects items and the gravitational items. The
subscripts m and s represent respectively the master
and the slave. State variables in the joint space of
the master and the slave manipulators are described
as q
i
, ˙q
i
, ¨q
i
∈ R
n×n
. T
i
indicates the control inputs.
∆(q
i
, ˙q
i
) and d
i
(t) represent the model uncertainties
and the external disturbances.
The impedance model of the slave system is writ-
ten as follow.
H
s
¨x
s
(t) + B
s
˙x
s
(t) + K
s
x
s
= f
e
, (2)
where H
i
, B
i
and K
i
are respectively inertial,
damping and stiffness matrices. x
s
, ˙x
s
, ¨x
s
∈ R
n×n
are
state variables in the work space. The state variables
in the work space may transferred to the joint space
via following nonsingular Jacobian matrices.
˙x
i
= J( ˙q
i
)
¨x
i
=
˙
J(q
i
) +
˙
J ¨q
i
(3)
where
J =
−l
1
sin(q
i1
) − l
2
sin(q
i1
+ q
i2
) −l
2
sin(q
i1
+ q
i2
)
l
1
cos(q
i1
) + l
2
cos(q
i1
+ q
i2
) l
2
cos(q
i1
+ q
i2
)
The tele-rehabilitation system has following prop-
erties (J Zhang, 2018).
• The inertia matrices M
i
are symmetric positive
definite matrices, M
i
= M
T
i
, and there exist the
upper and lower boundedness, M
down
I ≤ |M
i
| ≤
M
up
I (M
down
and M
up
are two positive constants)
•
˙
M
i
(q
i
)−2C
i
(q
i
, ˙q
i
) are skew-symmetric matrices.
• For all q
i
(t), ˙q
i
(t) ∈ R
n×1
, there exists a positive
scalar c
i
may render C
i
(q
i
(t), ˙q
i
(t)) ≤ c
3
| ˙q
i
|(1 +
|q
i
|) ≤ c
3
| ˙q
i
|, in which c
1
, c
2
, c
3
> 0 and | · | rep-
resents the Euclidean matrix norm.
• The linear parameterizable dynamic model of the
tele-rehabilitation system (in Eq.(1)) may be ex-
pressed as M
i
(q
i
(t)) ¨q
i
(t) + C
i
(q
i
(t), ˙q
i
(t)) ˙q
i
(t) +
G
i
(q
i
(t)) = Y
i
(q
i
(t), ˙q
i
(t), ¨q
i
(t))θ
i
, where
Y
i
(q
i
(t), ˙q
i
(t), ¨q
i
(t)) ∈ R
n×p
are a certain function
and θ
i
∈ R
p
are physical parameter vectors of the
master and the slave manipulators.
3 THE TRAJECTORY CONTROL
BASED ON THE HJI THEORY
AND RBF NEURAL NETWORK
3.1 The HJI Theory
The bilateral thele-rehabilitation system (in Eq.1)
may be rewritten as the following form.
˙x
i
(t) = f (x
i
) + g(x)d(t)
z(t) = h (x
i
)
(4)
where x(t), u(t), z(t) are respectively the state vari-
able, the input and the system evaluation index. d is
the external disturbances causing by communication
time delay, noises and so on.
Definition For the disturbance signal, its norm is de-
fined as kd(t)k
2
= {
R
∞
0
d
T
(t)d(t)dt}
1
2
, which may
measure the magnitude of the d(t) energy. In order
to evaluate the disturbance suppression ability of the
system, the performance index is defined as follow
J = sup
kd(t)k6=0
=
k z k
2
kdk
2
, (5)
where J is the L
2
gain of the system, indicating the ro-
bust performance. The smaller J results better robust
performance of the system.
According to (Schaft, 1992), the Hamilton-Jacobian-
Inequality theorem can be described as follow. For
a positive number γ, if there exists a positive definite
and differentiable function L(x) ≥ 0, and
˙
L ≤
1
2
{γ
2
kdk
2
− kzk
2
}, (∀d), (6)
then J ≤ γ.
3.2 The Trajectory Control and Its
Analysis
Assuming there is no time delay, the master is the
same as the slave manipulator, and both of manipu-
lators have the same initial state variables. Due to the
limitation of the paper, we merely introduce the mas-
ter trajectory control, and the slave adopts the same
trajectory control method. The desired trajectory is
noted by q
d
, and the trajectory tracking error is de-
fined as e = q − q
d
. The forwards feedback control
law is designed as
T = u + M ¨q
d
+C ˙q
d
+ G, (7)
where u is the feedback control law.
Substituting the Eq.(7) into the Eq. (1), the close
RBF Neural Network based Trajectory Control and Impedance Control of a Upper Limb Tele-rehabilitation Process
111

tele-rehabilitation system may change to the follow-
ing form,
M ¨e +C ˙e + ∆(q, ˙q) + d = u. (8)
Ordering ∆ f (q, ˙q)+d, we may get M ¨e+C ˙e+∆ f = u.
Taking the RBF neural network (RBFNN) to approx-
imate the ∆ f , the ∆ f is expressed as
∆ f = W
∗
f
σ
f
+ ε
f
, (9)
where ε
f
stands for the approximation error. σ
f
is the
RBF Gaussian function and W
∗
f
is the ideal weights
of the RBFNN. Combing Eq.(8) and Eq.(9), we may
acquire M ¨e +C ˙e +W
∗
f
σ
f
+ ε
f
= u.
Define
x
1
= e
x
2
= ˙e + αe, α > 0
(10)
then,
x
1
= x
2
− αx
1
M ˙x
2
= −Cx
2
+ ω −W
∗
f
− ε
f
+ u
ω = Mα ˙e +Cαe
(11)
Using the HJI inequality, rewritten the Eq. (11) to the
state space form as follow,
˙x = f (x) + g(x)d
z = h(x)
(12)
where f (x) =
x
2
− αx
1
1
M
(−Cx
2
+ ω −W
∗
f
σ
f
+ u)
,
g(x) =
0
1
M
, d = ε
f
. The evaluation index is
defined as follow. Due to d = ε, the approximation
error may be regarded as the external disturbance.
Therefore, the evaluation index is denoted by
z = x
2
= ˙e + αe, and its L
2
gain calculated by
J = sup
kε
f
k6=0
=
kzk
2
kε
f
k
2
.
The adaptive law of the tele-rehabilitation system is
designed as
˙
ˆ
W
f
= −ηx
2
σ
T
f
. (13)
Thus, the feedback control is expressed as
u
i
= −ω −
1
2γ
2
x
2
+
ˆ
W
f
σ
f
−
1
2
x
2
, (14)
where
ˆ
W
f
and σ
f
respectively note the weight of the
RBFNN and the output of the Gaussian function. That
is, the tele-rehabilitation system satisfies J ≤ γ. Ac-
cording to (Y wang, 2009), the stability is analyzed
as follow. The Lyapunov function is selected as
L =
1
2
x
T
2
Mx
2
+
1
2η
tr(
˜
W
T
f
˜
W
f
),
where
˜
W
f
=
ˆ
W
f
− W
∗
f
. Due to the properties of the
tele-rehabilitation system and the proposed feedback
control law, we may get following relations.
˙
L = x
T
2
M ˙x
2
+
1
2
x
T
2
˙
Mx
2
+
1
η
tr(
˙
˜
W
T
f
˜
W
f
)
= x
T
2
(−Cx
2
+ ω −W
∗
f
σ
f
− ε
f
+ u)
+
1
2
x
T
2
˙
Mx
2
+
1
η
tr(
˙
˜
W
T
f
˜
W
f
)
= x
T
2
(−Cx
2
−W
∗
f
σ
f
− ε
f
−
1
2γ
2
x
2
+
ˆ
W
f
σ
f
−
1
2
x
2
)
+
1
2
x
T
2
˙
Mx
2
+
1
η
tr(
˙
˜
W
T
f
˜
W
f
)
= x
T
2
(−ε
f
−
1
2γ
2
x
2
+
˜
W
f
σ
f
−
1
2
x
2
)
+
1
2
x
T
2
(
˙
M − 2C)x
2
+
1
η
tr(
˙
˜
W
T
f
˜
W
f
)
= −x
T
2
ε
f
−
1
2γ
2
x
T
2
x
2
+ x
T
2
˜
W
f
σ
f
−
1
2
x
T
2
x
2
+
1
η
tr(
˙
˜
W
T
f
˜
W
f
)
Order
H =
˙
L −
1
2
γ
2
kε
f
k
2
+
1
2
kzk
2
, (15)
then,
H = −x
T
2
ε
f
−
1
2γ
2
x
T
2
x
2
+ x
T
2
˜
W
f
σ
f
−
1
2
x
T
2
x
2
+
1
η
tr(
˙
˜
W
T
f
˜
W
f
)
−
1
2
γ
2
kε
f
k
2
+
1
2
kzk
2
Considering the following conditions,
• −x
T
2
ε
f
−
1
2γ
2
x
T
2
x
2
−
1
2
γ
2
kε
f
k
2
= −
1
2
k
1
γ
x
2
+ γε
f
k
2
≤ 0,
• x
T
2
˜
W
f
σ
f
+
1
η
tr(
˙
˜
W
T
f
˜
W
f
) = 0,
• −
1
2
x
T
2
x
2
+
1
2
kzk
2
,
we may easily get H ≤ 0. Depending on the definition
of H, we have
˙
L ≤
1
2
γ
2
kε
f
k
2
−
1
2
kzk
2
. Due to Eq.(6)
of the HJI theorem,we may deduce J ≤ γ, so that kzk
satisfies the performance index. That is, the trajectory
tracking error e
i
and ˙e conform to the convergency
requirement.
3.3 Adaptive Slave Impedance Control
The impedance model and the contact force between
the patient and the slave manipulator can be written
as follow.
H( ¨x − ¨x
m
) + B( ˙x − x
m
) + K(x − x
m
) = f
e
, (16)
where f
e
is the desired contact force between the im-
paired upper limb and the slave manipulator.. Since
we assume that there is not the time delay, the an-
gle and the angular velocity of the master manipu-
lator q, ˙q, ¨q may lossless send to the slave manipula-
tor. Via the transfer of the Jacobian matrix, we may
acquire the modified angular accelerator of the slave
manipulator. H, B and K are the inertia, the stiffness
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
112

and damping matrices parameters of the impedance
model. x, ˙x, ¨x are the position under the appropriate
contact force of patients.
Assuming that the tracking error is defined as ˜x =
x − x
m
, the reference model is expressed as follow,
¨x
m
+ λ
1
˙x
m
+ λ
2
x
m
= λ
2
f
e
, (17)
where λ
1
and λ
2
are positive numbers. For an uncer-
tain H, the adaptive law is set as follow,
U =
ˆ
H( ¨x
m
− 2λ
˙
˜x − λ
2
˜x), (18)
where λ is strictly positive and
ˆ
H is the estimation of
the inertial matrix.
Defining v = ¨x
m
− 2λ
˙
˜x − λ
2
˜x, and substituting the
Eq.(18) into Eq.(16), we may get the following re-
lation,
H ¨x =
ˆ
H( ¨x
m
− 2λ
˙
˜x − λ
2
˜x) =
ˆ
Hv. (19)
Setting
˜
H =
ˆ
H − H, the Eq.(19) may be transferred to
H( ¨x − v) =
˜
Hv. (20)
Define the tracking error function s as
s =
˙
˜x + λ˜x. (21)
From Eq. (19), it can be seen that the convergence of
s implies the the convergence of the position tracking
error ˜x and the velocity tracking error
˙
˜x.
Due to
¨x − v = ¨x − ¨x
m
+ 2λ
˙
˜x + λ
2
˜x
=
¨
˜x + λ
˙
˜x + λ(
˙
˜x + λ ˜x)
= ˙s + λs
, the Eq.(20) changes into
H( ˙s + λs) =
˜
Hv. (22)
That is, Hs ˙s = −λHs
2
+
˜
Hvs. Defining the Lyapunov
function as
V =
1
2
(Hs +
1
γ
˜m
2
), γ > 0. (23)
The derivation of V is as follows,
˙
V = Hs ˙s +
1
γ
˜
H
˙
˜
H
= −λHs
2
+
˜
Hvs +
1
γ
˜
H
˙
ˆ
H
= −λHs
2
+
˜
H(vs +
1
γ
˙
ˆ
H)
The adaptive law of the
ˆ
H is defined as
˙
ˆ
H = −γvs.
Thus, it is obvious that
˙
V = −λms
2
≤ 0. Due to
V ≥ 0,
˙
V ≤ 0, S and
˜
H are bounded depending on
(J LaSalle, 1961)(Hassan, 2002). As
˙
V ≡ 0, s = 0.
According to LaSalle invariance principle, the close
system are asymptotically stable. As t → 0, s → 0,
˜x → 0,
˙
˜x → 0.
4 NUMERICAL SIMULATION
In the simulation, the dynamic model set as follow,
M
11
(q
i
) = (m
1
+ m
2
)r
2
1
+ m
2
r
2
2
+ 2m
2
r
1
r
2
cos(q
i2
),
M
22
(q
i
) = m
2
r
2
2
M
12
(q
i
) = M
21
(q
i
) = m
2
r
2
2
+ m
2
r
1
r
2
cos(q
i2
),
C
11
(q
i
, ˙q
i
) = −m
2
r
1
sin(q
i2
) ˙q
2
,
C
22
(q
i
, ˙q
i
) = 0
C
12
(q
i
, ˙q
i
) = −m
2
r
1
r
2
sin(q
i2
)( ˙q
1
+ ˙q
2
)
C
21
(q
i
, ˙q
i
) = m
2
r
1
r
2
sin(q
i2
) ˙q
2
g
1
(q
i1
) = (m
1
+ m
2
)r
1
cos(q
i2
) + m
2
r
2
cos(q
1
+ q
2
),
g
2
(q
i2
) = m
2
r
2
cos(q
1
+ q
2
),
where m
1
and m
2
are respectively masses of the
upper limb and the forearm. r
1
and r
2
are the lengths
of the two links (the upper limb and the forearm). The
model uncertainties ∆(q
i
, ˙q
i
) is the uncertainty part of
the tele-rehabilitation dynamic model while d
i
repre-
sents the external disturbances. Set D = ∆(q
i
, ˙q
i
)+d
i
,
where
d
i
=
30sgnq
1
30sgnq
2
.
Real values in the numerical simulations
are used as follows:m
1
= m
2
= 1.5kg, r
1
= 1m,
r
2
= 0.8m. Ideal tracking signals are selected as
q
1d
= sint, q
2d
= sint, γ = 0.05. The with and
the center of the RBF Gaussian function choose
c
i
= [−1.5, −1.0, −0.5, 0, 0.5, 1.0, 1.5] and b
i
= 10.
Other parameters list as follows:λ
1
= 10, λ
2
= 25,
λ = 6. Initial conditions are set as ˙x
i
(0) = 0, x
i
= 0.5.
Applying the proposed trajectory tracking control
and impedance control to the master and the slave ma-
nipulators of the tele-rehabilitation system, results are
illustrated in the following Figures. from 3 to 12. In
the Figure. 3, the position signal and the speed track-
ing result are displayed. The ideal position signal and
the ideal speed signal mark with red solid lines while
the position tracking results and the speed tracking re-
sult are used by black dotted lines.
The details of the position tracking show in the
Figure.4. The ideal position of the upper limb and the
forearm represent by red solid lines while tracking re-
sults are marked with black dotted lines. The speed
tracking results are displayed in Figure. 5. The ideal
speed of the upper limb and the forearm represent by
red solid lines while tracking results are marked with
black dotted lines. The position tracking error and the
speed tracking error are showed in Figure. 6. The
control inputs of the upper limb and the forearm are
RBF Neural Network based Trajectory Control and Impedance Control of a Upper Limb Tele-rehabilitation Process
113
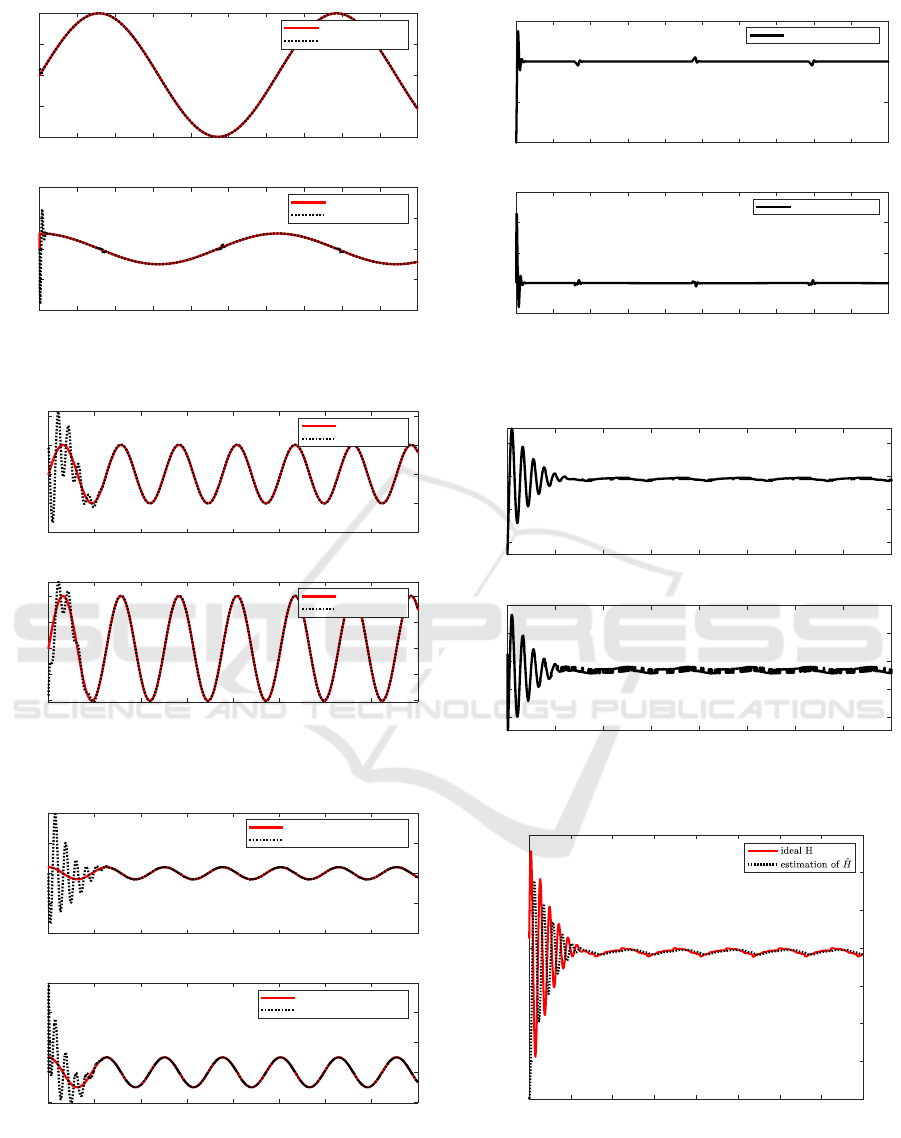
0 1 2 3 4 5 6 7 8 9 10
time(s)
-1
-0.5
0
0.5
1
position signal
ideal position signal
position tracking
0 1 2 3 4 5 6 7 8 9 10
time(s)
-4
-2
0
2
4
Speed tracking
ideal speed signal
speed tracking
Figure 3: The upper limb tele-rehabilitation process.
0 5 10 15 20 25 30 35 40
time(s)
-0.2
-0.1
0
0.1
0.2
Position tracking for upper limb
ideal position
position tracking
0 5 10 15 20 25 30 35 40
time(s)
-0.1
-0.05
0
0.05
0.1
Position tracking for forearm
ideal position
position tracking
Figure 4: The position tracking of the tele-rehabilitation
process.
0 5 10 15 20 25 30 35 40
time(s)
-1
-0.5
0
0.5
1
Speed tracking for upper limb
ideal speed for upper limb
speed tracking for upper limb
0 5 10 15 20 25 30 35 40
time(s)
-0.2
0
0.2
0.4
Speed tracking for forearm
ideal speed for forearm
speed tracking for forearm
Figure 5: The speed tracking of the tele-rehabilitation pro-
cess.
presented in Figure. 7. The figure 8 shows the es-
timation of
ˆ
H by the adaptive impedance control of
0 1 2 3 4 5 6 7 8 9 10
time(s)
-0.1
-0.05
0
0.05
position tracking error(cm)
position tracking error
0 1 2 3 4 5 6 7 8 9 10
time(s)
-2
0
2
4
6
Speed tracking error(m/s)
speed tracking error
Figure 6: The tracking error of the tele-rehabilitation pro-
cess.
0 5 10 15 20 25 30 35 40
time(s)
0
20
40
60
control input of upper limb (N.m)
0 5 10 15 20 25 30 35 40
time(s)
0
5
10
15
20
control input of forearm
Figure 7: The control input of the tele-rehabilitation pro-
cess.
0 5 10 15 20 25 30 35 40
time(s)
0
10
20
30
40
50
60
70
Ideal and estimation of H
Figure 8: The estimation of the impedance parameter of the
tele-rehabilitation process.
the slave manipulator. The contact force between the
patient and the slave manipulator is displayed in fig-
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
114
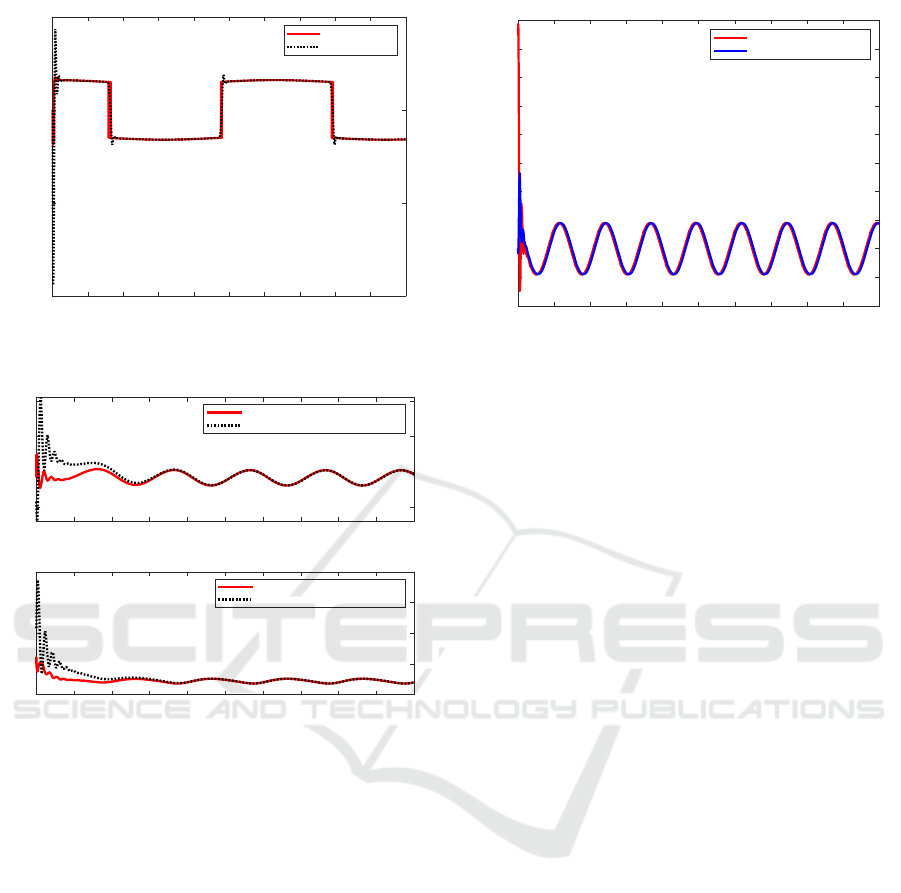
0 1 2 3 4 5 6 7 8 9 10
time(s)
-100
-50
0
50
Contact force of the slave side(N)
Practice Force
Estimated Force
Figure 9: The contact force of between the slave manipula-
tor and the patient.
0 2 4 6 8 10 12 14 16 18 20
time(s)
0
2
4
6
Uncertanties of system
Practical uncertainties of upper limb
Estimation uncertainties of upper limb
0 2 4 6 8 10 12 14 16 18 20
time(s)
-4
-2
0
2
4
Uncertanties of system
Practical uncertainties of forearm
Estimation uncertainties of forearm
Figure 10: The model uncertainties of the tele-rehabilitation
process.
ure 9. Model uncertainties of the upper limb and the
forearm are explained in Figure. 10. Figure. 11 intro-
duces the estimation of the external disturbances.
From results of numerical simulations, it may be
concluded that the patient may follow the training ex-
ercises trajectory according to the therapist through
the master trajectory tracking control. In the mean-
time, the therapist may sense the contact force of the
patient through the slave adaptive impedance control,
so that the therapist can momentarily adjust the train-
ing trajectory according to the severity of the patient.
5 CONCLUSIONS
The tele-rehabilitation process is studied in this pa-
per. In order to guide the training exercises of remote
patients, the contact force is an important issue to let
the therapist know how to strengthen or attenuate the
training exercises. At the same time, the trajectory
0 5 10 15 20 25 30 35 40 45 50
time(s)
-40
-20
0
20
40
60
80
100
120
140
160
Disturbances and its estimation
Disturbances
Estimation of disturbances
Figure 11: The external disturbances of the tele-
rehabilitation process.
tracking is also important so that different strengths
must be realized by different kinds of training exer-
cises. Aiming to solve the problems, we propose a
trajectory control based on the HJI theorem and the
RBF neural network for the master manipulator. Si-
multaneously, an adaptive impedance control is de-
signed so as to get the appropriate contact force of
the patient, for the purpose of protecting the patient
not to be impaired twice. Both of the trajectory con-
trol and the adaptive impedance control are analyzed
by the Lyapunov terrorem. Although the impedance
control is simple, it is easily to achieve in the prac-
tice. The proposed control methods are implemented
by numerical simulations. Results show the efficiency
and high performances.
ACKNOWLEDGEMENTS
This work was supported by the National Nat-
ural Science Foundation of China [grant num-
bers No.61906086, No.61802428], National Natu-
ral Science Foundation of Jiangsu province [BK.
20171019].
REFERENCES
Brainin, M. (2019). Stroke epidemiology in china: which
are the next steps? In Lancet Neurol. 18(4): 325-326.
F Azimifar, M Abrishamkar, B. F. (2017). Improving tele-
operation system performance in the presence of esti-
mated external force. In Robotics and ComputerCIn-
tegrated Manufacturing. 46:86C93.
GBDStrokeCollaborators (2018). Global, regional, and
country-specific lifetime risks of stroke, 1990 and
2016. In The New England Journal of Medicine.
379:2429-37.
RBF Neural Network based Trajectory Control and Impedance Control of a Upper Limb Tele-rehabilitation Process
115

GBDStrokeCollaborators (2019). Global, regional, and na-
tional burden of stroke, 19902016: a systematic anal-
ysis for the global burden of disease study 2016. In
Lancet Neurol. pii: S1474-4422(19)30034-1.
Gorelick, P. (2019). The global burden of stroke: persis-
tent and disabling. In Lancet Neurol. pii: S1474-
4422(19)30030-4.
Hassan, K. (2002). Nonlinear systems. In 3rd Ed. New
Jersey:Prentice Hall.
J LaSalle, S. L. (1961). Stability by lyapunov’s direct
method with applications. In New York. Academic
Press.
J Zhang, W Liu, L. G. L. L. Z. L. (2018). The master adap-
tive impedance control and slave adaptive neural net-
work control in underwater manipulator uncertainty
teleoperation. In Ocean Engineering. 165:465-479.
M Mendoza, I Bonilla, E. G. (2016). Impedance control
in a wave-based tele operator for rehabilitation motor
therapies assisted by robots. In computer methods and
programs in biomedicine. 123:54C67.
M Sharifi, S Behzadipour, H. S. M. T. (2017). Cooperative
modalities in robotic tele-rehabilitation using nonlin-
ear bilateral impedance control. In Control Engineer-
ing Practice. 67:52C63.
M Sharifi, H Salarieh, S. B. M. T. (2018). Beating heart
robotic surgery using bilateral impedance control:
Theory and experiments. In Biomedical Signal Pro-
cessing and Control. 45:256C266.
S Wu, B Wu, M. L. (2019). Stroke in china: advances and
challenges in epidemiology, prevention, and manage-
ment. In Lancet Neurol. 18(4):394-405.
Schaft, A. (1992). L2 gain analysis of nonlinear systems
and non linear state feedback h infinity control. In
IEEE Trans Autom Control. 37(6):770-784.
Y wang, W Sun, Y. X. S. M. (2009). Neural network based
robust tracking control for robots. In Int J Intel Auto
Soft Comput. 15(2):211-222.
Z Li, Y Jiang, H. L. (2019). Chinas response to the rising
stroke burden. In BMJ. 364-1879.
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
116
