
Validity of the Michaelis-Menten Approximation for the Stability
Analysis in Regulatory Reaction Networks
Takashi Naka
1
Faculty of Science and Engineering, Kyushu Sangyo University, Fukuoka, Japan
Keywords: Michaelis-Menten Approximation, Stability Analysis, Cellular Signalling Systems, Regulatory Reaction
Networks.
Abstract: Cellular signalling systems are comprised of enzymatic reaction cascades and organized as regulatory reaction
networks. The primary building block of the network is an enzymatic activation-inactivation cyclic reaction
such as phosphoryl modifications. We have investigated the effects of the network architectures and kinetic
parameter values on the stability such as the emergence of bi-stability or oscillations employing the canonical
Michaelis-Menten equation as the approximation for Michaelis-Menten-type reaction mechanisms in each of
enzymatic cyclic reaction. Although the Michaelis-Menten approximation has known to work well under an
assumption of a large excess of substrate over enzyme which is usually satisfied for metabolic pathways, the
approximation might not suit to regulatory reaction networks in which the required assumption might be
violated. In this study, comparing the predicted stabilities from the model with the Michalis-Menten
approximation and with the full set of reaction equations derived only from the law of mass action, the validity
of the Michaelis-Menten approximation was examined for the regulatory reaction networks over the possible
network architectures and kinetic parameter values elucidating that employing the Michalis-Menten
approximation might not be valid even in the analysis for the steady states such as the stability analysis.
1 INTRODUCTION
The Michaelis-Menten-type reaction mechanism has
been widely employed to construct the mathematical
models for analysing the dynamics and the stability
of the enzymatic reaction systems. Actually, the
mechanism has been devised as its approximation
form known as the Michaelis-Menten approximation
or the more simplified form such as the first order
equation or the higher order equation which is so-
called Hill equation to formulate the co-operativity
(Adler, Szekely, Mayo, & Alon, 2017; Kuwahara &
Gao, 2013; Ma, Trusina, El-Samad, Lim, & Tang,
2009; Shah & Sarkar, 2011; Sueyoshi & Naka, 2017;
Yao, Tan, West, Nevins, & You, 2011).
Although the Michaelis-Menten approximation
has known to work well under an assumption of a
large excess of substrate over enzyme which is
usually satisfied for metabolic pathways, the
approximation might not suit to regulatory reaction
networks in which the required assumption might be
1
http://www.is.kyusan-u.ac.jp/~naka/
violated since the same protein could have both roles
of the substrate and the enzyme simultaneously.
In this study, the cellular signalling systems are
formulated as the regulatory reaction networks where
the each node represents the enzymatic activation-
inactivation cyclic reaction such as phosphoryl
modifications and the each arc depicts their
regulations. Then, the effects of the Michaelis-
Menten approximation on the stability of the
regulatory reaction networks comprised of two
enzymes are analyzed to elucidate the validity of the
approximation in construction of the mathematical
models for the cellular signalling systems.
2 METHOD
All possible regulatory structures for the cellular
signalling systems comprised of two cyclic reaction
systems are formulated as the regulatory reaction
networks, and the stabilities are analysed. In
particular, the effects of the regulatory structures and
176
Naka, T.
Validity of the Michaelis-Menten Approximation for the Stability Analysis in Regulatory Reaction Networks.
DOI: 10.5220/0009093001760182
In Proceedings of the 13th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2020) - Volume 3: BIOINFORMATICS, pages 176-182
ISBN: 978-989-758-398-8; ISSN: 2184-4305
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
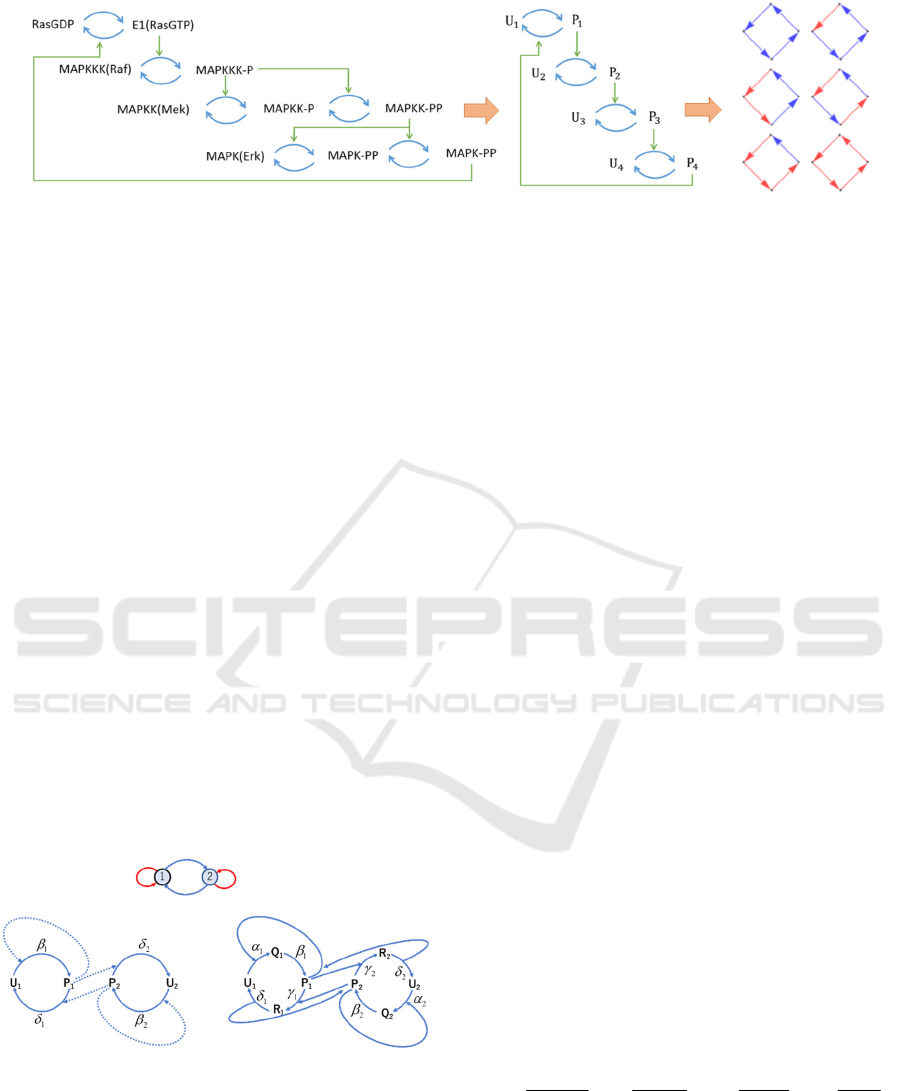
Figure 1: Regulatory reaction networks representing the MAPK cascade: the reaction scheme on the left; the simplified
reaction scheme on the middle; the regulatory reaction network representations on the right where red arrows depict positive
regulations, while blue arrows indicate negative regulations. The regulatory structure of the MAPK cascade is represented
by the four-node regulatory reaction network at the first column and the third row in the directed graphs shown on the right.
the parameter values of the systems on the number of
the stable equilibrium points are predicted.
Then, the aspects of the stability are compared
between the mathematical models employing the
Michaelis-Menten approximation and the models
derived only from the law of mass action for each
enzymatic reaction in the cyclic reaction systems.
2.1 Regulatory Reaction Networks
Figure 1 shows how the regulatory reaction networks
represent the cellular signalling systems with respect
to the MAPK cascade as an example, which is one of
the typical and the well-studied cellular signalling
systems (Ferrell, 1998; Jeschke, Baumgartner, &
Legewie, 2013; Kholodenko, 2006; Mai & Liu, 2013;
Qiao, Nachbar, Kevrekidis, & Shvartsman, 2007;
Volinsky & Kholodenko, 2013). The dual catalytic
reaction processes appeared in the third and the forth
cascades in MAPK cascade are simplified to the one
reaction step processes as shown in the middle. Red
arrows depict positive regulations where an activated
enzyme acts on another enzyme as the activating
Figure 2: Reaction schemes of the above regulatory reaction
network: employing the Michaelis-Menten approximation
on the bottom left; employing only the low of mass action
on the bottom right. Red and blue arrows on the top figure
depict the positive and negative regulations, respectively.
The solid lines on the bottom figures depict the associate
and dissociate chemical reactions, while the dotted lines
represent the enzymatic reactions foumulated by Michaelis-
Menten approximations.
enzyme, while blue arrows indicate negative
regulations where an activated enzyme acts on
another enzyme as the inactivating enzyme. Then,
the regulatory structure of the MAPK cascade is
represented by the four-node regulatory reaction
network at the first column and the third row in the
directed graphs shown on the right.
In this study, ten variations of the two-node
regulatory reaction networks shown as the legends of
the graphs in Fig. 4 are analysed. These networks are
all possible mutually regulatory reaction networks
with at most one positive regulation and one negative
regulation at each node. It should be noted that if one
of the positive or negative regulation at each node is
missing, a virtual regulation is added for the missing
regulation which catalyse with the maximum and
constant rate.
The Michaelis-Menten-type mechanisms are
employed as the reaction mechanisms in the
enzymatic cyclic reactions in each node. Figure 2
shows the mutual negative regulatory reaction
network with auto positive regulations as an example.
The representation of the network as the regulatory
reaction network is shown on the top. The left graph
and the right graph on the bottom depict the reaction
schemes employing the Michaelis-Menten
approximation and employing only the low of mass
action, respectively.
The activation reaction rate
and the
inactivation reaction rate
of node 1 in the model
employing the Michaelis-Menten approximation are
formulated as follows:
and
indicate the concentrations of the
active and inactive forms of the enzyme, respectively.
and
represent the Michaelis constants for the
activation and inactivation reaction, respectively.
Those concentrations of two enzymes and those
11 1 121 1 1 1 1
1111
11 11 1 1
,, ,
kPU lPP d k e l
MN
M
UNP a b
Validity of the Michaelis-Menten Approximation for the Stability Analysis in Regulatory Reaction Networks
177

Michaelis constants are relative, that is, normalized
by the total concentrations of the respective enzymes
which are assumed to be the same values for two
enzymes to simplify the formulations in this study.
Supposing the steady states, that is,
=
, with
the constant
=
/
leads to the following
equations:
The same equations of the variables with the
subscripts which numbers are exchanged are derived
for the node 2. The enzyme concentrations at the
steady state are obtained by solving these four
equations.
In the case that the Michaelis-Menten
approximation is not employed corresponding to the
reaction scheme on the bottom right in Fig. 2, the
respective reaction rates
,
,
, and,
are
formulated only from the law of mass action as
follows:
and
represent the relative concentrations of the
active and inactive forms of the enzyme, respectively.
and
depict the relative concentrations of the
substrate-enzyme complexes.
and
are the
normalized Michaelis constants for the activation and
inactivation reaction, respectively, as same as the case
with the model employing the Michaelis-Menten
approximation. Supposing the steady state drives the
following equations:
The same equations of the variables with the
exchanged subscripts are derived for the node 2. The
enzyme concentrations at the steady state are obtained
by solving these equations.
2.2 Stability Analysis
Steady states of the two-node regulatory reaction
networks are determined by the six parameters of
,
,
for the node 1 and
,
,
for the node 2.
In this study, the four Michaelis constants are set to
be the same value, that is, =
=
=
=
to reduce the dimension of the parameter space. The
analysis is performed over 11 discrete values of
such as 2
,2
,⋯,2
. The remaining parameters
and
are set to be the value of 2
, for which the
1000 values of p are taken randomly over the range
of −5 ≤ p ≤ 5. This range is determined to cover
the values of the parameters utilized in the
mathematical models for MAPK cascade (Brightman
& Fell, 2000; Hatakeyama et al., 2003; Huang &
Ferrell, 1996; Levchenko, Bruck, & Sternberg, 2000;
Schoeberl, Eichler-Jonsson, Gilles, & Muller, 2002).
The concentrations of each chemical species in
the regulatory reaction networks could be obtained by
solving the corresponding algebraic equations as
mentioned in section 2.1. However, the analytical
derivation is getting harder for higher order equations
due to the nonlinearity. Furthermore, the eigen values
of Jacobian matrix are required to evaluate the
stability at each equilibrium points (Heinrich &
Schuster, 1996). In this study, the number of stable
equilibrium points are obtained by the rather practical
way in which the convergent solutions are obtained
by solving the differential equations formulating the
dynamics of the regulatory reaction networks with a
number of initial states instead of solving the
corresponding algebraic equations analytically to
avoid the computational complications.
The parametric robustness is employed to
evaluate the stability quantitatively (Shah & Sarkar,
2011). The parametric robustness of the feature for
stability is defined as the ratio of applied parameter
sets exhibiting the feature. For instance, the
parametric robustness of the bi-stability is defined as
the ratio of the number of combinations of
and
yielding bi-stability to the total number of
combinations examined which is 1000 in this study.
High values of the parametric robustness imply the
robustness for the parametric perturbations which is
one of the important features in noisy environments
such as in cells.
3 RESULTS
The regulatory structures examined in this study yield
four types of stability, such as mono-stable, bi-stable,
tri-stable, and oscillatory. Most of the examined
cases exhibit mono-stability or bi-stability.
Figure 3 shows the result of the analysis for the bi-
stability. The row and the column of squares
correspond to the values of the Michaelis constants
and to the variation of the regulatory reaction
networks, respectively. Each square represents the
parameter space in logarithmic scales with the
abscissa of
and the ordinate of the
. The blue
dots and the red dots indicate the combination of
parameter values yielding bi-stability in the model
with the Michaelis-Menten approximation and in the
model without the Michaelis-Menten approximation,
respectively.
11 21
111
11 11
,1
PU P P
KPU
MU NP
111111111112111111
,, ,aPU dQ kQ bPP eR lR
11 11 11 21 1 11
11 112
,,
21
QM PU RN PP Q KR
PU Q R R
BIOINFORMATICS 2020 - 11th International Conference on Bioinformatics Models, Methods and Algorithms
178
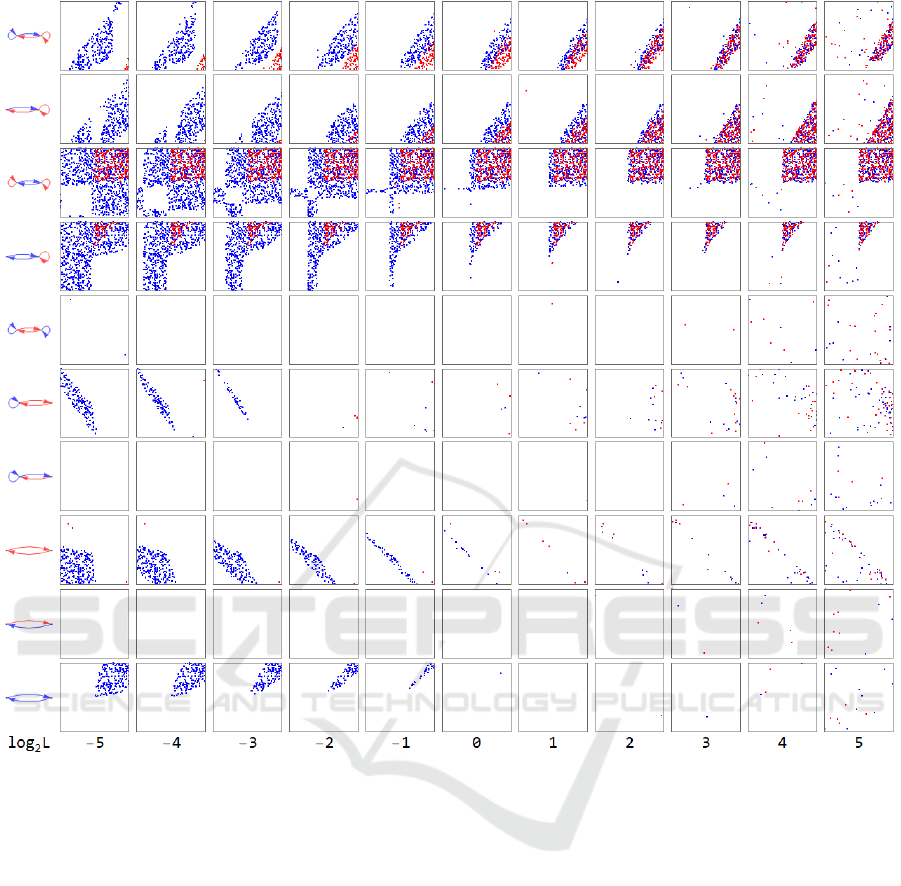
Figure 3: Parameter values yielding the bi-stabilities with respect to regulatory structures and the Michaelis constants. Each
square represents the parameter space in logarithmic scales with the abscissa of 1and the ordinate of the 2. The row
and the column of the squares correspond to the values of the Michaelis constants and to the examined variation of the two-
node regulatory reaction networks, respectively. The red arrows depict positive regulations, while the blue arrows indicate
negative regulations.
It is shown that the more combinations yielding
bi-stability for the model with the Michaelis-Menten
approximation were predicted than that for the model
without the Michaelis-Menten approximation in
some regulatory structures, especially in the area of
small values of the Michaelis constants. Furthermore,
it can be seen that each of the combination of the
parameters exhibiting bi-stability for the model
without the Michaelis-Menten approximation
remains at the same points regardless of the value of
the Michaelis constants.
Figure 4 shows the effects of Michaelis-Menten
approximation on the parametric robustness for the
emergence of bi-stability. The top and the bottom
graphs correspond to the aspect of the emergence of
bi-stability in the model with the Michaelis-Menten
approximation and in the model derived only from the
law of mass action, respectively. The abscissa and
the ordinate denote the values of the Michaelis
constants in logarithmic scale and the parametric
robustness, respectively. Each colour of the graph
corresponds to the individual regulatory reaction
network shown in the right side of the graph.
In the models utilizing the Michaelis-Menten
approximation, the parametric robustness for the
negative mutual regulatory network with two positive
auto-regulations or one positive auto-regulation is
quite high especially in the area for the small
Michaelis constants, which was reported in the
previous study (Sueyoshi & Naka, 2017). On the
Validity of the Michaelis-Menten Approximation for the Stability Analysis in Regulatory Reaction Networks
179
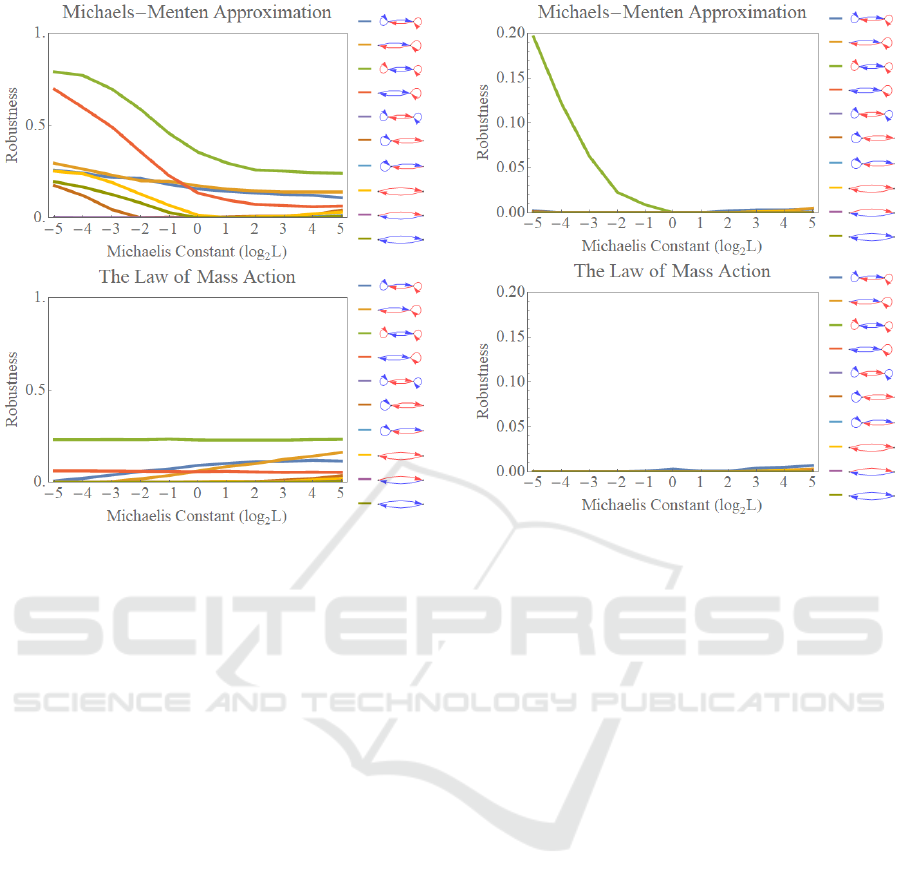
Figure 4: The effects of Michaelis-Menten approximation
on the parametric robustness for the emergence of bi-
stabilities. The robustness for the model with the Michaelis-
Menten approximation and with the law of mass action is
shown on the top, and on the bottom, respectively. Each
colour of the graph corresponds to the regulatory reaction
network shown in the right side of the graphs where the red
arrows depict positive regulations, while the blue arrows
indicate negative regulations.
contrary, in the models not utilizing the Michaelis-
Menten approximation, the parametric robustness has
hardly changed with respect to the values of the
Michaelis constants in both regulatory reaction
networks. The unchanged value of the parametric
robustness is as almost the same value as one for the
large value of the Michalis constant in the model
employing the Michaelis-Menten approximation.
Concerning the other regulatory structures, the
similar tendencies emanate while the parametric
robustness is much less on the whole.
Figure 5 shows the effects of Michaelis-Menten
approximation on the parametric robustness for the
emergence of tri-stability. The top and the bottom
graphs correspond to the aspect of the emergence of
tri-stability in the model with the Michaelis-Menten
approximation and in the model derived only from the
law of mass action, respectively. High parametric
robustness appears in the area of the small Michaelis
constants for the negative mutual regulatory network
with two positive auto-regulations which yields quite
high parametric robustness for bi-stability as
Figure 5: The effects of Michaelis-Menten approximation
on the parametric robustness for the emergence of tri-
stabilities. The robustness for the model with the Michaelis-
Menten approximation and with the law of mass action is
shown on the top, and on the bottom, respectively. Each
colour of the graph corresponds to the regulatory reaction
network shown in the right side of the graphs where the red
arrows depict positive regulations, while the blue arrows
indicate negative regulations.
mentioned before. However, the part of high
parametric robustness has vanished in the models not
employing the Michaelis-Menten approximation.
The slight emergence of tri-stability for the model
with the Michaelis-Menten approximation in the area
of large Michaelis constants is seen and the aspect of
the parametric robustness is as the almost same as for
the model without the approximation.
Figure 6 shows the effects of Michaelis-Menten
approximation on the parametric robustness for the
emergence of oscillations. The oscillations occur in
some regulatory reaction networks while their
parametric robustnesses are quite small. In the case
for the model with the Michaelis-Menten
approximation, the oscillations occur in the area of
the small Michaelis constants for the positive and
negative mutual regulations with a positive auto-
regulation. Furthermore, the oscillation appears in
the area of the large Michaelis constants for the
mutual positive regulations without auto-regulations.
However, the oscillations emerged in the area of
small Michaelis constant vanish in the models
BIOINFORMATICS 2020 - 11th International Conference on Bioinformatics Models, Methods and Algorithms
180
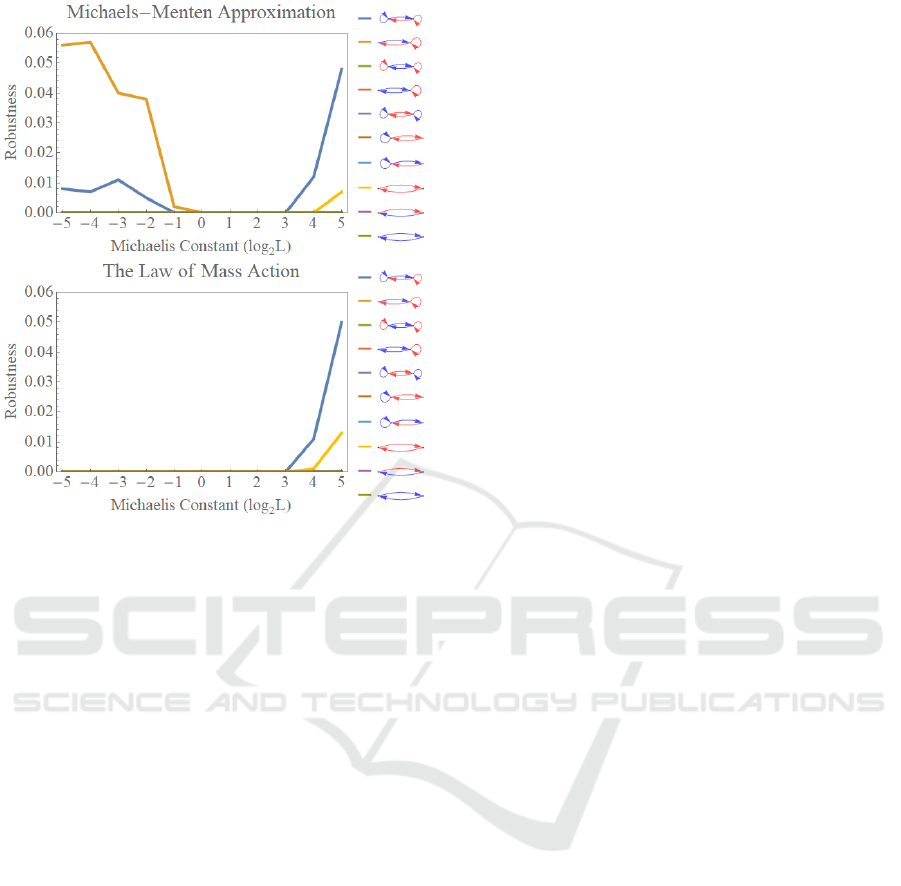
Figure 6: The effects of Michaelis-Menten approximation
on the parametric robustness for the emergence of
oscillations. The robustness for the model with the
Michaelis-Menten approximation and with the law of mass
action is shown on the top, and on the bottom, respectively.
Each colour of the graph corresponds to the regulatory
reaction network shown in the right side of the graphs
where the red arrows depict positive regulations, while the
blue arrows indicate negative regulations.
without the Michaelis-Menten approximation. The
aspect of the parametric robustnesses is almost the
same in two models.
Taken together, it is suggested that the parametric
robustness of stability might be overestimated on the
mathematical model employing the Michalis-Menten
approximation. This bias seems to be dominant in the
condition of the small Michaelis constants. On the
other hand, almost the same parametric robustnesses
are predicted in the area of the large Michaelis
constants. Therefore, it might be not valid to utilize
the Michaelis-Menten approximation for analysing
the properties even at the steady states. The validity
depends on the values of the Michaelis constants of
the enzymes comprising the cellular signalling
systems.
The quite large value of the Michaelis constant
implicates the much less associate rate than the
dissociate and catalytic rate, which means that the
concentrations of substrate-enzyme complex are
much less than the concentrations of the free
substrates and the enzymes. The Michaelis
approximation makes the substrate-enzyme
complexes not exist in the conservative laws.
Therefore, the large Michaelis constants might make
the effect of the absence of the complexes less. This
implication may be reason why the similar aspects are
observed about the emergence of stability for the two
models in the area of the large Michaelis constants.
4 CONCLUSIONS
In this study, the validity of the Michaelis-Menten
approximation was examined for a set of regulatory
reaction networks comprised of the two enzymatic
cyclic reactions, in which each enzyme also works as
the substrate each other such like cellular signalling
systems. As a result, it is suggested that the
mathematical models utilizing the Michaelis-Menten
approximation for an enzyme which has the small
Michaelis constant might overestimate the emergence
of the bi-stability and the oscillations even for
analysing the properties at the steady state.
Although it might be safer to construct a
mathematical model derived only from the law of
mass action without the Michaelis-Menten
approximation, it may cause a problem of high
computing cost. Furthermore, utilizing the
Michaelis-Menten approximations often makes it
possible to divide the target system into a number of
sub-systems due to omitting the substrate-enzyme
complexes. On the contrary, utilizing only the law of
mass action often cause the computational difficulty
due to intra-connections of each dynamics in the
entire system caused by the substrate-enzyme
complexes.
REFERENCES
Adler, M., Szekely, P., Mayo, A., & Alon, U. (2017).
Optimal Regulatory Circuit Topologies for Fold-
Change Detection. Cell Syst, 4(2), 171-181 e178.
Brightman, F. A., & Fell, D. A. (2000). Differential
feedback regulation of the MAPK cascade underlies the
quantitative differences in EGF and NGF signalling in
PC12 cells. FEBS Letters, 482, 169-174.
Ferrell, J. E., Jr. (1998). How regulated protein
translocation can produce switch-like responses.
Trends in Biochemical Science, 23, 461-465.
Hatakeyama, M., Kimura, S., Naka, T., Kawasaki, T.,
Yumoto, N., Ichikawa, M., et al. (2003). A
computational model on the modulation of mitogen-
activated protein kinase (MAPK) and Akt pathways in
heregulin-induced ErbB signalling. Biochemical
Journal, 373(Pt 2), 451-463.
Validity of the Michaelis-Menten Approximation for the Stability Analysis in Regulatory Reaction Networks
181

Heinrich, R., & Schuster, S. (1996). The regulation of
cellular systems. New York: Chapman & Hall.
Huang, C. F., & Ferrell, J. E., Jr. (1996). Ultrasensitivity in
the mitogen-activated protein kinase cascade.
Proceedings of the National Academy of Science of the
United States of America, 93, 10078-10083.
Jeschke, M., Baumgartner, S., & Legewie, S. (2013).
Determinants of cell-to-cell variability in protein kinase
signaling. PLoS Comput Biol, 9(12), e1003357.
Kholodenko, B. N. (2006). Cell-signalling dynamics in
time and space. Nat Rev Mol Cell Biol, 7(3), 165-176.
Kuwahara, H., & Gao, X. (2013). Stochastic effects as a
force to increase the complexity of signaling networks.
Sci Rep, 3, 2297.
Levchenko, A., Bruck, J., & Sternberg, P. W. (2000).
Scaffold proteins may biphasically affect the levels of
mitogen-activated protein kinase signaling and reduce
its threshold properties. Proceedings of the National
Academy of Science of the United States of America,
97(11), 5818-5823.
Ma, W., Trusina, A., El-Samad, H., Lim, W. A., & Tang, C.
(2009). Defining network topologies that can achieve
biochemical adaptation. Cell, 138(4), 760-773.
Mai, Z., & Liu, H. (2013). Random parameter sampling of
a generic three-tier MAPK cascade model reveals major
factors affecting its versatile dynamics. PLoS One, 8(1),
e54441.
Qiao, L., Nachbar, R. B., Kevrekidis, I. G., & Shvartsman,
S. Y. (2007). Bistability and oscillations in the Huang-
Ferrell model of MAPK signaling. PLoS Comput Biol,
3(9), 1819-1826.
Schoeberl, B., Eichler-Jonsson, C., Gilles, E. D., & Muller,
G. (2002). Computational modeling of the dynamics of
the MAP kinase cascade activated by surface and
internalized EGF receptors. Nature Biotechnology, 20,
370-375.
Shah, N. A., & Sarkar, C. A. (2011). Robust network
topologies for generating switch-like cellular responses.
PLoS Comput Biol, 7(6), e1002085.
Sueyoshi, C., & Naka, T. (2017). Stability Analysis for the
Cellular Signaling Systems Composed of Two
Phosphorylation-Dephosphorylation Cyclic Reactions.
Computational Molecular Bioscience, 7, 33-45.
Volinsky, N., & Kholodenko, B. N. (2013). Complexity of
receptor tyrosine kinase signal processing. Cold Spring
Harb Perspect Biol, 5(8), a009043.
Yao, G., Tan, C., West, M., Nevins, J. R., & You, L. (2011).
Origin of bistability underlying mammalian cell cycle
entry. Mol Syst Biol, 7, 485.
BIOINFORMATICS 2020 - 11th International Conference on Bioinformatics Models, Methods and Algorithms
182
