
ValidNet: A Deep Learning Network for Validation of Surface
Registration
Joy Mazumder
1,3
, Mohsen Zand
1,3
, Sheikh Ziauddin
1,3
and Michael Greenspan
1,2,3
1
Department of Electrical and Computer Engineering, Queen’s University, Kingston, Ontario, Canada
2
School of Computing, Queen’s University, Kingston, Ontario, Canada
3
Ingenuity Labs, Queen’s University, Kingston, Ontario, Canada
Keywords:
Surface Registration, 3D Object Recognition, Validation, Shared mlp Network.
Abstract:
This paper proposes a novel deep learning architecture called ValidNet to automatically validate 3D surface
registration algorithms for object recognition and pose determination tasks. The performance of many tasks
such as object detection mainly depends on the applied registration algorithms, which themselves are suscep-
tible to local minima. Revealing this tendency and verifying the success of registration algorithms is a difficult
task. We treat this as a classification problem, and propose a two-class classifier to distinguish clearly between
true positive and false positive instances. Our proposed ValidNet deploys a shared mlp architecture which
works on the raw and unordered numeric data of scene and model points. This network is able to perform two
fundamental tasks of feature extraction and similarity matching using the powerful capability of deep neural
network. Experiments on a large synthetic datasets show that the proposed method can effectively be used in
automatic validation of registration.
1 INTRODUCTION
The rigid registration of 3D surfaces is of central
importance to the processing of 3D data. Since
the initial introduction of the Iterative Closest Point
(ICP) Algorithm in the late 1990’s (Besl and McKay,
1992), there have been many variations proposed to
the basic approach to improve robustness, efficiency
and generality (Segal et al., 2009; Rusinkiewicz and
Levoy, 2001). Current research aims to address non-
rigid registration (Paiement et al., 2016; Yu et al.,
2017) and investigate machine learning approaches
(Schwarz et al., 2017; Pais et al., 2019).
The basic approach to rigid 3D surface registra-
tion applies local optimization, and therefore depends
upon initial conditions to resolve to a correct solu-
tion. In the case of ICP and its variants, an initial esti-
mate of the true rigid transformation needs to be pro-
vided which is “close enough” to the true solution,
lest the result be driven to a false positive (i.e., local
vs. global minimum). It is therefore expected that a
3D surface registration task will sometimes fail, by
returning a false positive. This failure mode is often
difficult to recognize and diagnose, as the distribution
of the surface residuals (i.e., distances between cor-
responding surface points and/or surfaces) between
ValidNet
Registration
Valid or Not
Registration
Output
Model
Segment
Figure 1: Overview of ValidNet. We proposed a deep neu-
ral network that takes two raw point clouds (model and seg-
ment) from a registration technique as input and provides
validity of the surface registration.
false positives and true positives can be similar.
There are some systems where a human is in the
loop to inspect the results from a registration task, in
which case the occasional failure may be a nuisance,
but is tolerable. There are also other desired uses of
3D surface registration, however, where registration
failure is less tolerable, and can lead to a catastrophic
system failure. One such desired use is automated
robot grasping and manipulation, which are common
tasks in industrial automation (Mahler and Goldberg,
2017). In this critical application, false positives in
registration can result in damage to equipment, as the
Mazumder, J., Zand, M., Ziauddin, S. and Greenspan, M.
ValidNet: A Deep Learning Networ k for Validation of Surface Registration.
DOI: 10.5220/0008988103890397
In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 4: VISAPP, pages
389-397
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
389

robot attempts to grasp a part that was incorrectly
identified and/or localized. Even small error rates of a
few percentage points, which are commonly accepted
in many general approaches, can be unacceptable in
this automation process.
This paper proposes a new approach for automatic
validation of registration algorithms. In our method,
we focus on the validation of 3D registration results
for rigid parts. A 3D segmentation algorithm is ini-
tially used to extract individual object instances from
a scene. A registration algorithm is then used to lo-
calize object hypotheses in the scene. Each hypoth-
esis is thus a segmented object matched with the ob-
ject model. Our algorithm categorizes each hypothe-
sis as a true positive or false positive. In particular,
the raw points of each segment and the object model
are considered as the inputs to the network. The pro-
posed network, called ValidNet, applies the powerful
capability of a Deep Neural Network (DNN). This
network can effectively extract required features and
match similarities between them. Thus, this archi-
tecture can learn to extract features and classify val-
idation hypotheses from the raw numeric data. The
overview of the proposed method is shown in Fig-
ure 1.
Intuitively, a reliable validation for surface reg-
istration can be useful for general pose determina-
tion. However, the proposed method is evaluated
for the time-sensitive application of robotic bin pick-
ing to emphasize its efficiency in real-time scenar-
ios. Some samples of real and synthetic 3D images
of bin picking scenes that are representative as input
to the system are illustrated in Figure 2. It is well
known that a large number (typically thousands to
millions) of image data are required to train DNNs,
and such a volume of ground truth datasets of real
images are not available for this task, and would be
expensive to generate. We therefore use a simple
method to generate synthetic datasets for the bin pick-
ing problem, as illustrated in Figure 2b. Similar to the
real-world data, the generated synthetic datasets con-
tain occlusion, clutter, noise, and missing information
(dropouts), and ground truth samples can be quickly
and easily generated in high volume for training pur-
poses.
2 RELATED WORK
Object recognition has been a major research direc-
tion in computer vision for many years. Its perfor-
mance is crucial in various application scenarios such
as image classification, image retrieval, scene under-
standing, visual tracking, and robot grasping and ma-
nipulation (Aldoma et al., 2012). A popular approach
is to transform the given 3D model to the scene, and
look for an accurate alignment of the model with the
objects in the scene (Papazov and Burschka, 2010;
Mian et al., 2006). Each object is finally recognized
if it is accurately aligned with the model. The ob-
ject recognition problem therefore depends upon sur-
face registration where object models are matched to
each object, and hypotheses verification is required to
reject the false detections. Although there are many
registration algorithms (Myronenko and Song, 2010;
Segal et al., 2009), this final validation stage remains
a challenge, as it has proven difficult to automati-
cally determine whether registration algorithms such
as ICP have succeeded or failed. Despite the ubiquity
and importance of surface registration in 3D process-
ing, there has been little previous work at registration
validation.
Early methods for validation focused on visual as-
sessment of the registration results. This was per-
formed by viewing image pairs and comparing their
contour overlays, alternate pixel displays, anatomi-
cal landmarks, or analytical models (Guehring, 2001;
Schnabel et al., 2001; Rogelj et al., 2002; Pappas
et al., 2005). These techniques were mostly based
on algorithms such as template matching and pat-
tern classification in 2D space. They were also
application-dependent. In industrial inspection, for
instance, (Guehring, 2001) compared the registered
dataset with its CAD description to verify the vali-
dation of a measured part. To this end, a weighted
pose estimation was used to determine the uncer-
tainty in the computed deviation. In medical imag-
ing, Schnabel et al. (Schnabel et al., 2001) proposed
to model tissue properties biomechanically for Mag-
netic Resonance (MR) mammography images. They
constructed finite element breast models to obtain the
average displacement of the whole breast volume.
A validation method was also presented in (Pappas
et al., 2005) to assess the CT–MR image registration
accuracy locally in all volume regions based on the
correspondence analysis of cortical bone structures on
the original images.
One interesting approach is to consider one hy-
pothesis at a time and use theresholding for verifica-
tion (Mian et al., 2006; Bariya and Nishino, 2010;
Papazov and Burschka, 2010). For example (Mian
et al., 2006) converted the point cloud of a scene into
a triangular mesh and constructed a tensor from ran-
domly selected vertices of this mesh. They ranked a
set of hypotheses according to a similarity measure
between the scene tensor and the tensors of the 3D
models in the library. The validation of each hypothe-
sis was achieved by transforming the 3D model to the
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
390

(a)
(b)
Figure 2: Synthetic data compared to the real-world data. (a) shows two real data samples and (b) represents two synthetic
samples which are obtained using our data generation procedure.
scene. (Bariya and Nishino, 2010) used a threshold
set on the number of supporting correspondences and
obtained a collection of hypotheses for each model.
The final hypothesis selection was based on the cal-
culation of overlap between the model and the scene.
(Papazov and Burschka, 2010) introduced an accep-
tance function for pruning hypotheses and validating
the model-scene correspondences. They used a hash
table to rapidly retrieve oriented scene and model
points. For each retrieved model point set, a rigid
transform aligning model and scene points was then
computed. The result was a hypothesis that the model
was present in the scene. The validity of this hypoth-
esis was finally evaluated by the acceptance function.
Instead of considering each model hypothesis indi-
vidually, (Aldoma et al., 2012) took into account the
whole set of hypotheses as a global scene model by
formulating this problem in terms of the minimization
of a global cost function.
In (Yang et al., 2015), the authors proposed a
global optimal solution to 3D registration by search-
ing the entire 3D rigid transformation space. They
also defined upper and lower bounds for the registra-
tion error function (L2 error metric defined in ICP).
However, their method was based on a branch-and-
bound search for the entire space, which was compu-
tationally expensive.
Instead of searching a huge space, we propose to
use a 3D segmentation model to obtain the object hy-
potheses. Thus, the whole object shape is preserved in
the corresponding descriptor. Segmented objects hy-
potheses in the scene will be obtained by applying a
registration algorithm using the object model. These
are the inputs to our ValidNet for validation. In par-
ticular, two main steps which are also common in the
other methods, i.e., feature extraction and similarity
matching are effectively modeled by a deep network
similar to PointNet (Qi et al., 2017) which is a lead-
ing approach that worked directly on the raw point
clouds as inputs. Deep learning strategies are able to
induce spatial–contextual features from the 3D geo-
metric data such as point clouds. Thus, the important
features can be captured using a set of learnable filters
at training time. Likewise, we employ an unordered
list of points and use a deep network to extract the
local and global features. In particular, we rely upon
the feature engineering of PointNet and use both clas-
sification and segmentation architectures in order to
effectively extract the local and global features. Sim-
ilarity matching, however, is another essential step,
and we additionally propose to use the dot product
and the max-pooling strategies for obtaining the high-
est similarity scores.
3 ValidNet FOR REGISTRATION
VALIDATION
A point cloud is a set of 3D points and can be repre-
sented by P
i
|i = 1, . . . , N where N is the total number
of points. Each P
i
is a vector that contains the position
of the i-th point. It may include any other useful infor-
mation such as color, intensity, or normal, although in
this work, we consider only the positional information
of each point.
Suppose we are given two point clouds as M and
S denoting a model and a segment in the scene, re-
spectively. We use m and n to respectively represent
the number of points in M and S. The transforma-
tion matrix that aligns M to S is found by the reg-
istration algorithm, and is denoted by T . Notably,
the segments are generated by applying a segmenta-
tion algorithm such as region growing (Rabbani et al.,
2006; Vo et al., 2015). Segmentation can beneficially
reduce the search space and make the registration pro-
cess faster.
The objective of validation is to quantify how well
the transformed model TM can represent the segment
S, or equivalently how well the inverse transformed
segment T
−1
S can represent the model M. The bene-
fit of transforming the segment to the model through
T
−1
S, is that this maps the segment to the same
canonical model pose, so that we do not have to con-
sider different model poses, which reduces and sim-
plifies network training. In other words, the network
ValidNet: A Deep Learning Network for Validation of Surface Registration
391
Similarit
y matrix,
X (m*n)
mlp
(1024-1024-
256)
mlp shared
(64,64)
mlp shared
(64,128,1024)
Maxpool
Maxpool
Maxpool
output
model
segment
1024
1024
mlp shared
(512,256,128)
m
m
*
64
n
*
64
m
*
1024
n
*
1024
m
*
3
n
*
3
m
*
1088
n
*
1088
m
*
128
n
*
128
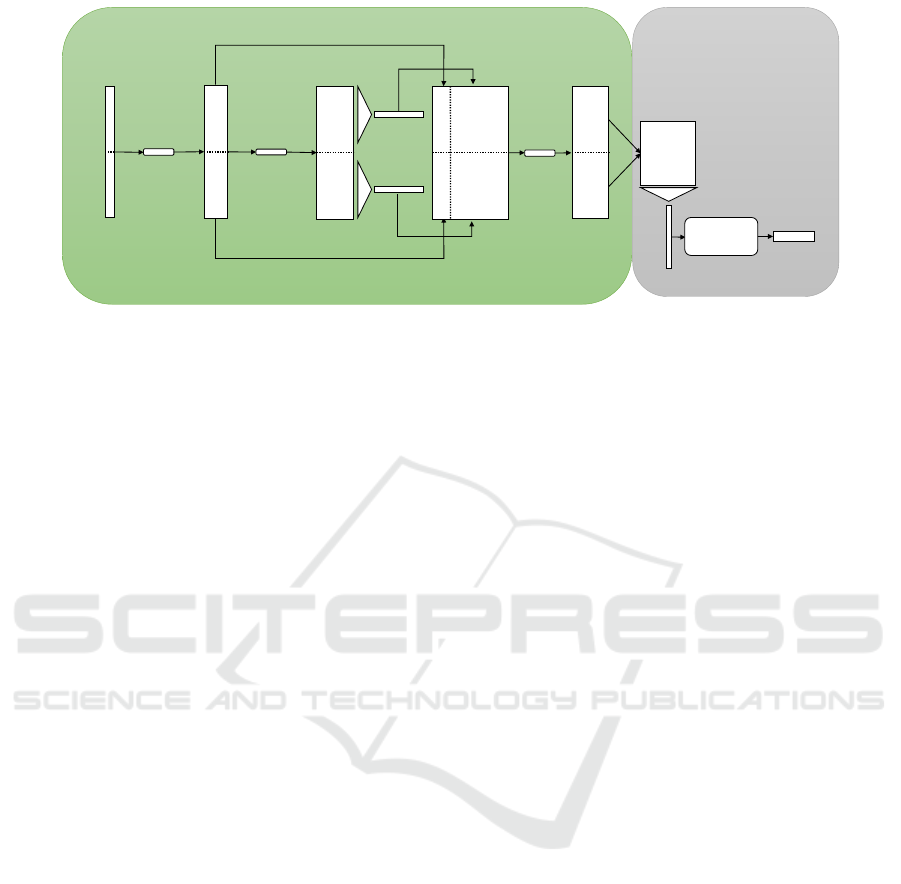
Figure 3: ValidNet for registration validation. The left part is the feature learning network that learns the features of the model
and the segment and the right part is the similarity finding network that measures the similarities between these features and
provides the validation probability of registration success.
does not need to learn the translation and rotational
invariance properties since the segments and model
are mapped to the same position. Another point is
that our method only uses position characteristics of
the point clouds, and other information such as color,
intensity, or normal are not employed. This not only
allows inputs from different sensors (which only cap-
ture position information) to be applicable, but also
can lead to faster computations.
The main framework of the proposed Validnet net-
work is shown in Figure 3. It consists of two parts,
including feature learning and similarity finding net-
work. The inputs to the network are vectors of size
(m ∗ 3) + (n ∗ 3) representing the overall points of a
set of segment and model pair.
The feature learning network learns the positional
information and characteristics of each point for both
model and segment. In particular, the local and global
information are accumulated in this part. It is intu-
itively similar to the PointNet segmentation network.
Likewise, we use a multi-layer perceptron network to
aggregate the global information.
The feature learning network consists of shared
mlp layers, skip connections, and symmetric func-
tions. In this network, initially five shared mlp layers
operate on each point independently. They are also
shared between all the model and the segment points.
These shared mlp layers map all the model points
and the segment points into a high dimensional space.
Two symmetric functions are used on the remapped
point-sets to leverage the global characteristics of the
model and the segment, respectively. Here, the max-
pool is used as a symmetric function. The captured
global characteristics are invariant to the segment’s
and the model’s point order.
After modeling the global characteristics, as
shown in Figure 3, the global vectors are concatenated
to the output of the second mlp layer. Finally, another
set of shared mlp layers are applied on the concate-
nated outputs of the model and the segment points to
generate a new set of point features that contains both
local and global information.
The similarity finding network measures the sim-
ilarities between obtained features of both model and
segment. It consists of a vector dot product, a sym-
metric function, and a feed forward network. In or-
der to find similarities between features learned in the
previous step, a similarity matrix X
m∗n
is calculated
where, each element x
i j
indicates the similarity be-
tween i-th model point and j-th segment point. If p
i
and q
j
represent feature vectors for i-th model point
and j-th segment point, respectively, then:
x
i j
= p
T
i
q
j
(1)
One essential characteristic is that if i-th model
point is accurately represented by any inversely trans-
formed scene point, a value along the i-th row will be
high. Hence, performing a max-pool along the row
preserves this information and makes the model in-
variant to scene input perturbation. A feed forward
network can finally classify this vector. As a result,
the output layer can provide the validation probability
of the registration algorithm. More specifically, the
outputs of the networks are two scores for two classes,
i.e. the positive (correctly registration) and negative
(incorrect registration) class. These scores represent
how accurately the registration method is able to find
the transformation matrix.
4 EXPERIMENTAL EVALUATION
In this section, first we will explain the data genera-
tion process for training and testing of our proposed
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
392
network. After that we will provide detailed exper-
imental results and comparison with two other tech-
niques. We will also present how ValidNet performs
under noisy conditions. Finally we will provide a vi-
sualization of our proposed network.
4.1 Dataset Generation
For training and testing of ValidNet, we generated
a large synthetic dataset containing 191,980 training
and 21,800 test samples. Our dataset generation pro-
cedure starts with modeling of synthetic bin, such as
might occur in a robotic bin picking task. In bin pick-
ing, the multiple objects in each bin are of a single
class, and are randomly arranged such that they ex-
hibit clutter and occlusions. The challenge is to be
able to determine the pose of each object to a high de-
gree of confidence, so that automated robotic grasp-
ing will succeed. For a realistic representation of the
environment for objects falling in a bin, we used the
Bullet Physics library (Coumans, 2015) which is a
physics engine that simulates collision, soft and rigid
body dynamics. Using this library, we modeled var-
ious physical scenarios related to bin picking prob-
lem such as gravity, center of mass, and collision with
other objects. This results in a reasonable modeling of
real-world scenarios with clutter and occlusion in the
scenes. Using the Bullet Physics library, we generated
2500 synthetic scenes with varying number of objects
(min=1, max=15, mean=4.28), and divided this data
into 2,250 training and 250 test scenes. Using the ori-
entations returned by the simulator, we then converted
these scenes into a 2.5D point cloud data. Figure 2b
shows two sample scenes from our dataset.
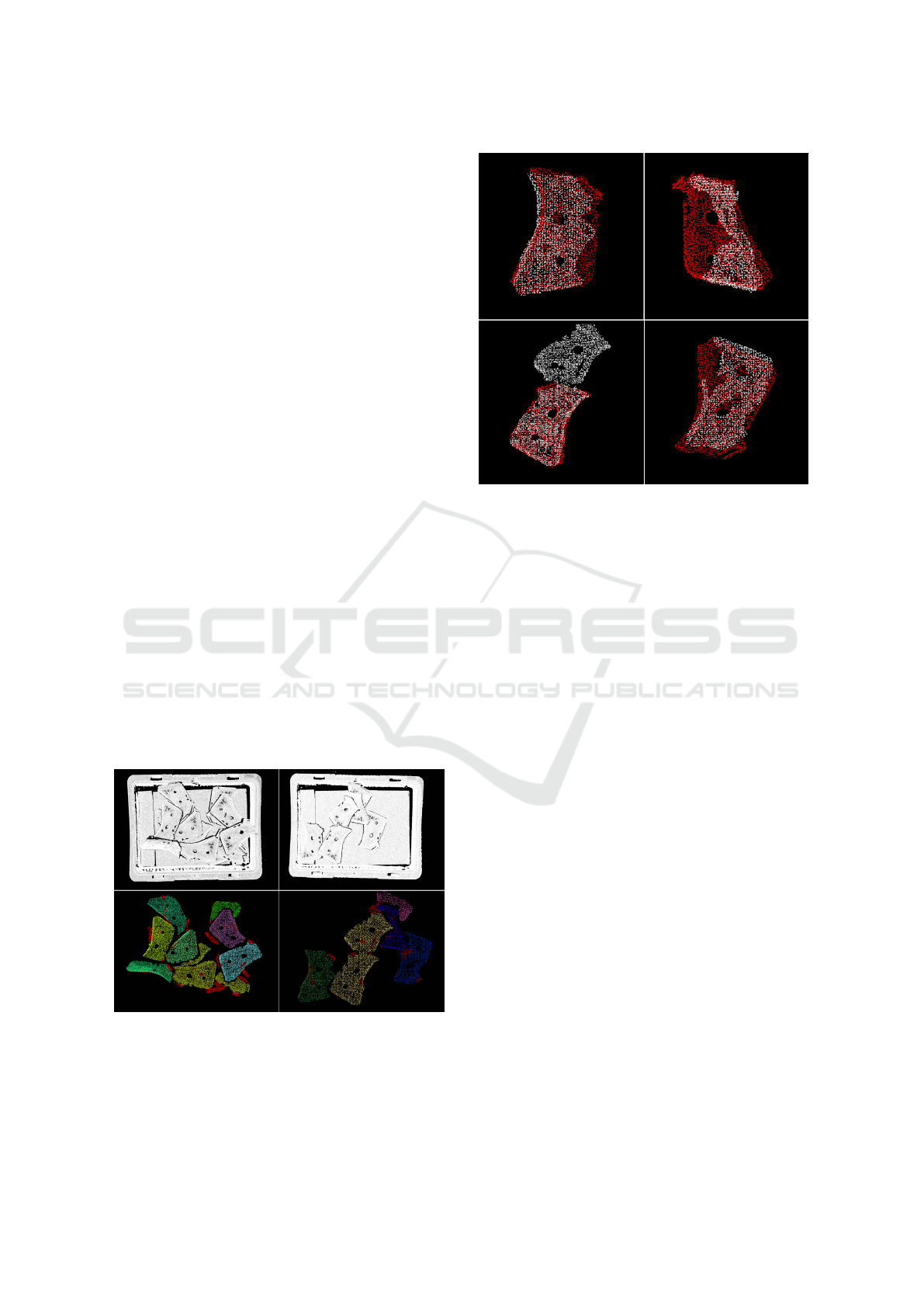
Figure 4: Two sample outputs of region growing segmenta-
tion.
The next step in our data generation pipeline is ob-
ject segmentation. We used region growing segmenta-
tion (Rabbani et al., 2006) to segment objects from the
Figure 5: Output of RANSAC-based registration.
scene. Two sample outputs from region growing seg-
mentation are shown in Figure 4, where the top two
images are the synthetic scenes and the bottom two
images are the outputs of the segmentation after re-
moving the background. The resulting segments were
then filtered to exclude those containing too many or
too few points.
Next we extracted FPFH (Rusu et al., 2009) fea-
tures from the model and the scene segments. These
features were then used to find a RANSAC-based reg-
istration transformation (Buch et al., 2013) between
the model and the segment resulting in an initial pose
estimation for the segment. A few sample outputs
from this step are shown in Figure 5. The model and
the segment are shown by the red and white points, re-
spectively. Note that the bottom left image indicates
an under segmentation case where two objects clus-
tered into a single object.
After RANSAC-based registration, we built a
dataset of 9599 training and 1090 test segments. To
generate more data for better training, we augmented
our dataset by introducing perturbations to the initial
poses of segments. For each segment, we generated
20 new poses by adding small translations and rota-
tions controlled by two Gaussian functions (mean=0,
σ=3 mm for translation, mean=0, σ=0.06 rad. for ro-
tation). This increased the training and test data sizes
to 191,980 and 21,800 samples, respectively.
The next step in the data generation pipeline is to
assign ground-truth labels to the generated segments.
Validation of registration results is a binary classifi-
cation problem where the positive class is the one
for which registration was successful and the nega-
ValidNet: A Deep Learning Network for Validation of Surface Registration
393

tive class indicates unsuccessful registrations. To as-
sign a class label to each segment, we ran the ICP
algorithm (Besl and McKay, 1992) on each model-
segment pair and used the ICP output to assign the
class label. If the centroids and principal axes of the
model and the segment were within some predefined
threshold, we labeled it as a positive class segment,
otherwise a negative class one. We used three differ-
ent thresholds corresponding to three different preci-
sion levels as shown in Table 1.
After that, we aligned the segment to the model’s
initial pose using the transformation matrix returned
by ICP. Finally, before feeding into the network, we
randomly sampled all the segments and models to a
fixed number of points. In our experiments, we used
m = n = 1, 024 points each for both the model and the
segment.
4.2 Training Process
For ValidNet training, we used ReLU activation func-
tion on all the shared mlp layers and fully connected
layers. For optimization, we used Adam optimizer
with a cross-entropy loss function. We used a batch
size of 8 and an initial learning rate of 0.000001 which
was reduced by a factor of 10 every 5 epochs. The net-
work was trained for 60 epochs on a single Amazon-
AWS GPU instance (≈ 8 hours on Tesla V100 GPU).
A dropout of 30% was used only for the fully con-
nected layers.
4.3 Results
In order to evaluate the effectiveness of our proposed
method, we calculated overall accuracy and average
class accuracy on all test samples in our dataset. We
also compared ValidNet results with that of Papazov
et al. (Papazov and Burschka, 2010) and PointNet (Qi
et al., 2017). PointNet is a well-known deep learning
model for point cloud classification. In order to use
PointNet for registration validation, we stacked two
input point clouds (segment and model) before pass-
ing to the PointNet network, as shown in Figure 6.
The results in terms of overall accuracy and aver-
age class accuracy for three different levels of match-
ing precision are shown in Table 2. Firstly, it can be
seen that different levels of matching precision does
not have any significant impact on the performance
of competing methods which shows that the meth-
ods adapted well to different thresholds. Secondly,
the results show that ValidNet outperforms Papazov
et al. and PointNet for both evaluation criteria and
all three precision levels. We believe that the major
reason for ValidNet’s better performance over Point-
Net is that the characteristics learned by ValidNet’s
feature extraction network is the combination of local
and global characteristics of a point cloud whereas
PointNet captures only global characteristics. For a
small misalignment between the model and the seg-
ment, the overall global information does not change
that much which makes it difficult for PointNet to
classify those cases correctly. On the other hand, the
local characteristics captured by ValidNet change sig-
nificantly resulting in a better classification accuracy.
Figure 7 shows some sample inputs for which
ValidNet successfully validated the registration re-
sults. Figure 8 shows some results where ValidNet
failed to validate correctly. By analyzing failure cases
for ValidNet, we noticed that most of the misclassi-
fications occur near the threshold level. The thresh-
olds we used to separate two classes (based on dis-
tance between centroid and angle between principle
axis) are relatively small making it hard even for hu-
mans to differentiate between two classes resulting in
most misclassifications near the threshold. In particu-
lar, the classification is determined by comparing the
results against the ground truth pose, which is subtle
and which may not be obvious in the human visual
comparison.
4.4 Robustness of ValidNet
Robustness against noise is an important property of
any machine vision system to cater for the unrelia-
bility of the sensor’s characteristics. We performed
an experiment to test the robustness of our proposed
method against noise. For each segment in the test
data, we added Gaussian noise on all the points inde-
pendently with mean 0 and specified standard devia-
tions in all three dimensions. The comparative results
are shown in Figure 9. Though accuracy of all tech-
niques suffer with increasing noise as expected, the
performance of ValidNet degrades more gracefully as
compared to that of PointNet and Papazov et al. As
noise level σ approaches 2, the discriminative abil-
ity of both PointNet and Papazov et al. reduces to
a random guess whereas ValidNet continues to per-
form well beyond that level as shown in Figure 9.
We believe that this greater robustness of ValidNet
against noise is due to its use of local characteristics
of points. For higher noise levels, points move farther
away from their original positions resulting in a dras-
tic change in the global shape of the object but the
change in points’ local characteristics remains rela-
tively less significant.
We saw that ValidNet performed well when it was
trained on noiseless data and tested on noisy data. We
performed another robustness experiment to evaluate
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
394
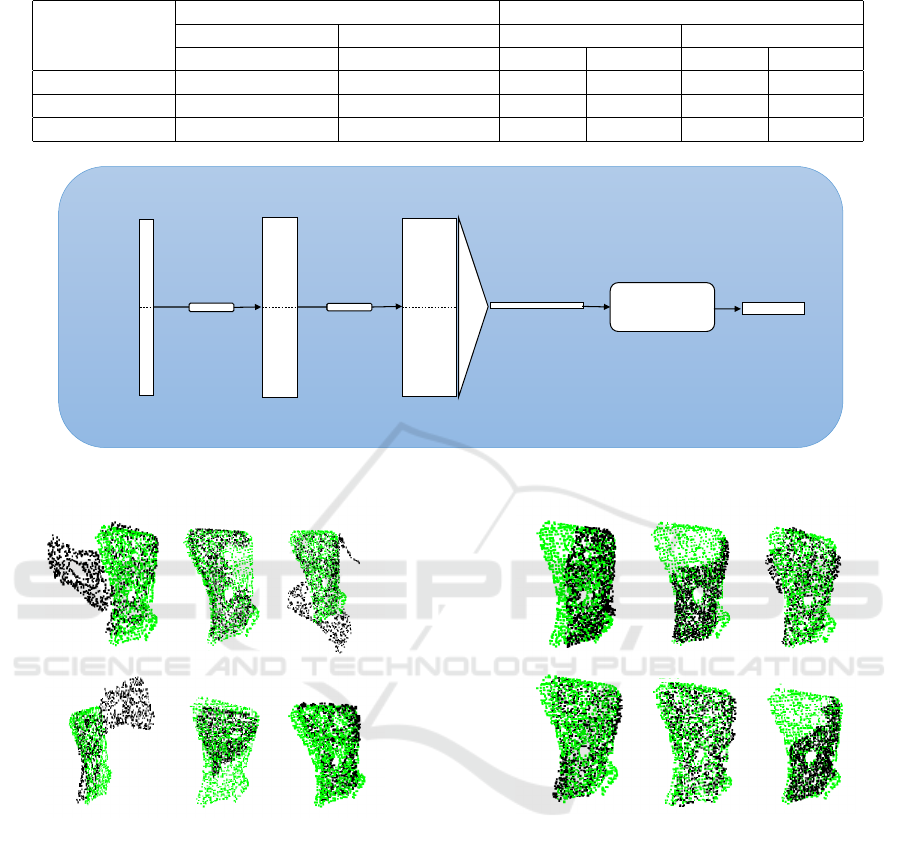
Table 1: Different levels of matching precision.
Precision-level Threshold Class Distribution
Train Test
Translation (mm) Rotation (radian) Positive Negative Positive Negative
High 4 0.12 77572 114408 8777 13023
Medium 4.5 0.14 94699 97281 10666 11134
Low 5 0.16 109920 82060 12395 9405
mlp shared
(64,64)
mlp shared
(64,128,1024)
model
segment
m
*
64
n
*
64
m
*
1024
n
*
1024
m
*
3
n
*
3
mlp
(1024-1024-
256)
Max
pool
output1024
Figure 6: PointNet for registration validation. It treats the model and the segment point clouds as a single point cloud, captures
their global relationship and provides the validation probability of registration success.
Figure 7: Some samples where ValidNet classified cor-
rectly. First row shows 3 images for positive class and sec-
ond row shows 3 images for negative class.
its performance when noise is added to training data
as well. The results are shown in Figure 10 . For both
ValidNet and PointNet, the reduction in accuracy with
noise is now much lower which is expected as the
networks have already seen noisy data during train-
ing. ValidNet again shows more robustness by out-
performing PointNet and Papazov et al. for all noise
levels.
4.5 Visualization of Results
To visualize how well ValidNet captures the required
matching information, we display activation output
Figure 8: Some samples where ValidNet failed to classify
correctly. First row shows 3 images for positive class and
second row shows 3 images for negative class.
of the max-pooling layer (after similarity matrix) as
a heat map in Figure 11. In the figure, registration
outputs along with heat maps of three samples each
for positive and negative classes are shown. The fig-
ure shows two alternate heat map representations for
each segment. The first one, that we call vector repre-
sentation, shows the activation output for 1024 points
sequentially in a vector (some width is added for bet-
ter visualization). The second one, that we call point
cloud representation, shows the activation output for
1024 points mapped to their locations in the input
point cloud segment.
The heat maps in Figure 11 shows clear differen-
tiation between the positive and the negative classes.
ValidNet: A Deep Learning Network for Validation of Surface Registration
395

Table 2: Performance comparison on our dataset.
High Precision Medium Precision Low Precision
Avg. Class Acc. Overall Acc. Avg. Class Acc. Overall Acc. Avg. Class Acc. Overall Acc.
Papazov et al. 64.57% 68.05% 65.502% 65.74% 65.89% 64.14%
PointNet 86.40% 86.95% 86.53% 86.60% 85.47% 86.63%
ValidNet 90.36% 89.47% 90.85% 90.81% 89.68% 90.11%
Figure 9: Effect of noise when trained on noiseless data and
tested on noisy data.
Figure 10: Effect of noise when noise is added on the train-
ing data as well
For the positive classes, the heat map is more towards
the yellow-red side (showing higher activation out-
puts) while for the negative classes, the heat map goes
more towards the blue region (showing lower acti-
vation outputs). The final fully connected layers of
our network perform the final classification based on
these values.
5 CONCLUSIONS
We have presented a novel approach for the open
problem of automatic validation. It is a deep learning
network to verify 3D surface registration results for
rigid parts. The proposed method is a shared mlp ar-
chitecture that treats the validation problem as a two-
class classification task. It has explored the potentials
of using deep learning for the validation task. Particu-
larly, this work reveals that feature learning and simi-
Figure 11: Visualization of ValidNet.
larity matching using deep neural network can be use-
ful in verifying the success of registration algorithms.
Working on segments instead of the complete scene
also reduces the search space and can be beneficial for
real-time applications. Moreover, it does not need to
learn the translation and rotational invariance proper-
ties since the scene segments are mapped to the same
canonical model pose. This work, however, can be
extended in several ways. For instance, it may be fur-
ther improved by using intensity data or other useful
information. In our future work, we will investigate
more experiments on different objects. We will also
tend to use this method as a post processing phase to
general object recognition to reduce false positives.
ACKNOWLEDGEMENTS
The authors would like to acknowledge Bluewrist
Canada, and the Natural Sciences and Engineering
Research Council of Canada for their support of this
work.
REFERENCES
Aldoma, A., Tombari, F., Di Stefano, L., and Vincze, M.
(2012). A global hypotheses verification method for
3d object recognition. In European conference on
computer vision, pages 511–524. Springer.
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
396

Bariya, P. and Nishino, K. (2010). Scale-hierarchical 3d
object recognition in cluttered scenes. In 2010 IEEE
computer society conference on computer vision and
pattern recognition, pages 1657–1664. IEEE.
Besl, P. J. and McKay, N. D. (1992). A Method for regis-
tration of 3-D shapes. In Sensor Fusion IV: Control
Paradigms and Data Structures, pages 586–607. In-
ternational Society for Optics and Photonics.
Buch, A. G., Kraft, D., Kamarainen, J.-K., Petersen, H. G.,
and Kr
¨
uger, N. (2013). Pose estimation using local
structure-specific shape and appearance context. In
2013 IEEE International Conference on Robotics and
Automation, pages 2080–2087. IEEE.
Coumans, E. (2015). Bullet physics simulation. In ACM
SIGGRAPH 2015 Courses, page 7. ACM.
Guehring, J. (2001). Reliable 3d surface acquisition, regis-
tration and validation using statistical error models. In
Proceedings Third International Conference on 3-D
Digital Imaging and Modeling, pages 224–231. IEEE.
Mahler, J. and Goldberg, K. (2017). Learning deep policies
for robot bin picking by simulating robust grasping
sequences. In Conference on Robot Learning, pages
515–524.
Mian, A. S., Bennamoun, M., and Owens, R. (2006).
Three-dimensional model-based object recognition
and segmentation in cluttered scenes. IEEE trans-
actions on pattern analysis and machine intelligence,
28(10):1584–1601.
Myronenko, A. and Song, X. (2010). Point set registra-
tion: Coherent point drift. IEEE transactions on pat-
tern analysis and machine intelligence, 32(12):2262–
2275.
Paiement, A., Mirmehdi, M., Xie, X., and Hamilton, M. C.
(2016). Registration and modeling from spaced and
misaligned image volumes. IEEE Transactions on Im-
age Processing, 25(9):4379–4393.
Pais, G. D., Miraldo, P., Ramalingam, S., Govindu, V. M.,
Nascimento, J. C., and Chellappa, R. (2019). 3dreg-
net: A deep neural network for 3d point registration.
arXiv preprint arXiv:1904.01701.
Papazov, C. and Burschka, D. (2010). An efficient
ransac for 3d object recognition in noisy and occluded
scenes. In Asian Conference on Computer Vision,
pages 135–148. Springer.
Pappas, I. P., Styner, M., Malik, P., Remonda, L., and
Caversaccio, M. (2005). Automatic method to as-
sess local ct–mr imaging registration accuracy on im-
ages of the head. American journal of neuroradiology,
26(1):137–144.
Qi, C. R., Su, H., Mo, K., and Guibas, L. J. (2017). Pointnet:
Deep learning on point sets for 3d classification and
segmentation. In Proceedings of the IEEE Conference
on Computer Vision and Pattern Recognition, pages
652–660.
Rabbani, T., Van Den Heuvel, F., and Vosselman, G. (2006).
Segmentation of point clouds using smoothness con-
straints. In ISPRS commission V symposium: image
engineering and vision metrology, pages 248–253. In-
ternational Society for Photogrammetry and Remote
Sensing (ISPRS).
Rogelj, P., Kovacic, S., and Gee, J. C. (2002). Validation of
a nonrigid registration algorithm for multimodal data.
In Medical Imaging 2002: Image Processing, volume
4684, pages 299–308. International Society for Optics
and Photonics.
Rusinkiewicz, S. and Levoy, M. (2001). Efficient variants
of the ICP algorithm. In 3D Digital Imaging and Mod-
eling (3dim), volume vol. 1, pages 145–153.
Rusu, R. B., Blodow, N., and Beetz, M. (2009). Fast point
feature histograms (fpfh) for 3d registration. In 2009
IEEE International Conference on Robotics and Au-
tomation, pages 3212–3217. IEEE.
Schnabel, J. A., Tanner, C., Smith, A. D. C., Hill, D. L.,
Hawkes, D. J., Leach, M. O., Hayes, C., Degenhard,
A., and Hose, R. (2001). Validation of non-rigid reg-
istration using finite element methods. In Biennial In-
ternational Conference on Information Processing in
Medical Imaging, pages 344–357. Springer.
Schwarz, M., Milan, A., Lenz, C., Munoz, A., Periyasamy,
A. S., Schreiber, M., Sch
¨
uller, S., and Behnke, S.
(2017). Nimbro picking: Versatile part handling
for warehouse automation. In 2017 IEEE Inter-
national Conference on Robotics and Automation
(ICRA), pages 3032–3039. IEEE.
Segal, A. V., Haehnel, D., and Thrun, S. (2009).
Generalized-icp. In Robotics: science and systems,
pages 435–442.
Vo, A.-V., Truong-Hong, L., Laefer, D. F., and Bertolotto,
M. (2015). Octree-based region growing for point
cloud segmentation. ISPRS Journal of Photogramme-
try and Remote Sensing, 104:88–100.
Yang, J., Li, H., Campbell, D., and Jia, Y. (2015). Go-
icp: A globally optimal solution to 3d icp point-set
registration. IEEE transactions on pattern analysis
and machine intelligence, 38(11):2241–2254.
Yu, W., Tannast, M., and Zheng, G. (2017). Non-rigid free-
form 2d–3d registration using a b-spline-based statis-
tical deformation model. Pattern recognition, 63:689–
699.
ValidNet: A Deep Learning Network for Validation of Surface Registration
397
