Mirror Symmetry Detection in Digital Images
L. Mestetskiy and A. Zhuravskaya
Moscow State University, Moscow, Russia
Keywords:
Mirror Symmetry, Measure of Symmetry, Fourier Descriptor, Contour Analysis.
Abstract:
This article proposes an approach to the recognition of symmetrical objects in digital images, based on a
quantitative asymmetry measure construction of such objects. The object asymmetry measure is determined
through the Fourier descriptor of a discrete object boundary points sequence. A method has been developed
for calculating the asymmetry measure and determining the most likely symmetry axis based on minimizing
the asymmetry measure. The proposed solution using the Fourier descriptor has a quadratic complexity in
the number of the object boundary points. A practical assessment of the efficiency and effectiveness of the
algorithm is obtained by computational experiments with silhouettes of aircraft in remote sensing images.
1 INTRODUCTION
Symmetry is an important classification feature in
solving various problems of analysis and recognition
of digital images and video. The mirror symmetry
property can be used when segmenting and classify-
ing objects. The orientation of symmetrical objects
can be determined on the image by the symmetry
axes found. For example, the symmetrical silhouettes
of aircraft and their orientation can be determined
among the many objects obtained by segmenting im-
ages in remote images (Fig. 1).
Methods for determining symmetric objects in im-
ages solve the problem in various settings, for exam-
ple, they look for objects with axial or central, global
or local symmetry (Liu et al., 2010), (Lee and Liu,
2012), (Widynski et al., 2014). Another important as-
pect of the method is the use of preliminary segmenta-
tion of objects in the image or working directly with
the image without preliminary processing. We con-
sider the problem of determining global axial sym-
metry for segmented images. It is assumed that the
segmentation of objects is carried out, but the quality
of this segmentation is not very high. An example is
shown in Fig. 1. Such a problem arises in the analysis
of images obtained by remote sensing of the Earth.
The image sizes are very large, the search for sym-
metrical objects without preliminary segmentation re-
quires a lot of computational time. The source im-
age is segmented based on thresholds or using trained
neural networks. The result is a binary image in which
it is necessary to recognize objects of a particular
class by their shape. In this case, objects in the binary
image are distorted by noise. Objects of the desired
class are symmetric, but their binary images are not
symmetrical in the strict mathematical sense. Thus,
the task is reduced to determining the degree of sym-
metry of binary image objects in order to further clas-
sify their shape. Moreover, algorithms for calculating
the degree of symmetry should be computationally ef-
ficient for use in processing a stream of large images.
Symmetry of human or animal figures can be used
for pose definition on an object silhouette. Based on
the symmetry evaluation of the object in the frame,
the correct shooting angle can be selected when the
camera is automatically positioned.
In order to determine whether an object is mirror
symmetric, it is enough to find its symmetry axis ex-
plicitly, or to establish that there is no symmetry axis.
This is an easy task for the human eye. Known algo-
rithms allow to find symmetry axes for perfectly sym-
metric objects. Such objects can be found in high-
quality images, where the symmetry shows up very
well and is easily evaluated (Zahn and Roskies, 1972),
(Yip et al., 1994). However, when automatic recogni-
tion of real digital images, there are problems asso-
ciated with the inevitable image segmentation errors
due to insufficient resolution, low contrast, poor illu-
mination, etc. Such errors are clearly visible in the
example in the figure 1. For these reasons, in prac-
tical work with real images and videos, the shape of
symmetrical objects is far from being perfect. There-
fore, the development of a reliable effective algorithm
for estimating the object symmetry in images is rele-
Mestetskiy, L. and Zhuravskaya, A.
Mirror Symmetry Detection in Digital Images.
DOI: 10.5220/0008976003310337
In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 4: VISAPP, pages
331-337
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
331

Figure 1: Symmetrical and asymmetrical objects in the air-
port image. Above is the original photo, below is the binary
image obtained as a result of segmentation.
vant and in demand in solving practical problems of
machine vision.
The disadvantage of the existing methods for solv-
ing the problems of determining the symmetry axis
and calculating the symmetry measure is the high
computational complexity. A naive search of bound-
ary point pairs with a comparison to some similar-
ity measure of the figure two halves to find the sym-
metry axis has a cubic complexity in the number of
boundary points. Among the more effective existing
algorithms for solving the described problems, two
classes of algorithms can be distinguished: methods,
the main part of which is the two halves compari-
son of the contour or skeletal object representation
(Van Otterloo, 1988), (Sheynin et al., 1999), (Yang
et al., 2008), (Kushnir et al., 2016), and methods for
analyzing halftone images, for example, using inte-
gral transformations (Karkishchenko and Mnukhin,
2012), (Lepskiy, 2013). The article (Fedotova et al.,
2016) presents an algorithm for refining the symmetry
axis for binary discrete images.
2 APPROACH TO ESTIMATING
THE SYMMETRY OF SHAPES
The proposed solution of the problem is based on the
symmetry estimator construction of figures in digital
images, which allows to rank on the basis of sym-
metry any figures, both symmetrical, but deformed as
a result of noise, and asymmetric. Our approach in-
cludes two elements:
• a finite set of possible straight lines-candidates for
the symmetry axis of the object iteration;
• the optimal symmetry axis selection based on cal-
culation of the measure of coincidence of the orig-
inal figure with the figure obtained by mirroring
relative to the candidate axis.
Formally the problem is formulated in the following
way. Denote:
• S is a figure, a closed one-connected region on the
Euclidean plane R
2
,
• G is a set of straight lines that have a non-empty
intersection with the figure S, each line g ∈ G is
given by a pair g = (s, α), where s ∈ S is the point
of the figure through which the line g passes, α is
the angle between the line g and the x-axis,
• S(g) is a figure obtained by symmetrically reflect-
ing S with respect to the straight line g ∈G,
• µ(S, S(g)) is a measure of the difference between
the figures S and S(g). If the figure coincides with
its symmetrical image, this value is 0.
The shape asymmetry coefficient is defined as
φ(S) = min
g∈G
µ(S, S(g)). (1)
Further the figure classification on the basis of
symmetry is performed by comparing this coefficient
with the selected threshold M. If φ(S) ≤ M, then
the figure is considered symmetric, if φ(S) > M, then
asymmetric.
Applied to a digital image, the figure S is a dis-
crete set of pixels. The set G consists of lines passing
through the centers of pixels, points with integer co-
ordinates. The solution of the problem (1) is reduced
to a combinatorial search of points from a finite set S
and finding the best value of the angle α, minimizing
the measure µ(S, S(g)).
Our proposed solution is based on the following
principles:
1. To calculate φ(S), only the set of lines passing
through the figure S boundary points is used. The
boundary ∂S of the figure S is described as a con-
tour, as a closed chain of pixels connected in an
8-adjacent neighborhood structure.
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
332

2. The calculation of the difference measure be-
tween a figure and its symmetric reflection with
respect to a straight line is determined based on
the Fourier descriptor of the figure boundary con-
tour.
The problem (1) solution is carried out on the ba-
sis of decomposition into two subtasks of minimiza-
tion:
φ(S) = min
s∈∂S
[min
0≤α<π
F(∂S, s, α)], (2)
where F(∂S, s, α) is a symmetry measure of the
boundary contour ∂S with respect to the line g =
(s, α). The external minimization problem solution
is based on iterating over the boundary contour ∂S
points for the time O(n), where n is the number of
pixels in the boundary contour. To solve the inner
subtask, we propose a method based on the use of the
boundary contour Fourier descriptor, which allows us
to find the best value of α at a given point s also in
time O(n). Thus, a joint problem solution has com-
plexity O(n
2
). This theoretical complexity estimate is
implemented in practice with a very small coefficient
value at n
2
by using two simple heuristic rules: one
for iterating over contour points in the outer subtask,
and the other for minimizing the functional in the in-
ner subtask.
The threshold M for classifying the figure accord-
ing to the asymmetry coefficient is determined exper-
imentally based on machine learning.
3 ESTIMATION OF OBJECTS
MIRROR SYMMETRY BASED
ON FOURIER DESCRIPTOR
Let the original object be a simply connected domain.
The set P = {(x
l
, y
l
)}
N−1
l=0
consists of the coordinates
of all boundary pixels of a silhouette in a 4-adjacent
neighborhood structure, and describes a closed curve
connected in an 8-adjacent neighborhood structure.
The contour construction methods are described in
(Mestetskiy, 2009). Convert P to a vector of com-
plex numbers: U = {u
l
= x
l
+ iy
l
}
N−1
l=0
. Then perform
a discrete Fourier transform for U , taking the distance
between neighboring points of the contour constant
(by construction, it can take the values {1,
√
2}).
f
l
= u
0
+
N−1
∑
k=1
u
k
·exp(−i ·
2π
N
·l ·k), l = 0, N −1.
The vector {f
l
}
N−1
l=0
will be called Fourier descriptor
of the contour U. We denote the complex conjugation
of x as x
∗
.
Definition 1. The contour U = {u
l
}
N−1
l=0
is called per-
fectly symmetric if the following conditions are satis-
fied:
Im(u
0
) = 0, u
l
= u
∗
N−l
, l = 1, N −1.
Statement 1. Let U = {u
l
}
N−1
l=0
be a perfectly sym-
metric contour. Then for the Fourier descriptor F =
{f
l
}
N−1
l=0
of the contour U the following equalities are
fulfilled:
Im( f
l
) = 0, l = 0, N −1.
Proof. For convenience, we introduce u
N
≡ u
0
and a
new contour
ˆ
U = {u
∗
N−l
}
N−1
l=0
, l = 0, N −1.
For the Fourier descriptor
ˆ
F = {
ˆ
f
l
}
N−1
l=0
of the con-
tour
ˆ
U, the following equalities are satisfied:
ˆ
f
l
=
N−1
∑
k=0
u
∗
N−k
·exp(−i ·
2π
N
·l ·k) =
= u
∗
0
+
N−1
∑
m=1
u
∗
m
·exp(−i ·
2π
N
·l ·(N −m)) =
= u
∗
0
+
N−1
∑
m=1
u
∗
m
·1 ·exp(i ·
2π
N
·l ·m) =
= u
∗
0
+
N−1
∑
m=1
(u
·
m
exp(−i ·
2π
N
·l ·m))
∗
=
= u
∗
0
+ (
N−1
∑
m=1
u
·
m
exp(−i ·
2π
N
·l ·m))
∗
=
= u
∗
0
+ ( f
l
−u
0
)
∗
= f
∗
l
, l = 0, N −1.
Since U is perfectly symmetric, U =
ˆ
U is executed.
Then f
l
=
ˆ
f
l
, f
l
=
ˆ
f
∗
l
, l = 0, N −1. So Im( f
l
) =
Im(
ˆ
f
l
) = 0 for all l ∈ 0, N −1.
The Fourier descriptor has the following proper-
ties (Theodoridis and Koutroumbas, 2003):
Lemma 1. Shifting the contour U to a fixed vector
∆u changes only one coefficient f
0
of the Fourier de-
scriptor.
Lemma 2. After rotating U by a given angle α
around the origin, all Fourier descriptor coefficients
f
l
are multiplied by the constant exp(iα).
Lemma 3. Let U
p
= {u
(l+p)modN
}
N−1
l=0
be the con-
tour obtained by cyclic shift of contour points U =
{u
l
}
N−1
l=0
by p positions, p ∈ 0, N −1, F = {f
l
}
N−1
l=0
is the Fourier descriptor of the contour U, F
p
=
{f
p
l
}
N−1
l=0
is the Fourier descriptor of the contour U
p
.
Then
f
p
l
= f
l
·exp(i ·
2π
N
·l · p), l = 0, N −1.
Mirror Symmetry Detection in Digital Images
333

Using the described facts about the behavior of the
Fourier descriptor under contour elementary transfor-
mations, we can generalize the statement 1 to an arbi-
trary symmetric contour:
Statement 2. Let the following conditions be satisfied
for the contour U = {u
l
}
N−1
l=0
:
1. The contour is symmetrical;
2. There is a contour point u
p
lying on the symmetry
axis;
3. The symmetry axis has an angle α to the abscissa
axis.
Let F = {f
l
}
N−1
l=0
be the Fourier descriptor of the con-
tour U. Then the following equality holds for all
l = 1..N −1:
Im[ f
l
·exp(i ·
2π
N
·l ·(N − p)) ·exp(−iα)] = 0.
Proof. Let’s perform a sequential shift of the con-
tour by ∆u = −u
p
and a rotation by the angle −α.
Next, we perform a cyclic shift of the obtained con-
tour points by N − p positions (now the initial point
of the contour is u
p
, lying on the axis of symmetry
which is coincides with the x-axis). The resulting
contour
e
U satisfies the conditions of the statement 1.
By performing inverse transformations of the Fourier
descriptor according to the rules of the lemmas 1, 2,
3, we obtain the necessary equalities.
In practice, in noisy images, the equalities from
statement 2 are only approximate.
We introduce a value characterizing the asymme-
try of the contour. If α is the approximate angle of the
symmetry axis passing through the point u
p
, then this
value is close to zero. To find the symmetry axis, we
will minimize it by α for each value of p:
t(α, p) =
N−1
∑
l=1
[Im( f
l
·exp(i ·
2π
N
·l ·(N − p) −iα))]
2
This value is the norm square of the Fourier coeffi-
cients imaginary parts deviation from zero after rotat-
ing by the angle −α when choosing u
p
as the origin
and starting point of the contour.
Calculate the optimal value of α given p, f
l
,
l = 1, N −1.
t(α, p) → min
α∈[0,π)
(3)
Denote f
p
l
= f
l
·exp(i ·
2π
N
·l ·(N − p)), l = 0, N −1
be Fourier coefficients after the shift of the contour
starting point. Let exp(−iα) = x +i ·y, f
p
l
= a
l
+i ·b
l
,
l = 1, N −1. It is clear that in this case x = cosα,
y = −sinα:
f
p
l
·exp(−iα) = (a
l
+ i ·b
l
) ·(x + i ·y) =
= (x ·a
l
−y ·b
l
) + i ·(x ·b
l
+ y ·a
l
),
t(α, p) =
N−1
∑
l=1
(x ·b
l
+ y ·a
l
)
2
=
= x
2
·
N−1
∑
l=1
b
2
l
+ 2xy ·
N−1
∑
l=1
(a
l
·b
l
) + y
2
·
N−1
∑
l=1
a
2
l
.
Denote k
1
=
∑
N−1
l=1
b
2
l
, k
2
= 2 ·
∑
N−1
l=1
(a
l
· b
l
),
k
3
=
∑
N−1
l=1
a
2
l
. Then (3) can be rewritten like this:
k
1
cos
2
α −k
2
cosα·sinα + k
3
sin
2
α → min
α∈[0,π]
The optimized function is continuously differentiable
by α, it is easy to find the local minima of the given
function on the segment (0, π). The minimum can
also be reached at the end of the segment. There
can be three local minima points α, denote them as
α
1
, α
2
, α
3
and the global minimum as α
p
.
α
1
=
(
π
4
, k
1
= k
3
1
2
(arctan(
k
2
k
1
−k
3
) mod π), k
1
6= k
3
,
α
2
= α
1
+
π
2
,
α
3
= 0.
The solution finally has the form:
k = argmin
i∈{1,2,3}
t(α
i
, p),
α
p
= α
k
.
To find the symmetry axis, we perform the de-
scribed procedure for finding the optimal angle for
each contour point, and in addition, calculate the fol-
lowing value of the descriptor coefficients deviation
from the found optimal axis for all possible p:
Q(p) =
q
∑
N−1
l=1
Im( f
p
l
·exp(−iα
p
))
2
N −1
The closer Q(p) is to zero, the more the found
line resembles the symmetry axis. Choose P =
argmin
p∈0,N−1
Q(p). The most suitable symmetry axis
passes through the selected vertex, and the value
Q(P) = Q makes sense as a asymmetry measure of
the figure. There is a classification criterion: we con-
sider a figure symmetric if the value Q for this figure
does not exceed the specified threshold M. The de-
scribed algorithm for calculating the asymmetry mea-
sure and determining the symmetry axis is quadratic
in terms of the contour points number. The M value
is determined based on training.
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
334

4 IMPROVING THE
COMPUTATIONAL
EFFICIENCY OF THE
ALGORITHM
Efficiency improvement is achieved by reducing the
search within the quadratic algorithm.
First, the symmetry axis of the figure must be the
symmetry axis of its convex hull, which can be con-
structed in subquadratic time, and due to this fact it
is enough to check only a few points from the con-
tour instead of a complete search p = 0, . . . , N −1.
Namely, on the symmetry axis can lie either a point-
vertex of the convex hull, or a point that lies on a
line passing through the center of mass (the arithmetic
mean of the contour points) and the middle of the con-
vex hull edge. Since all values are determined numer-
ically, we also check the small neighborhood of these
points (example in Fig. 2).
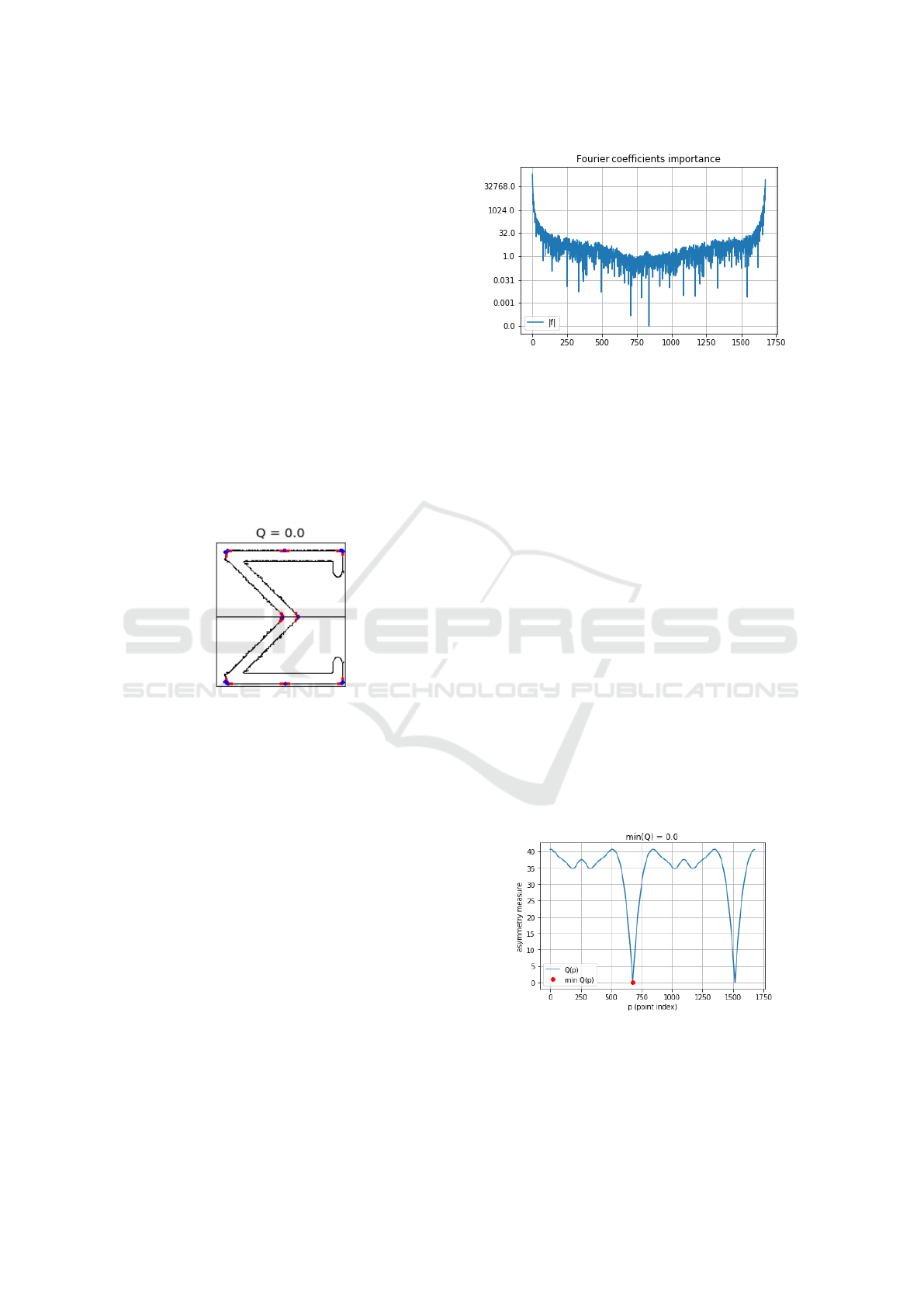
Figure 2: Silhouette of the Σ symbol. Blue dots are ver-
tices to iterate based on convex hull. The red dots are their
nearest neighbors. Q is the asymmetry measure.
Secondly, due to the distribution of the Fourier
descriptor coefficients modules, we can see that an
important contribution to the form description is
made by only a small number of Fourier coefficients,
namely having a large enough module. To speed up
the method, we calculate α
p
and Q(p) by a truncated
set of Fourier coefficients. That is, we sum only by
indices l where the Fourier coefficient module |f
l
| is
above a given threshold. Usually the first and last har-
monics are the most useful. There is an example in
Fig. 3. The absolute values of the Fourier coefficients,
except for f
0
, are invariant to transformations such
as shift, rotation and change of the contour starting
point, so this operation is correct. In fact, this proce-
dure is equivalent to conducting a contour frequency
filtering for approximate localization of the symmetry
axis, while losing some information about the original
circuit. In the small neighborhood of the found vertex
P, we calculate the full set of coefficients for the exact
determination of the figure symmetry measure.
Figure 3: The graph shows the coefficients importance for
the silhouette of the symbol Σ (logarithmic scale on the y-
axis).
The fast Fourier transform is performed in sub-
quadratic time, thus the final asymptotic of the al-
gorithm is O(NlogN + mk), where m is the num-
ber of contour points to iterate, k is the number of
Fourier coefficients to compute truncated sums. The
described heuristics work at m ≈ 0.05N, k ≈ 0.3N.
5 EXPERIMENTS
In the first experiment, a symmetric object silhouette
was chosen as the initial image, the symmetry axis
is parallel to the x-axis. There is a symbol Σ. The
contour is constructed as a boundary pixels sequence,
it consists of 1676 points. Next, the algorithm found
the value of the asymmetry measure equal to 0 (Fig.
2).
In the case of a symmetric object, the graph Q(p)
has two close local minima, one of which is global
(Fig. 4). These are values at two opposite contour
points lying on the symmetry axis.
Figure 4: The symbol Σ asymmetry measure with respect
to the symmetry axes passing through the various contour
points.
We will solve the following classification prob-
lem. Silhouettes of butterflies are given. It is required
Mirror Symmetry Detection in Digital Images
335

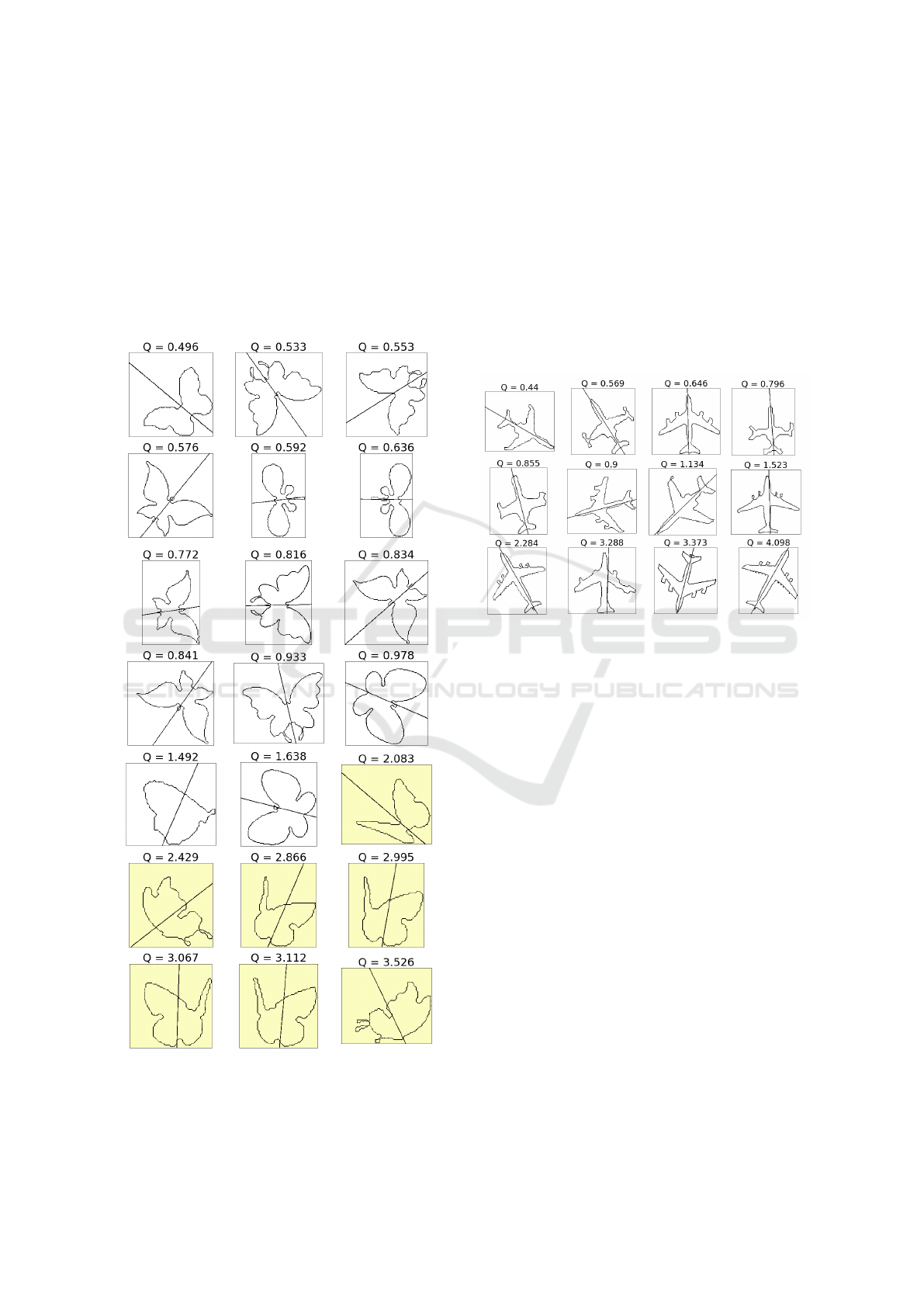
to classify from what position the picture is made:
from above or from the side. Silhouettes of the first
type are symmetrical, but allow noise as a result of
sampling and segmentation. Silhouettes of the second
type are not symmetrical. So, to solve the problem
it is enough to determine the symmetry measure of
each silhouette, and choose the optimal threshold to
maximize classifier accuracy. For the butterfly sam-
ple shown in Fig. 5, the threshold value was found to
be 2.
Figure 5: Q is an asymmetry measure. Silhouettes are or-
dered in Q ascending order. Yellow background indicates
silhouettes classified as asymmetrical.
Also earlier computational experiments were car-
ried out on real data: the aircraft silhouettes se-
lected from remote sensing of the Earth images are
given, it is required to determine the lines that spec-
ify these objects orientation (Mestetskiy and Zhu-
ravskaya, 2019). 2208 binary images with a size of
about 120 ×120 pixels were studied, the average im-
age processing time was 0.1 seconds, the orientation
was determined correctly in 98% of cases based on vi-
sual analysis, the errors are associated with sampling
error (low resolution of images). A few examples are
given in Fig. 6.
Figure 6: Q is an asymmetry measure. Silhouettes are or-
dered in Q ascending order.
6 CONCLUSION
A method for solving the classification problem of
symmetric and asymmetric binary silhouettes is de-
veloped. An efficient algorithm implementing the cre-
ated method is constructed. The reliability of the so-
lution is established by computational experiments.
A new measure of object symmetry is proposed. A
new axial symmetry criterion is formulated for a con-
nected object in a digital image. The applicability of
this criterion as a feature for solving the classification
problem is studied.
ACKNOWLEDGEMENTS
The work is executed at support of RFBR, grant 17-
01-00917.
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
336

REFERENCES
Fedotova, S., Seredin, O., and Kushnir, O. (2016). Algo-
rithms for refining the axis of mirror symmetry found
by comparing sub-chains of skeletal primitives. In Al-
goritmy utochneniya osi zerkal’noj simmetrii, najden-
noj metodom sravneniya podcepochek skeletnyh prim-
itivov. Izvestiya TulGU. Tekhnicheskie nauki, Tula,
Russia (in russian).
Karkishchenko, A. and Mnukhin, V. (2012). Symmetry
recognition in the frequency domain. 9th Conference
(International) on Intelligent Information Processing,
Moscow, pages 426–429.
Kushnir, O., Fedotova, S., Seredin, O., and Karkishchenko,
A. (2016). Reflection symmetry of shapes based on
skeleton primitive chains. International Conference
on Image and Signal Processing, Springer Interna-
tional Publishing.
Lee, S. and Liu, Y. (2012). Curved glide-reflection symme-
try detection. IEEE Trans. Pattern Anal. Mach. Intell.,
34(2):266–278.
Lepskiy, A. (2013). Determination of symmetry parame-
ters of objects in noisy images. Pattern recognition
and image analysis, Volume 23, Issue 3, Springer US,
September 2013, pages 408–414.
Liu, Y., Hel-Or, H., Kaplan, C., and Van Gool, L. (2010).
Computational symmetry in computer vision and
computer graphics. Found. Trends Comput. Graph.
Vis., 5(1-2):1–195.
Mestetskiy, L. (2009). Continuous morphology of binary
images: figures, skeletons, circulars. In Nepreryvnaya
morfologiya binarnyh izobrazheniy: figury, skelety,
cirkulyary. Fizmatlit, Moscow, Russia (in russian).
Mestetskiy, L. and Zhuravskaya, A. (2019). Method for
assessing the symmetry of objects on digital binary
images based on fourier descriptor. ISPRS - Interna-
tional Archives of the Photogrammetry, Remote Sens-
ing and Spatial Information Sciences. XLII-2/W12,
pages 143–148.
Sheynin, S., Tuzikov, A., and Volgin, D. (1999). Computa-
tion of symmetry measures for polygonal shapes. In-
ternational Conference on Computer Analysis of Im-
ages and Patterns, Springer Berlin Heidelberg, pages
183–190.
Theodoridis, S. and Koutroumbas, K. (2003). Pattern
Recognition. Second Edition. Elsevier.
Van Otterloo, P. (1988). A contour-oriented approach to
digital shape analysis. Technische Universiteit Delft.
Widynski, N., Moevus, A., and Mignotte, M. (2014). Local
symmetry detection in natural images using a particle
filtering approach. IEEE Transactions on Image Pro-
cessing, 23:5309–5322.
Yang, X., Adluru, N., Latecki, L., Bai, X., and Pizlo, Z.
(2008). Symmetry of shapes via self-similarity. Inter-
national Symposium on Visual Computing, Springer
Berlin Heidelberg., pages 561–570.
Yip, R., Tam, P., and Leung, D. (1994). Application of el-
liptic fourier descriptors to symmetry detection under
parallel projection. Pattern Analysis and Machine In-
telligence, IEEE Transactions on, 16:277–286.
Zahn, C. T. and Roskies, R. Z. (1972). Fourier descriptors
for plane closed curves. IEEE Transactions on Com-
puters, C-21(3):269–281.
Mirror Symmetry Detection in Digital Images
337