
Combining Evidential Clustering and Ontology Reasoning for Failure
Prediction in Predictive Maintenance
Qiushi Cao
1 a
, Ahmed Samet
2 b
, Cecilia Zanni-Merk
1 c
, Franc¸ois de Bertrand de Beuvron
2 d
and Christoph Reich
3 e
1
Normandie Universit
´
e/INSA Rouen, LITIS, 76000 Saint-
´
Etienne-du-Rouvray, France
2
ICUBE/SDC Team (UMR CNRS 7357)-Pole API BP 10413, 67412 Illkirch, France
3
Hochschule Furtwangen, 78120 Furtwangen, Germany
Keywords:
Industry 4.0, Predictive Maintenance, Ontologies, SWRL Rules, Evidential Clustering.
Abstract:
In smart factories, machinery faults and failures are detrimental to the efficiency and reliability of production
systems. To ensure the smooth operation of production systems, predictive maintenance techniques have
been widely used in a variety of contexts. In this paper, we tackle the machinery failure prediction task by
introducing a novel hybrid ontology-based approach. The proposed approach is based on the combined use
of evidential theory tools and semantic technologies. Among evidential theory tools, the Evidential C-means
(ECM) algorithm is used to assess the criticality of failures according to two main parameters (time constraints
and maintenance cost). In addition, domain ontologies with their rule-based extensions are used to formalize
the domain knowledge and predict the time and criticality of future failures. Case studies on synthetic data
sets and a real-world data set are used to validate the proposed approach.
1 INTRODUCTION
Within manufacturing processes, anomalies such as
machinery faults and failures may lead to the break
down of production lines. To avoid the outage situ-
ation and economic loss may be caused by machin-
ery faults and failures, predictive maintenance is a
vital methodology that has been widely used in dif-
ferent manufacturing processes. By collecting real-
time data from sensors and other information sources,
a predictive maintenance task tries to detect possi-
ble anomalies and hazards within different industrial
components.
To predict potential machinery failures, heteroge-
neous data are collected from multidimensional data
sources, including the machine historical data and
context data. For the analysis and management of
these data, data mining and machine learning tech-
niques are widely used for automatically discovering
knowledge from data sets. In the predictive main-
a
https://orcid.org/0000-0002-5858-0680
b
https://orcid.org/0000-0002-1612-3465
c
https://orcid.org/0000-0002-5189-9154
d
https://orcid.org/0000-0003-1324-2853
e
https://orcid.org/0000-0001-9831-2181
tenance domain, the prediction and assessment of
failure criticality is a critical issue for system users.
By obtaining criticality levels for different failures,
machine operators can prioritize maintenance actions
for higher criticality-level failures compared to lower
level ones. However, existing predictive maintenance
approaches in the manufacturing domain are limited
to the deployment of condition monitoring systems
for detecting anomalies and predicting the time of fu-
ture machinery failures, while lacking the solutions
for identifying the criticality of machinery failures
(Ansari et al., 2019). This brings obstacles to oper-
ators to perform appropriate maintenance actions by
considering different priorities. As the degradation
process of a piece of machinery often involves in-
herent randomness, techniques that can handle uncer-
tainty are required to avoid the outage situation of the
machinery and to ensure the smooth operation of the
production system.
In this paper, we propose a hybrid ontology-based
approach for the failure prediction tasks in Industry
4.0, which is based on the combined use of evidential
clustering and ontology reasoning. Since the predic-
tion of failure criticality suffers from the uncertainty
and imprecise knowledge, the ECM algorithm is used
to handle such kind of uncertainty and imprecision.
618
Cao, Q., Samet, A., Zanni-Merk, C., de Beuvron, F. and Reich, C.
Combining Evidential Clustering and Ontology Reasoning for Failure Prediction in Predictive Maintenance.
DOI: 10.5220/0008969506180625
In Proceedings of the 12th International Conference on Agents and Artificial Intelligence (ICAART 2020) - Volume 2, pages 618-625
ISBN: 978-989-758-395-7; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

On the other hand, domain ontologies with their rule-
based extensions are used to formalize the classifica-
tion results and predict the temporal constraints and
criticality of future failures.
The remainder of the paper is structured as fol-
lows. Section 2 introduces the existing solutions and
software that address the similar issues in predictive
maintenance. Section 3 gives the foundations and
background knowledge, including the introduction to
the evidence theory and ECM. Section 4 introduces
the proposed hybrid semantic approach for industry
4.0 predictive maintenance, where a domain ontology
and ontology reasoning process are presented. Sec-
tion 5 shows the experimental results we obtained on
several synthetic data sets and a real-world data set.
Section 6 concludes the paper.
2 STATE OF THE ART
In recent years, several efforts have been proposed to
facilitate the predictive maintenance in Industry 4.0.
As the manufacturing domain is becoming more dy-
namic and knowledge-intensive, several domain on-
tologies and their rule-based extensions were pro-
posed to facilitate knowledge representation and reuse
for the predictive maintenance in the industry. In this
section, we review the most relevant research works.
In (Zhou et al., 2015), an intelligent fault diag-
nosis method was proposed based on ontologies and
the Failure Mode, Effects and Criticality Analysis
(FMECA). The method was proposed to meet the de-
mands of fault diagnosis of wind turbines. In their
work, deep knowledge and the shallow knowledge
were extracted from FMECA and then modeled in the
form of ontologies. To perform failure diagnosis, the
knowledge is translated into the facts and rules for
ontology reasoning. The knowledge model for fleet
predictive maintenance, introduced in (Monnin et al.,
2011), was developed to handle contextual knowledge
within a fleet scale. In their work, semantic model-
ing techniques were used to define the context knowl-
edge and the structure of a fleet. The fleet knowledge
model has proved its practicability in the context of a
marine application.
In the manufacturing domain, there are also re-
search works considering the predictive maintenance
of production lines. In (Emmanouilidis et al., 2010),
a domain-specific ontology was developed to define
the main elements of a generic condition monitoring
system from an abstract level. The aim of the ontol-
ogy is to facilitate asset self-awareness and to support
production-level sustainable machinery operation. As
another knowledge-based approach, the prescriptive
maintenance model (PriMa) was designed for the pre-
scriptive maintenance of production systems in smart
factories (Ansari et al., 2019). Within the framework
of PriMa, ontologies and case-based reasoning are
used to build semantic learning and reasoning mod-
els. Results showed that the PriMa model enhances
two functional capabilities of production systems: the
efficient processing of heterogeneous big data, and the
effective generation of decision support measures and
recommendations for improving maintenance plans
(Ansari et al., 2019).
After examining the existing research works, we
observed that there is a missing link between the tem-
poral information of an anomaly (e.g., the occurrence
time of a future machinery failure) and the critical-
ity level of the anomaly. Also, the impact of the es-
timated economic cost of maintenance on the crit-
icality of the anomaly also remains uninvestigated.
To address these issues, we propose a novel hybrid
ontology-based approach for failure criticality predic-
tion. The prediction of failures relies on two critical-
ity descriptors: the temporal constraints of failures,
and the estimated maintenance cost for avoiding the
failures.
3 FOUNDATIONS AND
BACKGROUND KNOWLEDGE
This section introduces the foundations and theoreti-
cal background that are necessary for describing our
approach. It includes the background knowledge of
evidence theory and the ECM algorithm.
3.1 The Evidence Theory
The evidence theory (Dempster, 1967; Smets and
Kennes, 1994) is based on several fundamentals such
as the Basic Belief Assignment (BBA). A BBA m is
the mapping from elements of the power set 2
Θ
on to
[0, 1]:
m : 2
Θ
−→ [0,1],
where Θ is the frame of discernment. It is the set of
possible answers for a treated problem and is com-
posed of K exhaustive and exclusive hypotheses Θ =
{ω
1
,ω
2
,...,ω
K
}. A BBA m is written as follows:
∑
A⊆Θ
m(A) = 1
m(
/
0) ≥ 0.
(1)
Assuming that a source of information has a reliabil-
ity rate equal to (1 − α) where (0 ≤ α ≤ 1), such a
meta-knowledge can be taken into account using the
Combining Evidential Clustering and Ontology Reasoning for Failure Prediction in Predictive Maintenance
619

discounting operation introduced by(Shafer, 1976),
and is defined by:
(
m
α
(A) = (1 − α) × m(A) ∀A ⊂ Θ
m
α
(Θ) = (1 − α) × m(Θ) + α.
(2)
A discount rate α equal to 1 means that the source is
not reliable and the piece of information that is pro-
vided cannot be taken into account. On the contrary,
a null discount rate indicates that the source is fully
reliable and the piece of information that is provided
is entirely acceptable.
Within the evidence theory, several combination
rules have been introduced among which we find the
Dempster rule of combination (Dempster, 1967). As-
suming two BBAs m
1
and m
2
modelling two inde-
pendent reliable sources of information S
1
and S
2
, the
Dempster rule of combination is defined as follows:
m = m
1
⊕ m
2
, (3)
so that :
m(A) =
1
1 − m(
/
0)
∑
B∩C=A
m
1
(B) × m
2
(C) =
1
1 − m(
/
0)
m
∩
(A),
∀A ⊆ Θ,A 6=
/
0, (4)
where m(
/
0) is defined by:
m(
/
0) =
∑
B∩C=
/
0
m
1
(B) × m
2
(C) = m
∩
(
/
0). (5)
m(
/
0) represents the conflict mass between m
1
and m
2
.
The pignistic probability, denoted BetP, is pro-
posed by Smets et al. (Smets, 2005) within the Trans-
ferable Belief Model (TBM). In the decision phase,
the pignistic transformation consists in distributing
equiprobably the mass of a proposition A on its in-
cluded hypotheses. Formally, the pignistic probability
is defined by:
BetP(ω
n
) =
∑
A⊆Θ
|
ω
n
∩ A
|
|
A
|
× m(A) ∀ω
n
∈ Θ. (6)
where || is the cardinality operator.
3.2 Evidential c-means (ECM)
In the following, we present the ECM clustering ap-
proach (Masson and Denœux, 2008). The ECM al-
gorithm is based on the concept of credal partition,
which extends those of fuzzy and possibilistic ones.
To derive such a structure, we minimize the proposed
objective function:
J
ECM
(M,V ) ,
d
∑
i=1
∑
{ j/A
j
6=
/
0,A
j
⊆Θ}
c
α
j
m
β
i j
dist
2
i j
+
n
∑
i=1
δ
2
m
β
i
/
0
,
(7)
subject to:
∑
{ j/A
j
6=
/
0,A
j
⊆Θ}
m
i j
+ m
i
/
0
= 1 ∀i = 1,. ..,d, (8)
where m
i
/
0
and m
i j
respectively denote m
i
(
/
0) and
m
i
(A
j
). M is the credal partition M = (m
1
,. .. ,m
d
)
and V is a cluster centers matrix. c
α
j
is a weight-
ing coefficient and dist
i j
is the Euclidean distance. In
our case, we use the default values prescribed by the
authors in (Masson and Denœux, 2008), i.e. α = 1,
β = 2 and δ = 10.
3.3 Ontologies and SWRL Rules
In computer science, an ontology is a specification
of a representational vocabulary for a shared domain
(Gruber, 2009). Normally, it is designed to support
the sharing and reuse of domain knowledge among
different AI system components and also among sys-
tem users. An ontology consists of classes, individu-
als, relationships, functions, and other objects (Gru-
ber, 2009), which allows ontology reasoning to be
performed on individuals, for inferring new knowl-
edge.
Semantic Web Rule Language (SWRL) is based
on a combination of its sublanguages OWL DL and
OWL Lite with the RuleMarkup Language (Horrocks
et al., 2006). A SWRL rule is in the form of an impli-
cation between an antecedent (body) and consequent
(head), which can be interpreted in a way that when-
ever the conditions specified in the antecedent hold,
then the conditions specified in the consequent must
also hold (Horrocks et al., 2006). In SWRL, a rule has
the syntax: Antecedent → Consequent, where both
the antecedent (body) and consequent (head) contains
zero or more atoms.
4 THE HYBRID EVIDENTIAL
ONTOLOGY-BASED
APPROACH FOR PREDICTIVE
MAINTENANCE
This section introduces our proposed hybrid method
for failure time and criticality prediction. Fig. 1
shows the different steps within the approach. The
approach starts with the Sequential Pattern Mining
(SPM) on machine historical data (Agrawal et al.,
1995). The aim of SPM is to extract frequent sequen-
tial patterns which contain failure events as well as
their temporal information (e.g., the time stamp indi-
cating when the failure happened). Then, the ECM al-
gorithm is applied to cluster the failures according to
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
620

Figure 1: Different steps within the hybrid ontology-based approach for predictive maintenance.
their criticality, based on failure temporal constraints
and estimated maintenance cost. After the cluster-
ing, we label different clusters with criticality Low,
Medium, and High. With obtaining the results from
ECM, ontologies with its SWRL rule-based exten-
sions are used to predictive the criticality of a future
failure.
4.1 The Evidential Approach for
Failure Criticality Estimation
In our previous work (Cao et al., 2019), one ontology-
based condition monitoring method was proposed.
However, the method is based on crisp logic, and it
fails to classify the criticality of a failure into the cor-
rect category when there are uncertain situations. To
cope with this issue, an evidential approach which is
able to handle such type of uncertainty situations is
required. To do so, the times to failures described
in rules and the estimated maintenance cost are used
as training examples for ECM with 3 fixed clus-
ters/classes which represents three levels of critical-
ity: (i) high criticality, which indicates the time from
a normal condition to the failure is relatively short
and the production line should be stopped for immedi-
ate maintenance, or the estimated maintenance cost is
relatively high; (ii) medium criticality, indicating the
failure may happen after a moderate amount of time,
or the estimated maintenance cost is moderate; (iii)
low criticality, indicating the failure may happen in
the long future and machine operators will have suf-
ficient time to plan maintenance actions, or the esti-
mated maintenance cost is relatively low.
In this paper, we intend to consider two factors
to evaluate the criticality of a failure. Assuming a
prediction rule in a form R : A −−→
[t
i
,t
j
]
Failure that pre-
dicts the failure with a time interval with an Estimated
Maintenance Cost EMC. The time to failure and the
cost of the failure are valuable descriptors to assess
the criticality of a failure. Each rule R has a value of
support that evaluates its pertinence. We aim to use
both predicted maintenance cost and predicted tem-
poral constraints of the failure within a rule to assess
the criticality of a predicted failure.
Let us assume a sequence S classified by a rule R
as a failure in [t
i
,t
j
] with an EMC. A BBA is com-
puted from both parameters on the frame of discern-
ment {Low,Meduim, High} for each level of critical-
ity. Both m
S,Cost
and m
S,time
are discounted using the
support
1
of the used rule R as follows:
m
1−Sup(R)
S
= m
1−Sup(R)
S,Cost
⊕ m
1−Sup(R)
S,time
. (9)
m
1−Sup(R)
S
is the BBA obtained from the aggrega-
tion of the cost and the time to failure BBAs using
the Dempster rule of combination. 1 − Sup(R) is seen
as the reliability value used to discount the obtained
BBAs. The final level of criticality is decided upon
the use of the arguments of the maxima as follows:
4.2 The Manufacturing Failure
Prediction Ontology
To address the uncertain situations, we extend the the
ontology introduced in (Cao et al., 2019), by describ-
ing the nominal categories of classes. As a result, we
developed the Manufacturing Failure Predictive On-
tology (MFPO), within which the classes are associ-
ated with pignistic probabilities which range from 0
to 1. For example, in the ontology introduced in (Cao
et al., 2019), hasFailureCriticality is an object prop-
erty whose domain is the class Failure, and range is
the predefined individuals Low, Medium and High.
After applying the aforementioned method, this ob-
ject property is replaced by three data properties: has-
FailureCriticalityLow, hasFailureCriticalityMedium,
1
The Support is measure that evaluate the pertinence of
a rule based on its matching frequency within a database
and denoted Sup().
Combining Evidential Clustering and Ontology Reasoning for Failure Prediction in Predictive Maintenance
621

and hasFailureCriticalityHigh, and the sum of the nu-
meric values of these three data properties is 1.
H
n
= argmin
ω
n
∈Θ
BetP(ω
n
). (10)
Algorithm 1: Algorithm to transform a chronicle into a pre-
dictive SWRL rule, based on evidential c-means.
Require: S
F
: a chronicle within which the last state
(event) is a failure, E : a set of the states that are
described within a chronicle.
Ensure: R R: the SWRL rule to be constructed.
1: ls ← LastNon f ailureState(S
F
,E ) Extract
the last non-failure state before the failure within
a chronicle.
2: f ← theFailure(E) Extract the failure within a
chronicle.
3: R ←
/
0, A ←
/
0, C ←
/
0, Atom
a
←
/
0, Atom
c
←
/
0,
F
FailureCriticalityLow
= 0, F
FailureCriticalityMedium
= 0,
F
FailureCriticalityHigh
= 0.
4: for each e
i
∈ E do
5: pe ← ProceedingState(e
i
,S
F
) Extract the
proceeding state
6: se ← SubsequentState(e
i
,S
F
) Extract the
subsequent state
7: Atom
a
← pe ∧ se
8: A ← Atom
a
∧ pe ∧ se
9: end for
10: f td ← FailureTimeDuration(ls, f ) Extract the
time duration between the last non-failure state
and the failure.
11: mc ← MaintenanceCost(S
F
) Obtain the esti-
mated maintenance cost for the failure described
in this the chronicle.
12: F
FailureCriticalityLow
←
PignisticProbabilityLow( f td, mc)
13: F
FailureCriticalityMedium
←
PignisticProbabilityMedium( f td,mc)
14: F
FailureCriticalityHigh
←
PignisticProbabilityHigh( f td, mc)
15: C ← F
FailureCriticalityLow
∧ F
FailureCriticalityMedium
∧
F
FailureCriticalityHigh
∧ f td
16: R ← {A → C}
4.3 Ontology Reasoning for Failure
Time and Criticality Prediction
To predict time and criticality of future failures, we
propose SWRL rules (Horrocks et al., 2006) for on-
tology reasoning. The proposed SWRL rules reason
on the individuals in the MFPO ontology, and infer
new knowledge about failure prediction.
In this paper, we use the frequent chronicle min-
ing algorithm introduced in (Sellami et al., 2019) to
obtain chronicles, which are a special type of se-
quential patterns in a rule format. After that, SWRL
rules are proposed to formalize the mining results
and to predict failures. To enable the generation of
SWRL rules, in this work we propose a novel algo-
rithm to transform chronicles into SWRL predictive
rules. The pseudo-code of the rule transformation al-
gorithm is shown in Algorithm 1. It runs in four major
steps: i). The function LastNonfailureState extracts
the last non-failure state (event) within a chronicle,
and the function LastNonfailureState extracts the fail-
ure event within a chronicle; ii). For each time inter-
val in a chronicle, the two functions ProceedingEvent
and SubsequentEvent extract the proceeding and sub-
sequent events of it. Then the two events and this time
interval forms different atoms in the antecedent of the
rule, and they are treated as conjunctions; iii). The
ECM algorithm is applied to classify the failures ac-
cording to their criticality. The failures are classified
into three categories, and three object properties in
MFPO are used to represent the pignistic probability
to different clusters. The pignistic probabilities are
treated as a conjunction, to form the consequent of
the rule; iv). At last, a rule is constructed as an impli-
cation between the antecedent and the consequent.
5 EXPERIMENTAL RESULTS
We validate our approach on several synthetic data
sets and a real-world data set
2
. The experimentation
starts with the preprocessing of data, followed by the
chronicle mining step. The frequent chronicle mining
algorithm introduced in (Sellami et al., 2019) is used
to extract frequent chronicles.
5.1 Experimentation on Synthetic Data
Sets
The experimentation on synthetic data sets begin with
the frequent chronicle mining on synthetic data. To
do this, the synthetic data was transformed into the
form of pairs (event, time stamp), where each data
sequence finishes with a failure. With obtaining se-
quences that contain failures, the frequent chronicle
mining algorithm was used to extract the temporal
constraints among these sequential patterns. As re-
sults, frequent chronicles were obtained. Inside a
2
The source codes and data sets used in this paper
could be found at: https://github.com/caoppg/ICAART-
2020-paper-125.git
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
622

chronicle, events are ordered and temporal orders of
events are quantified with numerical bounds (Sellami
et al., 2019).
5.1.1 Classification of Failure Criticality using
ECM
After obtaining the chronicles, we then generate syn-
thetic data for the estimated maintenance cost. To do
this, the maintenance cost is generated as uniformly
distributed random numbers between [0,100]. In the
generated data, each value of maintenance cost is as-
sociated with a failure, indicating the estimated main-
tenance cost caused by the failure. In addition to the
temporal constraints of failures, maintenance cost is
considered as the second descriptor for the failure crit-
icality. The third step is to apply ECM on the syn-
thetic data set, for determining the criticality of fail-
ures based on their temporal constraints and estimated
maintenance cost. Following the evidential cluster-
ing approach introduced in Section 4.1, we obtained
the final level of criticality of the failures described
in chronicles. At last, the extracted frequent chroni-
cles are transformed into SWRL predictive rules (us-
ing Algorithm 1), and the ECM classification results
are also formalized by these rules. The following sub-
sections introduce the different steps in our experi-
mentation in details.
Table 1 shows the 10 failure chronicles (FC)
which have the highest chronicle support (CS) among
all extracted ones. In this figure, the numeric values
of the minimum time duration (Min
T D
, time unit: sec-
ond) among the last normal events and the failures,
the EMC for each chronicle, and the pignistic proba-
bility of the final criticality (PPFC) are presented. For
the classification results, the final level of a failure’s
criticality is shown inside the brackets within the last
column of the table.
5.1.2 The Generation of SWRL Rules based on
Chronicles and ECM Results
To formalize the failure classification results and to
predict the criticality of future failures, we generated
SWRL rules based on the obtained chronicles and
ECM classification results. To do this, Algorithm 1
was used to transform the failure chronicles and ECM
classification results into predictive SWRL rules. Fig.
2 presents an example SWRL rule that was generated
following our approach.
To evaluate the quality of the SWRL rules, two
measures are computed. The first measure is Accu-
racy. It is computed by Equation 11, where n
rc
is the
number of training examples that are covered by a rule
R and belonging to the class C. n
r ¯c
is the number of
training examples that are covered by a rule R but not
belonging to the class C. The second measure is Cov-
erage, which is computed by Equation 12. Within it,
n
¯rc
the number of training examples that are not cov-
ered by a rule R but belonging to the class C.
Accuracy(R) =
n
rc
n
rc
+ n
r ¯c
. (11)
Coverage(R) =
n
rc
n
rc
+ n
¯rc
. (12)
We use the above two equations to obtain the aver-
age value of Accuracy and Coverage for the SWRL
rules. Table 2 presents the two measures under differ-
ent chronicle support. We can observe from the table
that as the chronicle support increases, the accuracy of
rules also increases. It is reasonable since as the min-
imum threshold of extracted chronicles increases, we
obtain more relevant chronicles. On the other hand,
as the number of extracted rules decreases, the se-
quences that are covered by the rules decreases. This
is the reason why the average value of coverage shows
a downtrend.
5.2 Experimentation on a Real-world
Data Set
To evaluate the performance of the prediction and fail-
ure classification, we apply ECM on a real-world data
set. The real-world data set is called SECOM (Dua
and Graff, 2017), which contains measurements of
features of semi-conductor productions within a semi-
conductor manufacturing process.
We first compute the hard credal partition on the
SECOM data set. In total, at most 2
Θ
focal sets could
be obtained through credal partition, where Θ is the
frame of discernment. In our experimentation, Θ rep-
resents the three levels of failure criticality. For the
SECOM data set, we only use temporal constraints
of failures as the descriptor for criticality. The data
points on the empty set which have the highest masses
are removed as outliers before they are assigned to the
clusters.
Fig. 3 shows the hard credal partition computed
on the SECOM data set with the following parame-
ters: α = 1,β = 2, δ = 10, and ε = 10
−3
. As results,
6 focal elements are obtained, including the universal
set Θ
ω
= {ω
l
,ω
lm
,ω
m
,ω
mh
,ω
h
}. Each subset of Θ
ω
is represented by the convex hull. Among them, ω
l
is the focal set representing the low criticality class,
ω
m
is the focal set representing the medium critical-
ity class, and ω
h
is the focal set representing the high
criticality class. ω
lm
is the hesitation between the ω
l
and ω
m
classes, which is {ω
l
,ω
m
}. ω
mh
is the hesi-
tation between the ω
m
and ω
h
classes, which means
Combining Evidential Clustering and Ontology Reasoning for Failure Prediction in Predictive Maintenance
623

Figure 2: An example SWRL rule generated from a chronicle.
Table 1: Failure chronicles that have the 10 highest chronicle support, and their failure classification results.
C
F
Min
T D
EMC CS PPFC
C
F1
10 33.4163 96.19% 0.6652 (Medium)
C
F2
7 50.0472 95.61% 0.5049 (Medium)
C
F3
3 14.9865 94.48% 0.6140 (High)
C
F4
4 17.3388 94.21% 0.8739 (Medium)
C
F5
21 81.8148 92.94% 0.3921 (Low)
C
F6
3 65.9605 91.06% 0.8796 (High)
C
F7
11 68.1971 90.27% 0.4722 (Medium)
C
F8
24 9.6730 90.01% 0.6871 (Low)
C
F9
10 64.8991 86.93% 0.4266 (Medium)
C
F10
18 66.6338 86.87% 0.4030 (Low)
Table 2: Two rule quality measures under different chronicle support.
Chronicle support Accuracy Coverage
0.5 76.52% 74.26%
0.6 74.14 % 75.71%
0.7 76.98 % 74.35%
0.8 79.33% 70.49%
0.9 82.56% 68.10%
1 84.45% 67.71%
{ω
m
,ω
h
}. The center of each class is marked as a
cross.
It can be observed that the ω
h
class has the highest
number of training examples, and over half of the fail-
ures are classified into the ω
h
and ω
mh
classes. As the
value of a temporal constraint increases, the critical-
ity level of the failure decreases. We can see that the
evidential-based clustering extends the fuzzy and pos-
sibilistic methods by not only assigning data points to
single clusters but also to all subsets of the universal
set Θ
ω
. In this way, ECM provides more insights into
failures than the classical clustering methods.
To obtain the final level of criticality, the pignos-
tic probability BetP and the maxima of BetP are com-
puted. After comparing the BetP of the three classes,
the class with the maximum BetP is selected to rep-
resent the final level of criticality. Fig. 4 shows
the final criticality for the training examples in the
SECOM data set. ω
l
, ω
m
, ω
h
represents the low crit-
icality class, medium criticality class, and high criti-
cality class respectively. It can be seen that there is
no hesitation among different classes, which ensures
the final criticality to be determined based on a maxi-
mum of BetP of the three classes. An example of the
ECM clustering results on the training data is shown
in Table 3. We select rule #45 and show the obtained
BBAs and the pignistic probability of the final criti-
cality (PPFC) of the failure which is described within
this rule. Since the high criticality class is assigned
with the highest PPFC, the final decision on the criti-
cality level of this failure is high.
6 CONCLUSIONS
In this paper, the issue of failure prediction is tack-
led by introducing a hybrid ontology-based approach.
The proposed approach is based on the combined use
of evidential clustering and ontology reasoning tech-
niques, where temporal constraints of failures and the
estimated maintenance cost are used as training ex-
amples to evidential clustering, and domain ontolo-
gies with their rule-based extensions are used to for-
malize the classification results and predict the future
failures.
For future work, we will work on experience capi-
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
624
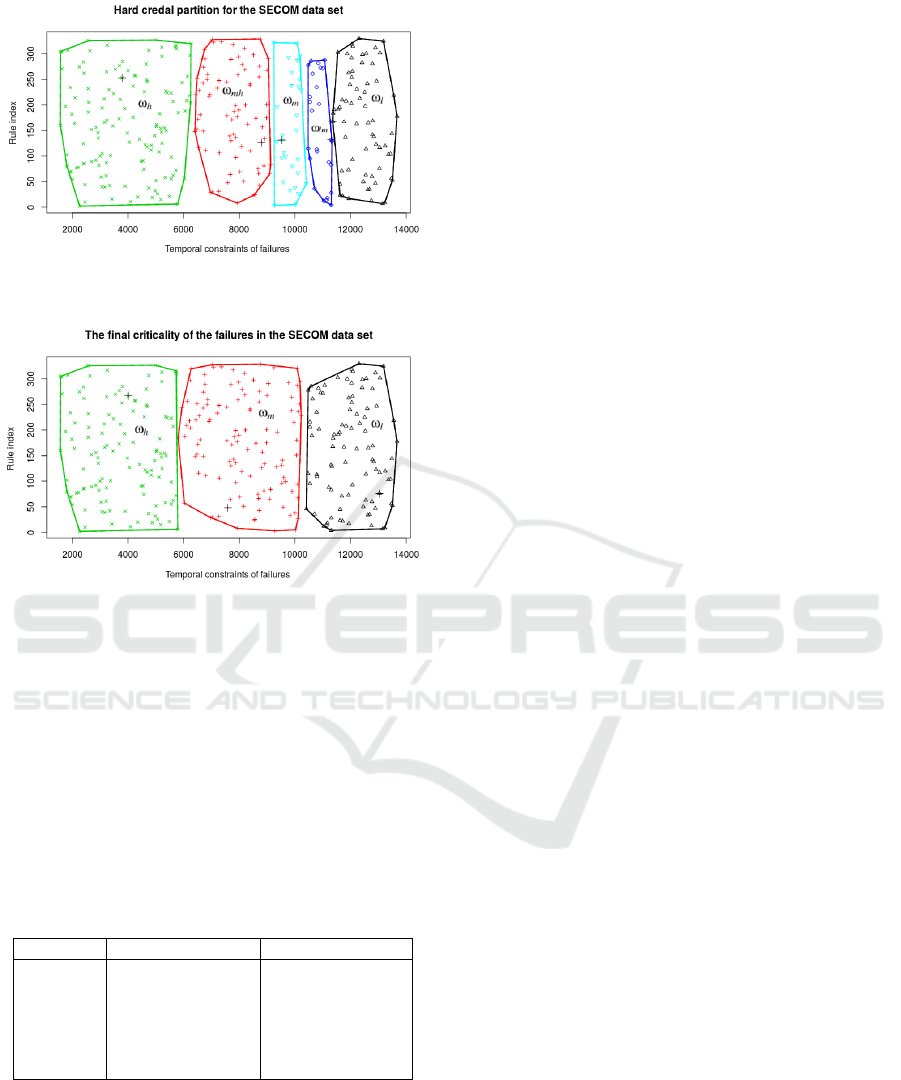
Figure 3: Hard credal partition for the SECOM data set.
Figure 4: Final criticality levels of failures in the SECOM
data set.
talization, which will support the failure classification
process in case of failure. To achieve this goal, expert
rules will be proposed and launched when the initial
rule base fails to predict the machine anomalies cor-
rectly. In this way, when the next time a similar situa-
tion needs to be addressed, the rule which capitalizes
domain experts’ experience will also be launched to
predict potential failures.
Table 3: Experimental results of a training example in the
SECOM data set.
Rule index BBAs of the failure PPFC
#45 m({ω
h
}) = 0.3174
m({ω
mh
}) = 0.2219
m({ω
m
}) = 0.2929
m({ω
lm
}) = 0.0181
m({ω
l
}) = 0.0485
m({Θ
ω
}) = 0.1012
BetP(ω
h
) = 0.4683
BetP(ω
m
) = 0.4391
BetP(ω
l
) = 0.0926
ACKNOWLEDGEMENTS
This work has received funding from INTER-
REG Upper Rhine (European Regional Development
Fund) and the Ministries for Research of Baden-
W
¨
urttemberg, Rheinland-Pfalz (Germany) and from
the Grand Est French Region in the framework of the
Science Offensive Upper Rhine HALFBACK project.
REFERENCES
Agrawal, R., Srikant, R., et al. (1995). Mining sequential
patterns. In icde, volume 95, pages 3–14.
Ansari, F., Glawar, R., and Nemeth, T. (2019). Prima: a pre-
scriptive maintenance model for cyber-physical pro-
duction systems. International Journal of Computer
Integrated Manufacturing, pages 1–22.
Cao, Q., Giustozzi, F., Zanni-Merk, C., de Bertrand de Beu-
vron, F., and Reich, C. (2019). Smart condition mon-
itoring for industry 4.0 manufacturing processes: An
ontology-based approach. Cybernetics and Systems,
pages 1–15.
Dempster, A. (1967). Upper and lower probabilities in-
duced by multivalued mapping. AMS-38.
Dua, D. and Graff, C. (2017). UCI machine learning repos-
itory.
Emmanouilidis, C., Fumagalli, L., Jantunen, E., Pistofidis,
P., Macchi, M., Garetti, M., et al. (2010). Condition
monitoring based on incremental learning and domain
ontology for condition-based maintenance. In 11th
International Conference on Advances in Production
Management Systems, APMS.
Gruber, T. (2009). Ontology. Springer.
Horrocks, I., Patel-Schneider, P. F., Boley, H., Tabet, S.,
Grosof, B., Dean, M., et al. (2006). Swrl: a semantic
web rule language combining owl and ruleml, 2004.
W3C Submission.
Masson, M.-H. and Denœux, T. (2008). ECM: An eviden-
tial version of the fuzzy c-means algorithm. Pattern
Recognition, 41(4):1384–1397.
Monnin, M., Abichou, B., Voisin, A., and Mozzati, C.
(2011). Fleet historical cases for predictive mainte-
nance. In The International Conference Surveillance,
volume 6, pages 25–26.
Sellami, C., Miranda, C., Samet, A., Tobji, M. A. B., and
de Beuvron, F. (2019). On mining frequent chronicles
for machine failure prediction. Journal of Intelligent
Manufacturing, pages 1–17.
Shafer, G. (1976). A Mathematical Theory of Evidence.
Princeton University Press.
Smets, P. (2005). Decision making in the TBM : The ne-
cessity of the pignistic transformation. International
Journal of Approximate Reasoning, 38:133–147.
Smets, P. and Kennes, R. (1994). The Transferable Belief
Model. Artificial Intelligence, 66(2):191–234.
Zhou, A., Yu, D., and Zhang, W. (2015). A research on in-
telligent fault diagnosis of wind turbines based on on-
tology and fmeca. Advanced Engineering Informatics,
29(1):115–125.
Combining Evidential Clustering and Ontology Reasoning for Failure Prediction in Predictive Maintenance
625
