
Correctness of an ATL Model Transformation from
SysML State Machine Diagrams to Promela
Georgiana Caltais, Stefan Leue and Hargurbir Singh
University of Konstanz, Germany
Keywords:
Model Transformation, ATL, SysML, Promela, Correctness, Observational Equivalence.
Abstract:
In this paper we discuss the correctness of an ATL-based model transformation from the systems engineering
modelling language SysML into Promela, the input language of the SPIN model checker. More precisely, we
reduce showing the correctness of the transformation to showing a notion of what we refer to as observational
equivalence of the SysML and the generated Promela models, respectively. This paves the way to a proof
technique that could be further exploited in order to argue the correctness of model transformations from
SysML to various model checkers, based on the observable actions generated by the systems under analysis.
1 INTRODUCTION
The implementation of a comprehensive Model-
Based Systems and Software Engineering (MBSSE)
methodology faces the challenge that, at least at the
time of writing, a plethora of disconnected, incongru-
ent and somewhat orthogonal modeling and analysis
methods and tools are available in academia and in-
dustrial practice. This becomes particularly evident
when considering modeling environments for safety-
critical system architectures, such as SysML (Ob-
ject Management Group, 2017a), on the one hand
side, and formal analysis and verification tools, such
as SPIN (Holzmann, 2004), NuSMV 2 (Cimatti
et al., 2002), UPPAAL (Bengtsson et al., 1995) or
PRISM (Kwiatkowska et al., 2004), just to mention
some of them, on the other hand. Modeling languages
supporting MBSSE, such as SysML, possess an, at
best, semi-formally defined semantics. With few ex-
ceptions, the semantics that the tools supporting these
languages offer are undocumented. Some of the tools
supporting UML-style languages offer a limited form
of commonly understood syntactic model represen-
tation, for instance using the XMI standard (Object
Management Group, 2015). On the other hand, for-
mal verification tools such as the ones cited above
possess a somewhat rigorous semantics, which is nec-
essary for the formal analysis to return meaningful
and reproducible results. These semantics are some-
times openly defined, at least in parts, but sometimes
deeply buried in the code of the analysis tool. For-
mal verification tools typically possess tool-specific,
sometimes rather idiosyncratic input languages.
However, linking the worlds of modeling and for-
mal analysis both syntactically and semantically is
highly desirable. This is in particular true in the
realm of MBSSE of safety-critical systems, where
formal assurance cases for the safety of a system are
of prime interest to industry, and society as a whole.
We claim that to enable an automated translation and
transformation process from MBSSE languages to
models understood by formal analysis and verifica-
tion tools is pivotal in order to obtain both syntacti-
cally and semantically dependable mappings between
these model domains. In particular, we maintain that
an excellent way to reach this goal is to use rule-based
transformations, such as it is for instance supported
by the Atlas Transformation Language (ATL) (Jouault
et al., 2008). While ATL based model transformation
rules define the syntactic correctness of these trans-
formations, it is the objective of this paper to consider
a framework for proving the semantic correctness of
ATL based model transformations. In doing so, we
will focus on the semantics of an SysML model as
defined by its state machine (stm) diagrams. Stm dia-
grams are derived from the Statechart (Harel, 1987)
notation and are widely used in UML and SysML
based MBSSE.
Contributions of this Paper. Related work doc-
umented in (Kölbl et al., 2018) has considered an
ATL-based translation from SysML into the input
language of various model checking tools, includ-
ing Promela (Holzmann, 2004), the input language of
the widely popular SPIN explicit state model checker.
The approach taken there defines ATL rules to trans-
late SysML into an intermediate model, and then uses
a hand-coded code generator for the translation from
the intermediate model to Promela.
360
Caltais, G., Leue, S. and Singh, H.
Correctness of an ATL Model Transformation from SysML State Machine Diagrams to Promela.
DOI: 10.5220/0008968303600372
In Proceedings of the 8th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2020), pages 360-372
ISBN: 978-989-758-400-8; ISSN: 2184-4348
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

We take this idea further and define an ATL trans-
lation from SysML to Promela as follows. We first
consider a suitable SysML source meta-model and
a Promela target meta-model. Then, we define an
ATL translation from SysML models conforming to
the aforementioned source meta-model into Promela
models conforming to the target meta-model. Note
that both the meta-models and the models are in XMI
format, as required by the ATL framework. Finally,
we provide a simple and straightforward hand-written
translation from the Promela models in XMI format
into Promela code.
The key contribution of this paper is then to show
that the ATL-based transformation above is correct.
The novelty of our approach consists in reducing the
correctness proof to showing that the SysML source
models and their corresponding Promela target mod-
els are observationally equivalent. The sets of obser-
vations are derived in accordance with the operational
semantics of SysML and Promela as in (Liu et al.,
2013; Weise, 1997), for instance.
In our case, observational equivalence coincides
with trace equivalence between the SysML models
and the Promela models. Consequently, safety prop-
erties proven during state space exploration of the
Promela models, including the presence of faults, also
hold of the SysML model from which the Promela
code was derived. Recall that safety properties can be
proven or disproven using reachability analysis.
More broadly speaking, the approach presented
here can be adapted to other ATL-based model to
model transformations as long as the involved mod-
els can be given an observational semantics similarly
to the one sketched in this paper.
Related Work. There is a wide plethora of work
dedicated to the topic of model transformation.
The results in (Mikk et al., 1998) tackle the trans-
lation of statecharts into Promela sequential or paral-
lel code. The main difference with our work is that the
approach is not based on ATL-like rule based trans-
formations, and no behavioural equivalence between
the two models is shown. Performance analysis of the
resulted code is performed.
(Anastasakis et al., 2007) proposes a declara-
tive model transformations in a formalism called Al-
loy (Jackson, 2019). The main difference with our
work is that Alloy does not have any built in notion of
state machine, hence the approach can only be used to
reason about static properties of the transformation.
Graph transformation based approaches to show-
ing correctness of model transformations in terms
of behavioural equivalence were proposed in (Dyck
et al., 2015; Engels et al., 2008), for instance.
ATL was not exploited in the aforementioned works.
In (Dyck et al., 2015), correctness is addressed in
the context of a more simplistic case study on trans-
forming lifelines into automata. In (Engels et al.,
2008), the authors show trace equivalence between
activity diagrams and the corresponding translated
TAAL (Rensink, 2006) programs.
The work in (Lano et al., 2015) introduces a sys-
tematic language-independent framework and tech-
niques for model transformation verification. As a
verification technique for statemachines transforma-
tions, the authors suggest showing preservation of
traces by proving preservation of a suitable invariant
formula.
For a more comprehensive study on formal verifi-
cation techniques for model transformations we refer
to the survey in (Amrani et al., 2015), for instance.
Closer related to our approach in this paper,
we address the following contributions. The work
in (Latella et al., 1999) proposes a transformation
from a behavioural subset of UML Statechart dia-
grams into Promela. The correctness of the approach
relies on a translation solely based on the operational
semantics of hierarchical automata. The benefits of
using a modular, syntax-based framework such as
ATL are, nevertheless, not exploited.
The verification of ATL transformations was also
addressed in (Büttner et al., 2012). The main differ-
ence with our work is that the correctness is estab-
lished based on an additional encoding of ATL into
OCL. The latter is further used to analyze different
properties of the transformations, but not a semantic
equivalence between the source and target models.
In (Troya and Vallecillo, 2011) the authors in-
troduce a formal semantics of the ATL language it-
self, using rewriting logic semantics implemented in
Maude (Clavel et al., 2003). The Maude toolkit is
then exploited to reason about the application of the
ATL rules, and syntactic properties of the target mod-
els. In our approach, the focus is on reasoning about
the semantic equivalence of the source and its trans-
lation into the target model.
Structure of the Paper. In Section 2 we provide an
overview of SysML, Promela and ATL. In Section 3
we discuss the ATL transformation from SysML into
Promela. Section 4 sets the basis for the observational
semantics of SysML and Promela. The correctness of
the ATL transformation is shown in Section 5. Con-
clusions and pointers to future work are provided in
Section 6.
Correctness of an ATL Model Transformation from SysML State Machine Diagrams to Promela
361
2 PRELIMINARIES
In this section we provide a brief overview of the
SysML, Promela and ATLAS Transformation Lan-
guage aspects relevant for our work.
2.1 SysML
The Systems modeling language (SysML) (Object
Management Group, 2017a), is a standardized, semi-
formal language for defining static and dynamic as-
pects of systems as well as their communication be-
havior. SysML uses a subset of the UML (Ob-
ject Management Group, 2017b). It encompasses,
amongst others, state-machine (stm) diagrams and, at
the same time, extends UML with block definition
and internal block definition diagrams.
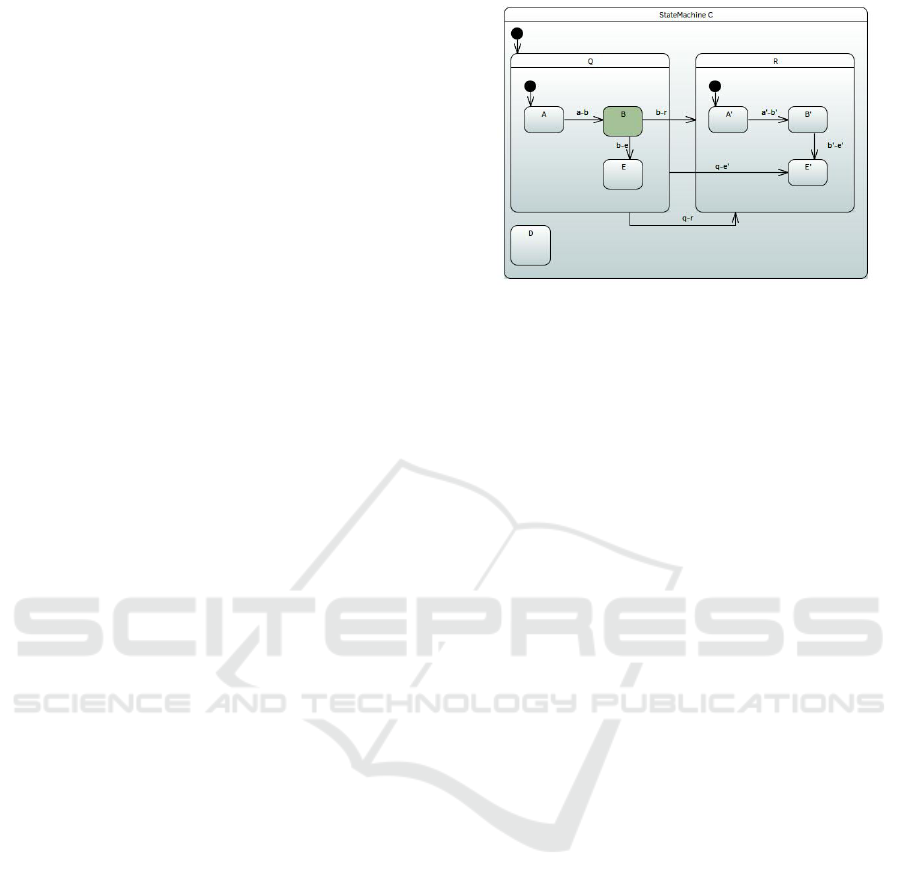
In this paper, we focus on stm diagrams like the
one in Fig. 1. A stm diagram consists of states and la-
belled transitions defining the behaviour of a system
component such as StateMachine C in Fig. 1. States
play the role of control locations for the system. In
Fig. 1, the current control location, or the active state
is B (note that B is coloured darker). Moreover, some
states are called “initial” and, intuitively, serve as en-
try points within the behaviour of a stm. See, for ex-
ample, states Q, A or R in Fig. 1. Each transition is
labelled with a guard that needs to be satisfied, and an
action that is performed whenever transiting between
the states. A guard in SysML can be a trigger wait-
ing for the occurrence of an event, or a check on a
variable value. An action can be the initialization of
an event or a variable value change. For an exam-
ple, the generic label a−b in Fig. 1 could be of shape
true/[x ← v], for the trivial guard true and the action
associating to variable x value v. Each component in
SysML can have multiple behaviors, but we restrict
each component to one behavior for our work. Hence,
we have one stm for each component. A system mod-
elled by means of several SysML components is un-
derstood as a set of associated stms operating concur-
rently. Note that stms can be hierarchical, i.e., they
consist of subsequent stms (such as Q in Fig. 1). We
refer to hierarchical stms as complex, and single-state
stms such as D in Fig. 1 as single, or simple. In this
paper, we limit ourselves to at most two-level stms.
The stms semantics is “run-to-completion”. The
semantics is defined with respect to an active state,
which is the current control location of the model.
If a complex state is active, it means that one of the
sub-states is active along with the complex state. We
restrict the behavioral information to transitions and
do not use the SysML semantics of state entry and
exit behaviors. Moreover, the model can only have
Figure 1: SysML Component.
one action per transition. SysML execution seman-
tics defines an event pool that stores events which are
available for “consumption”. The basic semantics de-
fines the execution environment for the selection of
an event from the event pool, but the precise mecha-
nism is not specified. The run-to-completion seman-
tics states that whenever the action of the current tran-
sition is completed, SysML will select an event from
the event pool to trigger a transition. The commu-
nication among processes in SysML is defined based
on First-In-First-Out (FIFO) queues, with the ability
to lose messages if the queue is full. In our work, we
consider message-based (a)synchronous communica-
tion, with simple messages lacking parameters and re-
turn values.
We support activity diagrams as a way to input the
communication information. The usage of activity di-
agrams is limited to sendSignalAction and callOpera-
tionAction with only one action per diagram.
2.2 Promela
Promela has similar syntax to the C programming
language, with guarded commands and communica-
tion primitives. Processes in Promela are defined
as proctypes and are concurrent in nature. Intu-
itively, such processes correspond to SysML compo-
nents. Promela syntax uses variables that can be de-
fined with both local and global scope. Additionally,
channels are constructs used according to the intended
operational semantics to send and receive messages
between processes. These channels are FIFO queues
and have user-defined size. A channel of size 0 cannot
save the message and is called synchronous: both the
sender and receiver processes need to be ready to per-
form the communication. Otherwise, the sender has
to wait. An asynchronous channel can become full
and the message is discarded, similarly to the SysML
behavior for full channels.
Listing (1) illustrates a toy Promela process en-
MODELSWARD 2020 - 8th International Conference on Model-Driven Engineering and Software Development
362
coding the SysML component in Fig. 1. The corre-
spondence is easy to follow: proctype C defines a
Promela process corresponding to the aforementioned
component C. Each state within C is associated with
a flattened state in Promela. For instance, state A in C
can be interpreted as state Q_A_ini in Promela. The
naming convention is made in order to preserve the
static information on the “ancestry” and “initial na-
ture” of A. Namely, A is within the hierarchical stm
Q and is also the initial state of Q. Q_A_ini has tran-
sitions without any guard. State label changes are de-
scribed with the goto statement. break defines states
with no behaviour.
1 proctype C {
2 Q_A_ini :
3 do
4 :: a -b -> goto Q_B ;
5 :: q -r -> goto R_A ’ _in i ;
6 :: q-e ’ -> goto R_E ’;
7 od
8 Q_B : [.. . ]
9 Q_E : [.. . ]
10 R_A ’ _in i :
11 do
12 :: a’ - b ’ -> R_B ’;
13 od
14 R_B ’: [...]
15 R_E ’:
16 do
17 :: br e a k ;
18 od
19 D:
20 do
21 :: br e a k ;
22 od
23 }
Listing 1: Promela Code of the SysML Component in
Fig. 1.
2.3 ATL
ATL (Jouault et al., 2008) is a domain specific lan-
guage which was designed to provide a framework for
rule-based model-to-model transformation of XMI
models. ATL has two benefits over conventional pro-
gramming languages: due to its rule-based nature it
provides syntactic correctness of the source and tar-
get models, and it supports uniqueness of the trans-
formation rules which means that each type of source
element will be mapped only once per target element.
ATL uses the concept of meta-models for representing
the structure of the models. A meta-model is a special
model that contains the meta-definitions of all model
elements used in the transformation. Intuitively, a
meta-model can be seen as a grammar, whereas the
corresponding model is given according to the rules
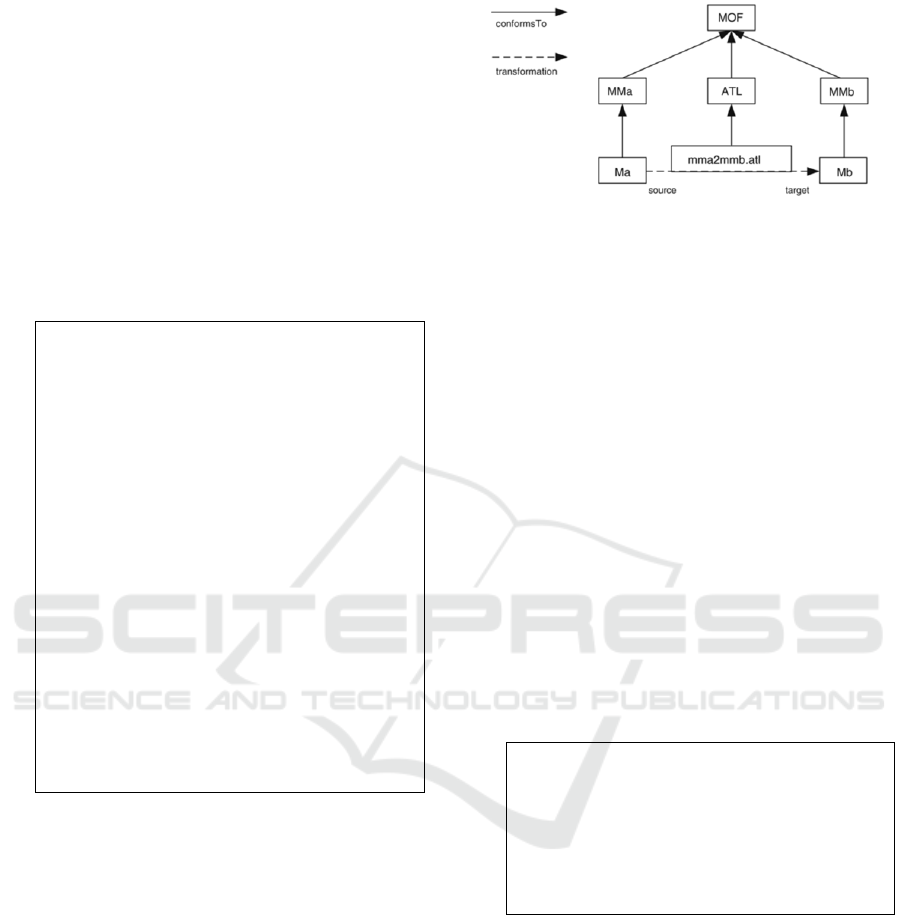
Figure 2: Overview of the ATL Transformation.
of the grammar. ATL requires meta-models for both
the source and the target models. The transformation
rules can refer to elements from the source and target
models.
The idea behind an ATL transformation is
sketched in Figure (2). ATL reads a source model Ma
which has to conform to a source meta-model MMa.
If the source model does not conform to the source
meta-model, ATL throws an error advising that the
source model is ill-defined. The ATL transformation
in mma2mmb.atl describes how a source model can
be converted to a target model Mb which conforms
to a target meta-model MMb. All meta-models must
conform to the meta-meta-model Meta Object Facility
(MOF). ATL defines its own syntax but also borrows
some functions from Java and OCL. All transforma-
tion rules in ATL are a set of mappings between the
source model elements and the target model elements
with imperative operations performed on the source
elements.
1 rule ex a m p l eATL {
2 from s : M M S y s M L ! S t ate (
3 s. name .startsWith(‘A ’)
4 )
5 to t : M M P r o m ela ! State (
6 n a me < - s . name , ID < - s . ID
7 )
8 }
Listing 2: ATL-code.
To illustrate the ATL translation mechanism, in
Listing 2 we define a sample rule which accepts
State elements from a SysML source model where
the name of the element starts with A. This set of
elements are then transformed to State elements of
the Promela target model where the name and ID at-
tributes are transferred.
Correctness of an ATL Model Transformation from SysML State Machine Diagrams to Promela
363
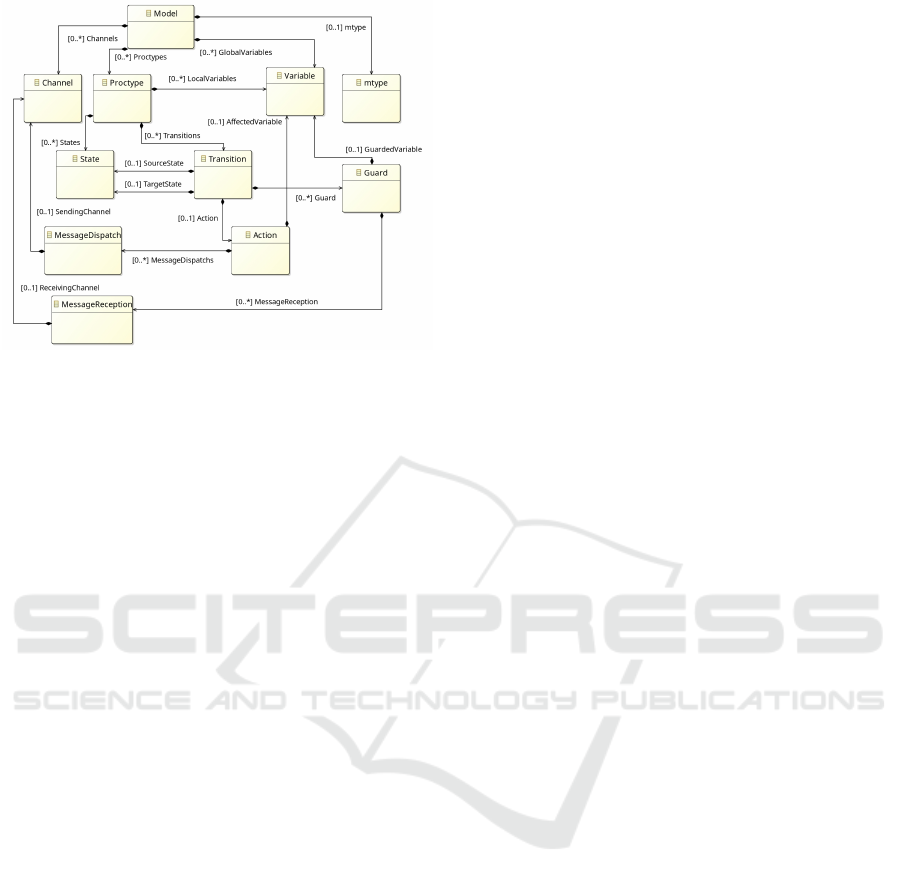
Figure 3: Class Diagram of the Promela Target Meta-
Model.
3 ATL TRANSFORMATION
FROM SysML TO Promela
As previously mentioned, the ATL transformation re-
lies on the meta-models of the source and target, re-
spectively. In short, ATL parses the SysML model
and checks whether it conforms to the UML 2.5.0
meta-model of Eclipse, encoded in XMI format. On
the Promela side, the equivalent class-diagram repre-
sentation of the XMI target meta-model is given in
Fig. 3. The referred class diagram encodes models
formed from several Proctype elements, which con-
sist of states and transitions labelled with actions and
guards, in the spirit of the Promela description in Sec-
tion 2.2.
The ATL transformation performs a syntactic con-
version of the SysML source model into the Promela
target model. The rules specify how the source model
elements must be processed and translated to the tar-
get model. It is important to observe that the conver-
sion from SysML into Promela is based on a “flat-
tening” procedure, which maps hierarchical state-
machines into corresponding proctypes. Intuitively,
the mapping transfers states and transitions as fol-
lows.
States:
(1) A simple state from SysML is translated into a
Promela state with the same name.
(2) All simple states within hierarchical SysML stms
are translated into Promela states respecting the
naming convention: the Promela names should
encode the “ancestry” and possibly the “initial na-
ture” information.
Transitions:
(3) If the source state of a SysML transition is simple,
then (a) if the SysML target is simple, then the
transition is translated into Promela directly or (b)
if the SysML target is complex, then the transition
is translated with the Promela target as the initial
state of the target hierarchical state-machine pre-
serving the naming convention.
(4) If the source state of the SysML transition is com-
plex, then (a) if the SysML target is simple, then
corresponding transitions originating from each
state of the hierarchical source state-machine are
translated into Promela (again, the naming con-
vention is fulfilled) or (b) if the SysML target is
complex, transitions as above are created with tar-
get as the initial state of the hierarchical target
state-machine (naming convention preserved).
The flattening procedure can be easily identified
based on the SysML source model in Listing 3 and
the derived Promela target model in Listing 4. Note
that both models are given in XMI format as required
by ATL, and provide corresponding encodings of the
component in Fig. 1.
The XMI format provides entries for the
Components (line 1 in Listing 3 and, line 1 in List-
ing 4) and entries for the InitialState of the pos-
sibly hierarchical stms (e.g., lines 2, 6 in Listing 3,
and line 2 in Listing 4). Each State entry has a name
and an ID that coincides with the name, in our ex-
amples. States have outgoing transitions specified via
their ID’s within the outTrans field. Additionally,
each transition is defined in terms of its label, Source
and Target, as expected.
Simple states such as D are translated directly from
SysML to Promela, as mentioned in (1) above. We
refer to line 3 in both Listing 3 and Listing 4 for the
corresponding entries.
Complex states are flattened as described in (2)
above. For instance, the complex state Q starting at
line 4 in Listing 3 is represented via the three enclosed
simple states Q_A_ini, Q_B and Q_E at lines 4, 8 and
13 in Listing 4. Observe that their ID’s are in accor-
dance with the naming convention.
For an example of a “simple to complex” transi-
tion as in (3)(b) above, we refer to the b-r labelled
transition at line 15 in Listing 3. Its Promela corre-
spondent is encoded at line 25 in Listing 3. Note how
in Promela, the target becomes the initial state of the
state-machine R.
An example of “complex to simple” transition as
in (4)(a) is the q-e’ labelled transition at line 32 in
Listing 3. On the Promela side, it is captured via
the transition at line 37 Listing 4. Observe how, the
source in Promela becomes the initial state of the hi-
erarchical stm Q.
MODELSWARD 2020 - 8th International Conference on Model-Driven Engineering and Software Development
364
A “complex to complex” transition as in (4)(b) is
given in Listing 3 at line 30. It corresponds to the
q-r labelled transition between the hierarchical stms
Q and R. The translation to Promela is realized in terms
of the q-r labelled transitions at lines 31, 33, 35 in
Listing 4. Observe that, all targets are the initial state
of R, whereas the sources are the stms enclosed within
Q.
1 < Co m p o n e n t C ID = C >
2 < Init i a l S tate Q / >
3 < S t a te D ID = D/ >
4 < S t a te Q ID = Q
5 outTrans = Qq - rR , Qq -e ’E
’>
6 < Init i a l S tate A / >
7 < S t a te A ID = A outTrans = Aa -
bB / >
8 < S t a te B ID = B
9 outTrans = Bb - eE , Bb - rR
/>
10 < S t a te E ID = E/ >
11 < T r a ns a - b ID = Aa - bB
12 Source = A Target = B / >
13 < T r a ns b - e ID = Bb - eE
14 Source = B Target = E / >
15 < T r a ns b - r ID = Bb - rR
16 Source = B Target = R / >
17 < S t a te / >
18 < S t a te R ID = R >
19 < Init i a l S tate A ’/ >
20 < S t a te A ’ ID = A ’
21 outTrans = A ’a ’ -b ’B
’/ >
22 < S t a te B ’ ID = B ’
23 outTrans = B ’b ’ -e ’E
’/ >
24 < S t a te E ’ ID = E ’/ >
25 < T r a ns a ’ - b ’ ID = A ’a ’-b ’ B ’
26 Source = A ’ Target
= B ’/ >
27 < T r a ns b ’ - e ’ ID = B ’b ’-e ’ E ’
28 Source = B ’ Target
= E ’/ >
29 < S t a te / >
30 < T r a ns q - r ID = Qq - rR
31 Source = Q Target =
R/ >
32 < T r a ns q -e ’ ID = Qq -e ’E ’
33 Source = Q Target =
E ’/ >
34 </ C ompone n t >
Listing 3: The XMI Source Model for the Component in
Fig. 1.
We continue by providing some details about the
actual ATL transformation rules encoding the map-
ping described above. Each of the discussed rules
is invoked with respect to the name-space of the el-
ements. Moreover, each rule works on a type of
1 < Co m p o n e n t C ID = C >
2 < I n i t i alSta t e Q _ A _ i n i / >
3 < State D ID = D / >
4 < State Q _ A _ i n i ID = Q_ A _ i n i
5 o u t T r a n s = Q_A_i nia - bQ_B ,
6 Q_ A _iniq - rR_A ’ _ini ,
7 Q_ A _iniq - e ’ R_E ’/ >
8 < State Q_B ID = Q_B
9 o u t T r a n s = Q_Bb - eQ_E ,
10 Q_Bb - rR_A ’ _ini ,
11 Q_Bq - rR_A ’ _ini ,
12 Q_Bq -e ’ R_E ’/ >
13 < State Q_E ID = Q_E
14 o u t T r a n s = Q_Eq - rR_A ’ _ini ,
15 Q_Eq -e ’ R_E ’/ >
16 < State R_A ’ _ini ID = R_A ’ _ini
17 o u t T r a n s = R_A ’ _inia ’ - b ’ R_B ’/ >
18 < State R_B ’ ID = R_B ’
19 o u t T r a n s = R_Ba ’-b ’ R_E ’/ >
20 < State R_E ’ ID = R_E ’/ >
21 < Trans a -b ID = Q _ A_ini a - bQ_B
22 S o urce = Q_A_ini T a r g e t = Q_ B
/>
23 < Trans b -e ID = Q_Bb - eQ_E
24 S o urce = Q_B T a r g e t = Q_E / >
25 < Trans b -r ID = Q_Bb - rR_A ’ _ ini
26 S o urce = Q_B T a r g e t = R_A ’ _ini
/>
27 < Trans a ’-b ’ ID = R_A ’ _inia ’ - b ’
R_B ’
28 S o urce = R_A ’ _ ini T a r g e t = R_B
’/ >
29 < Trans b ’-e ’ ID = R_Bb ’-e ’R_E ’
30 S o urce = R_B ’ Target = R_E ’/ >
31 < Trans q -r ID = Q_A_i n iq - rR_A ’
_in i
32 S o urce = Q _ A _ i n i T arget = R_A ’
_in i / >
33 < Trans q -r ID = Q_Bq - rR_A ’ _ ini
34 S o urce = Q_B Target = R_A ’ _ini
/>
35 < Trans q -r ID = Q_Eq - rR_A ’ _ ini
36 S o urce = Q_E Target = R_A ’ _ini
/>
37 < Trans q -e ’ ID = Q _A_ini q -e ’ R_E ’
38 S o urce = Q _ A _ i n i T arget = R_E
’/ >
39 < Trans q -e ’ ID = Q_Bq -e ’ R_E ’
40 S o urce = Q_B Target = R_E ’/ >
41 < Trans q -e ’ ID = Q_Eq -e ’ R_E ’
42 S o urce = Q_E Target = R_E ’/ >
43 </ C ompone n t >
Listing 4: The ATL-generated XMI Target Model.
source element and can be used to generate one or
more target elements. The transformation reads a
SysML model and extracts information which is tar-
geted through the rules. We navigate the model us-
ing subsequent calls to (lazy) sub-rules: the model
rule will call the component rule for each component
in the source model. The transformation completes
Correctness of an ATL Model Transformation from SysML State Machine Diagrams to Promela
365

1 lazy rule C 2P {
2 from s : M M S y s M L ! Component
3 to t : M M P r o m ela ! P r o c t y p e (
4 \\ c o l l e c t c o m p o n e n t a t tributes
5 ID <- s . id , [...]
6 )
7 do{
8 \\ i t e r a t e ove r co m p o n e n t s t ates
9 for ( p in s . n o r m alBe h a v iour .
states ){
10 if( p . subM a c h i nes .
ocl I s U ndef i n e d () ) {
11 \\ cal l sub - rul e for s i m p l e
states
12 t. S t ates <- thisModule. S2S
(p ) ;
13 }
14 else{
15 for ( q in p . s u b M a chines .
states ){
16 \\ ca ll sub - ru le for c o m p l e x
states
17 t. S t ates <- thisModule.
SMS2S ( q) ;
18 }
19 }
20 } [ . ..]
21 \\ i t e r a t e ove r co m p o n e n t s t ates
22 for (p in s. n o rmal B e h avio u r .
tran s i t i ons . union (thisModule.
Tra n s i tion L i s t )) {
23 \\ call sub - rul e fo r trans i t i o n s
24 if( p . sourc e )
25 t. Tr a n s i t ions <- thisModule.
T2T ( p );
26 } [ . ..] }
Listing 5: Component to Proctype Transformation.
when each relevant element is processed. The ATL
code in the listings of this section has been simplified
for presentation. The rule in Listing 5, for instance,
is used to transfer information about a component of
the SysML model and create an equivalent proctype
in the Promela model. The rule extracts information
about the simple states, complex states, and transi-
tions. This information is further sent to sub-rules for
processing.
Listing 6 defines a rule which is used to transfer
states which are of simple type and mark the initial
state, according to the naming convention. This rule
is a sub-rule of the component rule and operates on
elements received from its parent rule as parameters
(see line 12 in Listing 5).
In a similar fashion, we defined a rule which
for transferring SysML complex states into Promela.
This rule receives the children of the complex state as
parameters and names them according to the naming
convention. We also defined a rule which is used to
1 lazy rule S 2S {
2 from s : M M S y s M L ! S t ate
3 to t : M M P r o m ela ! State (
4 \\ c o l l e c t state a t t r ibutes
5 ID <- s . id
6 )
7 do{
8 \\ check if sta t e is i n i t i a l
9 if( s .refImmediateComposite() .
ini t i a l State . name = s . name ){
10 \\ annotate nam e wi t h ‘ ini tial ’
inf o
11 t. Nam e <- s . name .concat( ‘ _init
’) ;
12 t. IsIn i t i a l <- true ;
13 } } }
Listing 6: State to State Transformation.
transfer transitions along with the source and target
state information. This rule changes the source and
target states based on their type. So, if source is com-
plex, it will generate multiple transitions with source
state’s children as source. If target is complex then
target is changed to the initial state of the target state.
Our automated ATL-based tool for gen-
erating Promela models from SysML speci-
fications can be found at: https://github.com/
SysMLATL/SysMLPromelaTransformation
4 ENRICHING XMI MODELS
WITH OBSERVATIONAL
SEMANTICS
In this section we provide an observational semantics
of SysML and Promela models, on top of their XMI
encodings discussed in Section 3. Intuitively, this se-
mantics “collects” the sequences of actions that can
be executed by the SysML and Promela models, ac-
cording to associated operational semantics as in (Liu
et al., 2013; Weise, 1997), for instance.
At this point we would like to emphasize on the
uniformity of the proposed observational semantics.
The latter enables computing the possible observable
executions of both SysML and Promela models by us-
ing the same sets of semantic rules. This, despite the
fact that SysML allows the specification of hierarchi-
cal state-machines, whereas Promela does not.
The observational semantics will be further ex-
ploited in order to show the correctness of the ATL
transformation in terms of a notion of observational
equivalence of the SysML and the associated Promela
models.
We write obs to denote the set of traces w that can
be observed by executing a certain SysML/Promela
MODELSWARD 2020 - 8th International Conference on Model-Driven Engineering and Software Development
366

model. Executions w are words over SysML/Promela
actions. As usual, we write ε to denote the empty
word, and w
1
.w
2
to represent the concatenation of two
words w
1
and w
2
.
In order to mimic variable and channel updates,
we introduce a notion of memory (mem) that asso-
ciates values v to variables and, respectively, channels
x. Such an assignment is denoted by mem[x ← v]. A
lookup function is denoted by lkp(mem,x). For sim-
plicity, and without loss of generality, we assume that
all variables x within a model are “allocated” in the
memory and initialised with the default value ⊥.
The observational semantics will be given via
rules:
p
1
... p
n
c
1
... c
m
consisting of premises p
1
,..., p
n
and conclusions
c
1
,..., c
n
which capture sequences of observations
that simulate model executions and, whenever ap-
propriate, memory updates. Due to typesetting con-
straints, we sometimes syntactically split the semantic
rules into “shorter” rules such as, for instance:
p
1
... p
i
c
1
... c
j
p
i+1
... p
n
c
j+1
... c
m
Furthermore, in the subsequent sections we define a
series of notational conventions enabling the uniform
handling of the aforementioned XMI representations
and their observational semantics. More precisely, we
will provide equivalent, but more compact and mod-
ular representations of concurrent components and
their state-machines.
4.1 An Observational Semantics of
SysML
As seen in Section 3, SysML source models are
given as a “configuration” encoding a set of concur-
rent components C
i
, for i ∈ {1,..., N}. We write
C
1
| ... | C
N
, or |
i∈{1,...,N}
C
i
for these components.
Naturally, each such component is defined in terms
of a set of stms, a current state curr
C
and an initial
state ini
C
. When proving correctness of our transfor-
mation, we let curr
C
“evolve” according to the obser-
vational semantics of SysML provided later on in this
paper. Initially, the current state curr
C
is set to ini
C
.
A stm of C is given by: its ID, its type (that is
either complex and denotes a SysML hierarchical stm,
or simple and denotes a state), a set of sub-machines
(possibly empty, if type is simple), a set of transitions
and an initial state ini. A transition is defined over
the ID of its source (that corresponds to the ID of the
stm) and the ID of its target. More formally, a state-
machine SM
i
of a SysML component C can be given
as:
hID
i
,type
i
,
[
j∈{1,...,m}
{SM
i, j
},
[
l∈{1,...,r}
{ID
i
α
l
−→ ID
i,t
l
},ini
i
i
(1)
If type
i
is complex, then each SM
i, j
stands
for a simple sub-machine of SM
i
. Otherwise,
S
j∈{1,...,m}
{SM
i, j
} =
/
0, as expected. We define
ID(SM
i
) = ID
i
, type(SM
i
) = type(ID
i
) = type
i
and
ini(SM
i
) = ini(ID
i
) = ini
i
for a stm as in (1). Re-
call that, in accordance with the SysML semantics, ini
is the initial state of the sub-machine for hierarchical
stms. Naturally, for simple sub-machines (or states),
ini is defined as the associated ID.
In short, we write SM
i
∈ C in order to refer to a
(hierarchical) stm of C as in (1). Subsequently, we
write SM
i, j
∈ SM
i
in order to refer to a simple stm of
SM
i
.
For an example, the complex stm Q in Fig. 1 is
equivalently represented as:
SM
Q
= hQ,complex, {SM
A
,SM
B
,SM
E
},
{Q
q−e
0
−−−→ E
0
,Q
q−r
−−→ R},Ai
(2)
The simple sub-machine SM
B
, for instance, is given
as:
SM
B
= hB,simple,
/
0,{B
b−r
−−→ R, B
b−e
−−→ E},Bi
(3)
A component C is captured as:
C = [
[
i∈{1,...,n}
SM
i
,curr
C
,ini
C
]
(4)
with SM
i
as in (1), for i ∈ {1,..., n}.
For an example, component C in Fig. 1 is:
C = [{SM
Q
,SM
R
,SM
D
},B,Q]. (5)
Given C as in (4) and SM
i
as in (1), we write tr
1
C
(ID
i
)
for the set of “first-level” transitions:
[
l ∈ {1,. ..,r}
{ID
i,s
l
α
l
−→ ID
i,t
l
}.
Intuitively, these transitions originate in hierarchical
stms, or simple state machines at the top-most level
in a component C. Symmetrically, we write tr
2
C
(ID
i
),
for the “second-level” transitions:
[
j ∈ {1,.. . ,m}
tr
1
C
(ID(SM
i, j
)).
Correctness of an ATL Model Transformation from SysML State Machine Diagrams to Promela
367

These are transitions that originate in simple states of
the hierarchical stms of C. For the simplicity of nota-
tion, we write tr
i
C
to denote the set of all first, respec-
tively, second-level transitions of a component C, for
i = 1, respectively i = 2.
For an example, the set of first-level transitions tr
1
C
in Fig. 1 is:
{Q
q−r
−−→ R,Q
q−e
0
−−−→ E
0
}.
The set of second-level transitions is:
{B
b−r
−−→ R,A
a−b
−−→ B,B
b−e
−−→ E,A
0
a
0
−b
0
−−−→ B
0
,B
0
b
0
−e
0
−−−→ E
0
}.
We also define a “children” function that extracts the
ID’s of the sub-machines of a given stm:
ch(ID
i
,C)=
S
SM
i, j
∈Set
SM
{ID(SM
i, j
)} if Set
SM
6=
/
0
{ID
i
} [owise]
if ∃SM
i
∈ C s.t ID(SM
i
) = ID
i
and
Set
SM
= ∪
j={1,...,m}
{SM
i, j
| SM
i, j
∈ SM
i
}
(6)
With these ingredients at hand, we are ready to pro-
vide the semantics of the SysML stms relevant to our
purpose. Let C,C
i
,C
j
range over components of a
SysML “configuration” C
1
| . .. | C
N
. Let obs refer
to the current set of executions, and mem stand for the
content of the memory.
We proceed by first formalising asynchronous
communication. Intuitively, a transition ID
s
g/α
−−→ ID
t
,
where α is an action, can be triggered whenever (one
of the children of) its source matches the current state
of the enclosing component C, and the guard g is sat-
isfied. As a consequence, the observation set is en-
riched with the corresponding action α and the cur-
rent state becomes the initial state of the transition’s
target as in (7).
ID
s
g/α
−−→ ID
t
∈ tr
i
C
curr
C
∈ ch(ID
s
) lkp(mem,g) = true
curr
C
:= ini(ID
t
) obs := ∪
w∈obs
{w.α}
i ∈ {1, 2}
(7)
Variable or channel updates in the context of asyn-
chronous communication are handled in a similar
fashion, with the additional observation that the cor-
responding update is stored in the memory as shown
in (8).
ID
s
g/x←v
−−−−→ ID
t
∈ tr
i
C
curr
C
∈ ch(ID
s
) lkp(mem, g) = true
curr
C
:= ini(ID
t
) obs := ∪
w∈obs
{w.x ← v} mem[x ← v]
i ∈ {1, 2}
(8)
Synchronous communication is formalised as in (9).
The transition is triggered when its guard g is satisfied
and the synchronous action α can see its synchronous
reception g(α). In other words, we write g(α) as a
syntactic sugar for a guard g “waiting” to synchronise
with its counterpart α (here, by α we denote both an
action, and a variable/channel update). Note that the
synchronising transitions can be at different levels in
the corresponding (hierarchical) stms.
ID
s
i
g/α
−−→ ID
t
i
∈ tr
i
C
curr
C
∈ ch(ID
s
i
)
curr
C
:= ini(ID
t
i
)
ID
s
j
g(α)/β
−−−−→ ID
t
j
∈ tr
j
C
0
curr
C
0
∈ ch(ID
s
j
)
curr
C
0
:= ini(ID
t
j
)
lkp(mem,g) = true
obs := ∪
w∈obs
{w.α.β}
i, j ∈ {1, 2}
(9)
Synchronous variable or channel updates is handled
in a similar fashion, with an additional memory up-
date, as formalised in (10).
ID
s
i
g/x←v
−−−−→ ID
t
i
∈ tr
i
C
curr
C
∈ ch(ID
s
i
)
curr
C
:= ini(ID
t
i
)
ID
s
j
g(x←v)/β
−−−−−−→ ID
t
j
∈ tr
j
C
0
curr
C
0
∈ ch(ID
s
j
)
curr
C
0
:= ini(ID
t
j
)
lkp(mem,g) = true
obs := ∪
w∈obs
{w.(x ← v).β} mem[x ← v]
i, j ∈ {1, 2}
(10)
4.2 An Observational Semantics of
Promela
Similarly to the approach in Section 4.1, we base the
semantic rules of Promela on configurations C
1
| ... |
C
N
encoding the components C
i
within the XMI tar-
get model of the ATL transformation. The main dif-
ference with the SysML counterpart is that each such
component encloses a set of simple stms. The lat-
ter are “flattened” versions of the (hierarchical) stms
specified in SysML, derived as described in Section 3.
Recall that the flattening procedure entails simple
stms with ID’s built according to the naming conven-
tion encoding their “ancestry” and “initial nature”,
whenever the case. We formalize the naming con-
vention by means of the function in (11). Assume a
SysML component C (in essence, encoded as in (4)),
and let ID
k
refer to a stm of C (s.a, Q, A or D in Fig. 1).
The naming convention maps ID from the SysML
XMI to nmc(ID
k
,C) in the Promela XMI, where:
MODELSWARD 2020 - 8th International Conference on Model-Driven Engineering and Software Development
368

nmc(ID
k
,C) =
ID(SM
i
)_ID
k
_ini
if ∃SM
i
∈ C,∃SM
i, j
∈ SM
i
s.t.
ID(SM
i, j
) = ID
k
and
ID(SM
i, j
) = ini(SM
i
)
ID(SM
i
)_ID
k
if ∃SM
i
∈ C,∃SM
i, j
∈ SM
i
s.t.
ID(SM
i, j
) = ID
k
and
ID(SM
i, j
) 6= ini(SM
i
)
ID
k
[owise]
(11)
In words:
• If the stm ID
k
refers to a simple (and initial) state
within a hierarchical stm, then the ancestry-based
flattening keeps track of the enclosing parent (and
the initially information) as well. This is the case
of ID
k
= B and ID
k
= A.
• If the stm is a stm not enclosed within another ma-
chine, then there is no flattening. This is the case
of ID
k
= D.
Assume a SysML component C, consisting of n (hier-
archical) state-machines SM
i
, for i = {1,. . .,n}, each
of each consisting of a (possibly empty) set of sim-
ple state-machines SM
i, j
, for j = {1,... , m}, naturally
captured as:
C = [
S
i∈{1,...,n}
SM
i
,curr
C
,ini
C
]
SM
i
=
hID
i
,type
i
,
S
j∈{1,...,m}
{SM
i, j
},
S
l∈{1,...,r}
{ID
i
α
i
−→ ID
i,t
l
},ini
i
i
SM
i, j
= hID
i, j
,simple,
/
0,
S
k∈{1,...,o}
{ID
i, j
α
k
−→ ID
t
k
},ID
i, j
i
(12)
The corresponding “flattened” component C within
the XMI target model is:
C = [
[
i ∈ {1,... , n}
j ∈ {1,.. . ,m}
SM
i, j
∈ SM
i
({hID,simple,
/
0,T,IDi}),curr
C
,ini
C
]
(13)
where
ID = nmc(ini(SM
i, j
),C) and T stands for the
set of transitions
[
k = {1, . ..,o}
ID
i, j
α
k
−→ ID
t
k
∈ tr
1
(ID
i, j
)
{ID
α
k
−→ nmc(ini(ID
t
k
),C)} (14)
[
l = {1, . ..,r}
ID
i
α
l
−→ ID
t
l
∈ tr
1
(ID
i
)
ID
ch
∈ ch(ID
i
,C)
ID = nmc(ID
ch
,C)
{ID
α
l
−→ nmc(ini(ID
t
l
),C)} (15)
curr
C
= nmc(curr
C
,C) and ini
C
= nmc(ini(ini
C
),C).
For an example, the target XMI in Listing 4 is
equivalently represented as the component:
C = [{
hQ_A_ini,simple,
/
0,T
Q_A_ini
,Q_A_inii,
hQ_B,simple,
/
0,T
Q_B
,Q_Bi,
hQ_E,simple,
/
0,T
Q_E
,Q_Ei,
hR_A
0
_ini,simple,
/
0,T
R_A
0
,R_A
0
i,
hR_B
0
,simple,
/
0,T
R_B
0
,R_B
0
i,
hR_E
0
,simple,
/
0,T
R_E
0
,R_E
0
i,
hD,simple,
/
0,T
D
,Di
}
Q_B,Q_A_ini]
(16)
where, for instance, the transitions of the simple stm
Q_A_ini are
T
Q_A_ini
= {Q_A_ini
a−b
−−→ Q_B,
Q_A_ini
q−r
−−→ R_A
0
_ini,
Q_A_ini
q−e
0
−−→ R_E
0
}.
The “observational” semantics of Promela can be
now defined as in (7)–(10), based on a configuration
C
1
| ... | C
N
,
a set obs of executions, and the memory mem.
5 A PROOF OF CORRECTNESS
In this section we formalize the correctness of the
ATL transformation in Section 3, in terms of the
so-called observational equivalence of the associated
SysML and Promela XMI’s as in Sections 4.1 and 4.2.
Let MMS, MS, MMT and MT refer to the source
meta-model, source model, target meta-model and
target model, respectively, as in Section 3. We write
ATL(MMS,MS,MMT) = MT
as a shorthand for the aforementioned transformation.
Assume mem a memory-like structure whose vari-
ables could be initially set to the default value ⊥. Fur-
thermore, consider obs a set of observations. We write
|
i∈{1,...,N}
˜
C
i
mem obs
((7)−(10))
∗
−−−−−−−→
|
i∈{1,...,N}
˜
C
0
i
mem
0
obs
0
(17)
to denote the evolution of components
˜
C
i
, for i ∈
{1,..., N}, into
˜
C
0
i
, via the repeated application of
the semantic rules (7)–(10), given the memory mem
and a set of observations obs.
Intuitively, we say that a set of concurrent compo-
nents |
i∈{1,...,m}
C
i
are observational equivalent with
the concurrent components |
i∈{1,...,n}
C
i
whenever,
Correctness of an ATL Model Transformation from SysML State Machine Diagrams to Promela
369

given the same initial memory configuration, they
produce the same observations under the repeated ap-
plication of derivations
((7)−(10))
∗
−−−−−−−→.
Definition 1 (Observational Equivalence). Consider
a memory configuration mem and a set of observa-
tions obs. The concurrent components |
i∈{1,...,m}
C
i
are observational equivalent with the concurrent com-
ponents |
i∈{1,...,n}
C
i
whenever the following holds:
(a) If
|
i∈{1,...,m}
C
i
mem obs
((7)−(10))
∗
−−−−−−−→
|
i∈{1,...,m}
C
0
i
mem
0
obs
0
then there exists a derivation
|
i∈{1,...,n}
C
i
mem obs
((7)−(10))
∗
−−−−−−−→
|
i∈{1,...,n}
C
0
i
mem
0
obs
0
(b) Symmetrically.
We write |
i∈{1,...,m}
C
i
≈ |
i∈{1,...,n}
C
i
to denote
the observational equivalence above.
Theorem 1 (Correctness). Assume
ATL(MMS,MS,MMT) = MT.
Let |
i∈{1,...,N}
C
i
be the concurrent components asso-
ciated to MS, and |
i∈{1,...,N}
C
i
be the components of
MT. Then:
|
i∈{1,...,m}
C
i
≈ |
i∈{1,...,n}
C
i
.
Theorem 1 follows as a direct consequence of
Lemma 1.
Lemma 1. Assume
ATL(MMS,MS,MMT) = MT.
Let |
i∈{1,...,N}
C
i
denote the concurrent components
corresponding to MS, and |
i∈{1,...,N}
C
i
denote the
components of MT. Consider the initial memory con-
figuration mem and the initial set of observations obs.
Then:
(a) If
|
i∈{1,...,m}
C
i
mem obs
((7)−(10))
∗
−−−−−−−→
|
i∈{1,...,m}
C
0
i
mem
0
obs
0
then there exists a derivation
|
i∈{1,...,n}
C
i
mem obs
((7)−(10))
∗
−−−−−−−→
|
i∈{1,...,n}
C
0
i
mem
0
obs
0
(b) Symmetrically.
And, moreover,
nmc(curr
C
0
i
,C
0
i
) = curr
C
0
i
,∀i ∈ {1,... , N}.
for (a) and (b) above.
Observe that, apart from observational equiva-
lence, Lemma 1 guarantees equality of memory con-
tents and a one-to-one correspondence between the
current states of the SysML and Promela components.
Lemma 1 – Proof Sketch. The proof of both cases
“(a)” and “(b)” is by induction on the length of the
semantic rules derivation ((7) − (10))
∗
.
Remark 1. A direct consequence of Lemma 1 is that
observational equivalence coincides with trace equiv-
alence between the SysML models and the Promela
models. Hint: assume derivations
((7)−(10))
∗
−−−−−−−→ of
length 1.
6 DISCUSSION
In this paper we presented an ATL transforma-
tion from SysML hierarchical state-machines
into Promela, the input language of the SPIN
model-checker. The transformation is imple-
mented in an automated tool that can be found at
https://github.com/SysMLATL/SysMLPromelaTrans
formation
The ATL transformation is syntactic in na-
ture, whereas state-machines are inherently semantic.
Thus, the main challenge of our work consisted in fill-
ing the gap between the two worlds of syntax and
semantics, and proving the proposed transformation
correct. We chose to formulate the correctness result
in terms of a notion of observational equivalence be-
tween the SysML source models and the Promela tar-
get models. The interplay between syntax and seman-
tics can be better observed in the context of Lemma 1.
The proof of Lemma 1 shows that both models dis-
play the same observational behaviour by exploiting
the fact that the associated current states are in a one-
to-one correspondence which preserves the naming
convention characteristic to the flattening procedure
encoded within the ATL transformation.
We believe that our approach to proving correct-
ness can be easily adapted for similar ATL trans-
formations into the input languages of other model-
checkers. As future work we consider tackling more
such transformations.
It is beyond the scope of this paper to cover the
entire SysML. In this work, we mainly focused on
devising a methodology for proving semantic correct-
ness of the ATL syntactic transformation. Additional
aspects such as entry/exit behaviours, for instance,
could be handled in a rather straightforward fashion
by simply inserting additional states and transitions
MODELSWARD 2020 - 8th International Conference on Model-Driven Engineering and Software Development
370

labelled accordingly within the Promela model. Fur-
ther features of the SysML state-machines, such as
multiple-layer hierarchies, or time events, are left as
future work.
ACKNOWLEDGEMENTS
The work of Georgiana Caltais and Hargurbir Singh
was supported by the DFG project “CRENKAT”,
proj. no. 398056821.
REFERENCES
Amrani, M., Combemale, B., Lucio, L., Selim, G. M. K.,
Dingel, J., Traon, Y. L., Vangheluwe, H., and Cordy,
J. R. (2015). Formal verification techniques for
model transformations: A tridimensional classifica-
tion. Journal of Object Technology, 14(3):1:1–43.
Anastasakis, K., Bordbar, B., and Küster, J. (2007). Anal-
ysis of model transformations via alloy. In Baudry,
B., Faivre, A., Ghosh, S., and Pretschner, A., edi-
tors, Proceedings of the workshop on Model-Driven
Engineering, Verification and Validation (MoDeVVA
2007), Nashville, TN (USA), volume 5002, pages 47–
56. Springer.
Bengtsson, J., Larsen, K. G., Larsson, F., Pettersson, P., and
Yi, W. (1995). UPPAAL - a tool suite for automatic
verification of real-time systems. In Hybrid Systems,
volume 1066 of Lecture Notes in Computer Science,
pages 232–243. Springer.
Büttner, F., Egea, M., Cabot, J., and Gogolla, M. (2012).
Verification of ATL transformations using transfor-
mation models and model finders. In Aoki, T.
and Taguchi, K., editors, Formal Methods and Soft-
ware Engineering - 14th International Conference on
Formal Engineering Methods, ICFEM 2012, Kyoto,
Japan, November 12-16, 2012. Proceedings, volume
7635 of Lecture Notes in Computer Science, pages
198–213. Springer.
Cimatti, A., Clarke, E. M., Giunchiglia, E., Giunchiglia,
F., Pistore, M., Roveri, M., Sebastiani, R., and Tac-
chella, A. (2002). Nusmv 2: An opensource tool for
symbolic model checking. In CAV, volume 2404 of
Lecture Notes in Computer Science, pages 359–364.
Springer.
Clavel, M., Durán, F., Eker, S., Lincoln, P., Martí-Oliet, N.,
Meseguer, J., and Talcott, C. L. (2003). The Maude
2.0 system. In Nieuwenhuis, R., editor, Rewriting
Techniques and Applications, 14th International Con-
ference, RTA 2003, Valencia, Spain, June 9-11, 2003,
Proceedings, volume 2706 of Lecture Notes in Com-
puter Science, pages 76–87. Springer.
Dyck, J., Giese, H., Lambers, L., Schlesinger, S., and
Glesner, S. (2015). Towards the automatic verification
of behavior preservation at the transformation level
for operational model transformations. In Dingel, J.,
Kokaly, S., Lucio, L., Salay, R., and Vangheluwe, H.,
editors, Proceedings of the 4th Workshop on the Anal-
ysis of Model Transformations co-located with the
18th International Conference on Model Driven Engi-
neering Languages and Systems (MODELS 2015), Ot-
tawa, Canada, September 28, 2015., volume 1500 of
CEUR Workshop Proceedings, pages 36–45. CEUR-
WS.org.
Engels, G., Kleppe, A., Rensink, A., Semenyak, M.,
Soltenborn, C., and Wehrheim, H. (2008). From UML
activities to TAAL - towards behaviour-preserving
model transformations. In Schieferdecker, I. and Hart-
man, A., editors, Model Driven Architecture - Foun-
dations and Applications, 4th European Conference,
ECMDA-FA 2008, Berlin, Germany, June 9-13, 2008.
Proceedings, volume 5095 of Lecture Notes in Com-
puter Science, pages 94–109. Springer.
Harel, D. (1987). Statecharts: A visual formalism for com-
plex systems. Sci. Comput. Program., 8(3):231–274.
Holzmann, G. J. (2004). The SPIN Model Checker - primer
and reference manual. Addison-Wesley.
Jackson, D. (2019). Alloy: a language and tool for explor-
ing software designs. Commun. ACM, 62(9):66–76.
Jouault, F., Allilaire, F., Bézivin, J., and Kurtev, I. (2008).
ATL: A model transformation tool. Sci. Comput. Pro-
gram., 72(1-2):31–39.
Kölbl, M., Leue, S., and Singh, H. (2018). From SysML
to Model Checkers via Model Transformation. In
Gallardo, M. and Merino, P., editors, Model Check-
ing Software - 25th International Symposium, SPIN
2018, Malaga, Spain, June 20-22, 2018, Proceedings,
volume 10869 of Lecture Notes in Computer Science,
pages 255–274. Springer.
Kwiatkowska, M. Z., Norman, G., and Parker, D. (2004).
Probabilistic symbolic model checking with PRISM:
a hybrid approach. STTT, 6(2):128–142.
Lano, K., Clark, T., and Rahimi, S. K. (2015). A frame-
work for model transformation verification. Formal
Asp. Comput., 27(1):193–235.
Latella, D., Majzik, I., and Massink, M. (1999). Automatic
verification of a behavioural subset of UML statechart
diagrams using the SPIN model-checker. Formal Asp.
Comput., 11(6):637–664.
Liu, S., Liu, Y., André, É., Choppy, C., Sun, J., Wadhwa,
B., and Dong, J. S. (2013). A formal semantics for
complete UML state machines with communications.
In Johnsen, E. B. and Petre, L., editors, Integrated
Formal Methods, 10th International Conference, IFM
2013, Turku, Finland, June 10-14, 2013. Proceedings,
volume 7940 of Lecture Notes in Computer Science,
pages 331–346. Springer.
Mikk, E., Lakhnech, Y., Siegel, M., and Holzmann,
G. J. (1998). Implementing statecharts in PROME-
LA/SPIN. In 2nd Workshop on Industrial-Strength
Formal Specification Techniques (WIFT ’98), Octo-
ber 20-23, 1998, Boca Raton, FL, USA, pages 90–101.
IEEE Computer Society.
Object Management Group (2015). XML
metadata interchange, specification 2.5.1.
http://www.omg.org/spec/XMI/.
Object Management Group (2017a). OMG Sys-
tems Modeling Language, Specification 1.5.
http://www.omg.org/spec/SysML.
Correctness of an ATL Model Transformation from SysML State Machine Diagrams to Promela
371

Object Management Group (2017b). Unified
Modelling Language, Specification 2.5.1.
http://www.omg.org/spec/UML.
Rensink, A. (2006). Model checking quantified computa-
tion tree logic. In Baier, C. and Hermanns, H., editors,
CONCUR 2006 - Concurrency Theory, 17th Interna-
tional Conference, CONCUR 2006, Bonn, Germany,
August 27-30, 2006, Proceedings, volume 4137 of
Lecture Notes in Computer Science, pages 110–125.
Springer.
Troya, J. and Vallecillo, A. (2011). A rewriting logic se-
mantics for ATL. Journal of Object Technology, 10:5:
1–29.
Weise, C. (1997). An incremental formal semantics for
PROMELA. In In Proceedings of the Third SPIN
Workshop, SPIN97.
MODELSWARD 2020 - 8th International Conference on Model-Driven Engineering and Software Development
372
