CLARVA: Model-based Residual Veriﬁcation of Java Programs

Shaun Azzopardi

, Christian Colombo and Gordon Pace

Department of Computer Science, Faculty of ICT, University of Malta, Msida, Malta

Keywords:

Veriﬁcation, Model-based Analysis, Residual Analysis, Static Analysis.

Abstract:

Runtime veriﬁcation (RV) is an established approach that utilises monitors synthesized from a property lan-

guage (e.g. temporal logics or some form of automata) to observe program behaviour at runtime, determining

compliance of the program with the property at runtime. An issue with RV is that it introduces overheads at

runtime, while identifying a violation at runtime may be too late. This can be tackled by introducing light

analyses that attempt to prove parts of the property with respect to the program, leaving a residual property

that induces a smaller monitoring footprint at runtime and encodes some static guarantees. In this paper we

present CLARVA as a tool developed for this end for the RV tool LARVA. CLARVA transforms Java code

into an automaton-based model, and allows for the incorporation of control-ﬂow analyses that analyse this

model against Dynamic Automata with Timers and Events or DATES (the property language used by LARVA)

to produce residuals that produce an equivalent judgement at runtime.

1 INTRODUCTION

Veriﬁcation methods can be applied on an program

before or after its deployment. Ideally veriﬁcation is

done pre-deployment to ensure a misbehaving pro-

gram is not deployed, however precise formal ver-

iﬁcation before deployment can be expensive while

parts of the program may be dynamic or unknown

pre-deployment. Runtime veriﬁcation (RV) (Leucker

and Schallhart, 2009) is one approach to performing

post-deployment veriﬁcation by instrumenting an ap-

plication with a monitor that attempts to give a verdict

about the program’s compliance by analysing an exe-

cution preﬁx. However using only RV means no static

guarantees about the program can be given, while

RV introduces time and memory overheads at runtime

when performed synchronously with the program. In

this paper we present a tool addressing both of these

problems for LARVA, an established tool for the run-

time veriﬁcation of Java programs.

The LARVA (Colombo et al., 2009) approach ex-

pects speciﬁcations in the form of dynamic automata

with timers and events, or DATEs. This language al-

lows the developer to identify a set of program events

using AspectJ pointcuts (Kiczales et al., 2001), and an

automaton that captures the prohibited event traces.

These events are symbolic with parameters that are

only bound at runtime (Havelund et al., 2018). Tran-

https://orcid.org/0000-0002-2165-3698

sitions are triggered by such events, while they are

guarded by a condition on the program and monitor

variable state while possibly acting on the monitor

state (e.g. the monitor may keep a counter of the

times a certain method is called, prohibiting a cer-

tain number of subsequent calls). Moreover DATEs

allow for time-triggered events, and also for commu-

nication between multiple DATEs through channels,

making them more succinct and modular than simple

ﬁnite-state automata.

The runtime overheads induced by the LARVA ap-

proach is thus proportional to the number of times

DATE transitions are triggered at runtime and to the

expense of executing transition guards and actions.

There are several options for reducing runtime over-

heads then:

(i) reducing the number of times a program triggers

an event;

(ii) reducing the number of DATE transitions; and

(iii) reducing or optimising DATE transition guards

and actions.

Previous work considers sound approaches to per-

forming these reductions (Azzopardi et al., 2017),

with residual analyses ensuring that the reduced mon-

itor observations are equivalent to those of the origi-

nal, at least with respect to the program in question.

In this paper we introduce CLARVA (Azzopardi,

2019), a tool that is able to incorporate analyses that

352

Azzopardi, S., Colombo, C. and Pace, G.

CLARVA: Model-based Residual Veriﬁcation of Java Programs.

DOI: 10.5220/0008966603520359

In Proceedings of the 8th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2020), pages 352-359

ISBN: 978-989-758-400-8; ISSN: 2184-4348

effect such sound reductions based on a control-ﬂow

model of a Java program. CLARVA is thus intended

to be used for relatively inexpensive pre-deployment

analyses that produce a residual of a DATE and a pro-

gram with residual instrumentation that can be pre-

pared for deployment by LARVA. This was inspired

by CLARA (Bodden et al., 2010), a tool for similar

analyses but limited to ﬁnite-state automata and re-

ductions of instrumentation.

In Section 2 we discuss brieﬂy the background and

theoretical framework underpinning CLARVA, while

in Section 3 we discuss the architecture and process

of the tool. We illustrate the tool using a case study

in Section 4, discuss related work in Section 5, and

conclude in Section 6.

2 BACKGROUND

In this section we discuss some of the theoretical and

practical background behind CLARVA, introducing

brieﬂy LARVA (Colombo et al., 2009), how we model

programs, and a brief description of residual analyses.

2.1 The LARVA Approach

Common languages for speciﬁcations in the RV com-

munity can largely be classiﬁed as either logic- or

automata- based, with automata being also commonly

used behind the implementation of logic-based ap-

proaches, or as event- or state-based (Falcone et al.,

2018). LARVA falls under the event-based approaches

that use automata directly as the main speciﬁcation

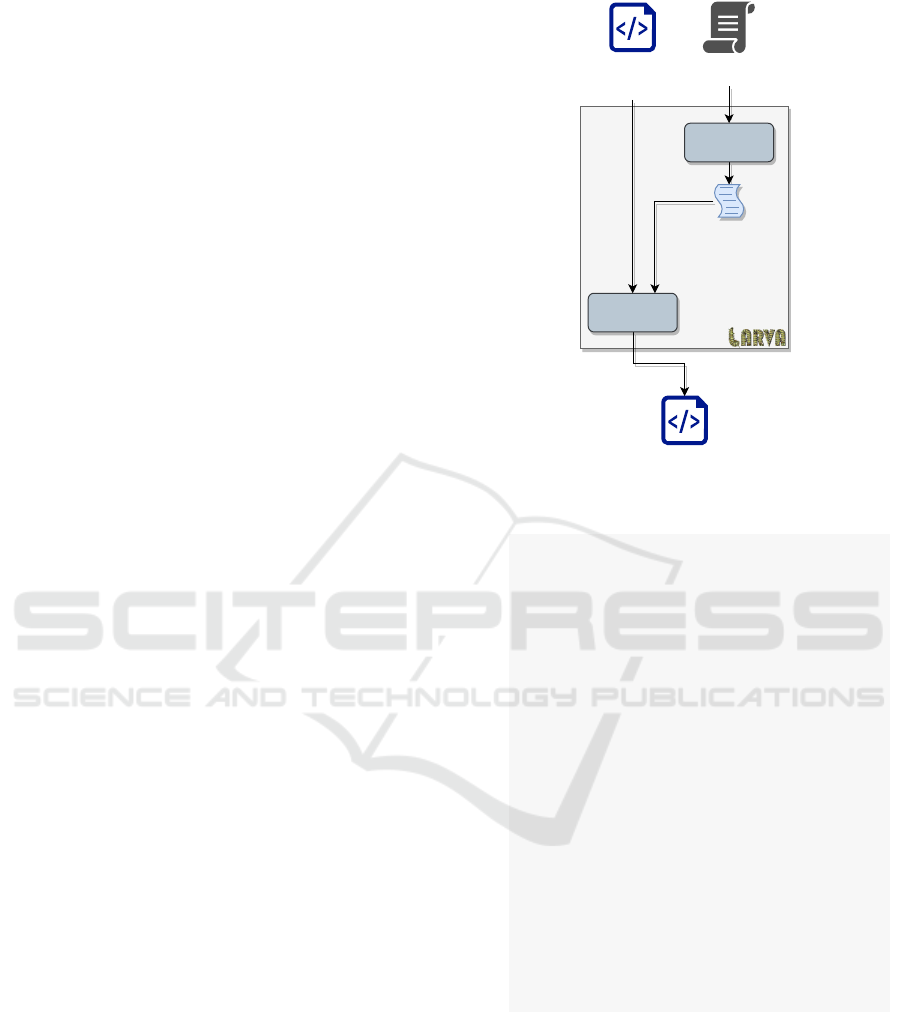
language. Figure. 1 illustrates a high-level view of

the process LARVA undertakes to produced a moni-

tored program. Here we discuss how LARVA handles

monitoring for program events and how the speciﬁca-

tion logic is represented using dynamic automata with

events and timers (DATEs). Listing. 1 is an example

of the LARVA speciﬁcation language, which we use

throughout this section.

2.1.1 Program Events

LARVA uses AspectJ pointcuts to allow the speciﬁca-

tion engineer ﬂexibility in specifying program events

of interest independent of the program implementa-

tion. These event deﬁnitions currently correspond to

Java method calls, with different matching modalities

(e.g. before the call, after, upon returning, or upon

throwing). For example, the LARVA event declaration

on lines 7-9 in Listing. 1 matches any return from a

call to a method named login and that has an integer

id parameter.

Monitored

Program

Code

DATE compiler

Event and

Business Logic

Advice

DATE

Script

AspectJ

compiler

Java

Program

Code

Figure 1: LARVA process.

1 GLOBAL{

2 VARIABLES{

3 i n t l i m i t = 25 0 ;

4 }

5 FOREACH( Us e r u ) {

6 EVENTS{

7 l o g i n ( User u1 )

8 = {

. l o g i n ( i n t i d ) u p o n R et u r n i n g

( ) }

9 whe r e { u1 = u s e r s . g e t ( i d ) ; u = u1 ; }

10 . . .

11 }

12 PROPERTY u s e r B e h a v i o u r {

13 STATES{

14 ACCEPTING { goo d }

15 BAD { bad}

16 NORMAL { l o g g e d I n }

17 STARTING { l o gg e dO u t }

18 }

19 TRANSITIONS{

20 l o gg e d I n −>lo g g ed O u t [ l o g i n ( u1 ) \ u1 .

a c t i v a t e d \ ]

21 . . .

22 }}}}

Listing 1: Partial view of a LARVA script.

The left-hand side of this declaration represents

the event as will be used in the DATE. Note how this

event is symbolic in that it is instantiated at runtime

with some program data (see Line 9). The right-hand

side syntax is close to that used by AspectJ for point-

cuts. The syntax also allows for a single DATE event

(left-hand declaration) to correspond to multiple pro-

gram events.

CLARVA: Model-based Residual Veriﬁcation of Java Programs

353

2.1.2 DATEs

Finite-state automata are traditionally parametrised

by a ﬁnite set of events, with transitions tagged by

these events and the automaton representing the ac-

ceptable set of event traces. As discussed in the pre-

vious section, events here are instead symbolic in that

they may have attached certain information about the

program. The event set here effectively is not ﬁnite —

note how for arbitrary n ∈ N then login(n) is an indi-

vidual event. The automata used by LARVA, DATEs,

are then forms of symbolic automata that are able to

deal with this inﬁnite set of events with a ﬁnite set of

states and transitions. Moreover DATEs allow us to

maintain some internal monitoring variable state, ef-

fectively allowing for a more succinct representation

than ﬁnite-state automaton.

A DATE transition is of the form: q− > q

[e\c\a],

where q and q

are automata states, e is a symbolic

event, c is a predicate on the event parameters (which

are bound at runtime) and the monitoring variable

state, and a is a transformation of the monitoring vari-

able state. For example, Line 20 in Listing. 1 deﬁnes

a transition that allows a user to login only when the

user account’s activated attribute is true.

2.1.3 Typestate

A concern in RV is that of typestate, where a monitor

is intended to be replicated for each object of a certain

type. For example, given a Stream object one may

want to ensure that each such object is not used after

it is closed. In this case typestate logic is used to en-

sure that a monitor is instantiated for each such object

at runtime, where the monitor only listens to events of

the object they are associated with. This functionality

is also present for DATEs, through the FOREACH con-

struct. In Listing. 1 Line 5 illustrates how the property

deﬁned by the script is parametrised by a User types-

tate, with each event identifying the relevant user (see

Line 9).

2.2 Modeling Programs

DATEs abstract away from program details through

DATE events. In the same manner when perform-

ing static analysis of a program it is ideal to work

at this level of abstraction rather than at the level

of program code. Moreover, since our speciﬁca-

tions are automata-based, representing programs in

an automata-based formalism allows us to exploit the

rich theory behind automata in performing veriﬁca-

tion and analysis. In CLARVA we choose to inter-

nally represent Java methods as non-deterministic au-

tomata with states representing Java statements and

transitions tagged with DATE events. A program is

thus represented as a set of such automata.

These automata in effect represent an over-

approximation of the possible execution traces of the

program. This is only sound and not complete be-

cause we are ignoring program data-ﬂow. In Section 4

we illustrate an example of such automata and their

corresponding Java methods.

2.3 Residual Analysis

CLARVA is essentially a tool for what we call residual

analysis. Here we give a brief semi-formal introduc-

tion to this approach.

The veriﬁcation problem is essentially whether a

program P satisﬁes a property π, which we denote by

P ` π. Residual analysis, given a program P, is con-

cerned with the reduction of the property π to a prop-

erty π

such that π and π

are interchangeable for the

purposes of veriﬁcation, i.e.

P ` π ⇐⇒ P ` π

This reduction does not occur blindly but by con-

sidering the known properties of the system, in effect

in the form of a model of the system (Azzopardi et al.,

2016). Then, a residual operation can take into ac-

count this model when producing a residual property.

This can be represented as follows, where the residual

operation is denoted by the symbol \:

P ` M =⇒ (P ` π \ M ⇐⇒ P ` π).

This notion allows us to use π \ M instead of π for

the purposes of veriﬁcation, with the guarantee that

the result is equivalent to verifying π, for any pro-

gram satisfying M. One question is how to acquire the

model M. An option is through analysis (which we do

in CLARVA by creating an automaton representation

of the program), while in other cases the program P

may be synthesized from an existing model M.

This condition is however too wide for the pur-

poses of RV. Consider that RV is concerned with the

compliance of single execution traces, while our ver-

iﬁcation operator here (`) is concerned with the com-

pliance of the whole program. Then, the residual con-

dition here does not guarantee that an event trace of

P will be given the same verdict by π \ M as by π.

Instead we can reﬁne this by considering the event

traces (with events from an alphabet A

) induced by

a program using an operator: T (P) : 2

∗

, and a trace

Note that here A represents a set of events. These events

can also be symbolic, e.g. the events may be associated with

a snapshot of the program variable state.

MODELSWARD 2020 - 8th International Conference on Model-Driven Engineering and Software Development

354

compliance operator 

P ` M =⇒ (∀t ∈ T (P) ·t  π \ M ⇐⇒ t  π).

This correctness condition is what we require

out of any property residual analysis included in

CLARVA, to ensure any reduced property can be used

for RV without any unexpected behaviour.

The overheads of RV are not associated only

with the property being monitored, but also with the

amount of instrumentation inserted into the program

to trigger property events. To model this consider that

a program P can be represented by a set of executions

(where STMT is the type of statements) Ex ⊆ 2

STMT

∗

and then instrumentation can be modeled as a func-

tion from executions to event traces inst

: STMT

∗

7→

∗

. Finally an instrumentation reduction of a program

with respect to a property, i.e. the function inst

P\π

, is

correct only if the event trace induced by an execution

preﬁx by both instrumentation functions is given the

same verdict by π (using pre for a function that gives

all the preﬁxes of a set of traces):

∀e ∈ pre(Ex) · inst

(e)  π ⇐⇒ inst

P\π

(e)  π.

This correctness condition for instrumentation re-

ductions ﬁnalises our brief treatment of the residual

analysis CLARVA incorporates. For a more in depth

treatment see (Azzopardi et al., 2017).

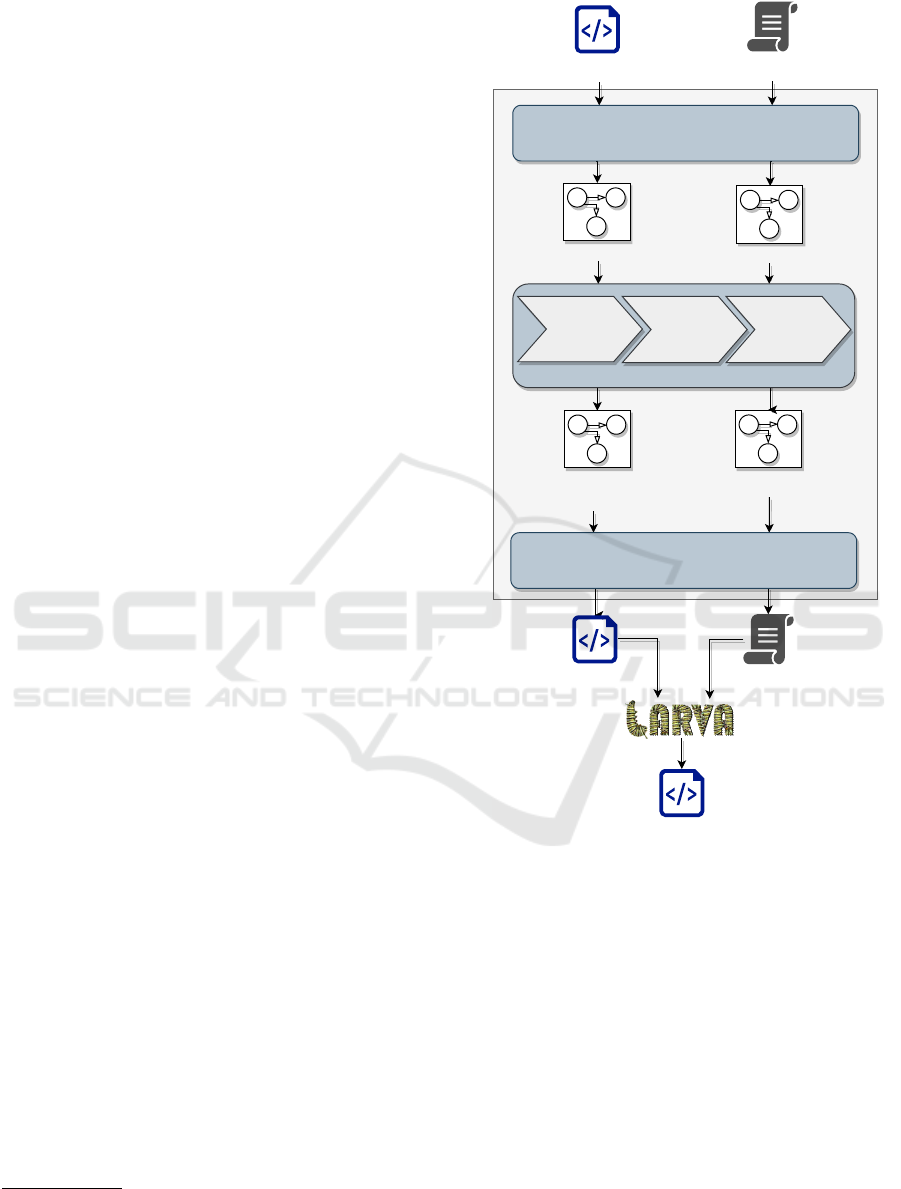
3 ARCHITECTURE

The CLARVA process is made up of three different

phases (Figure. 2): (i) the abstraction phase where the

Java code and LARVA script are abstracted into au-

tomata models; (ii) the residual analysis phase where

different residual analyses are applied in succession;

and (iii) the concretisation phase where the internal

representations are transformed into executable for-

mat.

During the abstraction phase the input program

and LARVA script are abstracted respectively by a

control-ﬂow model (as described in Section 2.2) and

a DATE (as described in Section 2.1.2). In the ab-

straction of programs the Java bytecode analyser Soot

(Vall

ee-Rai et al., 1999) is used to analyse the pro-

gram code and structure to create appropriate au-

tomata models of the program methods while the

DATE events are used to instrument these automata

with events. The resulting automata represent an

over-approximation of the execution traces of the pro-

gram at runtime with respect to the given DATE.

We require the condition that a program is compliant

with a property iff all its traces are also compliant with the

property: P ` π ⇐⇒ ∀t ∈ T (P) ·t  π.

DATE

Program Model

Residual

DATE

Program Model

with Residual

Instrumenation

Residual

Program

Code

Residual

Larva

Script

Optimised

Monitored

Program

Code

Program

Code

Larva

Script

Abstraction

Absent

Event

Analysis

Typestate

Absent

Event

Analysis

Control-Flow

Analysis

Residual Analysis

Concretisation

Figure 2: CLARVA process.

The residual analysis phase incorporates a number

of residual analyses, as described in (Azzopardi et al.,

2017), obeying the conditions deﬁned in Section 2.3.

These analyses compare the program model with the

DATE to produce reduced version of each. For ex-

ample, absent event analysis analyses the model to

identify events used by the DATE but not actually

triggered by the program and reducing the DATE ap-

propriately. The subsequent analyses introduce more

precision, e.g. typestate absent event analysis projects

the same analysis for every possible runtime typestate

object, and control-ﬂow analysis uses composition of

program and property automata to identify transitions

in the DATE that are never activated for any typestate.

CLARVA: Model-based Residual Veriﬁcation of Java Programs

355

Dually these can be used to identify instrumentation

points in the program that can be silenced (i.e. such

that they do not trigger events at runtime). These anal-

yses are subsequently more precise, using imprecise

and cheaper analyses to possibly reduce the expense

of the next stage. These analyses are performed mul-

tiple times until a ﬁx-point is reached. New residual

analyses can be introduced at this stage to create ﬁner

residuals.

The concretisation phase is the dual of the abstrac-

tion phase, using the internal abstractions to output a

Java program with optimised instrumentation and an

optimised monitor. The instrumentation identiﬁed as

unnecessary by the residual analysis phase is used to

transform the original Java code such that function

calls triggering events unnecessarily do not trigger

events after LARVA instrumentation. This transforma-

tion does not change the program behaviour although

it does introduce a new Java class through which calls

which should be instrumented pass through. The

residual LARVA script instruments methods in this

class instead of the original methods, while the mon-

itoring logic may also be reduced, when the analysis

phase proves the program cannot explore parts of the

DATE, and those parts of the DATE can be pruned.

4 CASE STUDY

Here we consider a case study to illustrate the

CLARVA approach. Listing. 2 illustrates the code of

a simple transaction menu that allows a user to lo-

gin, logout, transact, deposit, and delete their account,

while upon the user requesting deletion, their account

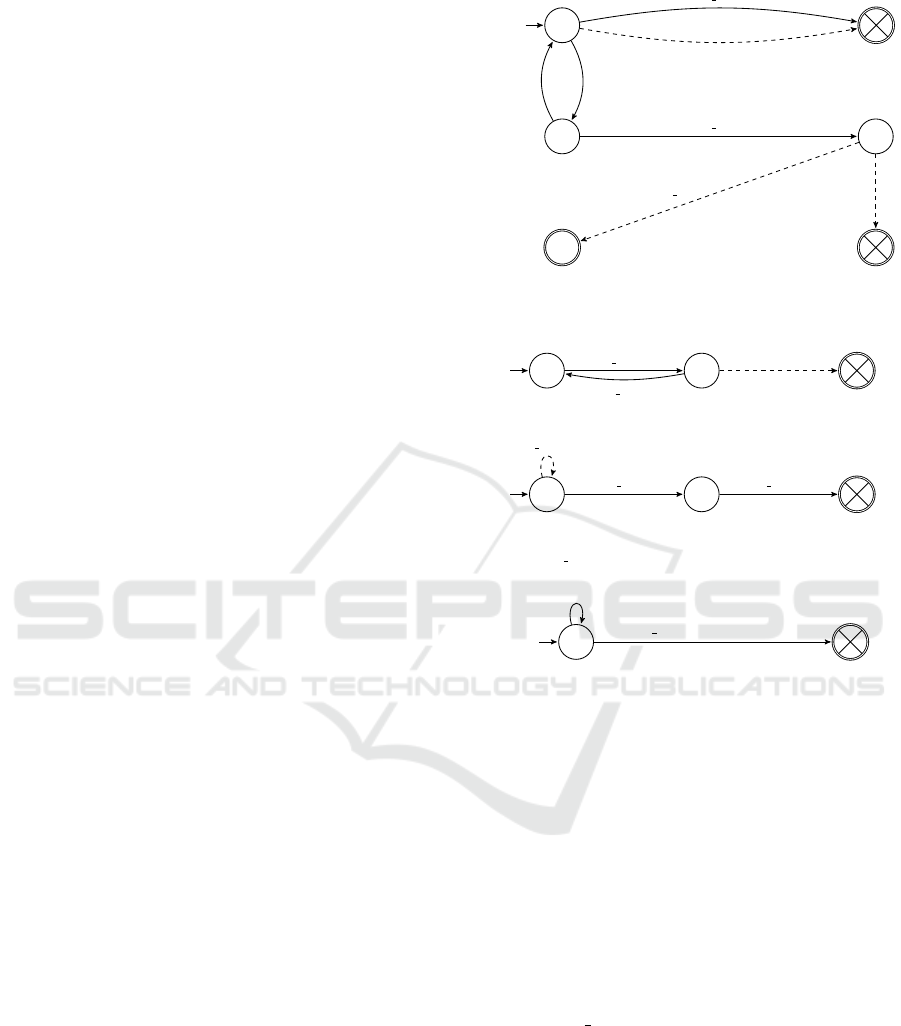
is removed from the list of users. Figure. 3 illustrates

a speciﬁcation for this program, where if the user is

logged out they are not allowed to delete account or

withdraw any funds, while they have a transaction

limit when logged in. Moreover during the process

of user deletion no deposits into the user’s account

are allowed.

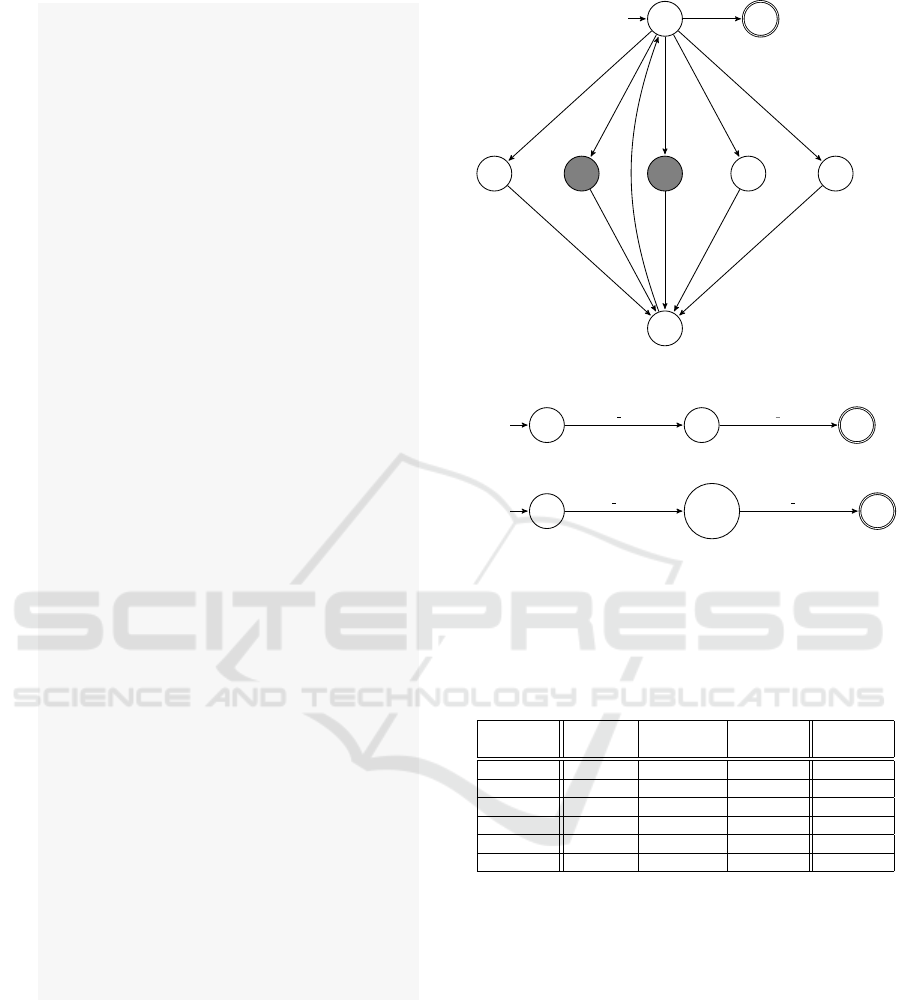
CLARVA processes the program Listing. 2 to pro-

duce automata for each method similar to those illus-

trated in Figure. 4. For illustration purposes these au-

tomata are more concise than those actually produced

by CLARVA, however they are equivalent language-

wise. Note also how the states of these automata are

annotated by the relevant program statement.

By analysing the DATE in Figure. 3a against the

models in Figure. 4 CLARVA’s analyses manage to:

(i) identify that the withdraw event is never actually

triggerable in the methods (note how it is never

called) and thus the withdraw transition in the

DATE can be safely removed;

start

delete enter(u)

withdraw(u)

logout(u)

delete enter(u)

deposit(u, val)

delete exit(u)

(a) Deletion and withdrawal only allowed after login of

an activated user, while no deposits are permitted during

deletion.

start

transact enter(u,val)

transact exit(u,val)

*(u)

(b) transact is atomic.

start

transact enter(u,val)

delete enter(u) transact enter(u,val)

start

transact enter(u,val)

| val +bal ≤ lim

7→ bal+ = val;

transact enter(u,val) | val + bal > lim

(d) transact respects limits.

Figure 3: Several properties expected out of Listing. 2,

with dashed transitions representing transitions removed af-

ter residual analysis.

(ii) that the delete method does not call the deposit

method and thus the respective transition can be

removed from the DATE;

(iii) since the deposit event is no longer used in the

residual DATE, the deposit event instrumented in

the menu method can be silenced (see Figure. 4a);

and

(iv) by analysing the DATE CLARVA identiﬁes that

the delete exit event does not need to be mon-

itored, since the residual DATE cannot violate

when at state q

and thus we can remove the re-

spective DATE transition and event instrumenta-

tion in the program. Similarly for Figure. 3b we

can determine that no other event occurs during a

transaction.

This purely control-ﬂow analysis however fails

for properties that require information about the pro-

gram’s variable state after an event occurs, e.g. to

MODELSWARD 2020 - 8th International Conference on Model-Driven Engineering and Software Development

356

1 Map<I n t e g e r , User> u s e r s ;

3 p u b l i c v o id menu ( ) {

4 i n t o p t i o n ;

5 User u ;

6 b o o l ean open = t r ue ;

7 . . .

8 w hi l e ( open ) {

9 sw i t c h ( o p t i o n ) {

10 c a s e 0 : i n t i d = /* get fr om inp ut */ ;

11 u = l o g i n ( i d ) ;

12 br eak ;

13 c a s e 1 : i f ( u ! = n u l l ) l o g o u t ( u . i d ) ;

14 br eak ;

15 c a s e 2 : i f ( u ! = n u l l ) {

16 f l o a t v a l = /* get f rom in put

*/ ;

17 i n t t o = /* get fr om input

*/ ;

18 i n t fr om = u . i d ;

19 i f ( u . b a l a n c e >= v a l )

20 t r a n s a c t ( from , to , v a l ) ;

21 }

22 br eak ;

23 c a s e 3 : i f ( u ! = n u l l ) {

24 f l o a t v a l = /* get f rom in put

*/ ;

25 i n t t o = u . i d ;

26 d e p o s i t ( t o , v a l ) ;

27 }

28 br eak ;

29 c a s e 4 : i f ( u ! = n u l l ) d e l e t e ( u ) ;

30 br eak ;

31 c a s e 5 : ope n = f a l s e ;

32 }

33 }

34 }

36 p u b l i c v o id d e l e t e ( U s e r u ) {

37 u s e r s . re mov e ( u ) ;

38 }

40 p u b l i c v o id t r a n s a c t ( i n t from , i n t to ,

41 double v a l ) {

42 i f ( u s e r s . g e t ( fro m ) . b a l >= v a l

43 && u s e r s . c o n t a i n s K e y ( t o ) ) {

44 u s e r s . g e t ( fr o m ) . b a l −= v a l ;

45 u s e r s . g e t ( t o ) . b a l += v a l ;

46 }

47 }

Listing 2: Example Java Program.

prove Figure. 3c we need to be able to determine that

after a delete the deleted user is no longer present

in the system and thus can no longer be acted upon.

However we can optimise the DATE by removing the

looping transition on the initial state, since it does not

have any effect. Another challenge is the variable

state of the DATE, e.g. consider Figure. 3d where

transitioning in the DATE depends on a bal variable

maintained by the DATE.

start

1320

logout(u)

deposit(u,val)

(a) menu method, with states 20 and 26 being call states,

respectively calling the transact and delete methods.

start

delete enter(u) delete exit(u)

(b) delete method.

start

38 −42

transact enter(u,val) transact exit(u,val)

Figure 4: Non-deterministic models of Listing. 2 methods,

with shaded states representing call states, and faded events

representing instrumentation silenced after analysis.

Table 1: Evaluation data of Figure. 3 monitored with and

without residual analysis, compared to without monitoring.

Users No. Original Monitored Residual. Savings

seconds % of orig. % of orig. % of mon.

500 30.86s 313.12% 261.31% 16.55%

600 35.11s 335.06%% 266.56% 20.44

700 40.98s 339.85% 262.57% 22.74%

800 47.17s 333.178% 275.98% 17.17%

900 53.04s 334.30% 272.61% 18.4%

1000 58.91s 334.19% 266.71% 20.19%

This case study was evaluated with a test harness

that creates a number of users with some initial de-

posit, that perform a number of transactions during

their lifetime, after which they are deleted. As a range

we chose to look at between 500 to 1000 users, with

increments of 100. We measured the time taken for

the test scenarios to execute:

(i) without monitoring;

(ii) with monitoring the original properties; and

(iii) with monitoring the residual properties.

We then computed the percentage of time saved

by the residual analysis by computing the difference

between time taken with the original monitoring as a

percentage of the latter time overheads.

CLARVA: Model-based Residual Veriﬁcation of Java Programs

357

Table. 1 shows the results of this benchmarking,

showing the increase in load to the transaction sys-

tem on the number of users increasing. However the

results show the monitoring overheads to remain rel-

atively stable even given the increase in load. The

residual analysis reduced the monitoring overheads

signiﬁcantly in this case (around 20%), however the

remaining overheads remain large. We do not mea-

sure the time taken for CLARVA to produce the resid-

uals since this was negligible.

We conclude that residual analysis can be useful in

reducing the overheads associated with runtime veriﬁ-

cation. This is however conditional on what the resid-

ual analysis manages to prove and prune. This exper-

iment’s artifacts, along with other case studies, can be

found in the CLARVA repository (Azzopardi, 2019).

5 RELATED WORK

CLARVA was inspired by CLARA (Bodden et al.,

2010), CompiLe-time Approximation of Runtime

Analyses, a tool for reducing the runtime overheads

required for monitoring properties representable as a

ﬁnite-state automaton. CLARA is a framework for

static analyses that optimise the program event instru-

mentation required to monitor a property by analysing

the control-ﬂow of the program. The ﬁrst two analy-

ses included in CLARVA, see Figure. 2, in fact are

inspired by existing CLARA analyses, while the third

analysis is novel. Unfortunately CLARA is no longer

maintained, while it uses an aspect weaver, abc (Al-

lan et al., 2005), that is also no longer maintained.

This motivated us to develop our own tool rather than

extending CLARA with DATEs. Moreover CLARA

only deals with residual instrumentation and does not

analyse properties in any meaningful manner to en-

code the static guarantees given by its analyses, unlike

CLARVA.

CLARVA currently only incorporates control-ﬂow

analysis for DATEs, since the program model (non-

deterministic automata) does not maintain any knowl-

edge about the program data-ﬂow. Work already ex-

ists to analyse the data-oriented aspects of a DATE

(i.e. transition guards) against the program, namely

that of STARVOORS (Chimento et al., 2015) (uniﬁed

STAtic and Runtime Veriﬁcation of Object-Oriented

Software) (Chimento et al., 2015). This tool uses

a syntactic superset of DATEs, namely ppDATEs,

that extend DATEs by allowing states to be tagged

by Hoare triples over method calls. However, a pp-

DATE is semantically equivalent to a set of DATEs;

in fact they are translated into DATEs for monitoring.

STARVOORS uses the Java theorem prover KEY

(Ahrendt et al., 2016) to prune these Hoare triples or

to make the conditions weaker, reducing what must

be proven at runtime by reducing the property. How-

ever STARVOORS does not consider attack program

instrumentation reductions directly, unlike CLARVA.

There is other work that uses a similar notion of a

property residual. (Dwyer and Purandare, 2008) anal-

yses the control-ﬂow of a program against a ﬁnite-

state automaton to identify sequences of statements

that always trigger the same behaviour in the prop-

erty. A summary-based approach here is used where

the instrumentation of such sequences is replaced by

new event symbols representing entry and exit into it

and appropriate transitions added to the automaton.

This is different from our approach where we simply

reduce the property and do not transform it.

Different work by (Lal et al., 2007; Beyer et al.,

2018) creates a residual program, in effect the part

of the program that was not proven safe by the anal-

ysis. In CLARVA we simply reduce instrumentation

and do not change program behaviour, while in this

other work the program is transformed into a smaller

program.

6 CONCLUSIONS AND FUTURE

WORK

In this paper we have introduced a tool, CLARVA,

for the static analysis of monitors based on symbolic

automata. This tool gives static guarantees by both

reducing the monitor logic left to prove at runtime

and by reducing the event instrumentation required of

the program. CLARVA currently incorporates control-

ﬂow analyses of the program by analysis of properties

against non-deterministic automata representations of

program methods.

Future iterations of the tool are planned to ex-

tend the process to be able to deal with communi-

cation between different DATEs. This is envisioned

to be possible through composing these communi-

cating DATEs. Another area for improvement is the

incorporation of data-ﬂow analysis by extending the

program model with data-oriented aspects, allowing

for more precise analysis and smaller residual proper-

ties. We explored this theoretically in another pub-

lication (Azzopardi et al., 2020), however we have

yet to implement this in CLARVA. We also plan

to apply the same approach to different program-

ming paradigms, including the LARVA variant for the

Ethereum blockchain (Azzopardi et al., 2018).

MODELSWARD 2020 - 8th International Conference on Model-Driven Engineering and Software Development

358

REFERENCES

Ahrendt, W., Beckert, B., Bubel, R., H

ahnle, R., Schmitt,

P. H., and Ulbrich, M., editors (2016). Deductive Soft-

ware Veriﬁcation - The KeY Book - From Theory to

Practice, volume 10001 of Lecture Notes in Computer

Science. Springer.

Allan, C., Avgustinov, P., Christensen, A. S., Hendren,

L., Kuzins, S., Lhot

ak, J., Lhot

ak, O., de Moor, O.,

Sereni, D., Sittampalam, G., and Tibble, J. (2005).

abc: The aspectbench compiler for aspectj. In Gl

uck,

R. and Lowry, M., editors, Generative Programming

and Component Engineering, pages 10–16, Berlin,

Heidelberg. Springer Berlin Heidelberg.

Azzopardi, S. (2019). CLARVA. https://github.com/

shaunazzopardi/clarva/.

Azzopardi, S., Colombo, C., and Pace, G. J. (2016). A

model-based approach to combining static and dy-

namic veriﬁcation techniques. In Leveraging Applica-

tions of Formal Methods, Veriﬁcation and Validation:

Foundational Techniques - 7th International Sympo-

sium, ISoLA 2016, Imperial, Corfu, Greece, October

10-14, 2016, Proceedings, Part I, pages 416–430.

Azzopardi, S., Colombo, C., and Pace, G. J. (2017).

Control-ﬂow residual analysis for symbolic automata.

In Francalanza, A. and Pace, G. J., editors, Proceed-

ings Second International Workshop on Pre- and Post-

Deployment Veriﬁcation Techniques, Torino, Italy, 19

September 2017, volume 254 of Electronic Proceed-

ings in Theoretical Computer Science, pages 29–43.

Open Publishing Association.

Azzopardi, S., Colombo, C., and Pace, G. J. (2020). A

technique for automata-based veriﬁcation with resid-

ual reasoning. In Model-Driven Engineering and

Software Development - 8th International Conference,

MODELSWARD 2020, Valletta, Malta, February 25-

27, 2020.

Azzopardi, S., Ellul, J., and Pace, G. J. (2018). Monitoring

smart contracts: CONTRACTLARVA and open chal-

lenges beyond. In The 18th International Conference

on Runtime Veriﬁcation.

Beyer, D., Jakobs, M.-C., Lemberger, T., and Wehrheim,

H. (2018). Reducer-based construction of conditional

veriﬁers. In Proceedings of the 40th International

Conference on Software Engineering, ICSE ’18, pages

1182–1193, New York, NY, USA. ACM.

Bodden, E., Lam, P., and Hendren, L. (2010). Clara: A

framework for partially evaluating ﬁnite-state runtime

monitors ahead of time. In Barringer, H., Falcone,

Y., Finkbeiner, B., Havelund, K., Lee, I., Pace, G.,

Ros¸u, G., Sokolsky, O., and Tillmann, N., editors,

Runtime Veriﬁcation, pages 183–197, Berlin, Heidel-

berg. Springer Berlin Heidelberg.

Chimento, J. M., Ahrendt, W., Pace, G. J., and Schneider,

G. (2015). Starvoors : A tool for combined static and

runtime veriﬁcation of java. In Bartocci, E. and Ma-

jumdar, R., editors, Runtime Veriﬁcation, pages 297–

305, Cham. Springer International Publishing.

Colombo, C., Pace, G. J., and Schneider, G. (2009). Larva

— safer monitoring of real-time java programs (tool

paper). In Proceedings of the 2009 Seventh IEEE In-

ternational Conference on Software Engineering and

Formal Methods, SEFM ’09, pages 33–37, Washing-

ton, DC, USA. IEEE Computer Society.

Dwyer, M. B. and Purandare, R. (2008). Residual checking

of safety properties. In Havelund, K., Majumdar, R.,

and Palsberg, J., editors, Model Checking Software,

pages 1–2, Berlin, Heidelberg. Springer Berlin Hei-

delberg.

Falcone, Y., Krsti

c, S., Reger, G., and Traytel, D. (2018). A

taxonomy for classifying runtime veriﬁcation tools. In

Colombo, C. and Leucker, M., editors, Runtime Veriﬁ-

cation, pages 241–262, Cham. Springer International

Publishing.

Havelund, K., Reger, G., Thoma, D., and Z

alinescu, E.

(2018). Monitoring Events that Carry Data, pages

61–102. Springer International Publishing, Cham.

Kiczales, G., Hilsdale, E., Hugunin, J., Kersten, M., Palm,

J., and Griswold, W. G. (2001). An overview of as-

pectj. In Proceedings of the 15th European Confer-

ence on Object-Oriented Programming, ECOOP ’01,

pages 327–353, London, UK, UK. Springer-Verlag.

Lal, A., Kidd, N., Reps, T., and Touili, T. (2007). Abstract

error projection. In Nielson, H. R. and Fil

e, G., edi-

tors, Static Analysis, pages 200–217, Berlin, Heidel-

berg. Springer Berlin Heidelberg.

Leucker, M. and Schallhart, C. (2009). A brief account of

runtime veriﬁcation. The Journal of Logic and Alge-

braic Programming, 78(5):293 – 303. The 1st Work-

shop on Formal Languages and Analysis of Contract-

Oriented Software (FLACOS’07).

Vall

ee-Rai, R., Co, P., Gagnon, E., Hendren, L., Lam,

P., and Sundaresan, V. (1999). Soot - a java byte-

code optimization framework. In Proceedings of the

1999 Conference of the Centre for Advanced Studies

on Collaborative Research, CASCON ’99, pages 13–.

IBM Press.

CLARVA: Model-based Residual Veriﬁcation of Java Programs

359