
The Bias-Expressivity Trade-off
Julius Lauw
† a
, Dominique Macias
† b
, Akshay Trikha
† c
, Julia Vendemiatti
† d
and George D. Monta
˜
nez
† e
AMISTAD Lab, Department of Computer Science, Harvey Mudd College, Claremont, CA 91711, U.S.A.
†
denotes equal authorship.
Keywords:
Machine Learning, Algorithmic Search, Inductive Bias, Entropic Expressivity.
Abstract:
Learning algorithms need bias to generalize and perform better than random guessing. We examine the flexi-
bility (expressivity) of biased algorithms. An expressive algorithm can adapt to changing training data, altering
its outcome based on changes in its input. We measure expressivity by using an information-theoretic notion
of entropy on algorithm outcome distributions, demonstrating a trade-off between bias and expressivity. To
the degree an algorithm is biased is the degree to which it can outperform uniform random sampling, but is
also the degree to which is becomes inflexible. We derive bounds relating bias to expressivity, proving the
necessary trade-offs inherent in trying to create strongly performing yet flexible algorithms.
1 INTRODUCTION
Biased algorithms, namely those which are more
heavily predisposed to certain outcomes than others,
have difficulty changing their behavior in response to
new information or new training data. Yet bias is
needed for learning (Monta
˜
nez et al., 2019). Given
a set of information resources (or a distribution over
them), an algorithm that can output many different re-
sponses is said to be more expressive than one that
cannot. We explore the inverse relationship between
algorithmic bias and expressivity for learning algo-
rithms. This work builds on recent results in theo-
retical machine learning, which highlight the neces-
sity of incorporating biases tailored to specific learn-
ing problems in order to achieve learning performance
that is better than uniform random sampling of the hy-
pothesis space (Monta
˜
nez et al., 2019). A trade-off
exists between specialization and flexibility of learn-
ing algorithms. While algorithmic bias can be viewed
as an algorithm’s ability to ‘specialize’, expressivity
characterizes the ‘flexibility’ of a learning algorithm.
Using the algorithmic search framework for learn-
ing (Monta
˜
nez, 2017b), we define a specific form of
a
https://orcid.org/0000-0003-4201-0664
b
https://orcid.org/0000-0002-6506-4094
c
https://orcid.org/0000-0001-8207-6399
d
https://orcid.org/0000-0002-6547-9601
e
https://orcid.org/0000-0002-1333-4611
expressivity, called entropic expressivity, which is a
function of the information-theoretic entropy of an
algorithm’s induced probability distribution over its
search space. Under this notion of expressivity, the
degree to which a search algorithm is able to spread
its probability mass on many distinct target sets cap-
tures the extent to which the same algorithm is said to
be capable of ‘expressing’ a preference towards dif-
ferent search outcomes. No algorithm can be both
highly biased and highly expressive.
2 RELATED WORK
Inspired by Mitchell’s work highlighting the impor-
tance of incorporating biases in classification algo-
rithms to generalize beyond training data (Mitchell,
1980), we propose a method to measure algorithmic
expressivity in terms of the amount of bias induced
by a learning algorithm. This paper delves further
into the relationships between algorithmic bias and
expressivity by building on the search and bias theo-
retical frameworks defined in (Monta
˜
nez et al., 2019).
Monta
˜
nez et al. proved that bias is necessary for a
learning algorithm to perform better than uniform ran-
dom sampling, and algorithmic bias was shown to en-
code trade-offs, such that no algorithm can be concur-
rently biased towards many distinct target sets. In this
paper, we apply these properties of algorithmic bias
to derive an upper bound on the level of bias encoded
Lauw, J., Macias, D., Trikha, A., Vendemiatti, J. and Montañez, G.
The Bias-Expressivity Trade-off.
DOI: 10.5220/0008959201410150
In Proceedings of the 12th International Conference on Agents and Artificial Intelligence (ICAART 2020) - Volume 2, pages 141-150
ISBN: 978-989-758-395-7; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
141
in a learning algorithm, in order to gain insights on
the expressivity of learning algorithms.
Within the statistical learning literature, there exist
various measures characterizing algorithmic expres-
sivity. For instance, the Vapnik-Chervonekis (VC) di-
mension (Vapnik and Chervonenkis, 1971) provides a
loose upper bound on algorithmic expressivity in gen-
eral by characterizing the number of data points that
can be exactly classified by the learning algorithm,
for any possible labeling of the points. However, the
disadvantages of the VC dimension include its inher-
ent dependence on the dimensionality of the space on
which the learning algorithm operates on (V’yugin,
2015), as well as the fact that it is only restricted
to classification problems. Building on the origi-
nal VC dimension idea, Kearns and Schapire devel-
oped a generalization of the VC dimension with the
Fat-shattering VC dimension by deriving dimension-
free bounds with the assumption that the learning al-
gorithm operates within a restricted space (Kearns
and Schapire, 1990). Further, Bartlett and Mendel-
son created Rademacher complexity as a more gen-
eral measure of algorithmic expressivity by eliminat-
ing the assumption that learning algorithms are re-
stricted within a particular distribution space (Bartlett
and Mendelson, 2003).
In this paper, we establish an alternative general
measure of algorithmic expressivity based on the al-
gorithmic search framework (Monta
˜
nez, 2017a). Be-
cause this search framework applies to clustering and
optimization (Monta
˜
nez, 2017b) as well as to the gen-
eral machine learning problems considered in Vap-
nik’s learning framework (Vapnik, 1999), such as
classification, regression, and density estimation, the-
oretical derivations of the expressivity of search al-
gorithms using this framework directly apply to the
expressivity of many types of learning algorithms.
3 SEARCH FRAMEWORK
3.1 The Search Problem
We formulate machine learning problems as search
problems using the algorithmic search framework
(Monta
˜
nez, 2017a). Within the framework, a search
problem is represented as a 3-tuple (Ω,T, F). The fi-
nite search space from which we can sample is Ω.
The subset of elements in the search space that we are
searching for is the target set T . A target function
that represents T is an |Ω|-length vector with entries
having value 1 when the corresponding elements of
Ω are in the target set and 0 otherwise. The external
information resource F is a finite binary string that
provides initialization information for the search and
evaluates points in Ω, acting as an oracle that guides
the search process. In learning scenarios this is typi-
cally a dataset with accompanying loss function.
3.2 The Search Algorithm
Given a search problem, a history of elements already
examined, and information resource evaluations, an
algorithmic search is a process that decides how to
next query elements of Ω. As the search algorithm
samples, it adds the record of points queried and in-
formation resource evaluations, indexed by time, to
the search history. The algorithm uses the history to
update its sampling distribution on Ω. An algorithm
is successful if it queries an element ω ∈T during the
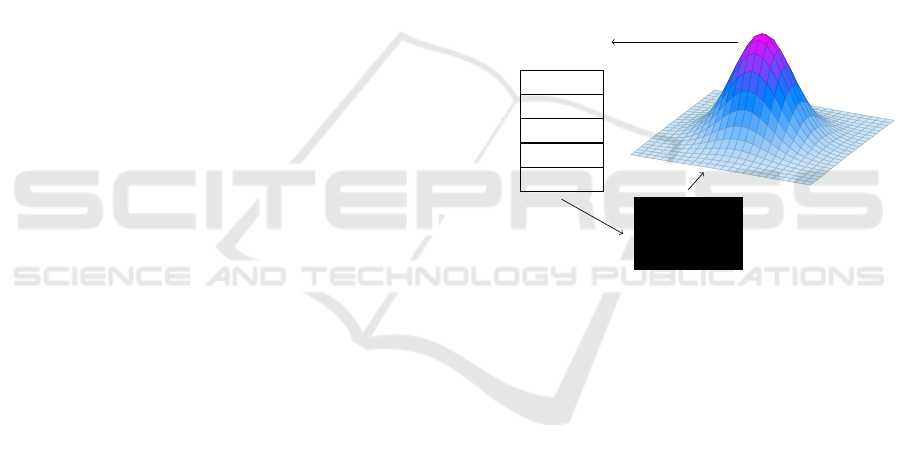
course of its search. Figure 1 visualizes the search
process.
P
i
Ω
next point at time step i
(ω, F(ω))
Black-Box
Algorithm
Search History
·
·
·
(ω
2
, F(ω
2
))
i = 5
(ω
0
, F(ω
0
))
i = 4
(ω
5
, F(ω
5
))
i = 3
(ω
4
, F(ω
4
))
i = 2
(ω
1
, F(ω
1
))
i = 1
Figure 1: As a black-box optimization algorithm samples
from Ω, it produces an associated probability distribution
P
i
based on the search history. When a sample ω
k
corre-
sponding to location k in Ω is evaluated using the external
information resource F, the tuple (ω
k
, F(ω
k
)) is added to
the search history.
3.3 Measuring Performance
Following Monta
˜
nez, we measure a learning algo-
rithm’s performance using the expected per-query
probability of success (Monta
˜
nez, 2017a). This quan-
tity gives a normalized measure of performance com-
pared to an algorithm’s total probability of success,
since the number of sampling steps may vary depend-
ing on the algorithm used and the particular run of
the algorithm, which in turn effects the total probabil-
ity of success. Furthermore, the per-query probability
of success naturally accounts for sampling procedures
that may involve repeatedly sampling the same points
in the search space, as is the case with genetic al-
gorithms (Goldberg, 1999; Reeves and Rowe, 2002),
allowing this measure to deftly handle search algo-
rithms that manage trade-offs between exploration
and exploitation.
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
142

The expected per-query probability of success is
defined as
q(T, F) = E
˜
P,H
"
1
|
˜
P|
|
˜
P|
∑
i=1
P
i
(ω ∈ T )
F
#
where
˜
P is a sequence of probability distributions over
the search space (where each timestep i produces a
distribution P
i
), T is the target, F is the information
resource, and H is the search history. The number of
queries during a search is equal to the length of the
probability distribution sequence, |
˜
P|. The outer ex-
pectation accounts for stochastic differences in multi-
ple runs of the algorithm, whereas the inner quantity
is equivalent to the expected probability of success for
a uniformly sampled time step of a given run.
4 BIAS
In this section, we review the definition of bias in-
troduced in (Monta
˜
nez et al., 2019) and restate some
results related to that concept, showing the need for
bias in learning algorithms.
Definition 4.1. (Bias between a Distribution over In-
formation Resources and a Fixed Target) Let D be a
distribution over a space of information resources F
and let F ∼D. For a given D and a fixed k-hot
1
target
function t (corresponding to target set t),
Bias(D,t) = E
D
[q(t,F)] −
k
|Ω|
= E
D
h
t
>
P
F
i
−
ktk
2
|Ω|
= t
>
E
D
P
F
−
ktk
2
|Ω|
= t
>
Z
F
P
f
D( f )d f −
ktk
2
|Ω|
where P
f
is the vector representation of the averaged
probability distribution (conditioned on f ) induced
on Ω during the course of the search, which implies
q(t, f ) = t
>
P
f
.
Definition 4.2. (Bias between a Finite Set of Informa-
tion Resources and a Fixed Target) Let U[B] denote
a uniform distribution over a finite set of information
resources B. For a random quantity F ∼ U[B], the
averaged |Ω|-length simplex vector P
F
, and a fixed
1
k-hot vectors are binary and have exactly k ones.
k-hot target function t,
Bias(B,t) = E
U[B]
[t
>
P
F
] −
k
|Ω|
= t
>
E
U[B]
[P
F
] −
k
|Ω|
= t
>
1
|B|
∑
f ∈B
P
f
!
−
ktk
2
|Ω|
.
Theorem 4.1 (Improbability of Favorable Informa-
tion Resources). Let D be a distribution over a set
of information resources F , let F be a random vari-
able such that F ∼ D, let t ⊆ Ω be an arbitrary fixed
k-sized target set with corresponding target function
t, and let q(t,F) be the expected per-query proba-
bility of success for algorithm A on search problem
(Ω,t,F). Then, for any q
min
∈ [0,1],
Pr(q(t,F) ≥ q
min
) ≤
p + Bias(D,t)
q
min
where p =
k
|Ω|
.
Theorem 4.2 (Conservation of Bias). Let D be a dis-
tribution over a set of information resources and let
τ
k
= {t|t ∈{0,1}
|Ω|
,||t|| =
√
k} be the set of all |Ω|-
length k-hot vectors. Then for any fixed algorithm A ,
∑
t∈τ
k
Bias(D,t) = 0
Theorem 4.3 (Famine of Favorable Information Re-
sources). Let B be a finite set of information re-
sources and let t ⊆ Ω be an arbitrary fixed k-size tar-
get set with corresponding target function t. Define
B
q
min
= {f | f ∈ B, q(t, f ) ≥ q
min
},
where q(t, f ) is the expected per-query probability of
success for algorithm A on search problem (Ω,t, f )
and q
min
∈ [0,1] represents the minimum acceptable
per-query probability of success. Then,
|B
q
min
|
|B|
≤
p + Bias(B,t)
q
min
where p =
k
|Ω|
.
Theorem 4.4 (Futility of Bias-free Search). For any
fixed algorithm A, fixed target t ⊆Ω with correspond-
ing target function t, and distribution over informa-
tion resources D, if Bias(D, t) = 0, then
Pr(ω ∈t; A) = p
where Pr(ω ∈ t;A) represents the single-query prob-
ability of successfully sampling an element of t using
A, marginalized over information resources F ∼ D,
and p is the single-query probability of success under
uniform random sampling.
The Bias-Expressivity Trade-off
143
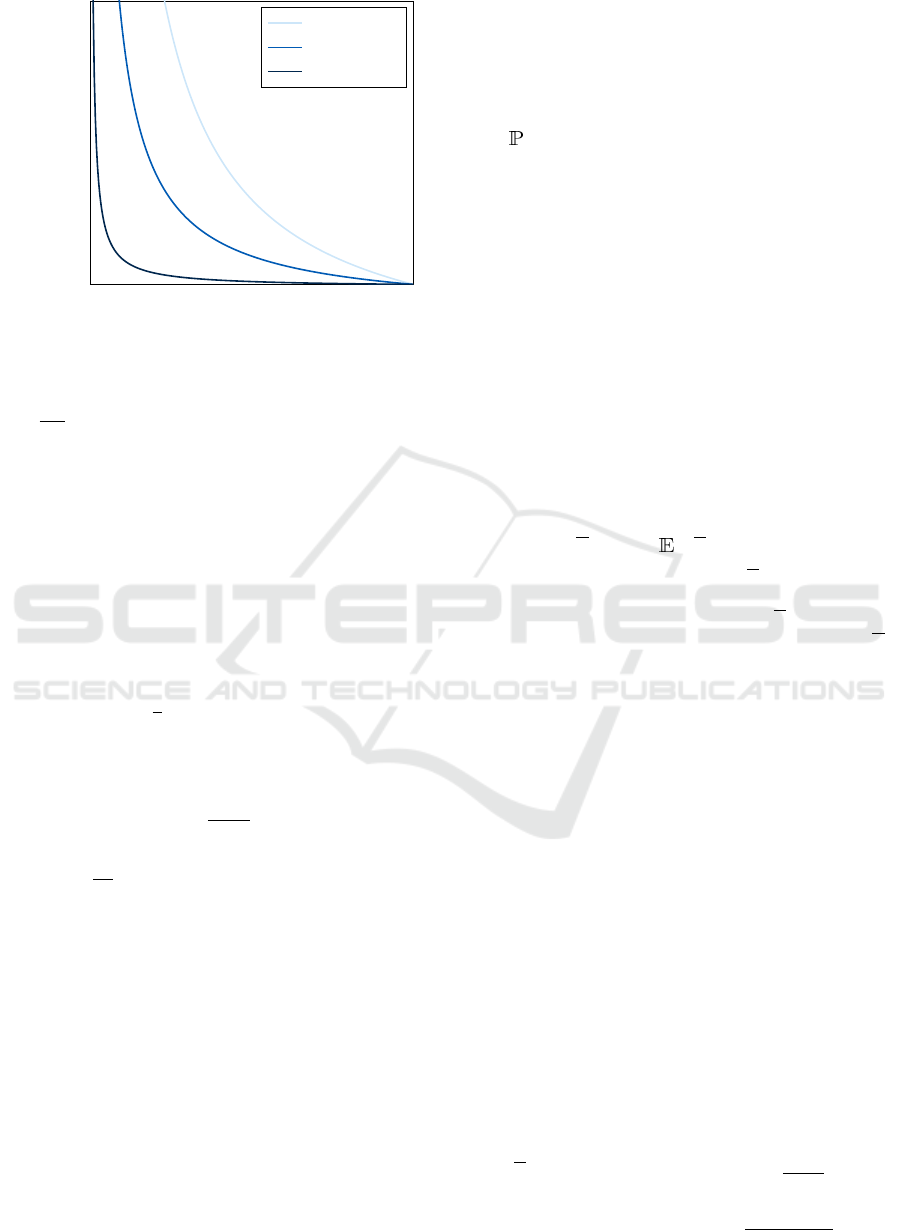
0 1
0
1
p
Upper Bound of Bias(D,t)
m = −0.3
m = −0.1
m = −0.01
Figure 2: This graph shows how the upper bound of the
supremum of the bias over all possible target sets of size
k varies with different values of p, for different values of
m =
p−1
p
.
5 MAIN RESULTS
Having reviewed the definitions of bias and prior re-
sults related to it, we now present our own results,
with full proofs given in the Appendix. We proceed
by presenting new results regarding bias and defining
entropic expressivity. We explore expressivity in rela-
tion to bias, demonstrating a trade-off between them.
Theorem 5.1 (Bias Upper Bound). Let τ
k
= {t|t ∈
{0,1}
|Ω|
,||t|| =
√
k} be the set of all |Ω|-length k-
hot vectors and let B be a finite set of information
resources. Then,
sup
t∈τ
k
Bias(B,t) ≤
p −1
p
inf
t∈τ
k
Bias(B,t)
where p =
k
|Ω|
.
Theorem 5.1 confirms the intuition that the bounds
on the maximum and minimum values the bias can
take over all possible target sets are related by at most
a constant factor. Note that from this theorem we can
also derive a lower bound on the infimum of the bias
by simply dividing by the constant factor.
We also consider the bound’s behavior as p varies
in Figure 2. As p increases, which can only happen
as the size of the target set k increases relative to the
size of Ω, the upper bound on bias tightens. This is
because if the target set size is a great proportion of
the search space, it is more likely that the algorithm
will do well on a greater number of target sets. Thus,
it will be less biased towards any given one of them,
by conservation of bias (Theorem 4.2).
Theorem 5.2 (Difference between Estimated and Ac-
tual Bias). Let t be a fixed target function, let D be
a distribution over a set of information resources B,
and let X = {X
1
,... ,X
n
} be a finite sample indepen-
dently drawn from D. Then,
(|Bias(X,t) −Bias(D,t)| ≥ ε) ≤2e
−2nε
2
.
This theorem bounds the difference in the bias de-
fined with respect to a distribution over information
resources, Bias(D, t), and the bias defined on a finite
set of information resources sampled from D. In prac-
tice, we may not have access to the underlying distri-
bution of information resources but we may be able
to sample from such an unknown distribution. This
theorem tells us how close empirically computed val-
ues of bias will be to the true value of bias, with high
probability.
Definition 5.1 (Entropic Expressivity). Given a dis-
tribution over information resources D, we define
the entropic expressivity of a search algorithm as the
information-theoretic entropy of the averaged strategy
distributions over D, namely,
H(P
D
) = H
D
[P
F
]
= H(U) −D
KL
(P
D
|| U)
where F ∼ D and the quantity D
KL
(P
D
|| U) is the
Kullback-Leibler divergence between distribution P
D
and the uniform distribution U, both being distribu-
tions over search space Ω.
Definition 5.1 uses the standard information-
theoretic entropy for discrete probability mass func-
tions, H(·). Our notion of expressivity characterizes
the flexibility of an algorithm by measuring the en-
tropy of its induced probability vectors (strategies) av-
eraged over the distribution on information resources.
Algorithms that place probability mass on many dif-
ferent regions of the search space will tend to have a
more uniform averaged probability vector. Entropic
expressivity captures this key aspect of the flexibility
of an algorithm.
We now present results relating this notion of ex-
pressivity to algorithmic bias.
Theorem 5.3 (Expressivity Bounded by Bias). Given
a fixed k-hot target function t and a distribution over
information resources D, the entropic expressivity of
a search algorithm can be bounded in terms of ε :=
Bias(D,t), by
H(P
D
) ∈
H(p + ε),
(p + ε)log
2
k
p + ε
+ (1 −(p + ε))log
2
|Ω|−k
1 −(p +ε)
.
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
144
This theorem shows that entropic expressivity is
bounded above and below with respect to the level of
bias on a fixed target. Table 1 demonstrates the dif-
ferent expressivity ranges for varying levels of bias.
While these ranges may be quite large, maximizing
the level of bias significantly reduces the range of pos-
sible values of entropic expressivity.
Table 1: Varying ranges of entropic expressivity for differ-
ent levels of bias on target t.
Bias(D,t) [t
>
P
F
] Expressivity Range
−p
(Minimum bias)
0 [0,log
2
(|Ω|−k)]
0
(No bias)
p [H(p),log
2
|Ω|]
1 −p
(Maximum bias)
1 [0,log
2
k]
Theorem 5.4 (Bias-expressivity Trade-off). Given a
distribution over information resources D and a fixed
target t ⊆ Ω, entropic expressivity is bounded above
in terms of bias,
H(P
D
) ≤ log
2
|Ω|−2Bias(D,t)
2
Additionally, bias is bounded above in terms of en-
tropic expressivity,
Bias(D,t) ≤
r
1
2
(log
2
|Ω|−H(P
D
))
=
r
1
2
D
KL
(P
D
|| U).
Theorem 5.4 demonstrates a trade-off between
bias and entropic expressivity. We bound entropic ex-
pressivity above in terms of bias and bias above in
terms of entropic expressivity such that higher values
of bias decrease the range of possible values of ex-
pressivity and higher values of expressivity decrease
the range of possible values of bias. Thus, a higher
level of bias on a specified target restricts the expres-
sivity of the underlying strategy distribution and a
higher level of expressivity on the underlying strategy
distribution restricts the amount of bias on any arbi-
trary target. Intuitively, this trade-off means that pref-
erences towards specific targets reduces the potential
flexibility of our algorithm over all elements and vice
versa.
Lastly, we give a corollary bound allowing us to
bound bias as a function of the expected entropy of
induced strategy distributions, rather than the entropic
expressivity.
Corollary 5.4.1 (Bias Bound Under Expected Ex-
pressivity).
Bias(D,t) ≤
r
1
2
(log
2
|Ω|−E
D
[H(P
F
)])
=
s
E
D
1
2
D
KL
(P
F
|| U)
.
6 CONCLUSION
Expanding results on the algorithmic search frame-
work, we supplement the notion of bias and define
entropic expressivity, as well as its relation to bias.
We upper bound the bias on an arbitrary target set
with respect to the minimum bias toward a target set
over all possible target sets of a fixed size. More-
over, we upper bound the probability of the difference
between the estimated bias and the true bias exceed-
ing some threshold, showing an exponential rate of
measure concentration in the number of samples. En-
tropic expressivity characterizes the degree of unifor-
mity for strategy distributions in expectation for an
underlying distribution of information resources. We
provide upper and lower bounds of the entropic ex-
pressivity with respect to the bias on a specified target
and we demonstrate a trade-off between bias and ex-
pressivity.
While bias is needed for better-than-chance per-
formance of learning algorithms, bias also hinders the
flexibility of an algorithm by reducing the different
ways it can respond to varied training data. Although
algorithms predisposed to certain outcomes will not
adapt as well as algorithms without strong predispo-
sitions, maximally flexible algorithms (those without
any bias) can only perform as well as uniform ran-
dom sampling (Theorem 4.4). This paper explores the
trade-off, giving bounds for bias in terms of expres-
sivity, and bounds for expressivity in terms of bias,
demonstrating that such a trade-off exists. Although
the notions of bias are different, the bias-expressivity
trade-off can be viewed as a type of bias-variance
trade-off (Geman et al., 1992; Kohavi et al., 1996),
where bias here is not an expected error but an ex-
pected deviation from uniform random sampling per-
formance caused by an algorithm’s inductive assump-
tions, and variance is not a fluctuation in observed er-
ror caused by changing data but is instead a “fluctu-
ation” in algorithm outcome distributions caused by
the same. Therefore, our results may provide new in-
sights for that well-studied phenomenon.
The Bias-Expressivity Trade-off
145

ACKNOWLEDGEMENTS
This work was supported in part by a generous grant
from the Walter Bradley Center for Natural and Arti-
ficial Intelligence.
REFERENCES
Bartlett, P. L. and Mendelson, S. (2003). Rademacher and
gaussian complexities: Risk bounds and structural re-
sults. J. Mach. Learn. Res., 3:463–482.
Geman, S., Bienenstock, E., and Doursat, R. (1992). Neu-
ral networks and the bias/variance dilemma. Neural
computation, 4(1):1–58.
Goldberg, D. (1999). Genetic algorithms in search op-
timization and machine learning. Addison-Wesley
Longman Publishing Company.
Kearns, M. J. and Schapire, R. E. (1990). Efficient
distribution-free learning of probabilistic concepts. In
Proceedings [1990] 31st Annual Symposium on Foun-
dations of Computer Science, pages 382–391 vol.1.
Kohavi, R., Wolpert, D. H., et al. (1996). Bias plus variance
decomposition for zero-one loss functions. In ICML,
volume 96, pages 275–83.
Mitchell, T. D. (1980). The need for biases in learning gen-
eralizations. In Rutgers University: CBM-TR-117.
Monta
˜
nez, G. D. (2017a). The Famine of Forte: Few Search
Problems Greatly Favor Your Algorithm. In 2017
IEEE International Conference on Systems, Man, and
Cybernetics (SMC), pages 477–482. IEEE.
Monta
˜
nez, G. D. (2017b). Why Machine Learning Works.
In Dissertation. Carnegie Mellon University.
Monta
˜
nez, G. D., Hayase, J., Lauw, J., Macias, D., Trikha,
A., and Vendemiatti, J. (2019). The futility of bias-
free learning and search. In AI 2019: Advances in Ar-
tificial Intelligence: 32nd Australasian Joint Confer-
ence, Adelaide, SA, Australia, December 2–5, 2019,
Proceedings, pages 277–288. Springer Nature.
Reeves, C. and Rowe, J. E. (2002). Genetic algorithms:
principles and perspectives: a guide to GA theory,
volume 20. Springer Science & Business Media.
Vapnik, V. and Chervonenkis, A. Y. (1971). On the uniform
convergence of relative frequencies of events to their
probabilities.
Vapnik, V. N. (1999). An overview of statistical learn-
ing theory. IEEE transactions on neural networks,
10(5):988–999.
V’yugin, V. (2015). VC Dimension, Fat-Shattering Dimen-
sion, Rademacher Averages, and Their Applications,
pages 57–74.
APPENDIX
Lemma 6.1 (Existence of subset with at most uni-
form mass). Given an n-sized subset S of the sample
space of an arbitrary probability distribution with to-
tal probability mass M
S
, there exists a k-sized proper
subset R ⊂ S with total probability mass M
R
such that
M
R
≤
k
n
M
S
.
Proof. We proceed by induction on the size k.
Base Case: When k = 1, there exists an ele-
ment with total probability mass at most
M
S
n
, since
for any element in S that has probability mass greater
than the uniform mass
M
S
n
, there exists an element
with mass strictly less than
M
S
n
by the law of total
probability. This establishes our base case.
Inductive Hypothesis: Suppose that a k-sized subset
R
k
⊂ S exists with total probability mass M
R
k
such
that M
R
k
≤
k
n
M
S
.
Induction Step: We show that there exists a subset
R
k+1
⊂ S of size k + 1 with total probability mass
M
R
k+1
such that M
R
k+1
≤
k+1
n
M
S
.
First, let M
R
k
=
k
n
M
S
−s, where s ≥ 0 represents
the slack between M
R
k
and
k
n
M
S
. Then, the total prob-
ability mass on R
k
c
:= S \R
k
is
M
R
k
c
= M
S
−M
R
k
= M
S
−
k
n
M
S
+ s.
Given that M
R
k
c
is the total probability mass on set
R
k
c
, either each of the n −k elements in R
k
c
has a uni-
form mass of M
R
k
c
/(n−k), or they do not. If the prob-
ability mass is uniformly distributed, let e be an ele-
ment with mass exactly M
R
k
c
/(n −k). Otherwise, for
any element e
0
with mass greater than M
R
k
c
/(n −k),
by the law of total probability there exists an element
e ∈ R
k
c
with mass less than M
R
k
c
/(n −k). Thus, in
either case there exists an element e ∈ R
k
c
with mass
at most M
R
k
c
/(n −k).
Then, the set R
k+1
= R
k
∪{e} has total probability
mass
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
146

M
R
k+1
≤ M
R
k
+
M
R
k
c
n −k
=
k
n
M
S
−s +
M
S
−
k
n
M
S
+ s
n −k
=
kM
S
(n −k) + n(M
S
−
k
n
M
S
+ s)
n(n −k)
−s
=
knM
S
−k
2
M
S
+ nM
S
−kM
S
+ ns
n(n −k)
−s
=
(n −k)(kM
S
+ M
S
) + ns
n(n −k)
−s
=
k + 1
n
M
S
+
s
n −k
−s
=
k + 1
n
M
S
+
s(1 + k −n)
n −k
≤
k + 1
n
M
S
where the final inequality comes from the fact that
k < n. Thus, if a k-sized subset R
k
∈ S exists such
that M
R
k
≤
k
n
M
S
, a k + 1-sized subset R
k+1
∈ S exists
such that M
R
k+1
≤
k+1
n
M
S
.
Since the base case holds true for k = 1 and the
inductive hypothesis implies that this rule holds for
k +1, we can always find a k-sized subset R
k
∈S such
that
M
R
k
≤
k
n
M
S
.
Lemma 6.2 (Maximum probability mass over a target
set). Let τ
k
= {t|t ∈ {0, 1}
|Ω|
,||t|| =
√
k} be the set
of all |Ω|-length k-hot vectors. Given an arbitrary
probability distribution P,
sup
t∈τ
k
t
>
P ≤ 1 −
1 −p
p
inf
t∈τ
k
t
>
P
where p =
k
|Ω|
.
Proof. We proceed by contradiction. Suppose that
sup
t∈τ
k
t
>
P > 1 −
1 −p
p
inf
t∈τ
k
t
>
P.
Then, there exists some target function t ∈τ
k
such that
t
>
P > 1 −
1 −p
p
inf
t∈τ
k
t
>
P.
Let s be the complementary target function to t such
that s is an |Ω|-length, (|Ω|−k)-hot vector that takes
value 1 where t takes value 0 and takes value 0 else-
where. Then, by the law of total probability,
s
>
P <
1 −p
p
inf
t∈τ
k
t
>
P.
By Lemma 6.1, there exists a k-sized subset of the
complementary target set with total probability mass
q such that
q ≤
k
|Ω|−k
(s
>
P)
<
k
|Ω|−k
1 −p
p
inf
t∈τ
k
t
>
P
=
k
|Ω|−k
|Ω|−k
k
inf
t∈τ
k
t
>
P
= inf
t∈τ
k
t
>
P.
Thus, we can always find a target set with total prob-
ability mass strictly less than inf
t∈τ
k
t
>
P, which is a
contradiction.
Therefore, we have proven that
sup
t∈τ
k
t
>
P ≤ 1 −
1 −p
p
inf
t∈τ
k
t
>
P.
Theorem 5.1 (Bias Upper Bound). Let τ
k
= {t|t ∈
{0,1}
|Ω|
,||t|| =
√
k} be the set of all |Ω|-length k-
hot vectors and let B be a finite set of information
resources. Then,
sup
t∈τ
k
Bias(B,t) ≤
p −1
p
inf
t∈τ
k
Bias(B,t)
where p =
k
|Ω|
.
Proof. First, define
m := inf
t∈τ
k
U[B]
[t
>
P
F
] = inf
t∈τ
k
Bias(B,t) + p
and
M := sup
t∈τ
k
U[B]
[t
>
P
F
] = sup
t∈τ
k
Bias(B,t) + p.
By Lemma 6.2,
M ≤ 1 −
1 −p
p
m.
Substituting the values of m and M,
sup
t∈τ
k
Bias(B,t) ≤ 1 − p −
1 −p
p
inf
t∈τ
k
Bias(B,t) + p
=
p −1
p
inf
t∈τ
k
Bias(B,t).
The Bias-Expressivity Trade-off
147

k
|Ω|−k
p + ε
1 - (p + ε)
k
|Ω|−k
p+ε
k
1−(p+ε)
|Ω|−k
Figure 3: Assuming positive bias, this figure shows two dis-
crete probability distributions over Ω. The top is of an al-
gorithm with high KL divergence while the bottom is of an
algorithm with low KL divergence.
Theorem 5.2 (Difference between Estimated and Ac-
tual Bias). Let t be a fixed target function, let D be
a distribution over a set of information resources B,
and let X = {X
1
,... ,X
n
} be a finite sample indepen-
dently drawn from D. Then,
(|Bias(X,t) −Bias(D,t)| ≥ ε) ≤2e
−2nε
2
.
Proof. Define
B
X
:=
1
n
n
∑
i=1
t
>
P
X
i
= Bias(X, t) + p.
Given that X is an iid sample from D, we have
E[B
X
] = E
"
1
n
n
∑
i=1
t
>
P
X
i
#
=
1
n
n
∑
i=1
E
h
t
>
P
X
i
i
= Bias(D,t) + p.
By Hoeffding’s inequality and the fact that
0 ≤ B
X
≤ 1
we obtain
(|Bias(X,t) −Bias(D,t)| ≥ ε)
= (|B
X
−E[B
X
]| ≥ ε) ≤2e
−2nε
2
.
Theorem 5.3 (Expressivity Bounded by Bias). Given
a fixed k-hot target function t and a distribution over
information resources D, the entropic expressivity of
a search algorithm can be bounded in terms of ε :=
Bias(D,t), by
H(P
D
) ∈
H(p + ε),
(p + ε)log
2
k
p + ε
+ (1 −(p + ε))log
2
|Ω|−k
1 −(p +ε)
.
Proof. Following definition 5.1, the expressivity of
a search algorithm varies solely with respect to
D
KL
(P
D
|| U) since we always consider the same
search space and thus H(U) is a constant value. We
obtain a lower bound of the expressivity by maximiz-
ing the value of D
KL
(P
D
||U) and an upper bound by
minimizing this term.
First, we show that H(p + ε) is a lower bound of
expressivity by constructing a distribution that devi-
ates the most from a uniform distribution over Ω. By
the definition of Bias(D,t), we place (p + ε) proba-
bility mass on the target set t and 1 −(p + ε) proba-
bility mass on the remaining (n −k) elements of Ω.
We distribute the probability mass such that all of the
(p + ε) probability mass of the target set is concen-
trated on a single element and all of the 1 −(p + ε)
probability mass of the complement of the target set is
concentrated on a single element. In this constructed
distribution where D
KL
(P
D
|| U) is maximized, the
value of expressivity is
H(P
D
) = −
∑
ω∈Ω
P
D
(ω)log
2
P
D
(ω)
= −(p + ε)log
2
(p + ε)
−(1 −(p + ε))log
2
(1 −(p +ε))
= H(p + ε)
where the H(p + ε) is the entropy of a Bernoulli dis-
tribution with parameter (p + ε). The entropy of this
constructed distribution gives a lower bound on ex-
pressivity,
H(P
D
) ≥ H(p + ε).
Now, we show that
(p+ε)log
2
h
k
p + ε
i
+(1−(p+ε))log
2
h
|Ω|−k
1 −(p +ε)
i
is an upper bound of expressivity by constructing a
distribution that deviates the least from a uniform dis-
tribution over Ω. In this case, we uniformly distribute
1
|Ω|
probability mass over the entire search space, Ω.
Then, to account for the ε level of bias, we add
ε
k
probability mass to elements of the target set and we
remove
ε
n−k
probability mass to elements of the com-
plement of the target set. In this constructed distribu-
tion where D
KL
(P
D
|| U) is minimized, the value of
expressivity is
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
148

H(P
D
) = −
∑
ω∈Ω
P
D
(ω)log
2
P
D
(ω)
= −
∑
ω∈t
1
|Ω|
+
ε
k
log
2
1
|Ω|
+
ε
k
−
∑
ω∈t
c
1
|Ω|
−
ε
|Ω|−k
log
2
1
|Ω|
−
ε
|Ω|−k
= −
∑
ω∈t
p + ε
k
log
2
p + ε
k
−
∑
ω∈t
c
1 −(p +ε)
|Ω|−k
log
2
1 −(p +ε)
|Ω|−k
= −k
p + ε
k
log
2
p + ε
k
−
(|Ω|−k)
1 −(p +ε)
|Ω|−k
log
2
1 −(p +ε)
|Ω|−k
= (p + ε)log
2
k
p + ε
+
(1 −(p + ε)) log
2
|Ω|−k
1 −(p +ε)
.
The entropy on this constructed distribution gives an
upper bound on expressivity,
H(P
D
) ≤ (p + ε)log
2
k
p + ε
+ (1 −(p + ε))log
2
|Ω|−k
1 −(p +ε)
.
These two bounds give us a range of possible values
of expressivity given a fixed level of bias, namely
H(P
D
) ∈
H(p + ε),
(p + ε)log
2
k
p + ε
+ (1 −(p + ε))log
2
|Ω|−k
1 −(p +ε)
.
Theorem 5.4 (Bias-expressivity Trade-off). Given a
distribution over information resources D and a fixed
target t ⊆ Ω, entropic expressivity is bounded above
in terms of bias,
H(P
D
) ≤ log
2
|Ω|−2Bias(D,t)
2
Additionally, bias is bounded above in terms of en-
tropic expressivity,
Bias(D,t) ≤
r
1
2
(log
2
|Ω|−H(P
D
))
=
r
1
2
D
KL
(P
D
|| U).
Proof. Let ω ∈t denote the measurable event that ω is
an element of target set t ⊆ Ω, and let Σ be the sigma
algebra of measurable events. First, note that
Bias(D,t)
2
= |Bias(D,t)|
2
= |t
>
E
D
[P
F
] −p|
2
= |t
>
P
D
−p|
2
= |P
D
(ω ∈t) − p|
2
≤
1
2
D
KL
(P
D
|| U)
=
1
2
(H(U) −H(P
D
))
=
1
2
(log
2
|Ω|−H(E
D
[P
F
]))
where the inequality is an application of Pinsker’s
Inequality. The quantity D
KL
(P
D
|| U) is the
Kullback-Leibler divergence between distributions
P
D
and U, which are distributions on search space
Ω.
Thus,
H(E
D
[P
F
]) ≤ log
2
|Ω|−2Bias(D,t)
2
and
Bias(D,t) ≤
r
1
2
(log
2
|Ω|−H(P
D
))
=
r
1
2
D
KL
(P
D
|| U)
=
r
1
2
(log
2
|Ω|−H(E
D
[P
F
])).
Corollary 5.4.1 (Bias Bound Under Expected Ex-
pressivity).
Bias(D,t) ≤
r
1
2
(log
2
|Ω|−E
D
[H(P
F
)])
=
s
E
D
1
2
D
KL
(P
F
|| U)
.
Proof. By the concavity of the entropy function and
Jensen’s Inequality, we obtain
E
D
[H(P
F
)] ≤ H(E
D
[P
F
]) ≤ log
2
|Ω|−2Bias(D,t)
2
.
The Bias-Expressivity Trade-off
149

Thus, an upper bound of bias is
Bias(D,t) ≤
r
1
2
D
KL
(P
D
|| U)
=
r
1
2
(log
2
|Ω|−H(E
D
[P
F
]))
≤
r
1
2
(log
2
|Ω|−E
D
[H([P
F
])])
=
s
E
D
1
2
D
KL
(P
F
|| U)
,
where the final equality follows from the linearity of
expectation and the definition of KL-divergence.
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
150
