
Visual Analysis of Billiard Dynamics Simulation Ensembles
Stefan Boshe-Plois
1
, Quynh Quang Ngo
1
, Peter Albers
2
and Lars Linsen
1
1
Westf
¨
alische Wilhelms-Universit
¨
at M
¨
unster, Germany
2
University of Heidelberg, Germany
Keywords:
Ensemble Visualization, Billiard Dynamics.
Abstract:
Mathematical billiards assume a table of a certain shape and dynamical rules for handling collisions. Some
trajectories exhibit distinguished patterns. Detecting such trajectories manually for a given billiard is cum-
bersome, especially, when assuming an ensemble of billiards with different parameter settings. We propose
a visual analysis approach for simulation ensembles of billiard dynamics based on phase-space visualizations
and multi-dimensional scaling. We apply our methods to the well-studied approach of dynamical billiards for
validation and to the novel approach of symplectic billiards for new observations.
1 INTRODUCTION
In the theory of mathematical dynamical systems the
main question is to investigate the long-term quali-
tative behavior of a system in terms of certain qual-
itative facets. Usually, these facets are phenomena
like periodicity and recurring patterns. Further, it
can be examined whether a system shows stable or
chaotic behavior and how robust it is to perturbations.
Mathematical billiards form a category of dynamical
systems (Birkhoff, 1927). They arise naturally from
physical laws of reflection and show connections to
problems like the motion of gas particles in a closed
environment. While the ultimate goal is to give an-
swers based on theoretical proofs, it is useful to have
well-founded suppositions indicating the direction to
head. We present visual analysis methods for sim-
ulation ensembles of billiard dynamics to form such
suppositions.
Billiards are defined on a table and the dynamics
are dependent on the shape of the table (Tabachnikov,
2005). If its boundary is defined via a function, a per-
turbation corresponds to slightly changing a param-
eter in the function. The question is what changes
occur due to such a perturbation, i.e., whether the bil-
liard trajectories exhibit a qualitatively different be-
havior. Since it is a priori unclear, which trajectories
would exhibit changing patterns and at what pertur-
bation levels, we propose to consider a simulation en-
semble with different shape parameters of the table,
compute a large amount of trajectories for each en-
semble member, and use visual analysis methods to
explore the generated data.
To analyze the trajectories of a single ensemble
member, we propose to visualize them in a phase
space spanned by the positions of collisions along
the boundary and directions. To analyze the changes
when altering the table’s parameters we compute pair-
wise dissimilarities between corresponding trajecto-
ries of ensemble members. These dissimilarities can
be visually encoded using a multidimensional scaling
(MDS) approach, which allows for the analysis of the
impact of the different table parameters on the dynam-
ics. Having identified interesting ensemble member
pairs from the MDS, we support a comparative visu-
alization of that pair by highlighting the deviations in
the trajectories.
While dynamical billiards (Birkhoff, 1927) have
been investigated in great depth, it has not yet been
addressed in detail whether other dynamics such as
symplectic billiards (Albers and Tabachnikov, 2018)
exhibit similar phenomena. We apply our approach
to dynamical billiards to validate our approach and to
symplectric billiards for novel findings.
2 RELATED WORK
In the visualization community, there have been many
attempts in trying to visually analyze dynamics. Tric-
oche et al. (Tricoche et al., 2012) study conserva-
tive dynamical systems using area-preserving maps.
They apply their method to two example dynamics to
reveal salient structure in the spatial domain. Boe-
ing et al. (Boeing, 2016) investigated chaos and self-
Boshe-Plois, S., Ngo, Q., Albers, P. and Linsen, L.
Visual Analysis of Billiard Dynamics Simulation Ensembles.
DOI: 10.5220/0008956201850192
In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 3: IVAPP, pages
185-192
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
185
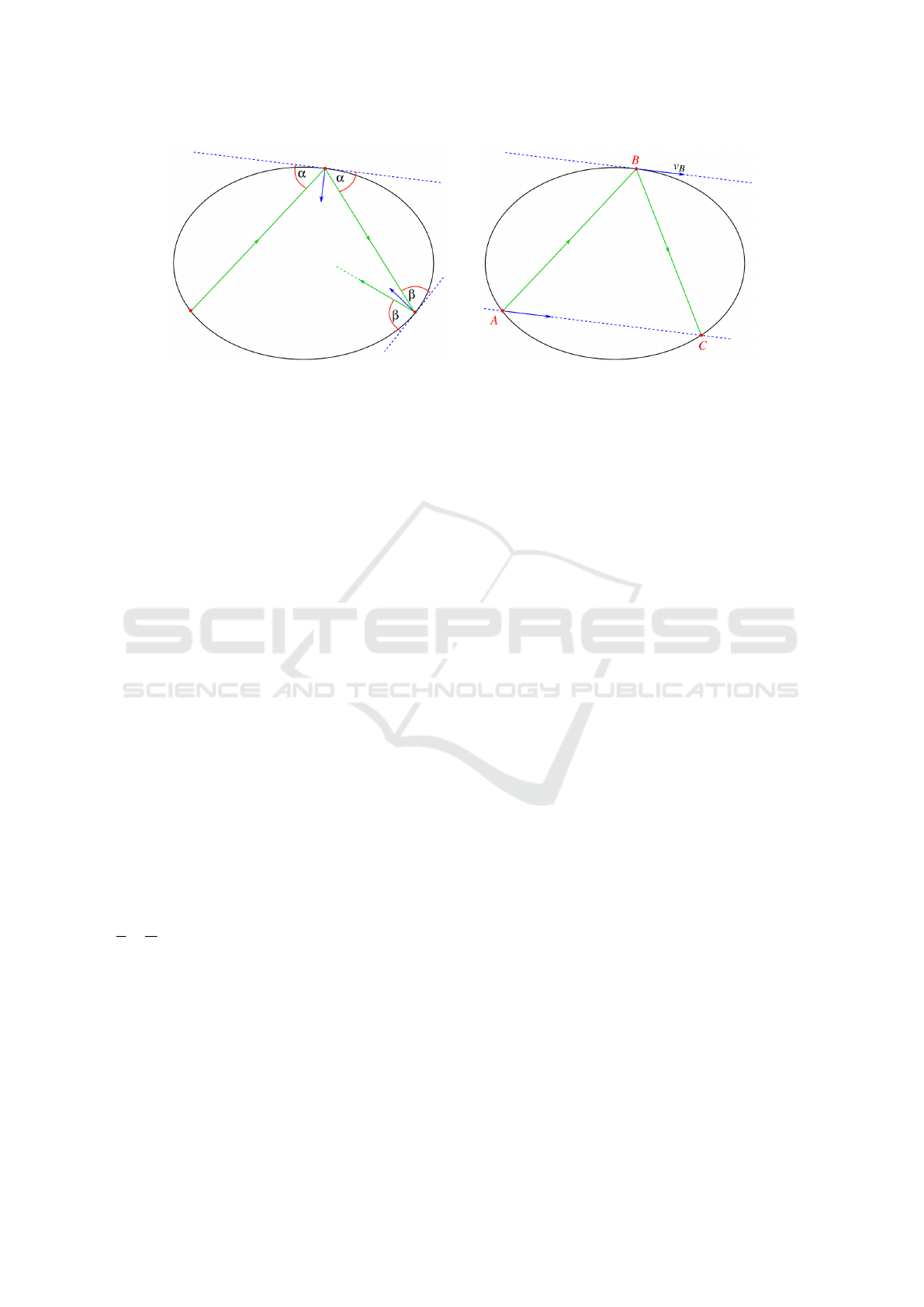
(a) standard dynamics (b) symplectic dynamics
Figure 1: Billiard dynamics.
similarity in non-linear systems. Ngo et al. (Ngo
et al., 2016) investigated dynamics on networks,
where they compute similarities between the dynam-
ics of the networks’ nodes, which are then visualized
using a multi-dimensional scaling (MDS) approach.
We also make use of MDS to visualize our data, but
apply it to compare simulation runs within an en-
semble of simulations. Kumpf et al. (Kumpf et al.,
2019) investigated ensembles to performed a sensibil-
ity analysis for weather forecasts based on correlation
measures. There aim was to identify regions of robust
prediction, which is related to parts of our goals. Fur-
ther approaches for dynamical systems exist in other
application scenarios. To our knowledge, this is the
first paper that investigates how visualization can sup-
port the analysis of billiard dynamics.
3 BACKGROUND AND
REQUIREMENT ANALYSIS
We first want to provide the mathematical background
for our investigations. A billiard model consists of a
table and dynamics. A billiard table is a convex do-
main Γ ⊂ R
2
with a smooth boundary γ := ∂Γ. Of
great interests are, in particular, elliptic billiard ta-
bles defined via a function F : R
2
→ R with F(x,y) =
x
r
a
+
y
w
b
−1, a,b > 0, and r, w ≥ 2. The elliptic billiard
table’s boundary is given by γ =
{
(x,y) | F(x,y) = 0
}
.
Γ is called a standard elliptic table, if r = w = 2, oth-
erwise a perturbed elliptic table.
The billiard dynamics consist of a rule set or algo-
rithm that determines a sequence of collision points
(A
n
)
n∈N
with A
n
∈ γ, which we call billiard trajec-
tory. One may simply imagine a massless billiard ball
that moves with unit speed and without friction. The
most natural kind of billiard dynamics are the dynam-
ical or Birkhoff billiards, as they arise from the laws
of elastic collision in physics. Therefore, we also re-
fer to them as standard dynamics. Assume we have
a collision point A on the boundary γ together with a
direction vector v
A
∈ R
2
. Then, from a point A with
direction v
A
, the subsequent point B is obtained as the
intersection of the line A + r · v
A
, r ∈ R with γ and
the subsequent direction is determined via the reflec-
tion law, i.e., the angle of incidence is the same as the
angle of reflection, see Figure 1(a).
The standard dynamics can be described as a vari-
ational problem: If A,B,C ∈ γ is a sequence of col-
lisions and we fix A and C, then the position of B
is defined by the condition that |AB| + |BC| is ex-
tremal. In symplectic billiards the dynamics are de-
rived from a related variational problem by the condi-
tion that the area of the triangle ABC is extremal (Al-
bers and Tabachnikov, 2018). The name symplectic
arises from the fact that the map describing the dy-
namics has the standard symplectic form ω as a gen-
erating function. Further mathematical details on the
form ω are beyond the scope of this paper. It suf-
fices to report that the resulting rules for the dynam-
ics can be reduced to taking the position of B to be
such that the vector C − A lies in the tangent space
T
B
γ. For computing trajectories on elliptical tables,
we start with two points A and B, compute the tan-
gent v
B
∈ T
B
γ, and calculate the root of the function
F(A + r · v
B
), see Figure 1(b) (Albers and Tabach-
nikov, 2018).
While structures in dynamical billiards have al-
ready been analyzed in much detail, advances for
symplectic billiards are recent. Initial questions that
are to be answered and respective expectations were
formulated by the domain scientists as follows:
• On a standard elliptic table, one would expect
clear structures that should be qualitatively inde-
pendent of parameters a and b for both dynamical
and symplectic billiards.
IVAPP 2020 - 11th International Conference on Information Visualization Theory and Applications
186
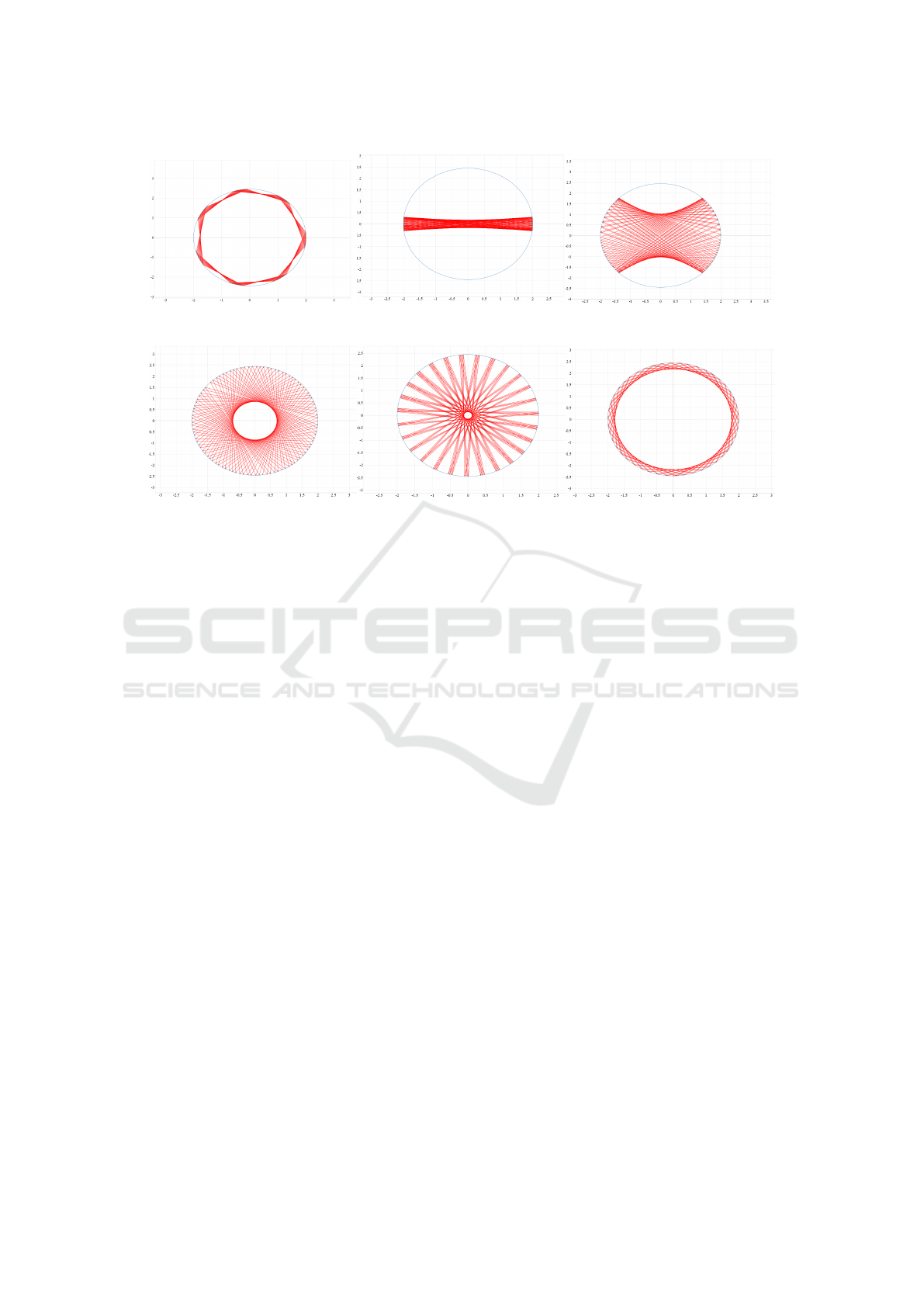
(a) standard dynamics (b) standard dynamics (c) standard dynamics
(d) symplectic dynamics (e) symplectic dynamics (f) symplectic dynamics
Figure 2: Trajectories with different starting conditions using boundary function F(x,y) = x
2
/4 + y
2
/6 − 1.
• On a perturbed elliptic table, there should occur
small anomalies (i.e., trajectories change in quali-
tative aspects) for dynamical billiards, but it is an
open question, whether the same is true for sym-
plectic billiards.
• If some trajectories change qualitatively when
perturbing the elliptic table, one would like to
know how they look like.
• It is unclear what happens, if one changes the pa-
rameters a and b on a perturbed elliptic table. It
would be interesting to see, whether there exist re-
lations between the two parameters depending on
their ratio.
To answer these questions, we generate and visu-
ally analyze simulation ensembles for both dynamical
and symplectic billiards by varying parameters r and
w as well as parameters a and b. For each ensemble
member, we compute a large amount of trajectories
with different starting collisions and directions for a
sufficiently large number of collisions.
From the expectations and questions formulated
by the domain scientists, we extracted the require-
ments to our analysis system as follows:
1. The highest-level goal is understand the influence
of the parameter settings on the dynamics. Hence,
we need to analyze the entire ensemble simulta-
neously.
2. When two ensemble runs differ, it would be of
interest to see, which of their trajectories differ.
Hence, we need a comparative visualization of
trajectories of two runs.
3. On the lowest level, one is interested in observing
individual simulation runs and observe the behav-
ior of their trajectories.
4 VISUAL ANALYSIS
In this section, we describe the visualization meth-
ods we developed for analyzing individual ensemble
members, ensemble member pairs, and entire ensem-
bles.
4.1 Phase-space Visualization
Our first aim is to visualize trajectories of a single
ensemble member (cf. Requirement 3). A straight-
forward visual encoding of a simulation outcome is
to render the trajectories on the table. Figure 2 shows
respective examples for standard and symplectic bil-
liards. The visualizations clearly exhibit patterns, but
only for a single trajectory. Obviously, displaying
many such trajectories simultaneously leads to visual
clutter. Therefore, we propose to visualize the set of
trajectories for a single ensemble member in a phase-
space configuration.
A phase space Ω for dynamical billiards consists
of a collision point on the boundary together with a
direction vector, i.e., Ω = γ × R
2
. Equivalently, it
Visual Analysis of Billiard Dynamics Simulation Ensembles
187

(a) Ω = S
1
× [0,π) (b) Ω = S
1
× [0,π)
(c) Ω = S
1
× S
1
(d) Ω = S
1
× S
1
Figure 3: Phase-space visualizations of sets of trajectories (with random color mapping) using boundary function F(x, y) =
x
2
/4 + y
2
/6 − 1 for standard (a,b) and symplectic dynamics (c,d).
can be defined by describing the direction using the
angle to the tangent at the collision point, i.e., Ω =
γ × [0,π]. Furthermore, one can apply a parametriza-
tion to the curve γ. Since γ is closed, we denote such
a parametrization as α : S
1
→ γ, which is equivalent
to α : [s,t] → γ with α(s) = α(t). The phase space
then becomes Ω = S
1
× [0, π] or Ω = [s,t] × [0,π].
For elliptical tables, we chose the parametrization
α(p) = arccos (hp − q
c
,v
c
i) with a center point q
c
∈ Γ
and a reference vector v
c
∈ S
1
. We used q
c
= (0, 0)
and v
c
= (1, 0). For symplectic billiards, a configu-
ration is not defined by a collision point and a direc-
tion vector, but by two consecutive collision points.
Hence, we define the phase space by Ω = S
1
× S
1
or
Ω = [s,t] × [s,t], respectively.
Having defined a phase space, a single trajectory
can be visualized by plotting the respective collisions
as dots in the phase space. A set of trajectories of
a single ensemble member can, then, be shown by
coloring each trajectory with a unique color. For
the color mapping we considered categorical color
maps, but given the large amount of trajectories, there
are not enough colors that can be sufficiently well
distinguished. Thus, random color mapping worked
equally well, i.e., each trajectory just got a randomly
assigned color. Figure 3 shows respective examples
for standard and symplectic billiards.
4.2 Comparative Visualization
Our Requirement 2 was to visually compare two en-
semble members to observe where and how trajecto-
ries differ, e.g., to highlight anomalies. From the jux-
taposed phase-space visualizations in Figure 4(a,b),
we can conclude that it is difficult to detect small
differences. Hence, the design choice would be to
compute an explicit visual encoding of computed dif-
ferences. To highlight the differences, we have to
compute the differences between two ensemble mem-
bers. More precisely, we have to compute the dif-
ferences of corresponding trajectories in the two en-
semble members. Using the phase-space representa-
tion of starting configurations for trajectory compu-
tations, we can generate matching starting conditions
for each ensemble member. Hence, when comparing
two ensemble members, we have a set of pairs of cor-
IVAPP 2020 - 11th International Conference on Information Visualization Theory and Applications
188

(a) standard elliptic table (b) perturbed elliptic table
(c) comparative visualization (d) symplectic dynamics
Figure 4: Juxtaposed visualization of two simulation runs using standard dynamics with parameters (a) a = 7,b = 4,r = 2, w =
2 and (b) a = 7,b = 4, r = 2.001,w = 2. (c) The comparative visualization highlights differences based on color mapping the
trajectories’ distances d
t
. (d) When perturbing the standard elliptic table (a = 4, b = 6, r = w = 2) by increasing parameters
r = 2.001 and w = 2.005, the comparative visualization for symplectic dynamics highlights qualitative changes in the form of
cyclic structures.
responding trajectories.
Let A = (A
j
)
1≤ j≤n
and B = (B
j
)
1≤ j≤n
be a pair of
corresponding trajectories. We define the difference
of two collision points using a Euclidean metric by
d
c
(A
j
,B
j
) =
|A
j,1
− B
j,1
|
2
T
+ |A
j,2
− B
j,2
|
2
T
1
2
with |x − y|
T
= min(|x − y|,l − |x − y|) being the dis-
tance of two points in an interval quotient space with
length l homeomorphic to S
1
. The difference of the
trajectories is, then, defined as the average difference
of the collision points, i.e.,
d
t
(A,B) =
∑
n
j=1
d
c
(A
j
,B
j
)
n
.
Having computed the distances d
t
(A,B) for all tra-
jectory pairs, we can highlight those trajectories A (or
B respectively), where the differences are strongest.
We achieve this by a applying a color mapping to the
trajectories that maps the distances (after normaliza-
tion to the unit interval) linearly from a background
color to a foreground color. Thus, the more different
trajectory A is from trajectory B the more it is empha-
sized. Figure 4(c) shows such a comparative visual-
ization of two ensemble members.
4.3 Ensemble Visualization
Our final aim is to fulfill Requirement 1, i.e., to al-
low for an analysis of an entire ensemble to investi-
gate the impact of the simulation parameters. Thus,
we need to compare ensemble members at a global
scale. Let S
1
and S
2
be two simulation runs each con-
taining m trajectories A
(i)
1≤i≤m
and B
(i)
1≤i≤m
. Building
upon the distance metric d
t
(A
(i)
,B
(i)
) for correspond-
ing trajectory pairs, we define the difference between
two simulation runs by the average of the distances of
all corresponding trajectory pairs, i.e., we define
d
s
(S
1
,S
2
) =
∑
m
i=1
d
t
(A
(i)
,B
(i)
)
m
.
We compute this distance for each pair of simulation
runs in a given ensemble. The pairwise distances for
Visual Analysis of Billiard Dynamics Simulation Ensembles
189

(a) influence of ratio a/b (b) influence of parameter r
(c) influence of parameter w (d) influence of ratio r/w
Figure 5: Color coding the MDS plots by parameter values for symplectic billiards ensemble shows that r and w are the key
parameters.
an ensemble of k simulation runs can be stored in a
symmetric k × k distance matrix
D = (d
s
(S
i
,S
j
))
1≤i, j≤k
.
The ensemble visualization shall depict the sim-
ilarities (or distances) of all ensemble members.
Hence, we want to find a 2D embedding, where the
2D Euclidean distances of the points that represent
the ensemble members in the embedding resemble the
distances stored in distance matrix D. This is exactly
the objective of the classical metric multi-dimensional
scaling (MDS) approach. Of course, plenty of other
embeddings exist in literature, but MDS reflects our
goal of preserving the computed distances by mini-
mizing the stress function (Kruskal and Wish, 1978).
For the implementation, we follow the standard so-
lution via an eigendecomposition of the Gram ma-
trix (Jung, ).
The outcome of the MDS step is visualized in the
form of a 2D scatterplot. Since our goal is to de-
tect the influence of the billiard table’s parameter, we
support color mapping of the scatterplot with respect
to interactively selected parameters or their ratio, see
Figure 5.
5 RESULTS AND DISCUSSION
We apply our methods to simulation ensembles for
standard and symplectic billiard dynamics to answer
the questions raised in Section 3. We first investigated
the impact of the choice of parameters a and b by con-
sidering a circular table (a = b = 1, r = w = 2) and
perturbing it slightly (a = 1.002). For standard dy-
namics, the phase-space visualizations on a circular
table exhibits straight trajectories, as the angles are
not changing, see Figure 6(a). However, when alter-
ing parameter a slightly, the behavior changes qualita-
tively, as trajectories with periodic orbits emerge, see
Figure 6(b). This finding confirms what was expected
and known from literature. Surprisingly though, this
IVAPP 2020 - 11th International Conference on Information Visualization Theory and Applications
190

(a) a = 1 (b) a = 1.002
Figure 6: Phase-space visualizations of standard dynamics on circular (a) and slightly perturbed circular table (b) show the
emergence of qualitatively different trajectories when changing parameter a.
was not true for symplectic dynamics, where phase-
space visualization for the perturbed table remained
qualitatively equivalent to Figure 6(a). When increas-
ing the ellipticity of the table (e.g., further increas-
ing parameter a), the phase-space visualizations for
standard dynamics exhibit more and more orbit struc-
tures, see Figure 3(a), while phase-space visualization
for symplectic dynamics still consists of horizontal
curves but with waves of increasing amplitudes, see
Figure 3(b).
As a second investigation, we looked into the im-
pact of the choice of parameters r and w by comparing
a standard elliptic table to a perturbed one. For stan-
dard dynamics, the phase-space visualizations seem
almost identical when slightly increasing r from 2 to
2.001, see Figure 4(a,b), but the comparative visu-
alization exhibits some structural changes, see Fig-
ure 4(c). In this investigation, the same holds true for
symplectic dynamics: The comparative visualization
in Figure 4(d) highlights emerging cyclic structures
for perturbed tables, which have not been observed
for the standard elliptic table (cf. Figure 3(b)).
Based on these initial investigation, we generated
ensembles with many different parameter configura-
tions. For standard dynamics, we generated initial
collisions by sampling the phase space equidistantly
with 23 position × 31 direction samples. For each
initial collision, we computed a trajectory with 200
collision points. These 23 × 31 trajectories are com-
puted for each ensemble member, where the ensem-
ble is formed by choosing parameters from ranges
a ∈ [4;4.004], b ∈ [5; 5.001], r = 2, and w ∈ [2; 2.009]
with step size 0.001. The MDS plot exhibits an arc
shape, see Figure 7. Color coding the plot to inves-
tigate the impact of the parameter, we can make the
following observations: The color transitions for pa-
rameters a, b, or their ratio a/b confirm the observa-
tion from above that these parameters locally affect
the outcome, see Figure 7(b,c). The color transitions
in Figure 7(b,c) form clusters, i.e., we see groups of
points where colors go from dark to bright and then
this pattern is repeated for the next group. Investigat-
ing the influence of parameter w in Figure 7(a) pro-
vides a different picture: There is a trend of having
brighter colors to the left of the arc and darker colors
to the right, but the transition is not monotonic. How-
ever, when investigating the color transition for ratio
r/w in Figure 7(d), we observe that there is a mono-
tonic color transition from bright to dark that clearly
follows the arc. Hence, we can formulate the suppo-
sition that ratio r/w is the dominant factor for signif-
icant changes, as runs occur the more similar in the
MDS plot the more they have a similar ratio. This is
in accordance with earlier studies in the field.
Finally, we generate a simulation ensemble for
symplectic dynamics using the same initial collisions
and trajectory lengths as above, while choosing pa-
rameters from ranges a ∈ [4; 4.006], b ∈ [6; 6.006],
r ∈ [2; 2.006], and w ∈ [2; 2.006] with step size 0.001.
Here, such studies had not been performed yet, but
is easily supported by our tool. Figure 5 shows that
parameters r and w and their ratio r/w are, again, re-
sponsible for generating main trends and clusters in
the MDS plots, while parameters a, b and their ratio
a/b are only responsible for small variations within
the clusters. Figure 5(a) clearly shows the color tran-
sitions only within each of the nine clusters for the
ratio a/b. For parameter r, there is a transition that
creates three stripes of brightness from the upper left
to the lower right. Similarly, for parameter w, there
is a transition that creates three stripes of brightness
from the lower left to the upper right. When combin-
ing the two parameters by looking at their ratio r/w,
there is a transition from left to right with five stripes.
Hence, we can conclude that for both standard and
symplectic dynamics changes of ratio r/w dominate
Visual Analysis of Billiard Dynamics Simulation Ensembles
191
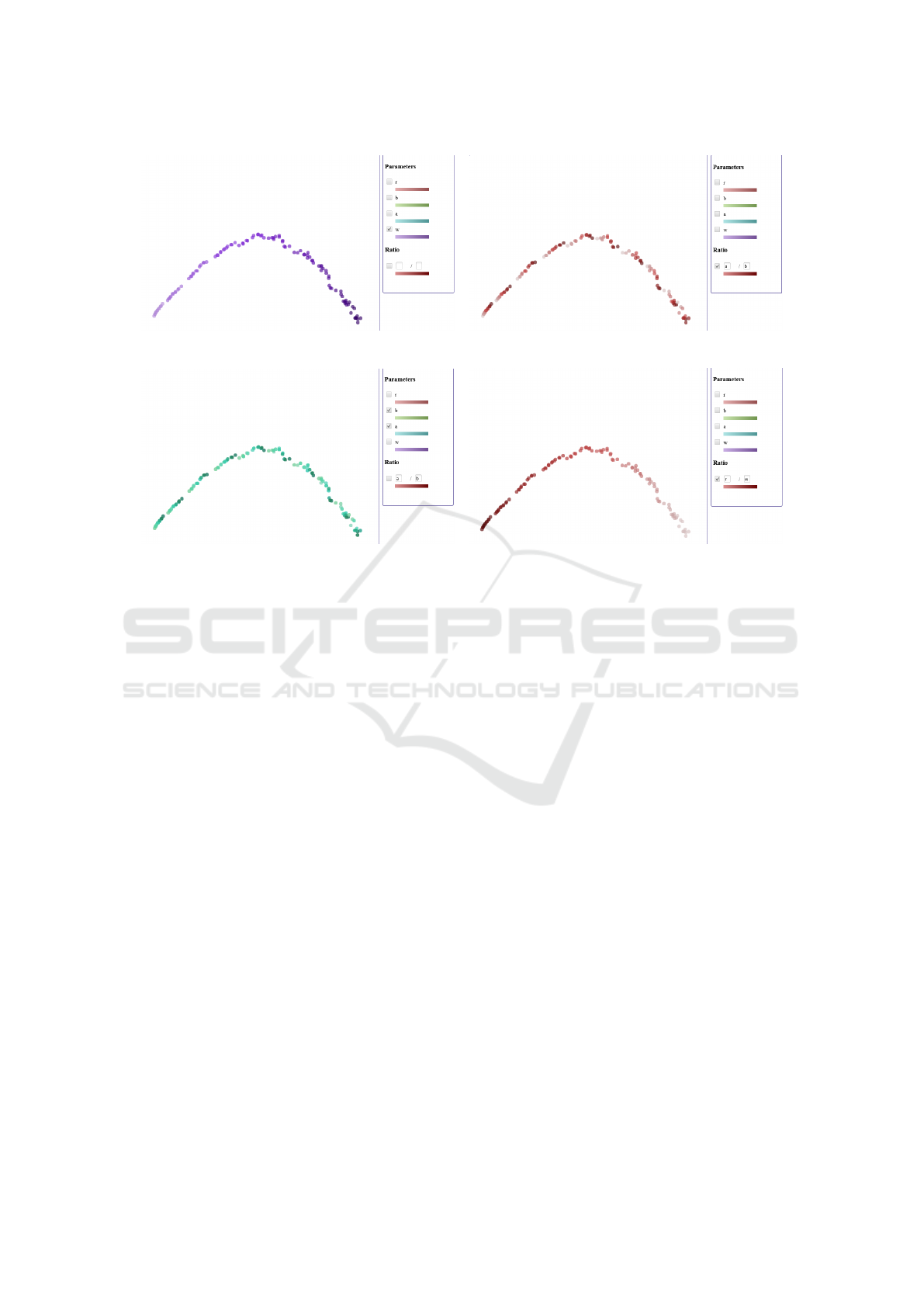
(a) influence of parameter w (b) influence of ratio a/b
(c) influence of parameters a and b (d) influence of ratio r/w
Figure 7: The main structure in the MDS visualization of the standard billiards ensemble is governed by ratio r/w.
over changes of ratio a/b. This is a novel finding that
had not been reported yet.
6 CONCLUSION
We have presented a novel approach to analyze bil-
liards using ensemble visualizations. For standard dy-
namics, we were able to confirm prior studies, while
for symplectic dynamics we made new discoveries
leading to suppositions that are a good starting point
for theoretical proofs.
REFERENCES
Albers, P. and Tabachnikov, S. (2018). Introducing sym-
plectic billiards. Advances in Mathematics, 333:822 –
867.
Birkhoff, G. (1927). Dynamical Systems. American Mathe-
matical Society / Providence, Estados Unidos. Amer-
ican Mathematical Society.
Boeing, G. (2016). Visual analysis of nonlinear dynamical
systems: Chaos, fractals, self-similarity and the limits
of prediction. Systems, 4:37.
Jung, S. Lecture Notes: Multidimensional scaling, Ad-
vanced Applied Multivariate Analysis.
Kruskal, J. and Wish, M. (1978). Multidimensional Scaling.
Number Nr. 11 in 07. SAGE Publications.
Kumpf, A., Rautenhaus, M., Riemer, M., and Westermann,
R. (2019). Visual analysis of the temporal evolution of
ensemble forecast sensitivities. IEEE Transactions on
Visualization and Computer Graphics, 25(1):98–108.
Ngo, Q. Q., H
¨
utt, M.-T., and Linsen, L. (2016). Visual
Analysis of Governing Topological Structures in Ex-
citable Network Dynamics. Computer Graphics Fo-
rum, 35(3):301–310.
Tabachnikov, S. (2005). Geometry and billiards. Stu-
dent Mathematical Library. 30. American Mathemat-
ical Society, Providence, RI; Mathematics Advanced
Study Semesters, University Park, PA,.
Tricoche, X., Garth, C., Sanderson, A., and Joy, K. (2012).
Visualizing Invariant Manifolds in Area-Preserving
Maps, pages 109–124. Springer Berlin Heidelberg,
Berlin, Heidelberg.
IVAPP 2020 - 11th International Conference on Information Visualization Theory and Applications
192
