
Structure Preserving Encoding of Non-euclidean Similarity Data
Maximilian M
¨
unch
1,2
, Christoph Raab
1,3
, Michael Biehl
2
and Frank-Michael Schleif
1
1
Department of Computer Science and Business Information Systems,University of Applied Sciences W
¨
urzburg-Schweinfurt,
D-97074 W
¨
urzburg, Germany
2
University of Groningen, Bernoulli Institute for Mathematics, Computer Science and Artificial Intelligence,
P.O. Box 407, NL-9700 AK Groningen, The Netherlands
3
Bielefeld University, Center of Excellence, Cognitive Interaction Technology, CITEC, D-33619 Bielefeld, Germany
Keywords:
Non-euclidean, Similarity, Indefinite, Von Mises Iteration, Eigenvalue Correction, Shifting, Flipping,
Clipping.
Abstract:
Domain-specific proximity measures, like divergence measures in signal processing or alignment scores in
bioinformatics, often lead to non-metric, indefinite similarities or dissimilarities. However, many classical
learning algorithms like kernel machines assume metric properties and struggle with such metric violations.
For example, the classical support vector machine is no longer able to converge to an optimum. One possible
direction to solve the indefiniteness problem is to transform the non-metric (dis-)similarity data into positive
(semi-)definite matrices. For this purpose, many approaches have been proposed that adapt the eigenspectrum
of the given data such that positive definiteness is ensured. Unfortunately, most of these approaches modify
the eigenspectrum in such a strong manner that valuable information is removed or noise is added to the data.
In particular, the shift operation has attracted a lot of interest in the past few years despite its frequently re-
occurring disadvantages. In this work, we propose a modified advanced shift correction method that enables
the preservation of the eigenspectrum structure of the data by means of a low-rank approximated nullspace
correction. We compare our advanced shift to classical eigenvalue corrections like eigenvalue clipping, flip-
ping, squaring, and shifting on several benchmark data. The impact of a low-rank approximation on the data’s
eigenspectrum is analyzed.
1 INTRODUCTION
Learning classification models for structured data is
often based on pairwise (dis-)similarity functions,
which are suggested by domain experts. How-
ever, these domain-specific (dis-)similarity measures
are typically not positive (semi-)definite (non-psd).
These so-called indefinite kernels are a severe prob-
lem for many kernel-based learning algorithms be-
cause classical mathematical assumptions such as
positive (semi-)definiteness (psd), used in the under-
lying optimization frameworks, are violated. For ex-
ample, the modified Hausdorff-distance for structural
pattern recognition, various alignment scores in bioin-
formatics, and also many others generate non-metric
or indefinite similarities or dissimilarities.
As a consequence, e.g., the classical Support Vec-
tor Machine (SVM) (Vapnik, 2000) has no longer a
convex solution - in fact, most standard solvers will
not even converge for this problem (Loosli et al.,
2016). Researchers in the field of, e.g., psychology
(Hodgetts and Hahn, 2012), vision (Scheirer et al.,
2014; Xu et al., 2011), and machine learning (Duin
and Pekalska, 2010) have criticized the typical re-
striction to metric similarity measures. (Duin and
Pekalska, 2010) pointed out many real-life problems
to be better addressed by, e.g., kernel functions that
are not restricted to be based on a metric. The use
of divergence measures (Schnitzer et al., 2012; Zhang
et al., 2009) is very popular for spectral data analy-
sis in chemistry, geo- and medical sciences (van der
Meer, 2006), and are in general not metric. Also, the
popular Dynamic Time Warping (DTW) (Sakoe and
Chiba, 1978) algorithm provides a non-metric align-
ment score, which is commonly used as a proximity
measure between two one-dimensional functions of
different length. In image processing and shape re-
trieval, indefinite proximities are frequently obtained
in the form of the inner distance (Ling and Jacobs,
2007) - another non-metric measure. Further promi-
nent examples of genuine non-metric proximity mea-
sures can be found in the field of bioinformatics where
Münch, M., Raab, C., Biehl, M. and Schleif, F.
Structure Preserving Encoding of Non-euclidean Similarity Data.
DOI: 10.5220/0008955100430051
In Proceedings of the 9th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2020), pages 43-51
ISBN: 978-989-758-397-1; ISSN: 2184-4313
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
43

classical sequence alignment algorithms (e.g., smith-
waterman score (Gusfield, 1997)) produce non-metric
proximities. Those domain-specific measures are ef-
fective but not particularly accessible in the mathe-
matical context. The importance of preserving the
non-metric part of the data is emphasized by many au-
thors. Multiple authors argue that the non-metric part
of the data contains valuable information and should
not be removed (Scheirer et al., 2014; Pekalska and
Duin, 2005).
There are two main directions to handle the prob-
lem of indefiniteness: using insensitive methods like
indefinite kernel fisher discrimination (Haasdonk and
Pekalska, 2008), empirical feature space approaches
(Alabdulmohsin et al., 2016), or correcting the eigen-
spectrum to psd.
Due to its strong theoretical foundations, Support
Vector Machine (SVM) has been extended for indef-
inite kernels in several ways (Haasdonk, 2005; Luss
and d’Aspremont, 2009; Gu and Guo, 2012). A re-
cent survey on indefinite learning is given in (Schleif
and Ti
˜
no, 2015). In (Loosli et al., 2016), a stabiliza-
tion approach was proposed to calculate a valid SVM
model in the Kr
˘
ein space, which can be directly ap-
plied to indefinite kernel matrices. This approach has
shown great promise in several learning problems but
used the so-called flip approach to correct the negative
eigenvalues, which is a substantial modification of the
structure of the eigenspectrum. In (Loosli, 2019),
a similar approach was proposed using the classical
shift technique.
The present paper provides a shift correction ap-
proach that preserves the eigenstructure of the data
and avoids cubic eigendecompositions. We also ad-
dress the limitation of the classical shift correction,
which renders to be impracticable and error-prone in
practical settings.
2 LEARNING WITH NON-PSD
KERNELS
Learning with non-psd kernels can be a challeng-
ing problem and may occur very quickly when using
domain-specific measures or noise occurs in the data.
The metric violations cause negative eigenvalues in
the eigenspectrum of the kernel matrix K, leading
to non-psd similarity matrices or indefinite kernels.
Many learning algorithms are based on kernel formu-
lations, which have to be symmetric and psd. The
mathematical meaning of a kernel is the inner product
in some Hilbert space (Shawe-Taylor and Cristianini,
2004). However, it is often loosely considered sim-
ply as a pairwise ”similarity” measure between data
items, leading to a similarity matrix S.
If a particular learning algorithm requires the use
of Mercer kernels and the similarity measure does not
fulfill the kernel conditions, then one of the mentioned
strategies have to be applied to ensure a valid model.
2.1 Background and Basic Notation
Consider a collection of N objects x
i
, i = {1,2,...,N},
in some input space X . Given a similarity function
or inner product on X , corresponding to a metric,
one can construct a proper Mercer kernel acting on
pairs of points from X . For example, if X is a finite-
dimensional vector space, a classical similarity func-
tion is the Euclidean inner product (corresponding to
the Euclidean distance) - a core component of various
kernel functions such as the famous radial basis func-
tion (RBF) kernel. Now, let φ : X 7→ H be a mapping
of patterns from X to a Hilbert space H equipped with
the inner product h·, ·i
H
. The transformation φ is, in
general, a non-linear mapping to a high-dimensional
space H and may, in general, not be given in an ex-
plicit form. Instead, a kernel function k : X × X 7→ R
is given, which encodes the inner product in H . The
kernel k is a positive (semi-)definite function such that
k(x, x
0
) = hφ(x),φ(x
0
)i
H
, for any x, x
0
∈ X . The ma-
trix K
i, j
:= k(x
i
,x
j
) is an N × N kernel (Gram) ma-
trix derived from the training data. For more general
similarity measures, subsequently, we also use S to
describe a similarity matrix. Such an embedding is
motivated by the non-linear transformation of input
data into higher dimensional H allowing linear tech-
niques in H . Kernelized methods process the em-
bedded data points in a feature space utilizing only
the inner products h·,·i
H
(Shawe-Taylor and Cristian-
ini, 2004), without the need to explicitly calculate φ,
known as kernel trick. The kernel function can be
very generic. Most prominent are the linear kernel
with k(x,x
0
) = hφ(x),φ(x
0
)i where hφ(x),φ(x
0
)i is the
Euclidean inner product and φ is the identity map-
ping, or the RBF kernel k(x,x
0
) = exp
−
||x−x
0
||
2
2σ
2
,
with σ > 0 as a free scale parameter. In any case,
it is always assumed that the kernel function k(x,x
0
)
is psd. However, this assumption is not always ful-
filled and the underlying similarity measure may not
be metric and hence not lead to a Mercer kernel. Ex-
amples can be easily found in domain-specific sim-
ilarity measures, as mentioned before and detailed
later on. Such similarity measures imply indefinite
kernels, preventing standard ”kernel-trick” methods
developed for Mercer kernels to be applied.
ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods
44

2.2 Eigenspectrum Approaches
A natural way to address the indefiniteness problem
and to obtain a psd similarity matrix is to correct
the eigenspectrum of the original similarity matrix
S. Popular strategies include eigenvalue correction by
flipping, clipping, squaring, and shifting. The non-
psd similarity matrix S is decomposed by an eigen-
decomposition: S = UΛU
>
, where U contains the
eigenvectors of S and Λ contains the corresponding
eigenvalues λ
i
. Now, the eigenvalues in Λ can be ma-
nipulated to eliminate all negative parts. Following
the operation, the matrix can be reconstructed, now
being psd.
Clip Eigenvalue Correction. All negative eigen-
values in Λ are set to 0. Such a spectrum clip leads
to the nearest psd matrix S in terms of the Frobe-
nius norm (Higham, 1988). Such a correction can be
achieved by an eigendecomposition of the matrix S,
a clipping operator on the eigenvalues, and the subse-
quent reconstruction. This operation has a complexity
of O(N
3
). The complexity might be reduced by either
a low-rank approximation or the approach shown by
(Luss and d’Aspremont, 2009) with roughly quadratic
complexity.
Flip Eigenvalue Correction. All negative eigenval-
ues in Λ are set to λ
i
:= |λ
i
| ∀i, which at least keeps
the absolute values of the negative eigenvalues and
keeps the relevant information (Pekalska and Duin,
2005). This operation can be calculated with O(N
3
)
or O(N
2
) if low-rank approaches are used.
Square Eigenvalue Correction. All negative
eigenvalues in Λ are set to λ
i
:= λ
2
i
∀i which ampli-
fies large and very small eigenvalues. The square
eigenvalue correction can be achieved by matrix
multiplication (Strassen, 1969) with ≈ O(N
2.8
).
Classical Shift Eigenvalue Correction. The shift
operation was already discussed earlier by different
researchers (Filippone, 2009) and modifies Λ such
that λ
i
:= λ
i
− min
i j
Λ ∀i. The classical shift eigen-
value correction can be accomplished with linear
costs if the smallest eigenvalue λ
min
is known. Oth-
erwise, some estimator for λ
min
is needed. A few es-
timators for this purpose have been suggested: ana-
lyzing the eigenspectrum on a subsample, making a
reasonable guess, or using some low-rank eigende-
composition. In our approach, we suggest employing
a power iteration method, for example the von Mises
approach, which is fast and accurate.
Spectrum shift enhances all the self-similarities
and therefore the eigenvalues by the amount of λ
min
and does not change the similarity between any two
different data points, but it may also increase the in-
trinsic dimensionality of the data space and amplify
noise contributions.
2.3 Limitations
Multiple approaches have been suggested to correct
the eigenspectrum of a similarity matrix and to obtain
a psd matrix (Pekalska and Duin, 2005; Schleif and
Ti
˜
no, 2015). Most approaches modify the eigenspec-
trum in a very powerful way and are also costly due
to an involved cubic eigendecomposition. In particu-
lar, the clip, flip, and square operator have an appar-
ent strong impact. While the clip method is useful in
case of noise, it may also remove valuable contribu-
tions. The clip operator only removes eigenvalues, but
generally keeps the majority of the eigenvalues unaf-
fected. The flip operator, on the other hand, affects
all negative eigenvalues by changing the sign and this
will additionally lead to a reorganization of the eigen-
values. The square operator is similar to flip but ad-
ditionally emphasizes large eigencontributions while
fading out eigenvalues below 1. The classical shift
operator is only changing the diagonal of the sim-
ilarity matrix leading to a shift of the whole eigen-
spectrum by the provided offset. This may also lead
to reorganizations of the eigenspectrum due to new
non-zero eigenvalue contributions. While this sim-
ple approach seems to be very reasonable, it has the
major drawback that all (!) eigenvalues are shifted,
which also affects small or even 0 eigenvalue contri-
butions. While 0 eigenvalues have no contribution in
the original similarity matrix, they are artificially up-
raised by the classical shift operator. This may intro-
duce a large amount of noise in the eigenspectrum,
which could potentially lead to substantial numerical
problems for employed learning algorithms, for ex-
ample, kernel machines. Additionally, the intrinsic
dimensionality of the data is increased artificially, re-
sulting in an even more challenging problem.
3 ADVANCED SHIFT
CORRECTION
To address the aforementioned challenges, we suggest
an alternative formulation of the shift correction, sub-
sequently referred to as advanced shift. In particu-
lar, we would like to keep the original eigenspectrum
structure and aim for a sub-cubic eigencorrection.
Structure Preserving Encoding of Non-euclidean Similarity Data
45

3.1 Algorithmic Approach
As mentioned in Sec. 2.3 the classical shift operator
introduces noise artefacts for small eigenvalues. In
the advanced shift procedure, we will remove these
artificial contributions by a null space correction. This
is particularly effective if non-zero, but small eigen-
values are also taken into account. Accordingly, we
apply a low-rank approximation of the similarity ma-
trix as an additional pre-processing step. The proce-
dure is summarized in Algorithm 1.
Algorithm 1: Advanced shift eigenvalue correction.
Advanced shift(S, k)
if approximate to low rank then
S := LowRankApproximation(S,k)
end if
λ := |ShiftParameterDetermination(S)|
B := NullSpace(S)
N := B · B
0
S
∗
:= S + 2 · λ · (I − N)
return S
∗
The first part of the algorithm applies a low-rank
approximation on the input similarities S using a re-
stricted SVD or other techniques (Sanyal et al., 2018).
If the number of samples N ≤ 1000, then the rank pa-
rameter k = 30 and k = 100, otherwise. The shift pa-
rameter λ is calculated on the low-rank approximated
matrix, using a von Mises or power iteration (Mises
and Pollaczek-Geiringer, 1929) to determine the re-
spective largest negative eigenvalue of the matrix. As
shift parameter, we use the absolute value of λ for
further steps. This procedure provides an accurate
estimate of the largest negative eigenvalue instead of
making an educated guess as suggested. This is par-
ticular relevant because the scaling of the eigenval-
ues can be very different between the various datasets,
which may lead to an ineffective shift (still remaining
negative eigenvalues) if the guess is incorrect. The
basis B of the nullspace is calculated, again by a re-
stricted SVD. The nullspace matrix N is obtained by
calculating a product of B. Due to the low-rank ap-
proximation, we ensure that small eigenvalues, which
are indeed close to 0 due to noise, are shrunk to 0 (Ilic
et al., 2007). In the final step, the original S or the
respective low-rank approximated matrix
ˆ
S is shifted
by the largest negative eigenvalue λ that is determined
by von Mises iteration. By combining the shift with
the nullspace matrix N and the identity matrix I, the
whole matrix will be affected by the shift and not only
the diagonal matrix. At last, the doubled shift factor
2 ensures that the largest negative eigenvalue
ˆ
λ
∗
of
the new matrix
ˆ
S
∗
will not become 0, but remains a
Table 1: Overview of the different datasets. Details are
given in the textual description.
Dataset #samples #classes
Balls3d 200 2
Balls50d 2,000 4
Gauss 1,000 2
Chromosomes 4,200 21
Protein 213 10
SwissProt 10,988 10
Aural Sonar 100 2
Facerec 945 10
Sonatas 1,068 5
Voting 435 2
Zongker 2,000 10
contribution.
Complexity: The advanced shift approach shown in
Algorithm 1 is comprised of various subtasks with
different complexities. The low-rank approximation
can be achieved with O(N
2
) as well as the nullspace
approximation. The shift parameter is calculated by
von Mises iteration with O(N
2
). Since B is a rect-
angular N × k matrix, the matrix N can be calculated
with O(N
2
).
The final eigenvalue correction to obtain
ˆ
S
∗
is also
O(N
2
). In summary, the low-rank advanced shift
eigenvalue correction can be achieved with O(N
2
) op-
erations. If no low-rank approximation is employed,
the calculation of N will cost O(N
2.8
) using Strassen
matrix multiplication.
In the experiments, we analyze the effect of our
new transformation method with and without a low-
rank approximation and compare it to the aforemen-
tioned alternative methods.
3.2 Structure Preservation
In our context, the term structure preservation refers
to the structure of the eigenspectrum. Those parts
of the eigenspectrum which are not to be corrected
to make the matrix psd should be kept unchanged.
The various eigen correction methods have a differ-
ent impact on the eigenspectrum as a whole and of-
ten change the structure of the eigenspectrum. Those
changes are: changing the sign of an eigenvalue,
changing its magnitude, removing an eigenvalue, in-
troducing a new eigenvalue (which was 0 before), or
changing the position of the eigenvalue with respect to
a ranking. The last one is particularly relevant if only
a few eigenvectors are used in some learning models,
like kernel PCA or similar methods. To illustrate the
various impact on the eigenspectrum, the plots (a)-(d)
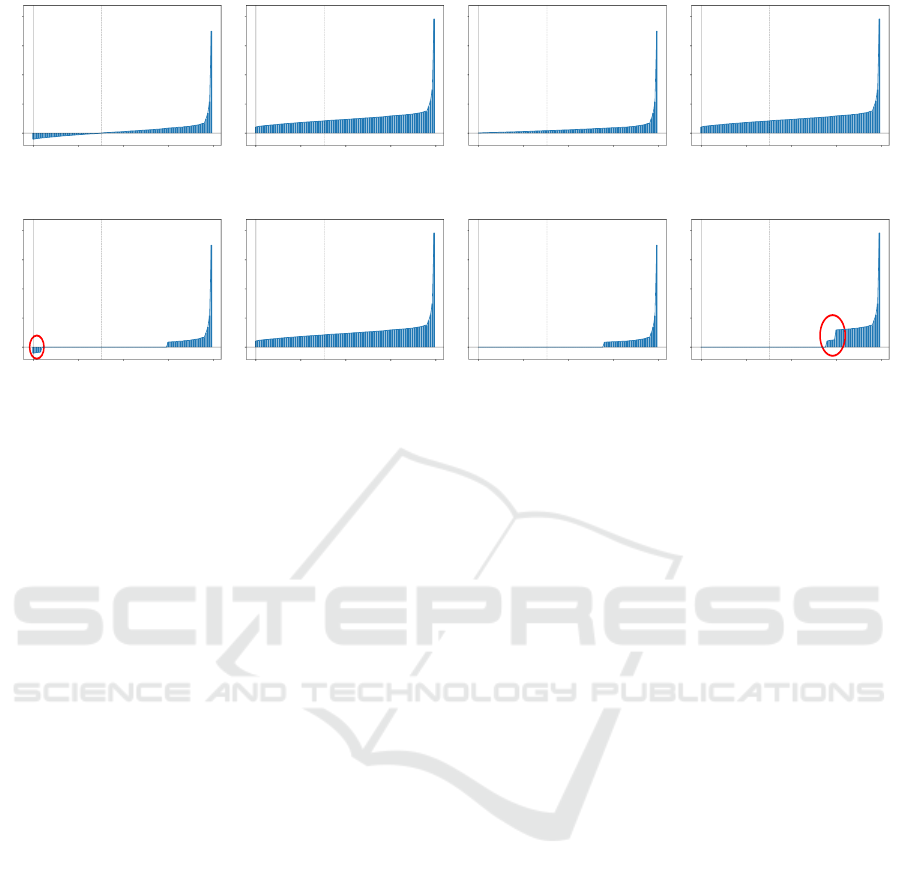
of Figure 1 plots (a)-(d), we show the eigencorrec-
tion methods on the original of an exemplary similar-
ity matrix, here the Aural-Sonar dataset. Obviously,
ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods
46
0 25 50 75 100
0
10
20
30
40
(a) Original
0 25 50 75 100
0
10
20
30
40
(b) Classic Shift
0 25 50 75 100
0
10
20
30
40
(c) Flip
0 25 50 75 100
0
10
20
30
40
(d) Advanced Shift
0 25 50 75 100
0
10
20
30
40
(e) Original low-rank
0 25 50 75 100
0
10
20
30
40
(f) Classic Shift low-rank
0 25 50 75 100
0
10
20
30
40
(g) Flip low-rank
0 25 50 75 100
0
10
20
30
40
(h) Advanced Shift low-rank
Figure 1: Eigenspectrum plots of the protein data set using the different eigenspectrum corrections. Plots (e) - (h) are generated
using a low-rank processing. The x-axis represents the index of the eigenvalue while the y-axis illustrates the value of the
eigenvalue. The dashed vertical bar indicates the transition between negative and non-negative eigenvalues. The classical shift
clearly shows an increase in the intrinsic dimensionality by means of non-zero eigenvalues. For flip and the advanced shift
we also observe a reorganization of the eigenspectrum.
the classical shift increases the number of non-zero
eigencontributions introducing artificial noise in the
data. The same is also evident for the advanced shift
(without low-rank approximation), but this is due to
a very low number of zero eigenvalues for this par-
ticular dataset and can be cured in the low-rank ap-
proach. The plots (e)-(h) show the respective correc-
tions on a low-rank representation of the Aural-Sonar
dataset. Obviously, the classical shift is still inappro-
priate whereas the advanced shift correction preserves
the structure of the spectral information. In contrast
to (f) and (g), the small negative eigenvalues from
(e) are still taken into account in (h), which can be
recognized by the abrupt eigenvalue step in the cir-
cle. In any case, clipping removes the negative eigen-
contributions leading to a plot similar to (a),(e) but
without negative contributions. The spectrum of the
square operations looks very similar to the results for
the flip method. Flip and square effect the ranks of
the eigenvalues, but square additionally changes the
magnitudes.
Although we only show results for the Aural-
Sonar data in this section, we observed similar find-
ings for the other datasets as well. This refers primar-
ily to the structure of the eigenspectrum, with hardly
eigenvalues close to zero. In particular, a more elab-
orated treatment of the eigenspectrum becomes evi-
dent, motivating our approach in favour of more sim-
ple approaches like classical shift or flip.
4 EXPERIMENTS
This part contains the results of the experiments
aimed at demonstrating the effectiveness of our pro-
posed advanced shift correction in combination with
low-rank approximation. The used data are briefly de-
scribed in the following and summarized in Table 1,
with details given in the references.
4.1 Datasets
We use a variety of standard benchmark data for
similarity-based learning. All data are indefinite with
different spectral properties. If the data are given as
dissimilarities, a corresponding similarity matrix can
be obtained by double centering (Pekalska and Duin,
2005): S = −JDJ/2 with J = (I −11
>
/N), with iden-
tity matrix I and vector of ones 1.
For evaluation, we use three synthetic datasets:
Balls3d/Balls50d consist of 200/2000 samples in
two/four classes. The dissimilarities are generated be-
tween two constructed balls using the shortest dis-
tance on the surfaces. The original data description
is provided in (Pekalska et al., 2006).
For working with Gauss data, we create two
datasets X, each consisting of 1000 data points in two
dimensions divided into two classes. Data of the first
dataset are linearly separable, whereas data of the sec-
ond dataset are overlapping. To calculate dissimilarity
Structure Preserving Encoding of Non-euclidean Similarity Data
47
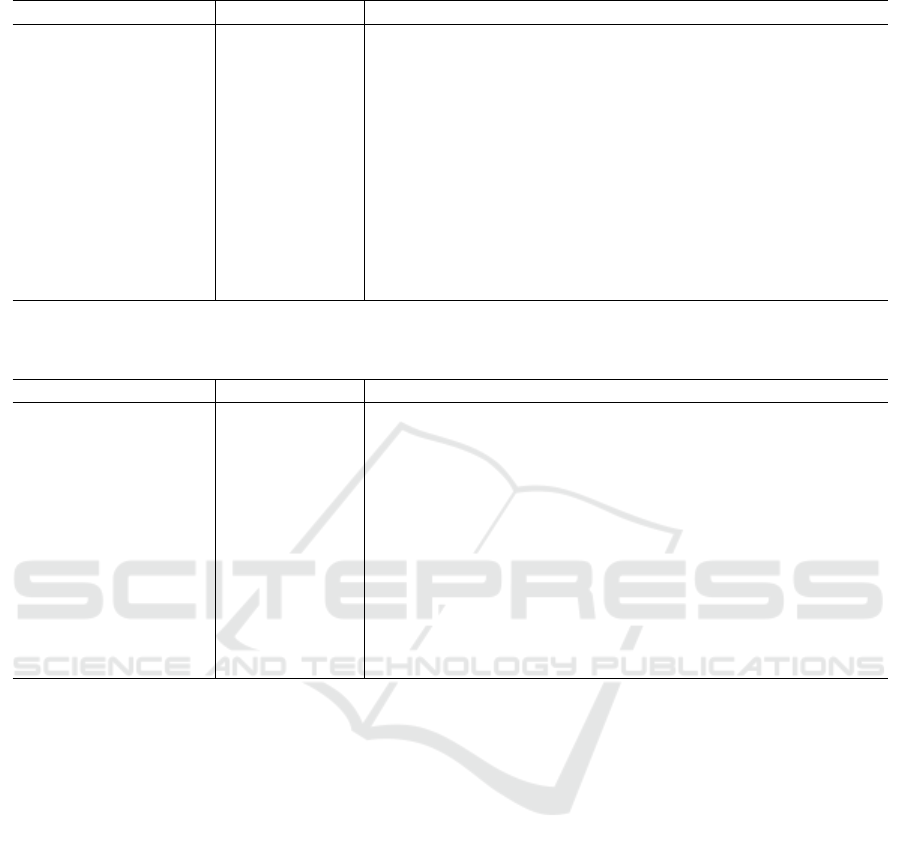
Table 2: Results using various eigen-correction methods on the original matrix. Best results are given in bold.
Dataset Advanced Shift Classic Shift Flip Clip Square
Aural Sonar 88.0 ± 0.07 90.0 ± 0.1 89.0 ± 0.08 91.0 ± 0.12 89.0 ± 0.09
Balls3d 42.5 ± 0.15 36.0 ± 0.06 98.0 ± 0.04 76.5 ± 0.08 55.0 ± 0.1
Balls50d 23.35 ± 0.03 20.5 ± 0.01 40.95 ± 0.02 28.45 ± 0.04 25.45 ± 0.04
Chromosomes 1.86 ± 0.0 not converged 97.86 ± 0.0 34.29 ± 0.03 96.71 ± 0.01
Facerec 88.99 ± 0.03 87.1 ± 0.03 85.61 ± 0.04 86.46 ± 0.04 85.82 ± 0.03
Gauss with overlap 89.3 ± 0.03 17.0 ± 0.02 91.4 ± 0.03 88.8 ± 0.02 91.2 ± 0.03
Gauss without overlap 98.5 ± 0.01 2.2 ± 0.01 100.0 ± 0.0 99.8 ± 0.0 100.0 ± 0.0
Protein 52.12 ± 0.06 55.37 ± 0.08 99.52 ± 0.01 93.46 ± 0.05 98.59 ± 0.02
Sonatas 82.87 ± 0.02 85.11 ± 0.02 91.01 ± 0.02 90.54 ± 0.03 93.45 ± 0.03
SwissProt 95.03 ± 0.01 96.2 ± 0.01 97.46 ± 0.0 97.46 ± 0.0 98.44 ± 0.0
Voting 95.65 ± 0.03 95.87 ± 0.03 96.79 ± 0.02 96.09 ± 0.02 96.78 ± 0.03
Zongker 92.15 ± 0.02 92.75 ± 0.02 97.65 ± 0.01 97.4 ± 0.01 97.25 ± 0.01
Table 3: Results using various eigen-correction methods on a low-rank approximated matrix. Best accuracies are given in
bold.
Dataset Advanced Shift Classic Shift Flip Clip Square
Aural Sonar 88.0 ± 0.13 89.0 ± 0.08 88.0 ± 0.06 86.0 ± 0.11 87.0 ± 0.11
Balls3d 100.0 ± 0.0 37.0 ± 0.07 96.0 ± 0.04 78.5 ± 0.05 55.0 ± 0.09
Balls50d 48.15 ± 0.04 20.65 ± 0.02 41.15 ± 0.03 27.2 ± 0.04 25.05 ± 0.02
Chromosomes 96.45 ± 0.01 not converged 97.29 ± 0.0 38.95 ± 0.02 96.07 ± 0.01
Facerec 62.33 ± 0.05 62.22 ± 0.07 63.27 ± 0.05 61.92 ± 0.07 86.13 ± 0.02
Gauss with overlap 91.6 ± 0.03 17.1 ± 0.03 91.5 ± 0.02 88.6 ± 0.03 91.3 ± 0.02
Gauss without overlap 100.0 ± 0.0 2.2 ± 0.01 100.0 ± 0.0 99.7 ± 0.0 100.0 ± 0.0
Protein 99.07 ± 0.02 58.31 ± 0.09 99.05 ± 0.02 98.59 ± 0.02 98.61 ± 0.02
Sonatas 94.29 ± 0.02 90.73 ± 0.02 94.19 ± 0.02 93.64 ± 0.04 93.44 ± 0.03
SwissProt 97.55 ± 0.01 96.48 ± 0.0 96.54 ± 0.0 96.42 ± 0.0 97.43 ± 0.0
Voting 97.24 ± 0.03 95.88 ± 0.03 96.77 ± 0.03 96.59 ± 0.04 96.77 ± 0.02
Zongker 97.7 ± 0.01 92.85 ± 0.01 97.2 ± 0.01 96.85 ± 0.01 96.75 ± 0.01
matrix D, we use D = tanh(−2.25 · X ·X
T
+ 2).
Further, we use three biochemical datasets:
The Kopenhagen Chromosomes data set consti-
tutes 4,200 human chromosomes from 21 classes rep-
resented by grey-valued images. These are transferred
to strings measuring the thickness of their silhouettes.
These strings are compared using edit distance. De-
tails are provided in (Neuhaus and Bunke, 2006).
Protein consists of 213 measurements in four
classes. From the protein sequences, similarities were
measured using an alignment scoring function. De-
tails are provided in (Chen et al., 2009).
SwissProt consists of 10,988 samples of protein
sequences in 10 classes taken as a subset from the
SwissProt database. The considered subset of the
SwissProt database refers to the release 37 mimicking
the setting as proposed in (Kohonen and Somervuo,
2002).
Another four datasets are taken from signal process-
ing:
Aural Sonar consists of 100 signals with two
classes, representing sonar signals dissimilarity mea-
sures to investigate the human ability to distinguish
different types of sonar signals by ear. Details are pro-
vided in (Chen et al., 2009).
Facerec dataset consists of 945 sample faces with
139 classes, representing sample faces of people,
compared by the cosine similarity as measure. De-
tails are provided in (Chen et al., 2009).
Sonatas dataset consists of 1068 sonatas from
five composers (classes) from two consecutive eras
of western classical music. The musical pieces were
taken from the online MIDI database Kunst der Fuge
and transformed to similarities by normalized com-
pression distance (Mokbel, 2016).
Voting contains 435 samples in 2 classes, repre-
senting categorical data, which are compared based
on the value difference metric (Chen et al., 2009).
Zongker dataset is a digit dissimilarity dataset.
The dissimilarity measure was computed between
2000 handwritten digits in 10 classes, with 200 en-
tries in each class (Jain and Zongker, 1997).
ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods
48

4.2 Performance in Supervised
Learning
We evaluate the performance of the proposed ad-
vanced shift correction on the mentioned datasets
against other eigenvalue correction methods using a
standard SVM classifier. The correction approaches
ensure that the input similarity, herein used as a kernel
matrix, is psd. Within all experiments, we measured
the algorithm’s accuracy and its standard deviation in
a ten-fold cross-validation shown in Table 2 and Table
3. The parameter C has been selected for each correc-
tion method by a grid search on independent data not
used during testing.
In Table 2, we show the classification performance
for the considered data and correction approaches.
The flip correction performed best, followed by the
square correction, which is in agreement with former
findings by (Loosli et al., 2016). The clip correction
is also often effective. Both shift approaches strug-
gle on a few datasets, in particular, those having a
more complicated eigenspectrum (see e.g. (Schleif
and Ti
˜
no, 2015)) and if the matrix is close to a full
rank structure.
In Table 3, which includes the low-rank approxi-
mation, we observe similar results to Table 2, but the
advanced shift correction performs much better also
in comparison to the other methods (also to the ones
without low-rank approximation). In contrast to Table
2, the low-rank approximation leads to a large num-
ber of truly zero eigenvalues making the advanced
shift correction effective. It becomes evident that be-
sides the absolute magnitude of the larger eigenval-
ues also the overall structure of the eigenspectrum is
important for both shift operators. The proposed ap-
proach benefits from eigenspectra with many close to
zero eigenvalues which occurs in many practical data.
In fact, many datasets have an intrinsic low-rank na-
ture, which we employ in our approach. In any case,
the classical shift increases the intrinsic dimension-
ality also if many eigenvalues have been zero in the
original matrix. This leads to substantial performance
loss in the classification models, as seen in Table 2
but also in Table 3. Surprisingly, the shift operator
is still occasionally preferred in the literature (Filip-
pone, 2009; Laub, 2004; Loosli, 2019) but not on a
large variety of data, which would have shown the ob-
served limitations almost sure. The herein proposed
advanced shift overcomes the limitations of the clas-
sical shift. Considering the results of Table 3, the ad-
vanced shift correction is almost preferable in each
scenario but should be avoided if low-rank approx-
imations have a negative impact on the information
content of the data. One of those rare cases is the Fac-
erec dataset which has a large number of small nega-
tive eigenvalues and many possibly meaningful posi-
tive eigenvalues. Any kind of correction of the eigen-
spectrum of this dataset addressing the negative part
has almost no effect - the largest negative eigenvalue
is −7e10
−4
. In this case, a low-rank approximation
removes large parts of the positive eigenspectrum re-
sulting in information loss. As already discussed in
former work, there is no simple answer to the correc-
tion of eigenvalues. One always has to consider char-
acteristics like the relevance of negative eigenvalues,
the ratio between negative and positive eigenvalues,
the complexity of the eigenspectrum, and the proper-
ties of the desired machine learning model. The re-
sults clearly show that the proposed advanced shift
correction is particularly useful if the negative eigen-
values are meaningful and a low-rank approximation
of the similarity matrix is tolerable.
5 CONCLUSIONS
In this paper, we presented an alternative formulation
of the classical eigenvalue shift, preserving the struc-
ture of the eigenspectrum of the data. Furthermore,
we pointed to the limitations of the classical shift in-
duced by the shift of all eigenvalues, including those
with small or zero eigenvalue contributions.
Surprisingly, the classical shift eigenvalue correc-
tion is nevertheless frequently recommended in the
literature pointing out that only a suitable offset needs
to be applied to shift the matrix to psd. However, it
is rarely mentioned that this shift affects the entire
eigenspectrum and thus increases the contribution of
eigenvalues that had no contribution in the original
matrix. As a result of our approach, the eigenval-
ues that had vanishing contribution before the shift re-
main irrelevant after the shift. Those eigenvalues with
a high contribution keep their relevance, leading to
the preservation of the eigenspectrum but with a pos-
itive (semi-)definite matrix. In combination with the
low-rank approximation, our approach was, in gen-
eral, better compared to the classical methods.
Future work on this subject will include a possible
adoption of the advanced shift to unsupervised sce-
narios. Another field of interest is the reduction of the
computational costs using advanced matrix approx-
imation and decomposition (Musco and Woodruff,
2017; Sanyal et al., 2018) in the different sub-steps.
Structure Preserving Encoding of Non-euclidean Similarity Data
49

ACKNOWLEDGEMENTS
We thank Gaelle Bonnet-Loosli for providing support
with indefinite learning and R. Duin, Delft University
for variety support with DisTools and PRTools.
FMS, MM are supported by the ESF program
WiT-HuB/2014-2020, project IDA4KMU, StMBW-W-
IX.4-170792.
FMS, CR are supported by the FuE program of
the StMWi,project OBerA, grant number IUK-1709-
0011// IUK530/010.
REFERENCES
Alabdulmohsin, I. M., Ciss
´
e, M., Gao, X., and Zhang, X.
(2016). Large margin classification with indefinite
similarities. Machine Learning, 103(2):215–237.
Chen, H., Tino, P., and Yao, X. (2009). Probabilistic classi-
fication vector machines. IEEE Transactions on Neu-
ral Networks, 20(6):901–914.
Duin, R. P. W. and Pekalska, E. (2010). Non-euclidean
dissimilarities: Causes and informativeness. In
SSPR&SPR 2010, pages 324–333.
Filippone, M. (2009). Dealing with non-metric dissimilar-
ities in fuzzy central clustering algorithms. Int. J. of
Approx. Reasoning, 50(2):363–384.
Gu, S. and Guo, Y. (2012). Learning SVM classifiers with
indefinite kernels. In Proc. of the 26th AAAI Conf. on
AI, July 22-26, 2012.
Gusfield, D. (1997). Algorithms on Strings, Trees, and Se-
quences: Computer Science and Computational Biol-
ogy. Cambridge University Press.
Haasdonk, B. (2005). Feature space interpretation of SVMs
with indefinite kernels. IEEE TPAMI, 27(4):482–492.
Haasdonk, B. and Pekalska, E. (2008). Indefinite kernel
fisher discriminant. In 19th International Conference
on Pattern Recognition (ICPR 2008), December 8-11,
2008, Tampa, Florida, USA, pages 1–4. IEEE Com-
puter Society.
Higham, N. (1988). Computing a nearest symmetric posi-
tive semidefinite matrix. Linear Algebra and Its Ap-
plications, 103(C):103–118.
Hodgetts, C. and Hahn, U. (2012). Similarity-based asym-
metries in perceptual matching. Acta Psychologica,
139(2):291–299.
Ilic, M., Turner, I. W., and Saad, Y. (2007). Linear system
solution by null-space approximation and projection
(SNAP). Numerical Lin. Alg. with Applic., 14(1):61–
82.
Jain, A. and Zongker, D. (1997). Representation and recog-
nition of handwritten digits using deformable tem-
plates. IEEE Transactions on Pattern Analysis and
Machine Intelligence, 19(12):1386–1391.
Kohonen, T. and Somervuo, P. (2002). How to make large
self-organizing maps for nonvectorial data. Neural
Netw., 15(8-9):945–952.
Laub, J. (2004). Non-metric pairwise proximity data. PhD
thesis, Berlin Institute of Technology.
Ling, H. and Jacobs, D. W. (2007). Shape classification
using the inner-distance. IEEE Trans. Pattern Anal.
Mach. Intell., 29(2):286–299.
Loosli, G. (2019). Trik-svm: an alternative decomposition
for kernel methods in krein spaces. In Verleysen, M.,
editor, In Proceedings of the 27th European Sympo-
sium on Artificial Neural Networks (ESANN) 2019,
pages 79–94, Evere, Belgium. d-side publications.
Loosli, G., Canu, S., and Ong, C. S. (2016). Learning svm
in krein spaces. IEEE Transactions on Pattern Analy-
sis and Machine Intelligence, 38(6):1204–1216.
Luss, R. and d’Aspremont, A. (2009). Support vector ma-
chine classification with indefinite kernels. Mathemat-
ical Programming Computation, 1(2-3):97–118.
Mises, R. V. and Pollaczek-Geiringer, H. (1929). Praktische
verfahren der gleichungsaufl
¨
osung . ZAMM - Journal
of Applied Mathematics and Mechanics / Zeitschrift
f
¨
ur Angewandte Mathematik und Mechanik, 9(2):152–
164.
Mokbel, B. (2016). Dissimilarity-based learning for com-
plex data. PhD thesis, Bielefeld University.
Musco, C. and Woodruff, D. P. (2017). Sublinear time low-
rank approximation of positive semidefinite matrices.
CoRR, abs/1704.03371.
Neuhaus, M. and Bunke, H. (2006). Edit distance based ker-
nel functions for structural pattern classification. Pat-
tern Recognition, 39(10):1852–1863.
Pekalska, E. and Duin, R. (2005). The dissimilarity repre-
sentation for pattern recognition. World Scientific.
Pekalska, E., Harol, A., Duin, R. P. W., Spillmann, B., and
Bunke, H. (2006). Non-euclidean or non-metric mea-
sures can be informative. In Structural, Syntactic, and
Statistical Pattern Recognition, Joint IAPR Interna-
tional Workshops, SSPR 2006 and SPR 2006, Hong
Kong, China, August 17-19, 2006, Proceedings, pages
871–880.
Sakoe, H. and Chiba, S. (1978). Dynamic program-
ming algorithm optimization for spoken word recog-
nition. Acoustics, Speech and Signal Processing,
IEEE Transactions on, 26(1):43–49.
Sanyal, A., Kanade, V., and Torr, P. H. S. (2018). Low
rank structure of learned representations. CoRR,
abs/1804.07090.
Scheirer, W. J., Wilber, M. J., Eckmann, M., and Boult,
T. E. (2014). Good recognition is non-metric. Pat-
tern Recognition, 47(8):2721–2731.
Schleif, F. and Ti
˜
no, P. (2015). Indefinite proximity learn-
ing: A review. Neural Computation, 27(10):2039–
2096.
Schnitzer, D., Flexer, A., and Widmer, G. (2012). A fast
audio similarity retrieval method for millions of music
tracks. Multimedia Tools and Appl., 58(1):23–40.
Shawe-Taylor, J. and Cristianini, N. (2004). Kernel Meth-
ods for Pattern Analysis and Discovery. Cambridge
University Press.
Strassen, V. (1969). Gaussian elimination is not optimal.
Numerische Mathematik, 13(4):354–356.
ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods
50

van der Meer, F. (2006). The effectiveness of spectral sim-
ilarity measures for the analysis of hyperspectral im-
agery. International Journal of Applied Earth Obser-
vation and Geoinformation, 8(1):3–17.
Vapnik, V. (2000). The nature of statistical learning the-
ory. Statistics for engineering and information sci-
ence. Springer.
Xu, W., Wilson, R., and Hancock, E. (2011). Determining
the cause of negative dissimilarity eigenvalues. LNCS,
6854 LNCS(PART 1):589–597.
Zhang, Z., Ooi, B. C., Parthasarathy, S., and Tung, A. K. H.
(2009). Similarity search on bregman divergence:
Towards non-metric indexing. Proc. VLDB Endow.,
2(1):13–24.
Structure Preserving Encoding of Non-euclidean Similarity Data
51
