A Formal Approach for the Analysis of the XRP Ledger Consensus

Protocol

Lara Mauri

1 a

, Stelvio Cimato

1 b

and Ernesto Damiani

1,2 c

Computer Science Department, Universit

a degli Studi di Milano, Milan, Italy

EBTIC - Khalifa University of Science and Technology, Abu Dhabi, U.A.E.

Keywords:

XRP Ledger, Ripple, Cryptographic Protocol, Consensus, Distributed Ledger.

Abstract:

Distributed ledger technology is envisioned as one of the cornerstones of promising solutions for building the

next generation of critical applications. However, there is still quite a bit of confusion and hype around the

real security guarantees this technology offers. This is especially due to the fact that for the vast majority

of existing blockchain-based consensus protocols it is really hard to ﬁnd sufﬁciently detailed documentation

that fully captures their behavior. A number of recent papers have formalized the behavior of Bitcoin-like

protocols in order to rigorously study the security and privacy properties of their underlying structure, but

surprisingly very little work has been devoted to the formalization of distributed ledger systems using BFT-

like approaches. In this work, we focus on XRP Ledger, better known as Ripple, and take the ﬁrst steps

towards the complete formalization of its consensus protocol. To this end, we have investigated all the existing

documentation and analyzed its source code. We present a formal description of its consensus protocol for

every step. Furthermore, we provide an accurate view of its security guarantees in terms of safety and liveness

and show how to increase the desired tolerance by changing the value of speciﬁc protocol parameters.

1 INTRODUCTION

Although the classical problem of achieving mutual

agreement in the presence of faulty nodes (Pease

et al., 1980) has been extensively studied in the liter-

ature from different perspectives (e.g. resiliency, net-

work connectivity, communication complexity, run-

ning time and channel reliability), interest in consen-

sus protocols has risen quite signiﬁcantly over the last

few years because of their application to various novel

settings such as blockchain systems. The novelty of

blockchain technology is a powerful combination of

well-known research results taken from distributed

computing, cryptography and game theory that to-

gether create a system providing a trustworthy service

to parties who otherwise have no reason to trust each

other. The term blockchain is self-explanatory and

denotes a distributed ledger (i.e. a public data struc-

ture) where inputs called transactions are aggregated

in the form of blocks which are added one after an-

other. A copy of the ledger is locally maintained by

https://orcid.org/0000-0002-4024-1015

https://orcid.org/0000-0003-1737-6218

https://orcid.org/0000-0002-9557-6496

all the nodes, which operate in a peer-to-peer commu-

nication setting and continuously send and validate

transactions in an attempt to update the state of the

shared ledger. In principle, any participant can pro-

pose the addition of a new block to the blockchain,

but this addition has to be approved by the other peers

to ensure its legitimacy.

The idea behind what is today known as the

Nakamoto consensus (or ledger consensus) was ﬁrst

conceptualized in 2008 with the birth of the Bitcoin

payment system (Nakamoto, 2008) and refers to the

consensus mechanism allowing the nodes in the Bit-

coin network to decide which next block to include

into the ledger. Speciﬁcally, the ultimate goal of

the consensus protocol is to ensure that parties have

a unique common view of the ledger even in the

presence of possible conﬂicting inputs and arbitrary

Byzantine behaviors of some network nodes. In or-

der to guarantee consistency between potentially dif-

ferent versions of the ledger, Bitcoin relies on the

concept known as proof-of-work (PoW), which re-

quires a party to invest computational power to af-

fect the behavior of the system. However, the ex-

traordinary amounts of energy it demands have raised

concerns over its sustainability and environmental im-

Mauri, L., Cimato, S. and Damiani, E.

A Formal Approach for the Analysis of the XRP Ledger Consensus Protocol.

DOI: 10.5220/0008954200520063

In Proceedings of the 6th International Conference on Information Systems Security and Privacy (ICISSP 2020), pages 52-63

ISBN: 978-989-758-399-5; ISSN: 2184-4356

pact. These limitations motivated an interesting re-

search direction that proposes the adoption of a new

class of consensus protocols based on the use of alter-

native resources (Bano et al., 2017; Wang et al., 2018)

− among them, the proof-of-stake (PoS) paradigm is

the most implemented so far. Such developments,

combined with recent efforts to leverage the core fea-

tures of blockchains for novel use cases in both ﬁnan-

cial and non-ﬁnancial domains (Rawat et al., 2019),

have led to a signiﬁcant increase in proposals for

blockchain-based solutions, with new software appli-

cations and services appearing daily. But this rush to

quickly enter the market poses serious risks to the en-

tire blockchain ecosystem since vulnerabilities of in-

sufﬁciently tested code can be exploited with signiﬁ-

cant consequences due to the decentralized nature and

irreversibility of the technology (Saad et al., 2019).

According to Halpin and Piekarska (2017), an

emerging ﬁeld that needs further research is the study

of the security and privacy properties of the structure

underlying blockchain-based systems. In this context,

the ﬁrst formal security analysis of the fundamental

principles behind the Nakamoto consensus was pro-

posed by Garay et al. (2015). In their work, the au-

thors presented an abstraction of the Bitcoin proto-

col in synchronous networks, which they referred to

as the Bitcoin backbone, and proved that it satisﬁes

certain security properties. Later, Pass et al. (2017)

extended the analysis to asynchronous networks, and

further reﬁnements of the initial model of computa-

tion were presented in subsequent works (Garay et al.,

2017, 2018). While a number of other papers have

studied the security of several PoW- and PoS-based

blockchains in a rigorous manner (Pass and Shi, 2017;

Badertscher et al., 2017; Daian et al., 2016; Kiayias

et al., 2017), it is worth noting that for the vast ma-

jority of existing blockchain protocols it is really hard

to ﬁnd sufﬁciently detailed information on the func-

tioning of the consensus mechanism they use (though

there is a lot of work presented online in the form of

white papers, pre-prints and blog posts). Moreover,

the majority of current research is focusing on study-

ing blockchains consistent with the so-called permis-

sionless setting, whereas much less attention has been

paid to the formalization of distributed ledger sys-

tems operating in permissioned settings, which em-

brace aspects of traditional Byzantine-fault tolerant

(BFT) consensus protocols. In contrast to permission-

less blockchains such as Bitcoin, permissioned ones

are operated by known entities and only a restricted

group of nodes can participate in the process for de-

termining the correct update of the ledger (Cachin and

Vukolic, 2017).

Motivated by this emerging new era of research,

in this work we focus our attention on XRP Ledger

− better known as Ripple (Ripple Labs Inc., a) −,

the third-largest digital currency in market capitaliza-

tion after Bitcoin and Ethereum. The XRP Ledger

protocol is a distributed payment system that uses a

unique consensus protocol which sets it apart from

previous approaches. Based on the idea of subjective

trust assumptions, in Ripple every participant is free

to specify which nodes it believes will behave cor-

rectly and which ones it considers faulty by means of

so-called Unique Node Lists (or UNLs). The fact that

the XRP Ledger protocol does not rely on a process

of mining to verify transactions has many advantages,

in terms of transaction speed, compared to other con-

sensus algorithms (Mauri et al., 2018). Indeed, while

for Bitcoin-like protocols transactions are conﬁrmed

after an hour on average, in the XRP Ledger network

the settlement process takes around 5 seconds, with a

throughput of up to 1500 transactions per second.

Although mentioned in several surveys on the

consensus mechanisms that govern the most popu-

lar blockchains (Xiao et al., 2019; Gramoli, 2017),

the Ripple protocol is often described in a vague and

not very clear way. By now the original white pa-

per (Schwartz et al., 2014) is deprecated, and avail-

able documentation about how the consensus process

works is restricted to the developer portal (Ripple

Labs Inc., b) and a recent analysis provided by the cre-

ators of Ripple themselves (Chase and MacBrough,

2018). Even if the latter presents a detailed explana-

tion of the Ripple algorithm and derives conditions

for its safety and liveness, there remains a degree

of uncertainty around many aspects of the protocol

and, in any case, not all steps have actually been de-

scribed. Furthermore, to date the only existing peer-

reviewed analysis of the XRP Ledger consensus pro-

tocol (Armknecht et al., 2015) was conducted on the

original white paper and showed that some speciﬁca-

tions were ﬂawed.

Our Contributions. In light of the above, we be-

lieve that having a clear and accurate description of

the XRP Ledger consensus protocol is fundamental

not only to gain in-depth understanding of its behav-

ior, but also to increase trust in the foundational prin-

ciples of the algorithm and identify its vulnerabilities.

To this end, we have carefully investigated all the ex-

isting documentation relating to XRP Ledger and, by

directly analyzing its source code (Ripple Labs Inc.,

c), we have created an in-depth description of the con-

sensus protocol for every step. In particular, our work

contributes in the following aspects: (1) taking the

ﬁrst steps towards the complete formalization of the

XRP Ledger Consensus Protocol; (2) providing an ac-

curate view of the current security guarantees of the

A Formal Approach for the Analysis of the XRP Ledger Consensus Protocol

protocol in terms of safety and liveness; (3) show-

ing how the inherent correlation between the safety

and liveness tolerances, the validation quorum and the

UNLs overlapping size can be leveraged to increase

either liveness or safety.

Organization. The remainder of the paper is or-

ganized as follows. Section 2 provides the neces-

sary background to understand the consensus mech-

anism powering the XRP Ledger network. Section 3

presents our formalization of the different phases of

the XRP Ledger Consensus Protocol, expressed by

means of a set-theoretic notation and mathematical

formulas. Section 4 reports and clariﬁes results from

a previous analysis with respect to safety and liveness

properties and extends it by showing that the value of

some protocol parameters can be changed to guaran-

tee more liveness or safety. Section 5 concludes and

proposes directions for future research.

2 BACKGROUND ON THE XRP

LEDGER NETWORK

2.1 Basic Concepts and Terminology

In the XRP Ledger network, the collaborative process

by which the shared replicated transaction system is

updated and kept consistently synchronized is known

as the XRP Ledger Consensus Protocol (or XRP LCP,

for short). The primary objective of each participant

involved in the XRP LCP is to advance the chain of

validated ledgers by reaching agreement on a new set

of transactions to apply to the prior ledger. The over-

all consensus process, which can be viewed as a pro-

gression through three phases − collection, deliber-

ation and validation − is controlled by the so-called

validators. Unlike simple tracking nodes, which are

uniquely responsible for relaying transactions from

clients throughout the network, participants acting as

validators perform the additional task of proposing

and revising candidate sets of transactions to be pro-

cessed.

Several permissioned blockchain platforms rely

on classical BFT consensus protocols, which typi-

cally require every node to know the entire set of

peers participating in the consensus process. How-

ever, one of the major challenges for those protocols

that prevents their wider adoption in blockchain sys-

tems is their scalability in terms of the number of

nodes (Vukoli

c, 2016). Conversely, the XRP Ledger

protocol does not rely on a strict notion of member-

ship and not every node has to trust all others. This

gives the XRP Ledger network a clear advantage over

BFT-based blockchains because it is more scalable in

terms of the number of nodes. In order to achieve con-

sensus, validators share information about their candi-

date transaction sets by exchanging signed messages

(whose format will be described in detail later on), but

nodes only consider messages sent by speciﬁc valida-

tors they believe will behave honestly. In particular,

each participant individually chooses which valida-

tors it will listen to when making decision about the

next ledger, and such choice is declared in the form

of a list, referred to as the Unique Node List (UNL),

which is locally maintained by each validator; valida-

tors belonging to the UNL are called trusted.

A fundamental component of the ﬁrst phase of the

consensus protocol is represented by the open ledger,

which is the ledger to which all pending transactions

are applied. When certain speciﬁc conditions are met,

the ledger is closed, and the closure implies that new

transactions are no longer accepted for inclusion in

the new version of the ledger. In essence, the set of

transactions included in the closed ledger constitutes

the ﬁrst position and reﬂects the validator’s initial be-

lief of which transactions should be considered for the

next ledger. Nodes are equipped with a public/private

key pair. Digital signatures are used to check that sub-

mitted transactions are correct, i.e. authorized to do

a speciﬁc set of actions, but also serve as a means

to authenticate the issuers of the messages received.

The fact that all protocol communications are signed

makes it possible to reliably identify validators in the

peer-to-peer network even if messages are relayed by

untrusted nodes.

As mentioned above, validators communicate by

means of messages in an attempt to reach network

agreement. One of such messages is represented by

the so-called proposals. At the start of the consen-

sus process, each node decides whether to operate as

an active or passive validator. A proposing valida-

tor is a normal participant taking on its own position

and sending proposals to other peers. Conversely, an

observing validator updates its position, but does not

propose it to its peers. The ﬁrst proposal issued by

a validator corresponds to its initial position, so pro-

posals can be seen as subsequent positions taken by

nodes as the network progresses. As we will see later,

the concept of dispute is strictly connected to that of

proposal. It is used to denote an individual transaction

that is either not included in a validator’s proposal or

not included in a trusted validator’s proposal.

In addition to the closed ledger, we can distinguish

two other types of ledger representing subsequent

evolutions, in terms of content validity and ﬁnality, of

the initial ledger version under consideration. Specif-

ically, the ledger resulting from the completion of de-

ICISSP 2020 - 6th International Conference on Information Systems Security and Privacy

liberation, known as the last closed ledger, is the most

recent ledger on which, from the point of view of a

single validator, the network reached agreement. This

ledger version is not immediately considered ﬁnal. In-

deed, a ledger is fully validated only once it passes a

certain validation threshold. It is only at that point that

it is considered authoritative and irrevocable, meaning

it becomes part of the permanent public history and its

content is truly reliable.

Lastly, a validation is a signed message containing

the hash of the last closed ledger, whose purpose is

to let trusted validators know which particular ledger

was built by the other validators and come to a com-

mon conclusion about which last closed ledger should

be considered authoritative (i.e. declared fully vali-

dated).

2.2 Informal Protocol Description

The XRP LCP proceeds in rounds and consists of

three different phases that are continually repeated to

process groups of transactions. The typical execution

of a single ledger round goes from collection to de-

liberation to validation. Below we provide a brief de-

scription of each phase:

• Collection: During this phase, validators collect

new incoming transactions, apply the well-formed

ones to their open ledger and subsequently relay

them to the other peers. When certain conditions

are met, each validator determines the open ledger

period should end and closes its ledger.

• Deliberation: Validators begin an iterative pro-

cess in which they try to establish consensus by

exchanging proposals with their trusted valida-

tors. Starting from their own position, they con-

tinuously change their view of the transaction set

by adding or removing disputed transactions from

their proposal and, after each update, they check

the percentage of trusted validators agreeing with

them. When a validator sees a supermajority

agreement, it declares that consensus has been

reached. Then, it creates a new last closed ledger

by applying the consensus transaction set to the

last validated ledger and issues a validation.

• Validation: Participants determine whether to

consider the outcome of deliberation (i.e. their

last closed ledger), fully validated by comparing

the hashes received from their trusted peers. The

decision is taken on the basis of the percentage

of agreement on the newly-created ledger. Only

when a quorum of validations for the same ledger

is reached, that ledger is deemed ﬁnal.

3 FORMALIZING THE XRP LCP

3.1 Preliminaries

In the XRP Ledger network, the shared global

ledger is actually a series of ledger versions (or

ledgers). A ledger is any quintuple of the form

L = hsn,h,h

−1

,ts,T i where sn is the sequence num-

ber of the ledger, h is the unique identifying hash of

the ledger’s contents, h

−1

is the h value of the pre-

vious ledger version this ledger was derived from, ts

is a timestamp, and T is a set of transactions. The

hash serves as a unique identiﬁer for the ledger and

its contents, whereas the sequence number identiﬁes

the order in which ledgers occur in the ledger chain.

The very ﬁrst ledger, known as the genesis ledger, has

sequence number 1; each successive ledger has a se-

quence number one greater than that of the preced-

ing one. We say a tuple L = hsn, h,h

−1

,ts,T i is valid

with respect to a predecessor (fully validated) ledger

= hsn

−1

,ts

i iff:

1. h

−1

= h

;

2. sn = sn

+ 1;

3. |Σ

| ≥ q

, where |Σ

| is the support of the ledger L

and q

is the minimum percentage of participation

required to reach network agreement.

Below we introduce the notation used in the formal-

ization of the XRP LCP provided in Section 3.2, as

well as the timing assumptions.

3.1.1 Notation

We denote by N the universe of nodes of the peer-

to-peer XRP Ledger network. Nodes play differ-

ent roles: client applications submit transactions to

server nodes, which are differentiated in tracking

nodes and validators. The consensus process is ex-

clusively driven by the latter. Since only validators

actively participate, check and validate all transac-

tions taking place in the system, we believe that for

the purposes of formalization it is meaningful to con-

sider only the subset N

⊂ N of participants, where

denotes exactly the nodes acting as validators. As

already mentioned, during the consensus process, val-

idators only evaluate proposals and validations issued

by their trusted nodes, discarding those received from

validators not belonging to their UNL. For any node

i ∈ N

, U NL

= {u : u ∈ N

, F(u)} denotes the set of

all nodes u for which F(u) is true, where F(u) means

that validator i trusts u. Also, we use n

= |U NL

to denote the size of node i’s UNL. Giving as a fact

that the individual choice to include (or omit) a given

transaction in the next ledger is inﬂuenced only by

A Formal Approach for the Analysis of the XRP Ledger Consensus Protocol

the trusted nodes’ messages, we decide not to directly

specify UNL membership every time (in our formal-

ization, we will specify this dependency only in the

context of the last phase). Deliberation and validation

phases are parameterized by q

and q

, respectively.

In particular, q

speciﬁes the consensus quorum (i.e.

the minimum number of validators having issued the

same proposal needed to declare consensus), whilst

− see the third condition required for ledger valid-

ity − represents the validation quorum (i.e. the min-

imum number of validations needed to fully validate

a ledger). Both these parameters are a function of a

constant k and n

, where n

is the previously deﬁned

size of UNL

. We let

and L

denote the open

ledger, the closed ledger and the last closed ledger of

node i, respectively. Moreover, we use

L to denote

the last fully validated ledger. tx is used to represent a

single transaction under consideration by consensus.

Any transactions excluded from a node’s proposal are

added to its local queue we denote by T

. For nota-

tional simplicity, we suppose the existence of another

set T

which contains all received new transactions.

Also, we use P

to denote the node i’s proposal of

candidate transactions and the symbol θ to indicate

the threshold for including a given transaction in the

proposal P

. Lastly, D

denotes the node i’s set of dis-

puted transactions, whereas σ

denotes a validation is-

sued by i. Table 1 provides a summary of the notation

used throughout this paper (some parts however will

be slightly modiﬁed to suit the context).

Table 1: Summary of notation.

The set of validators

i A validator in the network

UNL

i’s Unique Node List

The size of U NL

tx A single transaction

T A set of transactions

The set of queued transactions

The set of new transactions

The consensus quorum

The validation quorum

i’s open ledger

i’s closed ledger

i’s last closed ledger

L The last fully validated ledger

i’s proposal of transactions

i’s set of disputed transactions

i’s validation

3.1.2 Timing

An important aspect that must be considered when de-

signing any consensus protocol is the ability of parties

to reach a certain degree of synchronization during

the protocol execution. In the XRP Ledger network,

the protocol execution is driven by a heartbeat timer

which allows nodes to advance the consensus process.

In practice, at regular intervals each validator checks

whether the necessary conditions to move to the next

phase of the consensus protocol are met. Although

each validator can begin a new round of consensus at

arbitrary times based on when the initial round started

and the time taken to apply the transactions, the tran-

sition to both deliberation and validation phases can

only occur at the end of the heartbeat timer.

Furthermore, each node maintains an internal

clock that it uses when calculating its own close time,

i.e. the time at which the ledger has been closed (see

Sections 2.1 and 3.2.1 for details). In practice, at the

closure of the ledger (which reﬂects the end of col-

lection phase) each validator uses its current time as

the initial close time estimate and includes this value

in its initial position. Later, this approximate time is

rounded based on a dynamic resolution. As a result,

each validator uses the consensus process not only to

reach agreement with its trusted nodes about the set of

transactions, but also attempts to agree on a common

time for the closure of the ledger. Validators update

their close time positions in response to the effective

close time included in their trusted nodes’ positions,

and in this way, they can derive a common close time

for the ledger without the need to synchronize their

clocks. When there is no clear majority of trusted val-

idators agreeing on a close time, nodes agree to dis-

agree on an actual close time. Even though in this

case the network has no ofﬁcial close time, the effec-

tive close time of the ledger is set to 1 second past the

close time of the previous ledger.

Although reaching agreement on the effective

close time is part of the XRP LCP, in order to make

our formalization more readable, we decided to in-

clude in it only some fundamental protocol timing pa-

rameters.

3.2 In-depth Protocol Description and

Its Formalization

In Ripple, the ledger chain structure starts with the

genesis ledger and ends with the last fully validated

ledger. Generally, given the prior fully validated

ledger

L and a set T of new candidate transactions, the

execution of the XRP Ledger Consensus Protocol de-

termines an output ledger

which, together with the

previous validated ledgers, forms the ledger history.

As introduced in the foregoing section, the XRP LCP

is an asynchronous round-based protocol consisting

of three phases. The diagram of Fig. 1 shows the out-

ICISSP 2020 - 6th International Conference on Information Systems Security and Privacy

put expected from each phase from the perspective of

an individual node i ∈ N

: (a) the output of the col-

lection phase is represented by i’s initial proposal P

which contains the starting position taken by the val-

idator itself before considering any trusted validator

position; (b) at the end of the second phase, i builds

a new last closed ledger L

; (c) the validation phase

establishes which last closed ledger, amongst those

proposed by all participants, must be considered the

authoritative one (

We now proceed with the formalization of the

three main consensus phases. Note that in our formal-

ization we follow the ﬂow depicted in Fig. 1. That

is, we consider the perspective of a single validator

i ∈ N

, which makes decisions only by listening to

its unique node list UNL

. In order to formalize the

behaviour of the XRP LCP we referred to the cur-

rent implementation of the core XRP Ledger server,

called rippled, whose source code is available in the

GitHub repository (Ripple Labs Inc., c).

3.2.1 Collection

The ﬁrst stage of the process is a quiescent period al-

lowing the validator i to create an individual percep-

tion of the state of the network. This perception is

referred to as the open ledger. The node’s open ledger

is ﬁlled with the candidate transactions which failed

to be included in the last round (i.e. those queued in

), as well as newly submitted ones. i’s open ledger

contains the set of transactions T :

T = T

∪ T

, T ∈

(1)

Under normal circumstances, the closure of the ledger

occurs after a predetermined minimum time t

minclose

has elapsed and only if the open ledger contains at

least one transaction. Thus, i closes its open ledger if

the following holds:

T 6=

0 ∧ (t

open

≥ t

minclose

), T ∈

(2)

where t

open

is used to denote how long the ledger has

been open. We let

indicate that i’s open ledger

has been closed (superscript letter c). In other cases,

the protocol either (1) closes the ledger if more than

half of the proposers have closed the ledger or vali-

dated the last closed ledger, or (2) postpones the clo-

sure to the end of a certain idle interval so that it is

more likely to include some transactions in the next

ledger. Regardless of the condition which led to the

closure of the ledger, once the pre-close phase is com-

pleted, i establishes its initial position on the basis of

the transactions included in the newly closed ledger.

Then, i proposes it to its trusted validators in the form

of a proposal, i.e. a signed message containing the

transactions it believes should be included in the next

ledger (recall from Section 2.1 that a node not operat-

ing in a proposing mode maintains its position inter-

nally without sharing it with peers):

= {tx : tx ∈ T, T ∈

} (3)

Here the notation used for the proposal slightly dif-

fers from that given in Section 3.1.1; we introduced

the superscript 0 to denote that P

is the initial pro-

posal shared by i. Like ledgers, also proposals have a

sequence number that is incremented each time a val-

idator updates the transaction set contained therein.

As easy to guess, different nodes may receive dif-

ferent unconﬁrmed transactions due to network de-

lays. As this variation in arrival time allows for each

potential new ledger version to be different for each

node, immediately after sharing its initial position, i

considers all the proposals received from its trusted

validators and creates a dispute for each transaction

discovered not to be in common with the peer’s posi-

tion under consideration. We deﬁne the validator i’s

dispute set D

as:

= {tx : (tx ∈ P

∧ tx /∈ P

j6=i

)

∨ (tx /∈ P

∧ tx ∈ P

j6=i

)}

(4)

where r refers to one of the successive proposals is-

sued by i during deliberation (at this time, r = 0).

Also, the validator keeps track of each peer’s vote on

each disputed transaction (voting in favour of a dis-

puted transaction simply means believing that such

transaction should be included in the next ledger). For

each tx ∈ D

, we use v(tx) to denote the support given

to tx by i’s trusted validators:

v(tx) = | j 6= i : tx ∈ P

| (5)

where, as before, r is currently 0 (in a more advanced

stage of the process, i.e. during deliberation, P

will

refer to the most recent proposal issued by j).

Unless they are part of a peer’s proposal, transac-

tions received after the closure of the ledger are not

considered until the next round.

3.2.2 Deliberation

In order to achieve consensus on the speciﬁc set of

transactions to be processed next, i begins an itera-

tive process during which it issues updated proposals

(i.e. updates of its initial position), which are modi-

ﬁed based on the support obtained by each individual

transaction. A heartbeat timer is the key ingredient

that drives the consensus process forward: it is only

on timer calls, which occur at a regular frequency, that

i adjusts and issues new proposals (see Section 3.1.2).

Going into detail, the mechanism allowing differ-

ences between peers’ proposals to converge is based

A Formal Approach for the Analysis of the XRP Ledger Consensus Protocol

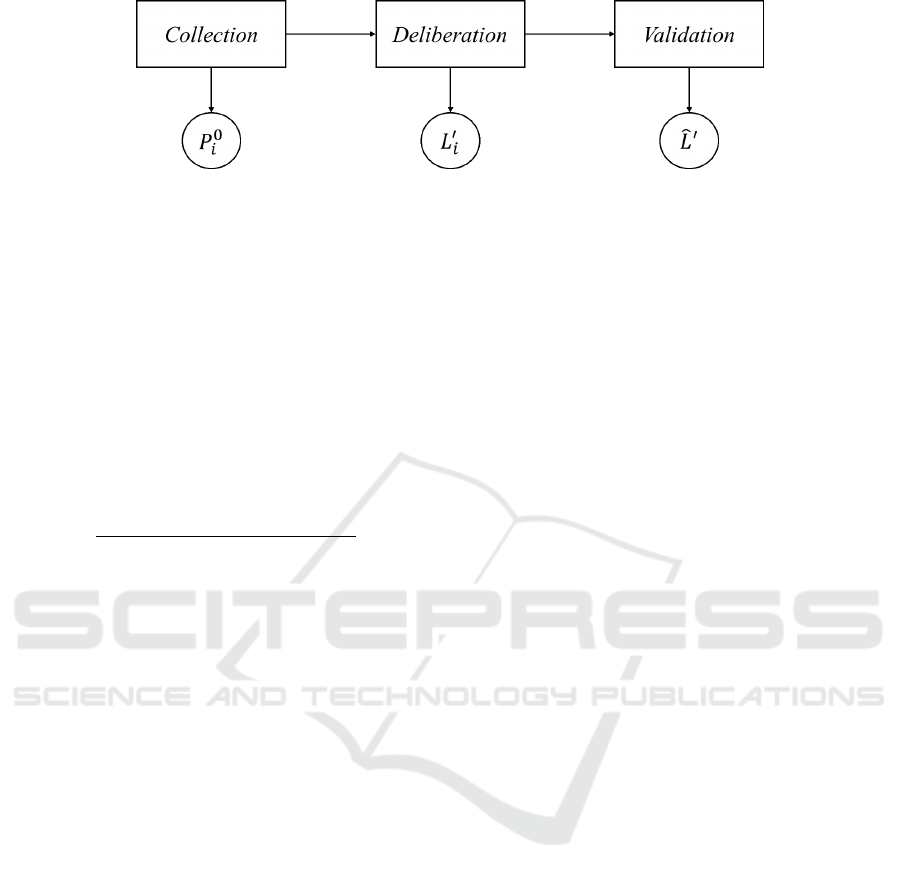
Figure 1: Output of each phase from the perspective of a single validator i.

on a majority voting scheme. The evaluation of the

achieved convergence degree is performed taking the

value of a certain threshold θ as a reference. In turn,

the value θ depends on a parameter d which expresses

the percentage of time that consensus is expected to

take to converge. Speciﬁcally, d is a function of the

previous round duration, which corresponds to the du-

ration of the last deliberation phase (measured from

closing the open ledger to accepting the consensus re-

sult) and the duration of the deliberation phase for the

current consensus round:

d = f (t

(deliberation−1)

, t

deliberation

) =

deliberation

· 100

max(t

(deliberation−1)

, t

minconsensus

)

(6)

where t

minconsensus

(currently, 5 seconds) expresses the

minimum amount of time to consider that consensus

was reached in the previous round.

As deliberation proceeds, i changes its candidate

transaction set in response to what its trusted valida-

tors propose. As a result, i may either add a dis-

puted transaction to its current set if the percentage of

trusted validators that have proposed the same trans-

action in their most recent proposal exceeds the afore-

mentioned threshold θ or, otherwise, remove it. New

proposals are formalized as follows:

= {tx : (tx ∈ P

∧ tx /∈ D

)

∨ (tx ∈ D

∧ (v(tx) ≥ θ))}.

(7)

The current implementation uses an initial threshold

for inclusion of 0.5. This means that if a particular

disputed transaction is supported by half of the val-

idators or more, i agrees to include it in its set. On the

contrary, a transaction that, at this early stage, does

not have the support of at least 50% of the trusted

nodes, is removed from i’s position. Omitted transac-

tions are added to the transaction queue T

and con-

sidered again for inclusion in the next ledger version.

Therefore, the queue is updated whenever a transac-

tion is removed from a proposal:

= T

∪ {tx : tx ∈ D

∧ (v(tx) < θ)}. (8)

The speciﬁc values of θ are subject to change, in ac-

cordance to the XRP Ledger implementation. De-

pending on the value of the function d (deﬁned in Eq.

6), θ can currently assume one of the following val-

ues:











0.5 d < 50

0.65 50 ≤ d < 85

0.7 85 ≤ d < 200

0.95 otherwise

(9)

After changing its transaction view, i broadcasts its

new proposal (increasing the related sequence num-

ber) and determines whether consensus has been

reached − in case i has not changed its set of trans-

actions, no new proposal needs to be issued. Consen-

sus can be declared only if there is a supermajority

support for each of the transactions the candidate set

contains. Formally, the support of a proposal P

expressed as follows:

v(P

) = |{ j 6= i : P

= P

}|. (10)

Actually, consensus is reached when the following

three conditions are met: (a) a certain minimum

amount of time has elapsed since deliberation be-

gan, (b) at least 3/4 of the previous round proposers

are participating or the current deliberation phase is

longer (of a given minimum amount of time) than

the deliberation phase of the previous round, (c) i,

together with its trusted peers, has reached the per-

centage threshold q

above which consensus can be

declared. However, for the purpose of formalization,

the really meaningful condition is the third. Hence,

we assume i declares consensus reached when the fol-

lowing holds:

v(P

) ≥ q

, q

= k · n

(11)

where n

is the number of trusted nodes belonging to

UNL

(see Section 3.1.1) and k = 0.8 in the current

implementation. Once consensus is reached, i builds

a new last closed ledger L

by adding the agreed-upon

set of transactions to the prior fully validated ledger

L ∪ {tx ∈ P

: v(P

) ≥ q

} (12)

and then, it broadcasts its resulting ledger in the form

of a signed message σ

containing the identifying hash

of this ledger. At this point, the round is completed

and i now builds a new open ledger on top of the last

closed ledger. As previously said, the open ledger

ICISSP 2020 - 6th International Conference on Information Systems Security and Privacy

represents the basis of any validator’s initial proposal

and hence, the ﬁrst transactions to be added to the

new open ledger are those held over from the previ-

ous consensus round. Next, all valid transactions that

in the previous round were received after the ledger

was closed are applied. In practice, the protocol starts

a new round of consensus before the third phase, i.e.

validation, ends. Each participant begins a new col-

lection phase concurrently, preparing its proposal for

the next ledger version while the consensus process

related to the prior ledger version is ongoing. Accord-

ingly, at any given time, the process is characterized

by a series of in-progress open ledgers, individual par-

ticipants’ last closed ledgers that have not been fully

validated and historical ledgers that have been fully

validated.

3.2.3 Validation

At the end of deliberation, as seen above, validators

independently build what they believe the next state

of the ledger should be. Due to latency in propagating

transactions throughout the network, different valida-

tors may compute different last closed ledgers. These

ledger versions have the same sequence number, but

different hash values that uniquely identify their con-

tents (see Section 3.1). It is important to note that the

sequence number and the hash correlate 1:1 only for

fully validated ledgers. Thus, for a given sequence

number, only one ledger version can ever be fully val-

idated. In order to converge on a universal status of

the ledger and, consequently, resolve the above dif-

ferences, i checks how many trusted validators have

built a last closed ledger equal to its own by compar-

ing its validation, i.e. the hash of the ledger it com-

puted, with the hashes received from its peers; among

all the most recent validations, i considers only those

with the greatest sequence number. We denote by Σ

the set of trusted validators that published the same

validation hash as the validator i:

= { j ∈ UNL

: σ

= σ

}. (13)

Based on these validations, i recognizes whether the

previous consensus round succeeded or not. In partic-

ular, the node declares its last closed ledger L

fully

validated in the event that a supermajority agreement

on the calculated hash is reached. Therefore, if i de-

tects that it is in the majority, having built a ledger that

received enough matching validations to meet the val-

idation quorum q

, it considers the ledger fully vali-

dated. Formally, L

is declared fully validated iff:

|Σ

| ≥ q

, q

= k · n

(14)

where, as for the consensus quorum q

(cf. Eq. 11),

the constant k is 0.8. Conversely, if i is in the minority,

it cannot consider its ledger instance fully validated.

Instead, it has to ﬁnd the supermajority ledger, i.e.

the one with the sufﬁcient number of validations (and

highest sequence number), and accept it as the new

fully validated ledger:

= L

: (x = i ∨ x ∈ U NL

) ∧ (|Σ

| ≥ q

). (15)

Lastly, in case for a given sequence number no last

closed ledger meets q

, no ledger is declared fully

validated and i switches to a strategy allowing it to

determine the preferred last closed ledger for the next

consensus round (see (Chase and MacBrough, 2018)

for an overview on this strategy).

To summarize, the three outputs depicted in Fig. 1

correspond to Eq. 3, 12 and 15 respectively.

4 XRP LEDGER PROPERTIES

4.1 Safety and Liveness

One of the fundamental problems in distributed com-

puting is ensuring that in a system where processors

exchange information, all correct processes make a

decision and eventually reach a common understand-

ing or agreement even if one or more processors have

failed. There are several ﬂavors of the consensus

problem (Pease et al., 1980), but all variations are sub-

ject to conditions similar to the following:

• Validity: If every process begins with the same

initial value v, then the ﬁnal decision of a non-

faulty process must be v;

• Agreement: Final decisions by non-faulty proces-

sors must be identical;

• Termination: Every non-faulty process must even-

tually decide.

These conditions are intended to capture two crucial

properties, namely safety and liveness. The former,

which derives from the conjunction of validity and

agreement, traditionally guarantees that something

bad will never happen. On the other hand, liveness

guarantees that something good will happen eventu-

ally, and derives from the termination condition. In

the context of the XRP Ledger network, the above

deﬁnitions can be reﬁned as follows:

• Safety: If an honest node fully validates a ledger

L, then all honest nodes cannot fully validate a

contradictory ledger L

6= L;

• Liveness: If an honest node broadcasts a valid pro-

posal P to all honest nodes, then P will eventually

be accepted by all nodes and included in a fully

validated ledger.

A Formal Approach for the Analysis of the XRP Ledger Consensus Protocol

The phenomenon called fork is the biggest threat to

the ability of a distributed ledger system to operate

properly and produce results that can be relied upon.

In the XRP Ledger network, the occurrence of a fork

corresponds to the situation in which two honest val-

idators fully validate conﬂicting ledgers, i.e. ledgers

having the same sequence number, but different iden-

tifying hash value.

As already mentioned, the XRP LCP features a

layered notion of trust. The network is divided into

subsets of nodes that are collectively trusted to not

collude in an attempt to defraud the other peers, and

each node has complete discretion in selecting its

own UNL. Since validators have inﬂuence only over

nodes conﬁgured to trust them, the presence of a cer-

tain honest validator in more UNLs directly implies a

higher inﬂuence by that validator on the process of de-

termining the next ledger state. As a result, protocol

safety relies on the fact that the majority of the val-

idators act honestly and it is strongly dependent on the

degree of intersection between the UNLs of every pair

of nodes. The original Ripple whitepaper (Schwartz

et al., 2014) provided an initial analysis of the over-

lap condition required to ensure consistency, coming

to the conclusion that the needed minimum overlap

was roughly 1/5 of the UNL size. Later, an indepen-

dent analysis (Armknecht et al., 2015) proved that the

above condition was insufﬁcient and suggested that

the correct bound was > 2/5 of the UNL size. To be

precise, they showed that in order to ensure the ab-

sence of any fork, the intersection set size between

the UNL of any two validators needs to be > 40%

of the maximum UNL size. A recent work by Chase

and MacBrough (2018) provided a further analysis of

the XRP Ledger Consensus Protocol and also derived

new conditions for its safety and liveness, changing

the expectation for the overlap requirement. In the

remainder of this section, we show the major ﬁnd-

ings of Chase and MacBrough which will be useful in

the subsequent section. Prior to this, we present the

model used to analyze the safety and liveness of the

protocol.

The network is modeled as if an adversary is in

full control of at most t

nodes in U NL

for any val-

idator i. The nodes controlled by the adversary are

called Byzantine and can deviate from the protocol

by performing at least one of the following actions:

(i) not responding to messages; (ii) sending incor-

rect messages; (iii) sending differentiated messages

to different nodes. On the contrary, we consider as

honest any node that follows exactly the prescribed

XRP LCP. The honest proportion is equal to n

− t

Due to the FLP Impossibility Result (Fischer et al.,

1985), safety and liveness cannot be simultaneously

guaranteed by any consensus algorithm in the pres-

ence of arbitrary asynchrony and Byzantine nodes. In

(Chase and MacBrough, 2018), the authors assumed

a weak form of asynchrony in order to prove that the

system is able to not fall in a state where some hon-

est nodes can never fully validate a new ledger. This

last assumption, however, does not seem to be suf-

ﬁcient to guarantee that the system cannot get stuck

even in networks where two UNLs disagree only by

few nodes. In this regard, the paper showed an exam-

ple where even with 99% UNL overlap and no Byzan-

tine faults, the system fails to successfully apply the

preferred branch strategy, consequently maintaining

a ledger chain with two distinct branches (in other

words, the nodes are unable to determine a preferred

chain of ledgers to converge on). It follows that, actu-

ally, only in the restricted case in which the network

consists of a single agreed-upon UNL with an arbi-

trary number of extra nodes, the XRP LCP cannot get

stuck.

The most relevant contribution by Chase and

MacBrough was the re-analysis of the overlap con-

dition required to ensure safety. According to them,

the XRP LCP guarantees fork safety if for every pair

of nodes i, j the following holds:

i, j

+ n

− q

i, j

(16)

where O

i, j

= |UNL

∩UNL

|, q

= k · n

(cf. Eq. 14)

and t

i, j

= min{t

i, j

} is the maximum number of

allowed Byzantine faults in U NL

∩UNL

− here we

have slightly changed the original notation in order to

adapt it to the one used in our formalization. Assum-

ing 80% validation quorum (q

) (as prescribed in the

actual implementation) and 20% faults (t

i, j

), the con-

dition in essence requires roughly > 90% UNL agree-

ment.

4.2 Analysis

In order to provide a more accurate view of the secu-

rity provisions of the XRP LCP in terms of safety and

liveness, here we make some observations about the

three key parameters of the protocol, i.e. UNL over-

lap, validation quorum and tolerated Byzantine nodes,

considering also the discussion recently appeared on

the Ripple GitHub repository (Wilson, 2018). We in-

vestigate the values O

i, j

, q

and t

i, j

displayed in Eq.

16 and in the following we show how safety and live-

ness tolerances are related to each other and vary ac-

cording to the assumptions made on the above param-

eters.

To this end, we ﬁnd it convenient to introduce two

additional parameters, namely µ

and µ

, which de-

note the size of the set of surplus nodes for UNL

ICISSP 2020 - 6th International Conference on Information Systems Security and Privacy

Figure 2: µ

and µ

are the set sizes of surplus nodes in

UNL

and UNL

, respectively, that is the nodes in U NL

that are not in common with UNL

and viceversa:

= n

− O

i, j

, µ

= n

− O

i, j

(Fig. 2). Moreover, we

denote by t

the safety fault tolerance and by t

the

liveness tolerance of the system, i.e. the maximum

number of Byzantine nodes the XRP LCP tolerates in

order to guarantee safety and liveness, respectively.

Given a pair of nodes i, j with their respective

UNLs, and assuming that n

< n

and both UNLs

have the same percentage of faulty nodes, t

i, j

min{t

i, j

} = t

. By substituting O

i, j

with n

− µ

in Eq. 16, we get the following inequality:

< −

−

+ q

. (17)

On the other hand, the liveness tolerance t

is given

by:

< n

− q

. (18)

In general, a consensus protocol providing results that

can be relied upon is preferable, rather than one that

is able to progress in the presence of faulty nodes but,

at the same time, reports impaired results that could

undermine consistency. As a result, in order to obtain

a validation quorum q

whose safety fault tolerance t

meets or exceeds the liveness tolerance t

, we can use

≥ n

− q

and get the following:

− q

< −

−

+ q

. (19)

4.2.1 Unique UNL

Let us now consider the simplest case where the

XRP Ledger network consists of a single agreed-upon

UNL. In this case, n

= n

= n, and, consequently,

= µ

= 0. By Eq. 19, we obtain q

> (3/4)n,

meaning that when there is 100% agreement on par-

ticipants, reaching a 75% validation quorum is sufﬁ-

cient to fully validate a ledger. Therefore, in Eq. 16

we have n > n/2 + n − (3/4)n + t

, from which we

obtain t

(= t

) < (1/4)n, whereas from Eq. 18 we

obtain t

< n–(3/4)n = (1/4)n. As a result, in case

UNL

= UNL

and q

= 0.75n, both the tolerances are

0.25n. This means that when less than 25% of trusted

nodes are Byzantine, the protocol functions properly.

Keeping valid the assumption U NL

=UNL

, now

we show how t

and t

vary when q

is equal to 0.8n,

as required by the current XRP LCP speciﬁcation. In

this case, the value of the two tolerances are no longer

equal: t

< (3/10)n, and t

< (1/5)n. Compared to the

previous case in which q

= 0.75n, here the liveness

tolerance is lower than the safety fault tolerance, and

this implies that the system ability to not get stuck is

slightly weakened.

4.2.2 Overlapping UNLs

So far the analysis has focused on the circumstance

where the network is composed of a unique UNL.

However, the validation quorum increase takes on

greater signiﬁcance in the context in which the UNLs

of any two nodes i, j do not completely overlap, i.e.

when at least one of the two parameters µ

and µ

> 0. In this regard, we now turn our attention to the

total non-overlapping component resulting from the

sum of the two individual surpluses µ

and µ

of Eq.

17:

+ µ

< −n + 2q

− 2t

. (20)

Let us now consider two cases in which we set the

validation quorum ﬁrst to 80% and then to 90% of the

nodes. In the former case, q

= 0.8n and assuming

= 0.2n, we can safely allow up to a non-overlap

of 0.2n. In the latter case, q

= 0.9n and assuming

= 0.1n, the maximum non-overlap we can safely

allow is 0.6n. Thus, as the above bounds show, as q

increases, the degree of freedom of any node in the

choice of validators to trust, in turn, increases.

To conclude, if we want the system to have a little

more liveness, we can increase the sizes of the sur-

plus node sets µ

and µ

. Recalling that t

depends on

the quantity n

− q

, as the values µ

and µ

increase,

we obtain a higher validation quorum (cf. Eq. 19),

and hence the maximum number of allowed Byzan-

tine nodes to guarantee liveness increases. Let us con-

sider an overlap of 90%, i.e. a non-overlap of 10%. If

the safety fault tolerance is 0.2n

, from Eq. 16 we ob-

tain q

> 0.75n

, and t

< 0.25n

. In contrast, if the

safety fault tolerance is 0.25n

, we obtain q

> 0.8n

and hence, t

< 0.2n

. From this analysis, it emerges

that safety and liveness tolerances, validation quorum,

and UNLs overlapping set size are strictly correlated,

and it is possible to tune these parameters according

to the desired properties the system needs to satisfy.

Currently, if no conﬁguration changes are made,

each node adopts the default and recommended UNL

provided by Ripple. This essentially implies that no

disagreement on the participants in the network is al-

lowed, since all the nodes listen to a single list of val-

idators. Accordingly, the XRP LCP is really able to

A Formal Approach for the Analysis of the XRP Ledger Consensus Protocol

guarantee that the network cannot get stuck as long as

the number of Byzantine nodes within the system is

limited.

5 CONCLUSIONS

Understanding the fundamental mechanisms and

security properties of the structure underlying

blockchain-based protocols is becoming increasingly

important. Thus, detailed analyses and formalizations

of existing distributed ledger systems are crucial to

prove the correctness of the algorithms and gain con-

ﬁdence that they achieve their goals.

In this paper, we have presented a formalization

of the XRP Ledger Consensus Protocol, whose func-

tioning has been studied in a rather superﬁcial way

so far. To the best of our knowledge, our work is the

ﬁrst one that describes the phases of the Ripple pro-

tocol in such great detail, trying to avoid ambiguities

in deﬁning its behavior. We have included the analy-

sis of two key security properties, namely safety and

liveness, based upon which the efﬁcacy of the proto-

col can be determined. Furthermore, we have shown

that the correlation between some protocol parame-

ters can be leveraged to meet a desired liveness/fault

tolerance. Our work represents the ﬁrst step towards

the complete analysis of the XRP Ledger Consensus

Protocol and opens several research directions. For

instance, our set-theoretic approach could serve as the

basis for the construction of an extended formalism

that is capable of capturing the behaviour of the pro-

tocol by means of a strictly formal language. Also

the use of different model-driven approaches and au-

tomated veriﬁcation tools can greatly beneﬁt from our

speciﬁcation efforts and facilitate the comprehensive

description of the protocol. For the immediate future,

we plan to extend our work considering the formal-

ization of additional security properties and using dif-

ferent models of computation.

REFERENCES

Armknecht, F., Karame, G. O., Mandal, A., Youssef, F.,

and Zenner, E. (2015). Ripple: Overview and Out-

look. In Conti, M., Schunter, M., and Askoxylakis,

I., editors, Trust and Trustworthy Computing, pages

163–180, Cham. Springer International Publishing.

Badertscher, C., Maurer, U., Tschudi, D., and Zikas, V.

(2017). Bitcoin as a Transaction Ledger: A Compos-

able Treatment. In Katz, J. and Shacham, H., editors,

Advances in Cryptology – CRYPTO 2017, pages 324–

356, Cham. Springer International Publishing.

Bano, S., Sonnino, A., Al-Bassam, M., Azouvi, S., Mc-

Corry, P., Meiklejohn, S., and Danezis, G. (2017).

Consensus in the Age of Blockchains. CoRR,

abs/1711.03936.

Cachin, C. and Vukolic, M. (2017). Blockchain Consensus

Protocols in the Wild. CoRR, abs/1707.01873.

Chase, B. and MacBrough, E. (2018). Analysis of the XRP

Ledger Consensus Protocol. CoRR, abs/1802.07242.

Daian, P., Pass, R., and Shi, E. (2016). Snow White:

Provably Secure Proofs of Stake. Cryptology ePrint

Archive, Report 2016/919.

Fischer, M. J., Lynch, N. A., and Paterson, M. S. (1985).

Impossibility of Distributed Consensus with One

Faulty Process. J. ACM, 32(2):374–382.

Garay, J., Kiayias, A., and Leonardos, N. (2015). The Bit-

coin Backbone Protocol: Analysis and Applications.

In Oswald, E. and Fischlin, M., editors, Advances

in Cryptology - EUROCRYPT 2015, pages 281–310,

Berlin, Heidelberg. Springer Berlin Heidelberg.

Garay, J., Kiayias, A., and Leonardos, N. (2017). The Bit-

coin Backbone Protocol with Chains of Variable Dif-

ﬁculty. In Katz, J. and Shacham, H., editors, Ad-

vances in Cryptology – CRYPTO 2017, pages 291–

323, Cham. Springer International Publishing.

Garay, J. A., Kiayias, A., Leonardos, N., and Panagiotakos,

G. (2018). Bootstrapping the Blockchain, with Appli-

cations to Consensus and Fast PKI Setup. In Abdalla,

M. and Dahab, R., editors, Public-Key Cryptography

– PKC 2018, pages 465–495, Cham. Springer Interna-

tional Publishing.

Gramoli, V. (2017). From Blockchain Consensus Back to

Byzantine Consensus. Future Generation Computer

Systems.

Halpin, H. and Piekarska, M. (2017). Introduction to Secu-

rity and Privacy on the Blockchain. EuroS&P 2017 -

2nd IEEE European Symposium on Security and Pri-

vacy, Workshops.

Kiayias, A., Russell, A., David, B., and Oliynykov, R.

(2017). Ouroboros: A Provably Secure Proof-of-

Stake Blockchain Protocol. In Katz, J. and Shacham,

H., editors, Advances in Cryptology – CRYPTO 2017,

pages 357–388, Cham. Springer International Pub-

lishing.

Mauri, L., Cimato, S., and Damiani, E. (2018). A Compar-

ative Analysis of Current Cryptocurrencies. In Pro-

ceedings of the 4th International Conference on In-

formation Systems Security and Privacy - Volume 1:

ICISSP, pages 127–138. INSTICC, SciTePress.

Nakamoto, S. (2008). Bitcoin: A Peer-to-Peer Electronic

Cash System.

Pass, R., Seeman, L., and Shelat, A. (2017). Analysis of

the Blockchain Protocol in Asynchronous Networks.

In Coron, J.-S. and Nielsen, J. B., editors, Advances

in Cryptology – EUROCRYPT 2017, pages 643–673,

Cham. Springer International Publishing.

Pass, R. and Shi, E. (2017). The Sleepy Model of Consen-

sus. In Takagi, T. and Peyrin, T., editors, Advances

in Cryptology – ASIACRYPT 2017, pages 380–409,

Cham. Springer International Publishing.

Pease, M., Shostak, R., and Lamport, L. (1980). Reach-

ICISSP 2020 - 6th International Conference on Information Systems Security and Privacy

ing Agreement in the Presence of Faults. J. ACM,

27(2):228–234.

Rawat, D. B., Chaudhary, V., and Doku, R. (2019).

Blockchain: Emerging Applications and Use Cases.

CoRR, abs/1904.12247.

Ripple Labs Inc. (a). Ripple. https://ripple.com/. Last

checked on Oct, 2019.

Ripple Labs Inc. (b). XRP Ledger Dev Portal.

https://xrpl.org/index.html. Last checked on Oct,

2019.

Ripple Labs Inc. (c). Ripple Source, GitHub repository.

https://github.com/ripple/rippled/tree/develop/src/

ripple. Last checked on Oct, 2019.

Saad, M., Spaulding, J., Njilla, L., Kamhoua, C. A., Shetty,

S., Nyang, D., and Mohaisen, A. (2019). Explor-

ing the Attack Surface of Blockchain: A Systematic

Overview. CoRR, abs/1904.03487.

Schwartz, D., Youngs, N., and Britto, A. (2014). The Rip-

ple Protocol Consensus Algorithm. Ripple Labs Inc.

White Paper.

Vukoli

c, M. (2016). The Quest for Scalable Blockchain

Fabric: Proof-of-work vs. BFT Replication. In Ca-

menisch, J. and Kesdo

gan, D., editors, Open Problems

in Network Security, pages 112–125, Cham. Springer

International Publishing.

Wang, W., Hoang, D. T., Xiong, Z., Niyato, D., Wang, P.,

Hu, P., and Wen, Y. (2018). A Survey on Consensus

Mechanisms and Mining Management in Blockchain

networks. CoRR, abs/1805.02707.

Wilson, B. (2018). Raise quorum / increase fault tol-

erance. https://github.com/ripple/rippled/issues/2604.

Last checked on Oct, 2019.

Xiao, Y., Zhang, N., Lou, W., and Hou, Y. T. (2019).

A Survey of Distributed Consensus Protocols for

Blockchain Networks. CoRR, abs/1904.04098.

A Formal Approach for the Analysis of the XRP Ledger Consensus Protocol