Anomaly Event Detection based on People Trajectories for Surveillance

Videos

Rensso Mora Colque

, Edward Cayllahua

, Victor C. de Melo

, Guillermo Camara Chavez

and

William Robson Schwartz

Universidad Cat

olica San Pablo, DCC, Arequipa, Per

Universidade Federal de Ouro Preto, ICEB, Ouro Preto, Brazil

Universidade Federal de Minas Gerais, DCC, Belo Horizonte, Brazil

Keywords:

Anomaly Recognition, Trajectory Analysis, Recurrent Autoencoder.

Abstract:

In this work, we propose a novel approach to detect anomalous events in videos based on people movements,

which are represented through time as trajectories. Given a video scenario, we collect trajectories of normal

behavior using people pose estimation techniques and employ a multi-tracking data association heuristic to

smooth trajectories. We propose two distinct approaches to describe the trajectories, one based on a Convolu-

tional Neural Network and second based on a Recurrent Neural Network. We use these models to describe all

trajectories where anomalies are those that differ much from normal trajectories. Experimental results show

that our model is comparable with state-of-art methods and also validates the idea of using trajectories as a

resource to compute one type of useful information to understand people behavior; in this case, the existence

of rare trajectories.

1 INTRODUCTION

Abnormal event detection for video surveillance

refers to the problem of ﬁnding patterns in sequences

that do not conform to expected events (Du et al.,

2013). It is a challenging problem because the deﬁ-

nition of anomaly is subjective to the particular scene

context, giving origin to a large number of interpre-

tations. For instance, someone running at a marathon

can be considered a normal event, while someone run-

ning during a regular working day due to an emer-

gency, can be considered an anomalous event. There-

fore, the difﬁculty of anomaly recognition is related

to the semantics that is observed in the scene.

Due to the wide number of interpretations, deﬁn-

ing algorithms that suit in any anomaly event is a

very difﬁcult problem. Consequently, most models

focus in extracting features based on movement and

appearance from spatiotemporal regions (Popoola and

Wang, 2012). Nevertheless, this type of informa-

tion might be affected by noise due to complex back-

grounds, illumination changes and poor lighting con-

ditions. Following new trends in computer vision, this

issue can be minimized by using high level semantic

information, such as object detection and pose estima-

tion, allowing to also model anomaly from contextual

information directly.

In this work, we exploit high level information

to create a robust representation for anomaly recog-

nition. Our approach models people movements by

leveraging from body skeletons obtained through a

state-of-the-art pose estimator. The reference points

are extracted from body skeleton and aggregated

through time, thus building a trajectory. Each trajec-

tory is then represented using deep neural networks to

better encode its morphology. Our hypothesis is that

trajectories are able to encode the necessary informa-

tion from movement to recognize certain anomalous

events. Since our proposed approach is based on tra-

jectories, it is more robust to the aforementioned is-

sues that affect classical approaches based on move-

ment and appearance; furthermore, an advantage of

using trajectories is that the localization of the par-

ticular individual performing an anomalous event is

easily retrieved. In addition, trajectories allow other

applications, such as people behavior analysis. We

illustrate this application by using clustering models,

such that it is possible to characterize the rarity of tra-

jectories (Zhou et al., 2012). It is important to high-

light that the proposed model is oriented to scenes

where people detector techniques and tracking algo-

rithms can offer a good representation, thus, crowded

Colque, R., Cayllahua, E., C. de Melo, V., Chavez, G. and Schwartz, W.

Anomaly Event Detection based on People Trajectories for Surveillance Videos.

DOI: 10.5220/0008952401070116

In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 5: VISAPP, pages

107-116

ISBN: 978-989-758-402-2; ISSN: 2184-4321

107

scenes are not considered in the scope of this research.

The novelty and contributions of this work are

summarized as follows. (i) A spatial and temporal tra-

jectory descriptor for anomaly event detection based

on deep neural networks, aiming at describing trajec-

tories by their morphology. (ii) A novel approach for

anomaly recognition extracted from higher level in-

formation. (iii) An heuristic for multi-object tracking

for data association based on Kalman ﬁlter. (iv) An

experimental evaluation regarding trajectories and the

relation between anomalies and rarity.

This paper presents a literature review in Sec-

tion 1. Section 2 exposes our approach for anomaly

recognition and rare event analysis. Section 3 con-

tains our experiment results, which show that our

model is competitive with other state of art methods,

and also enforces the idea of using trajectories for

other type of analysis. Section 4 concludes this study

presenting a discussion about advantages and limita-

tions of the complete study.

Related Works

Due to the success of Deep Neural Networks (DNN),

researchers started to employ them to solve the

anomaly recognition problem (Kiran et al., 2018). For

instance, CNN-based approaches describe anoma-

lies by creating models that combine optical ﬂow

and texture information from spatiotemporal re-

gions (Sabokrou et al., 2018). Models that use AE or

Convolutional AE (CAE) (Ribeiro et al., 2017) aim

at describing events in non-supervised fashion. Thus,

anomalies are representations that differ from normal

(i.e., an anomaly occurs when the AE is not able to

perform a satisfactory reconstruction). Similar to AE,

GAN-based approaches learn the normal behavior us-

ing a generative model (Ravanbakhsh et al., 2017),

in which anomalies are recognized by the discrimina-

tor since the generator built an anomaly representa-

tion based in normal situations. Furthermore, RNN

models usually appear accompanied with DNN, spe-

cially for movement data (Chong and Tay, 2017). The

idea is to combine the recurrent information of what

is considered normal and create a representation of

it. Nevertheless, most of these models depend on the

camera position. Thus, these models learn speciﬁc

patterns of the camera view which cannot be trans-

ferred to other views without retraining. Similarly

to handcrafted features (De Almeida et al., 2017),

these techniques also extract texture (appearance) and

movement (ﬂow) information. On the other hand, in

our model, the source of information for anomaly rep-

resentation is different. Speciﬁcally, our model ex-

tracts information from trajectories. An important dif-

ference with these models is the fact that our model is

not affected by large color intensity changes.

Anomaly recognition models based on trajecto-

ries (Wang et al., 2008) are among ﬁrst approaches

in visual anomaly recognition. The main drawback of

this model was the problem of people detection and

trajectory building. However, with novel approaches

and technologies, this issue has been progressively re-

duced. The model proposed by Cosar et al. (Cosar

et al., 2017) considers trajectories to build regions

which are examined in a time lapse to ﬁnd texture

and movement information. The process is divided

into two phases: description and ﬁltering. Li et al.(Li

et al., 2013) proposed a technique that describes the

scene using a sparse representation of overlapping tra-

jectories, these trajectories are grouped and abnormal

events are recognized when they differs much from

any cluster. While Saini et al. (Saini et al., 2018) used

trajectories to train a Hidden Markov Model (HMM)

combined with genetic algorithm to detect anoma-

lies by their low probability,the model proposed by

Zhou et al. (Zhou et al., 2015) developed a method

based on HMM and feature clustering. An impor-

tant difference between these approaches and ours

is that our model does not segment the trajectories

in parts or blocks, it focuses in complete trajectory.

Furthermore, for surveillance purposes, region based

models analyze motion characteristics, which are not

meaningful without accurate localization of the tar-

gets. Thus, trajectories present the complete event

that contains the anomaly.

2 PROPOSED APPROACH

In this section, we present the proposed approach for

anomaly detection comprising four main steps: (i)

reference point estimation, (ii) tracking building, (iii)

feature extraction, and (iv) anomaly and rare trajec-

tory detection. Figure 1 presents an overview of our

approach.

2.1 Reference Point Estimation

The ﬁrst stage of our model computes the reference

points in a frame, they represent a determinate per-

son. In the literature, we can ﬁnd accurate object

and person detectors (Redmon and Farhadi, 2017).

These detectors provide the bounding box of the de-

tected person/object. Although, the person is inside

the bounding box, the four points deﬁning the bound-

ing box do not represent a reliable reference to lo-

cate the person inside this bounding box, due to the

bounding box varying size. For instance, a person

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

108

with stretched arms will have a larger bounding box

than a person with closed arms. Another case where

the bounding box coordinates are not reliable as ref-

erence points is when the detector detects a group of

persons and their bounding box changes in size in ev-

ery frame. To overcome this, our approach deﬁnes the

reference point of a person as the joint point between

body and head. This is a very robust reference point,

as it rarely changes and it more stable compared to the

movements of other parts in the body (Morais et al.,

2019). In order to compute this reference point, we

use a multi-person pose estimator (Cao et al., 2017).

This model extracts the person skeleton including the

point between head and body parts.

2.2 Trajectory Building

The next step of our approach is to create the trajec-

tories for each person. The goal is to connect ref-

erence points, relating them frame by frame and la-

beling the set with a person identiﬁer. Multi-object

tracking is a np-hard problem (Betke and Wu, 2016).

Therefore, inspired on (Girdhar et al., 2018), we in-

troduce an algorithm (see Alg. 1) that aims to offer a

straightforward alternative to complex multi-tracking

Figure 1: Overview of our approach. Given a body skeleton,

we select reference points that are used to build trajectories.

A sequence of such reference points consists of a trajectory.

Then, we describe the normalized trajectories using two dif-

ferent techniques, a convolutional descriptor based on CNN

or a recurrent descriptor modeled using a RNN. During the

testing phase, we recognize anomalies and rare trajectories

by comparing the descriptors extracted from each test sam-

ple regarding the trained model.

models. Given a tracklet set T and a set of reference

points R

observed at a frame j, our algorithm asso-

ciates the reference points with their respective track-

lets; the algorithm also creates a new tracklet if a new

person observation appears. Initially, T is an empty

set (T =

0); after the ﬁrst iteration, any new reference

point is associated to a tracklet.

Algorithm 1: Trajectory Builder algorithm.

1: procedure TRAJECTORY(T , R

)

2: for each r ∈ R

3: for each t ∈ T do

4: S[r,t] ← Scr(r, t),

5: M ← Munkres(S),

6: T ← Update(R

, T , M)

7: return T

The algorithm computes the relationship between

one reference point and its corresponding tracklet.

For a frame j + 1, we compute a set of reference

points R

j+1

, in order to associate every element in

j+1

to a tracklet in T , which contains a Kalman ﬁl-

ter K. This model allow us to predict from R

the

new positions of such reference points in the frame

j + 1. Our algorithm computes the best ﬁtting track-

let t for a r ∈ R

j+1

, we build a matrix M

|×|T |

that

contains the scores between a tracklet and each refer-

ence point. From this matrix, we can look for the best

match between a reference point and a tracklet.

To compute the score point between a tracklet t =

(l, pr,K,P) and reference point r, l is subtracted from

r and pr in such a way that l is considered as coordi-

nate origin. Let be the result of a = (¯r. ¯pr)/k¯rk.k ¯prk,

this value is truncated between [−1,1]. Thus, the an-

gle between r and pr is θ

k, j

= arccos(a) is in the range

[0,π]. The ﬁnal score is given by

Scr(r,t) =







k, j

if δ

< th + b f ,

k, j

× τ if δ

< k ¯prk,

π × τ otherwise,

(1)

where δ

= kp− prk is the distance between reference

point r and the predicted point pr, b f = th/(2 × |P|)

is a value that is inversely proportional to the num-

ber of elements in the set P, δ

= kr − pr/2k is the

distance from point r and the middle point of l and

pr, as l is the origin of coordinates then, this point is

half pr, the variable th is a threshold value that is set

before the process and depends on the size of people

in the video, and τ ≥ 2 is a penalty value. The idea

of the score function is to assign a low value to the

compared point that is closer to the predicted point,

as we can see in Figure 2. Using the variable b f ,

we extend the initial threshold and balance the initial

prediction of the Kalman model, speciﬁcally for the

Anomaly Event Detection based on People Trajectories for Surveillance Videos

109

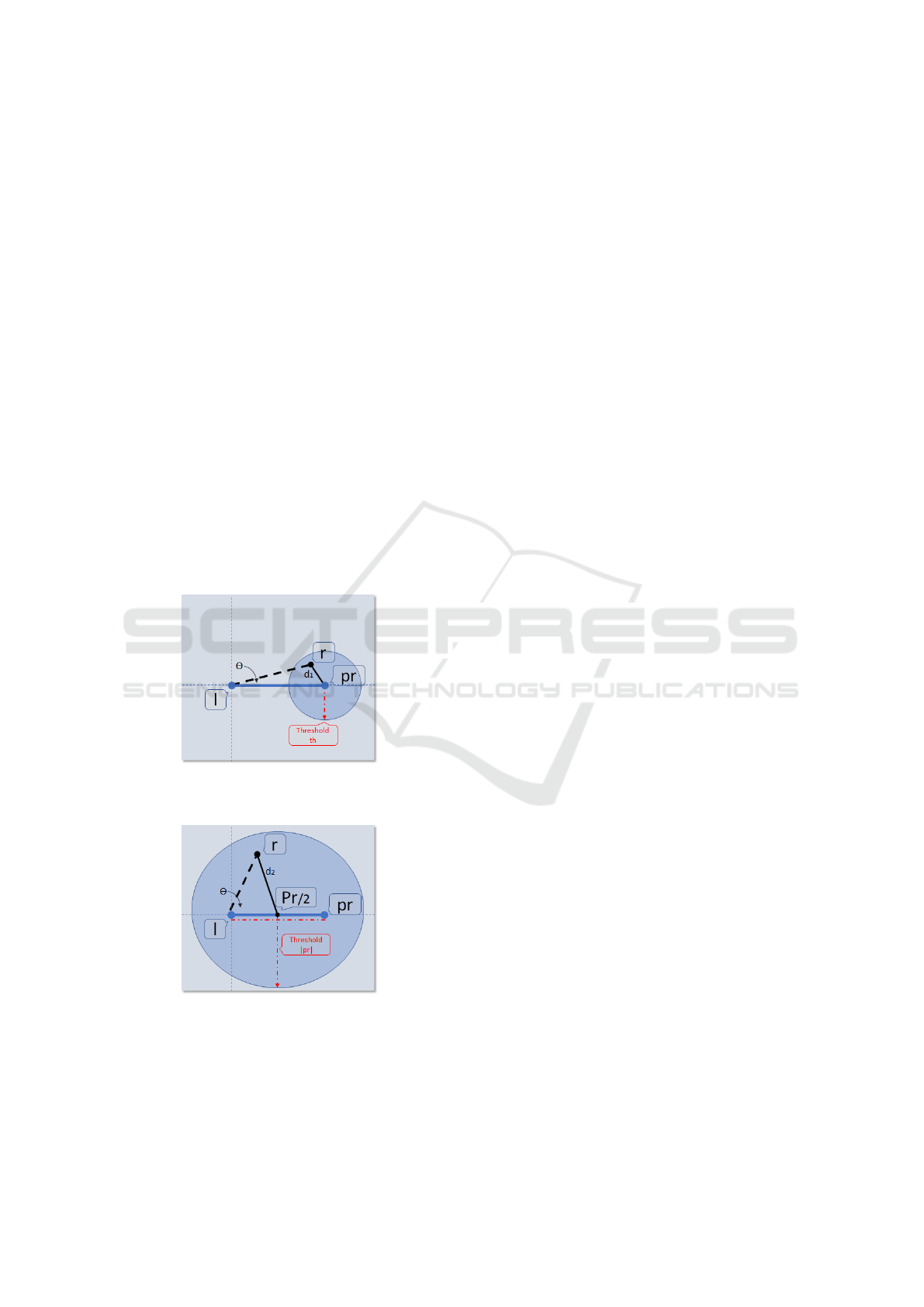
initial points, where the Kalman model is not stable.

Initially, the variable b f allow us to be more robust in

the ﬁrst iterations of the algorithm, where there is not

enough information about trajectories and the Kalman

ﬁlter produce predictions with noise. Variable b f de-

creases as there are more detected points in the trajec-

tory. The second case of the score function is when

the point is not sufﬁciently near to the predicted point

but it is close to the trajectory ﬂow, as shown in Fig-

ure 3. The idea in this case is to cover a greater region

where candidate point could move, including a little

region behind the last trajectory point. In last case, the

candidate point is outside of the possible regions of

movement. The set M contains all the scores between

reference points in R and tracklets in T . In the next

state, our approach computes the best distribution us-

ing Munkres’ algorithm (Zhu et al., 2016) to solve

the assignment problem. After that, the points are as-

signed to a speciﬁc trajectory. Unassigned points cre-

ate new tracklets. Finally, all trajectories update their

information (Kalman model and predicted point), and

trajectories that do not present changes within time

lapse are closed and saved to avoid confusing with

new trajectories.

Figure 2: Example of situation when a predicted point of

Kalman is near to a candidate point.

Figure 3: Example of situation when a predicted point of

Kalman is far from a candidate point.

2.3 Trajectory Point Reduction and

Augmentation

Once every trajectory is collected, the trajectories

must have the same number of points to use this infor-

mation as input for the models. Therefore, we reduce

or increase the number of points up to a certain value

by employing a point reduction or point augmentation

process. The problem in the ﬁrst process lies in the

choice of signiﬁcant points. To solve this, our model

selects the points that better represent the shape of

the trajectory, giving preference to the points where

there is more variation, such as curves. To select these

points, the model applies the second derivative to the

set of points. The highest values represent the curves

in the shape of trajectory. Thus, our model chooses

the interest points by sorting from largest to the small-

est the values obtained by the second derivative. Fig-

ure 4 illustrates the idea of this process, where the ﬁrst

row depicts the images with the ﬁrst derivatives of the

trajectories, the highest values are the key points, and

the second row shows the chosen points. Hence, with

this heuristic, we reduce the number of points in a tra-

jectory. For the point augmentation, our model per-

forms a straightforward strategy. Depending on the

number of required points, they are introduced in the

middle of two consecutive points. This process is per-

formed initially in the original set of points, if more

points are needed, the process is repeated until the

number of necessary points is reached. Finally, all

the trajectories have the same number of points n.

2.4 Feature Extraction

Unsupervised representation learning has become an

important tool for anomaly detection. An autoencoder

is a neural network trained through backpropagation

that provides a dimensionality reduction by minimiz-

ing the reconstruction error on the training set (Kiran

et al., 2018). Our approach presents two feature ex-

traction models based on unsupervised learning: ﬁrst

descriptor TAoT-M, based on an image representation

extracted from a convolutional autoencoder, and sec-

ond descriptor TAoT-T, which directly utilizes the tra-

jectory information in a recurrent autoencoder. In-

spired by (Zhang and Lu, 2004), the idea of the ﬁrst

descriptor (based on convolution) is to ﬁnd a repre-

sentation that depicts the trajectory as a complete en-

tity (i.e., without segmenting or dividing it). There-

fore, the goal is to describe the morphology of the

trajectory. To accomplish this goal, our approach

computes the variation between each pair of points

belonging to a given trajectory into two matrices:

angular (referred to as AG) and radial (RD), which

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

110

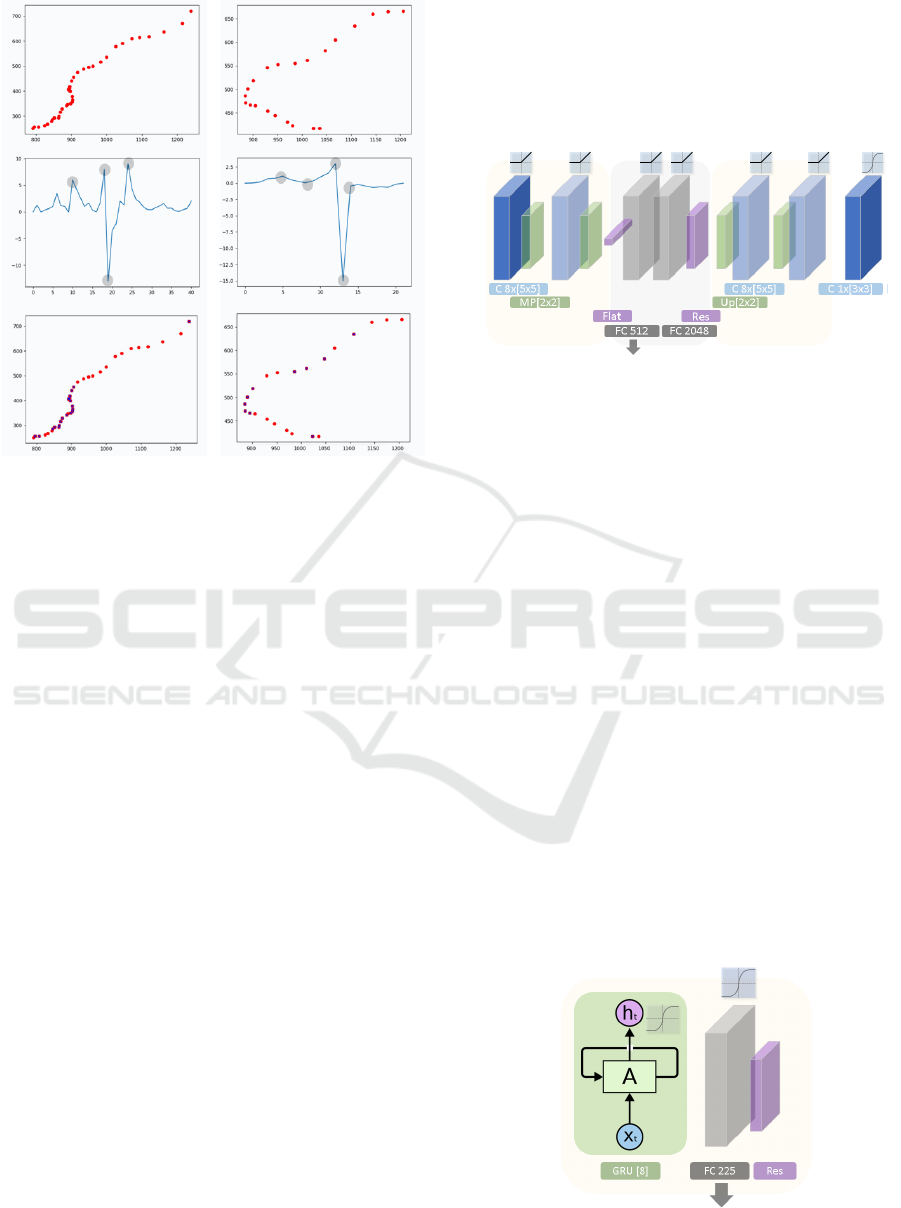
Figure 4: Examples for point selection when the number

or points have to be reduced. The ﬁrst row corresponds

to trajectory examples. the second row is the set of ﬁrst

derivative, circles show some interest points. The third row

presents the selected points marked in blue.

are square matrices of dimension n × n. The posi-

tion AG

a,b

is ﬁlled with the angle formed by points

, p

∈ T

. Similarly, the position RD

a,b

is ﬁlled

with the magnitude of the vector formed by points

, p

∈ T

. Thus, local information is saved in places

that are near to the diagonal of the matrix, while the

global information appears closer to the edges of the

matrix. Radial matrix RD is symmetric, while in the

angular matrix, the values are complements between

superior and inferior triangular sections of the matrix.

These images are n × n matrices, where n is the tra-

jectory’s number of points.

Afterwards, these images are described by a con-

volutional autoencoder. Similar to Kasparavi

ciut

e ap-

proach (Kasparavi

e et al., 2019), our ﬁrst descrip-

tor is a Encoder and decoder model, which is com-

posed by two convolutional layers, each layer with

eight ﬁlters, whose convolutional mask size is 5 × 5,

followed by max pooling and up sampling layers of

size 2 × 2. In the middle of this representation, the

convolutional autoencoder architecture presents two

fully connected layers, with 512 and 2048 neurons,

respectively, at the end of the decoder part ﬂatten and

reshape layer are used to synthesize the information.

The idea of this architecture is to ﬁnd a semantic rep-

resentation from angular and radial matrices. This

network is trained with only normal trajectory images

normalized between [0, 1]. After the model computes

the weights, trajectory features are extracted from the

ﬁrst fully connected layer (512). The feature vector

is the concatenation of outputs of angular and radial

convolutional autoencoder. Hence, the ﬁnal represen-

tation is a vector of 1024 dimensions. Figure 5 depicts

the autoencoder architecture.

Figure 5: Architecture for convolutional autoencoder.

The second descriptor builds the feature vectors

using a recurrent autoencoder. Similar to the previ-

ous model, the idea in this approach is to ﬁnd an en-

tire representation for the trajectory by correlating the

morphology and the temporal information. Thus, the

proposed network learns the temporal trajectory pat-

terns. Composed by only three layers, it begins with

a recurrent cell, which in our approach is a Gated Re-

current Unit (GRU) (Chung et al., 2014). We opted to

use GRU instead of other recurrent architectures, such

as LSTM, because they are better suited for small

training sets (Chung et al., 2014). The input for this

cell is the set of overlapping segments that compose

the trajectory. The next element is a fully connected

layer with 225 neurons. Both layers, recurrent cell

and fully connected utilize sigmoid as activation func-

tion. At the end of the pipeline, the model reshapes

the output to the same input size, thus the recurrent

autoencoder can learn the trajectory patterns. This

network is also trained with only normal trajectories.

The ﬁnal descriptor for a trajectory is the output of the

fully connected layer, a vector comprising 225 dimen-

sions. Figure 6 presents the architecture for recurrent

autoencoder.

Figure 6: Architecture for recurrent autoencoder.

Anomaly Event Detection based on People Trajectories for Surveillance Videos

111

2.5 Anomaly Recognition and Rare

Trajectory Identiﬁcation

In the last step, our model is divided in two ap-

proaches: anomaly trajectory detection and rare tra-

jectory identiﬁcation. While the ﬁrst addresses the

problem of identifying anomalies, the second il-

lustrates an application of people behavior analy-

sis by characterizing uncommon trajectories. The

strategy for anomaly detection is simple, our model

computes nearest neighbor for each point in test-

ing (Mora Colque et al., 2017). Thus, if the distance

of this point is smaller than a threshold ∆, at least

for one point in training, then this test point is nor-

mal. Otherwise, if the distance to any training point

is larger than the threshold ∆, then it is considered an

anomalous point or trajectory. Each descriptor were

tested separately. In rare trajectory identiﬁcation, we

suppose that points that represent common trajecto-

ries make clusters in the space, and anomalies are iso-

lated points or they are in groups with few elements.

Thus, our model groups the trajectories using a clus-

tering Afﬁnity Propagation (AP) model. An advan-

tage of using an AP model is that it does not need to

set the number of clusters. Thus, given a trained and

testing features, these representations can be seen as

points in the space, where anomalies can be consid-

ered as outliers (Aggarwal, 2013). The second aims

to ﬁnd rare patterns, in fact, rare trajectories are whose

that are not common, and possibly they are found in

small clusters far from common.

3 EXPERIMENTAL RESULTS

In this section, we present our experimental evalua-

tion. First, we describe the results regarding anomaly

detection and then present the results achieved on the

rare trajectory recognition task. Experiments were

performed on the following datasets: Subway (Adam

et al., 2008), Avenue (Lu et al., 2013), and our pro-

posed video dataset, named Laboratory.

The setup for the tracking step depends on the

video scene. Each dataset has a different setup, ba-

sically due to the people that appear on the scene be-

ing near or far from the camera. We ﬁxed the num-

ber of points per trajectory to n = 64. For the recur-

rent autoencoder, the GRU input is the trajectory di-

vided in segments, each segment composed of eight

points with an overlap of four points between them

for each segment. This autoencoder was trained af-

ter 200 epochs, using sigmoid function for the ac-

tivation and hard sigmoid the recurrent activation.

We employed mean square error as loss function and

AdaDelta algorithm for optimizer. For the convolu-

tional autoencoder, the training phase was limited to

300 epochs, using mean square error as loss func-

tion and the Adam optimizer algorithm. The aver-

age loss value during training were 0.0001 and 0.01

for recurrent and convolutional networks respectively.

These protocols were the same for all datasets. The

∆ ∈ [0,10] value for KNN distance algorithm is used

to build the Receiver Operating Characteristic (ROC)

curves.

3.1 Anomaly Recognition

The subway dataset (Adam et al., 2008) is composed

of two sequences. The ﬁrst video sequence, known

as Entrance Gate, has a time length of one hour and

36 minutes and the second video, called Exit Gate

has length of 43 minutes. Entrance Gate is a se-

quence recorded from a subway entrance gate view.

The ground-truth in this clip presented both types

of anomalies: walking on wrong way and jumping

the ticket gate. For this sequence, we compare our

results with the state-of-the-art approaches proposed

by (Roshtkhari and Levine, 2013) (Sparce), (Cheng

et al., 2015) (GPR), (Li et al., 2014) (Bayes),

(Saligrama and Chen, 2012) (Agr) and (Mora Colque

et al., 2017). Figure 7 shows our experimental results

and the comparison with the state-of-the-art. Our re-

current descriptor achieved a promising result com-

pared with recent methods in the literature. However,

our convolutional descriptor missed some anomalies,

speciﬁcally the ticket jumping, because the convolu-

tional autoencoder aims to describe the morphology

of the trajectory and when the people jump the ticket

gate the morphology of the trajectory is similar with

other normal trajectories. The Exit Gate clip contains

data recorded from a subway exit. In this case, the

ground-truth considers only people walking in wrong

way. We compare our results with (Li et al., 2014)

(Bayes) and (Mora Colque et al., 2017) (HOFME)

methods. Figure 8 presents the results for this clip,

in this case, our recurrent descriptor outperforms the

other models. The convolutional descriptor reports

low AUC compared with the other methods in this set

as well.

Train Sequence. The train sequence is part of a set of

videos for anomaly detection proposed by (Zaharescu

and Wildes, 2010). This video clip has a view from

the interior of a train coach and is the only sequence

in the dataset that contains people in the scenes. It

has 19,218 frames which are very challenging due

to drastic variation in lighting conditions and cam-

era jitter. The anomalies in this sequence comprise

people coming out and moving on the train. For

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

112

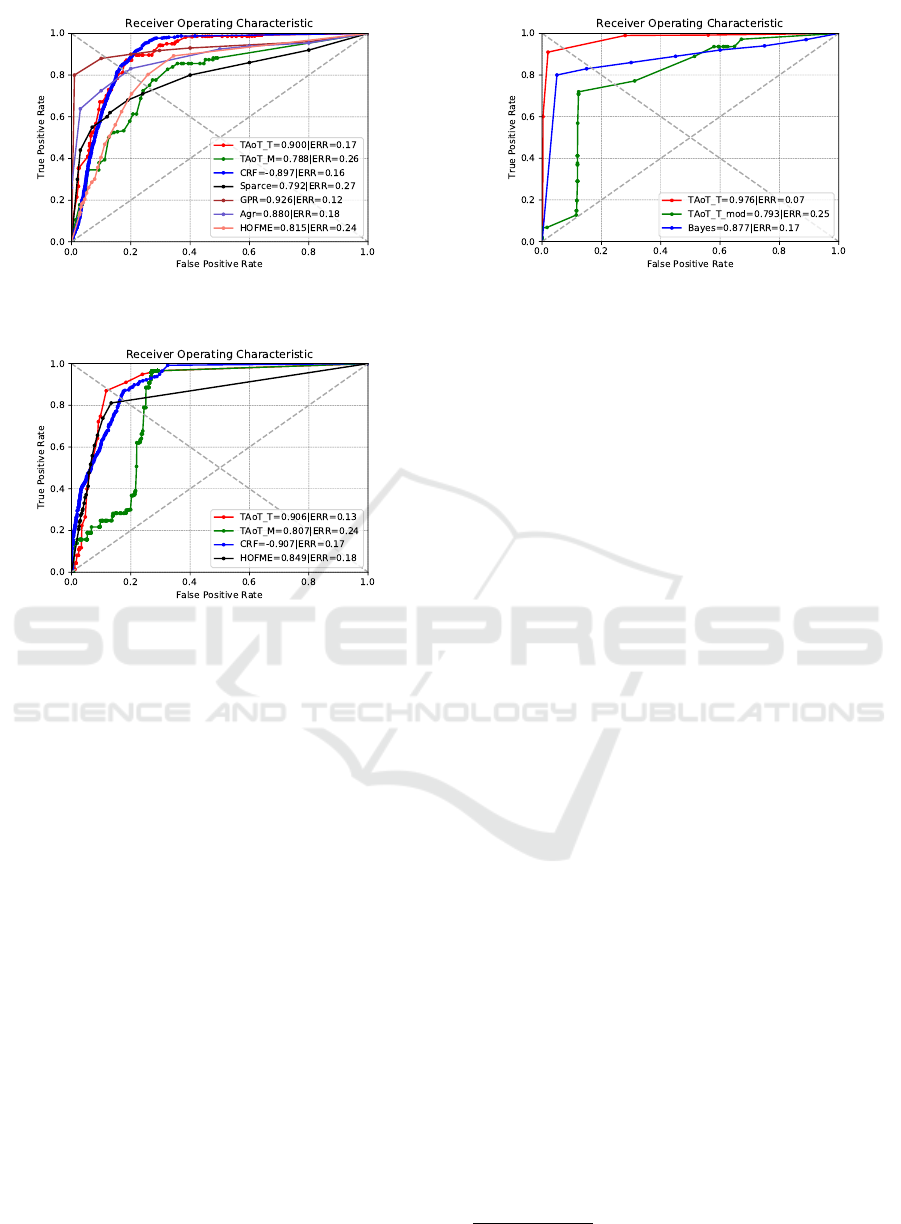
Figure 7: Experimental results and comparison with the

state-of-the-art on the Entrance.

Figure 8: Experimental results and comparison with the

state-of-the-art on the Exit.

this video sequence, we present two results, where

“TAoT-T-mod” (green colored curve) and “TAoT-T”

(red colored curve), both using recurrent descriptor.

The ﬁrst experiment was performed training with 800

frames and testing with the rest of the video. The sec-

ond experiment “TAoT-T”, which follows the original

ground-truth validation protocol, the number of train-

ing frames are 800 and for testing only the last 5000.

These experiments have two goals, ﬁrst we want to

evaluate our recurrent descriptor, which presents bet-

ter results for anomaly detection in a difﬁcult light-

ing condition sequence. Figure 9 shows our results

and the results achieved by the Bayes method (Cheng

et al., 2016). The second experiment obtained better

results because the information for trajectories were

clear in contrast with the ﬁrst aforementioned exper-

iment. Also, according to the results shown in Fig-

ure 9, our model outperforms the Cheng’s method

because, to build the trajectories, our model utilizes

a pose estimation/person detector, which is robust to

problems of illumination changes, camera movement,

shadows, etc.

Avenue Dataset. Introduced by (Lu et al., 2013), the

avenue dataset contains videos from entrance avenue

at the Chinese University of Hong Kong (CUHK) and

is composed of 16 training videos and 21 test clips.

Figure 9: ROC curves for Train sequence.

Testing videos include both normal and anomalous

events. It comprises three types of anomalies: run-

ning, wrong direction and abnormal object. Abnor-

mal object sequences contains a person that pulls up a

backpack. In this work, we did not test the sequences

that contain this type of anomalies. Thus, our exper-

iments were performed without sequences 5, 10, 12,

13, 14, 16, 17 and 20. All videos for training were

used to tune the network. In this experiment, we just

tested the recurrent descriptor. According to Table 1,

TAoT-T achieves the best result in sequence 18 and

the worst in sequence 19. In this last sequence, the

missed anomaly is a person walking in a wrong direc-

tion towards the camera, but due to the projection, the

generated trajectory was too small. Such issues could

be minimized by employing depth information. We

should add that we cannot compare this experiment

with other works in the literature due to sequence

reduction in our experiments. However, comparing

only the mean AUC with other studies (Hasan et al.,

2016)(Kiran et al., 2018) our results are still compet-

itive.

The experiments performed to identify rare trajec-

tories intend to separate or identify trajectories that

are not usual. The criterion is simple, clustering tra-

jectories to segment common from uncommon. Rare

trajectories are useful because they are not necessarily

anomalies, but could be suspicious events that would

trigger an alarm. For these experiments, we introduce

a novel dataset called Laboratory, which contains one

month of recordings of the entrance of a laboratory

The video resolution is 1280 × 720, recorded at a

frame rate of 30 FPS. The videos have length between

30 seconds and four minutes. The ground-truth is

based on people behavior, for instance, a person stay-

ing for a long time at the door or going around suspi-

ciously. For training, we selected 10 days of record-

ings (1,100 normal trajectories), and the remaining

Videos and ground-truth annotations will be provided

soon.

Anomaly Event Detection based on People Trajectories for Surveillance Videos

113

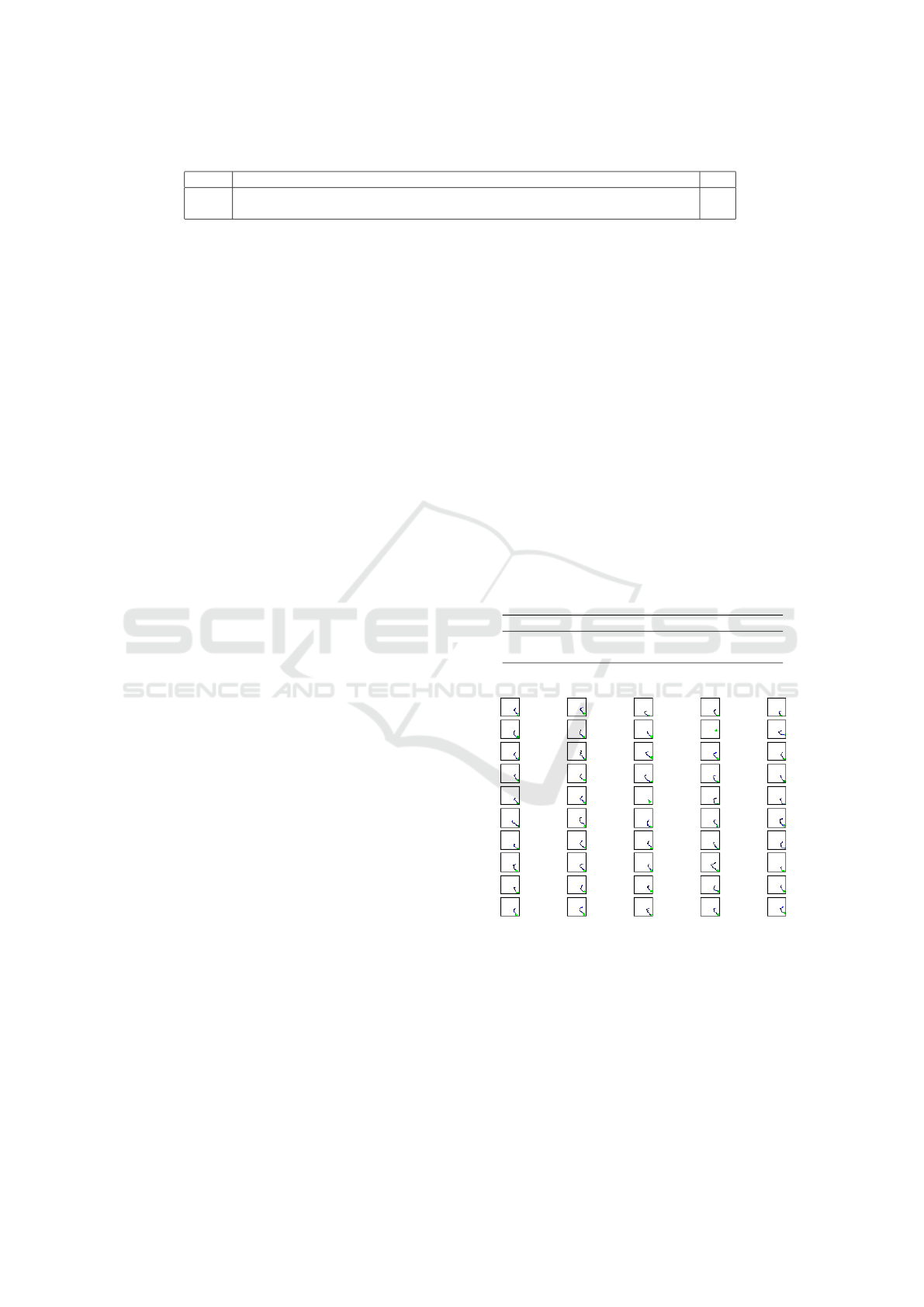
Table 1: AUC and ROC for Avenue sequences. Highlighted in bold, we present our best and worst result.

Seq. 1 2 3 4 6 7 8 9 11 15 18 19 21 µ

AUC .69 .80 .44 .94 .84 .88 .82 .80 .74 .50 .95 .22 .61 .71

ERR .45 .24 .53 .22 .21 .21 .29 .29 .34 .47 .9 .51 .35 .32

for testing (2,946 normal and abnormal trajectories).

Videos contain at least one person and might have up

to 10 people in the same scene.

We evaluate both the convolutional descriptor and

recurrent descriptor. In our data “TAoT-T” represen-

tations generates 58 clusters, where most of anoma-

lies appear in clusters with few elements. “TAoT-

M” feature vectors generate 141 clusters, also, low

populated clusters contains the anomalous trajecto-

ries. Note that without any previous information

about anomalies these events that are in clusters with

few elements could be considered as rare events. An-

other important aspect to highlight is that our descrip-

tors encode important information about trajectories

like: morphology, orientation and speed.

3.2 Rare Trajectory Identiﬁcation

The experiments performed to identify rare trajecto-

ries intend to separate or identify trajectories that are

not usual. The criterion is simple, clustering trajecto-

ries to segment common from uncommon. Rare tra-

jectories are useful because they are not necessarily

anomalies, but could be suspicious events that would

trigger an alarm. For these experiments, we introduce

a novel dataset called Laboratory.

The Laboratory dataset contains one month of

recordings of the entrance of a laboratory. The video

resolution is 1280 × 720, recorded at a frame rate

of 30 FPS. The videos have length between 30 sec-

onds and four minutes. The ground-truth is based

on people behavior, for instance, a person staying

for a long time at the door or going around suspi-

ciously. For training, we selected 10 days of record-

ings (1,100 normal trajectories), and the remaining

for testing (2,946 normal and abnormal trajectories).

Videos contain at least one person and might have

up to 10 people in the same scene. Therefore, each

video is labeled as normal which means that people

just enter or leaving the room where their trajectories

are smoothed lines or curves, in contrast to anoma-

lous sequences where people remaining in the scene

for long time, thus their trajectories present a complex

morphology.

We evaluate both the convolutional descriptor and

recurrent descriptor. Table 2 shows the clustering re-

sults, which reports the number of clusters created,

the cluster with the smallest number of trajectories

and the one with largest number. Clusters with a

small number of trajectories are trajectories that have

unusual morphology, but are not necessarily anoma-

lies. We see that TAoT-M creates more clusters than

TAoT-T, and, therefore, is able to ﬁnd more rare tra-

jectories. This shows that TAoT-M is better at encod-

ing more ﬁne-grained differences between the trajec-

tories. Despite this, TAoT-T still yields better results

on anomaly detection, since it is able to group spa-

tially similar trajectories, while anomalies have very

dissimilar morphology. Figures 10 and 11 show an

example of rare trajectory identiﬁcation, these images

are thumbnails from original trajectories, the circle

(green) represents the initial point of each trajectory.

It is important to highlight that our descriptors pre-

serve also the direction as well as the morphology

of the trajectories. Normal cluster, like the example

in Figure 10, contains normal trajectories, in contrast

with anomaly cluster, as the example in Figure 11,

contains anomaly trajectories inside.

Table 2: Clustering chart for Rare Trajectory Identiﬁcation.

Descriptor N. Clus. Min. Ele Max. Ele

TAoT-T 58 5 212

TAoT-M 141 3 133

Figure 10: Example of normal cluster and rare cluster us-

ing Convolutional descriptor. This cluster has 73 elements

(only 50 presented) and correspond to a normal situation.

4 CONCLUSIONS

In this work, we proposed a new method to detect

anomalous events based on the trajectory informa-

tion of person/objects. Tracking people in very crowd

scenes is a difﬁcult task, in some cases many trajec-

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

114

Figure 11: Example of normal cluster and rare cluster using

Convolutional descriptor. This cluster contains 10 elements,

it presents anomaly trajectories.

tories may be related to one person. However, the

idea is to warn the existence of strange events and

one trajectory is enough to identify the person. Thus,

in our study we propose a straightforward heuristic

for multi-person tracking, the idea of this approach

is to obtain a smooth trajectory for people. Other

tracking models could be used as long as the result

is faithful to the movement of the person and that

considers a ﬁxed point of reference. Following the

experiment results, the Recurrent descriptor suits bet-

ter for anomaly trajectory recognition, while convolu-

tional descriptor works ﬁne for rare trajectory analy-

sis, this is due to characteristics of convolutional de-

scriptor, that groups the trajectories by morphology,

which is a interesting property to cluster. As future

work, we plan to evaluate other person/object track-

ing algorithms. We can also explore new representa-

tion of trajectories based on a mixture of Recurrent

autoencoder and adversarial autoencoders (Makhzani

et al., 2016) that better discriminates the abnormal tra-

jectories so we have an improved detection of outliers.

REFERENCES

Adam, A., Rivlin, E., Shimshoni, I., and Reinitz, D. (2008).

Robust real-time unusual event detection using mul-

tiple ﬁxed-location monitors. IEEE Transactions

on Pattern Analysis and Machine Intelligence, pages

555–560.

Aggarwal, C. C. (2013). Outlier analysis. Springer Pub-

lishing Company, Incorporated.

Betke, M. and Wu, Z. (2016). Data Association for Multi-

Object Visual Tracking, volume 6. Synthesis Lectures

on Computer Vision.

Cao, Z., Simon, T., Wei, S.-E., and Sheikh, Y. (2017). Real-

time multi-person 2d pose estimation using part afﬁn-

ity ﬁelds. In The IEEE Conference on Computer Vi-

sion and Pattern Recognition (CVPR).

Cheng, K.-w., Chen, Y.-t., and Fang, W.-h. (2015). Gaussian

Process Regression-Based Video Anomaly Detection

and Localization With Hierarchical Feature Represen-

tation. IEEE Transactions on Image Processing, pages

5288–5301.

Cheng, K. W., Chen, Y. T., and Fang, W. H. (2016). An efﬁ-

cient subsequence search for video anomaly detection

and localization. Multimedia Tools and Applications,

pages 15101–15122.

Chong, Y. S. and Tay, Y. H. (2017). Abnormal event detec-

tion in videos using spatiotemporal autoencoder. Lec-

ture Notes in Computer Science (including subseries

Lecture Notes in Artiﬁcial Intelligence and Lecture

Notes in Bioinformatics), pages 189–196.

Chung, J., Gulcehre, C., Cho, K., and Bengio, Y. (2014).

Empirical evaluation of gated recurrent neural net-

works on sequence modeling. In NIPS 2014 Workshop

on Deep Learning, December 2014, pages 1–9.

Cosar, S., Donatiello, G., Bogorny, V., Garate, C., Alvares,

L. O., and Bremond, F. (2017). Toward Abnormal

Trajectory and Event Detection in Video Surveillance.

IEEE Transactions on Circuits and Systems for Video

Technology, pages 683–695.

De Almeida, I. R., Cassol, V. J., Badler, N. I., Musse, S. R.,

and Jung, C. R. (2017). Detection of Global and Lo-

cal Motion Changes in Human Crowds. IEEE Trans-

actions on Circuits and Systems for Video Technology,

pages 603–612.

Du, D., Qi, H., Huang, Q., Zeng, W., and Zhang, C. (2013).

Abnormal event detection in crowded scenes based

on Structural Multi-scale Motion Interrelated Patterns.

Proceedings - IEEE International Conference on Mul-

timedia and Expo, pages 1–8.

Girdhar, R., Gkioxari, G., Torresani, L., Paluri, M., and

Tran, D. (2018). Detect-and-Track: Efﬁcient Pose Es-

timation in Videos. Proceedings of the IEEE Com-

puter Society Conference on Computer Vision and

Pattern Recognition, pages 350–359.

Hasan, M., Choi, J., Neumann, J., Roy-Chowdhury, A. K.,

and Davis, L. S. (2016). Learning Temporal Regular-

ity in Video Sequences. IEEE Conference on Com-

puter Vision and Pattern Recognition, pages 1–31.

Kasparavi

e, G., Thelin, M., Nordin, P., S

oderstam, P.,

Magnusson, C., and Almljung, M. (2019). Online

encoder-decoder anomaly detection using encoder-

decoder architecture with novel self-conﬁguring neu-

ral networks and pure linear genetic programming for

embedded systems. In Proceedings of the 11th In-

ternational Joint Conference on Computational Intel-

ligence - ECTA, (IJCCI 2019), pages 163–171. IN-

STICC, SciTePress.

Kiran, B. R., Thomas, D. M., and Parakkal, R. (2018).

An overview of deep learning based methods for un-

supervised and semi-supervised anomaly detection in

videos. J. Imaging, 4:36.

Li, C., Han, Z., Ye, Q., and Jiao, J. (2013). Visual abnormal

behavior detection based on trajectory sparse recon-

struction analysis. Neurocomputing, pages 94–100.

Li, W., Mahadevan, V., and Vasconcelos, N. (2014).

Anomaly detection and localization in crowded

scenes. IEEE Transactions on Pattern Analysis and

Machine Intelligence, pages 18–32.

Lu, C., Shi, J., and Jia, J. (2013). Abnormal event detec-

tion at 150 fps in matlab. In 2013 IEEE International

Conference on Computer Vision, pages 2720–2727.

Anomaly Event Detection based on People Trajectories for Surveillance Videos

115

Makhzani, A., Shlens, J., Jaitly, N., and Goodfellow, I.

(2016). Adversarial autoencoders. In International

Conference on Learning Representations.

Mora Colque, R. V. H., Caetano, C., De Andrade, M. T. L.,

and Schwartz, W. R. (2017). Histograms of Opti-

cal Flow Orientation and Magnitude and Entropy to

Detect Anomalous Events in Videos. IEEE Transac-

tions on Circuits and Systems for Video Technology,

27:673–682.

Morais, R., Le, V., Tran, T., Saha, B., Mansour, M., and

Venkatesh, S. (2019). Learning regularity in skele-

ton trajectories for anomaly detection in videos. In

The IEEE Conference on Computer Vision and Pat-

tern Recognition (CVPR).

Popoola, O. P. and Wang, K. (2012). Video-based abnormal

human behavior recognition, a review. IEEE Transac-

tions on Systems, Man, and Cybernetics, Part C Ap-

plications and Reviews, pages 865–878.

Ravanbakhsh, M., Nabi, M., Sangineto, E., Marcenaro, L.,

Regazzoni, C., and Sebe, N. (2017). Abnormal event

detection in videos using generative adversarial nets.

In 2017 IEEE International Conference on Image Pro-

cessing (ICIP), pages 1577–1581.

Redmon, J. and Farhadi, A. (2017). Yolo9000: Better,

faster, stronger. 2017 IEEE Conference on Computer

Vision and Pattern Recognition (CVPR), pages 6517–

6525.

Ribeiro, M., Lazzaretti, A. E., and Lopes, H. S. (2017).

A study of deep convolutional auto-encoders for

anomaly detection in videos. Pattern Recognition Let-

ters, pages 1–10.

Roshtkhari, M. J. and Levine, M. D. (2013). Online dom-

inant and anomalous behavior detection in videos. In

2013 IEEE Conference on Computer Vision and Pat-

tern Recognition, pages 2611–2618.

Sabokrou, M., Fayyaz, M., Fathy, M., Moayed, Z., and

Klette, R. (2018). Deep-anomaly: Fully convolutional

neural network for fast anomaly detection in crowded

scenes. Computer Vision and Image Understanding.

Saini, R., Pratim Roy, P., and Prosad Dogra, D. (2018). A

segmental HMM based trajectory classiﬁcation using

genetic algorithm. Expert Systems with Applications,

pages 169–181.

Saligrama, V. and Chen, Z. (2012). Video anomaly detec-

tion based on local statistical aggregates. Proceedings

of the IEEE Computer Society Conference on Com-

puter Vision and Pattern Recognition, pages 2112–

2119.

Wang, X., Ma, K. T., Ng, G.-W., and Grimson, W. (2008).

Trajectory analysis and semantic region modeling us-

ing a nonparametric Bayesian model. 2008 IEEE Con-

ference on Computer Vision and Pattern Recognition,

pages 1–8.

Zaharescu, A. and Wildes, R. (2010). Anomalous behaviour

detection using spatiotemporal oriented energies, sub-

set inclusion histogram comparison and event-driven

processing. In Proceedings of the 11th European Con-

ference on Computer Vision: Part I, pages 563–576.

Zhang, D. and Lu, G. (2004). Review of shape representa-

tion and description techniques. Pattern Recognition,

pages 1–19.

Zhou, B., Wang, X., and Tang, X. (2012). Understanding

collective crowd behaviors: Learning a mixture model

of dynamic pedestrian-agents. In 2012 IEEE Con-

ference on Computer Vision and Pattern Recognition,

pages 2871–2878.

Zhou, S., Shen, W., Zeng, D., and Zhang, Z. (2015). Un-

usual event detection in crowded scenes by trajectory

analysis. ICASSP, IEEE International Conference on

Acoustics, Speech and Signal Processing - Proceed-

ings, pages 1300–1304.

Zhu, H., Liu, D., Zhang, S., Zhu, Y., Teng, L., and Teng, S.

(2016). Solving the Many to Many assignment prob-

lem by improving the Kuhn-Munkres algorithm with

backtracking. Theoretical Computer Science, pages

30–41.

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

116