
Visual Exploration of 3D Shape Databases Via Feature Selection
Xingyu Chen
1,2 a
, Guangping Zeng
1 b
, Ji
ˇ
r
´
ı Kosinka
2 c
and Alexandru Telea
3 d
1
School of Computer and Communication Engineering, University Science and Technology Beijing, Beijing, China
2
Bernoulli Institute, Faculty of Science and Engineering, University of Groningen, The Netherlands
3
Utrecht University, The Netherlands
Keywords:
Content-based Shape Retrieval, Multidimensional Projections, Feature Selection, Visual Analytics.
Abstract:
We present a visual analytics approach for constructing effective visual representations of 3D shape databases
as projections of multidimensional feature vectors extracted from their shapes. We present several methods
to construct effective projections in which different-class shapes are well separated from each other. First,
we propose a greedy heuristic for searching for near-optimal projections in the space of feature combina-
tions. Next, we show how human insight can improve the quality of the constructed projections by iteratively
identifying and selecting a small subset features that are responsible for characterizing different classes. Our
methods allow users to construct high-quality projections with low effort, to explain these projections in terms
of the contribution of different features, and to identify both useful features and features that work adversely
for the separation task. We demonstrate our approach on a real-world 3D shape database.
1 INTRODUCTION
Recent developments in 3D content creation and 3D
content acquisition technologies, including modeling
and authoring tools and 3D scanning techniques, have
led to a rapid increase in the number and complex-
ity of available 3D models. Such models are typi-
cally stored in so-called shape databases (ShapeNet,
2019; ITI DB, 2019). Such databases offer next var-
ious mechanisms enabling users to browse or search
them to locate models of interest for a specific appli-
cation at hand.
As shape databases increase, so does the diffi-
culty that users have in locating models of inter-
est therein (Tangelder and Veltkamp, 2008). Typi-
cal mechanisms offered to support this task include
searching by keywords, browsing the database along
one or a few predefined hierarchies, or content-based
shape retrieval (CBSR). While efficient for certain
scenarios, all these mechanisms have limitations:
Keyword search assumes a good-quality labeling of
shapes with relevant keywords, and also that the user
is familiar with relevant search terms. Hierarchy
browsing is most effective when the organization of
a
https://orcid.org/0000-0002-3770-4357
b
https://orcid.org/0000-0003-0494-3877
c
https://orcid.org/0000-0002-8859-2586
d
https://orcid.org/0000-0003-0750-0502
shapes follows the way the user wants to explore
them. Finally, CBSR works well when the user aims
to search for shapes similar to an existing query shape.
Besides the above targeted use-cases, more
generic ones involve users who simply want to ex-
plore the entire database to see what it contains. This
is relevant in cases where users want to first get a good
overview of what a database contains before deciding
to invest more effort into exploring or using it; and
also in cases where users do not have specific searches
in mind. Existing mechanisms offered for the above
scenarios are linear in nature, showing either a small
part of the database at a single time and/or asking the
user to perform lengthy navigations to create a mental
map of the database itself, much like when navigating
a web domain.
We address this task by a different, visual, ap-
proach. We construct a compact and scalable
overview of an entire shape database, with shapes or-
ganized by similarity. We offer details-on-demand
mechanisms to enable users to control the separa-
tion quality of the similar-shape groups in the visual
overview; understand what makes a set of shapes sim-
ilar (or two or more sets of shapes different); and find
features that have high, respectively little, value for
the shape classification task. Our approach is sim-
ple to use; requires no prior knowledge of the orga-
nization of a shape database; nor a prior organization
42
Chen, X., Zeng, G., Kosinka, J. and Telea, A.
Visual Exploration of 3D Shape Databases Via Feature Selection.
DOI: 10.5220/0008950700420053
In Proceedings of the 15th Inter national Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 3: IVAPP, pages 42-53
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

or labeling of the database; handles any type of 3D
shape represented by a polygon mesh; and scales vi-
sually and computationally to real-world large shape
databases. Additionally, our proposal is useful for
both end users (who aim to explore a shape database)
and technical users (who aim to engineer features to
query or classify shapes in such databases).
This paper is structured as follows. Section 2 out-
lines related work in exploring 3D shape databases.
Section 3 details our pipeline that consists of shape
normalization, feature extraction, and dimensionality
reduction. Section 4 presents our automatic and user-
driven methods for constructing high-quality projec-
tions for exploring shape databases, and demonstrates
these on a real-world shape database. Section 6 con-
cludes the paper.
2 RELATED WORK
Searching and exploring 3D shape databases can be
structured along three modalities, as follows.
Keyword search uses words to search for shapes
whose annotation data contains those words. It
is the simplest to support, and therefore old-
est and most widespread form of search for
3D content, present in many shape databases,
such as TurboSquid (TurboSquid, Inc., 2019) and
Aim@Shape (Aim@Shape, 2019), to mention just a
few. Such databases allow providers to upload mod-
els with associated keywords for subsequent search.
However, keyword lists are only weakly structured,
possibly containing redundant or vague keywords, po-
tentially added this way to increase exposure rate.
Besides general-purpose databases of this type, more
specialized ones exist, such as containing 3D shapes
related to space exploration (NASA, 2019). Overall,
keyword search is popular and widely supported, but
works best for targeted searches performed by users
aware of a database’s organization, require a good an-
notation with specific keywords, and is less effective
for overall exploration.
Hierarchical exploration systems organize shapes
along different criteria, following an existing tax-
onomy of the targeted 3D shape universe at hand.
Such systems support exploration (apart from key-
word search) by allowing users to browse the
hierarchy, with shapes or shape categories de-
picted by thumbnails, much like when exploring
a file system. Examples of such systems are the
Princeton Shape Benchmark (Shilane et al., 2004),
Aim@Shape (Aim@Shape, 2019), or the ITI 3D
search engine (ITI DB, 2019) that allows browsing
multiple hierarchically-organized shape databases.
Hierarchy browsing supports browsing better than
keyword-based search. Yet, it typically only allows
examining a single path (shape subset) at a time, and
cannot provide a rich global overview of an entire
database. Moreover, its effectiveness relies on the
provided hierarchy, which may or may not match the
way users see the grouping of shapes.
Content Based Shape Retrieval (CBSR) allows
users to search for shapes similar to a given query
shape, and therefore depend far less on an upfront or-
ganization of the database in terms of suitable key-
words or hierarchies and/or on the user’s familiar-
ity with these. Good surveys of CBSR methods
are provided by (Bustos et al., 2005; Tangelder and
Veltkamp, 2008). These methods essentially extract
a high-dimensional descriptor from the query and
database shapes, and then search and retrieve the most
similar shapes to the query based on a suitable dis-
tance metric in descriptor space. Many types of de-
scriptors and distance metrics have been proposed, as
follows. Global descriptors, such as shape elongation,
eccentricity, and compactness, are simple, yet crude
ways to discriminate between highly different shapes.
Local descriptors, such as saliency, shape thickness,
and shape contexts capture more fine-grained shape
details (Shtrom et al., 2013; Rusu et al., 2009; Shapira
et al., 2008; Tasse et al., 2015). Topological descrip-
tors, such as based on curve skeletons (Jalba et al.,
2012) or surface skeletons (Feng et al., 2016) cap-
ture the part-whole shape structure. Finally, view-
based descriptors capture the appearance of the shape
from multiple viewpoints (Cyr and Kimia, 2001; Shen
et al., 2003). Kalogerakis et al. (Kalogerakis et al.,
2010) provide a tool to compute several types of shape
features. Apart from such hand-engineered descrip-
tors, deep learning has proved effective in automat-
ically extracting low-dimensional representations of
shape with high accuracy for query tasks (Su et al.,
2015). CBSR frees the user from the burden of speci-
fying keywords or choosing explicit navigation paths
in a hierarchy to examine a shape database. Addition-
ally, CBSR assists in finding the most similar shapes
to a given prototype (query). However, CBSR does
not readily support the task of general-purpose explo-
ration of a shape database, e.g., seeing how all the
shapes within it are organized in terms of similarity.
Summarizing the above, keyword search, hierar-
chical exploration, and CBSR offer largely comple-
mentary mechanisms for exploring a shape database,
and can be readily combined in a 3D database ex-
ploration system. However, as outlined, none of
these methods offer a compact, complete, and detailed
overview of an entire database. Moreover, such mech-
anisms do not explain why a set of shapes are deemed
Visual Exploration of 3D Shape Databases Via Feature Selection
43

similar. In earlier work, Rauber et al. (Rauber et al.,
2015) have used interactive feature selection to im-
prove image classification, which is related, but not
the same, to our goal of exploring data collections.
Such functionalities are essential in contexts where
users do not know precisely what they are looking
for, and would like to understand the information con-
tained in a database before proceeding to more spe-
cific queries.
3 PROPOSED METHOD
To support the overall exploration of 3D shape
databases, we propose to augment existing mecha-
nisms (keyword search, hierarchies, and CBSR) by
a visual navigation approach. Our approach allows
users to see a complete overview of an entire database
and the way shapes are organized within in terms of
similarity. Next, it allows selecting specific shapes
or shape properties and finding similar shapes (from
the perspective of one or several such properties), and
also finding out how properties discriminate between
different shapes. We now detail our approach.
3.1 Overview
We start by introducing some notations. A mesh
m = (V = {x
i
}, F = { f
j
}) is a collection of vertices
x
i
⊂ R
3
and faces f
j
, assumed to be triangles for sim-
plicity. A shape database is a set of shapes M = {m
k
}.
No restrictions are placed here, i.e., shapes can be of
different kinds, sampling resolutions, and require no
extra organization or annotations, e.g., classes or hi-
erarchies.
Our key idea is to present a visual overview
of M in which every shape m
k
is represented by
a thumbnail rendering thereof, and visual distances
between two shapes m
i
and m
j
reflect their simi-
larity. The visual overview is interactively linked
with detail views in which users can explore spe-
cific shape details. The combination of overview and
details, following Shneiderman’s visual exploration
mantra (Shneiderman, 1996), enables both free and
targeted exploration of the shape database along the
use-cases outlined in Sec. 2.
We create our overview-and-detail visual explo-
ration as follows. First, we preprocess all meshes
in M so as to normalize them in terms of sampling
resolution and size. Secondly, we extract local fea-
tures from all meshes m ∈ M (Sec. 3.3). These fea-
tures capture the respective shapes at a fine level of
detail. Next, we aggregate local features into fixed-
length feature vectors (Sec. 3.4). Finally, we use
a dimensionality-reduction algorithm to project the
shapes, represented by their feature vectors, onto 2D
screen space (Sec. 3.5). We describe all these steps
next.
3.2 Preprocessing
Since we do not pose any constraint on the shapes in
M, these can come with virtually any sampling reso-
lution, orientation, and at any scale. Such variations
are known to pose problems when computing virtu-
ally any type of shape descriptor (Bustos et al., 2005).
Hence, as a first step, we normalize all shapes m ∈ M
by first remeshing them, with a target edge-length of
1% of m’s bounding-box diagonal. Next, we translate
and scale the remeshed shapes to fit the [−1, 1]
3
cube.
3.3 Local Feature Extraction
To characterize shapes, we extract several so-called
local features from each. Such features describe the
shape at or in the neighborhood of every vertex x
i
∈ m
and are therefore good at capturing local characteris-
tics. We compute seven local feature types, as fol-
lows.
Gaussian Curvature (Gc): Gaussian curvature de-
scribes the overall flatness of a shape close to a given
point. For every vertex x ∈ m we compute its Gaus-
sian curvature as
Gc(x) = 2π −
∑
f ∈F(x)
θ
x, f
, (1)
where F(x) is the set of faces in F incident with x and
θ
x, f
is the angle in face f at vertex x.
Average Geodesic Distance (Agd): We estimate the
geodesic distance d(x, y) between a pair of vertices
x and y of m as the geometric length of the short-
est path in the edge connectivity graph of m be-
tween x and y. This distance can be easily and ef-
ficiently estimated using Dijkstra’s shortest-path al-
gorithm with A* heuristics and edge weights equal
to edge lengths. More accurate estimations of the
geodesic distance between two points on a polygonal
mesh exist, including computing the distance field (or
transform) DT (x) of x over F and tracing a stream-
line in −∇DT (x) from x until it reaches y (Peyre and
Cohen, 2005); GPU minimization of cut-length using
pivoting slice planes passing through x and y (Jalba
et al., 2013); or hybrid search techniques (Verma and
Snoeyink, 2009). While more accurate than the Di-
jkstra approach we use, these methods are consid-
erably more complex to implement, slower to run,
and require careful tuning and/or specialized plat-
forms (GPU support). For a detailed comparison of
IVAPP 2020 - 11th International Conference on Information Visualization Theory and Applications
44
geodesic estimation methods on polygonal meshes,
we refer to (Jalba et al., 2013). More importantly, we
do not use the individual geodesic lengths, but aggre-
gate them into per-shape feature vectors (Sec. 3.4). As
such, high geodesic estimation precision is less im-
portant.
Given the above, we estimate the average geodesic
distance of a vertex x as
Agd(x) =
∑
y∈V
d(x, y)
|V |
. (2)
Normal Diameter (Nd): We first estimate the surface
normal at a vertex x as
n(x) =
∑
f ∈F(x)
n( f )θ
x, f
, (3)
where n( f ) is the outward normal of face f . Given
the above, let r be a ray starting at x and advancing
in the direction −n(x). The normal diameter Nd(x)
is then the distance along r from x to the closest face
f ∈ F \F(x).
Normal Angle (Na) and Point Angle (Pa): These
features describe how vertices x ∈ V are spread
around the shape itself. In detail, let e
1
be the domi-
nant eigenvector of the shape covariance matrix given
by all vertices V . As known, e
1
gives the direction
in which the shape spreads the most. Next, for every
vertex x ∈ V , we define the normal angle Na(x) as the
angle (dot product) between e
1
and the surface nor-
mal n(x); and the Point Angle Pa(x) as the angle (dot
product) between e
1
and the vector c − x, where c is
the barycenter of m.
Shape Context (Sc): The shape context descriptor
is a 2D histogram that characterizes how vertices of
a shape are ‘seen’ in terms of distance and orienta-
tion from a given vertex of that shape (Belongie et al.,
2001). For a vertex x ∈ V , the shape context de-
scribes the number of vertices in V that are within
a given distance range and direction range to x. To
compute Sc, we first build a local coordinate system
at every vertex x, using the eigenvectors of the shape
covariance matrix in the neighborhood of x. This
ensures that this coordinate system is aligned with
the shape locally — one of its axes will be the nor-
mal n(x), whereas the two other ones are tangent to
the surface of m at x. Next, we discretize the ori-
entations around x into the eight octants of the local
coordinate system, and distances using a set of bins
(distance ranges) (t
i
,t
i+1
) defined by a distance-set
T = {0, t
1
,t
2
, . . . , t
n
, 1}, n ∈ N
+
. In practice, we use
T = [0, 0.1, 0.3, 1]. Hence, for each vertex x, we get a
shape context vector with 8 × 3 = 24 elements.
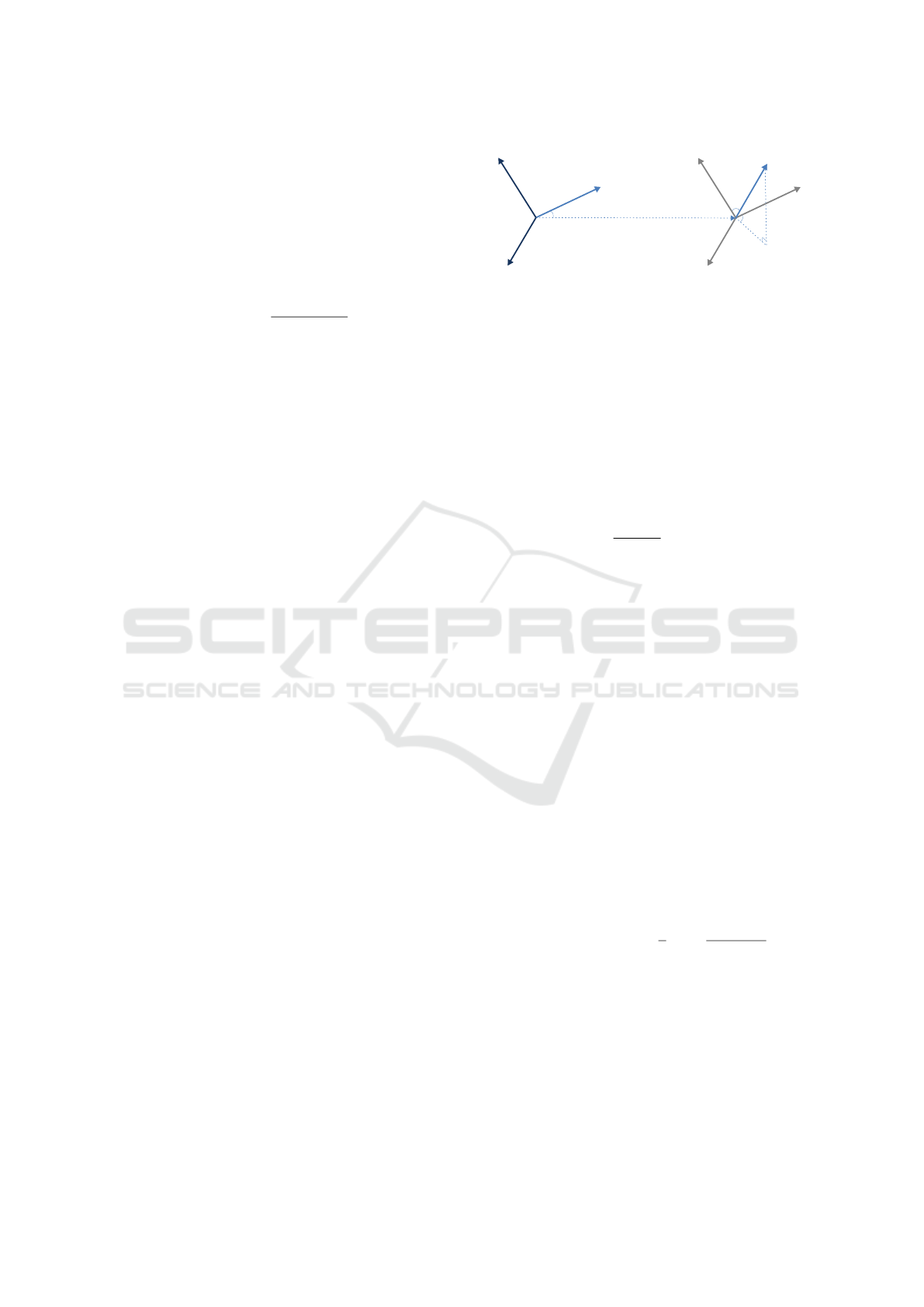
Point Feature Histogram (PFH): PFH (Rusu et al.,
2009) is a complex descriptor that captures the local
geometry in the vicinity of a vertex. Given a pair of
u = m
v = (
¯
y − y) × u
w = u × v
y
¯
y − y
¯
y
w
v
u
φ
α
θ
¯
m
Figure 1: PFH descriptor computation (Shtrom et al., 2013).
vertices y and
¯
y, one first defines a local coordinate
frame (u, v, w) as
u = m,
v = (
¯
y − y) × u,
w = u × v,
(4)
where m is the vertex normal at y (Fig. 1). Next, the
variation of the shape geometry between points y and
¯
y is captured by three polar coordinates
α = v ·
¯
m,
φ = u ·
¯
y − y
k
¯
y − yk
,
θ = arctan2(w ·
¯
m, u ·
¯
m),
(5)
where
¯
m is the vertex normal at
¯
y. Next, three
histograms are built to capture the distributions of
α, φ, θ for a given vertex x by considering all pairs
(y,
¯
y) ∈ N
x,k
× N
x,k
in the k-nearest neighbors N
x,k
of x. In practice, we set k = 30 and use 5 bins for
each histogram. This delivers a PFH feature vector of
5
3
= 125 entries.
Fast Point Feature Histogram (FPFH): While PFH
models a neighborhood N
x,k
by all its point-pairs, the
Simplified Point Feature Histogram (SPFH) models
N
x,k
by the characteristics of the pairs (x, y ∈ N
x,k
).
We proceed analogously to binning the α, φ, θ distri-
butions in three histograms of 11 bins each, obtain-
ing a feature vector of 3 × 11 = 33 elements. With
this vector, we finally compute the FPFH value of a
vertex x following (Rusu et al., 2009) as the distance-
weighted average of the SPFH values over the neigh-
borhood N
x,k
as
FPFH(x) = SPFH(x) +
1
k
∑
y∈N
x,k
SPFH(y)
kx − yk
. (6)
3.4 Feature Vector Computation
The features described in Sec. 3.3 are local, i.e., they
take different values for every mesh vertex x ∈ V . To
be able to compare meshes to each other, we need to
reduce these to same-length global descriptors. For
this, we use a simple histogram-based solution that
aggregates the values of every local descriptor, at all
Visual Exploration of 3D Shape Databases Via Feature Selection
45

vertices of a mesh, into a fixed-length (10 bin) his-
togram. Note that some descriptors are by definition
high-dimensional — for instance, the shape context
Sc has 24 dimensions. Hence, for a d-dimensional
descriptor, we compute a histogram having 10d bins.
Table 1 shows the local features, their dimensional-
ity, and the number of bins used to quantize each.
Summarizing, we reduce every shape m to a 1870-
dimensional feature vector F .
3.5 Dimensionality Reduction
So far, we have reduced a shape database M to a
set of |M| 1870-dimensional feature vectors. We
next create a visual representation of the shape
database by projecting all these vectors onto 2D us-
ing the well-known t-SNE dimensionality reduction
method (van der Maaten and Hinton, 2008). Sim-
ply put, t-SNE constructs a 2D scatterplot P(M) =
{P(m
k
)}, where every shape m
k
∈ M is represented
by a point P(m) ∈ R
2
, so that the distances between
scatterplot points reflect (encode) the similarities of
their feature vectors.
An important concern when proposing such a rep-
resentation is to gauge its quality. To do this, we
use the classes (labels) of the shapes. For a database
where each shape m has a categorical label c(m) ∈ C,
where C is a set of categories (e.g., keywords describ-
ing the different shapes in a database), we define the
neighborhood hit NH(m) as the proportion of the k-
nearest neighbors of P(m) that have the same label
c(m) as m itself (Paulovich et al., 2008). In prac-
tice, we set k = 10, following related applications
that gauge projection quality (Paulovich et al., 2008).
With this, we can next define the neighborhood hit of
an entire class c ∈ C as
NH
c
(c) =
∑
m∈M:c(m)=c
NH(m)
|m ∈ M : c(m) = c|
. (7)
Finally, at the highest aggregation level, we define the
neighborhood hit for an entire scatterplot P(M) for a
Table 1: Local features, their dimensionalities and binning.
Name Dimensionality Bins
Gaussian curvature (Gc) 1 10
Average geodesic distance (Agd) 1 10
Normal diameter (Nd) 1 10
Normal angle (Na) 1 10
Point angle (Pa) 1 10
Shape context (Sc) 24 240
Point Feature Histogram (PFH) 125 1250
Fast Point Feature Histogram (FPFH) 33 330
Total 1870
shape database M as
NH
s
(M) =
∑
m∈M
NH(m)
|M|
. (8)
The above two NH metrics describe how a mesh
(point in the 2D projection scatterplot) is separated
from points of different kinds: NH
c
shows whether
a group of points representing same-class meshes is
well separated in a scatterplot (something we desire
since we want next to use the scatterplot to answer the
question “How many shape classes are in a database,
and how similar are they to each other?”). NH
s
shows
how well a whole scatterplot can represent an entire
shape database. Both NH metrics range between 0
and 1, with higher values indicating better separation,
which is preferred.
4 APPLICATIONS
We next demonstrate our visual exploration ap-
proach on a subset of the Princeton Shape Bench-
mark (Shilane et al., 2004) having 280 meshes from
14 classes, with 20 meshes from each class. As out-
lined earlier, these meshes are not labeled, hierarchi-
cally organized, or otherwise preprocessed.
4.1 Optimal Scatterplot Creation
The projection scatterplot (Sec. 3.5) is the central
view that shows an entire shape database. Hence,
creating a good scatterplot is important for all explo-
ration tasks addressed next. In this section, we ex-
plore the following questions:
Q1: How can we create a good projection scatterplot?
Q2: Which features are best for grouping simi-
lar shapes (and, conversely, separating different
shapes) in the scatterplot?
Q3: Which is the minimal set of features required to
generate a good-quality scatterplot?
Concerning Q1, we could directly create and
examine a t-SNE projection of the whole shape
database as encoded by the 1870-dimensional fea-
ture vectors we extracted (Sec. 3.4). However, us-
ing t-SNE is not always easy, especially for high-
dimensional data: This method maps similarities (of
feature vectors) non-linearly to 2D distances; also,
tuning t-SNE’s parameters to yield a good embed-
ding of high-dimensional feature vectors is notori-
ously hard (Wattenberg, 2016). Hence, we first ex-
plore the simpler solution of projecting only subsets
of all extracted features. As we have 8 feature types
(Tab. 1), a natural idea is to try all combinations of
IVAPP 2020 - 11th International Conference on Information Visualization Theory and Applications
46
NH value highlow
B
A
features: Gc, Na, Pa, Agd, PFH NH
s
: 0.859
plier: 1.0
teddy: 0.985
cup: 0.98
ant: 0.975
fish: 0.945
chair: 0.895
glasses: 0.88
airplane: 0.875
table: 0.87
human: 0.855
hand: 0.805
fourleg: 0.765
bird: 0.66
octopus: 0.53
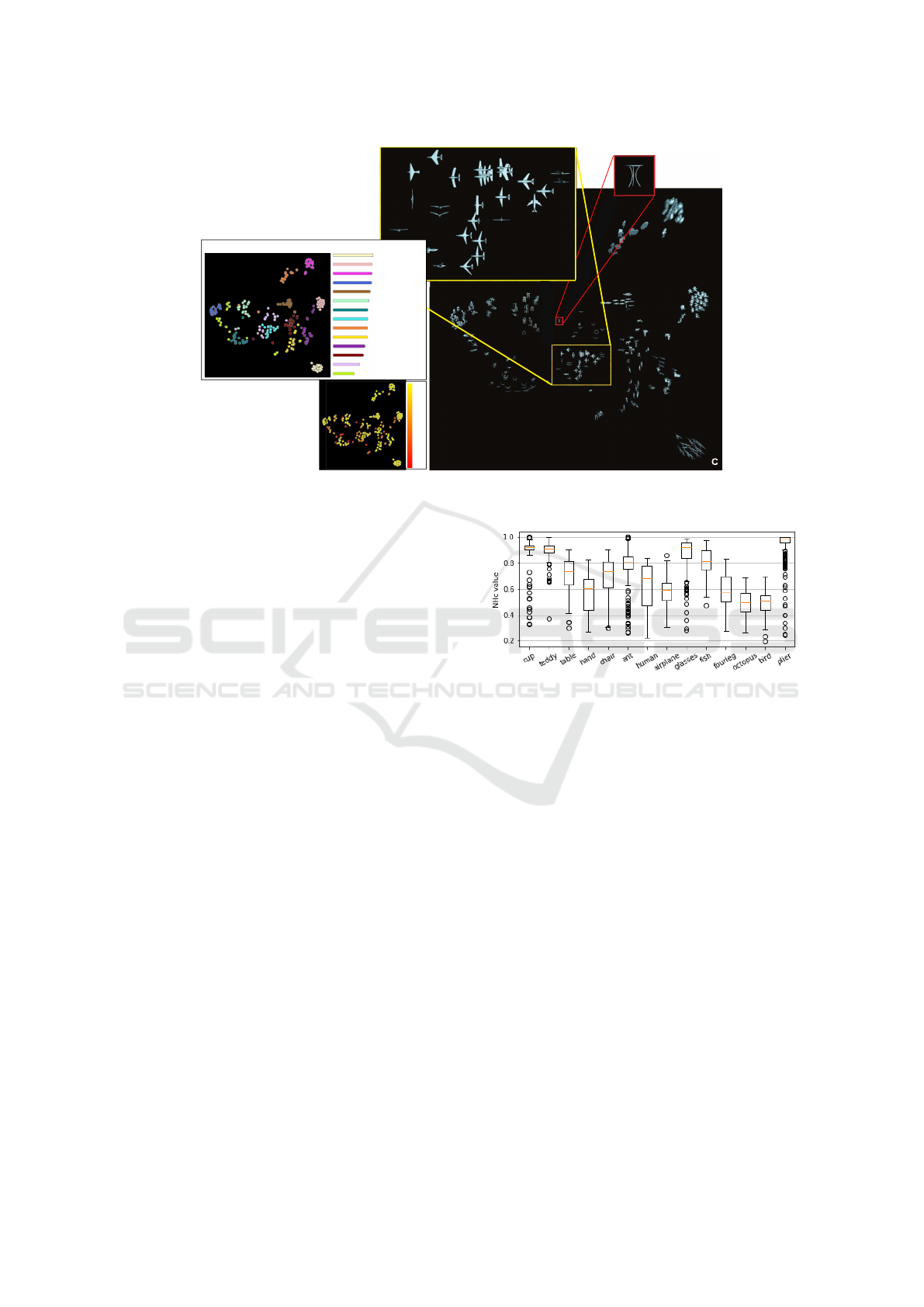
Figure 2: Three views of the optimal projection scatterplot for the Princeton Shape Database, depicting classes and their NH
c
values and the overall plot quality NH
s
(A), per-shape NH values (B), and actual shape thumbnails (C).
groups of feature types. This yields 2
8
−1 = 255 pos-
sible projection scatterplots. Following the scagnos-
tics idea (Tukey and Tukey, 1988; Wilkinson et al.,
2006), we compute all these scatterplots (using t-
SNE) and select the one having the highest quality,
measured by its NH
s
value.
Figure 2 shows three views of the optimal projec-
tion scatterplot, as follows. Image A shows the scat-
terplot with points (shapes m ∈ M) colored by their
class value c(m). The text atop this image indicates
the feature subset leading to this optimal scatterplot
(highest NH
s
= 0.859 value), namely (Gc, Na, Pa,
Agd, PFH). The bar chart in image A shows the NH
c
values for all classes, with high values (well sepa-
rated classes) at the top. From this, we can see that
pliers are perfectly separated from all other classes
(NH
pliers
= 1), while octopus is least well separated
(NH
octopus
= 0.53). Image B shows the optimal scat-
terplot colored by NH values for all shapes, ranging
between red (low NH) to yellow (high NH). Red
points in this image show shapes which are not pro-
jected well — that is, placed close to shapes having
different classes. Finally, image C shows the opti-
mal scatterplot with shapes depicted by thumbnails.
From this image, we find that shapes of the classes pli-
ers, teddies, cups, ants, and fishes are well projected.
However, birds are mixed with airplanes; and fourlegs
are mixed with humans and hands. The octopus class
is visually split in the projection into several parts.
While this optimal scatterplot is not perfect, it is still
formally the best one we can create given the combi-
nations of our 8 available features. Indeed, while class
separation is not perfect, closely-projected shapes are
Figure 3: NH
c
statistics for the 14 classes in the shape
database for all considered 255 projection scatterplots.
still quite similar. For instance, ants are surrounded by
octopuses, which is arguably logical, since both shape
types have many thin and spread legs. Similarly, air-
planes and birds are close to each other; indeed, both
have wings and are relatively flat.
Figure 3 shows boxplot statistics of the NH
c
val-
ues for the 14 shape classes in our database for the
255 created projection scatterplots. Ideally, we would
like to see that every class has a very high NH
c
value.
However, we see that birds and octopuses have quite
low NH
c
values, confirming the insights obtained ear-
lier by visually examining the projection (Fig. 2).
Finally, Fig. 4 shows a complete view of how fea-
tures affect the quality of the produced projections.
The bar chart shows the NH
s
values of all possible
255 projections created by combining our 8 features
types, sorted in increasing values from left to right.
The matrix plot below the bar chart shows which fea-
tures (color coded according to the legend at the right)
are used by which projection. Projections using more
than one feature have blue bars; projections that use
exactly one feature have their bars colored by the re-
Visual Exploration of 3D Shape Databases Via Feature Selection
47
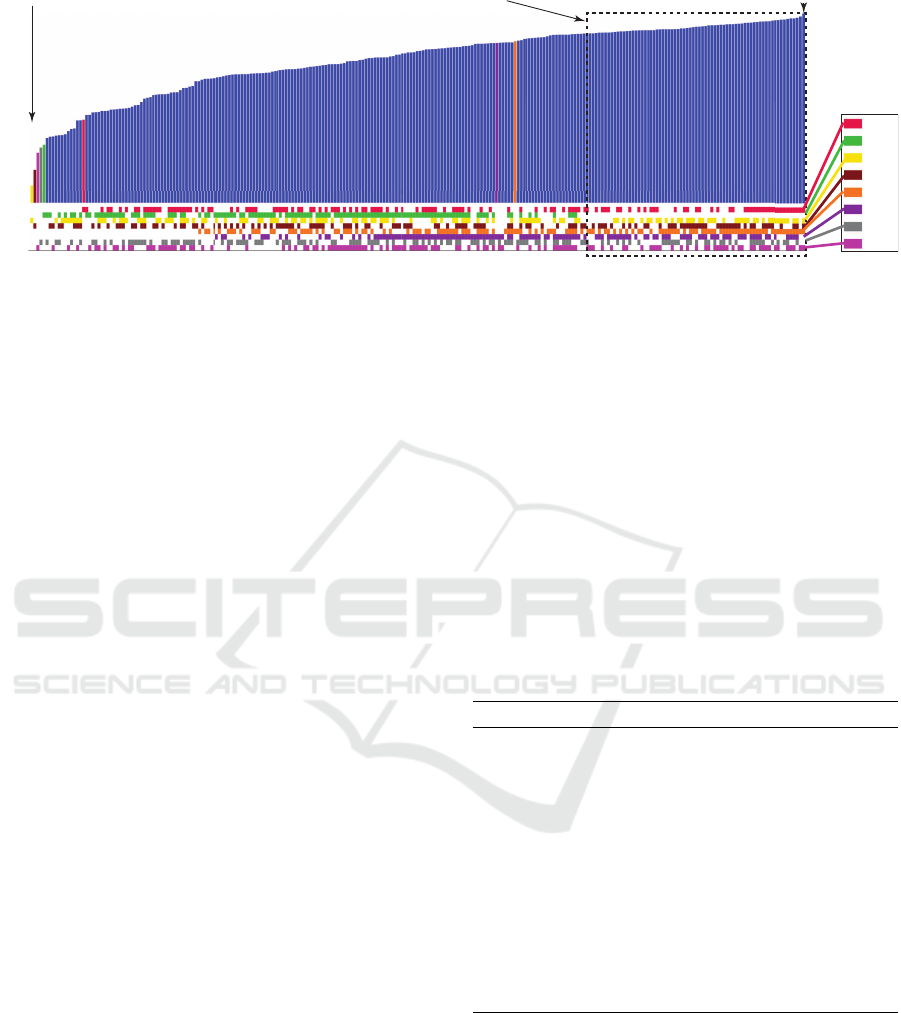
Gc
Sc
Na
Pa
PFH
FPFH
Agd
Nd
0.83
0.0
NH
s
Feature
Legend
best projectionworst projection
top 30% best projections
Figure 4: A bar chart showing the NH
s
scores of 255 projections, sorted on increasing value (best projections to the right,
worst ones to the left). The color blocks under a bar show which features are used for that projection (the feature color legend
on the right). Bars which are not blue only use one feature, whose identity colors the bar. Scanning the color matrix below the
bars row-wise tells us which projections use which features. We see that PFH (orange) and FPFH (purple) are good features
since their blocks are close to the right. Conversely, Sc (green) is not a very useful feature since its blocks are spread to the
left.
spective feature. This plot gives us several insights:
(1) The quality difference between the best and worst
projections is significant (NH
s
0.831 vs 0.38), with
better projections using more features than poor ones;
(2) some features are really instrumental in achieving
high quality, e.g. PFH (orange) and FPFH (purple),
which appear consistently in the right of the matrix
plot in Fig. 4, whereas other features are actually ad-
versely affecting quality, e.g. Sc (green) which ap-
pears in the left of the matrix plot. This indicates ei-
ther that Sc is not a useful feature for discriminating
classes in this database or that it is poorly evaluated,
e.g., by an insufficiently dense sampling. (3) Over-
all, the right of the matrix is more full than its left
part, which means that using more features produces
better segregating projections, although the relation
is not monotonic. (4) The highest-quality projections
(roughly, rightmost third of the bar chart) consistently
use the same mix of features (Gc, Na, Pa, PFH, FPFH,
Agd, Nd). (5) The patterns in the matrix plot of dif-
ferent features look different, which means there are
no redundant features in the considered set.
4.2 Fast Computation of Near-optimal
Projection Scatterplot
Computing all possible scatterplots given a feature
vector F to find the optimal one is expensive, espe-
cially when the set F is large. We next propose a
greedy algorithm to accelerate this task (Alg. 1). The
parameter s gives the maximum size of the feature-set
to search for. For every search iteration,
s
|F |
fea-
ture combinations are examined, and the best one, in
terms of the realized NH
s
value, is retained. Better so-
lutions are obtained for larger s values, at the expense
of longer search times. When s = |F |, Alg. 1 com-
pares all possible 2
|F |
feature combinations. From
our tests, a quite good solution in terms of NH
s
value
can be found by setting s = 1. For this setting, the
time complexity of our algorithm is O(|F |
2
).
Table 2 shows the results of our greedy algorithm,
executed 5 times, to account for the stochastic nature
of the t-SNE projection. For every round, we indi-
cate the time taken by exhaustive search vs our greedy
search, and also the number of t-SNE projections be-
ing evaluated. We see that our algorithm yields prac-
tically the same NH
s
quality as the exhaustive search,
but is roughly 5 times faster.
Algorithm 1: Computing near-optimal feature sets.
Input: Set of features F ; maximal size s, 1 ≤ s ≤ |F |, of
feature-set to search for,
Output: Near-optimal feature set C,
1: C := ø, C
new
:= ø;
2: repeat
3: C := C
new
4: for each F
sub
⊆ F , |F
sub
| ≤ s do
5: C
temp
:= (C ∪ F
sub
) − (C ∩ F
sub
)
6: if NH
s
(C
temp
) > NH
s
(C
new
) then
7: C
new
:= C
temp
;
8: end if
9: end for
10: until (C
new
= C );
11: return C ;
4.3 User-driven Projection Engineering
Section 4.2 showed how we can automatically se-
lect features from the eight existing feature classes
(Tab. 1) to create a projection scatterplot which best
separates shapes from different classes. However, us-
ing this automatic approach has some disadvantages:
(1) It is expensive, even when using the proposed
IVAPP 2020 - 11th International Conference on Information Visualization Theory and Applications
48
1. model and feature selector
2. original scatterplot
6. separation
control
selected features
4. scoring
methods
5. refined scatterplot
3. feature scoring view
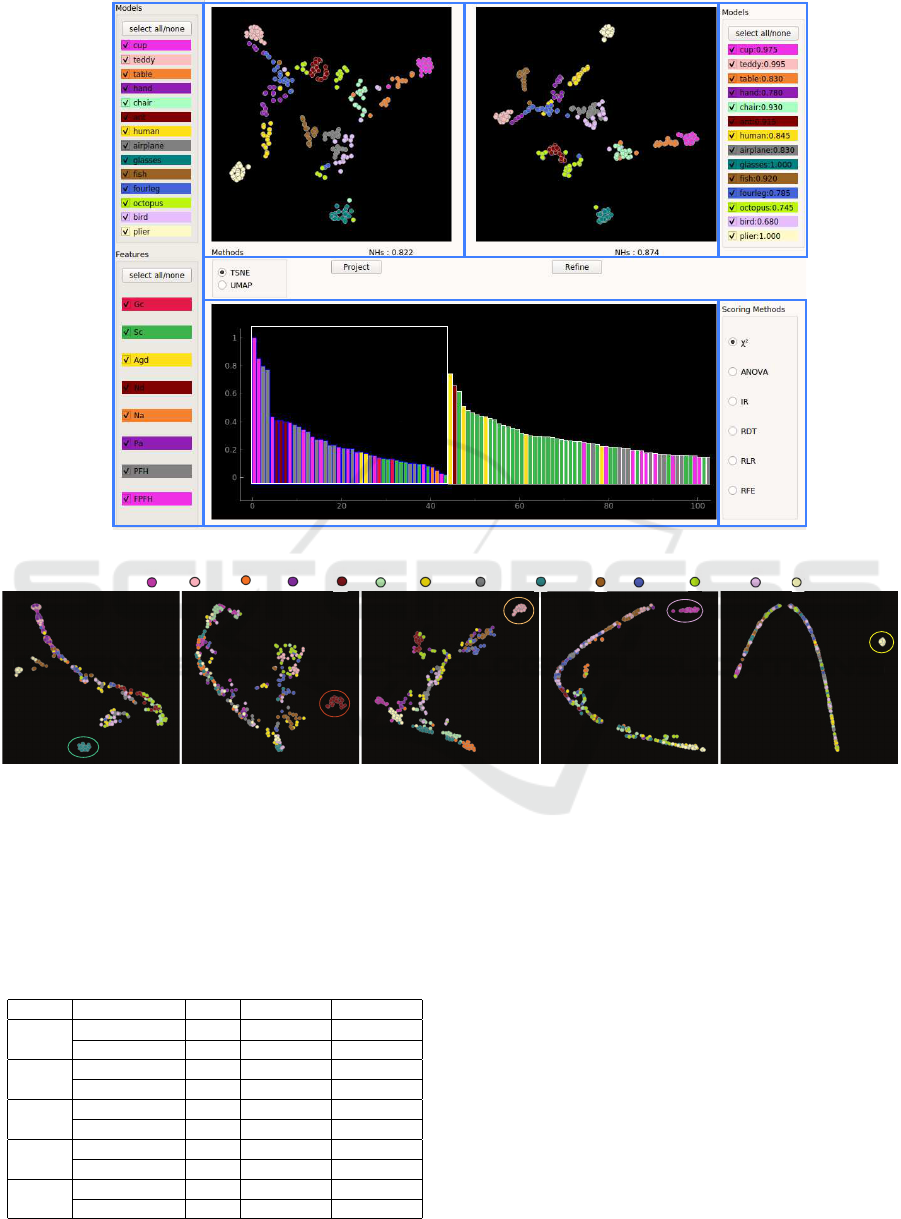
Figure 5: A user-driven projection engineering tool and its six views (Sec. 4.3).
a) glasses: (Sc:1,PFH:1) b) ant: (Pa:1,FPFH:1,FPH:1) c) teddy: (Nd:2,Gc:1) d) cup: (Agd:1,FPFH:1) e) pliers: (PFH:1)
glasses
ant
teddy
cup
pliers
cup teddy table hand ant chair human airplane glasses fish fourleg octopus bird plierscupClasses:
Figure 6: Finding minimal number of feature-bins able to separate five shape classes from the rest of the database. Notation
name:i indicates that i bins of feature name are used.
greedy algorithm for feature selection. (2) It is too
coarse-grained: All features of the same type, e.g.,
the 24 shape-context Sc features are either selected
all, or ignored, when constructing the projection. (3)
Table 2: Performance of the greedy algorithm.
Round Search method NH
s
Time (secs) t-SNE runs
1
Exhaustive 0.831 459.74 255
Greedy 0.831 103.49 56
2
Exhaustive 0.830 452.12 255
Greedy 0.830 84.98 48
3
Exhaustive 0.829 453.70 255
Greedy 0.820 70.24 40
4
Exhaustive 0.832 445.47 255
Greedy 0.832 111.71 64
5
Exhaustive 0.824 447.66 255
Greedy 0.824 97.39 55
It is too simplistic: There are cases when, for in-
stance, we want to optimize for separation of certain
classes more, based on problem-specific constraints.
Hence, user input in deciding which feature combi-
nation leads to the optimal projection is crucial.
We next address question Q2, rephrased as: How
can we pick ‘good’ feature-bins (from the total set of
1870 bins) that separate classes in the way we desire
in a specific context? For this, we propose an interac-
tive tool based on feature scoring (Fig. 5) which con-
tains several views (1–6) that allow the user to explore
the effect of features on separating classes of shapes
in the database, and also select subsets of features that
lead to a desired, better, class separation. We explain
these views via an overview-and-details-on-demand
workflow, as follows:
Visual Exploration of 3D Shape Databases Via Feature Selection
49
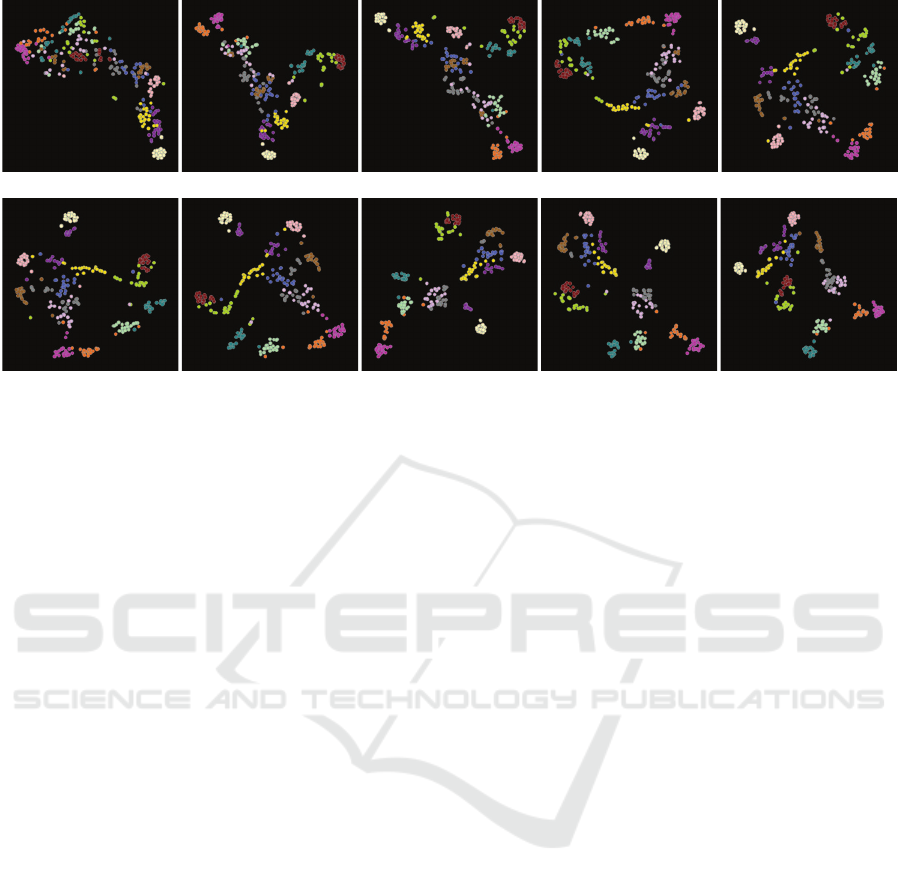
a) hand (10, 0, 0.584) b) table (5, 0, 0.745) c) airplane (3, 0, 0.750) d) octopus (11, 0, 0.816) e) fish (5, 0, 0.815)
f) glasses (5, 0, 0.825) g) bird (1, 0, 0.837) h) airplane, fish, bird
(
5, 0, 0.870)
i) airplane (
10, 0, 0.880)
j) all (
4, 8, 0.873)
Figure 7: Incremental creation of high-quality projection scatterplot that separates all classes well. In each step, a few feature-
bins (having high scores, count indicated in green) are selected to separate one or several classes from the rest, and a few
feature-bins (having low scores, count indicated in red) are removed from the selection. NH
s
at each step are rendered blue.
Model and Feature Selector (1): The user starts
by selecting the shape classes and feature types of
interest in this view. This allows them to specify
if they are interested in separating specific classes
(which are then to be selected) or, alternatively, inter-
ested in separating equally well all classes from each
other (in which case, all classes should be selected).
For instance, from our earlier experiments discussed
in Sec. 4.1, we saw that birds are hard to separate
from airplanes. The user can then select only these
two classes in view (1) to explore how to increase
their separation. Separately, one can select the feature
types (of the 8 computed ones) to use for creating the
scatterplot. This is useful to examine, or debug, the
effect of a specific feature type. Classes are categor-
ically color-coded, and the same colors are used in
the scatterplots (2, 5). Similarly, feature types are cat-
egorically color-coded with the same colors used in
the feature scoring view (3).
Original Scatterplot (2): This view shows a scatter-
plot using all shape classes vs all feature types chosen
in the selector (1). It acts as a starting point for the
exploration, which can next be refined to e.g. pro-
duce better separation of desired classes or instances
(shapes) using the feature scoring views (3, 4) dis-
cussed next. Scatterplots can be computed either with
the t-SNE or UMAP (McInnes et al., 2018) projec-
tion methods. t-SNE spreads similar points better
over the available 2D space, but takes longer to com-
pute. UMAP creates denser clusters separated by
more whitespace, but is faster to execute. For a trade-
off of these two techniques, we refer to a recent sur-
vey (Espadoto et al., 2019).
Feature Scoring Views (3, 4): Each bar in the bar-
chart (3) shows the discriminative score of every el-
ement f
i
of the 1870-dimensional feature vector, i.e.,
how much f
i
contributes to separating class c
i
from
a few or from all other classes c
j
6= c
i
selected for
exploration in view (1), depending on the separation
control (6, discussed later). Colors identify to which
feature types the elements f
i
belong. For instance,
the several purple bars in Fig. 5(3) correspond to the
330 bins that the FPFH feature (colored purple in
Fig. 5(1)) has. Scores are computed with six scor-
ing methods(Rauber et al., 2015): chi-squared, one-
way ANOVA, Randomized Decision Trees (RDT),
Randomized Linear Regression (RLR), iterative re-
lief (IR), and Recursive Feature Elimination (RFE),
which can be chosen by the user in panel (4). The bar-
chart supports two tasks: First, it shows how the many
bins that each feature is represented by contributes to
the separation power of that feature. Secondly, it al-
lows fine-grained examination of the effect of each
such bin on the class separation: Users can freely se-
lect specific bins (from the 1870 available ones) to
create a new projection. The selected bins are dis-
played with a blue border and listed, in decreasing
score order, before the unselected ones, in the bar-
chart. The new projection created by the user-selected
bins is shown in view (5).
Refined Scatterplot (5): This scatterplot shows in-
stances from the classes selected in view (1), pro-
jected according to the specific feature-bins selected
in the barchart (3). This is thus a refined view of
IVAPP 2020 - 11th International Conference on Information Visualization Theory and Applications
50

the original projection (1). By comparing the re-
fined scatterplot with the original one, one can thus
see how fine-grained selection of every single of the
1870 feature-vector components can improve the pro-
jection or parts thereof. In other words, obtaining
an optimal projection is achieved in two steps: First,
one can select entire features (in view 1). This corre-
sponds to considering or ignoring entire features that
capture different aspects of shape. Upon obtaining a
suitable projection, one can refine it by selecting or
deselecting individual bins for the selected features.
This corresponds to considering or ignoring ranges
of the values of the features under exploration.
Separation Control (6): As mentioned, feature scor-
ing measures how well selected features separate a
class c
i
from one or several classes c
j
6= c
i
. The view
(6) allows controlling this. The view shows all shape
classes c
i
in the database. If all classes are selected
in view (6), scoring will measure how well a class c
i
is separated from each of the other classes c
j
6= c
i
. If
only one class c
i
is selected in (6), then scoring will
measure the separation of c
i
from ∪
j6=i
c
j
. This way,
one can flexibly measure the separation of arbitrary
groups of classes rather than only the separation of
individual classes themselves.
4.4 Use-cases
We demonstrate the added value of our user-driven
projection engineering by answering several practical
questions, as follows.
A. What is the minimal number of feature values, and
which are these, that are sufficient to separate a given
class of shapes from all others (Q3, Sec. 4.1)?
Figure 6 illustrates this use-case for the classes
glasses (a), ant (b), teddy (c), cup (d), and pliers
(e). For each class, we select the respective class in
the model selector (Fig. 5(1)) and use next the fea-
ture scoring view (Fig. 5(3)) and separation control
(Fig. 5(6)) to find the feature values (bins of the 1870-
dimensional feature vector) that best separate this
class from the remaining ones. We assess separation
both visually, using the refined projection (Fig. 5(5))
and its corresponding NH
s
score. We find, this way,
that these classes can be separated very well from the
rest of the database by a maximally three, and some-
times just one, feature bin(s) of the 1870 computed
ones, as indicated in Fig. 6. This is, we believe, a
quite powerful (and novel) result as it indicates that
very little computational effort is needed for classify-
ing shapes in the Princeton Shape Database (and, by
extension, in other similar databases). In turn, this
can considerably increase the scalability of applica-
tions such as shape retrieval and classification.
Agd Nd FPFH
cupteddyant
low
high
feature value
Figure 8: Feature-bins (Agd 6
th
bin, Nd 1
st
bin, and FPFH
6
th
bin) mapped on three shapes. This shows how these
specific feature bins can effectively separate these shapes.
B. How can we explain the discriminatory power of
the features found in use-case A?
The computed feature scoring and the clear separation
shown in the refined projection scatterplots (Fig. 6)
are, in principle, enough to let us choose the mini-
mal set of feature-bins needed to separate a class from
all others. However, it is useful to double-check and
explain this discriminatory power, to ensure that the
features found this way indeed reflect meaningful dif-
ferent properties of the respective shape classes. For
this, we choose shapes from the analyzed classes in
use-case A and color them by the values of the fea-
tures found in the same step to be strongly character-
istic of specific classes. Figure 8 shows this for three
such shapes and feature-bins, respectively. As visi-
ble, the three feature-bins take indeed different values
for the three shapes. Atop of this insight (which we
already knew from the analysis shown in Fig. 6), we
also see now that the Nd feature has indeed low values
on thin shape parts and large values on thick ones, re-
spectively. Similarly, we see that the Agd is large for
shape protrusions (e.g. ant and teddy legs) but is small
for central shape parts (e.g. teddy rump). The FPFH
feature is harder to interpret visually; still, we can see
how it gets high values on roughly round shape parts
(teddy head and ant’s first and last segments) and low
values elsewhere.
C. How can we create a good scatterplot which sepa-
rates well all classes?
Figure 7 shows an example workflow for this task.
We start here with a scatterplot that uses all 1870 fea-
tures. Next, we search, using the feature scoring view
(Fig. 5(3)), for the feature-bins that are most discrimi-
natory, i.e., have highest scores, for each of the classes
in our database, starting with the hand class (we could
start from any other class). As we progress investigat-
Visual Exploration of 3D Shape Databases Via Feature Selection
51

ing subsequent classes, we add feature-bins which are
discriminatory for these newly visited classes. At the
end, when we have considered all classes, we also re-
move features, from the already added ones, which
have low scores (that is, bring the least discrimina-
tion value or even work adversely for this task). The
entire process can be done in one to two minutes.
The different images in Fig. 7 show us how the qual-
ity (NH
s
value) of the scatterplot almost monotoni-
cally improves as we add more feature-bins by con-
sidering new classes. Note that, in this process, we
may visit a certain class several times (e.g. airplane),
as features that score high for it may appear several
times during the exploration as we add other classes.
The final result (Fig. 7j) contains all 14 classes, has
a value NH
s
= 0.873, and is obtained with a total set
of 51 feature-bins. Note that this final NH
s
value is
higher than the one we found by the exhaustive search
(NH
s
= 0.831, Tab. 1). Indeed, our manual search is
more fine-grained, as it allows us to consider individ-
ual feature-bins (of the 1870 in total), whereas the au-
tomatic search only considered entire features (of the
8 in total). Also, note that obtaining this result by ex-
haustive search would be prohibitively expensive, as
this would involve searching all 2
1870
combinations.
5 DISCUSSION
We discuss next several aspects of our method, as fol-
lows:
Dimensionality Reduction: Currently, we directly
reduce dimensionality of our 1870-dimensional fea-
ture vector to 2D using either t-SNE or UMAP. How-
ever, this may be too hard a task for these projection
methods to perform, while in the same time preserv-
ing neighborhoods. Another approach is to use more
dedicated methods, such as autoencoders, to reduce
dimensionality to a lower value, and then project this
low-dimensional dataset to 2D using t-SNE or UMAP.
However, it has to be checked whether this approach
can yield final 2D scatterplots that better preserve
the structure of the shape database. Concerning the
choice of projection techniques, we used t-SNE and
UMAP as these techniques are known for their abil-
ity to separate well, in the visual space, clusters of
similar observations, as opposed to other projection
techniques (Espadoto et al., 2019).
Scalability: Our method depends on two key param-
eters in this respect, namely the number of shapes in
the database to be explored, and the number of fea-
tures which are extracted from each shape. From
a computational viewpoint, feature extraction can be
done offline, as shapes are changed and/or new shapes
are added to the database. Since, typically, shape
databases do not change with a high frequency, such
an offline extraction can be done without impeding
the performance of the end user. Moreover, features
can be extracted in parallel, both among themselves
and over different shapes. We compute the t-SNE pro-
jection using the scikit-learn implementation, which
projects several hundreds of instances in a few sec-
onds; the UMAP implementation, provided by the au-
thors (McInnes et al., 2018), works in real time for
this dataset size. If needed, other, faster projections
can be used (Pezzotti et al., 2017). From a visualiza-
tion viewpoint, the scatterplot, barchart, and matrix
plot metaphors we use scale well to hundreds of thou-
sands of points (shapes) and tens of features.
Evaluation: One important aspect concerning our
proposal is evaluating its effectiveness for different
types of tasks and users. In detail, we identify end
users, for whom tasks involve getting an overview of a
shape database, finding similar groups of shapes, find-
ing which features make two shape groups similar (or
different), and finding outlier shapes; and technical
users, for whom tasks involve selecting a small set of
features able to create effective visualizations for the
first user group. We consider such evaluations to be
part of future work.
6 CONCLUSION
We have presented an interactive visual analytics sys-
tem for exploring 3D shape databases for CBSR ap-
plications. After reducing shapes to high-dimensional
feature vectors following standard feature extraction,
we visualize the similarity structure of a database by
using dimensionality reduction. To this end, we offer
several mechanisms for creating projections in which
different shape classes are separated well from each
other. First, we use a scagnostics approach to gener-
ate near-optimal projections based on maximizing the
quality of resulting projections, using a greedy heuris-
tic to optimize the search for suitable feature-sets.
Next, we propose a visual analytics approach to en-
able users to select a small feature subset for separat-
ing specific classes, generate high-separation projec-
tions for all classes, and gauge the separation power
(thus, added-value) of all available features. We show
that this visual analytics approach allows generating
projections with better separation quality than auto-
matic approaches, and also helps finding both dis-
criminating features (to be used in a CBSR system)
and confusing features (of little value for such sys-
tems). Our approach can be applied to any 3D shape
database and feature-set, allowing CBSR engineers to
IVAPP 2020 - 11th International Conference on Information Visualization Theory and Applications
52

streamline the process of designing and selecting ef-
fective features for shape classification and retrieval.
We demonstrate our work on a real-world 3D shape
database.
Several extensions of this work are possible, as
follows. First and foremost, performing a user study
to gauge how well our approach can support explo-
ration tasks of typical end users, is an important addi-
tion. Secondly, since our approach is generic, it could
be used to optimize feature selection in other applica-
tions beyond CBSR, e.g., in image classification.
REFERENCES
Aim@Shape (2019). Aim@shape digital shape workbench
5.0. http://visionair.ge.imati.cnr.it.
Belongie, S., Malik, J., and Puzicha, J. (2001). Shape con-
text: A new descriptor for shape matching and object
recognition. In Proc. NIPS, pages 831–837.
Bustos, B., Keim, D., Saupe, D., Schreck, T., and Vranic, D.
(2005). Feature-based similarity search in 3D object
databases. ACM Comput Surv, 37(4):345–387.
Cyr, C. M. and Kimia, B. B. (2001). 3D object recognition
using shape similiarity-based aspect graph. In Proc.
IEEE ICCV, pages 254–261.
Espadoto, M., Martins, R., Kerren, A., Hirata, N., and
Telea, A. (2019). Towards a quantitative survey
of dimension reduction techniques. IEEE TVCG.
doi:10.1109/TVCG.2019.2944182.
Feng, C., Jalba, A. C., and Telea, A. C. (2016). Improved
part-based segmentation of voxel shapes by skeleton
cut spaces. Mathematical Morphology –Theory and
Applications, 1(1).
ITI DB (2019). The informatics & telematics institute
database. http://3d-search.iti.gr/3DSearch/index.html.
Jalba, A., Kustra, J., and Telea, A. (2012). Surface and
curve skeletonization of large 3D models on the GPU.
IEEE TPAMI, 35(6):1495–1508.
Jalba, A., Kustra, J., and Telea, A. (2013). Computing sur-
face and curve skeletons from large meshes on the
GPU. IEEE TPAMI, 35(6):783–799.
Kalogerakis, E., Hertzmann, A., and Singh, K. (2010).
Learning 3D mesh segmentation and labeling. ACM
TOG, 29(4).
McInnes, L., Healy, J., and Melville, J. (2018). Umap: Uni-
form manifold approximation and projection for di-
mension reduction. arXiv:1802.03426.
NASA (2019). Nasa 3D resources. https://nasa3d.arc.nasa.
gov.
Paulovich, F. V., Nonato, L. G., Minghim, R., and Lev-
kowitz, H. (2008). Least square projection: A fast
high-precision multidimensional projection technique
and its application to document mapping. IEEE
TVCG, 14(3):564–575.
Peyre, G. and Cohen, L. (2005). Geodesic computations for
fast and accurate surface remeshing and parameteri-
zation. Progress in Nonlinear Differential Equations
and Their Applications, 63:151–171.
Pezzotti, N., Lelieveldt, B. P., van der Maaten, L., H
¨
ollt,
T., Eisemann, E., and Vilanova, A. (2017). Approxi-
mated and user steerable t-SNE for progressive visual
analytics. IEEE TVCG, 23(7):1739–1752.
Rauber, P. E., da Silva, R. R. O., Feringa, S., Celebi, M. E.,
Falc
˜
ao, A. X., and Telea, A. C. (2015). Interactive im-
age feature selection aided by dimensionality reduc-
tion. In Proc. EuroVA, pages 19–23.
Rusu, R. B., Blodow, N., and Beetz, M. (2009). Fast point
feature histograms (FPFH) for 3D registration. In
Proc. IEEE Intl. Conf. on Robotics and Automation,
pages 3212–3217.
ShapeNet (2019). ShapeNet online repository. https://www.
shapenet.org.
Shapira, L., Shamir, A., and Cohen-Or, D. (2008). Con-
sistent mesh partitioning and skeletonisation using
the shape diameter function. The Visual Computer,
24(4):249–262.
Shen, Y.-T., Chen, D.-Y., Tian, X.-P., and Ouhyoung, M.
(2003). 3D Model Search Engine Based on Lightfield
Descriptors. In Eurographics 2003 - Posters. Euro-
graphics Association.
Shilane, P., Min, P., Kazhdan, M., and Funkhouser, T.
(2004). The Princeton shape benchmark. In Proc.
SMI, pages 167–178. http://shape.cs.princeton.edu/
benchmark.
Shneiderman, B. (1996). The eyes have it: A task by
data type taxonomy for information visualizations. In
Proc. IEEE Symp. on Visual Languages, pages 336–
343.
Shtrom, E., Leifman, G., and Tal, A. (2013). Saliency de-
tection in large point sets. In Proc. IEEE ICCV, pages
3591–3598.
Su, H., Maji, S., Kalogerakis, E., and Learned-Miller, E.
(2015). Multi-view convolutional neural networks for
3D shape recognition. In Proc. IEEE ICCV, pages
945–953.
Tangelder, J. and Veltkamp, R. (2008). A survey of content
based 3D shape retrieval methods. Multimedia Tools
and Applications, 39(3):441–471.
Tasse, F., Kosinka, J., and Dodgson, N. (2015). Cluster-
based point set saliency. In Proc. IEEE ICCV, pages
163–171.
Tukey, J. and Tukey, P. (1988). Computer graphics and ex-
ploratory data analysis: An introduction. In The Col-
lected Works of John W. Tukey: Graphics: 1965-1985.
TurboSquid, Inc. (2019). Turbosquid shape repository.
https://www.turbosquid.com.
van der Maaten, L. and Hinton, G. (2008). Visualizing high-
dimensional data using t-SNE. J Mach Learn Res,
(9):2579–2605.
Verma, V. and Snoeyink, J. (2009). Reducing the mem-
ory required to find a geodesic shortest path on a large
mesh. In Proc. ACM GIS, pages 227–235.
Wattenberg, M. (2016). How to use t-SNE effectively. https:
//distill.pub/2016/misread-tsne.
Wilkinson, L., Anand, A., and Grossman, R. (2006). High-
dimensional visual analytics: Interactive exploration
guided by pairwise views of point distributions. IEEE
TVCG, 12(6):1363–1372.
Visual Exploration of 3D Shape Databases Via Feature Selection
53
