
Efficiency of Meme Usage in Evolutionary Algorithm
Jaroslav Janacek and Marek Kvet
Faculty of Management Science and Informatics, University of Žilina, Univerzitná 8215/1, 010 26 Žilina, Slovakia
Keywords: Location, Emergency Medical Service System, Approximate Approach, Evolutionary Algorithm, Meme.
Abstract: Emergency medical service system design attracts attention of a broad researcher and practitioner community
due to increasing public demand for more safe life. A basic model of the design problem is known as the
weighted p-median problem. Large instances of the problem as are hard to solve in general and very often it
is necessary to obtain a series of solutions to be able to offer a spectrum of various solutions. For this purpose,
an evolutionary metaheuristic seems to be a suitable tool, as it processes simultaneously a family of solutions.
A standard evolutionary algorithm is based on developing a population using some nature inspired operations
with solutions-members of the population, which produce candidates for population updating. This
evolutionary process is characterized by fast improvement of the best-found-solution at the beginning and
very slow improvement at the end, when the best-found-solution is near to the optimal one. To improve the
first phase of the evolutionary process, numerous authors recommend to plug increasing procedures called
memes in the process. Within this paper, we will study an impact of the meme plugin on acceleration of the
evolutionary process, when big instances of the weighted p-media problem are solved. The study will be
performed on instances of an emergency service system design problem solved by genetic algorithm with
elite set and the studied meme will be based on exchange neighborhood searching.
1 INTRODUCTION
The emergency service system design problem
represents a hard solvable combinatorial problem,
where p service center locations should be selected
from a finite set of possible center locations so that
disutility perceived by system users be minimal
(Brotcorne et al., 2003, Doerner et al., 2005,
Jánošíková and Žarnay, 2014, Jánošíková et al., 2019,
Marianov and Serra, 2002, Reuter-Oppermann et al.,
2017). Disutility is often computed as a sum of
weighted time-distances from individual users’
locations to the nearest service center, where the
weights correspond to frequency of emergency events
at the individual users’ locations. The emergency
service system design problem can be presented and
solved as a weighted p-median problem by an exact
optimization algorithm (Avella el al, 2007, Current et
al., 2002, Elloumi et al., 2004, García et al., 2011,
Guerriero et al. 2016, Janáček, 2008, Sayah and
Irnich, 2016). The exact approaches were mostly
based on so called radial formulation of the p-median
problem and this formulation also enables
construction of a fast approximate approach (Janáček
and Kvet, 2016).
In spite of existence of the exact and approximate
fast approaches, there are many situations, which are
not covered by enough efficient solving tools. It
concerns very large instances of the p-median
problem or necessity of producing a series of good
different solutions. Such a demand can be satisfied
my metaheuristic approaches (Gendreau, and Potvin,
2010).
As the problem can be studied as searching across
a set of unit hypercube vertices, genetic algorithm
represents a suitable tool for obtaining good solution
in predetermined computational time (Daskin,. 2015,
Reeves, 2010, Sastry and Goldberg, 2005, Rybičková
et al., 2016 ). Nevertheless, the progress of the best-
found-solution objective function value along
computational time resembles convex decreasing
function, which converges slowly to the optimal
value. To accelerate convergence of an evolutionary
algorithm in general, many authors recommend
plugging an improving heuristic called meme in the
evolutionary process (Resende, 2004, Moscato and
Cotta, 2010, Gupta and Ong, 2019,). We concentrate
our effort on memes based on neighborhood
searching, where the neighborhood of a current
solution is represented by all p-median solutions,
Janacek, J. and Kvet, M.
Efficiency of Meme Usage in Evolutionary Algorithm.
DOI: 10.5220/0008946301650171
In Proceedings of the 9th International Conference on Operations Research and Enterprise Systems (ICORES 2020), pages 165-171
ISBN: 978-989-758-396-4; ISSN: 2184-4372
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
165

which can be obtained from the current solution by
replacing a current center location with an
unoccupied one. The increasing neighborhood
searching process can be restricted by several means,
e.g. by limited number of objective function
evaluations. Within the paper, we deal with meme
efficiency in the above mentioned evolutionary
process. We want to answer the question, under
which conditions can meme usage improve the
process convergence and when the meme complexity
represents such a computational burden that the
process becomes inefficient.
The paper is organized in the following way. The
next section concisely describes a genetic algorithm
including a special implementation of its basic
operations of crossover and mutation. The third
section gives an insight in an efficient increasing
meme construction used for hybridization of the
genetic algorithm. The fourth section introduces a
way of measuring of convergence speed and
comments on possible meme application in the
genetic algorithm. The fifth section contains results
of the numerical experiments aimed at solving the
meme efficiency problem. The last section
summarizes the obtained findings.
2 GENETIC ALGORITHM FOR
P-MEDIAN PROBLEM
A genetic algorithm (GA) imitates a naturel process
of species development in general. The algorithm
processes a current population of individuals, where
each individual corresponds to a solution of the
solved problem. So called fitness of an individual
usually reflects objective function value of the
associated solution. The algorithm starts with creation
of an initial population of different individuals-
solutions and computing their fitness values. Then,
the evolutionary process is simulated by creating
candidates for a new population, by forming the new
population and by a way of population exchange. This
process is repeated until a termination rule is met, e.g.
until used computational time reaches a given limit.
Pool of the candidates is created using two operations
performed on individuals selected from the current
population, where the selection is performed
randomly and probability of an individual choice
depends on its fitness. The first of the operations is
called crossover and it combines a pair of individuals
and creates two new individuals. The new individuals
are subjected to the second operation – mutation and
then, they are inserted into the pool of candidates.
After the pool has been completed, the new
population is formed by selection of some individuals
from the pool and by including some elite individuals
of the current population. Creating of the new
population is completed by fitness evaluation of each
individual and by updating the best-found-solution.
As can be seen, no special improving algorithm is
included into the basic evolutionary process. Quality
of the resulting solution is achieved only by the two
selections (parent’s selection for crossover and the
selection of individuals for new population from the
pool) and by keeping the best-found-solution or so
called elite sub-set of the current population.
Efficiency of GA algorithm implementation is
determined by a design of the two mentioned
operations, which usually exploit characteristics of
the solved problem to speed up the algorithm
performance. In the studied case, the emergency
system design problem is solved.
The emergency system design consists of choice
of p service center locations from the set I consisting
of m possible service center locations so that the min-
sum objective function reflecting system users’
disutility is minimal. It is assumed that the system
users are concentrated at a finite set J of users’
locations, where b
j
denotes a volume of weight of user
j
J, e.g. b
j
may correspond to an average number of
emergency calls from the user’s location j. If symbol
d
ij
denotes the integer time-distance between
locations i
I and j
J, and if the service center
deployment is described by zero-one m-dimensional
vector y of variables y
i
denoting the center location by
unit value, we can describe the problem by the
formula (1).
min{ min{ : , 1}
:{0,1}, }
jij i
jJ
m
i
iI
bdiIy
yp
y
(1)
As concerns the emergency system design, it is
assumed that a user demand is satisfied from the
nearest service center. From the mathematical point
of view, the set of some vertices of m-dimensional
hypercube is searched through, to obtain optimal
solution.
The studied genetic algorithm is not able to find
the optimal solution in general, but it tries to produce
as good as possible solution using the specific
crossover and mutation operations. Both the
operations are designed so that the resulting offspring
are feasible solutions, i.e. they contains exactly p
located centers.
ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems
166

The suggested operation of crossover is
performed with two individuals-parents x and y,
where each parent is represented by a vector
consisting of m zero-one components. Each
component corresponds to one possible service center
location and unit value of component i indicates that
the associated solution-individual locates a service
center at the possible service location. Thus, each
vector contains exactly p units and m-p zeros at the m
positions. Comparing the associated components of
vectors x and y, it can be found that the components
can be categorized into three classes. The first class
consists of components, at which positions the both
vectors have the zero values. The second class
consists of u components with units in the both
vectors and the third class contains b components, at
which one vector has unit value and the other has zero
value. As totally 2p units are contained in the both
vectors and 2u units are placed at components from
the second class, then b=2p-2u units occupy positions
of the third class, i.e. b is even number.
The suggested crossover operation lets offspring’s
components of the first and second class unchanged
and distributes the b units randomly among the
offspring’s components of the third class so that each
offspring gets exactly b/2 units.
This way, each offspring represents a feasible
solution of the p-median problem.
The mutation used in this genetic algorithm is
based on the exchange operation, which randomly
chooses a position occupied by a center and moves it
at some unoccupied position, which is also chosen
randomly.
As concerns the parent selection for crossover, a
tournament approach is used in the studied case of
GA. Elite set for the new generation completion is
defined as the set of BSize different individuals with
the best fitness values withdrawn from the current
population.
Diversity of the new population is assured by
exclusion of individuals, fitness of which is equal to
a fitness value of already accepted individual of the
new population.
3 MEME FOR P-MEDIAN
PROBLEM
Generally, noun “meme” denotes an arbitrary
heuristic, which can improve some input solution of
the solved problem (Gupta and Ong, 2019). Within
this paper, we will concentrate on a special case of
memes designed as an intensification tool for
metaheuristics, which solve p-median problem. The
studied meme is increasing heuristic based on
neighborhood searching applied to a current p-
median solution, where the neighborhood of the
current solution consists of all p-median solutions,
which differ from the current one in exactly one
located service center. If the meme is run, the
neighborhood of the current solution is searched
through by inspecting results of the individual
exchanges occupied center locations for unoccupied
ones. The searching process proceeds until either a
limited number t of inspections is reached or an
admissible exchange is found. In the second case, a
current solution is updated by the better one and
neighborhood searching is repeated until either t
inspections have been performed or the current
neighborhood has been inspected unless an
admissible solution has been found.
The meme can be described by following five
steps, where I denotes the set of all possible center
locations, P denotes the set of p chosen center
locations, which determine the current solution. F(P)
represents value of the objective function value
connected with the solution P. Definition of the
function value F(P) is described in the formula (1).
Meme(P,t)
0. Initialize F
*
=F(P), P
*
=P, C=I-P,
done=false, s=0, mark all elements of P and
C as uninspected, and go to step 1.
1. If there is any uninspected element of P and
done=false and s<t hold, choose an
uninspected element i from P and perform
step 2, otherwise go to step 4.
2. If there is any uninspected element of C and
done=false and s<t hold, choose an
uninspected element j from C and perform
step 3, otherwise mark element i as
inspected and all elements of C as
uninspected and go to step 1.
3. Set s=s+1, P = (P-{i}){j} and compute
F(P), mark j as inspected. If F(P)<F
*
, then
set F
*
=F(P) and P
*
=P and done=true. Go to
step 2.
4. If s≥t or done=false, then terminate, the
resulting solution is P
*
and its objective
function is F
*
, else if done=false, then set
P=P
*
, C=I-P, done=false, mark all elements
of P and C as uninspected and go to step 1.
Efficiency of the above presented standard
exchange algorithm obviously depends on a way of
objective function value computing. If the objective
function value of a solution P is computed in a
Efficiency of Meme Usage in Evolutionary Algorithm
167
standard way according to formula presented in
model (1), then complexity of the computational
process is O(J.P ), where J .denotes cardinality of
the set J of users and the cardinality P equals to the
number p of located centers.
In our implementation of the process, we make
use of the fact that most of the inspected solutions P
differ from the current solution P only in one service
center. It enabled us to compute the objective function
value F(P) with complexity O(2J ). This effect was
achieved by determining and saving the first and
second minimal values of the set {d
ij
: i
P} for each
jJ. These data are used for fast computation of
objective function value of any solution P, which
differs from P in only one element.
This meme can be used in the genetic algorithm
for p-median problem solving, to improve some
portion of individuals from the pool of candidates or
elite set before creating new population.
4 MEME APPLICATION AND
CONVERGENCE OF
EVOLUTIONARY PROCESS
To be able to study impact of meme usage on an
evolutionary process, some way of convergence
evaluation must be defined. We want to study
characteristics of the evolutionary process limited by
given computational time. As the tested heuristic
need not reach the exact optimum, but it generally
produces near-to-optimal solutions in the given time,
there is no use to define quality of process
convergence only by the objective function value of
the resulting solution. That is why, we suggest the
following measure based on progress of the best-
found-solution objective function value in the
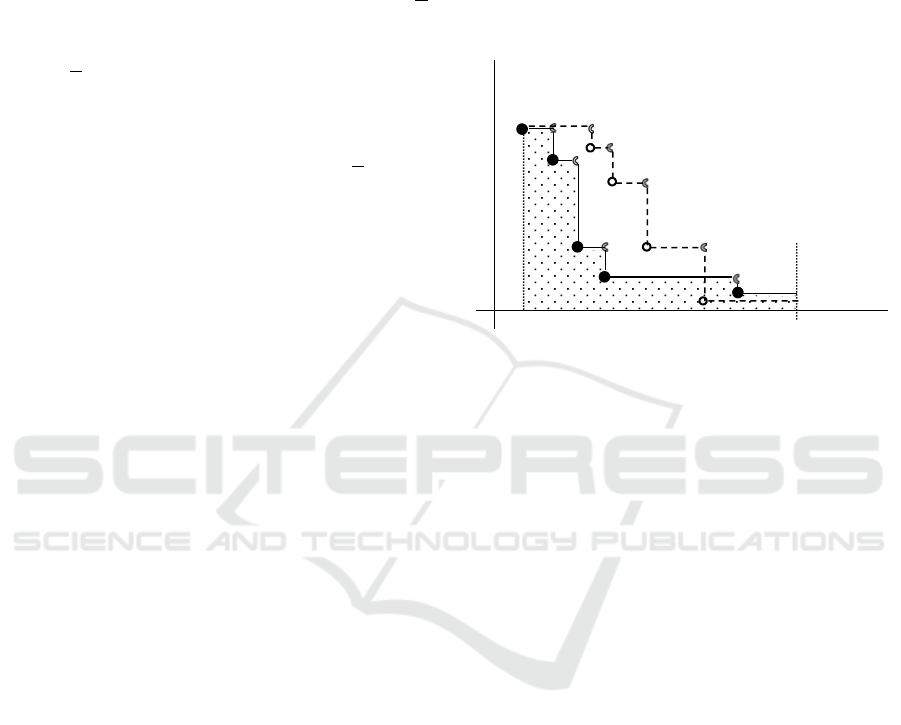
running time. Intuitively, we consider that the process
depicted in Figure 1 by bold lines is better than the
process depicted by the dash lines.
Applied measure of the convergence quality is
defined here as the area below the graph determined
by the progress.
In the remainder of the paper, we will study
influence of meme usage on convergence of the
evolutionary process. Due to big computational time
demand of the suggested meme, we restricted our
study only on the case, when a meme is applied at
most once in population exchange and, in addition, it
will be applied to the best solution of the current
population. Under these assumptions, we will study
following schemes of meme applications.
a) A meme is applied to the best solution of the
current population before the new population
is created.
b) A meme is applied with given constant
probability to the best solution of the current
population.
c) A meme is applied with probability, which
decreases with the number of performed
population exchanges.
Figure 1: Possible progresses of the objective function
values of the best found solutions depending on the running
time of the GA. Dotted area below the full line curve
represents possible evaluation of the associated process
convergence.
5 NUMERICAL EXPERIMENTS
To perform the planned study, the genetic algorithm
including the above described meme was
programmed in programming language JAVA in
NetBeansIDE 7.3 and the associated experiments
were run on a PC equipped with the Intel® Core™ i7
5500U processor with the parameters: 2.4 GHz and
16 GB RAM. The used benchmarks were obtained
from the road network of Slovak self-governing
regions. The mentioned instances are further denoted
by the names of capitals of the individual regions
followed by triples (XX, m, p), where XX is
commonly used abbreviation of the region
denotation, m stands for the number of possible centre
locations (cardinality of the set I) and p is the number
of service centres, which are to be located in the
mentioned region. The list of instances follows:
Bratislava (BA, 87, 14), Banská Bystrica (BB, 515,
36), Košice (KE, 460, 32), Nitra (NR, 350, 27),
Prešov (PO, 664, 32), Trenčín (TN, 276, 21), Trnava
(TT, 249, 18) and Žilina (ZA, 315, 29).
All cities and villages with corresponding number
b
j
of inhabitants were taken into account. The
coefficients b
j
were rounded to hundreds. The set of
Running time
Objective of the best found solution
Time limit
ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems
168
communities represents both the set J of users’
locations and the set I of possible center locations as
well.
To verify the results obtained for the regular self-
governing regions, we constructed bigger
benchmarks by union of the original regions. Thus,
we obtained the additional instances (ESR, 1124,
112), (WSR, 1792, 180) and (HSR, 2916, 273).
Parameters of the studied genetic algorithm were
set up at the following most fitting values according
to preliminary experiments. The size of the
population (PopSize) was determined to correspond
with cardinality of so called near-to-maximal
uniformly deployed set of p-median problem for
given m and p (Janáček and Kvet, 2019, Kvet and
Janáček, 2019). The size of elite set (BSize) was equal
to (1/3)PopSize and the size of pool of candidates was
(3/2)PopSize. The probability of mutation was set up
at the value of 0.3. The computational time of one
original benchmark solution was 5 seconds. The
maximal solving time of the additional benchmarks
was set up to 20 seconds.
Each run of the genetic algorithm was repeated 50
times with the same benchmark and average results
are reported in the following tables.
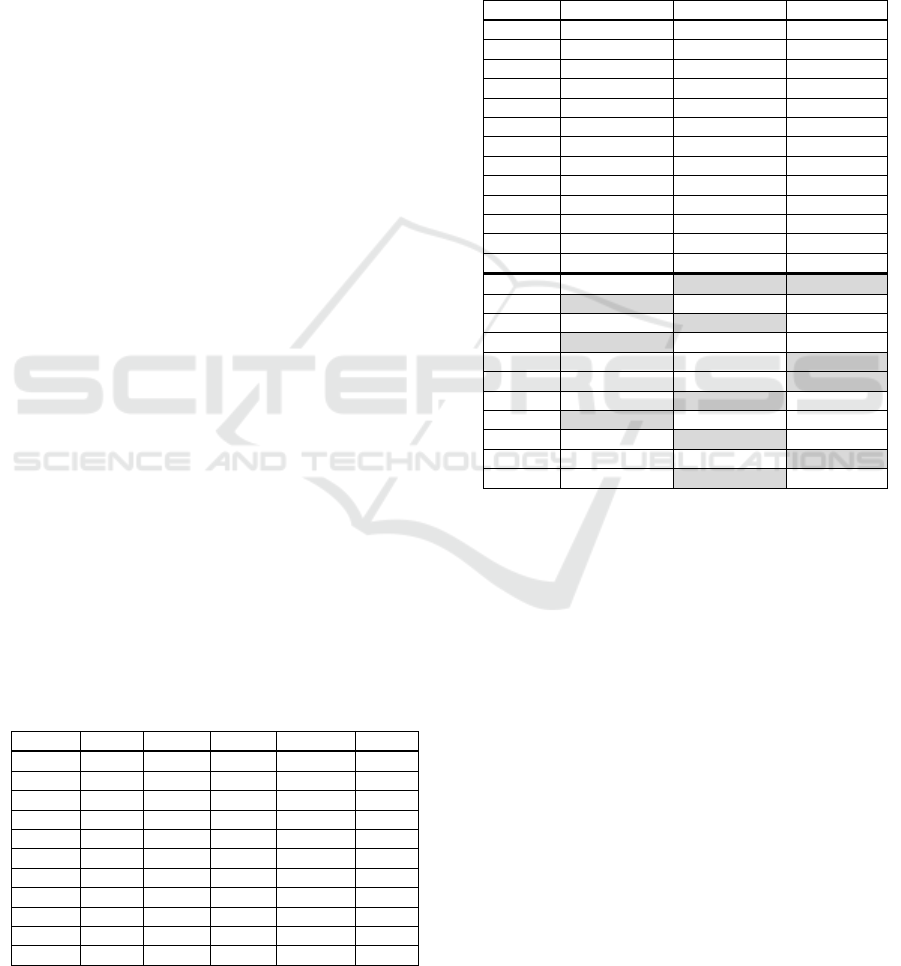
Table 1 gives an overview of the benchmarks,
their exact optimal solutions (optSol) and results of
the standard version of the above described genetic
algorithm without any meme application.
The table refers about size of population
(PopSize), average resulting objective function value
(bestFit), number of population exchanges during run
of the algorithm (noPop). The column labeled by
“RedArea” contains evaluation of the algorithm
convergence described in the previous section. In the
tables is given so called reduced area, which differs
from the full area by subtracting the product of bestFit
and associated time of the run.
Table 1: Characteristics of benchmarks and results of
standard version of the genetic algorithm without meme
application.
Region optSol PopSize bestFit RedArea noPop
BA 19325 23 19325 9 98368
BB 29873 172 30083 5233 625
KE 31200 60 31290 3172 2428
NR 34041 83 34051 1393 2891
PO 39073 232 39352 6809 464
TN 25099 137 25099 403 2939
TT 28206 212 28206 470 2384
ZA 28967 112 28971 1329 1951
ESR 40713 200 42696 82574 355
WSR 108993 200 124605 906515 111
HSR 161448 200 296142 296142 19
An individual experiment using the scheme a) and
b) were organized so that the meme described in
Section 3 for t= p*64 was applied to the best solution
of the current population with the probability 1/(2
T
)
for parameter values T= 0, 1, …,5. It must be noted
that experiments for T= 0 correspond to the case a),
where the meme is applied once to the best solution
in each population.
Table 2: Reduced area of the experiments a) and b).
Reg\T 0 1 2
BA 14 9 8
BB 5487 5092 4610
KE 3288 2911 2672
NR 1735 1466 1334
PO 7733 7116 6781
TN 509 455 415
TT 511 482 479
ZA 1562 1432 1328
ESR 104056 95287 89018
WSR 1022991 959206 908363
HSR 1496960 1475589 1457807
Reg\T 3 4 5
BA 7 6 6
BB 4604 4838 4790
KE 2657 2519 2668
NR 1113 1165 1238
PO 6647 6384 6365
TN 405 406 401
TT 454 436 449
ZA 1214 1240 1295
ESR 86416 83311 86312
WSR 905763 895335 877440
HSR 1452485 1444251 1455430
Comparing the column for T=0 of the Table 2 to
the column RedArea of the Table 1, it can be found
that meme application has worsen convergence of the
algorithm. This effect can be explained by big
computational demand of the used meme, which has
lowered the number of population exchanges
(compare the column for T=0 of the Table 3 to the
column noPop of the Table 1) and thus it decreases
efficiency of the evolutionary operations. Our
experiments showed that lower probability of the
meme application (for T=3, 4, 5) can considerably
improve the convergence of hybridized GA
algorithm.
Efficiency of Meme Usage in Evolutionary Algorithm
169
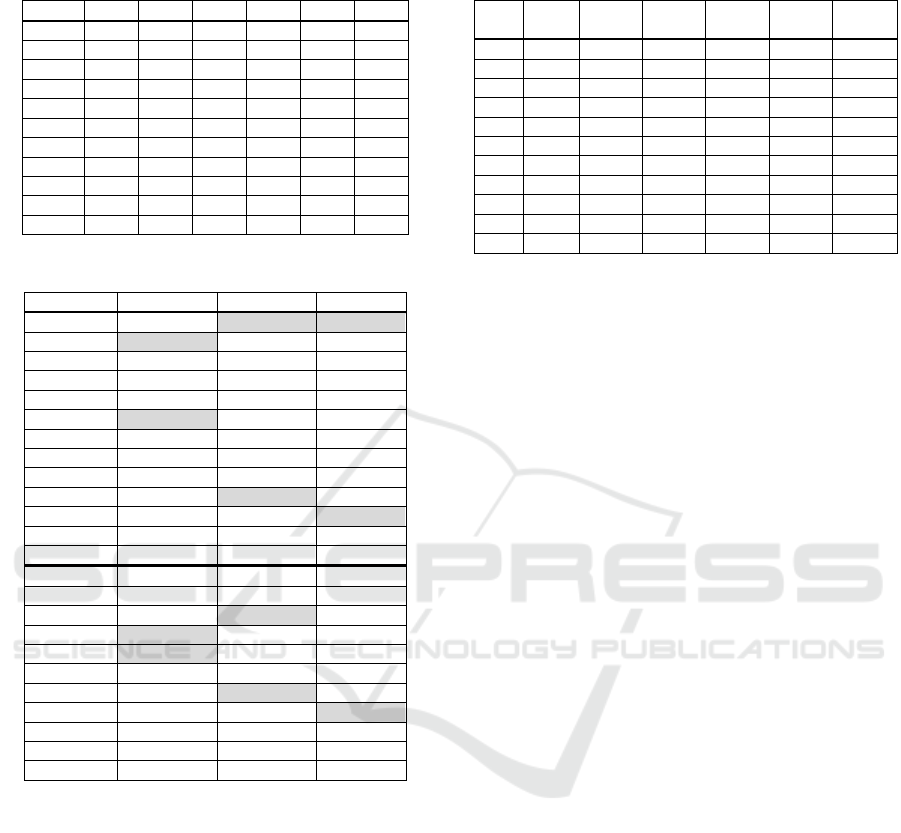
Table 3: Number of population exchanges of the
experiments a) and b).
Reg\T 0 1 2 3 4 5
BA 18636 31502 47893 64861 78899 88472
BB 402 487 538 566 586 597
KE 945 1376 1750 2051 2223 2319
NR 1341 1868 2331 2636 2832 2957
PO 321 380 418 442 451 452
TN 1667 2137 2488 2699 2832 2900
TT 1593 1932 2140 2265 2322 2377
ZA 1052 1350 1558 1694 1779 1829
ESR 245 290 318 335 345 348
WSR 79 93 102 107 109 111
HSR 17 18 19 20 20 20
Table 4: Reduced area of the experiments c).
Reg\T 0 1 2
BA 10 9 9
BB 4854 4986 4867
KE 3185 3144 3351
NR 1185 1261 1444
PO 6995 6801 6991
TN 418 438 421
TT 491 512 499
ZA 1427 1346 1389
ESR 78515 79120 79679
WSR 849673 843178 845608
HSR 1441520 1488013 1433971
Reg\T 3 4 5
BA 10 10 10
BB 4873 5162 5219
KE 3004 2713 2746
NR 1152 1241 1241
PO 6651 6798 7098
TN 448 448 461
TT 485 477 479
ZA 1370 1331 1328
ESR 82681 84750 89350
WSR 863891 884460 903266
HSR 1503572 1464120 1511966
The experiments for scheme c) were performed
for the situation, when the probability Pr of meme
application was dynamically lowered with the
increasing number noP of performed population
exchanges according to (2), where T is so called
shaping parameter of the probability progress.
(1 ) / 2
Pr
T
noP
e
(2)
In this case, the convergence of GA has been also
improved in comparison to the standard GA
algorithm, but the improvement was not as big as in
case of the scheme b). Contrary to scheme b), it must
be noted that bigger value of the parameter T in
scheme c) according to (2) means slower decrease of
probability depending on noP.
Table 5: Number of population exchanges of the
experiments c).
Reg\
T
0 1 2 3 4 5
BA 99985 100213 100248 100342 100380 100255
BB 603 615 617 609 604 599
KE 2399 2436 2420 2450 2429 2388
NR 3081 3119 3128 3113 3083 3080
PO 452 458 461 460 458 446
TN 2932 2952 2968 2958 2938 2938
TT 2303 2318 2335 2323 2319 2300
ZA 1823 1826 1815 1810 1802 1802
ESR 363 363 363 362 356 350
WSR 118 119 118 117 113 106
HSR 20 20 19 19 18 18
6 CONCLUSIONS
The paper reports on research conducted to increase
the efficiency of the genetic algorithm in cases where
real-time emergency service system instances need to
be resolved and, in addition, a whole set of good
alternative solutions is required. To estimate
contribution of genetic algorithm hybridization, we
studied an impact of the meme plugin on acceleration
of the evolutionary process applied to the emergency
system design.
The performed experiments showed that usage of
meme in the evolutionary process need not inevitably
contribute to acceleration of the process. Two
schemes of random meme application were suggested
and their influence on evolutionary process
convergence was studied. It was found that suitable
setting of application probability may lead to
considerable improvement of the evolutionary
process.
Future research may be aimed at a deeper research
of the meme application and parameter tuning
including learning process and other tools of artificial
intelligence.
ACKNOWLEDGEMENTS
This work was supported by the research grants
VEGA 1/0342/18 “Optimal dimensioning of service
systems”, VEGA1/0089/19 “Data analysis methods
and decisions support tools for service systems
supporting electric vehicles”, and VEGA 1/0689/19
“Optimal design and economically efficient charging
infrastructure deployment for electric buses in public
transportation of smart cities” and APVV-15-0179
“Reliability of emergency systems on infrastructure
with uncertain functionality of critical elements”.
ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems
170

REFERENCES
Avella, P., Sassano, A. and Vasil'ev, I. 2007. Computational
study of large scale p-median problems. Mathematical
Programming, 109: pp. 89-114.
Brotcorne, L., Laporte, G., Semet, F. 2003. Ambulance
location and relocation models. European Journal of
Operational Research 147, pp. 451–463
Current, J., Daskin, M., Schilling, D. 2002. Discrete
network location models. In Drezner Z. (ed) et al.
Facility location. Applications and theory, Berlin,
Springer, pp 81-118
Daskin, M., S. 2015. The p-Median Problem. Location
Science, edited by G. Laporte, S. Nickel and F.
Saldanha da Gama, Springer, pp. 21-45
Doerner, K. F., et al. 2005. Heuristic Solution of an
Extended Double-Coverage Ambulance Location
Problem for Austria. Central European Journal of
operations research, Vol. 13, No 4, pp. 325-340
Elloumi, S., Labbé, M., Pochet, Y. 2004. A new formulation
and resolution method for the p-center problem.
INFORMS Journal on Computing 16, pp. 84-94
García, S., Labbé, M., Marín, A. 2011. Solving large p-
median problems with a radius formulation. INFORMS
Journal on Computing, Vol. 23, No 4, pp. 546-556
Gendreau, M., Potvin, J. 2010. Handbook of Metaheuristics,
Springer Science & Business Media, 648 p.
Guerriero, F., Miglionico, G., Olivito, F. 2016. Location
and reorganization problems: The Calabrian health care
system case. European Journal of Operational
Research 250, pp. 939-954
Gupta, A., Ong, Y. 2019. Memetic Computation: The
Mainspring of Knowledge Transfer in a Data-Driven
Optimization Era, Springer, 2019, 104 p.
Janáček, J. 2008. Approximate Covering Models of
Location Problems. In Lecture Notes in Management
Science: Proceedings of the 1st International
Conference ICAOR, Yerevan, Armenia, pp. 53-61
Janáček, J., Kvet, M. 2016. Sequential approximate
approach to the p-median problem. Computers &
industrial engineering, Vol. 94, pp. 83-92.
Janáček, J., Kvet, M. 2019. Usage of uniformly deployed
set for p-location min-sum problem with generalized
disutility. In SOR 2019: International symposium on
Operational Research, Bled, Slovenia, pp. 494-499
Jánošíková, Ľ., Žarnay, M. 2014. Location of emergency
stations as the capacitated p-median problem. In
International scientific conference: Quantitative
Methods in Economics-Multiple Criteria Decision
Making XVII, Virt, Slovakia
Jánošíková, Ľ. et al. 2019. An optimization and simulation
approach to emergency stations relocation. Central
European Journal of Operations Research, Vol. 27.
No. 3, pp. 737-758
Kvet, M., Janáček, J. 2019. Population diversity
maintenance using uniformly deployed set of p
-location
problem solutions. In SOR 2019: International
symposium on Operational Research, Bled, Slovenia,
pp. 354-359
Marianov, V., Serra, D. 2002. Location problems in the
public sector. In Drezner, Z. (Ed.). Facility location -
Applications and theory, Berlin: Springer, pp. 119-150
Reeves, C., R. 2010. Genetic Algorithms. Handbook of
Metaheuristics, edited by M. Gendreau and Jean-Yves
Potvin, Second Edition, Springer, pp. 109-139
Resende, M., G., C. 2004. A Hybrid Heuristic for the p-
Median Problem. Journal of Heuristics, 10, Kluwer
Academic Publishers, pp. 59-88
Moscato, P., Cotta, C. A 2010. Modern Introduction to
Memetic Algorithms. Handbook of Metaheuristics,
edited by M. Gendreau and Jean-Yves Potvin, Second
Edition, Springer, pp. 141-183
Reuter-Oppermann, M., van den Berg, P. L., Vile, J. L.
2017. Logistics for Emergency Medical Service
systems. Health Systems, Vol. 6, No 3, pp 187-208
Rybičková, A., Burketová, A., Mocková, D. 2016. Solution
to the lacating – routing problem using a genetic
algorithm. In SmaRTT Cities Symposiuum Prague,
Prague, pp. 1 - 6
Sastry, K., Goldberg, D. 2005. Genetic Algorithms. Search
Methodologies: Introductory Tutorials in Optimization
and Decision Support Techniques, edited by E. K.
Burke, G. Kendall, Springer, pp. 97-125
Sayah, D., Irnich, S. 2016. A new compact formulation for
the discrete p-dispersion problem. European Journal of
Operational Research, Vol. 256, No 1, pp. 62-67
Efficiency of Meme Usage in Evolutionary Algorithm
171
