
Acquisition of Optimal Connection Patterns for Skeleton-based Action
Recognition with Graph Convolutional Networks
Katsutoshi Shiraki, Tsubasa Hirakawa, Takayoshi Yamashita and Hironobu Fujiyoshi
Chubu University, Kasugai, Aichi, Japan
Keywords:
Graph Convolutional Networks, Multitask Learning, Skeleton-based Action Recognition.
Abstract:
Action recognition from skeletons is gaining attention since skeleton data can be easily obtained from depth
sensors and highly accurate pose estimation methods such as OpenPose. A method using graph convolutional
networks (GCN) has been proposed for action recognition using skeletons as input. Among the action recog-
nition methods using GCN, spatial temporal GCN (ST-GCN) achieves a higher accuracy by capturing skeletal
data as spatial and temporal graphs. However, because ST-GCN defines human skeleton patterns in advance
and applies convolution processing, it is not possible to capture features that take into account the joint rela-
tionships specific to each action. The purpose of this work is to recognize actions considering the connection
patterns specific to action classes. The optimal connection pattern is obtained by acquiring features of each
action class by introducing multitask learning and selecting edges on the basis of the value of the weight matrix
indicating the importance of the edges. Experimental results show that the proposed method has a higher clas-
sification accuracy than the conventional method. Moreover, we visualize the obtained connection patterns by
the proposed method and show that our method can obtain specific connection patterns for each action class.
1 INTRODUCTION
Human action recognition has been actively stud-
ied due to its importance in video surveillance sys-
tems and sports analysis. Conventional human action
recognition methods use appearance, optical flows,
and skeletons as inputs (Tran et al., 2015) (Simonyan
and Zisserman, 2014) (Limin et al., 2016) (Wu,
2012). The use of skeletons is attracting attention be-
cause their skeletal data can be captured using depth
sensors and high-precision pose estimation methods
such as OpenPose (Zhe et al., 2017) and they can
be easily adapted to changes in the environment and
viewpoint. As skeletal data contains the coordinates
of each joint for each frame, many action recog-
nition methods based on skeletons do not consider
the relationships between joints (Vemulapalli et al.,
2014) (Hongsong and Liang, 2017) (Liu et al., 2017).
To consider such a relationships, actions can poten-
tially be determined by expressing skeletons in a
graph composed of nodes and edges connecting them.
When skeletons are represented as a graph, nodes cor-
respond to joint coordinates and edges correspond to
the relationship between joints. Therefore, it is pos-
sible to consider the relationship between joints and
recognize complex actions. A method using graph
convolutional networks (GCN) has been proposed for
action recognition with graph skeletons as input (Si-
jie et al., 2018) (Li et al., 2018). A GCN is a convo-
lutional neural network that takes graph structures as
input, enabling it to extract features considering the
relationship of connected nodes. GCN are also used
in fields such as image classification, document clas-
sification, and compound classification (Joan et al.,
2014) (Defferrard et al., 2016) (Gilmer et al., 2017).
The spatial temporal GCN (ST-GCN) is an action
recognition method that achieved a high recognition
accuracy by introducing a spatial graph that considers
the relationship between joints and a temporal graph
that considers temporal movement. However, only a
human skeleton pattern is defined in advance as the
connection pattern of the graph used in the spatial
graph. Therefore, since the convolution is performed
only with the human skeletal pattern, it is difficult to
consider the relationship between distant joints. In the
case of performing action recognition, the relation-
ship between distant joints is important for many mo-
tions, such as the relationship between arms and legs
when throwing. In addition, the relationship between
important joints may be different for each action.
In this work, we propose an action recognition
method that considers the optimal connection pat-
tern for each action. By constructing a connection
pattern for each action, the optimal feature between
302
Shiraki, K., Hirakawa, T., Yamashita, T. and Fujiyoshi, H.
Acquisition of Optimal Connection Patterns for Skeleton-based Action Recognition with Graph Convolutional Networks.
DOI: 10.5220/0008934603020309
In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 5: VISAPP, pages
302-309
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
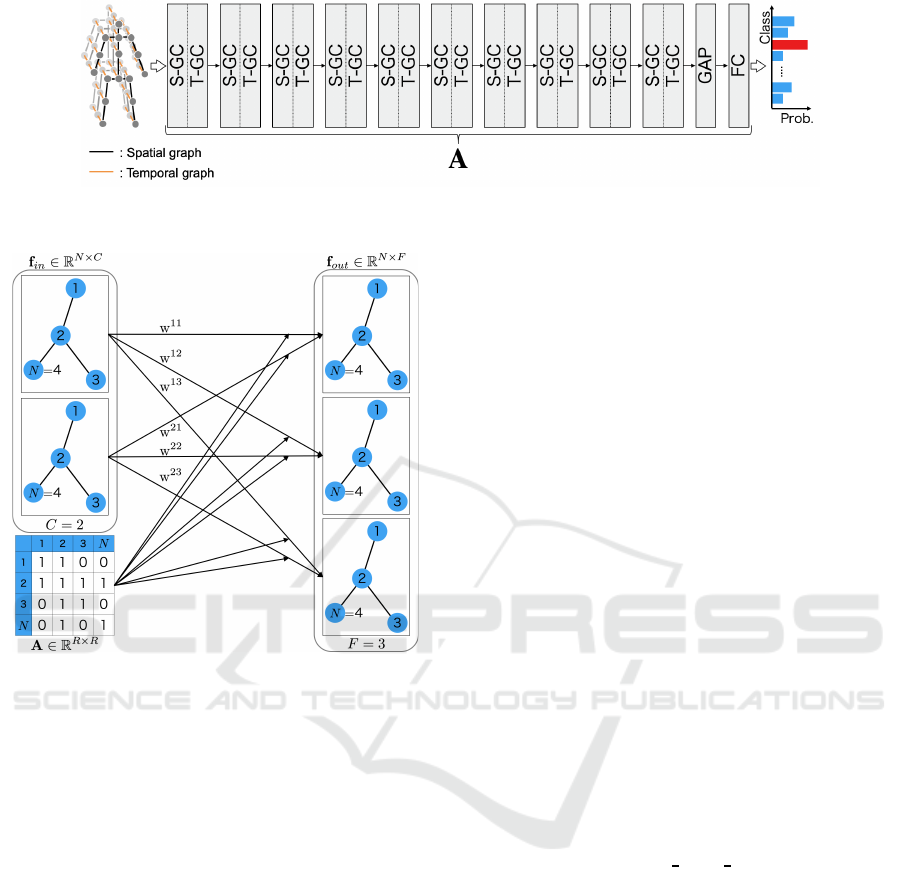
Figure 1: ST-GCN network architecture.
Figure 2: Graph convolution processing.
joints is extracted for each action. Also, instead of
using a pre-defined optimal connection pattern, it is
possible to construct one automatically during learn-
ing. In the proposed method, we introduce multitask
learning framework and classify each action class as
binary classification problem. This enables the pro-
posed method to define different connection patterns
for each task (i.e., each action class) and the optimal
pattern is obtained by updating the connection pat-
terns during learning. To update the connection pat-
tern, we focus on the weight matrix indicating edge
importance and select the more important edge on the
basis of weight value. We propose an action recogni-
tion method that obtains the optimal connection pat-
tern for each action by repeatedly updating the pattern
during learning.
2 RELATED WORKS
ST-GCN is an action recognition method that rep-
resents skeletons as graphs. This method achieves
a higher recognition accuracy than that of conven-
tional methods as skeletons are represented as spa-
tial and temporal graphs. A spatial graph considers
the relationship between joints by connecting joints
in the same frame, and a temporal graph considers the
temporal movement of joints by connecting the same
joints between frames. The ST-GCN network archi-
tecture is shown in Figure 1. Spatial graph convolu-
tion (S-GC) and temporal graph convolution (T-GC)
are used for the convolution processing of the spatial
and temporal graphs, respectively, followed by global
average pooling (Min et al., 2014).
ST-GCN recognizes action using a GCN to ob-
tain a feature map by convolution processing, similar
to a general convolutional neural network. However,
the general convolution process cannot be applied to
graphs because each node has a different number of
adjacent nodes. Therefore, the convolution process-
ing of graphs in ST-GCN has been achieved in the
literature (Kipf and Welling, 2017). An outline of the
graph convolution process is shown in Figure 2. For
a spatial graph with N nodes, we condider a graph
convolution process with C dimensional node feature
f
in
∈ R
N×C
. The output f
out
∈ R
N×F
of the number of
feature maps F is obtained by Equation (1) using the
adjacency matrix
ˆ
A ∈ R
N×N
and the weight matrix
W ∈ R
C×F
.
f
out
= Λ
−
1
2
ˆ
AΛ
−
1
2
f
in
W, (1)
where
ˆ
A is obtained by Equation (2) using the adja-
cency matrix A ∈ R
N×N
and the unit matrix I ∈ R
N×N
indicating the loop of the graph.
ˆ
A = A+ I (2)
The adjacency matrix A is a matrix indicating the con-
nection relation of nodes. Each element A
ij
of the
adjacency matrix A indicates the connection relation-
ship between the nodes i and j, and is obtained by
Equation (3).
A
ij
=
(
1 (node i, j is connected),
0 (node i, j is not connected).
(3)
Λ in Equation (1) is a diagonal matrix whose diagonal
component is the eigenvalue of the graph Laplacian,
Acquisition of Optimal Connection Patterns for Skeleton-based Action Recognition with Graph Convolutional Networks
303
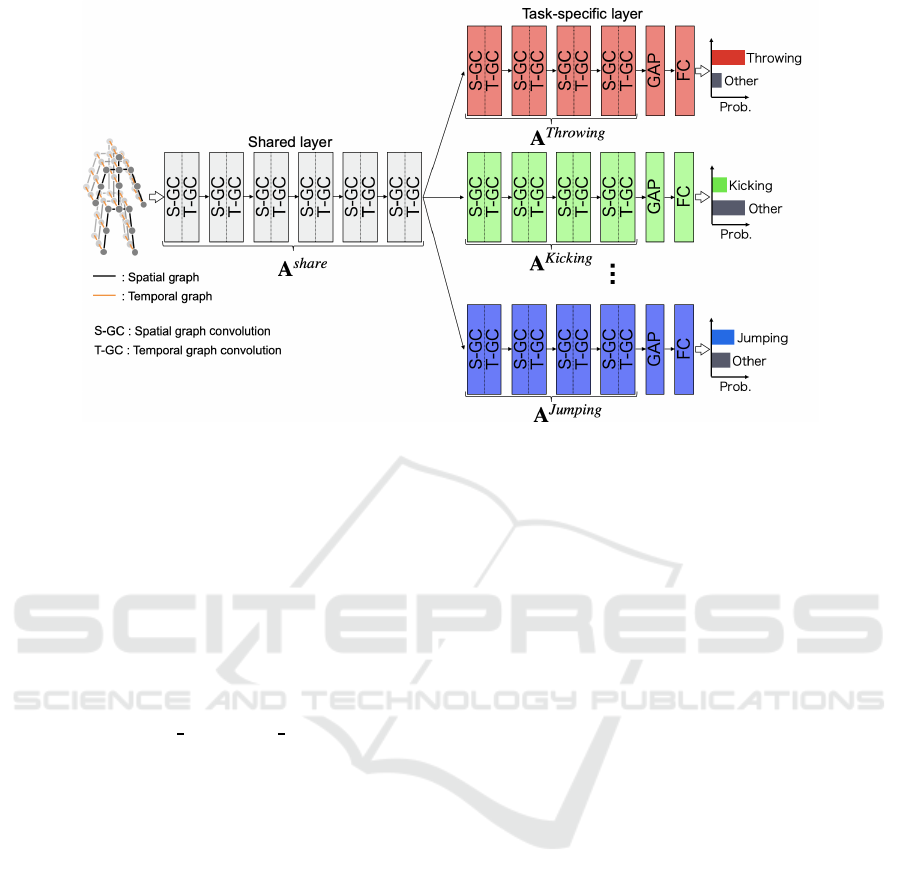
Figure 3: Network architecture of the proposed method.
and its diagonal component is Λ
ii
=
∑
j
(A
ij
+ I
ij
).
The output feature map can be expressed as a (C,V,T)
dimensional tensor with C dimensions, N nodes, and
T frames. Therefore, the convolution processing of
the temporal graph can be implemented by that of the
arbitrary kernel size 1 × Γ. In ST-GCN, a learning
weight matrix M ∈ R
N×N
is proposed to consider the
importance of edges in action recognition. The learn-
ing weight matrix M is added to the graph convolution
process as show in Equation (4).
f
out
= Λ
−
1
2
(
ˆ
A◦ M)Λ
−
1
2
f
in
W, (4)
where ◦ is the element-wise product. By taking the
element product of the adjacency matrix
ˆ
A and the
learning weight matrix M, a weight can be given
to each edge. Updating M increases the weight of
edges connected to important nodes. The classifica-
tion accuracy of ST-GCN has been reported to have
improved by adding the learning weight matrix M to
the graph convolution process.
3 PROPOSED METHOD
The convolutionprocessing of the spatial graph in ST-
GCN is performed only with the connection pattern
of a human skeleton. Since convolution processing
is performed only between adjacent joints, the rela-
tionship between distant joints such as right and left
hands, and hands and feet is not considered. Also, the
relationship of important joints in action recognition
may differ depending on the action. For example, in
the throwing action, both the right leg and arm are
important because the right leg is the axis leg and the
object is thrown with the right arm. Moreover, since
the whole body moves in the jumping action, the rela-
tionship between the whole body is important for ac-
tion recognition. In this work, we propose an action
recognition method that automatically obtains the op-
timal connection pattern for each action class. The
network of the proposed method is shown in Figure
3. The details of the proposed method are described
below.
3.1 Extraction of Action Features by
Multitask Learning
We introduce multitask learning to extract features
specific to each action class. Multitask learning is a
method in which multiple tasks can be learned on one
neural network. Our proposed method performs two-
class classification between specific classes and other
classes in each task of multitask learning. The shared
part of the network extracts common features from all
action classes, and each task extracts specific features
from each action class. Also, to obtain the connection
pattern of each action class, an independent adjacency
matrix is used in the shared layer and a specific task
layer of the network.
3.2 Obtaining the Optimal Connection
Pattern by Updating the Adjacency
Matrix
The adjacency matrix is updated during learning to
obtain connection patterns specific to each action
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
304

Figure 4: Network architecture with additional multi-class classfication layer.
class. We focus on the learning weight matrix M pro-
posed in ST-GCN. M gives weights to each edge by
Equation (4), and updating M increases the weight of
edges connected to important nodes. Therefore, the
optimal connection pattern can be obtained by select-
ing important edges on the value of M. The initial
values of the adjacency matrix are all 1, that is, all
nodes are connected. The adjacency matrix is updated
by leaving only K edges with large weights from the
value of the learning weight matrix M. Edge weights
without connections are not considered. As such, the
reduced edge does not connect the nodes again. Also,
to maintain the loop in the graph, the diagonal com-
ponent of the adjacency matrix is always 1 regardless
of the weight value. The updated adjacency matrix
is then converted into a symmetric matrix to form an
undirected graph. That is,
ˆ
A
ji
= 1 when
ˆ
A
ij
= 1.
Let A
share
be the adjacency matrix of the shared
part and A
t
be that of task t. The learning weight
matrix M exists in each S-GC layer. Therefore, the
adjacency matrix A
t
of each task is updated with the
value M
t
obtained by adding all the learning weight
matrices of task t. The algorithm for updating the ad-
jacency matrix is shown in Algorithm 1. After updat-
ing, graph convolution processing is performed using
the obtained adjacency matrix. The number of edges
is gradually reduced by repeatedly updating the ad-
jacency matrix during learning. As a result, only an
edge with a large weight remains, so an optimum con-
nection pattern for action recognition can be obtained.
Algorithm 1: Adjacency matrix update algorithm.
Input: A
t
of size N × N : Adjacency matrix of task t
M
t
of size N×N: Learning weight matrix of
task t
K: Number of edges to leave
Output:
ˆ
A
t
of size N × N : Updated adjacency ma-
trix of task t
1:
ˆ
A
t
← N × N identity matrix
2: s = 0
3: while s < K do
4: (i, j) ← argmaxM
t
5: M
t
ij
← 0
6: M
t
ji
← 0
7: if i 6= j then
8: if A
t
ij
6= 0 then
9:
ˆ
A
t
ij
← 1
10:
ˆ
A
t
ji
← 1
11: s ← s+ 1
12: end if
13: end if
14: end while
3.3 Multi-class Classification Layer
In the proposed method shown in Figure 3, each task
is classified into two classes. Therefore, when one
data is input, the classification result is output for each
task. For this reason, there is a possibility that the in-
put data is classified into multiple classes. Our pro-
posed method solves this problem by introducing a
multi-class classification layer. Figure 4 shows the
network structure when performing multi-class clas-
sification. The feature map obtained by GAP for
Acquisition of Optimal Connection Patterns for Skeleton-based Action Recognition with Graph Convolutional Networks
305
each task is the input to the additional fully connected
layer. To train the additional fully connected layer, we
fix the network weights trained by only the additional
fully connected layer and the S-GC and T-GC layers.
4 EXPERIMENTS
To show that the reduction of edges leads to the
improvement of accuracy, an evaluation experiment
was performed in which the number of edges was
changed. The optimal number of edges was deter-
mined from the experimental results. To verify the
effectiveness of the proposed method, a second evalu-
ation experiment based on identification accuracy was
performed. By visualizing the acquired adjacency
matrix, we confirmed that connection patterns spe-
cific to each action class could be acquired. The de-
tails of the dataset, learning conditions, experimental
results, and visualization of the adjacency matrix are
described below.
4.1 Dataset
NTU-RGB+D dataset, a dataset for action recogni-
tion with skeletons, is was used for the experiments
(Shahroudy et al., 2016). The dataset has a total of
60 different action classes, including daily actions
such as walking and sitting, and sports actions such
as throwing and kicking. Data was taken from three
viewpoints simultaneously, the front and 45 degrees
to the left and right. A skeleton comprises 3D coordi-
nates (X, Y, Z) based on information from a Kinect v2
depth sensor and have 25 joints. In this work, we ex-
perimented with three action classes (throwing, kick-
ing, jumping). The number of input frames T was 80.
The NTU-RGB+D dataset recommends two eval-
uation methods: cross-subject and cross-view. Cross-
subject is a method that separates 40 subjects into a
learning data group and an evaluationdata group. Pre-
determined data for 20 subjects are used for learning.
The evaluation is based on data from subjects who
were not used for learning. The number of samples
for learning and evaluation is 2,010 and 830, respec-
tively. Cross-view is a method that separates the data
of the three viewpoints taken by learning and evalua-
tion. The learning uses data taken from the 45 degree
direction, and the evaluation uses that from the front.
The number of samples for learning and evaluation is
1,900 and 950, respectively.
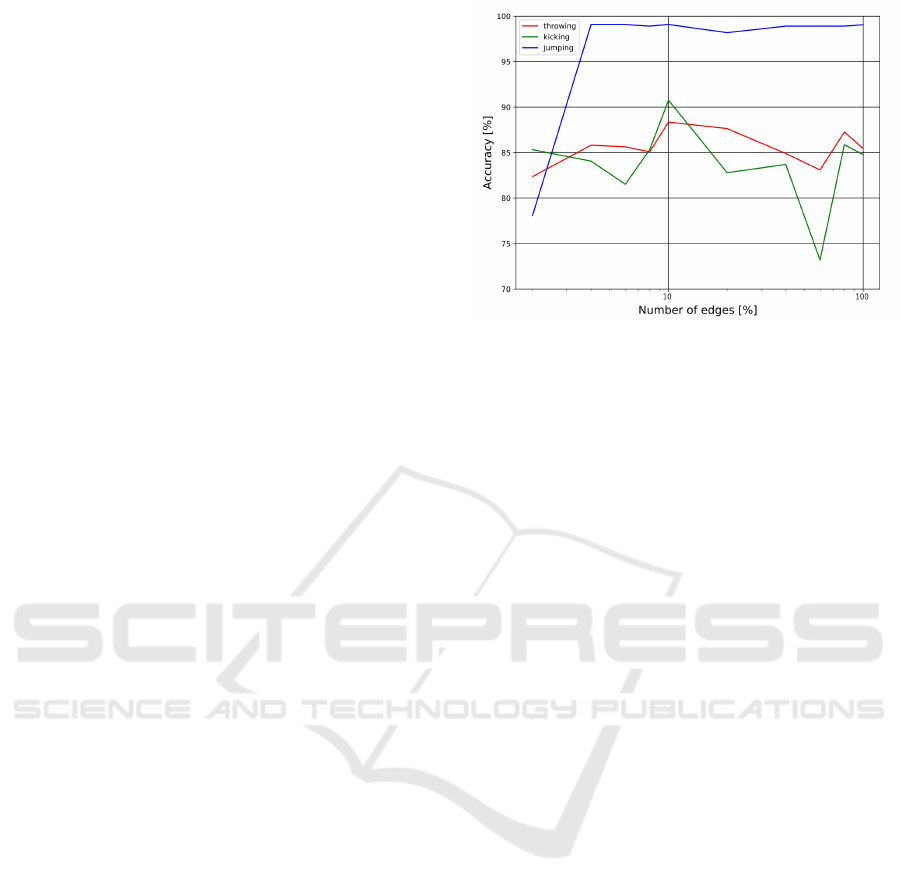
Figure 5: Accuracy per number of connected edges.
4.2 Network Architecture
The network of the proposed method consists of a
convolutional block of spatial and temporal graphs.
A block first has a spatial GCN, followed by a batch
normalization layer, a ReLU layer, a temporal GCN,
a dropout layer, a batch normalization layer and a
ReLU layer. The kernel size Γ for temporal GCN is
set to 9, and the drop rate for the dropout layer is set
to 0.5. The shared part has six blocks. The first four
blocks have 64 channels and the remaining blocks
have 128 channels for output. The task-specific part
consists of four blocks. There are 128 output channels
for the first block and 256 channels for the following
three blocks. The output of the task-specific part is
input into the GAP layer and softmax classifier for
classification.
During training, we set the batch size as 16. We
use the SGD algorithm. The initial learning rate is 0.1
and decays by 0.1 every 20 epochs. In fine tuning, the
learning rate is set to 0.0001 and the model is train for
20 epoch.
4.3 Experimenting using a Different
Number of Edges
To show that edge reduction affects recognition accu-
racy, we experimented by changing the number of re-
duced edges. Experiments were performed using two
classes, a specific class and one from other classes.
For the other-class one, data randomly selected from
action classes other than throwing, kicking, and jump-
ing were used. The model used was a network of ten
layers with convolution processing for the spatial and
temporal graphs. We set the number of learnings to
100 epochs. The adjacency matrix was updated at 40,
50, 60 and 70 epochs, and the edges were gradually
reduced. The recognition accuracy was evaluated by
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
306
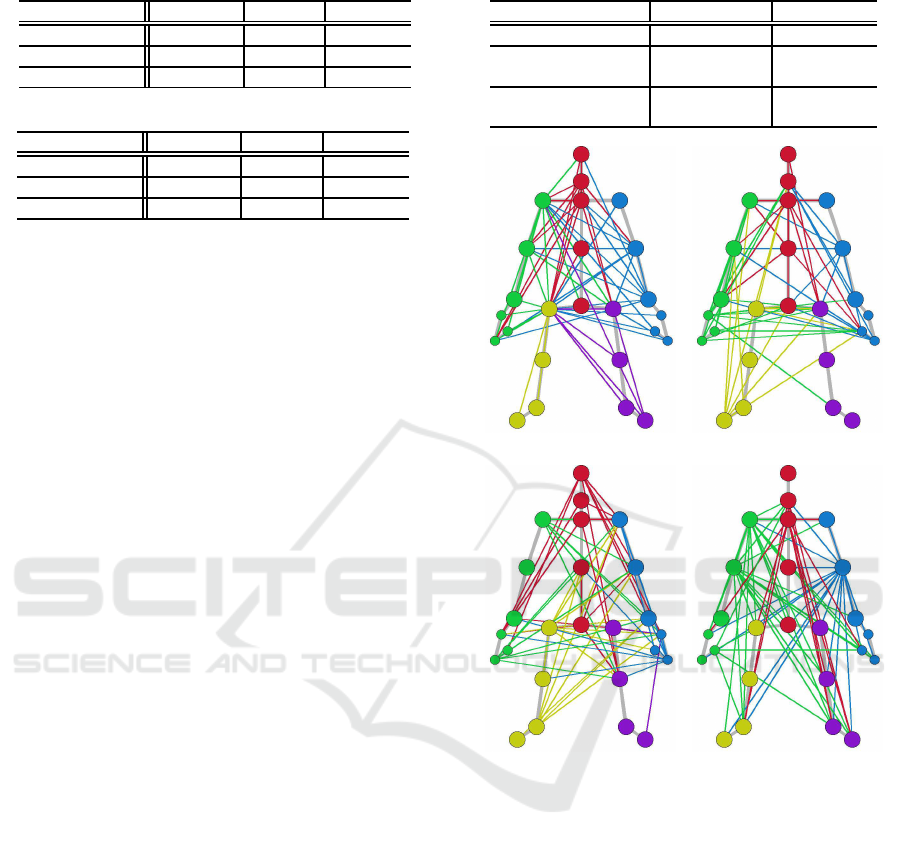
Table 1: Accuracy of each action class in cross-subject [%].
Throwing Kicking Jumping
ST-GCN 86.91 90.94 99.63
Ind. Network 88.36 90.76 99.09
M.T. Network 96.86 96.98 99.74
Table 2: Accuracy of each action class in cross-view [%].
Throwing Kicking Jumping
ST-GCN 93.72 94.02 98.64
Ind. Network 93.23 93.98 99.01
M.T. Network 97.57 96.43 99.26
calculating the difference in the number of edges at
70 epochs. If all edges are connected, the number of
edges is 600, excluding loops.
The experimental results are shown in Figure
5. The results of the throwing, kicking, and jump-
ing classes showed the highest recognition accuracy
with 10% edges. The recognition accuracy at 10%
is 88.36% for throwing, 90.76% for kicking, and
99.09% for jumping. From the results, it can be seen
that a higher accuracy can be obtained by connect-
ing only joints that strongly affectaction than learning
with all edges connected. This indicates that reducing
the number of edges affects recognition accuracy.
4.4 Accuracy Comparison Experiment
4.4.1 Learning Conditions
For this experiment,the number of learning was set to
100 epochs, and the adjacency matrix was updated at
40, 50, 60, and 70 epochs. Each update of the ad-
jacency matrix reduces the number of edges by 20%
of the total number of edges in the initial state. That
is, the number of edges after the update at 70 epochs
is 60. The adjacency matrix was not updated in the
shared part. The initial value of the learning weight
matrix M was set to M
ij
= 1/N using the number of
nodes N of the graph.
4.4.2 Experimental Results
Tables 1 and 2 show the classification accuracies of
each action class of the proposed method and ST-
GCN on the basis of cross-subject and cross-view, re-
spectively. There are two proposed methods, an in-
dependent network (Ind. Network) that learns each
class by two-class classification, and a multitask net-
work (M.T. Network) that learns three classes with a
multitask structure. When comparing M.T. Network
with ST-GCN, cross-subject improved accuracy by an
average of 5.4 points and cross-view by an average of
2.4 points. Also, the accuracy of the throwing class
is particularly improved. The relationship between
Table 3: Tree-class classification accuracy [%].
Cross-subject Cross-view
ST-GCN 92.38 94.68
M.T. Network
w/o class. layer
95.49 95.57
M.T. Network
w/ class. layer
96.61 97.05
(a) Shared (b) Throwing
(c) Kicking (d) Jumping
Figure 6: Visualization of the adjacency matrix at 70
epochs.
the arm and the leg is important for the throwing ac-
tion, and the relationship between the distant joints is
more important than that of other action. Therefore,
the recognition accuracy can be improved by consid-
ering the features between distant joints, not captured
by ST-GCN, by the proposed method.
Table 3 shows the results of classification accu-
racy when three classes are classified. The M.T. Net-
work w/o class. layer is a model that does not include
a multi-class classification layer. Classification accu-
racy is based on the inference result of the class with
the highest class probability obtained from each task.
The M.T. Network w/ class. layer model includes a
multi-class classification layer used to obtain the clas-
sification accuracy. The results show that the M.T.
Network w/ class. layer model improved classifica-
Acquisition of Optimal Connection Patterns for Skeleton-based Action Recognition with Graph Convolutional Networks
307

(a) Throwing
(b) Kicking
(c) Jumping
Figure 7: Visualization examples of connection patterns. Top: ST-GCN. Bottom: Proposed method.
tion accuracy by 4.23 points in cross-subject and 2.37
points in cross-view. This shows the effectiveness of
the proposed method.
4.4.3 Visualization of Adjacency Matrix
Figure 6 shows the adjacency matrixes of the shared
part and the throwing, kicking, and jumping action
classes at 70 epochs. Since the adjacency matrix of
the shared part is not updated, all nodes are connected
after learning, but only the top 60 with the largest
edge weights are drawn. Out of the two-way edges
connecting the nodes, the edges are drawn in the same
color as the node to which the edge with the higher
weight is connected. The resultant drawing is the con-
nection pattern when learning with cross-subject. The
pattern of the shared part (Figure 6(a)) shows that the
whole body is considered because the edges are con-
nected to the whole body. In the throwing class pat-
tern (Figure 6(b)), many of the subjects performed the
throwing action with their right hand, so the edges
are concentrated on the right arm and the right leg,
which is the pivot foot. Similarly, in the the kicking
class pattern (Figure 6(c)), the edge concentrates on
the right leg because many subjects kicked with their
right leg. In addition, the edges are concentrated on
the head when kicking. This is because many sub-
jects face the throwing point of the throw instead of
the object, but kicking is done by facing the object. In
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
308

the jump class pattern (Figure 6(d)), the whole body
moves, so the edges are concentrated at the center of
the body and also concentrated on the right arm.
Figure 7 shows an example of rendering the ac-
quired connection pattern on the dataset videos. Fig-
ure 7(a) shows that in the throwing class, the right
arm greatly moves and the edges are concentrated on
the right arm. Similarly, in the kicking class (Fig-
ure 7(b)), the right leg greatly moves and the edges
are concentrated on the right leg. Also, when throw-
ing, the participant is looking at the target, and when
kicking, the participant is looking at the kicking ob-
ject. In the jump class (Figure 7(c)), the arm greatly
moves with the movement of the whole body, so the
edges are concentrated on the center of the body and
the right arm. From these results, it can be seen that
the edges are concentrated on nodes with large move-
ments for each operation class, and connection pat-
terns specific to operation classes were successfully
acquired.
5 CONCLUSIONS
In this work, we proposed an action recognition
method considering connection patterns that are spe-
cific to action classes. In the proposed method, fea-
tures unique to each action class were acquired by
introducing multitask learning, and the optimal con-
nection for each action class was obtained by updat-
ing the adjacency matrix on the basis of the learning
weight matrix indicating the importance of edges dur-
ing learning. Evaluation experiments demonstrated
that the proposed method improved classification ac-
curacy in all action classes evaluated compared to ST-
GCN. Moreover, by visualizing the connection pat-
tern, we confirmed that patterns specific to each action
class were generated. Future work includes learning
methods that can obtain the optimal number of edges
for each action class.
REFERENCES
Defferrard, M., Bresson, X., and Vandergheynst, P. (2016).
Convolutional neural networks on graphs with fast lo-
calized spectral filtering. In Neural Information Pro-
cessing Systems.
Gilmer, J., Schoenholz, S. S., Riley, P. F., Vinyals, O., and
Dahl, G. E. (2017). Neural message passing for quan-
tum chemistry. In International Conference on Ma-
chine Learning.
Hongsong, W. and Liang, W. (2017). Modeling temporal
dynamics and spatial configurations of actions using
two-stream recurrent neural networks. In Computer
Vision and Pattern Recognition.
Joan, B., Wojciech, Z., Arthur, S., and Yann, L. (2014).
Spatial networks and locally connected networks on
graphs. In International Conference on Learning Rep-
resentations.
Kipf, T. N. and Welling, M. (2017). Semi-supervised clas-
sification with graph convolutional networks. In Inter-
national Conference on Learning Representations.
Li, C., Cui, Z., Zheng, W., Xu, C., Ji, R., and Yang,
J. (2018). Action-attending graphic neural network.
IEEE Transactions on Image Processing, 27(7):3657–
3670.
Limin, W., Yuanjun, X., Zhe, W., Yu, Q., Dahua, L., Xi-
aoou, T., and Luc, V. (2016). Temporal segment net-
works: Towards good practices for deep action recog-
nition. In European Conference on Computer Vision.
Liu, M., Liu, H., and Chen, C. (2017). Enhanced skeleton
visualization for view invariant human action recogni-
tion. Pattern Recogn, 68(C):346–362.
Min, L., Qiang, C., and Shuicheng, Y. (2014). Network in
network. In 2nd International Conference on Learn-
ing Representations.
Shahroudy, A., Liu, J., Ng, T.-T., and Wang, G. (2016). Ntu
rgb+d: A large scale dataset for 3d human activity
analysis. In Computer Vision and Pattern Recogni-
tion.
Sijie, Y., Yuanjun, X., and Dahua, L. (2018). Spatial tem-
poral graph convolutional networks for skeleton-based
action recognition. In Association for the Advance-
ment of Artificial Intelligence.
Simonyan, K. and Zisserman, A. (2014). Two-stream con-
volutional networks for action recognition in videos.
In Advances in Neural Information Processing Sys-
tems.
Tran, D., Bourdev, L., Fergus, R., Torresani, L., and Paluri,
M. (2015). Learning spatiotemporal features with 3d
convolutional networks. In International Conference
on Computer Vision.
Vemulapalli, R., Arrate, F., and Chellappa, R. (2014). Hu-
man action recognition by representing 3d skeletons
as points in a lie group. In Computer Vision and Pat-
tern Recognition.
Wu, Y. (2012). Mining actionlet ensemble for action recog-
nition with depth cameras. In Conference on Com-
puter Vision and Pattern Recognition.
Zhe, C., Tomas, S., Shih-En, W., and Yaser, S. (2017). Real-
time multi-person 2d pose estimation using part affin-
ity fields. In Conference on Computer Vision and Pat-
tern Recognition.
Acquisition of Optimal Connection Patterns for Skeleton-based Action Recognition with Graph Convolutional Networks
309
