
Efficient Computation of Base-pairing Probabilities in Multi-strand RNA
Folding
Ronny Lorenz
1 a
, Christoph Flamm
1 b
, Ivo L. Hofacker
1,2 c
and Peter F. Stadler
1,3,4,5,6 d
1
Institute for Theoretical Chemistry, University of Vienna, W
¨
ahringerstraße 17, A-1090 Wien, Austria
2
Bioinformatics and Computational Biology, Faculty of Computer Science, University of Vienna, W
¨
ahringerstraße 29,
A-1090 Wien, Austria
3
Bioinformatics Group, Department of Computer Science, Interdisciplinary Center for Bioinformatics,
and Competence Center for Scalable Data Services and Solutions Dresden/Leipzig, Universit
¨
at Leipzig H
¨
artelstraße 16-18,
D-04107 Leipzig, Germany
4
Max Planck Institute for Mathematics in the Sciences, Inselstraße 22, D-04103 Leipzig, Germany
5
Facultad de Ciencias, Universidad National de Colombia, Sede Bogot
´
a, Colombia
6
Santa Fe Institute, 1399 Hyde Park Road, Santa Fe NM 87501, U.S.A.
Keywords:
RNA Folding, Interacting RNAs, Partition Function, Outside Recursion, Cubic-time Algorithm.
Abstract:
RNA folding algorithms, including McCaskill’s partition function algorithm for computing base pairing prob-
abilities, can be extended to N ≥ 2 interacting strands by considering all permutations π of the N strands. For
each π, the inside dynamic programming recursion for connected structures needs to be extended by only a
single extra case corresponding to a base pair connecting exactly two connected substructures. This leaves
the cubic running time unchanged. A straightforward implementation of the corresponding outside recur-
sion, however results in a quartic algorithm. We show here how cubic running time asymptotically equal
to McCaskill’s partition function algorithm can be achieved by introducing linear-size auxiliary arrays. The
algorithm is implemented within the framework of the ViennaRNA package and conforms to the theoretical
performance bounds.
1 INTRODUCTION
RNA molecules not only form intramolecular base
pairs but also interact with other RNAs according to
the same rules to form hetero-polymeric complexes.
RNA-RNA interactions play an important role in eu-
karyotic gene regulation, see (Guil and Esteller, 2015)
for a recent review: The best known example is the
binding of microRNAs (miRNAs) to their mRNA tar-
gets in post-transcriptional gene silencing. Recently,
a plethora of different modes of action have been re-
ported. Both small interfering RNAs (siRNAs) and
long non-coding RNAs (lncRNAs) can regulate splic-
ing. The lncRNA TINCR binds several mRNAs to
control translation. MiRNAs as well as other ncRNAs
are involved in the regulation of miRNA biogenesis
from their primary precursors. LncRNAs may act as
a
https://orcid.org/0000-0002-2144-698X
b
https://orcid.org/0000-0001-5500-2415
c
https://orcid.org/0000-0001-7132-0800
d
https://orcid.org/0000-0002-5016-5191
“sponges” to bind and sequester miRNAs. A zoo of
small RNAs (sRNAs) has also been described in pro-
caryotes, many of which act a regulators of translation
by directly binding to their mRNA targets, reviewed
e.g. in (Dutta and Srivastava, 2018). Hetero-duplexes
between spliceosomal RNAs are crucial for the as-
sembly of the spliceosome, and many of the chemi-
cal modifications of ribosomal RNAs require the base
pairing between small nucleolar RNAs (snoRNAs)
and rRNAs. Recent advances in trancriptome-wide
experimental approaches have revealed an unexpected
extent of RNA-RNA interactions (Gong et al., 2018),
suggesting that – similar to the protein case – com-
plexes composed of more than two RNAs may also
play important roles. Such higher order complexes
have already be considered extensively in synthetic
biology (Isaacs et al., 2006; Chappell et al., 2015).
RNA structures are efficiently modeled by their
secondary structures, i.e., at the level of discrete
base pairs. Together with a set of empirically
well-supported energy parameters for the stacking
Lorenz, R., Flamm, C., Hofacker, I. and Stadler, P.
Efficient Computation of Base-pairing Probabilities in Multi-strand RNA Folding.
DOI: 10.5220/0008916600230031
In Proceedings of the 13th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2020) - Volume 3: BIOINFORMATICS, pages 23-31
ISBN: 978-989-758-398-8; ISSN: 2184-4305
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
23

of base pairs and the destabilizing effects of un-
paired “loops” (Turner and Mathews, 2010), effi-
cient dynamic programming algorithms are avail-
able to compute ground state structures (Zuker and
Stiegler, 1981) as well as the partition function of the
equilibrium ensemble of secondary structures (Mc-
Caskill, 1990). Most routine applications consider
only pseudoknot-free structures, i.e., structures with-
out crossing base pairs (i, j) and (k,l) with i < k <
j < l, see (Reidys, 2011). The same physical prin-
ciples govern the interaction of two or more RNA
molecules, and thus similar combinatorial models are
applicable. The interaction of two or more RNA
strands naturally leads to a class of structures that
includes pseudoknot-like structures and thus is dif-
ficult to handle computationally. An example is the
RIP model of Alkan et al. (2006), for which the com-
putation of base-pairing probabilities is still feasi-
ble for pairs of RNAs (Chitsaz et al., 2009; Huang
et al., 2009). A combinatorial model that captures the
multi-strand case was introduced by Mneimneh and
Ahmed (2015). A greedy, helix-based approach that
allows essentially unrestricted matchings is described
by Bindewald et al. (2011). The combination of local
structures and interactions can be formalized also as
a constrained maximum weight clique problem (Leg-
endre et al., 2019). An alternative class of approaches
restricts the interaction of a pair of RNAs to a single
sequence region in each partner, making it possible to
decompose the energy of interaction in contributions
for unfolding the interaction sites and their hybridiza-
tion (Busch et al., 2008; M
¨
uckstein et al., 2008; Bern-
hart et al., 2011).
Here we are concerned with a simplified model
that excludes such pseudoknot-like features (and thus
also some important types of interactions including
kissing-hairpins). We stipulate that the heterpoly-
meric complex can be understood as secondary struc-
ture formed by a conceptual concatenation of the in-
teracting strands. The corresponding folding prob-
lems thus remains equivalent to the case of a single
RNA molecule (Zuker and Stiegler, 1981; McCaskill,
1990). For two strands, this model has been analyzed
in detail by Dimitrov and Zuker (2004), Andronescu
et al. (2005), and Bernhart et al. (2006). Even for
multiple (N > 2) strands, the folding problem remains
very similar to the single strand folding problem in
this setting. It suffices to assign different energy con-
tributions to substructures (“loops”) that contain one
or more breakpoints between strands (Dirks et al.,
2007). An implementation for the general case is
available in NUPACK (Zadeh et al., 2011). Kinetic sim-
ulations of multi-strand cofolding have been studied
by Schaeffer et al. (2015).
It is important to note that binding energies be-
tween strands in heteropolymeric structures are in-
trinsically concentration dependent because the num-
ber of particles changes when polymeric structures
are formed (Dimitrov and Zuker, 2004). In parti-
tion function computations it is therefore important to
treat complexes separately that are composed of dif-
ferent compositions of strands. RNAcofold (Bernhart
et al., 2006) handles this issue as a post-processing
step: first a partition function Z
AB
over all confor-
mation of two strands is computed, from which the
contribution Z
A
Z
B
of the separated monomers is sub-
tracted. This approach quickly becomes tedious for
higher-order interactions, however. In NUPACK, Dirks
et al. (2007) therefore introduced a different strategy
in which partition functions are computed that sum
only over conformations that are connected. This
does not significantly change the recursions of Mc-
Caskill’s algorithm for a single RNA molecule (Mc-
Caskill, 1990). This approach reduced the complica-
tions arising from disconnected structures but in re-
turn complicated the outside recursion, i.e., the com-
putations of base pairing probabilities.
The computation of base-pairing probabilities for
multiple interacting RNAs conceptually follows Mc-
Caskill’s outside recursions (McCaskill, 1990). The
key issue is that in order to compute the probability
of a base pair (k,l) one needs to explicitly handle
the case that the focal base pair (k,l) is located in a
loop L with closing pair (i, j) that contains exactly
one concatenation point (“nick”) between strands in
the loop L . As a consequence, the structure on the se-
quence interval [i, j] becomes disconnected upon re-
moval of the pair (i, j). While conceptually simple,
the practical difficulties arise from the fact that all par-
tition function variables computed in the inside recur-
sions only cover connected substructures, and hence
the cases with a nick in the exterior loop need to be
handled separately. It is the purpose of this contribu-
tion to show how this can be achieved efficiently.
2 INSIDE RECURSION
Consider N ≥ 1 RNA strands with a total length n.
We are interested here in the ensemble of connected
structures that are crossing free in at least one permu-
tation of the strands, that is, if (i, j) is a base pair, then
(k, l) with i < k < j is a base-pair only if i < l < j.
As shown in (Dirks et al., 2007), the sets of crossing
free structures are invariant under circular permuta-
tions of the strands, while the sets of connected struc-
tures generated from other permutations of strands π
are disjoint. As an immediate consequence, it is pos-
BIOINFORMATICS 2020 - 11th International Conference on Bioinformatics Models, Methods and Algorithms
24
sible, therefore, to compute the base pairing proba-
bilities p
k,l
in a given complex of N RNA strands
as (weighted) sums of the base pairing probabilities
p
k,l
[π] of all permutations π that fix the first strand
(Dirks et al., 2007). Each permutation π contributes
with a weight proportional to its partition function
Q[π], i.e., p
k,l
=
∑
π
w(π)p
k,l
[π] with w(π) = Q[π]/Q,
where Q :=
∑
π
Q[π] is the total partition function of
the complex. It thus suffices to investigate the inside
and outside recursions for a fixed permutation π. We
can therefore assume that the strands are indexed by
s = 1, ... , N and the nucleotides are numbered con-
secutively by i = 1,... n.
The standard energy model for RNA folding dis-
tinguishes three types of “loops”: hairpin loops,
which contain no further interior base pairs, interior
loops, which contain exactly one interior base pair,
and multi-branch loops (multi-loops for short), con-
taining two more consecutive pairs. Stacked base
pairs, the main stabilizing contribution of RNA struc-
tures, are treated as special case of interior loops.
While energy contributions for hairpin and interior
loops are tabulated as function of sequence and length
of the unpaired stretches, a linear approximation is
used for multiloops. This both reduced the number of
parameters to a manageable size and ensures that the
recursions require O(n
3
) time and O (n
2
) space.
As discussed in detail in (Dirks et al., 2007),
the main difference between McCaskill’s original
approach (McCaskill, 1990) to computing partition
functions and the generalization to multi-strand prob-
lems is the interpretation of the variables: instead of
computing partitions over all structures, the computa-
tions are restricted to connected structures. Interest-
ingly, this introduces only a small modification to the
standard recursions.
Denote by Q
i j
the partition function over all
crossing-free connected structures on the interval
[i, j]. Analogously, Q
B
i j
denotes the partition function
over all crossing-free connected structures on the in-
terval [i, j] that are enclosed by the base-pair (i, j).
For hairpin loops, which contain no interior base
pairs, i and j thus must be located on the same or con-
secutive strands. Interior loops have a single enclosed
base pair (p,q) with i < p < q < j. Multi-branch
loops are handled in the standard RNA folding model
based on a linear approximation of the folding energy
that makes it possible to decompose every multi-loop
into its closing base pairs (i, j ), a part Q
M
i+1,u
con-
taining at least one stem, and a part Q
1
u+1, j−1
com-
prising exactly one stem, see (McCaskill, 1990) for
details. If the structure on [i, j] to which the closing
pair is added is already connected, the recursions are
the same as in McCaskill’s original algorithm. In the
Q
i+1,
Q
+1,j−1ω(s) ω(s)
(s)ω (s+1)α
i
j
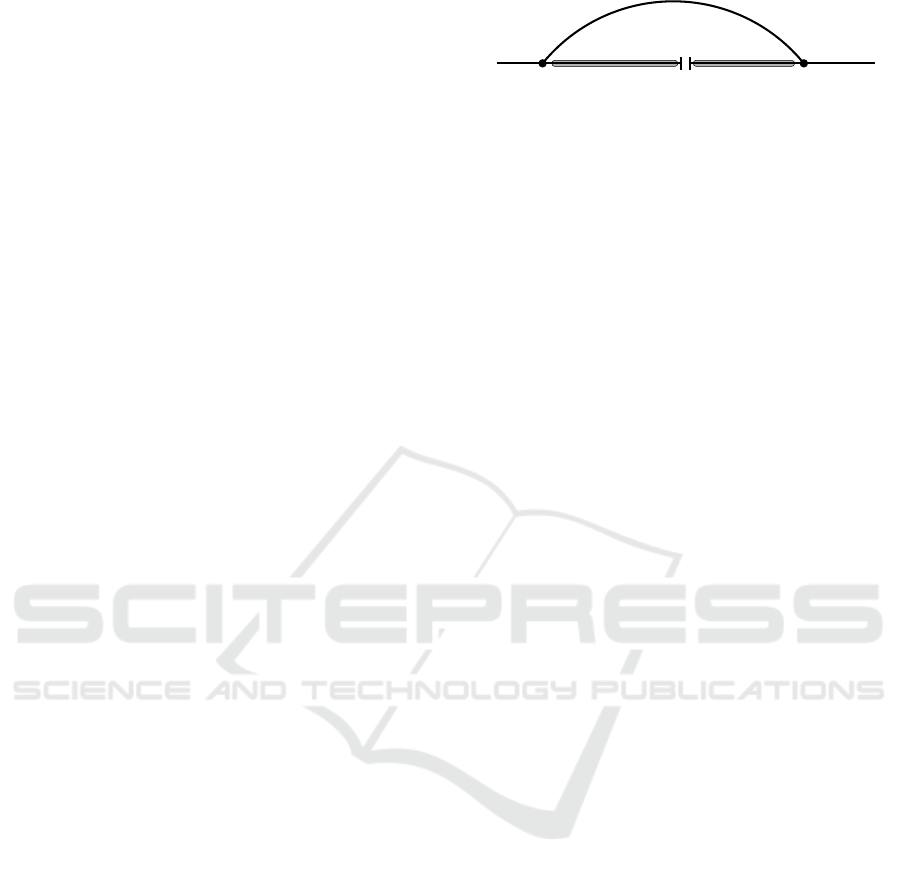
Figure 1: Nicked loop case in the inside recursion. The
base pair (i, j), as usual represented by an arc, connects
two connected components separated by a single nick be-
tween ω(s) and α(s + 1) = ω(s) + 1. Since nicked loops
are exterior, connected secondary structures on the intervals
[i + 1,ω(s)] and [α(s + 1), j −1] contribute independently.
Note that the nick can also be adjacent to i or j, in which
case one of the two intervals is empty, and thus formally
contributes as factor of 1 to the partition function.
multi-strand case, however, connected structures also
arise by combining exactly two disjoint connected
components by means of the closing pair (i, j). This
gives rise to an additional term in the decomposition
of Q
B
i j
(Dirks et al., 2007).
From an energetic point of view, the loop closed
by (i, j) is an external loop. Using ω(s) to denote 3’-
most nucleotide position of strand s, the contribution
of “nicked loops” is
Q
N
i j
=
∑
s:i≤ω(s)≤j
e
−ε
i j
/RT
Q
i+1,ω(s)
Q
ω(s)+1, j−1
(1)
with the additional constraint that either i and i + 1 as
well as j −1 and j must be on the same strand, or the
nick is adjacent to the base pair, in which case either
i = ω(s) and j −1 and j are on the same strand, or j −
1 = ω(s) and i and i + 1 are on the same strand. The
energy term ε
i j
contains only the so-called dangling
end terms (Turner and Mathews, 2010). A graphical
representation is given in Fig. 1.
3 OUTSIDE RECURSION
Complementary to the structures on [k,l] enclosed by
a pair (k,l), McCaskill’s approach considers the en-
semble of partial secondary structure on [1,k] ∪· [l,n]
that contain the base pair (k,l). Such “outside en-
sembles” can always be constructed as complements
of “inside ensembles” (H
¨
oner zu Siederdissen et al.,
2015). For fixed π, we consider here the partition
function
b
Q
k,l
[π] over all connected partial secondary
structures outside of the base pair (k, l). Clearly a
secondary structure containing (k, l) is connected if
and only if both the substructures inside and out-
side of (k,l) are connected. Thus
b
Q
k,l
[π]Q
B
k,l
[π] is
the partition function over all connected structures
that contain the pair (k, l) and the base pairing prob-
abilities for fixed π can be computed as p
k,l
[π] =
b
Q
k,l
[π]Q
B
k,l
[π]/Q[π], where Q[π] = Q
1,n
[π] is the parti-
tion function over all connected secondary structures.
Efficient Computation of Base-pairing Probabilities in Multi-strand RNA Folding
25

The base pairing probability p
k,l
in a given complex
of RNAs is therefore given by
p
k,l
=
∑
π
w(π)p
k,l
[π] =
1
Q
∑
π
b
Q
k,l
[π]Q
B
k,l
[π]. (2)
As outlined in (Dirks et al., 2007), these values can
then be used to obtain further derived quantities such
as expected number of base pairs connecting any two
strands. Equ.(2) implies that it suffices to compute the
p
k,l
[π] separately for all π. From here on, we therefore
suppress the reference to the fixed permutation π.
Following McCaskill (1990),
b
Q
k,l
can be com-
puted from three mutually exclusive subsets of struc-
tures: (1) the contribution
¯
Q
k,l
of structures in which
(k, l) is not enclosed by any other base pair and (2) the
contribution of structures in which (k,l) is enclosed
by another base pairs (i, j). The second case can
further be subdivided into two disjoint contribution
˘
Q
k,l
+
¨
Q
k,l
depending on whether the loop enclosed
by (i, j) contains (2a) no nick or (2b) exactly one
nick. If there were two or more nicks, the structure
would not be connected. The recursions for
¯
Q
k,l
and
˘
Q
k,l
are identical to the ones developed by McCaskill
(1990). They have been presented repeatedly in the
literature, we therefore do not recall them here. The
na
¨
ıve implementation of the recursions for
¯
Q
k,l
and
˘
Q
k,l
requires O(n
4
) time. With the help of auxiliary
arrays of size O(n), however, they can be modified
to allow evaluation in cubic time (McCaskill, 1990;
Lorenz et al., 2011).
Here, we study the additional multi-strand case
¨
Q
k,l
in detail. The notation below is consistent with
implementation in the ViennaRNA package. Follow-
ing Lorenz et al. (2011) we also allow terms of the
form Q
i,i−1
= 1, denoting empty intervals. This con-
siderably simplifies the notation since boundary cases
do not need to be treated explicitly. For each strand
s we define α(s) and ω(s) to denote its 5’-most and
3’-most nucleotide position with respect to the fixed
order to the strands. To this end, we write σ(i) for
the strand that contains position i, i.e., σ(i) = s iff
α(s) ≤ i ≤ ω(s). The same-strand indicator function
is given by ξ
i
= 1 if σ(i) = σ(i + 1) and ξ
i
= 0 other-
wise. We write
¯
ξ
i
:= 1 −ξ
i
.
In order to compute
¨
Q
k,l
we separately consider
the case that the single nick in the loop containing
(k, l) is located 5’ (left) of (k,l), i.e., between i and k,
and the case that the nick is found 3’ (right) of (k,l),
i.e., between l and j. Clearly, these cases are mutually
exclusive.
Hence we can write
¨
Q
k,l
=
¨
Q
5
0
k,l
+
¨
Q
3
0
k,l
(3)
with
¨
Q
5
0
k,l
=
∑
1≤i<k
l< j≤n
b
Q
i, j
Q
l+1, j−1
× (4)
∑
s|i≤ω(s)<k
Q
i+1,ω(s)
Q
ω(s)+1,k−1
¨
Q
3
0
k,l
=
∑
1≤i<k
l< j≤n
b
Q
i, j
Q
i+1,k−1
× (5)
∑
s|l<α(s)≤j
Q
l+1,α(s)−1
Q
α(s), j−1
In this form, the computation of a single entry
¨
Q
k,l
requires O (n
2
N) operations for N strands with a to-
tal length n, leading to an overall running time of
O(n
4
N). This time complexity is much worse than
cubic running time of all other components of the par-
tition function algorithm. Since the pairing probabil-
ities need to be computed for all (N −1)! non-cyclic
permutations of the strands, the additional factor nN
is a serious practical burden. Our goal is therefore to
reduce the time complexity by rearranging the recur-
sions for
¨
Q
5
0
k,l
and
¨
Q
3
0
k,l
at the expense of introducing
additional arrays to store intermediate results.
4 COMPUTING
¨
Q
k,l
IN CUBIC
TIME
Let us assume that position l is fixed and we com-
pute the values of
¨
Q
k,l
consecutively for all k. The
basic idea is then to pre-compute and store contribu-
tions that depend only on l and are required for all k.
Let us first consider
¨
Q
5
0
k,l
, i.e., Equ.(4). Fixing the sec-
ond index k only affects the number of choices for i
and s. Moreover, a particular strand s already deter-
mines the number of choices for i, since i ≤ω(s). We
may, therefore, pre-compute parts of the outside con-
tribution for each s with ω(s) < l and all possible i,
and j. We store these values in auxiliary array
Y
5
0
s
= ξ
l
∑
j>l
ξ
j−1
Q
l+1, j−1
× (6)
b
Q
ω(s), j
+
∑
i<ω(s)
ξ
i
·
b
Q
i, j
·Q
i+1,ω(s)
.
This array has size O (N) and each entry is computed
on O(n
2
) time, hence the total effort is O (n
2
N). Fig-
ure 2 gives a graphical representation of the contri-
BIOINFORMATICS 2020 - 11th International Conference on Bioinformatics Models, Methods and Algorithms
26

|
|
|
|
Figure 2: Auxiliary arrays for RNAmultifold base pair probabilities. The first line consists of a schematic representation
of all contributions that need to be considered when a base pair (k, l) is enclosed by another pair (i, j) and effectively forms a
loop with a strand-change (nicked loop). We explicitly distinguish the two cases
¨
Q
5
0
k,l
and
¨
Q
3
0
k,l
, where the nick appears to the
left (5
0
) and to the right (3
0
) of the pair (k,l), respectively. To efficiently compute both contributions, we introduce the two
auxiliary arrays Y
5
0
s,l
and Y
3
00
s,k
(2nd line) to store and re-use pre-computed contributions that are independent of the choice of
i and j. This reduces the effort to compute
¨
Q
5
0
k,l
and
¨
Q
3
0
k,l
to a sum over the strands s. Still, for different l and k, parts of the
contributions stored in these two auxiliary arrays are computed repeatedly. Hence, to keep the computational effort as small
as possible, we add two further arrays Y
5
00
s, j
and Y
3
0
s,i
(3rd line) to store these parts for reuse. Finally, both multi-strand cases can
be evaluated for all possible pairs (k,l) in O(n
2
N) total time.
butions captured by Y
5
0
s
. We can now re-write Equa-
tion (4) as
¨
Q
5
0
k,l
=
¯
ξ
k−1
Y
5
0
σ(k−1)
+ ξ
k−1
∑
s|ω(s)<k
Q
ω(s)+1,k−1
Y
5
0
s
.
(7)
Each of the O(n
2
) is now computed in O(nN) time,
hence we have already reduced the complexity by a
factor of n. A further reduction is obtained by ob-
serving that parts required to compute Y
5
0
s
for l can be
re-used when Y
5
0
s
is computed for l −1. This is due
to the fact that the major difference between consec-
utive entries is only a single extra value of j. On the
expense of an additional O (nN) memory and explic-
itly denoting k, we re-write (6) as
Y
5
0
s,l
= ξ
l
Y
5
00
s,l+1
+
∑
j>l+1
Q
l+1, j−1
·Y
5
00
s, j
(8)
Y
5
00
s, j
= ξ
j−1
b
Q
ω(s), j
+
∑
i<ω(s)
ξ
i
b
Q
i, j
·Q
i+1,ω(s)
.(9)
Since Y
5
00
s, j
is independent of l and k, we can even re-
use the corresponding stored contributions throughout
all computations for any pair (k,l). However, care has
to be taken to properly interleave the computations
of Y
5
00
s, j
into the part that loops over variable l. More
precisely, the required contributions
b
Q
i, j
only become
available for l < j. Still, the time complexity to pre-
fill all Y
5
00
s, j
is O(n
2
N). Hence, the time complexity for
(8) reduces to O(n), and the overall time complexity
to compute (7) becomes O(n
2
N).
Let us now focus on the second case and assume
that the single nick is located 3
0
of base pair (k,l).
Here, we can apply the same re-arrangement and pre-
computation as above. First, we observe that fixing a
value of k only affects the possible choices of i. But
this time, the contributions to the left of the nick do
not contain a re-usable factor independent of k. This
is due to the fact that (i) we always require the full
contribution of Q
i+1,k−1
and (ii) the strand-changes
we need to consider only depend on the current value
of l. There are contributions on the right, however,
that can be pre-computed. Consider the O(nN) terms
Y
3
0
s,i
= ξ
i
b
Q
i,α(s)
+
∑
j>α(s)
ξ
j−1
b
Q
i, j
Q
α(s), j−1
(10)
These terms are independent of both k and l. Hence
they need to be computed only once and can then be
re-used for any pair (k, l). Using equ.(10), equ.(5) can
be rewritten as
¨
Q
3
0
k,l
= ξ
k−1
∑
i<k
ξ
i
Q
i+1,k−1
× (11)
¯
ξ
l
Y
3
0
σ(l+1),i
+ ξ
l
∑
s|α(s)>l
Q
l+1,α(s)−1
Y
3
0
s,i
,
which can be evaluated in total time O (n
3
N) for all
k and l at the expense of storing the nN auxiliary
values Y
3
0
s,i
. Still, the effort asymptotically exceeds
McCaskill’s cubic-time algorithm by a factor O(N).
To further reduce the computational time, we ob-
serve that the order of summation in equ.(11) can be
changed in such a way that the inner sum becomes
independent of l. We can therefore pre-compute
Y
3
00
s,k
= ξ
k−1
∑
i<k
ξ
i
Q
i+1,k−1
Y
3
0
s,i
(12)
for all possible k and any strand s in total time O(n
2
N)
and store it with additional memory requirements of
O(nN). Taken together, we have now removed the
Efficient Computation of Base-pairing Probabilities in Multi-strand RNA Folding
27

dependence of k from l, and can, therefore, re-use (12)
for all pairs (k, l). Similar to equ. (7), equ. (5) can now
be rewritten as
¨
Q
3
0
k,l
=
¯
ξ
l
Y
3
00
σ(l+1),k
+ ξ
l
∑
s|α(s)>l+1
Q
l+1,α(s)−1
Y
3
00
s,k
. (13)
and be evaluated in O(n
2
N) time provided that the
O(nN) values of Y
3
00
s,k
are stored. Again, due to the de-
pendence of Y
3
0
s,i
on
b
Q
i, j
, proper interleaving into the
recursion is necessary. But this can be easily achieved
by filling Y
3
0
σ(l+1),i
for all i if ξ
l
= 1 and subsequently
re-compute Y
3
00
s,k
. Figure 2 gives a graphical represen-
tation of the class of structures contributing to Y
3
00
s,k
.
The additional effort to compute the auxiliary ar-
rays thus matches the added effort for the inside re-
cursion of the multi-strand problem, namely O(n
2
N)
time, though with extra O (nN) space. In any rea-
sonable application scenario, the number of strands
is much smaller than their total length, i.e., N n.
Under this assumption, the additional resources re-
quired for the multi-strand version of McCaskill’s
partition function algorithms therefore are asymptoti-
cally negligible compared to the cubic running time
and quadratic memory consumption of the single-
strand problem.
5 IMPLEMENTATION AND
BENCHMARKING
The inside and outside recursions for a fixed permu-
tation π of strands has been implemented as part of
ViennaRNA package (Hofacker et al., 1994; Lorenz
et al., 2011). This initial version of RNAmultifold,
which is available as part of release 2.5.0alpha,
is primarily intended for testing and benchmark-
ing. Although functional, it does not yet provide
all features of partition function algortihms. For in-
stance, no corresponding minimum energy folding al-
gorithm is available at this point. Future versions
of RNAmultifold will feature further optimizations
making use of the fact that for N > 2 strands some
parts of the arrays for different permutations are the
same and thus need not be recomputed.
A generic difficulty in practical implementations
of partition function algorithms are overflow and un-
derflow errors due to the exponential terms. The
ViennaRNA package therefore does not directly com-
pute the partition functions as outlined above. In-
stead, scaled partition functions of the form z
i j
:=
Z
i j
/ζ
j−i+1
are computed. The scaling constant ζ is an
a priori estimate of
n
√
Z, i.e., the average contribution
of a single nucleotide to the overall partition func-
tion (Hofacker et al., 1994). It can be estimated by
ζ = exp(−E
∗
/nRT ), where E
∗
is the expected ground
state energy. As described by Hofacker et al. (1994), ζ
can be estimated for connected structures with a sim-
ple regression model. This scaling keeps the values
of Z
i j
and its restricted versions sufficiently close to
unity to avoid overflow and underflow errors for se-
quence lengths of at least n ≤ 10
4
. Since the effect of
the nicks on the ground state energy is bounded above
by the sum of the energies of the loops that contain the
nicks, ζ can be estimated with sufficient accuracy to
ensure numerical stability from the ground state en-
ergy of the concatenation of the strands, i.e., by ig-
noring the nicks.
In order to benchmark the performance of our im-
plementation we compare running time and mem-
ory consumption of the preliminary version of
RNAmultifold with RNAfold (Lorenz et al., 2011),
RNAcofold (Bernhart et al., 2006), and NUPACK
(Zadeh et al., 2011). As input we generated 10 ran-
dom sequences for each length and subdivided these
into a different number of strands. This choice of
benchmark data is designed to minimize sequence-
specific variations between instances with different
numbers of strands. The performance measurements
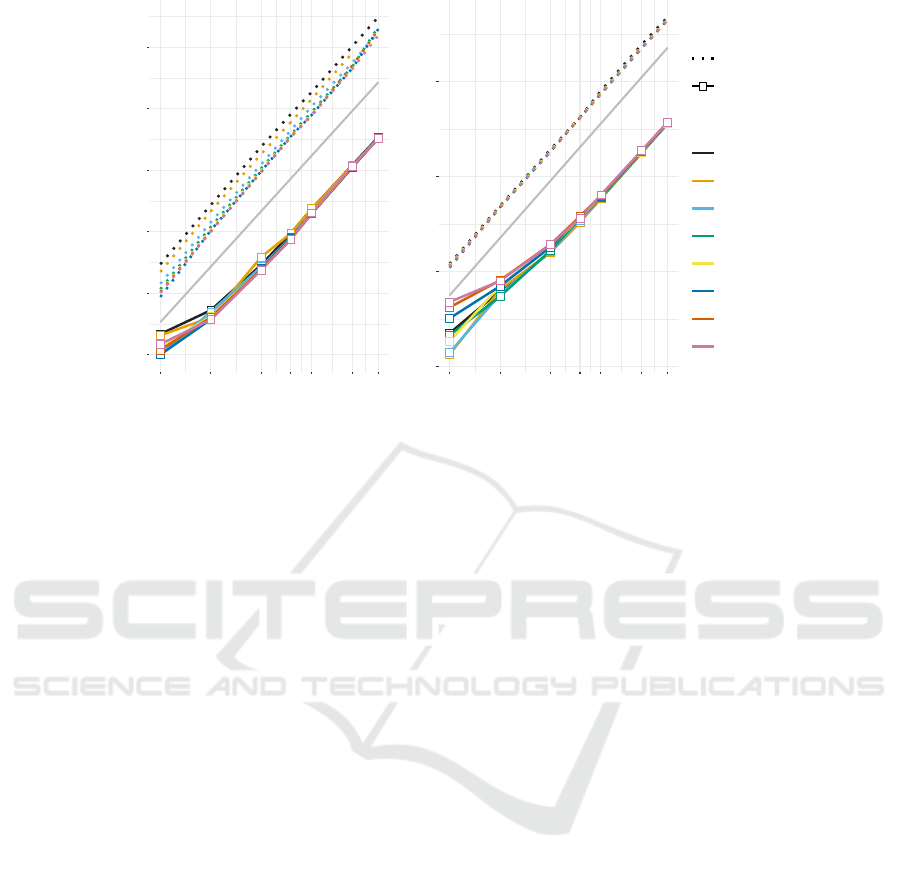
for RNAmultifold and NUPACK are summarized in
Fig. ??. We also compared RNAmultifold with the
previously available components of the ViennaRNA
package.
RNAfold, and RNAcofold use identical energy
parameters. As expected, for N = 1 the results
of RNAmultifold and RNAfold coincide within the
expected numerical inaccuracies; for N = 2 we
obtained the same output for RNAmultifold and
RNAcofold. We observed no significant differences
in memory consumption. RNAfold is 10-15% faster
than RNAmultifold. In contrast, we found that
the outside recursion of RNAmultifold is approxi-
mately twice as fast as the version implemented in
RNAcofold. Because of the small differences be-
tween RNAmultifold and RNAfold or RNAcofold,
resp., the latter are not shown separately in Fig. ??.
As expected from the theoretical considerations
above, we find that both memory consumption and
running time of RNAmultifold becomes independent
of N for large n. The number of strands plays a not-
icable role only when the average length of individ-
ual strands is smaller than about 20 nt. We found,
furthermore, that RNAmultifold consistently outper-
forms NUPACK 3.2.2. For large sequences, the inside
recursion of RNAmultifold is about 35×and the out-
side recursion is about 50-65× faster. The memory
consumption is about 7× lower.
BIOINFORMATICS 2020 - 11th International Conference on Bioinformatics Models, Methods and Algorithms
28
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
10
−2
10
−1
10
0
10
1
10
2
10
3
150 300 600 9001200 2100 3000
Running Time [s]
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
10
2
10
3
10
4
10
5
150 300 600 9001200 2100 3000
Memory Consumption [kB]
Tool
●
NuPack
RNAmultifold
# Strands
●
●
●
●
●
●
●
●
1
2
5
10
15
20
25
30
Total sequence length [nt]
Figure 3: Comparison of the performance measures for NUPACK (version 3.2.2) and RNAmultifold for different total
sequence length n and different number N of strands. Each data point is the average over 10 random instances. The thin lines
indicate O(n
3
) and O(n
2
) for running time and memory consumption, respectively.
RNAmultifold uses the full framework for han-
dling constraints in the ViennaRNA package and
thus supports user-defined hard and soft constraints
(Lorenz et al., 2016), such as experimental probing
data or forbidden base pairs. It also handles intra-
strand G-quadruplexes in the same way as in case of
a single strand (Lorenz et al., 2013).
6 FUTURE WORK
We have shown here that the base pairing probabilities
in the multi-strand RNA folding problem can be com-
puted in O(n
3
) time and O (n
2
) space for a fixed per-
mutation π of the strands. We provide an implementa-
tion within the framework of the ViennaRNA package
that has negligible overhead compared to RNAfold
and RNAcofold. The performance gain compared to
NUPACK, at present the only competing software, is
nearly an order of magnitude in memory and about
a factor of 50 in running time.
A full-fledged implementation of multi-strand
folding will also include a minimum free energy rou-
tine as well as a facility to enumerate suboptimal
structures (Wuchty et al., 1999). Here, one has to take
special care to properly treat the energy penalties as-
sociated with structures with symmetries that appear
in particular in homo-dimers and -multimers (Ho-
facker et al., 2012). Stochastic backtracing makes it
possible to sample individual structures with Boltz-
mann probabilities (Tacker et al., 1996; Ding et al.,
2004). As a straightforward extension of the parti-
tion function algorithms, this feature will also become
available with the next release of RNAmultifold. We
also plan to implement the extension of RNA folding
grammar necessary to handle multiple ligand bind-
ing sites (Forties and Bundschuh, 2010) again mak-
ing use of the constraints framework of Lorenz et al.
(2016). A closer inspection of the folding recursions
for different permutations π and π
0
shows that parts
of the arrays are identical. In a forthcoming version
of RNAmultifold we will utilize this fact to further
reduce the computational efforts.
The concentration dependence of the different
multi-strand complexes under equilibrium conditions
are of practical importance in particular for design
tasks. Since the partition functions computed here
refer to connected structures, i.e., complexes with a
given composition, it is easy to compute the equi-
librium constants for the association/dissociation of
complexes: For reactions of the form A
1
A
2
...A
k
+
B
1
B
2
...B
l
A
1
A
2
...A
k
B
1
B
2
...B
l
we have equilibrium
constants K = Z
A
1
A
2
...A
k
B
1
B
2
...B
l
/Z
A
1
A
2
...A
k
Z
B
1
B
2
...B
l
.
As described previously in the literature (Dimitrov
and Zuker, 2004; Bernhart et al., 2006; Dirks et al.,
2007), the law of mass action together with mass con-
servation leads to a system of non-linear equations for
the concentrations that, by detailed balance, is guar-
anteed to have a unique positive solution. This makes
it possible to compute the equilibrium concentrations
given only the total concentrations of the RNA strands
as input.
Efficient Computation of Base-pairing Probabilities in Multi-strand RNA Folding
29

For the complete analysis, RNAmultifold will be
extended to automatically enumerate all permutations
π and all complexes consisting of subsets of the in-
put strands up to a maximum interaction order. It will
then compute equilibrium constants and solve the re-
sulting non-linear system of equations to obtain con-
centrations for each complex. To reduce the combi-
natorial explosion of permutations and compositions,
users will be able to supply a list of complexes that are
of interest. An automatic selection of the maximal in-
teraction order may be achieved by starting with the
smallest complexes, increasing the maximum interac-
tion order step by step, until the computed equilibrium
concentrations do not change significantly anymore.
AVAILABILITY
RNAmultifold can be downloaded as
part of ViennaRNA Package 2.5.0a1 from
www.tbi.univie.ac.at/RNA.
ACKNOWLEDGMENTS
This work was supported in part by the German Fed-
eral Ministry of Education and Research (BMBF,
project no. 031A538A, de.NBI-RBC, to PFS and
project no. 031L0164C, RNAProNet, to PFS), and the
Austrian science fund FWF (project no. I 2874 “Pre-
diction of RNA-RNA interactions”, project no. F 43
“RNA regulation of the transcriptome”, to ILH).
REFERENCES
Alkan, C., Karakoc¸, E., Nadeau, J. H., Sahinalp, S. C.,
and Zhang, K. Z. (2006). Rna-rna interaction predic-
tion and antisense rna target search. J. Comput. Biol.,
13:267–282.
Andronescu, M., Zhang, Z. C., and Condon, A. (2005).
Secondary structure prediction of interacting RNA
molecules. J. Mol. Biol., 345:987–1001.
Bernhart, S. H., M
¨
uckstein, U., and Hofacker, I. L. (2011).
RNA accessibility in cubic time. Algorithms Mol
Biol., 6:3.
Bernhart, S. H., Tafer, H., M
¨
uckstein, U., Flamm, C.,
Stadler, P. F., and Hofacker, I. L. (2006). Partition
function and base pairing probabilities of RNA het-
erodimers. Algorithms Mol. Biol., 1:3.
Bindewald, E., Afonin, K., Jaeger, L., and Shapiro, B. A.
(2011). Multistrand rna secondary structure prediction
and nanostructure design including pseudoknots. ACS
Nano, 5:9542–9551.
Busch, A., Richter, A., and Backofen, R. (2008). IntaRNA:
efficient prediction of bacterial sRNA targets incorpo-
rating target site accessibility and seed regions. Bioin-
formatics, 24:2849–2856.
Chappell, J., Watters, K. E., Takahashi, M. K., and Lucks,
J. B. (2015). A renaissance in RNA synthetic biology:
new mechanisms, applications and tools for the future.
Curr. Op. Chem. Biol., 28:47–56.
Chitsaz, H., Salari, R., Sahinalp, S. C., and Backofen, R.
(2009). A partition function algorithm for interacting
nucleic acid strands. Bioinformatics, 25:i365–i373.
Dimitrov, R. A. and Zuker, M. (2004). Prediction of hy-
bridization and melting for double-stranded nucleic
acids. Biophys. J., 87:215–226.
Ding, Y., Chan, C. Y., and Lawrence, C. E. (2004). Sfold
web server for statistical folding and rational design
of nucleic acids. Nucleic Acids Res, 32:W135–W141.
Dirks, R. M., Bois, J. S., Schaeffer, J. M., Winfree, E., and
Pierce, N. A. (2007). Thermodynamic analysis of in-
teracting nucleic acid strands. SIAM Rev., 49:65–88.
Dutta, T. and Srivastava, S. (2018). Small RNA-mediated
regulation in bacteria: A growing palette of diverse
mechanisms. Gene, 656:60–72.
Forties, R. A. and Bundschuh, R. (2010). Modeling the in-
terplay of single stranded binding proteins and nucleic
acid secondary structure. Bioinformatics, 26:61–67.
Gong, J., Ju, Y., Shao, D., and Zhang, Q. C. (2018). Ad-
vances and challenges towards the study of RNA-
RNA interactions in a transcriptome-wide scale.
Quant Biol, 6:239–252.
Guil, S. and Esteller, M. (2015). RNA-RNA interactions
in gene regulation: the coding and noncoding players.
Trends Biochem Sci., 40:248–256.
Hofacker, I. L., Fontana, W., Stadler, P. F., Bonhoeffer,
L. S., Tacker, M., and Schuster, P. (1994). Fast
folding and comparison of RNA secondary structures.
Monatsh. Chem., 125:167–188.
Hofacker, I. L., Reidys, C. M., and Stadler, P. F. (2012).
Symmetric circular matchings and RNA folding.
Discr. Math., 312:100–112.
H
¨
oner zu Siederdissen, C., Prohaska, S. J., and Stadler, P. F.
(2015). Algebraic dynamic programming over general
data structures. BMC Bioinformatics, 16:19:S2.
Huang, F. W. D., Qin, J., Reidys, C. M., and Stadler, P. F.
(2009). Partition function and base pairing probabil-
ities for RNA-RNA interaction prediction. Bioinfor-
matics, 25:2646–2654.
Isaacs, F. J., Dwyer, D. J., and Collins, J. J. (2006). RNA
synthetic biology. Nat Biotechnol., 24:545–554.
Legendre, A., Angel, E., and Tahi, F. (2019). RCPred: RNA
complex prediction as a constrained maximum weight
clique problem. BMC Bioinformatics, 20:128.
Lorenz, R., Bernhart, S. H., H
¨
oner zu Siederdissen, C.,
Tafer, H., Flamm, C., Stadler, P. F., and Hofacker, I. L.
(2011). ViennaRNA Package 2.0. Alg. Mol. Biol.,
6:26.
Lorenz, R., Bernhart, S. H., Qin, J., H
¨
oner zu Siederdis-
sen, C., Tanzer, A., Amman, F., Hofacker, I. L., and
Stadler, P. F. (2013). 2D meets 4G: G-quadruplexes
BIOINFORMATICS 2020 - 11th International Conference on Bioinformatics Models, Methods and Algorithms
30

in RNA secondary structure prediction. IEEE Trans.
Comp. Biol. Bioinf., 10:832–844.
Lorenz, R., Hofacker, I. L., and Stadler, P. F. (2016). RNA
folding with hard and soft constraints. Alg. Mol. Biol.,
11:8.
McCaskill, J. S. (1990). The equilibrium partition function
and base pair binding probabilities for RNA secondary
structure. Biopolymers, 29:1105–1119.
Mneimneh, S. and Ahmed, S. A. (2015). Multiple RNA in-
teraction: beyond two. IEEE Trans. Nanobioscience,
14:210–219.
M
¨
uckstein, U., Tafer, H., Bernhard, S. H., Hernandez-
Rosales, M., Vogel, J., Stadler, P. F., and Hofacker,
I. L. (2008). Translational control by RNA-RNA inter-
action: Improved computation of RNA-RNA binding
thermodynamics. In Elloumi, M., K
¨
ung, J., Linial, M.,
Murphy, R. F., Schneider, K., and Toma, C. T., editors,
BioInformatics Research and Development — BIRD
2008, volume 13 of Comm. Comp. Inf. Sci., pages
114–127, Berlin. Springer.
Reidys, C. M. (2011). Combinatorial Computational Biol-
ogy of RNA. Springer, Berlin, Heidelberg, D.
Schaeffer, J. M., Thachuk, C., and Winfree, E. (2015).
Stochastic simulation of the kinetics of multiple in-
teracting nucleic acid strands. In Phillips, A. and Yin,
P., editors, DNA 2015, volume 9211, Basel. Springer
International.
Tacker, M., Stadler, P. F., Bornberg-Bauer, E. G., Hofacker,
I. L., and Schuster, P. (1996). Algorithm independent
properties of RNA structure prediction. Eur. Biophy.
J., 25:115–130.
Turner, D. H. and Mathews, D. H. (2010). NNDB: the near-
est neighbor parameter database for predicting stabil-
ity of nucleic acid secondary structure. Nucleic Acids
Res, 38:D280–D282.
Wuchty, S., Fontana, W., Hofacker, I. L., and Schuster, P.
(1999). Complete suboptimal folding of RNA and
the stability of secondary structures. Biopolymers,
49:145–165.
Zadeh, J. N., Steenberg, C. D., Bois, J. S., Wolfe, B. R.,
Pierce, M. B., Khan, A. R., Dirks, R. M., and Pierce,
N. A. (2011). NUPACK: Analysis and design of nu-
cleic acid systems. J. Comput. Chem., 32:170–173.
Zuker, M. and Stiegler, P. (1981). Optimal computer folding
of large RNA sequences using thermodynamics and
auxiliary information. Nucleic Acids Res., 9:133–148.
Efficient Computation of Base-pairing Probabilities in Multi-strand RNA Folding
31
