Solitons in a Dual-core System with a Uniform Bragg Grating
and a Bragg Grating with Dispersive Reflectivity
Bellal Hossain and Javid Atai
School of Electrical and Information Engineering, The University of Sydney, NSW 2006, Australia
Keywords:
Gap Soliton, Kerr Nonlinearity, Dispersive Reflectivity.
Abstract:
The existence and stability of gap solitons in a dual-core optical fiber made of a uniform and a nonuniform
Bragg grating with Kerr nonlinearity are considered. The nonuniformity in the one of the cores originates
from the presence of dispersive reflectivity. It is found that quiescent soliton solutions exist throughout the
bandgap. Stability analysis shows that there exist vast areas within the bandgap where stable solitons exist.
1 INTRODUCTION
Solitons are nonlinear waves that maintain their pro-
file for a long distance (or time). They have been ob-
served in a variety of physical systems such as wa-
ter, plasma and optical materials. In optical materi-
als, solitons are formed when the nonlinearity of the
medium is balanced by the dispersion (Chiao et al.,
1964).
In periodic optical media such as Fiber Bragg grat-
ings (FBGs), due to the coupling between the forward
and reflected waves gives rise to an induced disper-
sion which can be up to 6 orders magnitude greater
than that of silica. Gap solitons (GSs) are formed
when the induced dispersion in the FBG is balanced
by the nonlinearity of medium (De Sterke and Sipe,
1994). In the last few decades, GSs have attracted
much attention and have been studied in numerous
theoretical (Aceves and Wabnitz, 1989; Malomed and
Tasgal, 1994; Barashenkov et al., 1998) and experi-
mental works (De Sterke et al., 1997; Eggleton et al.,
1999).
GSs have a number of interesting features one of
which is that their velocity can range from zero to
speed of light in the optical medium. Zero velocity
or slow solitons have potential applications in optical
buffers and memory elements (Krauss, 2008). The
existencxe and dynamics of GSs have been studied
in different structures and nonlinearities such as dual-
core systems (Mak et al., 1998a; Atai and Malomed,
2000), nonuniform Bragg gratings (Atai and Mal-
omed, 2005; Baratali and Atai, 2012), photonic crys-
tal waveguides (Neill and Atai, 2007; Monat et al.,
2010), cubic-quintic nonlinearity (Atai and Malomed,
2001; Dasanayaka and Atai, 2010) and quadratic non-
linearity (Conti et al., 1997; Mak et al., 1998b).
Dual-core and dual-modesystems possess rich dy-
namical features (Atai and Chen, 1992; Mak et al.,
2004; Chen and Atai, 1998; Chen and Atai, 1995).
In particular, a dual-core system with non-identical
cores can provide superior switching performance
than the dual-core systems with identical cores (Atai
and Chen, 1993; Bertolotti et al., 1995). In this paper,
we consider the existence and stability of gap solitons
in a dual-core system with Kerr nonlinearity where
one core has a uniform Bragg grating and the other is
equipped with a Bragg grating with dispersive reflec-
tivity.
2 THE MODEL
Propagation of light in a dual-core nonlinear coupled
system with one core having a uniform Bragg grating
and the other being equipped with a Bragg grating and
dispersive reflectivity can be represented mathemati-
cally by the following equations:
iu
1t
+ iu
1x
+ u
1

1
2
|u
1
|
2
+ |v
1
|
2

+v
1
+ λu
2
+ mv
1xx
= 0,
iv
1t
− iv
1x
+ v
1

1
2
|v
1
|
2
+ |u
1
|
2

+u
1
+ λv
2
+ mu
1xx
= 0,
iu
2t
+ iu
2x
+ u
2

1
2
|u
2
|
2
+ |v
2
|
2

+v
2
+ λu
1
= 0,
iv
2t
− iv
2x
+ v
2

1
2
|v
2
|
2
+ |u
2
|
2

+u
2
+ λv
1
= 0.
(1)
76
Hossain, B. and Atai, J.
Solitons in a Dual-core System with a Uniform Bragg Grating and a Bragg Grating with Dispersive Reflectivity.
DOI: 10.5220/0008909700760079
In Proceedings of the 8th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2020), pages 76-79
ISBN: 978-989-758-401-5; ISSN: 2184-4364
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

In Eqs. (1), u
1,2
and v
1,2
stand for forward- and
backward-propagating waves of the cores 1 and 2, re-
spectively. m > 0 denotes dispersive reflectivity and
λ is the coupling coefficient between the two cores.
It is worth noting that m > 0.5 may not be physically
realizable (Atai and Malomed, 2005). Therefore, we
have limited our analysis to 0 ≤ m < 0.5.
To determine the bandgap within which GSs may
exist, the linear spectrum of the system needs to be
analyzed. To this end, the dispersion relation for
the model by is derived by substituting u
1,2
, v
1,2
∼
exp(ikx − iωt) into linearized form of Eqs. (1) which
leads to the following equation:
ω = ±

k
2
− mk
2
+ λ
2
∓
1
2

m
4
k
8
− 4m
3
k
6
+4m
2
λ
2
k
4
+ 4m
2
k
4
− 16mλ
2
k
2
+ 16λ
2
k
2
+16λ
2

1
2
+1+
1
2
m
2
k
4

1
2
.
(2)
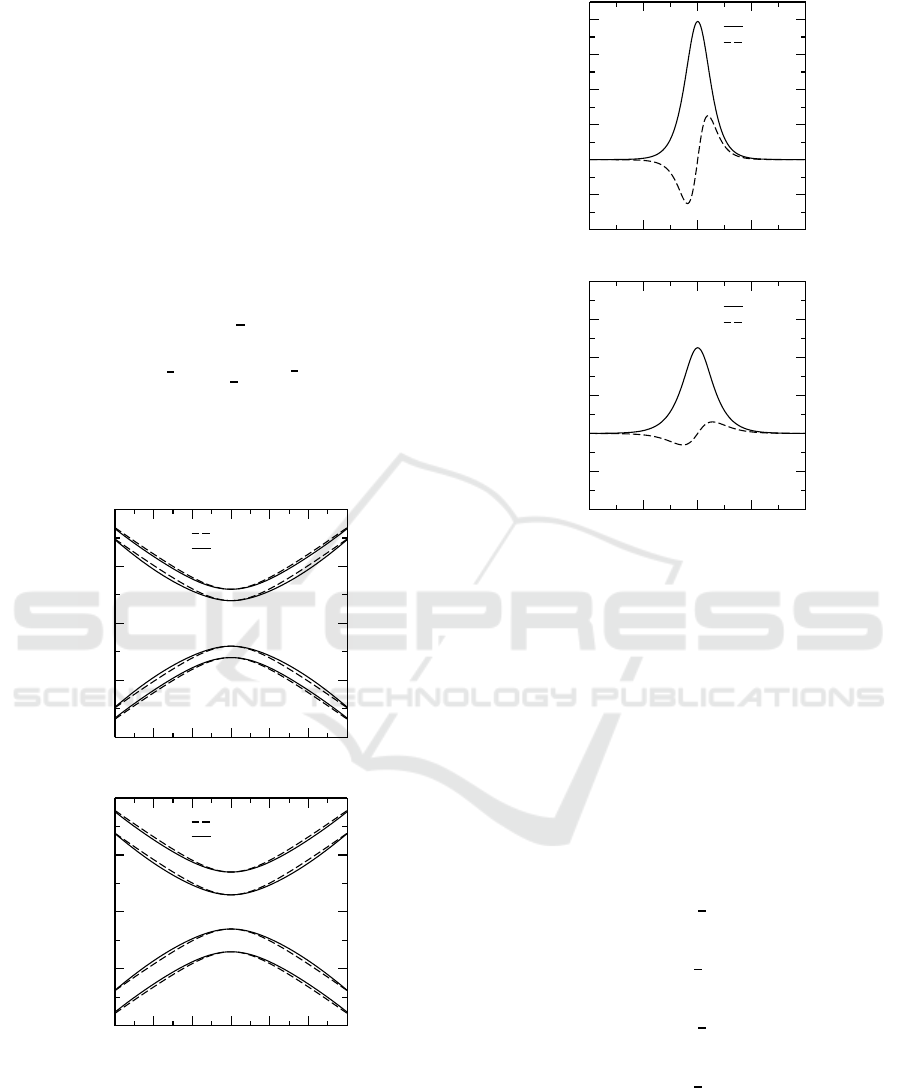
Figure 1 represents the dispersion diagram or bandgap
specturm in (k, ω) plane. It is evident that the bandgap
shrinks as λ increases.
-3 -2 -1 0 1 2 3
k
-4
-2
0
2
4
ω
m = 0.0
m = 0.2
(a)
-3 -2 -1 0 1 2 3
k
-4
-2
0
2
4
ω
m = 0.0
m = 0.2
(b)
Figure 1: Examples of bandgap spectrum for (a) λ = 0.2,
m = 0.0, 0.2 and (b) λ = 0.4, m = 0.0, 0.2.
-10
-5
0
5
10
x
-0.4
-0.2
0
0.2
0.4
0.6
0.8
Re(u )
Im(u )
(a)
1
1
-10
-5
0
5
10
x
-0.2
-0.1
0
0.1
0.2
0.3
Re(u )
Im(u )
(b)
2
2
Figure 2: Examples of for (a) u
1
and (b) u
2
at λ = 0.2,
m = 0.2, ω = 0.4.
3 QUIESCENT GAP SOLITON
SOLUTIONS
The stationary GS solutions must be obtained numer-
ically using the relaxation algoritm since there are no
analytical solutions for Eqs. (3). The soliton so-
lutions are sought as u(x,t) = U (x)exp(−iωt) and
v(x,t) = V (x)exp(−iωt). Substituting these ansatz
into Eqs. (1) results in the following equations:
ωU
1
+ iU
1x
+U
1

1
2
|U
1
|
2
+ |V
1
|
2

+V
1
+ λU
2
+ mV
1xx
= 0,
ωV
1
− iV
1x
+V
1

1
2
|V
1
|
2
+ |U
1
|
2

+U
1
+ λV
2
+ mU
1xx
= 0,
ωU
2
+ iU
2x
+U
2

1
2
|U
2
|
2
+ |V
2
|
2

+V
2
+ λU
1
= 0,
ωV
2
− iV
2x
+V
2

1
2
|V
2
|
2
+ |U
2
|
2

+U
2
+ λV
1
= 0.
(3)
Figure 2 shows the real and imaginary parts of u
1
and
u
2
(note that v
1
= −u
∗
1
and v
2
= −u
∗
2
) and Figure 3
displays the amplitudes of u
1
and u
2
. Our analysis
shows that quiescent soliton solutions exist through-
out the bandgap.
Solitons in a Dual-core System with a Uniform Bragg Grating and a Bragg Grating with Dispersive Reflectivity
77

-10
-5
0
5
10
x
0
0.2
0.4
0.6
0.8
|u |
m=0.2
m=0.4
(a)
1
-10
-5
0
5
10
x
0
0.1
0.2
|u |
m=0.2
m=0.4
(b)
2
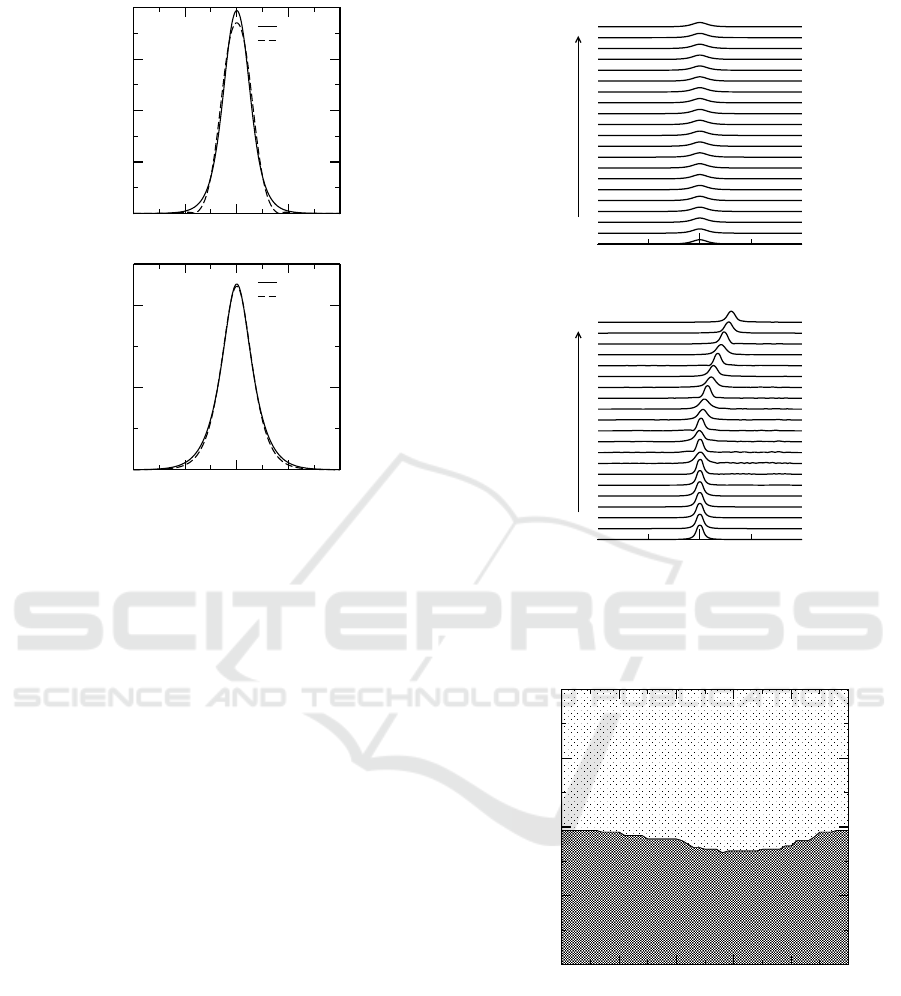
Figure 3: Examples of amplitude variation of (a) u
1
and (b)
u
2
at λ = 0.2, ω = 0.4, m = 0.2, 0.4.
4 STABILITY ANALYSIS OF
QUIESCENT GAP SOLITONS
To analyze the stability of the solitons in the model,
we have solved Eqs. (1) numerically using the sym-
metrized split-step Fourier method. Figure 4 shows
the examples of propagation of stable and unstable
solitons. In the case of unstable solitons, it is found
that they generally shed some energy in the form of
radiation and they either evolve to a moving soli-
ton (see Figure 4(b)) or if they are highly unstable
they are completely destroyed. Figure 5 shows the
stability diagram for λ = 0.2 in the plane of (m, ω).
An important feature of this stability diagram is that
there is a vast region within the bandgap where stable
quiescent solitons exist. Moreover, the stabilization
effect of dispersive reflectivity is more pronounced
for moderate values m (i.e. when m is in the range
0.2 < m < 0.4).
5 CONCLUSIONS
The existence and stability of gap solitons are con-
sidered in a coupled system with Kerr nonlinearity
where one core has a uniform Bragg grating and
the other has a Brag grating with dispersive reflec-
-30 0 30
x
0
2000
t
(a)
-30 0 30
x
0
2000
t
(b)
Figure 4: Examples of propagation of (a) stable soliton at
λ = 0.2, m = 0.2, ω = 0.7 and (b) unstable soliton at λ =
0.2, m = 0.2, ω = −0.7. Here only u
1
component is shown.
0 0.1 0.2 0.3 0.4
0.5
m
-0.8
-0.4
0
0.4
0.8
ω
Stable
Unstable
Figure 5: The stability diagram of quiescent gap solitons at
λ = 0.2.
tivity. The analysis of the linear spectrum of the
model shows that there exists a genuine bandgap in
the model where solitons can exist. The size of the
bandgap shrinks as the coupling coefficient between
the cores is increased. Quiescent soliton solutions are
found throughout the bandgap.
Stability analysis of quiescent solitons shows that
stable and unstable solitons exist in the system. Un-
PHOTOPTICS 2020 - 8th International Conference on Photonics, Optics and Laser Technology
78

stable solitons may either evolve to a moving soliton
or are completely destroyed. Nontrivial stability bor-
ders have been identified in the plane of (m, ω).
REFERENCES
Aceves, A. and Wabnitz, S. (1989). Self-induced trans-
parency solitons in nonlinear refractive periodic me-
dia. Physics Letters A, 141(1-2):37–42.
Atai, J. and Chen, Y. (1992). Nonlinear couplers com-
posed of different nonlinear cores. Journal of applied
physics, 72(1):24–27.
Atai, J. and Chen, Y. (1993). Nonlinear mismatches be-
tween two cores of saturable nonlinear couplers. IEEE
journal of quantum electronics, 29(1):242–249.
Atai, J. and Malomed, B. A. (2000). Bragg-grating solitons
in a semilinear dual-core system. Physical Review E,
62(6):8713.
Atai, J. and Malomed, B. A. (2001). Families of bragg-
grating solitons in a cubic–quintic medium. Physics
Letters A, 284(6):247–252.
Atai, J. and Malomed, B. A. (2005). Gap solitons in bragg
gratings with dispersive reflectivity. Physics Letters A,
342(5-6):404–412.
Barashenkov, I., Pelinovsky, D., and Zemlyanaya, E.
(1998). Vibrations and oscillatory instabilities of gap
solitons. Physical review letters, 80(23):5117.
Baratali, B. and Atai, J. (2012). Gap solitons in dual-core
bragg gratings with dispersive reflectivity. Journal of
Optics, 14(6):065202.
Bertolotti, M., Monaco, M., and Sibilia, C. (1995). Role of
the asymmetry in a third-order nonlinear directional
coupler. Optics communications, 116(4-6):405–410.
Chen, Y. and Atai, J. (1995). Polarization instabilities in
birefringent fibers: A comparison between continuous
waves and solitons. Phys. Rev. E, 52:3102–3105.
Chen, Y. and Atai, J. (1998). Stability of fundamental soli-
tons of coupled nonlinear schr¨odinger equations. Opt.
Commun., 150(1):381 – 389.
Chiao, R. Y., Garmire, E., and Townes, C. H. (1964). Self-
trapping of optical beams. Phys. Rev. Lett., 13:479–
482.
Conti, C., Trillo, S., and Assanto, G. (1997). Doubly reso-
nant bragg simultons via second-harmonic generation.
Phys. Rev. Lett., 78:2341–2344.
Dasanayaka, S. and Atai, J. (2010). Stability of bragg grat-
ing solitons in a cubic–quintic nonlinear medium with
dispersive reflectivity. Physics Letters A, 375(2):225–
229.
De Sterke, C. and Sipe, J. (1994). Gap solitons progress in
optics. North-Holland, 33:203–260.
De Sterke, C. M., Eggleton, B. J., and Krug, P. A. (1997).
High-intensity pulse propagation in uniform gratings
and grating superstructures. Journal of lightwave
technology, 15(8):1494–1502.
Eggleton, B. J., de Sterke, C. M., and Slusher, R. (1999).
Bragg solitons in the nonlinear schr¨odinger limit: ex-
periment and theory. JOSA B, 16(4):587–599.
Krauss, T. F. (2008). Why do we need slow light? Nature
Photonics, 2(8):448.
Mak, W. C., Chu, P., and Malomed, B. A. (1998a). Solitary
waves in coupled nonlinear waveguides with bragg
gratings. JOSA B, 15(6):1685–1692.
Mak, W. C., Malomed, B. A., and Chu, P. L. (2004). Sym-
metric and asymmetric solitons in linearly coupled
bragg gratings. Physical Review E, 69(6):066610.
Mak, W. C. K., Malomed, B. A., and Chu, P. L. (1998b).
Three-wave gap solitons in waveguides with quadratic
nonlinearity. Phys. Rev. E, 58:6708–6722.
Malomed, B. A. and Tasgal, R. S. (1994). Vibration modes
of a gap soliton in a nonlinear optical medium. Phys-
ical Review E, 49(6):5787.
Monat, C., De Sterke, M., and Eggleton, B. (2010). Slow
light enhanced nonlinear optics in periodic structures.
Journal of Optics, 12(10):104003.
Neill, D. R. and Atai, J. (2007). Gap solitons in a hollow
optical fiber in the normal dispersion regime. Physics
Letters A, 367(1-2):73–82.
Solitons in a Dual-core System with a Uniform Bragg Grating and a Bragg Grating with Dispersive Reflectivity
79