DynaLoc: Real-Time Camera Relocalization from a Single RGB Image

in Dynamic Scenes based on an Adaptive Regression Forest

Nam-Duong Duong

, Amine Kacete

, Catherine Soladie

, Pierre-Yves Richard

and J

ome Royan

IRT b-com, 1219 Avenue des Champs Blancs, 35510 Cesson-S

evign

e, France

IETR/CentraleSupelec, Avenue de la Boulaie, 35576 Cesson-S

evign

e, France

Keywords:

Camera Relocalization, Adaptive Regression Forest, Hybrid Approach, Single RGB Image.

Abstract:

Camera relocalization is an important component in localization systems such as augmented reality or robotics

when camera tracking loss occurs. It uses models built from known information of a scene. However, these

models cannot perform in a dynamic environment which contains moving objects. In this paper, we propose

an adaptive regression forest and apply it to our DynaLoc, a real-time camera relocalization approach from a

single RGB image in dynamic environments. Our adaptive regression forest is able to ﬁne tune and update

continuously itself from evolving data in real-time. This is performed by updating a relevant subset of leaves,

which gives uncertain predictions. The results of camera relocalization in dynamic scenes report that our

method is able to address a large number of moving objects or a whole scene to gradually change in order to

obtain high accuracy avoiding accumulation of error. Moreover, our method achieves results as accurate as the

best state-of-the-art methods on static scenes dataset.

1 INTRODUCTION

Camera pose estimation is a key feature of Aug-

mented Reality (AR), robot navigation and au-

tonomous vehicles (self-driving), which requires an

accurate tracking of camera viewpoint in a 3D space.

The main solution of camera pose estimation for com-

mercial systems is known as Simultaneously Local-

ization And Mapping (SLAM) (Davison et al., 2007;

Klein and Murray, 2007; Mur-Artal et al., 2015; En-

gel et al., 2014; Tateno et al., 2017). SLAM processes

an ordered sequence of images. In the case of fast

camera motion or sudden change of viewpoint such

as with a hand-held camera, tracking failure interrupts

camera pose estimation. When this happens, camera

relocalization is needed to retrieve camera pose af-

ter tracking lost, rather than restarting the localization

again from scratch. However, the existing camera re-

localization methods in SLAM need to store a large

set of key-points or key-frames. Consequently, mem-

ory usage as well as processing time increase with re-

spect to the size of models.

Recently, machine learning approaches for cam-

era relocalization have appeared to tackle these con-

straints. These methods (Kendall et al., 2015; Kendall

and Cipolla, 2016; Walch et al., 2017; Clark et al.,

2017) can estimate camera pose in real-time from

each image. However, limitations of these methods

lie in their moderate accuracy and the lack of con-

ﬁdence score for each pose estimation. To improve

the accuracy as well as address uncertainty prediction

in deep learning approaches, (Shotton et al., 2013;

Guzman-Rivera et al., 2014; Valentin et al., 2015;

Brachmann et al., 2016; Duong et al., 2018) presented

hybrid methods using random forest and geometric al-

gorithms for camera relocalization with higher accu-

racy. Such methods are robust to illumination changes

and partial occlusion. Yet, these machine learning

based methods and hybrid methods still fail to chal-

lenge dynamic scenes with moving objects.

Moving objects are often encountered in many

augmented reality scenarios such as maintenance,

assembly and quality control task for Manufactur-

ing and Construction application where: devices are

equipped only with a single RGB camera, scenes are

changing gradually over time, tasks requires work-

bench scale 3D registration. Dynamic data is not a

challenge dedicated to camera relocalization. But it

also appears in many other applications using ma-

chine learning. Indeed, for machine learning in gen-

eral, a model is learned from a set of training data.

If data is changing and the learned model is not

able to update itself, this model is no longer accu-

rate. Thus, these methods require an adaptive learning

Duong, N., Kacete, A., Soladie, C., Richard, P. and Royan, J.

DynaLoc: Real-Time Camera Relocalization from a Single RGB Image in Dynamic Scenes based on an Adaptive Regression Forest.

DOI: 10.5220/0008902906430653

In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 4: VISAPP, pages

643-653

ISBN: 978-989-758-402-2; ISSN: 2184-4321

643

model which has the capacity to update rapidly to the

changes of data in order to maintain the accuracy of

the learned model.

In this paper, we focus on handling challenges of

dynamic data for generic machine learning as well as

for camera relocalization. Our contributions are di-

vided into two parts as follows.

Our ﬁrst contribution is to propose an online up-

dating regression forest process. We call it Adaptive

Regression Forest - ARF. The main idea is that the

ARF updates instantly a subset of leaves which gives

uncertain predictions. It is performed by two main

originalities based on detection and update of uncer-

tain leaves.

The ﬁrst originality of our ARF is to detect the

leaves giving uncertain predictions. There are two cri-

teria for a leaf to become a passive leaf: having a high

variance of predictive model; giving repeatedly a re-

sult rather different from the other leaves.

The second originality of our ARF is to update

in real time passive leaves of the regression forest

model. This is performed by re-modeling their pre-

dictive model from new computed labels. These la-

bels are computed based on results given by the other

leaves (actives leaves). Note that the update is only

performed on passive leaves and not on the whole re-

gression forest model. This process leads to select rel-

evant data to update efﬁciently at runtime the model.

The second contribution is to present our Dy-

naLoc. It is a real time camera relocalization in dy-

namic scenes based on the generic ARF. For this ap-

plication, the ARF predicts 3D points in the world co-

ordinates system which correspond to 2D points in the

image. The originality is to keep the structure of the

forest (trees and nodes) by using invariant SURF fea-

ture at split nodes as proposed in (Duong et al., 2018).

A last contribution concerns the creation of a pub-

lic database to evaluate camera relocalization meth-

ods. It is the ﬁrst public database including dynamic

scenes, which is one of the most important challenge

for (re)localization methods.

In the following sections, we ﬁrst present the re-

lated work in section 2. Our adaptive regression for-

est is described in section 3. Section 4 presents our

DynaLoc that is a real-time camera relocalization in

dynamic scenes based on the adaptive regression for-

est. Section 5 shows and discusses our results on rigid

scenes dataset and on our dynamic scenes dataset. Fi-

nally, section 6 provides some conclusions and per-

spectives.

2 RELATED WORK

In this section, we ﬁrst present camera localization

(SLAM) methods in dynamic environment. Then, we

introduce state-of-the-art camera relocalization meth-

ods and their limit regarding dynamic scenes.

2.1 SLAM in Dynamic Environment

Dynamic environment with moving objects is still

known as a difﬁcult challenge in camera localization

community. The most typical methods to address this

challenge are RANSAC algorithms. RANSAC con-

siders data on moving objects as outliers in order to

eliminate them in camera pose estimation process.

However, if a large number of objects move, the num-

ber of outliers will be superior to the number of in-

liers. In this case, RANSAC algorithm processes in-

correctly. In recent years, several SLAM methods fo-

cus on this speciﬁc issue of dynamic scenes.

Most works perform detection and segmentation

of moving objects in each frame. This is to avoid their

inﬂuence on the camera pose estimation. (Wangsirip-

itak and Murray, 2009; Riazuelo et al., 2017; Bescos

et al., 2018) detect and track the known dynamic ob-

jects or movable objects e.g. people, vehicles. (Sun

et al., 2017; Alcantarilla et al., 2012) detect mov-

ing objects by using optical ﬂow between consecutive

frames. Nevertheless, these methods try to remove

moving objects to compute camera pose. Hence,

they cannot process in scenes where the whole scene

changes gradually.

To overcome this, (Newcombe et al., 2015) pro-

posed a real-time dense dynamic scene reconstruction

and tracking based on depth images by using a single

rigid volumetric TSDF (Truncated Signed Distance

Function). This method requires a RGB-D camera to

robustly detect moving objects based on ICP (Iterative

Closest Point) algorithm, which is not our application

case. (Tan et al., 2013) proposes another SLAM ap-

proach that can detect any changes by projecting the

map feature into the current frame. In real-time, it can

update the 3D points cloud and keyframes stored in a

memory to add new elements or remove those which

do not exist anymore. This allows to address the chal-

lenge of whole scene changing gradually. Yet, it has

the limitations of geometric approaches, that we detail

below.

2.2 Camera Relocalization Methods

The camera relocalization methods can be classi-

ﬁed into three different groups, namely: geometric

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

644

approaches; deep learning approaches; hybrid ap-

proaches.

Geometric Approaches are methods that use ge-

ometric point correspondences in order to calculate

camera pose. These methods ﬁrst extract a set of

sparse features (Sattler et al., 2011; Baatz et al.,

2012; Sattler et al., 2017) or dense features (New-

combe et al., 2011; Engel et al., 2014; Glocker et al.,

2015) from each frame. Then, these features are

matched with keypoints of a scene model. Eventu-

ally, camera pose is determined by minimizing feature

re-projection error. These methods require a scene

model that includes a set of keypoints attached to fea-

ture vectors and 3D positions in the world coordi-

nates. This model is constructed from a set of im-

ages of the scene by performing Structure from Mo-

tion (SfM) (Sattler et al., 2011; Baatz et al., 2012;

Sattler et al., 2017) or encoding a set of keyframes

(Mur-Artal et al., 2015; Glocker et al., 2015). Most of

these geometric methods attempt to reduce the com-

putational complexity of feature matching. (Sattler

et al., 2011; Sattler et al., 2017) use a visual vocabu-

lary for efﬁcient 2D-to-3D matching. Even so, since

the matching time depends on the size of the model,

this reduces considerably the scalability.

Deep Learning Approaches in camera relocal-

ization are usually considered as a supervised regres-

sion problem. A regression model is learned from the

labeled data (images with their 6-DoF camera poses)

of the known scenes. (Kendall et al., 2015) was the

ﬁrst to propose the use of deep learning as an end-to-

end camera pose estimation approach. (Kendall and

Cipolla, 2016) generates a probabilistic pose estima-

tion by using dropout after every convolutional layer.

(Walch et al., 2017) is an improvement of PoseNet’s

architecture with spatial Long Short Term Memory

(LSTM) added after CNN layers, that aims at reduc-

ing the dimension of the feature vector, thus providing

important improvements in localization performance.

(Kendall and Cipolla, 2017) solves an ambiguity of

scale factor between location error and orientation er-

ror in the loss function of (Kendall et al., 2015) by

a novel loss function based on re-projection error.

(Clark et al., 2017) exploits the temporal informa-

tion by using a LSTM to predict camera pose based

on multiple consecutive frames. However, all these

methods exhibit low relocalization accuracy so far.

Hybrid Approaches estimate camera pose by

fusing both machine learning approaches and geomet-

ric approaches. Machine learning part is applied to

learn and predict 3D position of each pixel in world

coordinates instead of 6-DoF camera pose as pre-

sented in deep learning approaches above. Then, geo-

metric part infers camera pose from these correspon-

dences. The ﬁrst hybrid methods are based on the

regression forest to fast deﬁne 2D-3D point (Brach-

mann et al., 2016) or 3D-3D point (Shotton et al.,

2013; Guzman-Rivera et al., 2014; Valentin et al.,

2015; Meng et al., 2017) correspondences. (Brach-

mann et al., 2017; Brachmann and Rother, 2018),

instead, uses a deep learning architecture to predict

scene coordinates. (Duong et al., 2018) proposes a

sparse feature regression forest learning with a novel

split function aiming at accelerating computational

time and keeping high accuracy. (Cavallari et al.,

2017) proposes an on-the-ﬂy training camera relocal-

ization from RGB-D images which deals with how

to accelerate learning a new scene. It adapts a pre-

trained forest to a new scene by retaining the internal

nodes. Yet, it needs to update all the leaves with the

ground truth of this new scene.

However, all camera relocalization methods men-

tioned above are not suitable for dynamic scenes

with moving objects. Indeed, geometrical model or

learned model are built from rigid scenes. There-

fore, when some objects move, these models are no

longer accurate to infer camera pose. To overcome

this challenge, we expand the real-time accurate hy-

brid method based on the regression forest (Duong

et al., 2018) to our ARF method. The ARF model

is able to update only a subset of uncertain leaves to

quickly modify without any interruption the trained

model according to changes of the scene such as mov-

ing objects.

3 ADAPTIVE REGRESSION

FOREST

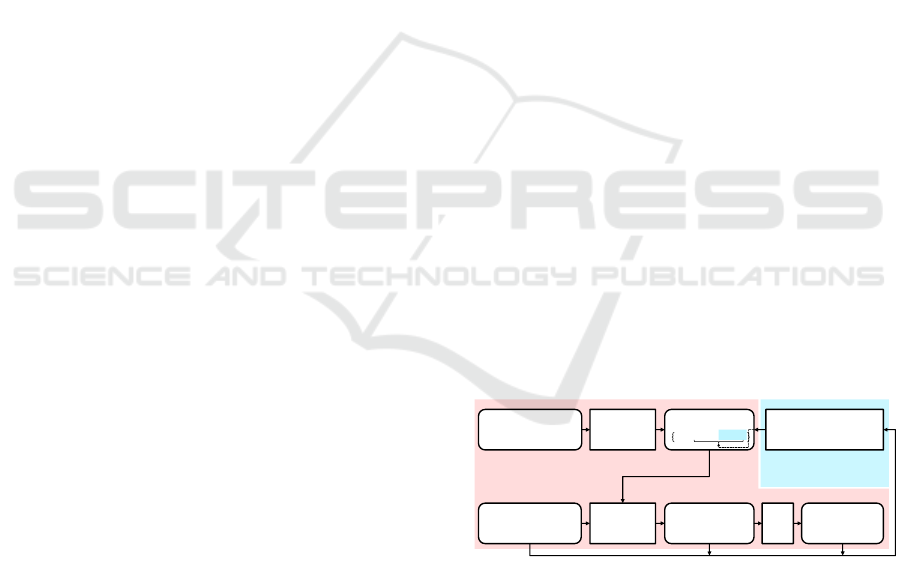
RF Train

Training data with

labels {



, 



}

RF Model





 



 



Testing data

{



}

RF Test

Leaves

predictions {





}





Result Ω with

score 



RF update

Regression Forest

Pipeline

Our contribution

Figure 1: Adaptive regression forest pipeline. The common

regression forest method (red components) is extended with

an online update step (blue component). It reﬁnes predictive

model in real-time from new computed labels.

In this section, we ﬁrst introduce the common regres-

sion forest pipeline which our method is based on.

Then, we explain the limitations of this pipeline and

how we overcome them by using our ARF method.

Finally, we detail our ARF methodology including:

adaptive leaf; passive leaves detection and passive

leaves update.

DynaLoc: Real-Time Camera Relocalization from a Single RGB Image in Dynamic Scenes based on an Adaptive Regression Forest

645

3.1 Regression Forest Pipeline

Fig. 1 presents the common regression forest pipeline

(components in red) including two phases: training

and testing. A regression forest is a set of N deci-

sion trees F = {T

}. Each tree T

= {θ

split

,θ

pred

}

consists of split functions θ

split

at internal nodes and

predictive models θ

pred

at leaf nodes. These parame-

ters are learned from a set of labeled data {φ(d

),m

where φ(d

) is the feature vector extracted from data

with the label m

. The split function θ

split

is a weak

learner. It is used to split a subset of data into left

child node and right child node. The weak learner

is trained to maximize an objective function aiming

to reduce variance. The training terminates when the

tree reaches a maximum depth or when a node has

few data. The predictive model at each leaf node is

represented by a distribution θ

pred

= N (m, ¯m,Σ

). It

is computed from a set of labels m of data reaching

this leaf. m and Σ

are respectively the mean and the

covariance of the Gaussian distribution.

For testing phase, each testing data that is repre-

sented by a set of features {φ(d

)} passes through the

regression forest model to obtain multiple leaves pre-

dictions {l

}, in which l

is a prediction of the deci-

sion tree j for the feature φ(d

). All predictions are

combined to compute the ﬁnal output result Ω with

a conﬁdence score s

con f

by using a post-processing

function f

post

3.2 Limitations of Regression Forest

In the regression forest, leaves with a high variance

are not informative. They make noisy predictions.

Thus, all leaves whose variance is greater than a

threshold T

var

are discarded to eliminate noise and im-

prove accuracy. This leads to the fact that a subset of

leaves are stored in the regression forest, but they are

never used.

Another challenge of regression forest and of ma-

chine learning methods in general is facing dynamic

data. Because a regression model is learned from

static data, the pretrained regression model will be no

longer accurate if some data change. In this case, it

requires re-training from scratch a whole model with

a redeﬁnition of data labels.

3.3 Methodology

To overcome the limitations of the regression forest,

we propose an adaptive regression forest. It is an ex-

tension of the common regression forest pipeline by

adding an update step, as shown in Fig. 1 (in blue).

At the beginning, we assume that a regression forest

is learned from initial training data. Then, in runtime,

their labels change. The update step of our ARF im-

proves consecutively the accuracy of the regression

forest model. It adapts robustly to dynamic data as

well as reﬁnes unused leaves (see 3.2). This is per-

formed by updating leaf nodes based on input data

}, predictions {l

} and ﬁnal output result Ω.

In this section, we ﬁrst give the deﬁnitions of our

ARF parameters. Then, we describe the two main

steps of our update process: passive leaves detection

and passive leaves update. This ARF update is de-

tailed in Fig. 2.

3.3.1 Deﬁnitions of ARF Parameters

Several concepts are used in our ARF: active/passive

leaf, good/bad prediction, validation function, conﬁ-

dence score. We present them in this subsection.

The parameters of each tree of a regression forest

is extended to the ARF model {θ

split

,θ

pred

,θ

update

where θ

update

= {s,n

f alse

data

} are the parameters

used in the update process.

s denotes the status of a leaf: s ∈ {0 : passive,1 :

active}. A passive leaf is a leaf whose prediction is

not accurate, see 3.3.2 for more details. We call it

passive because those leaves are not used during the

ﬁnal process that use the random forest prediction. In

contrary, predictions which come from active leaves

are used to estimate ﬁnal result. Therefore, the post-

processing function in our ARF is deﬁned as follows:

Ω = f

post

({d

= 1}) (1)

Where s

is the status of the leaf of the tree j corre-

sponding to the feature vector φ(d

f alse

denotes the number of consecutive times an

active leaf gives a bad prediction (see 3.3.2). S

data

is a

stack of data that stores the data d

and the ﬁnal result

Ω at each passive leaf. We need it for passive leaves

update (see 3.3.3).

We introduce a validation function f

val

to deﬁne

good and bad predictions.

val

( f

err

(Ω,d

)) =

(

1, f

err

(.) < T

val

, good

0, otherwise, bad

(2)

Where f

err

(Ω,d

) denotes an error function of

each leaf prediction l

based on the output Ω and input

data d

. T

val

is an error threshold in order to determine

good/bad predictions.

After the validation step, we obtain n

good

and n

bad

predictions. A score s

con f

is calculated to evaluate the

conﬁdence score of ﬁnal result:

con f

good

+ n

bad

(3)

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

646

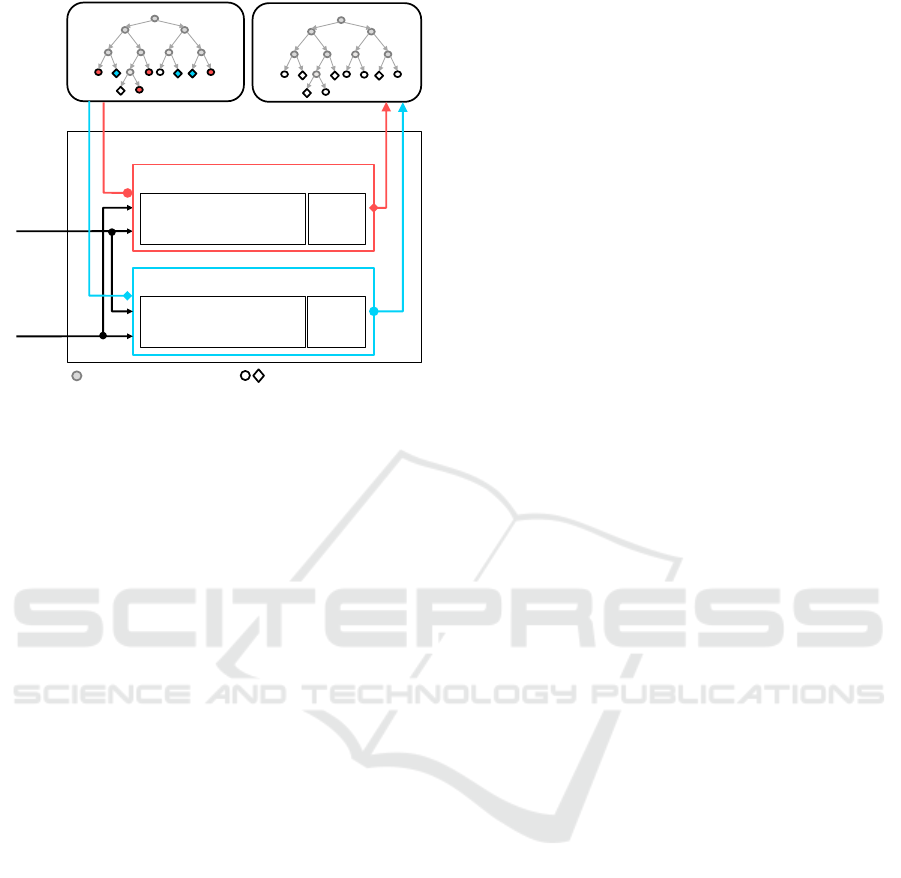
Label data arriving at

passive leaves

Update

𝑨𝑹𝑭

𝒕−𝟏

𝑨𝑹𝑭

𝒕

a) Passive leaves detection

b) Passive leaves update

Testing

data at

time t

Result Ω

𝑡

Leaves

Predictions

{𝑙

𝑗

𝑖

}

𝑡

ARF Update

: Internal node

: Active/passive leaves

Blue and Red: predicted active leaves and passive leaves

Active leaves

Passive leaves

Detected passive leaves

Activated passive leaves

with 𝑠

𝑐𝑜𝑛𝑓

𝑡

{𝜙(𝑑

𝑖

)}

𝑡

Define good/bad

predictions at active leaves

Detect

Figure 2: Adaptive regression forest update process. The

predictive models at leaf nodes evolve by part over time

without training from scratch a whole new model. ARF

performs simultaneously two steps: passive leaves detec-

tion and passive leaves update.

If this conﬁdence score is greater than T

con f

, the up-

date of ARF will be proceeded based on the output

result Ω. T

con f

is a conﬁdence threshold to ensure

that the output result is reliable. It aims at limiting

accumulation of errors during the update process.

3.3.2 Passive Leaves Detection

Passive leaves detection aims at detecting leaves be-

ing no longer relevant and change their status to pas-

sive. After the initial training phase, the status of each

leaf is deﬁned by:

s =

(

1,active, tr(Σ

) < T

var

0, passive, otherwise

(4)

Where tr(Σ

) is the trace of the covariance matrix Σ

var

is a threshold to deﬁne passive leaves. In the test-

ing phase, an active leaf becomes a passive leaf, when

it gives consecutively uncertain results. Fig. 2-a) il-

lustrates the passive leaves detection. We ﬁrst deﬁne

good/bad predictions from a set of active leaves pre-

dictions based on the validation function (2). We then

use n

f alse

to count the number of consecutive times an

active leaf is considered as a bad prediction. Finally,

if n

f alse

> T

f alse

, this active leaf becomes a passive

leaf and its status is assigned to 0 (passive). T

f alse

is a

detection threshold to ensure that this leaf is really an

uncertain leaf. n

f alse

is reassigned to 0 as soon as the

active leaf gives a good prediction once. This aims

at avoiding mistakes of determining good/bad predic-

tion from the error function (2) due to noisy data.

3.3.3 Passive Leaves Update

The passive leaves update aims at remodeling the pre-

dictive models of passive leaves from new estimated

labels. These new labels are calculated based on the

estimated result Ω and input data {d

}. Fig. 2-b)

shows the passive leaves update step. It only pro-

cesses at predicted passive leaves. When a feature

φ(d

) passes through our forest and terminates in a

passive leaf, we ﬁrstly collect the corresponding input

data d

and the result Ω in a stack of data S

data

asso-

ciated to this passive leaf. These elements stored in

the stack of data allow to compute new labels of data.

When the number of data in the stack at a passive leaf

is large enough |S

data

| > T

data

is a threshold to

ensure that the number of data is sufﬁcient to learn a

new distribution), we calculate labels m

of d

by us-

ing a labeling function:

= f

label

data

) (5)

And then a Gaussian distribution of this leaf is mod-

eled from these labels {m

}. Finally, the status of this

leaf is deﬁned by the function (4). The stack of data

data

is reset. The passive leaves update and passive

leaves detection are performed at the same time to ac-

celerate ARF system.

4 CAMERA RELOCALIZATION

IN DYNAMIC SCENES

In this section, we introduce our DynaLoc, a real-

time camera relocalization method from only RGB

images in dynamic scenes. Inspired by (Duong et al.,

2018), we propose a hybrid method merging our ARF

(described in the section 3) and geometric methods.

Our ARF is applied to learn and predict 2D-3D point

correspondences. The geometric part uses PnP and

RANSAC algorithms in order to compute camera

pose from these correspondences. Fig. 3 illustrates

our DynaLoc pipeline. Our method is summarized in

three principal steps. Firstly, we present how to ini-

tially train the ARF from RGB images. Then, camera

pose estimation is performed based on the ARF and

geometric algorithms. Finally, we detail the online

ARF update process for camera relocalization.

4.1 Initial ARF Training

The ARF is initialized according to the training step

detailed in (Duong et al., 2018). An ARF is learned

from a set of labeled feature vectors {φ(d

),m

} which

are extracted from a set of RGB training images. φ(d

)

DynaLoc: Real-Time Camera Relocalization from a Single RGB Image in Dynamic Scenes based on an Adaptive Regression Forest

647

SURF Feature Extraction

Camera Pose with Inliers/Outliers

3D Scene Coordinates

Passive leaves

detection and

update

Adaptive

Regression Forest

Model

PnP

RANSAC

Inliers/Outliers

Camera pose

Keypoints

Features

Figure 3: DynaLoc: Real-time camera relocalization in dynamic scenes based on the ARF. We apply the ARF to hybrid camera

relocalization: from a set of SURF feature detected on each RGB image, the ARF predicts a set of 3D world coordinates.

They correspond to active leaves (green and red points). Then PnP and RANSAC algorithms determine inliers (green points)

to estimate camera pose and reject outliers (red points). Finally, if the camera pose is precisely estimated, the ARF is updated

by using the estimated camera poses, inliers, outliers and 2D positions of keypoints.

is a SURF feature vector extracted around a 2D key-

point position d

. m

is the 3D point in the world co-

ordinates system corresponding to d

. The label m

is deﬁned by running triangulation algorithm (Hart-

ley and Zisserman, 2005) for each pair of matching

keypoints (d

) of two RGB images, whose poses

(Ω

,Ω

) are supposed to be known in advance by us-

ing a localization system (marker based, 3D model

based, SLAM, tracking, etc.):

(

× (KΩ

−1

) = 0

× (KΩ

−1

) = 0

(6)

Where K is the matrix of the camera intrinsic param-

eters.

Each tree of ARF is initially trained by a ran-

dom subset of data to determine the split func-

tions. We use whole SURF feature vector as pro-

posed in (Duong et al., 2018) and adaptive leaf nodes

{θ

split

,θ

pred

,θ

update

} (see 3.3). Each leaf node stores

the 3D positions corresponding to a set of SURF fea-

tures reaching it which is represented by a Gaussian

distribution N (m,m,Σ

). The status s of each leaf of

ARF is deﬁned by the status deﬁnition function (4).

f alse

is assigned to 0 and S

data

is initialized by an

empty set.

4.2 Camera Pose Estimation

Firstly, a set of SURF keypoints and features

,φ(d

)} is extracted from each RGB input image.

They pass through the ARF {T

} to achieve a set

of predictions {l

} that contains 3D world coordi-

nates predictions { ˆm

} corresponding to 2D SURF

keypoints {d

}. All 2D-3D correspondences coming

from active leaves are used to estimate camera pose

based on the post-processing function (1). In cam-

era relocalization, f

post

function of ARF is deﬁned by

PnP and RANSAC functions in order to remove bad

predictions (outliers) and keep good predictions (in-

liers). RANSAC generates a set of hypothetical poses

{Ω

} by performing PnP on random subsets of 2D-3D

point correspondences. The best inliers are deﬁned

by maximizing the number of inliers corresponding

to each hypothesis based on the validation function

(2), in which the error function f

err

(.) is deﬁned as a

re-projection error function:

err

(Ω,d

) = kd

− KΩ

−1

ˆm

(7)

The ﬁnal camera pose Ω is carried out by running

PnP once on all inliers to minimize the sum of re-

projection error.

4.3 Online ARF Update

The ARF in our DynaLoc keeps the internal nodes

and the structures of the trees. It only updates con-

tinuously predictive models at uncertain leaf nodes to

adapt to the changes in dynamic scenes. The update

process is based on two main steps: passive leaves

detection and passive leaves update, as described in

section 3.3.

In the passive leaves detection (see 3.3.2), the

good and bad predictions correspond to inliers and

outliers respectively which are deﬁned in section 4.2.

In the passive leaves update (see 3.3.3), the stack S

data

of each passive leaf collects constantly 2D positions

of SURF keypoints and camera poses (d

,Ω

). The la-

beling function (5) is deﬁned by the triangulation al-

gorithm (Hartley and Zisserman, 2005). From a pair

of data in the stack (d

,Ω

) and (d

,Ω

), the label m

is computed based on the triangulation function (6).

Thus, a set of T

data

data at each passive leaf deﬁnes

a set {m

} of

data

·(T

data

−1)

3D points. A new Gaus-

sian distribution N (m, ¯m,Σ

) is modeled based on

3D points. The function (4) validates the status of

new leaf model.

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

648

Table 1: DynaScenes dataset. A RGB images dataset is used to evaluate camera relocalization methods in dynamic scenes.

Infos

DynaScene-01 DynaScene-02 DynaScene-03 DynaScene-04

Train Test Train Test Train Test Train Test

Seq-00 Seq-01 Seq-02 Seq-00 Seq-01 Seq-02 Seq-00 Seq-01 Seq-02 Seq-00 Seq-01 Seq-02

#Frames 669 681 681 831 1136 1075 743 842 1140 958 1395 2109

Occlusion No No No No Yes No No No No No Yes Yes

Illumination change No No No No No No No Yes No No Yes Yes

Moving objects 0% 0% 30% 0% 0% 60% 0% 0% 100% 0% 0% 100%

A key feature of this update process is that the

function (4) can eliminate the new model and reset the

data buffer at leaf nodes when the variance is too high

(outliers). Thus, changes of the scene such as mov-

ing/coming objects or wrong camera pose estimation,

generating inconsistent 3D points during triangulation

step, will not damage the model. Nevertheless, when

a moving object will become stationary again, the tri-

angulation function will estimate correct labels, and

the variance will become low enough to reactivate the

leaf. Thus, the model is updated to remain accurate

when the scene has changed.

5 EXPERIMENTS

In this section, we ﬁrst present the datasets used in

our experiments. Especially, we introduce our dataset

including dynamic scenes, we call it DynaScenes

dataset. Then, we demonstrate the usefulness of our

ARF on both static and dynamic scenes by compar-

ing it with a regression forest (RF) approach. Finally,

we compare our DynaLoc with state-of-the-art RGB

camera relocalization methods.

5.1 Datasets

We evaluate our method on two datasets, both static

and dynamic scenes, to compare with state-of-the-art

methods. These datasets are indoor scenes. Each one

provides intrinsic matrix of camera, thousands of im-

ages of different trajectories at 640 × 480 resolution

and annotations (camera pose for each frame).

The 7-scenes Dataset (Shotton et al., 2013) con-

tains seven static scenes in room-scale. Each scene in-

cludes some RGB-D image sequences which are cap-

tured around a single room and annotated by using

Kinect Fusion (Newcombe et al., 2011). The data is

challenging with texture-less surface, repeated struc-

ture or fast movement of the camera, that provides

many blurry images.

The DynaScenes Dataset

is a completely new

dataset for camera relocalization proposing dynamic

environments. To create challenging dynamic scenes

with gradually moving objects, we simulates real sce-

narios as augmented reality based maintenance on a

workbench where users teleport sequentially objects

from one location to another. We also inject chal-

lenges of illumination changes and occlusion into this

dataset. This dataset consists of four scenes. Each

one contains three absolutely different RGB image se-

quences of the same scene (one training sequence and

two testing sequences). More detail characteristics of

this dataset are given in Tab. 1. The ground truth of

camera pose is accurately acquired by using a HTC

Vive tracker rigidly attached on the camera. The cam-

era can move around within a visible area of two light-

house base stations. This allows us to continuously

track the orientation and trajectory of the tracker. A

rigid transformation matrix between tracker pose and

camera pose is estimated by using the hand-eye cali-

bration method (Tsai and Lenz, 1988). Camera pose

is found based on tracker pose and this transformation

matrix. We perform a synchronization to get image

frame and tracker pose at the same time.

5.2 ARF versus RF

ARF Performance on Dynamic Scenes. Fig. 4

shows the performance of our ARF compared to a re-

gression forest with chosen leaves (RF) on a dynamic

sequence which contains objects moving gradually.

The results demonstrate that when objects are static,

both approaches achieve high accurate localization as

shown at beginning of Fig. 4-a,b). As soon as more

than 30% of objects move, the RF approach has large

error because the number of inliers reduces rapidly.

On the other hand, the accuracy of our DynaLoc is

maintained thanks to the ARF update process. Fig. 4-

d) gives the evolution of the number of active leaves

over time. When some objects move, the correspond-

ing active leaves are deﬁned as passive leaves and the

percentage of active leaves drops. When these ob-

jects return to a static state, this percentage increases

https://github.com/duongnamduong/DynaScenes-

dataset

DynaLoc: Real-Time Camera Relocalization from a Single RGB Image in Dynamic Scenes based on an Adaptive Regression Forest

649

0 200 400 600 800 1000

a) Translation error (cm)

0 200 400 600 800 1000

b) Rotation error (degree)

0 200 400 600 800 1000

100

c) Percentage of inliers

0 200 400 600 800 1000

100

d) Percentage of active leaves

0 20 40 60 80 100

Percentage of moving objects

ARF

Figure 4: Detail results of our DynaLoc based the ARF

(blue) and RF (red) on DynaScene-03/Seq-02. a), b) trans-

lation error in centimeter and rotation error in degree. c) the

percentage of number of inliers at each frame. d) the per-

centage of active leaves compares to the number of leaves

used at each frame for predictions. The background color

present the percentage of objects in the scene that have

moved since the beginning.

01/01 02/01 03/01 04/01 01/02 02/02 03/02 04/02

Scenes

100

RF-all leaves RF-chosen leaves ARF

b) scenes with moving objects

a) scenes without moving objects

Figure 5: Comparison our DynaLoc based on the ARF

(blue) to RF approaches using all leaves (red) and chosen

leaves (green) with T

var

= 0.1 on DynaScenes dataset by

measuring the percentage of test images where the pose er-

ror is below 5cm and 5°.

again thanks to the passive leaves update step. That is

why the inliers percentage remains sufﬁciently high,

as shown in Fig. 4-c). Furthermore, although the ARF

update is proceeded based on estimated results, the

error accumulation is very small. The rotation and

translation errors before and after movements are ap-

proximately equal as shown in Fig. 4-a,b). Therefore,

our DynaLoc can handle a whole scene with gradual

changes.

In Fig. 5-b), we compare the results of our Dy-

naLoc with the RF approaches (with or without cho-

sen leaves) on dynamic scenes. We report that the ac-

Ground-truth

DynaLoc

Figure 6: Comparison results between DynaLoc and RF on

a dynamic sequence.

0 100 200 300 400 500 600

Frames

100

Percentage of active leaves

ARF

Figure 7: The percentage of active leaves in the whole re-

gression forest at each frame for the ARF strategy (blue) and

a regression forest strategy (green) on the static sequence

01/01.

curacy of RF approaches drastically drops when the

scene changes, whereas our DynaLoc remains stable.

Fig. 6 also shows results on a part of the sequence

Dyna-03/Seq-02. For this example, when some ob-

jects move gradually, the result of our DynaLoc is

still accurate. Conversely, the RF approach fails com-

pletely.

Fine-tune Predictive Model on Static Scenes. Our

ARF also improves the predictive model on static

scenes. Indeed, Fig. 5-a) shows that the removal of

uncertain leaves signiﬁcantly improves accuracy (RF

chosen leaves gives better results than RF all leaves).

And the ARF update increases accuracy further than

the static strategy (RF). This is due to our ARF ﬁne-

tunes the predictive model from online data. Firstly,

we discard the uncertain predictive models given by

passive leaves. Then, these predictive models are re-

calculated based on active leaves update. Fig. 7 shows

the percentage of active leaves in the forest on the

static sequence DynaScene-01/Seq-01 with a variance

threshold T

var

= 0.1. Our ARF update increases the

number of active leaves.

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

650

5.3 Comparison to State-of-the-Art

Methods

Baselines. We compare our method to three differ-

ent RGB camera relocalization approaches: sparse

feature based (Sattler et al., 2017), machine learning

based (Kendall and Cipolla, 2017) and hybrid based

(Brachmann et al., 2016; Brachmann et al., 2017;

Brachmann and Rother, 2018; Duong et al., 2018)

methods. All baselines use RGB-D images for the

training phase and a single RGB image for the testing

phase. We report our results on both static scenes and

dynamic scenes.

Table 2: Comparison of our method with a hybrid method

based on a regression forest (Duong et al., 2018). The ac-

curacy is evaluated by median pose errors on DynaScenes

dataset.

Sequence (Duong et al., 2018) DynaLoc

Dyna-01/Seq-01 2.9cm, 1.9° 2.6cm, 1.7°

Dyna-02/Seq-01 3.2cm, 2.6° 3.0cm, 2.5°

Dyna-03/Seq-01

1.9cm, 1.4° 1.4cm, 1.2°

Dyna-04/Seq-01 4.3cm, 3.8° 3.3cm, 1.9°

Dyna-01/Seq-02 4.7cm, 2.9° 2.2cm, 1.6°

Dyna-02/Seq-02 7.2cm, 5.1° 3.5cm, 2.7°

Dyna-03/Seq-02 19.8cm, 14.3° 2.2cm, 1.5°

Dyna-04/Seq-02 25.6cm, 20.6° 3.2cm, 1.7°

Average 8.7cm, 6.6° 2.7cm, 1.9°

Table 3: Comparison of our method with state-of-the-art

methods. The accuracy is evaluated by median pose errors

on 7 scenes dataset.

Scene Active Search PoseNet2 DSAC++ DynaLoc

Chess 0.04m,2.0° 0.13m,4.5° 0.02m,0.5° 0.03m,1.3°

Fire 0.03m,1.5° 0.27m,11.3° 0.02m,0.9° 0.02m,1.2°

Heads 0.02m,1.5° 0.17m,13.0° 0.01m,0.8° 0.02m,1.3°

Ofﬁce 0.09m,3.6° 0.19m,5.6° 0.03m,0.7° 0.04m,1.5°

Pumpkin 0.08m,3.1° 0.26m,4.8° 0.04m,1.1° 0.05m,1.6°

Kitchen 0.07m,3.4° 0.23m,5.4° 0.04m,1.1° 0.04m,1.7°

Stairs 0.03m,2.2° 0.35m,12.4° 0.09m,2.6° 0.07m,1.9°

Average 0.05m,2.5° 0.23m,8.1° 0.04m,1.1° 0.04m,1.5°

Table 4: Comparison of our method with state-of-the-art

methods. The accuracy is measured by the percentage of

test images where the pose error is below 5cm and 5°on 7

scenes dataset.

Scene (Brachmann et al., 2016) DSAC (Duong et al., 2018) DynaLoc

Chess 94.9% 97.4% 73.1% 75.2%

Fire 73.5% 71.6% 79.5% 82.3%

Heads 49.1% 67.0% 80.1% 81.8%

Ofﬁce 53.2% 59.4% 54.5% 58.2%

Pumpkin 54.5% 58.3% 55.1% 56.7%

Kitchen 42.2% 42.7% 52.2% 54.5%

Stairs 20.1% 13.4% 41.0% 41.6%

Average 55.2% 58.5% 62.2% 64.3%

DynaScenes Dataset. We ﬁrst compare our method

to the hybrid method (Duong et al., 2018) on Dy-

naScenes dataset. Tab. 2 shows median camera pose

error for each sequence. Our results are moderately

better than (Duong et al., 2018) on the sequences

Table 5: Comparison of our method with DSAC++ in term

of runtime. Training time per scene and testing time per

image.

DSAC++ DynaLoc

Conﬁguration

GPU Tesla K80

Intel Core i7-7820HK

Intel Xeon E5-2680

Training time 1-2 days 5-10 minutes

Testing time 220ms 55ms (5ms for ARF update)

01,02,03,04/01 where there are challenging partial

occlusion, illumination changes without moving ob-

jects. Both methods achieve high accuracy thanks to

the use of SURF features and RANSAC algorithm.

However, on the remaining sequences, (Duong et al.,

2018) only obtains moderate accuracy for two scenes

Dyna-{01,02}/Seq-02 that contain respectively 30%

and 60% moving objects. For the scenes Dyna-

{03,04}/Seq-02 where all the objects move gradu-

ally, the accuracy of (Duong et al., 2018) drops sig-

niﬁcantly because RANSAC cannot eliminate a lot of

outliers on moving objects. Inversely, our method still

estimates precisely thanks to passive leaves detection

and update.

7 Scenes Dataset. Our method is also as accurate as

the state-of-the-art methods on static scenes. This is

demonstrated by results on 7 scenes dataset shown in

Tab. 3 and Tab. 4. Tab. 3 reports that our results

clearly outperform PoseNet2 (Kendall and Cipolla,

2017) on all scenes. And they are slightly better than

Active Search (Sattler et al., 2017) on this dataset

except for the translation error on the stairs scene.

The results also show that the accuracy of our method

is approximately equal to DSAC++ (Brachmann and

Rother, 2018). Tab. 4 shows the results of our

method, of the hybrid methods (Brachmann et al.,

2016; Brachmann et al., 2017; Duong et al., 2018)

using another metric: the percentage of test images

where the pose error is below 5cm and 5°. This met-

ric gives a better evaluation of the stably of a method

on this dataset. Regarding result of each scene, our

method achieves the best results on four scenes: Fire,

Heads, Kitchen and Stairs. Our method achieves bet-

ter accuracy than (Duong et al., 2018) on all scenes.

This indicates that the update of ARF from current

data improves signiﬁcantly the accuracy of the ini-

tially learned model. In term of the runtime, our

method is much faster than DSAC++ for both train-

ing and testing, as shown in Tab. 5.

DynaLoc: Real-Time Camera Relocalization from a Single RGB Image in Dynamic Scenes based on an Adaptive Regression Forest

651

6 CONCLUSION

In this paper, we proposed an adaptive regression for-

est that can update itself during the test phase with

current observations to tackle the challenge of dy-

namic data. This is performed by detecting and up-

dating passive leaves of a regression forest. We apply

our adaptive regression forest to our DynaLoc, a real-

time and accurate camera relocalization from a singe

RGB image in dynamic scenes with moving objects.

Our DynaLoc achieves high accuracy on our dynamic

scenes dataset. Moreover, our method is as accurate

as the state-of-the-art methods on static scenes dataset

but performs more quickly both training and testing

time.

REFERENCES

Alcantarilla, P. F., Yebes, J. J., Almaz

an, J., and Bergasa,

L. M. (2012). On combining visual slam and dense

scene ﬂow to increase the robustness of localization

and mapping in dynamic environments. In Robotics

and Automation (ICRA), 2012 IEEE International

Conference on, pages 1290–1297. IEEE.

Baatz, G., K

oser, K., Chen, D., Grzeszczuk, R., and Polle-

feys, M. (2012). Leveraging 3d city models for rota-

tion invariant place-of-interest recognition. Interna-

tional Journal of Computer Vision, 96(3):315–334.

Bescos, B., Facil, J. M., Civera, J., and Neira, J. (2018).

Dynaslam: Tracking, mapping, and inpainting in dy-

namic scenes. IEEE Robotics and Automation Letters,

3(4):4076–4083.

Brachmann, E., Krull, A., Nowozin, S., Shotton, J., Michel,

F., Gumhold, S., and Rother, C. (2017). Dsac - differ-

entiable ransac for camera localization. In The IEEE

Conference on Computer Vision and Pattern Recogni-

tion (CVPR).

Brachmann, E., Michel, F., Krull, A., Ying Yang, M.,

Gumhold, S., et al. (2016). Uncertainty-driven 6d

pose estimation of objects and scenes from a single

rgb image. In Proceedings of the IEEE Conference

on Computer Vision and Pattern Recognition, pages

3364–3372.

Brachmann, E. and Rother, C. (2018). Learning less is

more-6d camera localization via 3d surface regres-

sion. In Proc. CVPR, volume 8.

Cavallari, T., Golodetz, S., Lord, N. A., Valentin, J., Di Ste-

fano, L., and Torr, P. H. S. (2017). On-the-ﬂy adap-

tation of regression forests for online camera relocal-

isation. In The IEEE Conference on Computer Vision

and Pattern Recognition (CVPR).

Clark, R., Wang, S., Markham, A., Trigoni, N., and Wen, H.

(2017). Vidloc: A deep spatio-temporal model for 6-

dof video-clip relocalization. In The IEEE Conference

on Computer Vision and Pattern Recognition (CVPR).

Davison, A. J., Reid, I. D., Molton, N. D., and Stasse, O.

(2007). Monoslam: Real-time single camera slam.

IEEE transactions on pattern analysis and machine

intelligence, 29(6):1052–1067.

Duong, N.-D., Kacete, A., Soladie, C., Richard, P.-Y., and

Royan, J. (2018). Accurate sparse feature regression

forest learning for real-time camera relocalization. In

2018 International Conference on 3D Vision (3DV),

pages 643–652. IEEE.

Engel, J., Sch

ops, T., and Cremers, D. (2014). Lsd-slam:

Large-scale direct monocular slam. In European Con-

ference on Computer Vision, pages 834–849. Springer.

Glocker, B., Shotton, J., Criminisi, A., and Izadi, S. (2015).

Real-time rgb-d camera relocalization via randomized

ferns for keyframe encoding. IEEE transactions on

visualization and computer graphics, 21(5):571–583.

Guzman-Rivera, A., Kohli, P., Glocker, B., Shotton, J.,

Sharp, T., Fitzgibbon, A., and Izadi, S. (2014). Multi-

output learning for camera relocalization. In Proceed-

ings of the IEEE Conference on Computer Vision and

Pattern Recognition, pages 1114–1121.

Hartley, R. and Zisserman, A. (2005). Multiple view geom-

etry in computer vision. Robotica, 23(2):271–271.

Kendall, A. and Cipolla, R. (2016). Modelling uncertainty

in deep learning for camera relocalization. Proceed-

ings of the International Conference on Robotics and

Automation (ICRA).

Kendall, A. and Cipolla, R. (2017). Geometric loss func-

tions for camera pose regression with deep learning.

Proceedings of the IEEE Conference on Computer Vi-

sion and Pattern Recognition.

Kendall, A., Grimes, M., and Cipolla, R. (2015). Posenet: A

convolutional network for real-time 6-dof camera re-

localization. In Proceedings of the IEEE International

Conference on Computer Vision, pages 2938–2946.

Klein, G. and Murray, D. (2007). Parallel tracking and map-

ping for small ar workspaces. In Mixed and Aug-

mented Reality, 2007. ISMAR 2007. 6th IEEE and

ACM International Symposium on, pages 225–234.

IEEE.

Meng, L., Chen, J., Tung, F., Little J., J., Valentin, J., and

Silva, C. (2017). Backtracking regression forests for

accurate camera relocalization. In IEEE/RSJ Interna-

tional Conference on Intelligent Robots and Systems

(IROS 2017).

Mur-Artal, R., Montiel, J. M. M., and Tardos, J. D. (2015).

Orb-slam: a versatile and accurate monocular slam

system. IEEE Transactions on Robotics, 31(5):1147–

1163.

Newcombe, R. A., Fox, D., and Seitz, S. M. (2015). Dy-

namicfusion: Reconstruction and tracking of non-

rigid scenes in real-time. In Proceedings of the IEEE

conference on computer vision and pattern recogni-

tion, pages 343–352.

Newcombe, R. A., Izadi, S., Hilliges, O., Molyneaux, D.,

Kim, D., Davison, A. J., Kohi, P., Shotton, J., Hodges,

S., and Fitzgibbon, A. (2011). Kinectfusion: Real-

time dense surface mapping and tracking. In Mixed

and augmented reality (ISMAR), 2011 10th IEEE in-

ternational symposium on, pages 127–136. IEEE.

Riazuelo, L., Montano, L., and Montiel, J. (2017). Semantic

visual slam in populated environments. In 2017 Eu-

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

652

ropean Conference on Mobile Robots (ECMR), pages

1–7. IEEE.

Sattler, T., Leibe, B., and Kobbelt, L. (2011). Fast image-

based localization using direct 2d-to-3d matching. In

2011 International Conference on Computer Vision,

pages 667–674. IEEE.

Sattler, T., Leibe, B., and Kobbelt, L. (2017). Efﬁcient &

effective prioritized matching for large-scale image-

based localization. IEEE transactions on pattern anal-

ysis and machine intelligence, 39(9):1744–1756.

Shotton, J., Glocker, B., Zach, C., Izadi, S., Criminisi, A.,

and Fitzgibbon, A. (2013). Scene coordinate regres-

sion forests for camera relocalization in rgb-d images.

In Proceedings of the IEEE Conference on Computer

Vision and Pattern Recognition, pages 2930–2937.

Sun, Y., Liu, M., and Meng, M. Q.-H. (2017). Improving

rgb-d slam in dynamic environments: A motion re-

moval approach. Robotics and Autonomous Systems,

89:110–122.

Tan, W., Liu, H., Dong, Z., Zhang, G., and Bao, H. (2013).

Robust monocular slam in dynamic environments. In

Mixed and Augmented Reality (ISMAR), 2013 IEEE

International Symposium on, pages 209–218. IEEE.

Tateno, K., Tombari, F., Laina, I., and Navab, N. (2017).

Cnn-slam: Real-time dense monocular slam with

learned depth prediction. In The IEEE Conference on

Computer Vision and Pattern Recognition (CVPR).

Tsai, R. Y. and Lenz, R. K. (1988). Real time versatile

robotics hand/eye calibration using 3d machine vi-

sion. In Robotics and Automation, 1988. Proceed-

ings., 1988 IEEE International Conference on, pages

554–561. IEEE.

Valentin, J., Nießner, M., Shotton, J., Fitzgibbon, A., Izadi,

S., and Torr, P. H. (2015). Exploiting uncertainty in

regression forests for accurate camera relocalization.

In Proceedings of the IEEE Conference on Computer

Vision and Pattern Recognition, pages 4400–4408.

Walch, F., Hazirbas, C., Leal-Taixe, L., Sattler, T., Hilsen-

beck, S., and Cremers, D. (2017). Image-based local-

ization using lstms for structured feature correlation.

In The IEEE International Conference on Computer

Vision (ICCV).

Wangsiripitak, S. and Murray, D. W. (2009). Avoiding mov-

ing outliers in visual slam by tracking moving objects.

In ICRA, volume 2, page 7.

DynaLoc: Real-Time Camera Relocalization from a Single RGB Image in Dynamic Scenes based on an Adaptive Regression Forest

653