
Discrete Focus Group Optimization Algorithm for Solving Constraint
Satisfaction Problems
Mahdi Bidar, Malek Mouhoub and Samira Sadaoui
Department of Computer Science, University of Regina, Regina, Canada
Keywords: Constraint Satisfaction Problems (CSPs), Nature-inspired Techniques, Optimization, Metaheuristics.
Abstract: We present a new nature-inspired approach based on the Focus Group Optimization Algorithm (FGOA) for
solving Constraint Satisfaction Problems (CSPs). CSPs are NP-complete problems meaning that solving
them by classical systematic search methods requires exponential time, in theory. Appropriate alternatives
are approximation methods such as metaheuristic algorithms which have shown successful results when
solving combinatorial problems. FGOA is a new metaheuristic inspired by a human collaborative problem
solving approach. In this paper, the steps of applying FGOA to CSPs are elaborated. More precisely, a new
diversification method is devised to enable the algorithm to efficiently find solutions to CSPs, by escaping
local optimum. To assess the performance of the proposed Discrete FGOA (DFGOA) in practice, we
conducted several experiments on randomly generate hard to solve CSP instances (those near the phase
transition) using the RB model. The results clearly show the ability of DFGOA to successfully find the
solutions to these problems in very reasonable amount of time.
1 INTRODUCTION
A wide variety of real world applications, including
scheduling, planning (Mouhoub, 2003),
configuration (Mouhoub & Sukpan, 2012) and
timetabling (Hmer & Mouhoub, 2016), can be seen
as constraint problems. Over the last four decades,
researchers have focused on developing effective
algorithms including systematic and approximation
methods for tackling these problems modeled using
the Constraint Satisfaction Problem (CSP)
framework (Dechter, 2003). A CSP includes a finite
set of variables,
,…,
, for every variable
, a finite set of values (or domain
, and a finite
set of constraints
,…,
that restrict the
values that variables can simultaneously take. A
CSP solution,
,…,
where
∈
, is the assignment of values to each
variable such that all constraints are satisfied. When
solving a CSP, we might be looking for one, many
or all solutions (Solnon, 2002). In the case where a
solution does not exist, the problem is inconsistent.
As a matter of fact, many of the real world problems
are over-constrained and do not have a solution. In
this particular case, the goal is to look for an
assignment satisfying the largest number of
constraints. This latter notion is the generalized
definition of CSPs which is called Max-CSPs
(Freuder, 1992).
The most well-known systematic search
algorithm for solving CSPs is Backtracking
(Dechter, 2003). This algorithm incrementally
attempts to extend a partial solution toward a
complete one by assigning values to variables in a
particular sequence. Given that CSPs are NP-hard
problems, solving them with systematic search
methods requires an exponential time, O(d
n
), where
n is the number of variables and d their domain size.
Despite this limitation, the running time, in practice,
of Backtracking can be improved through constraint
propagation (Dechter, 2003). However this latter
algorithm has limitations for those hard to solve
problems (Solnon, 2002).
An alternative is to use incomplete methods like
metaheuristic algorithms. Although these algorithms
do not guarantee to find a solution to a CSP (nor
they can prove the inconsistency of over-constrained
problems), they are often capable solving CSPs in a
reasonable amount of time. Metaheuristics explore
search spaces, using a compromise between
exploitation and exploration in order to find a
solution. The main inspiration sources of these
algorithms are swarm intelligence, biological
322
Bidar, M., Mouhoub, M. and Sadaoui, S.
Discrete Focus Group Optimization Algorithm for Solving Constraint Satisfaction Problems.
DOI: 10.5220/0008877803220330
In Proceedings of the 12th International Conference on Agents and Artificial Intelligence (ICAART 2020) - Volume 2, pages 322-330
ISBN: 978-989-758-395-7; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

processes as well as chemical and physical systems.
Over the last two decades, these algorithms have
become very popular due to their successes in
dealing with combinatorial problems and CSPs in
particular.
For instance, in (Solnon, 2002) a new approach
based on Ant Colony Optimization (ACO) is
presented for solving CSPs. The basic idea of this
work was to keep track of promising areas by laying
pheromone on them. This pheromone information is
used then as a heuristic for assigning appropriate
values to the problem variables. The performance of
the proposed ACO algorithm is boosted using local
search methods.
The Firefly Algorithm (FA) is another powerful
metaheuristic which has been successfully adopted
to CSPs as shown in (Bidar, 2018) and (Bidar,
Mouhoub, & Sadaoui, 2018). In these works,
discrete version of FAs (called discrete FA or DFA)
were proposed and evaluated on different CSP
instances generated using the model RB. In (Fister,
2013) the applicability of FA for solving graph
coloring problems has been investigated. In this
work, a heuristic swap local search has been
employed to improve the overall search.
In (Breaban, 2007), a new discrete Particle
Swarm Optimization algorithm (PSO) is proposed
for solving CSPs. The new algorithm is obtained
after transforming a continuous PSO into its discrete
version as well as adopting important features such
as velocity and new positions of the particles. In
(Bidar & Mouhoub, 2019), a new discrete PSO was
proposed for solving CSPs in dynamic environment
(Dynamic CSPs (DCSPs)). In this work all the
features of the standard PSO redefined to be able to
deal with discrete problems like CSPs. This method
successfully applied to DCSPs and achieved very
promising results.
In (Eiben, 1994), Genetic Algorithms (GAs)
have been investigated for solving CSPs and their
applications including, Graph Coloring Problems
(GCPs) and N-Queen problems. In this regard,
several experiments have been conducted and their
results reported in the paper.
In (Abbasian, 2016) a new parallel architecture,
called Hierarchical Parallel Genetic Algorithm
(HPGA) has been proposed for solving CSPs. In
addition to exploring the search in parallel, through a
set of Islands of Parallel GAs (PGAs), this proposed
algorithm uses a new operator, called the Genetic
Modifier (GM) that injects good solutions to these
islands. These good solutions are obtained after
gathering useful information from constraint
violations in previous runs and ordering variables
according to (Mouhoub, 2011).
Other attempts for solving variants of CSPs have
also been proposed, such as in (Salari, 2008) where
ACO has been proposed for tackling GCPs. Here,
the authors present a new Max-Min ACO where at
each iteration Kempe Chain local search is applied
to boost the search. In (Mouhoub & Wang, 2008)
and (Mouhoub & Wang, 2006), the authors adopted
the ACO algorithm to quadratic assignment
problems using CSPs framework. In these works
they proposed new random walks strategies to
improve the stochastic local search of the standard
ACO in order to address the weakness of the ACO
in getting stuck in local optimum solution and
immature convergence. They also proposed a new
forward look ahead strategy to improve the
exploitation feature of the algorithm.
In (Cui, 2008), an improved PSO algorithm is
reported for solving GCPs. In this regard, a
disturbance factor is used in order to improve the
performance of the solving algorithm. The idea
behind the disturbance factor is to help the algorithm
escape local optimum by choosing some particles
(according to a probability function which
corresponds to the hardest problems to solve) and
resetting their velocities. This addresses one of the
main shortcomings of PSOs which consists of
immature convergence.
Recently, Fattahi and Bidar have proposed a new
metaheuristic, namely the Focus Group
Optimization Algorithm (FGOA) based on human
collaborating behavior in finding the best solution
for a problem through group discussion (Fattahi,
2018). The results of the experiments conducted on
different benchmarking functions including the
constrained and unconstrained ones, have shown the
high performance of FGOA and the potential it has
to dealing with problems under constraints. This has
motivated us to develop a discrete version of FGOA
that we call, Discrete FGOA (DFGOA), in order to
deal with CSPs.
To assess the performance of the proposed
DFGOA in practice, we conducted several
experiments on randomly generate hard to solve
CSP instances (those near the phase transition) using
the RB model. The results clearly show the ability of
DFGOA to successfully find the solutions to these
problems in very reasonable amount of the time.
Discrete Focus Group Optimization Algorithm for Solving Constraint Satisfaction Problems
323

2 FOCUS GROUP
OPTIMIZATION ALGORITHM
(FGOA)
FGOA is a new metaheuristic algorithm proposed by
Fattahi and Bidar (Fattahi, 2018) for global
optimization tasks. This algorithm is inspired by
collaborative behavior of a group’s members in
sharing their ideas on a subject in an attempt to
develop an appropriate solution for that problem.
The pseudo-code of FGOA is presented in
Algorithm 1. To get the best solution to a given
problem, FGOA works as follows. All members
share their solutions through group communication
and discussion, in an iterative manner, and under the
supervision of an agent called the Note Taker. Each
member’s solution is getting affected by the other
members’ solutions. This impact is calculated
according to (1):
∑
(1)
where,
is the impact of other participants’
solutions on the solution of participant i in k
th
iteration,
is the solution of the participant i in
iteration k,
is the best solution of participant j
achieved before iteration k, and
is the impact of
participant j which should be calculated based on the
cost of the best solution achieved by participant j. w
is the inertia weight. It is a real value in the interval
[0, 1].
Initialization
while (termination criterion is not met)
for i=1 to N // N is the population size
. IC = getCindex (PBC)
. Calculate the impact of other solutions on Solution i:
∑
. Apply impact limits on
. . Update
based on
. Apply limits on
by facilitator
. Evaluate the
. Update
based on
and
end for
Update NBC
k
k=k+1
end while
: impact of other solutions on Solution i in k
th
iteration
: Best Solution of i
th
Participant in k
th
iteration
: Solution of i
th
Participant in k
th
iteration
NBC
k
: Best Cost in k
th
iteration
IC
i
: Impact Coefficient belong to i
th
Participant
w: Inertia Weight
: Cost of i
th
Participant in k
th
iteration
PBC: Best Cost of all Participants
Rnd: Random Number
getCindex: A function that returns the Impact Coefficient based on PBC
Algorithm 1: Pseudo code of FGOA.
must be kept within the lower and the upper
bounds of impact as shown below in (2), as we need
to enforce some constraints to do so.
max
,
min
,
(2)
Finally, the solution of participant i is updated based
on the impact of the other solutions which is
calculated using (1):
(3)
The upper and lower bounds are enforced on the
participants’ solutions by (4) to keep them within the
bounds of the problem:
max
,
min
,
(4)
3 DISCRETE FOCUS GROUP
OPTIMIZATION ALGORITHM
(DFGOA)
The basic version of the FGOA has been developed
to deal with continuous problems (∈
). To
apply it to CSPs where search spaces are discrete
(∈
), we need a discretization of this algorithm
as described in the following subsections.
A. Potential Solution Representation
Let us consider a CSP with 6 variables,
,
,
,
,
,
, define on a domain
1,2,3,4
. A candidate solution is represented in
Figure 1.
Figure 1: Solution representation.
B. Fitness Function
Given that solving CSPs consists in finding a
complete assignment satisfying all the constraints
(or the one minimizing the number of constraints in
the case of over-constrained problems), we define
the fitness function as the total number of violated
constraints, for the given potential solution.
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
324

C. Solution Update
We define the impact factor parameter for each
potential solution based on its quality according to
(5).
∑
|
|
(5)
Here, IF(i) is the impact factor of participant i
which will take an important role in the next steps to
affect the other participants’ solutions,
is the
new impact factor of participant i, nPop is the
population size, Nvar is the number of variables of
the problem, rand(1) generates a random number in
(0,1) and
and
are the qualities of solutions
i and j respectively.
, the impact coefficient, is a random
number in (0,1) and is assigned to each solution. In
this regard, a set of nPop random numbers is
generated and is based on the quality assigned to
each solution (the more quality a solution has, the
larger the value will be assigned to).
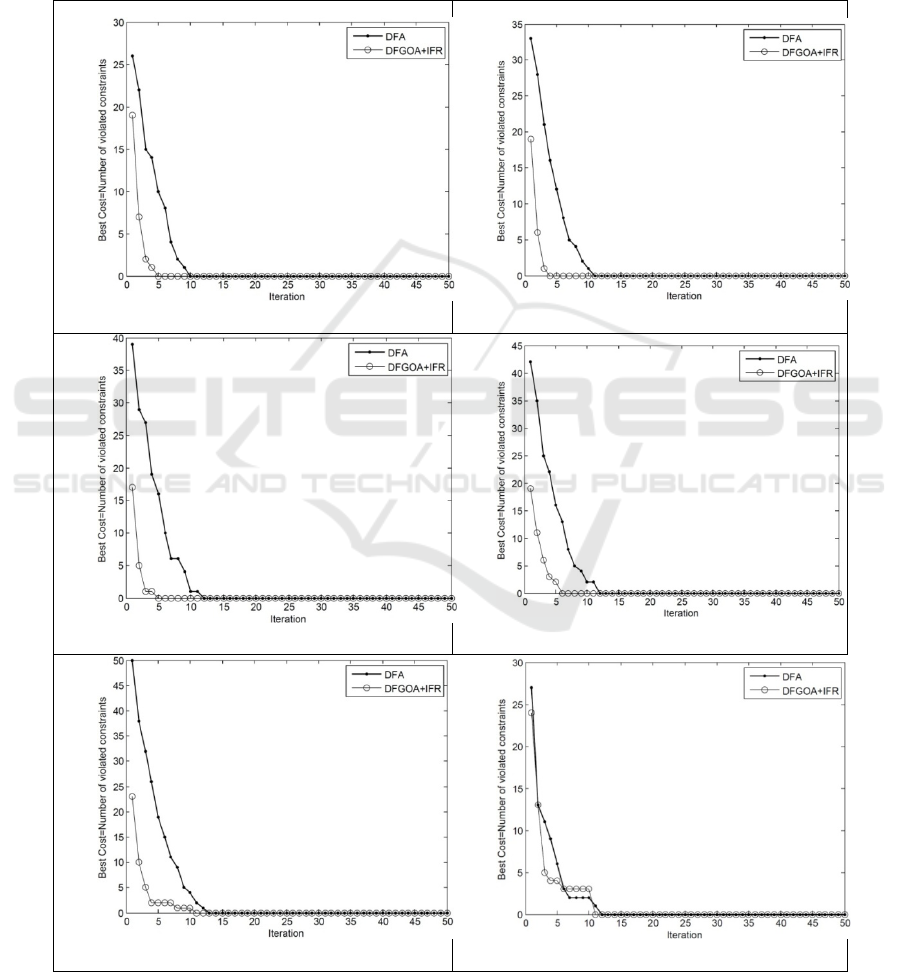
As an example, Table 1 shows this process for a
minimization problem for a set of given solutions
with associated qualities.
Table 1: Assignmnet of Impact Coefficient to
each Solution for Given Instance Problem (RD are
generated random numbers).
S1 S2 S3 S4 S5 S6 S7 S8
F(
)
21 20 18 14 10 7 8 2
RD
0.71 0.51 0.07 0.18 0.40 0.59 0.24 0.14
IC(i)
0.18 0.21 0.24 0.40 0.51 0.63 0.59 0.71
D. Affecting other participants’ Solutions
In a discrete problem space, affecting a solution can
be interpreted as replacing its variables’ values with
the corresponding values of the better solution with
an appropriate probability. This is done in order to
avoid the immature convergence of the algorithm. In
our proposed algorithm, this replacement is done by
considering IF() as the probability of this
replacement. In our experimentation, we normalize
the Impact Factor between 0 and 1 according to (6).
1
(6)
Here,
and
are the
expected qualities of the best and the worst
solutions. In fact, the larger IF(i), the more chance
participant i (
) has to impact the other participant’
solutions. This replacement is done according to (7).
,
←
,
and
(7)
,
is the replacement equation, rnd is a
random number in (0,1). Figure 2 indicates the steps
through which
is being affected by
.
According
to this figure, the corresponding variables in two
solutions with equal values remain unchanged.
However, the other variables’ values of
are
replaced with probability IF(1)=0.3, by the
corresponding variables’ values of
.
V
1
V
2
V
3
V
4
V
5
V
6
:
1 3 2 4 1 1
:
3 1 3 4 2 3
→
1
st
step → 3 4
2
nd
step→ 3 1 4
3
rd
step→ 3 1 2 4
4
th
step→ 3 1 2 4 2
5
th
step→ 3 1
2
4
2
1
Figure 2: Steps showing how participant 2 (S
2
) is affected
by participant 1 (S
1
).
At the first, second and forth steps above, the
variables’ values of
remained unchanged.
However, in third and fifth steps,
variables values
are replaced by those of
,
resulting in
312421
.
E. Solutions Diversification
One of the main challenges when searching for a
solution is the risk of being trapped in a local
optimum. This immature convergence is caused by
the lack of diversity in potential solutions. To
overcome this issue, diversification via
randomization is adopted to enable the algorithm to
search problem spaces more efficiently.
In this regard, solutions that are different from
the current ones are generated which results in
higher probability of escaping local optimum and,
hopefully, get optimal solutions.
In this regard, we use a controlling parameter,
called CP, to detect if the FGOA has been trapped in
local optimum, and this happens when it cannot
make further improvements. This parameter, through
(8), monitors the progress trend of the algorithm and
if, for some iterations, not enough progress has been
made by the algorithm, this parameter enables a
randomization method to diversify the solutions.
Discrete Focus Group Optimization Algorithm for Solving Constraint Satisfaction Problems
325
∑
1
(8)
IN is the current iteration number, WS is the
window size, and GB(i) is the global best solution in
iteration i. Here, window size determines the number
of iterations to be considered to determine if an
acceptable progress has been made by the algorithm.
If CP is less than the user-defined threshold value,
the algorithm activates a new randomization method
called IF Randomization (IFR).
F. IF Randomization (IFR)
We have employed IF Randomization method for
diversifying the solutions. According to this method
based on the Impact Factor (IF) of a solution, a
variable value of a given solution is replaced with
another value which is randomly chosen from its
domain with probability
1
(as shown in
Figure 3).
The probability
1
causes more quality
solutions to be subject to less changes in their
variables values. The procedure of IF Randomization
is presented in Figure 4.
V
1
V
2
V
3
V
4
V
5
V
6
:
1 3 2 4 1 1
Select variables with
probability 1
.
3 2
1
Assign new values for
the selected variables.
4
3 2
2 3
1
Figure 3: Process of diversification of a solution
considering probability 1
.
Procedure IF Randomization
b I
f
CP<Threshold
a For k=1:Nvar
A rnd=rand()
b if rnd<(1-IF(k))
2
m Temp← randomly choose value d∈D
g S
k←Temp
h Endif
a Endfor
1 Endif
Figure 4: IF Diversifier scheme.
4 EXPERIMENTATION
To assess the performance of our DFGOA, we use
the model RB (Xu, 2000) to randomly generate
binary CSP instances (CSPs with constraints
involving only pair of variables).
The model RB is based on the model B and has
the advantage of generating those hard instances that
are close to the phase transition.
The model RB has two controlling parameters p
and r, and two critical values
and
.The relation
between these two parameters and their
corresponding critical values determines if a
generated CSP instance is solvable or not. More
precisely, if
and
, a random CSP
instance generated using the model RB is solvable
with a high probability (close to 1) as the number of
the variables approach the infinity. If
and
, a CSP instance is unsolvable with
probability close to 1.
Each CSP instance is generated as follows using
the parameters n, p, α and r where n is the number of
CSP variables, p (0 < p < 1) is the constraint
tightness (ratio of the number of eligible tuples over
the Cartesian product of the domains of the involved
variables), and r and α (0 < r, α < 1) are two positive
constants used by the model RB.
1. Select with repetition random
constraints. Each random constraint is formed by
selecting k of n variables (without repetition). r is the
number of constraints for each CSP.
2. For each constraint, we uniformly select without
repetition q=pd
k
incompatible pairs of values,
where d = n
α
is the domain size of each variable and
each constraint involves 1
compatible
tuples of values (2 for binary CSPs).
All the variables have the same domain
corresponding to the first d natural numbers (0 ...
d−1). According to (Xu, 2000), the phase transition
is calculated as follows:
= 1 − e
−α/r
. Solvable
problems are therefore generated with P<
.
The proposed method and Model RB have been
implemented by MATLAB R2013b and all
experiments have been performed on a PC with Intel
Core i7-6700K 4.00 GHz processor and 32GB RAM.
We compare our algorithm with the DFA
presented in (Bidar, 2018) on the same test bed in
terms of population size (30) and considering the best
tuned parameters for both algorithms.
CSP instances are generated with different
tightness value ranging from 0.1 to 0.6. We consider
CSPs with 100 variables. The results are compared in
terms of Success Rate (SR), Running Time (RT) and
the Number of the Violated Constrained (NVC). The
window size for our DFGOA is 3 and the threshold
value is 0. Therefore, if for 3 successive iterations no
improvement has been made, DFGOA activates the
IF Diversifier. To normalize IF (see (6)) the worst
solution (the one that violates all the constraints) has
a fitness value equal to the total number of
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
326
constraints and subsequently the best solution is the
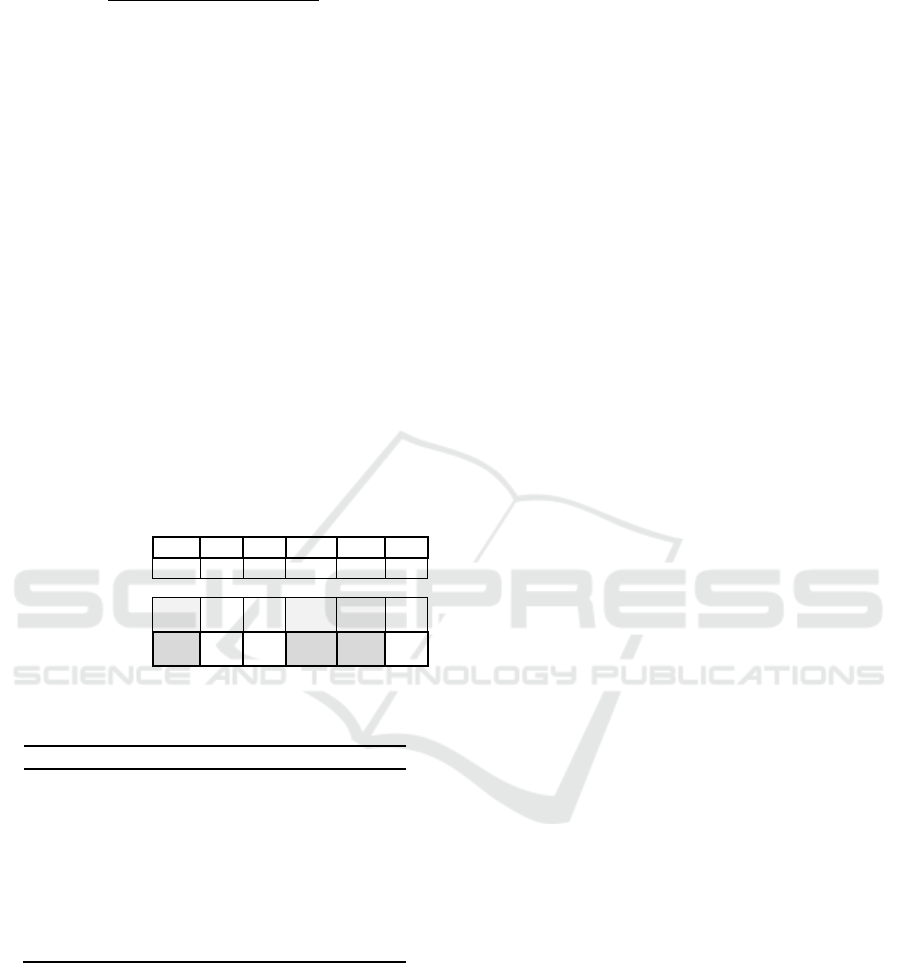
one with fitness equal to zero. Figure 5 compare the
convergence trend of the proposed DFGOA+IFR and
DFA on CSPs with 100 variables. From the figures,
we can see how both metaheuristic algorithms
converge to the best solutions in a very good amount
of the time.
We also compare the results of the experiments
achieved by DFGOA, DFA and variants of
systematic search methods, namely, Backtracking
(BT), Forward Checking (FC), and Full Look Ahead
(FLA) (Dechter, 2003). The results are reported in
Tables 2.
Since all methods achieved the best solution in all
experiments, this table only report the running time
of different methods for achieving the best solution.
Tightness=0.35, DFGOA+IFR Running Time=20.2440, DFA
Running Time=24.7091
Tightness=0.4, DFGOA+IFR Running Time=26.1065, DFA
Running Time=29.9511
Tightness=0.45, DFGOA+IFR Running Time=36.9663, DFA
Running Time=36.5480
Tightness=0.5, DFGOA+IFR Running Time=25.3553, DFA
Running Time=40.2505
Tightness=0.55, DFGOA+IFR Running Time=39.1651, DFA
Running Time=42.9272
Tightness=0.60, DFGOA+IFR Running Time=67.2543,
DFA Running Time=58.2602
Figure 5: Comparing convergence trend of the DFGOA and DFA on CSPs with 100 variables and a tightness from 0.3 to 0.
Discrete Focus Group Optimization Algorithm for Solving Constraint Satisfaction Problems
327
FC and FLA have been developed to improve the
performance of BT, in practice, by reducing the
domain sizes (and consequently the search space)
through constraint propagation (Dechter, 2003).
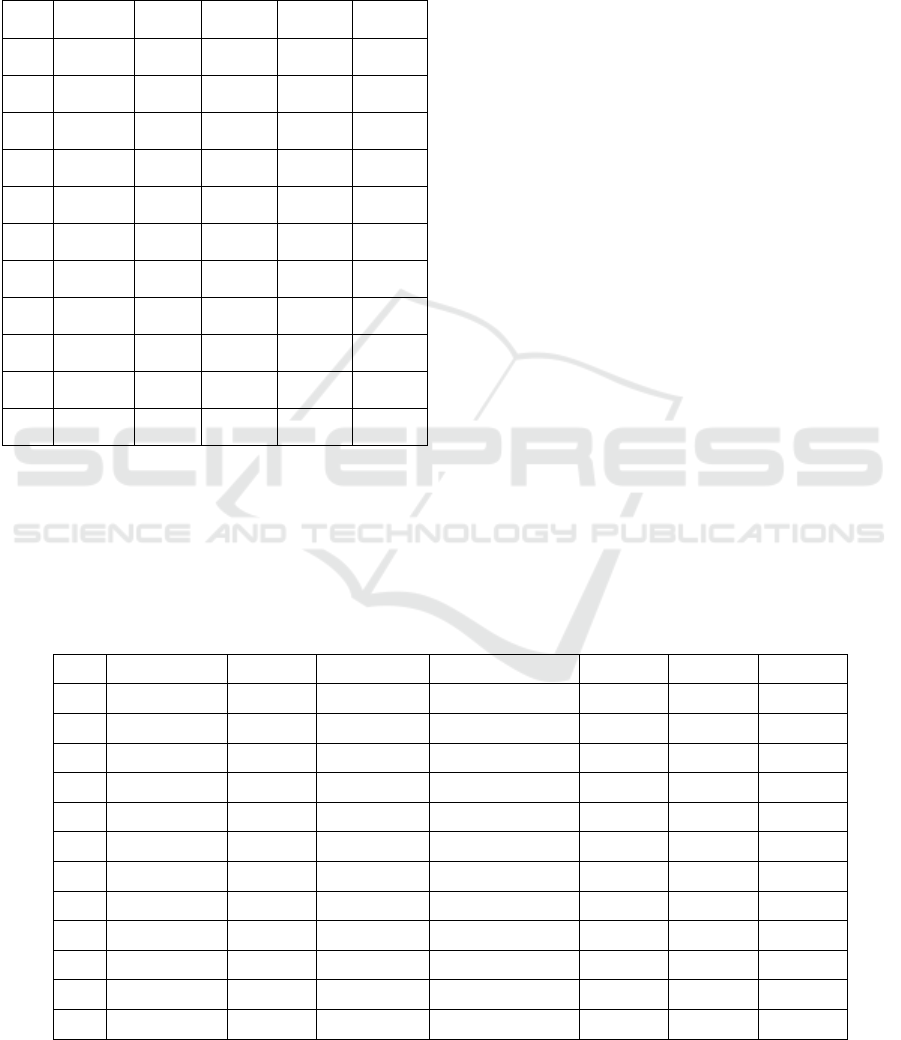
Table 2: Achieved Results (RT) by DFGOA and
Systematic Methods on CSPs with 100 Variables.
P
DFGOA
+IFR
DFA
BT FC FLA
0.1
2.694 6.0216 9.370 9.433 5.1778
0.15
9.012 8.418 20.321 16.428 15.3742
0.2
12.273 17.628 40.067 39.443 26.3828
0.25
14.483 14.026 49.523 47.175 39.3856
0.3
18.001 15.416 91.067 61.410 56.7726
0.35
19.830 21.849 141.969 101.679 100.783
0.4
19.903 30.539 158.854 149.838 124.532
0.45
26.443 31.810 196.688 148.484 145.761
0.5
34.699 38.109 306.486 198.877 165.945
0.55
39.739 43.627 296.960 239.307 213.962
0.6
46.565 55.126 416.111 323.019 252.535
The results show that although all methods are
successful in getting the complete solutions, DFA
and DFGOA outperform the systematic search
techniques.
DFGOA shows however better performance than
DFA and this is mainly due to its ability in
diversifying the solutions thanks to our IF
Randomization.
For further investigations, we compared the
results achieved by FGOA and DFA with those
achieved by the following GA variants (Abbasian,
2016). These comparisons are based on success rate
(SR) and number of violated constraints (NVC).
MPC: GA with multi parent crossover
(Abbasian, 2016).
OPC: Standard Genetic Algorithm with one
point crossover (Abbasian, 2016).
PSC: GA with Parental Success Crossover
proposed in (Abbasian, 2016).
HPGA+PSC: Hierarchical Parallel Genetic
Algorithm.
HPGA+GM+PSC: Hierarchical Parallel Genetic
Algorithm with proposed GM operator in
(Abbasian, 2016) and PSC crossover.
The results of these experiments are presented in
Table 3. As we can see, DFGOA and DFA achieved
the complete solutions (solutions that satisfy all
constraint) in all experiments.
HPGA+GM+PSC achieved the best performance
and was able to find the solutions with tightness
ranging from 0.1 to 0.55 with 100% success rate.
For those with a tightness of 0.6, the success rate is
79%, meaning complete solutions are found 79% of
time.
The other versions of GA were unable to solve
CSP instances near the phase transition.
For example, MPC’s success rate in dealing with
CSPs with tightness equal to 0.6 is 0% with 78
fitness average of its best achieved solutions.
Table 3: Achieved Results by DFGOA, DFA and variants of Genetic Algorithms on CSPs with 100 Variables.
DFGOA+IFR DFA HPGA+PSC HPGA+GM+PSC MPC OPC PSC
P SR, NVC SR, NVC SR, NVC SR, NVC SR, NVC SR, NVC SR, NVC
0.1
100%, 0 100%, 0 100%, 0 100%, 0 100%,0 100%, 0 100%, 0
0.15
100%, 0 100%, 0 100%, 0 100%, 0 0, 4 100%, 0 100%, 0
0.2
100%, 0 100%, 0 100%, 0 100%, 0 0, 9 27%, 0 100%, 0
0.25
100%, 0 100%, 0 100%, 0 100%, 0 0, 17 0, 3 100%, 0
0.3
100% ,0 100% ,0 100% ,0 100% ,0 0, 25 0, 5 100%, 0
0.35
100%, 0 100%, 0 100%, 0 100%, 0 0, 28 0, 10 100%, 0
0.4
100%, 0 100%, 0 100%, 0 100%, 0 0, 37 0, 12 62%, 0
0.45
100%, 0 100%, 0 100%, 0 100%, 0 0, 45 0, 27 0, 5
0.5
100%, 0 100%, 0 100%, 0 100%, 0 0, 53 0, 30 0, 9
0.55
100%, 0 100%, 0 73%, 0 100%, 0 0, 69 0, 42 0, 15
0.6
100%, 0 100%, 0 0, 3 79%, 0 0, 78 0, 62 0, 17
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
328

5 CONCLUSION
We propose the discrete version of the Focus
Group Optimization Algorithm (FGOA) for
solving CSPs. In this regard, we described in
details all the necessary steps needed for DFGOA.
Moreover, in order to deal with local optimum, we
devised and proposed a new method for
diversifying the potential solutions. The
performances of DFGOA when augmented with
this diversification method have been assessed by
conducting experiments on random CSP instances
generated by the model RB. Comparing to other
metaheuristics as well as systematic search
methods, DFGOA shows better running time even
for the hardest instances.
In the near future, we plan to apply the
DFGOA for solving different variants of the CSP.
First, we will tackle over-constrained CSPs. In this
particular case, a solution does not exist and the
goal is to find one that maximizes the total number
of solved constraints. This latter problem is called
the max-CSP.
We will also consider the case where CSPs are
solved in a dynamic environment. In this regard,
the challenge is to solve the problem, in an
incremental way, when constraints are added or
removed dynamically.
Finally, we will consider the case where
constraints are managed together with quantitative
preferences. This problem is captured with the
weighted CSP (Schiex, Fargier, & Verfaillie,
1995), where two types of constraints are
considered: soft constraint that can be violated
with associated costs and hard constraints that
must be satisfied. The goal here is to find an
optimal solution satisfying all the hard constraints
while minimizing the total cost related to soft
constraints.
REFERENCES
Bidar, M., & Mouhoub, M. (2019). Discrete Particle
Swarm Optimization Algorithm for Dynamic
Constraint Satisfaction with Minimal Perturbation.
2019 IEEE International Conference on Systems,
Man and Cybernetics (SMC), 4353–4360.
Bidar, M., Mouhoub, M., & Sadaoui, S. (2018). Discrete
Firefly Algorithm: A New Metaheuristic Approach
for Solving Constraint Satisfaction Problems. 2018
IEEE Congress on Evolutionary Computation, CEC
2018 - Proceedings.
Hmer, A., & Mouhoub, M. (2016). A multi-phase hybrid
metaheuristics approach for the exam timetabling.
International Journal of Computational Intelligence
and Applications, 15(4), 1–22.
Mouhoub, M. (2003). Dynamic Path Consistency for
Interval-based Temporal Reasoning. IASTED
International Multi-Conference on Applied
Informatics, 21, 393–398.
Mouhoub, M., & Sukpan, A. (2012). Conditional and
composite temporal CSPs. Applied Intelligence,
36(1), 90–107. https://doi.org/10.1007/s10489-010-
0246-z
Mouhoub, M., & Wang, Z. (2006). Ant colony with
stochastic local search for the quadratic assignment
problem. Proceedings - International Conference on
Tools with Artificial Intelligence, ICTAI, 127–131.
Mouhoub, M., & Wang, Z. (2008). Improving the Ant
Colony Optimization Algorithm for the Quadratic
Assignment Problem. 2008 IEEE Congress on
Evolutionary Computation, CEC 2008, 250–257.
Dechter, R., and David C. Constraint processing.
Morgan Kaufmann, 2003.
Salari, E., and Kourosh E. "An ACO algorithm for the
graph coloring problem." Int. J. Contemp. Math.
Sciences 3, no. 6 (2008): 293-304.
Lü, Z., and Jin-Kao H. "A memetic algorithm for graph
coloring." European Journal of Operational Research
203, no. 1 (2010): 241-250.
Cui, G., Limin Q., Sha Liu, Yanfeng W., Xuncai Z., and
Xianghong C. "Modified PSO algorithm for solving
planar graph coloring problem." Progress in Natural
Science 18, no. 3 (2008): 353-357.
Solnon, C. "Ants can solve constraint satisfaction
problems." IEEE transactions on evolutionary
computation 6, no. 4 (2002): 347-357.
Bidar, M., Malek M., Samira S., and Mohsen Bidar.
"Solving Constraint Satisfaction Problems Using
Firefly Algorithms." In Advances in Artificial
Intelligence: 31st Canadian Conference on Artificial
Intelligence, Canadian AI 2018, Toronto, ON,
Canada, May 8–11, 2018, Proceedings 31, pp. 246-
252. Springer International Publishing, 2018.
Fattahi, E., Mahdi B., and Hamidreza R. K. "Focus
Group: An Optimization Algorithm Inspired by
Human Behavior." International Journal of
Computational Intelligence and Applications 17, no.
01 (2018): 1850002.
Fister Jr, I., Xin-She Y., Iztok F., and Janez B. "Memetic
firefly algorithm for combinatorial optimization."
arXiv preprint arXiv:1204.5165 (2012).
Breaban, M., Madalina I., and Cornelius C. "A new PSO
approach to constraint satisfaction." In Evolutionary
Computation, 2007. CEC 2007. IEEE Congress on,
pp. 1948-1954. IEEE, 2007.
Eiben, A. E., P-E. Raué, and Zsófia R. "Solving
constraint satisfaction problems using genetic
algorithms." In Evolutionary Computation, 1994.
IEEE World Congress on Computational
Intelligence., Proceedings of the First IEEE
Conference on, pp. 542-547. IEEE, 1994.
Abbasian, R., and Malek M. "A new parallel ga-based
method for constraint satisfaction problems."
Discrete Focus Group Optimization Algorithm for Solving Constraint Satisfaction Problems
329

International Journal of Computational Intelligence
and Applications 15, no. 03 (2016): 1650017.
Freuder, Eugene C., and Richard J. Wallace. "Partial
constraint satisfaction." Artificial Intelligence 58, no.
1-3 (1992): 21-70.
Xu, Ke, and Wei Li. "Exact phase transitions in random
constraint satisfaction problems." Journal of
Artificial Intelligence Research 12 (2000): 93-103.
Mouhoub, M, and Jafari Jashmi, B. “Heuristic
techniques for variable and value ordering in CSPs.”
GECCO 2011: 457-464, 2011.
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
330
