Using Unsupervised Machine Learning for Plasma Etching Endpoint

Detection

Imen Chakroun

, Thomas J. Ashby

, Sayantan Das

, Sandip Halder

, Roel Wuyts

and Wilfried Verachtert

Exascience Life Lab, IMEC, Leuven, Belgium

Advanced patterning, IMEC, Leuven, Belgium

Keywords:

Plasma Etch, Endpoint Detection, Principal Component Analysis, Clustering Algorithms.

Abstract:

Much has been discussed around the advent of Industry 4.0 tools to improve yield across front-end and back-

end semiconductor manufacturers. One of these tools is the etch endpoint detection (EPD) systems. It is

essential to optimize the etch process by precisely landing on the underlying layers, because over-etching can

cause underlying layer damage. In this work, we explore unsupervised machine learning for automatically

identifying the endpoint during plasma etching of low open-area wafers using optical emission spectroscopy.

1 INTRODUCTION

Traditionally, the main driving force for the semicon-

ductor industry is the continuous shrinking of device

feature sizes, thereby incorporating more devices per

unit area, reducing manufacturing cost and enhanc-

ing performance. However, the shrinking of feature

size leads to a decrease in the process window im-

posing extremely tight requirement not only for the

critical dimension (CD), but also for the edge and

width roughness of spaces and trenches, of contacts

and lines and 0f tip to tip (T2T) values. At sub-10nm

technology nodes these parameters have signiﬁcant

inﬂuence on the overall device performance. It has

been seen that CD and edge and width roughness and

T2T values are highly inﬂuenced by the plasma etch-

ing process. After the lithography process, the target

material to etch from the wafer surface reacts selec-

tively with the plasma without affecting the underly-

ing layers. Excess over etching can cause underlying

layer damage, CD variations and inﬂuence the rough-

ness if lines/trenches, resulting in yield loss. Thus, it

is essential to optimize the etch process by precisely

landing on the underlying layers. EndPoint Detection

(EPD) is a technique that can help here.

During the plasma etch process speciﬁc gases

are pumped into a chamber where they are turned

into plasma by means of microwaves. The resulting

plasma interacts with the exposed surface of the wafer

in a highly controlled fashion. As said, it is critical to

avoid excessive over-etching because it can damage

the underlying layers causing device failures and sub-

Figure 1: Mutliwavelength Optical Emission Spectra during

main etch of oxide experiments.

sequent yield reduction. As a mean to control the pro-

cess, etch endpoint detection (EPD) has received great

attention (H. Noh and Han., 2015) (H. Henry Yue and

Toprac., ). The most widely used method for endpoint

detection is to monitor the optical emission trace of

reactive gases in the plasma using optical emission

spectroscopy (OES) (Chen, 1996) (Puggini, 2015).

OES is popular because OES measurements can be

collected non-intrusively during wafer processing and

because they provide real-time plasma chemical in-

formation, making them more reliable. The measure-

ments correspond to the variation of the optical emis-

sion intensity of the plasma as a function of the re-

actants and by-products inside the etch chamber. Us-

ing this method, the endpoint is identiﬁed by monitor-

ing the intensity of an emission peak corresponding

Chakroun, I., Ashby, T., Das, S., Halder, S., Wuyts, R. and Verachtert, W.

Using Unsupervised Machine Learning for Plasma Etching Endpoint Detection.

DOI: 10.5220/0008877502730279

In Proceedings of the 9th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2020), pages 273-279

ISBN: 978-989-758-397-1; ISSN: 2184-4313

273

to a particular reactant or product that show a pro-

nounced variation at a certain time. However, using

few manually selected wavelengths as an endpoint de-

tection technique is only appropriate for high open

areas. For low open area etches, tracking individual

wavelengths often yields to an insufﬁcient signal-to

noise ratio (SNR). In small sample areas, changes in

the optical signal are very small making it difﬁcult to

detect the etching endpoint. Moreover, if the view-

port for optical-emission monitoring becomes blurred

due to prolonged use of the etching system, optical-

emission monitoring becomes impossible and regular

maintenance of these observation windows is required

(H. Jang and Chae., 2017). Other classical methods

simply time the etch. In this case the resulting EPD

is only valid for a very short number of runs before

process drift and noise render the results ineffective.

Figure 2: Principal component model of three dimensional

data set lying primarily in a single plane. (Barry M. Wise,

et al., 1996).

In this work, high-resolution multi-wavelength

OES data is used to provide the necessary sensitiv-

ity for detecting subtle endpoint signals. Detecting

etch endpoint from multi-wavelength OES data us-

ing existing simple methods is challenging. This is

because these simple methods usually rely on ﬁnd-

ing a representative wavelength for each gas and each

material used. Moreover, multi-wavelength OES data

is high-dimensional and large, since it encapsulates

measurements as a function of wavelength, time and

intensity. Figure 1 plots a sample of 1200 spectral

channels from 200 to 2000nm.

To overcome these challenges, data analysis tech-

niques have been applied for etching processes (Pug-

gini, 2015) (Goodlin, 2002). In this work, we com-

bine feature extraction with unsupervised machine

learning to extract key components that capture the

endpoint signal. We ﬁrst apply Principal Compo-

nent Analysis (PCA) to the raw data. PCA uses an

orthogonal transformation to convert a set of corre-

lated variables into a new set of linearly uncorrelated

variables called principal components. It’s often used

Figure 3: Schematic of a plasma etch chamber.

as a data compression algorithm or feature extraction

technique. Therefore, we believe that PCA is suit-

able for extract small partial signal changes of mul-

tivariate signals as demonstrated in (H. L. Maynard

and Ibbotson, 1996; S. Hong and Park, 2003). After-

wards, unsupervised clustering techniques such as the

balanced iterative reducing and clustering using hier-

archies algorithm (BIRCH) (Tian Zhang and Livny.,

1997) are applied. The remainder of the paper is

organized as follows: in Section 2 an overview of

existing research work using machine learning tech-

niques for EPD is given. In Section 3, our approach

for EPD using unsupervised machine learning tech-

nique is presented. Experimental settings and results

are described in Section 4. In Section 5, we provide a

summary of the work and possible future research.

2 RELATED WORK

PCA has been suggested as a method for analyz-

ing optical emission spectra due to its ability to dra-

matically reduce the dimensionality of large amounts

of OES data. For example, Rangan et al (S. Ran-

gan and Poolla, 1997) used PCA-reduced OES data

to form a linear dynamical model capable of detect-

ing endpoints and transition times in plasma etch.

(A. d’Aspremont and Lanckriet, 2007) used sparse

PCA for selecting key wavelengths from OES data.

In (Goodlin, 2002), the authors reviewed statistical

methods for OES in endpoint detection and suggested

a novel method for weighting OES according to SNR.

In (Han et al., 2008), the PCA algorithm was modiﬁed

to determine the loading vector from the model wafer,

and the score vector from the real-time data of the tar-

get wafer to reduce the processing time.

Due to their ability to synthesize nonlinear re-

ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods

274

lationships from process data, artiﬁcial neural net-

works found application in the prediction of etch end-

point detection (H. L. Maynard and Ibbotson, 1996).

(S. Hong and Park, 2003) compared the use of PCA

and ANNs for feature extraction from OES data and

proposed a further ANN model for the reduced data.

Similarly, (Kim and Kim., 2004) compared ANN

and PCA but reported a signiﬁcant performance im-

provement with partial OES models compared to con-

ventional PCA-reduction. Other supervised machine

learning techniques such as support vector machines

(SVM) have been used in (K. Han and Chae., ) for

endpoint detection based on OES measurement. In

(H. Jang and Chae., 2017), analyzing the optical emis-

sion spectra with a K-means clustering algorithm is

proposed on raw data.

In the next section we will explain how our pro-

posed technique improves on the related work pre-

sented here.

3 ENDPOINT DETECTION

USING PCA AND CLUSTERING

In this section we document the two main steps of our

method, namely i) PCA for dimensionality reduction

and variable selection, and ii) BIRCH clustering.

3.1 Dimensionality Reduction and

Variable Selection

OES data are difﬁcult to deal with since the number

of variables (wavelengths) is usually larger than the

number of measurements. In such cases, each vari-

able can be obtained as a linear combination of the

others making uncovering the true relationship be-

tween the different variables difﬁcult. Principal com-

ponent analysis (PCA) is a good candidate technique

for dealing with such data being an established statis-

tical method for multivariate data compression and in-

formation extraction. Its basic idea is to extract com-

binations of variables or factors (commonly expressed

in percentage of explained variance) capable of recon-

structing the majority of the information of the orig-

inal high dimensional data. The concept of principal

components is shown graphically in Figure 2 showing

a three dimensional data set where the data lie primar-

ily in a plane. The dimension reduction is achieved by

identifying the principal directions, called principal

components, in which the data varies. PCA assumes

that the directions with the largest variances are the

most ”important”. In this example, the ﬁrst PC aligns

with the greatest variation in the data. The second PC

axis is the second most important direction and it is

orthogonal to the ﬁrst PC axis.

3.2 Clustering Techniques for Endpoint

Detection

Etch endpoint detection is an unsupervised problem

since no real ground truth can be used to control the

data analysis technique. In production, EPD is based

on best practices and domain expertise. Recall also

that the basic idea of EPD is to ﬁnd a change point or

variation in the OES spectra that may alert about etch

rate limit. This means we are looking for two disjoint

group of points in the spectral curve that are sepa-

rated by a change in the signal that deﬁne the before-

endpoint and after-endpoint status. Hence, the idea

of using unsupervised machine learning algorithms

such as clustering which is the process of gathering

objects in groups called clusters without prior knowl-

edge only based on their similarity between each

other and difference with objects from other groups.

(H. Jang and Chae., 2017) also used clustering tech-

niques for enhancing sensitivity of dielectric plasma

etching EPD. In their case, K-means was applied on

raw normalized data. In this work, hierarchical clus-

tering is used via the balanced iterative reducing and

clustering using hierarchies (BIRCH) algorithm with

PCA as a dimensionality reduction technique. Using

K-means cluster in real-time application is tricky be-

cause the load applied to the processor increases with

continuous data collection and normalization of the

optical signals. Moreover, K-means is very sensitive

to noise and outliers since a small number of such data

can substantially inﬂuence the centroids. BIRCH is

an online-learning clustering algorithm, it’s an incre-

mental method that does not require the whole data

set in advance. It is also local where each cluster-

ing decision is made without scanning all data points

and currently existing clusters. It does not inspect all

data points or all currently existing clusters equally

for each ’clustering decision’ and performs heuristic

weighting based on the distance between these data

points (Tian Zhang and Livny., 1997).

As aforementioned, the aim here is to construct

two disjoint group of points representing the before

and after etch endpoint. To construct such clusters,

the OES data is split in batches that are normalized.

PCA is applied and the output is fed to the birch algo-

rithm. The resulting clusters are then evaluated using

the silhouette score. The silhouette score (Rousseeuw,

1987) refers to a method of interpretation and valida-

tion of consistency within clusters of data, it measures

the cohesion of the cluster (how similar an object is to

its own cluster) and the separation compared to other

Using Unsupervised Machine Learning for Plasma Etching Endpoint Detection

275

Figure 4: Simpliﬁed process ﬂow for the etch process.

clusters. The silhouette ranges from -1 to 1 where co-

efﬁcient values near 1 indicate that the sample is far

away from the neighboring clusters, values of 0 indi-

cate that the sample is on or very close to the decision

boundary between two neighboring clusters and neg-

ative values indicate that those samples might have

been assigned to the wrong cluster.

4 EXPERIMENTS

4.1 Experimental Settings

Etch Process: In Reactive-Ion Etching (REI), a

high frequency electromagnetic ﬁeld (HF) is applied

to the upper electrode and low frequency ﬁeld (LF) to

the bottom electrode. The schematic of a plasma etch

chamber is shown in Figure 3. During the plasma etch

process the wafer is positioned on the bottom elec-

trode and is held ﬁrmly in place by electrostatic chuck

(ESC). The LF power applied to the bottom electrode

determines the ion energy directing positive ions in

the plasma onto the wafer and is responsible for phys-

ical etching. On the other hand, the HF applied to

the top electrode inﬂuences the plasma density and is

responsible for generating radicals for chemical etch-

ing.

In a production process, wafers are grouped in

lots and processed sequentially undergoing several

etching steps. Lots are also processed sequentially

through etch chambers, interspersed with cleaning

and maintenance operations. Cleaning cycles are

typically done between each lot to remove the by-

products of plasma etching that build up on the cham-

ber walls, and are detrimental to etching performance.

Creation and Collection of Data: In major spec-

trometers, several channels are used each one record-

ing a single wavelength. Wavelength intensity mea-

surements are taken without interruption with a ﬁxed

sampling rate during processing of wafers. The re-

sulting dataset is for every etching step a chronologi-

cally ordered values for a set of wafers. In this work,

21 wafers have been used. The wavelength intensities

were measured during 500 to 1100 seconds at a sam-

pling rate of 1 second using 1200 channels. For easy

reading, the presented results are for one wafer.

A simpliﬁed process ﬂow for the etch process is

illustrated in Figure 4. In this study our focus will be

on two steps in this process. For the remaining of the

paper, we call Step A for the SOC etch step and Step

B for the Oxide etch step.

4.2 Experimental Results

In Figures 5a and 6a, we plot the time series behav-

ior of a sample OES spectrum for the wafer under in-

vestigation and the two etching steps A and B. It’s

clear from the ﬁgure that due to the big range of wave-

lengths, manually checking the variations in the sig-

nals is difﬁcult or impossible. Thinking of selecting

some dominant wavelengths based on domain knowl-

edge is also misleading and incomplete. As an exam-

ple, in Figures 5b and 6b four dominant spectral chan-

nels for the two aforementioned steps are plotted. For

step B, in Figure 6b, the raw signal is almost uniform

for three of the selected wavelengths and smoothly

decreases over time for the 387nm wavelength. No

distinct change point can be detected manually. How-

ever, in Figure 5b, one ﬁrst big slope can be noticed

around 30 seconds and a second smoother change can

be seen between 70 and 90 seconds.

We applied ﬁrst PCA to this dataset formatted as

an T × W matrix, where T is the number of exper-

imental runs and W is the number of measurements

collected for each wavelengths. For every etching

step a different matrix is considered. The results ob-

tained by applying PCA to the complete OES spec-

trum presented in Figures 5a and 6a are plotted in

Figures 7a and 7b respectively. In both plotted PCA

ﬁrst components, we can clearly identify two big vari-

ations in the signal: for Step A, in Figure 7a, in

the interval [20 seconds,40 seconds]. For Step B,

in Figure 7b, a big variations is observed between

50 and 65 seconds and a slighter one in the interval

[25 seconds,35 seconds]. Compared to the original

multi-wavelength signal, the new representation sim-

pliﬁes and condenses the data while keeping the same

amount of information. Indeed, we report in Table

ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods

276

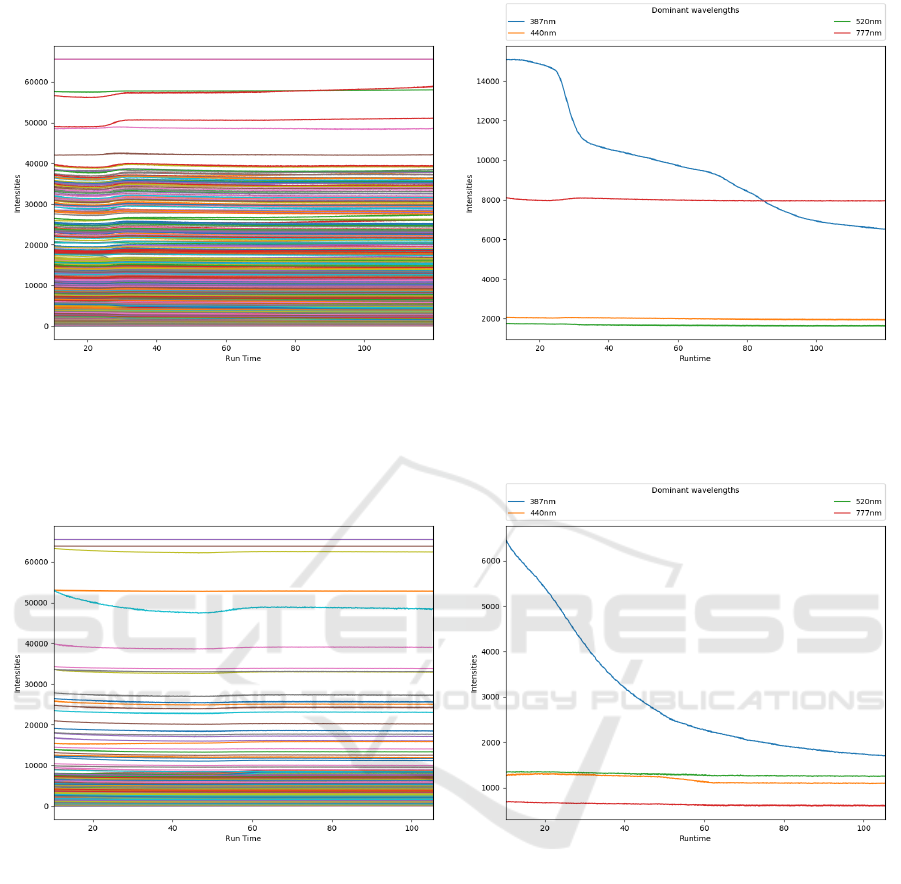
(a) Optical Emission Spectra during oxide etching

experiments.

(b) Time series behavior of the selected dominant spectral

channels.

Figure 5: Step A.

(a) Optical Emission Spectra during oxide etching

experiments.

(b) Time series behavior of the selected dominant spectral

channels.

Figure 6: Step B.

1 some of the explained variance randomly selected

from the experimented wafers. On average, the per-

centage of variance explained by the ﬁrst component

is 0.913 for step A and 0.936 for step B.

In Figures 8a and 8b, we plot the silhouette score

computed on the output of the clustering algorithm for

step A and B respectively. As already explained, the

silhouette score reﬂects the cohesion inside the clus-

ter and the separation with other clusters. For Step A,

in Figure 8a, the silhouette reaches a maximum value

of 0.79 around 45 seconds and strongly decreases few

seconds later around 57 seconds. For the rest of the

runtime the values are roughly constant around 0.62.

The peak value of the silhouette score at 45 seconds

indicates that the data can be separated at that time

and this separation can be deﬁned as the etching end-

point. In Figure 8b, the silhouette score is plotted for

step B. A ﬁrst ﬂat interval is observed around 45 sec-

onds, a maximum value is reached afterwards around

70 seconds. The values are constants around 0.6 for

the rest of the experiment. We suspect the endpoint

here to happen around the 70 seconds which corre-

sponds to the maximum value of the silhouette score.

Using Unsupervised Machine Learning for Plasma Etching Endpoint Detection

277

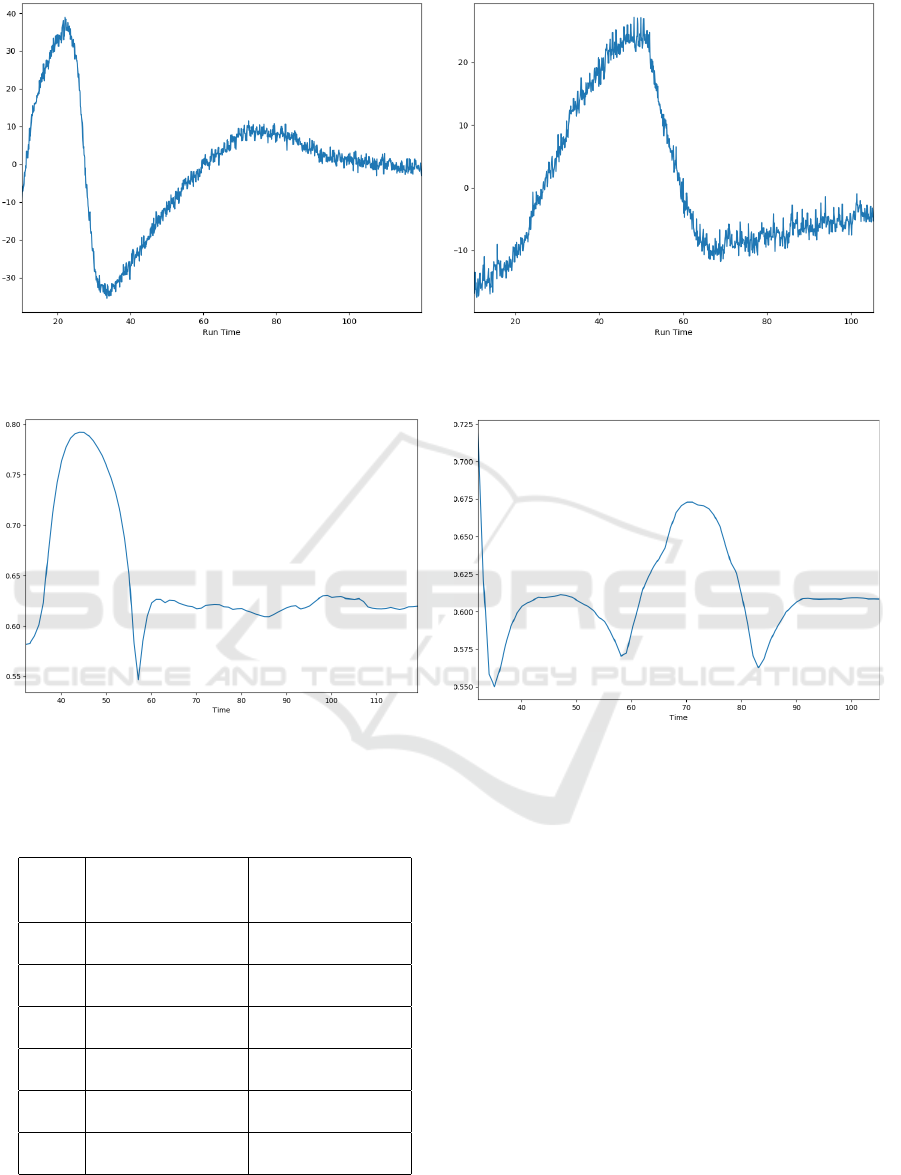
(a) Step A (b) Step B

Figure 7: Plotting PCA ﬁrst component.

(a) Step A (b) Step B

Figure 8: Silhouette score computed for the birch algorithm.

Table 1: Explained variances after PCA for randomly se-

lected wafers.

Wafer Explained variance

Step A

Explained variance

Step B

1 0.943 0.903

2 0.914 0.927

3 0.905 0.941

4 0.904 0.945

5 0.9027 0.950

6 0.908 0.950

5 CONCLUSION

In this work, we applied unsupervised machine learn-

ing techniques for identifying etch endpoint detection

using high-resolution multi-wavelength OES data.

PCA is ﬁrst applied on the raw data to extract mean-

ingful variables. Afterwards, the birch clustering is

used to separate the data divided into batches in two

clusters corresponding to the before-EPD and after-

EPD. Satisfactory decision about etch endpoint were

possible based on clearer variations in the silhouette

score which was used as a metric for cluster separa-

tion. As further improvement of this work, we should

be looking into methods that can produce the correct

response even when the input data is corrupted by

noise.

ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods

278

ACKNOWLEDGEMENT

This project has received funding from the Electronic

Component Systems for European Leadership Joint

Undertaking under grant agreement No 826589. This

Joint Undertaking receives support from the European

Unions Horizon 2020 research and innovation pro-

gram and Netherlands, France, Italy, Belgium, Ger-

many, Austria, Hungary and Israel.

REFERENCES

A. d’Aspremont, L. E. Ghaoui, M. J. and Lanckriet, G.

R. G. (2007). A direct formulation for sparse pca us-

ing semideﬁnite programming. In SIAM Rev., volume

49 no 3, page 434–448.

Chen, R., H. H. S. C. G. M. (1996). Plasma etch model-

ing using optical emission spectroscopy. Journal of

Vacuum Science & Technology, 14:1901–1906.

Goodlin, B. E. (April 2002). Multivariate endpoint detec-

tion of plasma etching processes. PhD thesis, Univ. of

Texas, Austin.

H. Henry Yue, S. Joe Qin, J. W. and Toprac., A. Plasma

etching endpoint detection using multiple wave-

lengths for small open-area wafers.

H. Jang, H. Lee, H. L. C. K. and Chae., H. (February 2017).

Sensitivity enhancement of dielectric plasma etching

endpoint detection by optical emission spectra with

modiﬁed k-means cluster analysis. In IEEE Trans-

actions on Semiconductor Manufacturing, volume 30.

issue 1.

H. L. Maynard, E. A. Rietman, J. T. C. L. and Ibbotson,

D. E. (1996). Plasma etching endpointing by monitor-

ing radio-frequency power In Journal of Electrochem.

Society, volume 143 no 6, pages 2029–2035.

H. Noh, D. K. and Han., S. (2015). Real time endpoint

detection in plasma etching using real-time decision

making algorithm. In China Semiconductor Technol-

ogy International Conference, Shangai., pages 1–3.

Han, K., Yoon, E. S., Lee, J., Chae, H., Han, K. H., and

Park, K. J. (2008). Real-time end-point detection us-

ing modiﬁed principal component analysis for small

open area sio2 plasma etching. In Industrial & Engi-

neering Chemistry Research, volume 47, no 11, pages

3907–3911.

K. Han, S. Kim, K. J. P. E. S. Y. and Chae., H. Principal

component analysis based support vector machine for

the endpoint detection of the metal etch process. In

Proc. IFAC World Congr.

Kim, B. and Kim., S. (2004). Partial diagnostic data to

plasma etch modeling using neural network. In Mi-

croelectron. Eng., volume 75 no 4, pages 397–404.

Puggini, L., M. S. (2015). Extreme learning machines for

virtual metrology and etch rate prediction. In 26th

IEEE Irish Signals and Systems Conference (ISSC),

pages 1–6.

Rousseeuw, P. J. (1987). Silhouettes: A graphical aid to

the interpretation and validation of cluster analysis. In

Journal of Computational and Applied Mathematics,

volume 20, pages 53–65.

S. Hong, G. M. and Park, D.-C. (2003). Neural network

modeling of reactive ion etching using optical emis-

sion spectroscopy data. In IEEE Trans. Semicond.

Manuf., volume 16 no 4, pages 598–6081–6.

S. Rangan, C. S. and Poolla, K. (1997). Modeling and ﬁlter-

ing of optical emission spectroscopy data for plasma

etching systems. In IEEE International Symposium of

Semiconducter Manufacturing, page B41–B44.

Tian Zhang, R. R. and Livny., M. (January 1997). Birch: A

new data clustering algorithm and its applications. In

Data Min. Knowl. Discov., pages 141–182.

Using Unsupervised Machine Learning for Plasma Etching Endpoint Detection

279