
Automated Synthesis of ATL Transformations from Metamodel
Correspondences
Kevin Lano
a
and Shichao Fang
b
King’s College London, London, U.K.
Keywords:
Model Transformations, ATL.
Abstract:
In this paper we describe techniques for semi-automatically synthesising transformations from metamodel
correspondences, in order to accelerate transformation development. We provide a strategy for synthesising
complete ATL transformations from correspondences, and evaluate the approach using examples from the
ATL zoo.
1 INTRODUCTION
Model transformations (MT) are central elements
of model-driven engineering (MDE). However, MT
specifications are often difficult to manually con-
struct, and MT definition requires a high level of ex-
pertise in particular MT languages. The development
of transformations can be a time-consuming process,
which limits the agility of MDE. Therefore it is in-
teresting to examine to what extent the transforma-
tion development process can be automated. Previous
work has shown that it is possible to automatically
recognise correspondences between source and target
metamodels of a proposed transformation, and to use
these as the basis of a transformation definition (Fang
and Lano, 2019; Kessentini et al., 2014; Schwichten-
berg et al., 2014).
In this paper we look in detail at how transfor-
mations can be constructed from the identified cor-
respondences, and define a process for synthesising
ATL transformations. We evaluate the benefits of the
process in terms of the reduction of effort expended in
MT construction, and in terms of the improved qual-
ity of the resulting transformations.
a
https://orcid.org/0000-0002-9706-1410
b
https://orcid.org/0000-0002-3556-4346
2 DERIVING
TRANSFORMATION
SPECIFICATIONS FROM
METAMODELS
Transformations operate on source and target meta-
models, usually one source metamodel MM
1
, and one
target metamodel MM
2
. When a transformation de-
veloper is starting to construct a MT specification,
their first task is usually to identify which classes and
features of MM
1
should be mapped to which classes
and features of MM
2
. In other words, what the cor-
respondence relation m (mapping) of MM
1
and MM
2
classes should be, and what the correspondence rela-
tion fm (feature mapping) of MM
1
and MM
2
features
should be.
As an example, Figure 1 shows the
metamodels of the ATL Class2Relational
transformation case from the ATL zoo
(www.eclipse.org/atl/atlTransformations). The
source metamodel MM
1
is Class, on the LHS, the
target metamodel MM
2
is Relational, on the RHS.
We have implemented different techniques for
recognising m and fm, based on structural, linguistic
and semantic similarities of MM
1
and MM
2
ele-
ments (Fang and Lano, 2019). These have been
defined as a plugin to the Eclipse Agile UML tools
(projects.eclipse.org/projects/modeling.agileuml).
Metamodels are imported as KM3 or Ecore files.
For example, the correspondence of Class to Table
and of Attribute to Column in the above case are
recognised by the structural similarity of these ele-
ments, whilst DataType in MM
1
and Type in MM
2
Lano, K. and Fang, S.
Automated Synthesis of ATL Transformations from Metamodel Correspondences.
DOI: 10.5220/0008873702630270
In Proceedings of the 8th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2020), pages 263-270
ISBN: 978-989-758-400-8; ISSN: 2184-4348
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reser ved
263

Figure 1: Class and Relational metamodels.
are linguistically similar. We primarily use struc-
tural similarity to identify class and feature correspon-
dences, with linguistic and semantic similarity as sec-
ondary criteria.
To formalise class and feature correspondences,
we use an abstract transformation notation called T L .
The notation expresses class correspondences of E to
F by the notation E 7−→ F, and feature correspon-
dences of f to g by the notation f 7−→ g.
A T L specification consists of a set of rules of the
form
{PreCond} E 7−→ F
p
1
7−→ q
1
.
.
.
p
n
7−→ q
n
where the p
i
are features (owned, inherited or com-
posed) of E, or OCL expressions in such features, and
the q
i
are distinct features of F. The optional PreCond
is a boolean-valued OCL expression in the p
i
.
The meaning of a class mapping {C} E 7−→ F as a
model transformation rule is that for every instance e
of E that satisfies C, there is a corresponding instance
e
0
of F. By default, distinct instances of E map to
distinct instances of F. A feature mapping p 7−→ q of
{C} E 7−→ F means that for corresponding instances
e : E, e
0
: F, the value of e
0
.q is the interpretation (e.p)
0
of e.p via the class mappings.
For Class2Relational, the initial automatically-
derived correspondences are:
NamedElt 7−→ Named
name 7−→ name
Class 7−→ Table
name 7−→ name
attr 7−→ col
Attribute 7−→ Column
name 7−→ name
owner 7−→ owner
type 7−→ type
Classifier 7−→ Type
name 7−→ name
DataType 7−→ Type
name 7−→ name
Having obtained such possible correspondences,
the next step of a MT specifier is typically to exam-
ine them for incompleteness or inconsistency. In the
above example, we notice that the reference feature
super of Class is not used by the discovered mappings
(incompleteness), and in addition, there is a potential
inconsistency in that Class is mapped to Table, but
Table is not a specialisation of (or equal to) the image
Type of Classifier, even though Class is a specialisa-
tion of Classifier.
Our tools partially automate this step by recog-
nising cases of incompleteness and inconsistency,
proposing solutions (additional or alternative map-
pings) to resolve them, and asking the user to con-
firm these solutions. Table 1 summarises the different
checks which we use.
For the case of feature mapping incompleteness in
Class2Relational, because the unused source feature
super is a self-association on Class, the system pro-
poses to replace attr 7−→ col by the mapping
Set{self }→closure(
super)→unionAll(attr) 7−→ col
of all defined attributes of a class to the columns of a
table, ie., all attributes of the class itself and of all its
ancestors are mapped to columns of the table corre-
sponding to the class.
Because of the inheritance conflict in the targets
of the class mappings, the additional class mapping
Class 7−→ Type
name 7−→ name
is also proposed: this is a ‘vertical entity splitting’
of Class (Lano et al., 2018b): each Class instance
in a source model is represented by both a Type in-
stance and a Table instance in the resulting Relational
model
1
.
1
The target classes must have no common MM
2
super-
class which is a type/element type of some g ∈ ran(fm)
MODELSWARD 2020 - 8th International Conference on Model-Driven Engineering and Software Development
264
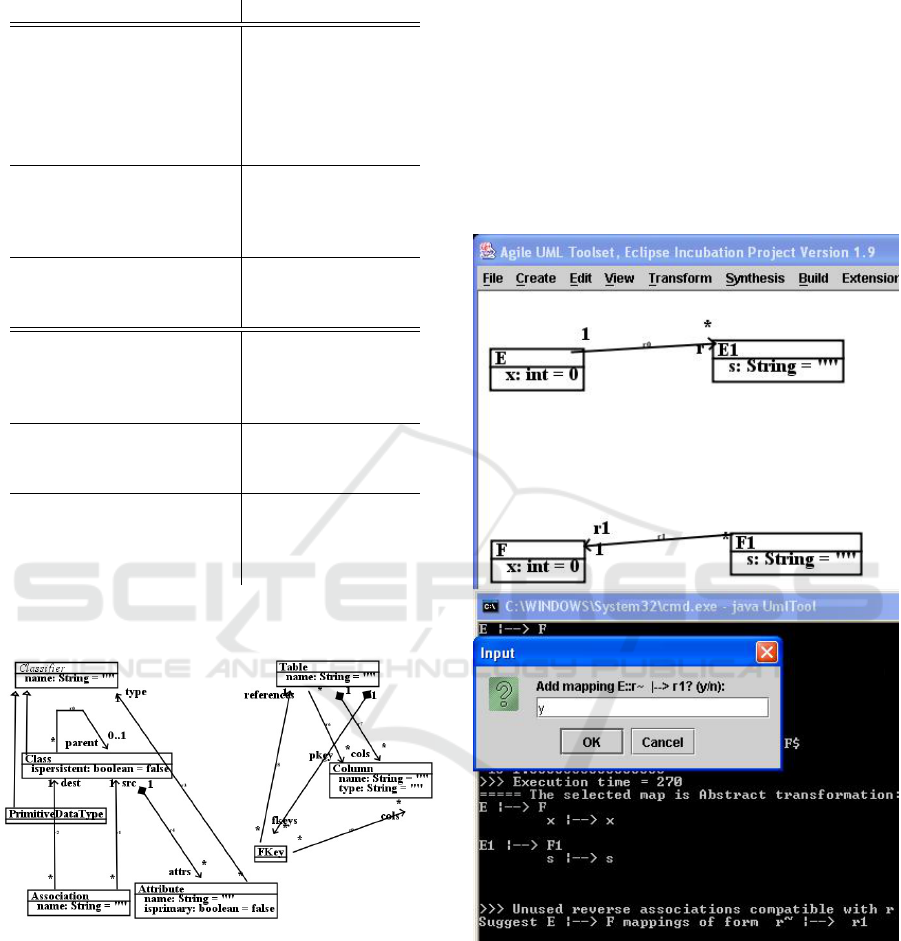
Table 1: Consistency and completeness checks.
Issue Correction
Class mapping Retarget Sub
Sub 7−→ T mapping, or add
for Sub subclass of E, target splitting map
has T not subclass/or Sub 7−→ F
equal to F, where
E 7−→ F
Two directions of Modify one
bidirectional association r feature mapping
not mapped to mutually to ensure
reverse target features consistency
Source, target features Propose modified
have different mappings
multiplicities
Unused target subclasses Introduce
F1 of F, where condition F1C
E 7−→ F and mapping
{F1C}E 7−→ F1
Unused source Suggest class or
or target feature mapping
feature f that uses f
Feature mapping Propose concrete
f 7−→ r.g subclass RSub of
with r : R of abstract R for instantiation
type/element type of r.
A more complex example is the Simple-
Class2SimpleRDB case from the ATL zoo (Figure 2).
Figure 2: SimpleClass2SimpleRDB metamodels.
In this case there is incompleteness in the ini-
tial feature mapping, because it omits the target fea-
ture Table :: pkey and the source feature Attribute ::
isPrimary. Because Class :: attrs is already mapped
to a target feature, the system proposes the additional
mapping
attrs→select(isPrimary) 7−→ pkey
of Class 7−→ Table. Further unused source boolean
features can be used for class mapping conditions, eg.,
{isPersistent} Class 7−→ Table.
Another case of feature mapping incompleteness
is when an association is navigated in opposite direc-
tions in the two metamodels, ie., there are matchings
E 7−→ F, E1 7−→ F1 of classes, but an association
E →
r
E1 in MM
1
should correspond to the reverse
direction rr
∼
of an association F1 →
rr
F in MM
2
.
To detect such cases, we look for unmatched source
reference features E :: r where there is an unmatched
target reference feature F1 :: rr whose (unnamed) re-
verse direction is type-compatible with r. Figure 3
shows a typical situation.
Figure 3: Reversing association direction.
The expression matching
E→select(ex | self = ex.r) 7−→ rr
is then proposed as an additional E1 7−→ F1 map-
ping, in the case that r is of 1-multiplicity. For ∗-
multiplicity r the matching is
E.allInstances()→select(
ex | ex.r→includes(self )) 7−→ rr
For SimpleClass2SimpleRDB, such a case arises
in the mapping of Association to FKey. Association ::
Automated Synthesis of ATL Transformations from Metamodel Correspondences
265

dest should be mapped to FKey :: references, and
Association :: src should be mapped to the opposite
direction of Table :: fkeys. The system recognises this
and adds the additional mapping to Class 7−→ Table.
Feature mapping inconsistencies may arise be-
cause the two directions of bidirectional associations
must be mapped in mutually consistent ways. If there
is a mapping
E 7−→ F
r1 7−→ rr1
where r1 : E → E1 has reverse reference r2 : E1 → E,
and rr1 : F → F1 has reverse rr2 : F1 → F, then any
mappings E1 7−→ F1 or of subclasses E2 of E1 to
F1 or to subclasses of F1 should include the feature
mapping r2 7−→ rr2. If instead a different mapping
for r2 is present, the user is asked to resolve this
conflict. This situation arises in the SQL to KM3
case, where the automatically derived correspondence
Table 7−→ Class has columns 7−→ structuralFeatures,
but Column 7−→ StructuralFeature has table 7−→ type
instead of the correct mapping table 7−→ owner.
The SQL to KM3 case also illustrates a form of
class mapping incompleteness, in which some con-
crete classes Fi (here, Reference and Attribute) are
not the targets of any class mapping, but they have
a superclass F in MM
2
which is a target of a map-
ping E 7−→ F (here, Column 7−→ StructuralFeature).
The system prompts the user to define more specific
mappings
{Cond1} E 7−→ F1
{Cond2} E 7−→ F2
for disjoint conditions Cond1, Cond2. This is the
‘horizontal entity splitting’ pattern of (Lano et al.,
2018b). Unused boolean attributes of E are pro-
posed as candidates for such discriminator conditions
Cond1, Cond2, however the user can define their own
conditions – in this example the conditions are the
somewhat obscure comment.size() = 0 and its nega-
tion.
A related feature mapping incompleteness issue
arises with composed target features r.f where r is
of an abstract class element type R. In order to pro-
duce an executable implementation, some concrete
subclass of R must be chosen as the type of r.
Finally, some proposed class mappings may be
recognised as spurious and unnecessary, if there is no
feature mapping p 7−→ q which uses the class map-
ping.
In general, the process of refining correspon-
dences based on identified incompleteness and incon-
sistencies can simulate the decisions which a human
MT expert might make. Indeed the automated detec-
tion of all such issues can ensure that many potential
semantic gaps and conflicts in a transformation speci-
fication are identified and resolved prior to implemen-
tation. A purely manual specification process could
result in some issues being missed.
3 MAPPING FROM T L TO ATL
Once a complete and consistent T L specification is
obtained, the next step is to generate an implemen-
tation of this in a particular MT language, such as
QVTr, QVTo, UML-RSDS, ETL or ATL.
We describe how QVTr implementations of T L
transformations can be derived in (Fang and Lano,
2019). Because ATL (Eclipse, 2019) is a more im-
perative language than QVTr, and also more restricted
in its declarative part than QVTr, the mapping of T L
specifications to ATL is more complex. In this section
we describe the steps of this mapping.
For each T L rule {Cond} E 7−→ F, with F a
concrete class, there is an ATL matched rule of the
schematic form
rule E2F
{ from ex : MM1!E ( ex.Cond )
to fx : MM2!F
( ... )
}
In the case that there are two or more T L rules for E
with the same conditions Cond, these must be com-
bined into a single ATL rule with multiple output pat-
tern elements.
For example, rules E 7−→ F1 and E 7−→ F2 with
concrete F1, F2 would be implemented by:
rule E2F1F2
{ from ex : MM1!E
to f1x : MM2!F1
( ... ),
f2x : MM2!F2
( ... )
}
This means also that source expressions e of el-
ement type E must be disambiguated when used
on the RHS of bindings: t ← e refers to e con-
verted to F1 elements via E2F1F2, whilst t ←
thisModule.resolveTemp(e, ‘f 2x’) refers to e con-
verted to F2 elements via the rule.
A feature mapping f 7−→ g is represented by an
ATL binding g ← ex.f in cases where f and g are
not composed. Source compositions r.f for f of
1 multiplicity, r of ∗ multiplicity, are evaluated as
ex.r→collect( x | x.f ).
MODELSWARD 2020 - 8th International Conference on Model-Driven Engineering and Software Development
266

In the case of a feature mapping f 7−→ r.g, where r
is of 1-multiplicity, of concrete class element type R,
a new output pattern element rx : MM2!R is defined:
rule E2F
{ from ex : MM1!E ( ex.Cond )
to fx : MM2!F
( r <- rx ),
rx : MM2!R
( ... )
}
The bindings for rx implement the feature mappings
for f 7−→ g, and for other mappings k 7−→ l, for each
k 7−→ r.l which is a feature mapping of the E 7−→ F
mapping.
In the case that there is a direct mapping f 7−→ r
and also composed mappings g 7−→ r.h, a do clause is
needed for the composed mappings:
rule E2F
{ from ex : MM1!E ( ex.Cond )
to fx : MM2!F
( r <- ex.f )
do
{ fx.r.h <- ex.g; }
}
where r is of 1 multiplicity.
For 0..1 and for *-multiplicity r, a do clause im-
plementation of g 7−→ r.h instead has the form
for (rx in fx.r)
{ rx.h <- ex.g; }
If there are cases of mappings f 7−→ r.g where f
and r are of *-multiplicity, then instead sets of R el-
ements are created using unique lazy or called rules.
In this case, if f has a class element type E1, the map-
ping f 7−→ r.g in cases where r and f have * multiplic-
ity can be implemented by introducing a new unique
lazy rule:
rule E2F
{ from ex : MM1!E ( ex.Cond )
to fx : MM2!F
( r <- ex.f->collect( e1x |
thisModule.MapE12Rg(e1x) ) )
}
unique lazy rule MapE12Rg
{ from e1x : MM1!E1
to rx : MM2!R
( g <- e1x )
}
The effect of this approach is to produce a set of R
objects, one for each element e1x of ex.f . Again,
R must be a concrete class for this to be valid.
An example of this situation is the supertypes 7−→
generalization.parent mapping in the MOF2UML
case.
If f is of 0..1 multiplicity and r of * or 0..1 multi-
plicity, then the assignment to r is
r <- Set{ex.f}->collect( e1x |
thisModule.MapE12Rg(e1x) )
Further updates to the r with additional mappings
k 7−→ r.l with l of higher or equal upper multiplicity
to k must be handled in the do clause of the E2F rule,
via a statement
for (rx in fx.r)
{ rx.l <- ex.k; }
Further updates to the r with additional mappings
k 7−→ r.l with l of smaller upper multiplicity than k
require the creation of additional R objects:
( r <- ex.k->collect( e2x |
thisModule.MapE22Rl(e2x)) )
If instead f has a value element type T, the map-
ping f 7−→ r.g can be implemented by introducing a
new called rule:
rule E2F
{ from ex : MM1!E ( ex.Cond )
to fx : MM2!F
( r <- ex.f->collect( tx |
thisModule.MapT2Rg(tx) ) )
}
rule MapT2Rg(tx : T) : MM2!R
{ to rx : MM2!R
( g <- tx )
}
Table 2 summarises the translation from T L to
ATL for composed target feature mappings f 7−→ r.g,
where there is no direct mapping h 7−→ r.
The synthesised ATL satisfies the quality recom-
mendations of (Eclipse, 2019):
• Use standard and unique lazy rules in preference
to lazy rules – lazy rules are not needed by our
translation.
• Avoid imperative constructs and the use of
resolveTemp – imperative code and called rules
are only needed in cases of composite target fea-
tures. resolveTemp is only needed in cases of ver-
tical entity splitting.
• Use collect in preference to iterate – iterate is
only needed to define the closure operator, oth-
erwise collect is used.
More precisely, the situation with regard to the
quality flaws of (Lano et al., 2018a) is that cycles
of calling dependencies (CBR
2
> 0) are not possi-
ble, while errors of excessive fan-in, fan-out and
Automated Synthesis of ATL Transformations from Metamodel Correspondences
267

Table 2: Generated ATL for composite target feature mappings f 7−→ r.g of E 7−→ F.
r multiplicity f multiplicity g multiplicity ATL implementation
1 any any r ← rx for new OutPatternElement rx : MM2!R (...)
rx binding is
g ← ex.f for g upper multiplicity ≥ f upper multiplicity,
g ← ex.f →any() otherwise.
All bindings due to E 7−→ F mappings k 7−→ r.l
are defined in the rx pattern.
* 1 any r ← rx for new OutPatternElement rx : MM2!R (...)
rx binding is g ← ex.f
* or 0..1 0..1 any r ← Set{ex.f }→collect(e1x | thisModule.MapE12Rg(e1x))
Additional k 7−→ r.l with
upper multiplicity k ≤ upper multiplicity l:
for (rx in fx.r) { rx.l ← ex.k; }
Additional k 7−→ r.l with
upper multiplicity k > upper multiplicity l:
r ← ex.k→collect(e2x | thisModule.MapE22Rl(e2x))
* * any r ← ex.f →collect(e1x | thisModule.MapE12Rg(e1x))
Additional k 7−→ r.l are treated as for f 0..1 multiplicity
calling dependencies can arise only because of calls
to data conversion operators or to auxiliary unique
lazy/called rules in the case of composite target fea-
tures. Duplicate code may arise if two subclasses E1,
E2 of a source class E have common feature map-
pings – this duplication could be removed by using
ATL rule inheritance. Excessive rule and transforma-
tion size may occur due to the size of the metamodels.
4 EVALUATION
We evaluated the approach using several cases from
the ATL transformation zoo. For these cases we gen-
erated a solution using only the provided metamod-
els in KM3 or Ecore format. The procedure detailed
in Section 2 was followed with interactive enhance-
ment of the initially derived metamodel correspon-
dences. In Table 3 we compare our derived ATL
transformation with the manually-constructed solu-
tions of the zoo cases, in terms of their size and the
number of technical debt flaws in the transforma-
tion according to the quality flaw categories of (Lano
et al., 2018a). We also quantify the recall, precision
and f-measure of our matching result with respect to
the class and feature mappings defined by the orig-
inal manually-created transformations. In terms of
quality, the synthesised transformations have lower
numbers of flaws, and lower flaw density (the aver-
age flaw density of the generated transformation ver-
sions is 0.008 flaws/LOC, compared to 0.0172 for the
original versions). All the examples are available at
https://nms.kcl.ac.uk/kevin.lano/mtsynthesis.
Table 4 shows some estimates of the relative
amount of work involved in the manual and auto-
mated construction of the ATL zoo case versions. We
estimate effort in terms of how many manual changes
are necessary to the automatically-synthesised class
and feature mappings (additional to changes identi-
fied by the interactive improvement process), and the
semantic complexity of the original versions, as the
total number of class and feature mappings. The ex-
ecution time for the automated synthesis of the initial
T L specifications is also shown (times are the same
for a transformation and its inverse because our tool
generates these together).
These results show that a relatively small amount
(less than 10% of the feature/class mappings) of trans-
formation content needs to be manually modified or
created, for the versions produced by our transforma-
tion synthesis process.
5 RELATED WORK
For metamodel matching, there are established bench-
mark cases, and results of different approaches on
these benchmarks are given in (Addazi et al., 2016;
Fang and Lano, 2019; Kessentini et al., 2014; Voigt
and Heinze, 2010). We show in Table 5 that our meta-
MODELSWARD 2020 - 8th International Conference on Model-Driven Engineering and Software Development
268

Table 3: Evaluation on ATL zoo cases.
Case Original Original Recall Precision F-measure New New
size (LOC) flaws size (LOC) flaws
Ports 31 0 1.0 1.0 1.0 28 0
PetriNet2PathExp 70 1 0.78 1.0 0.875 27 0
Class2Relational 97 2 1.0 0.88 0.94 35 0
PathExp2PetriNet 104 0 0.94 1.0 0.97 40 0
SimpleClass2 302 10 1.0 0.87 0.93 38 0
SimpleRDB
Ant2Maven 324 4 0.84 0.99 0.91 317 2
Maven2Ant 360 3 0.92 0.91 0.91 332 2
MOF2UML 585 8 0.69 0.78 0.73 255 3
MySQL2KM3 613 13 0.79 0.81 0.8 48 1
UML2MOF 935 18 0.53 0.8 0.64 220 3
Averages 342.1 5.9 0.85 0.9 0.87 134 1.1
Table 4: Effort of manual/automated versions of cases.
Case Execution Changed Original
time (ms) maps maps
Ports 70 0 7
PetriNet2 133 0 11
PathExp
Class2 60 0 28
Relational
PathExp2 133 0 19
PetriNet
SimpleClass2 285 2 16
SimpleRDB
Ant2Maven 326,769 1 136
Maven2Ant 326,769 7 112
MOF2UML 66,953 32 184
MySQL2KM3 859 5 128
UML2MOF 66,953 31 165
model matching approach produces similar overall re-
sults to the SBSE approach of (Kessentini et al., 2014)
on the benchmarks, and therefore is superior to the re-
sults of other approaches with regard to these bench-
marks, such as (Addazi et al., 2016; Voigt and Heinze,
2010). In terms of efficiency, the execution times on
the benchmarks are generally lower than the results of
(Kessentini et al., 2014), although we use determinis-
tic algorithms instead of the evolutionary algorithm
approach of (Kessentini et al., 2014).
Several existing works on recognising metamodel
correspondences are based on the concept of similar-
ity flooding (Melnik et al., 2002; Addazi et al., 2016;
Fabro and Valduriez, 2009; Garces et al., 2009): that
if two metamodel elements c1, c2 (eg., classes) are
connected to elements e1, e2 with a known similar-
ity v, then c1 and c2’s estimated similarity can be
modified based on v and the strength of the connec-
tions. However this approach only takes into account
pairwise similarities, whilst in practice many-to-many
similarities may exist between metamodels (eg., a
group of classes in MM
1
can be related to a group in
MM
2
). Thus our matching approach considers global
and n-to-m matches of metamodel elements as a ba-
sis for metamodel correspondences. A similar global
structural matching approach using graph similarity is
described in (Voigt and Heinze, 2010), however they
rely on an initial manually-constructed ‘seed’ match-
ing of classes, and on planarization of metamodel
graphs, which our approach does not need. In this
paper and in (Fang and Lano, 2019) we consider 15
of the 20 ‘gold standard’ cases of (Voigt and Heinze,
2010), and we achieve an average F-score of 0.79 on
these, compared to 0.58 in (Voigt and Heinze, 2010).
Other approaches to synthesising transformations
from correspondences are (Fabro and Valduriez,
2009) and (Garces et al., 2009). (Fabro and Valduriez,
2009) defines case-specific patterns to create transfor-
mations for particular source and target metamodels,
however we define general-purpose patterns and con-
sistency and completeness checks to identify and re-
fine correspondences for arbitrary metamodel pairs.
For example, the mutual consistency of feature map-
pings of the two directions of a bidirectional associ-
ation is a logical property which must hold for any
semantically-valid transformation, and hence a pro-
posed mapping m, fm must satisfy this property or be
modified to satisfy it. (Fabro and Valduriez, 2009)
does not consider the quality of generated transforma-
tions, and its ATL generation approach does not ap-
pear to address the issue of composed target features,
which considerably complicates ATL production.
The AMW tool of (Garces et al., 2009) provides
a means to define customised matching criteria and
techniques. This requires more substantial interven-
tion from the developer than our approach, which is
Automated Synthesis of ATL Transformations from Metamodel Correspondences
269
Table 5: Evaluation on cases of (Kessentini et al., 2014).
Case Precision Recall F Precision Recall F Execution
(SBSE) (SBSE) (SBSE) time (s)
WebML2EER 0.65 1.0 0.79 0.69 0.72 0.70 0.116
EER2Ecore 0.6 1.0 0.75 0.48 0.59 0.52 0.188
WebML2Ecore 0.7 0.74 0.72 0.82 0.69 0.74 0.125
EER2UML1.4 0.8 0.86 0.83 0.71 0.72 0.71 0.172
EER2UML2.0 0.61 0.67 0.64 0.67 0.72 0.68 0.422
WebML2UML1.4 0.53 0.62 0.57 1.0 0.84 0.91 0.203
WebML2UML2.0 0.79 0.75 0.77 0.91 0.73 0.81 0.219
Ecore-UML1.4 0.76 0.64 0.69 1.0 0.66 0.79 104.5
Ecore-UML2.0 0.76 0.78 0.77 0.64 0.89 0.75 510
UML1.4-UML2.0 0.9 0.6 0.72 1.0 0.67 0.8 393
Average 0.71 0.77 0.73 0.79 0.72 0.74
primarily automated and requires relatively low man-
ual intervention. It is unclear if AMW is able to gen-
erate complex ATL for cases of composed target fea-
tures.
Transformation construction by example is an-
other approach for semi-automated transformation
derivation (Balogh and Varro, 2008). Transforma-
tion rules are inferred from examples of the intended
transformation inputs and outputs (models). Example
source and target models could also be used to en-
hance our approach, to identify detailed feature map-
pings which cannot be inferred from feature typing
(eg., 2 ∗ x 7−→ y for integer-typed features x and y).
6 CONCLUSIONS
We have described a process for synthesising ATL
transformations from metamodel correspondences,
based on analysis of the consistency and complete-
ness of these correspondences. The approach is novel
in attempting to formally emulate the processes which
a software engineer would informally undertake when
creating a transformation.
We have shown that this approach can produce
correct and effective transformations, with a higher
quality than manually-produced transformation code,
and that development times for transformations can
be reduced in principle by the approach.
REFERENCES
Addazi, L., Cicchetti, A., Rocco, J. D., Ruscio, D. D.,
Iovino, L., and Pierantonio, A. (2016). Semantic-
based model matching with EMFCompare. In ME
2016, CEUR-WS vol. 1706, pages 40–49.
Balogh, Z. and Varro, D. (2008). Model transformation by
example using inductive logic programming. SoSyM.
Eclipse (2019). Atl user guide. eclipse.org.
Fabro, M. D. D. and Valduriez, P. (2009). Towards the
efficient development of model transformations us-
ing model weaving and matching transformations.
SoSyM.
Fang, S. and Lano, K. (2019). Extracting correspondences
from metamodels using metamodel matching. In PhD
symposium, STAF 2019.
Garces, K., Jouault, F., Cointe, P., and Bezivin, J. (2009).
Managing model adaptation by precise detection of
metamodel changes. In ECMDA-FA, LNCS vol. 5562,
pages 34–49.
Kessentini, M., Ouni, A., Langer, P., Wimmer, M., and
Bechikh, S. (2014). Search-based metamodel match-
ing with structural and syntactic measures. JSS,
(97):1–14.
Lano, K., Kolahdouz-Rahimi, S., Sharbaf, M., and Alfraihi,
H. (2018a). Technical debt in model transformation
specifications. In ICMT 2018.
Lano, K., Kolahdouz-Rahimi, S., Yassipour-Tehrani, S.,
and Sharbaf, M. (2018b). A survey of model trans-
formation design patterns in practice. JSS.
Melnik, S., Garcia-Molina, H., and Rahm, E. (2002). Sim-
ilarity flooding: a versatile graph-matching algorithm
and its application to schema matching. In ICDE
2002.
Schwichtenberg, S., Gerth, C., Huma, Z., and Engels, G.
(2014). Normalising heterogeneous service descrip-
tion models with generated qvt transformations. In
ECMFA 2014, LNCS vol. 8569, pp. 180–195.
Voigt, K. and Heinze, T. (2010). Metamodel matching
based on planar graph edit distance. In ICMT 2010,
LNCS vol. 6142, pages 245–259.
MODELSWARD 2020 - 8th International Conference on Model-Driven Engineering and Software Development
270
