Approximate Conditional Independence Test using Residuals

Shinsuke Uda

Medical Institute of Bioregulation, Kyushu University, 3-1-1 Maidashi Higashi-ku Fukuoka 812-8582, Japan

Keywords:

Information Theory, Conditional Mutual Information, Permutation Test, Biological Data Analysis.

Abstract:

Conditional mutual information is a useful measure for detecting the association between variables that are

also affected by other variables. Though permutation tests are used to check whether the conditional mutual

information is zero to indicate mutual independence, permutations are difﬁcult to perform because the other

variables in a dataset may be associated with the variables in question. This problem is particularly acute

when working with datasets of small sample size. This study aims to propose a computational method for

approximating conditional mutual information based on the distribution of residuals in regression models. The

proposed method can implement the permutation tests for statistical signiﬁcance by translating the problem

of measuring conditional independence into the problem of estimating simple independence. Additionally,

a reliability of p-value in permutation test is deﬁned to omit unreliably detected associations. We tested

our proposed method’s performance in inferring the network structure of an artiﬁcial gene network against

comparable methods submitted to the Dream4 challenge.

1 INTRODUCTION

Recent progress in the ﬁeld of information technology

has made the analysis of high-dimensional datasets

possible with novel analytic techniques. However,

these techniques remain in development stage due to

some problems faced to the curse of dimensional-

ity (Hastie et al., 2001). When three variables may

be dependent on each other, we may want to ex-

amine the associations between variables X and Y

while ignoring the effects of Z, which apparently

boosts/depresses association. The dataset is of high

dimension and X ⊂ ℜ, Y ⊂ ℜ and Z ⊂ ℜ

are con-

tinuous random variables. Conditional mutual infor-

mation is a statistically robust measure to quantify the

association between variables while removing the ef-

fects of other variables, without assuming a particular

model distribution. X and Y are conditionally inde-

pendent given Z if and only if the conditional mutual

information between X and Y given Z is zero, and

vice versa. Conditional independence can serve as a

measure to infer the network structure of associations

between variables (Pearl, 2009). Perfect conditional

independence between X and Y given Z indicates that

no edge connects nodes X and Y . In inference net-

works, in most of the cases, it is assumed that the

dimensions of X and Y are one, therefore, hereafter,

https://orcid.org/0000-0001-6221-3587

we will assume it. While conditional mutual infor-

mation has theoretical advantages, there are two dif-

ﬁculties for inferring network from ﬁnite sample size

datasets. First, estimating conditional mutual infor-

mation is computationally difﬁcult if the dimension of

Z is high, even if X and Y are one-dimensional. Sec-

ond, though conditional independence is detected by

examining whether conditional mutual information is

zero or not, the conditional mutual information esti-

mated from a dataset with ﬁnite sample size is rarely

zero due to statistical errors, even if the variables are

conditionally independent.

To infer the associations in high-dimension net-

works, statistical tests must be employed to examine

whether the conditional mutual information is close

to zero or not. A permutation test is a powerful strat-

egy for this analysis and involves generating the ex-

pected data distribution of the null hypothesis with-

out making any assumptions about the distribution of

the actual data. Permutations are not easy to apply

for examining the conditional independence between

X and Y given Z, because Z may be associated with

X and/or Y , and the permutations of X and Y ignore

the inﬂuence of Z. This problem can be addressed by

grouping the data in resampling, but this approach re-

quires a large sample. This article proposes a compu-

tational method for approximating conditional mutual

information. The method translates the test for condi-

tional independence with a simple independence test

Uda, S.

Approximate Conditional Independence Test using Residuals.

DOI: 10.5220/0008866102970304

In Proceedings of the 12th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2020) - Volume 2, pages 297-304

ISBN: 978-989-758-395-7; ISSN: 2184-433X

297

using the distribution of residuals in regression mod-

els of X or Y against Z. With this translation of the

problem, permutations can be used to isolate the as-

sociations between X and Y. Additionally, a reliabil-

ity of p-value in permutation test is deﬁned to omit

unreliably detected associations.

The biological datasets compiled in recent years

are of high dimension, because of technological de-

velopments in measurement techniques that allow

the measurement of greater numbers of molecular

species. The structure of associations between molec-

ular species can be expressed as a regulatory network

when seeking insight into biological phenomena. To

test our proposed analytic method with a widely avail-

able dataset, the method was used to infer the ar-

tiﬁcial gene network structure in the Dream4 chal-

lenge dataset (Schaffter et al., 2011). Next, Section

2 presents related works including comparable meth-

ods of gene network inference, Section 3 introduces

the proposed method for approximating conditional

mutual information, Section 4 discusses the results of

artiﬁcial gene network inference, and Section 5 con-

cludes the paper.

2 RELATED WORK

Mutual information

I(X;Y ) =

dxdy p(x, y)log

p(x, y)

p(x)p(y)

is a statistical measure to quantify association be-

tween X and Y . Mutual information combining with

permutation test is a promising method to examine

statistical dependence between variables and applied

to analyzing gene expression data sets(Daub et al.,

2004). Conditional mutual information

I(X;Y |Z) =

dxdydz p(x, y,z)log

p(x, y|z)

p(x|z)p(y|z)

is a statistical measure to quantify association be-

tween X and Y given Z removing the effect of other

variables Z. Therefore, conditional mutual informa-

tion would be a more suitable measure to infer di-

rect association than mutual information. However,

estimating conditional mutual information is com-

putationally difﬁcult if the dimension of Z is high,

and permutations are not easy to apply for examining

conditional independence, in general. The proposed

method enables us to examine conditional indepen-

dence by permutation test and applied to inference of

gene network.

A number of methods to infer gene network were

reported. ARACNE (Margolin et al., 2006) and

CLR (Faith et al., 2007) are network-inference meth-

ods based on information theoretic approach. Both

determine the presence of an edge between nodes

by calculating the mutual information of the two

nodes. ARACNE employs data-processing inequal-

ities to eliminate weakest associations in every closed

triplet of nodes. The procedure would be exact if the

network structure was a tree. On the contrary, CLR

compares each value of mutual information between

nodes to the empirically determined distribution of all

the mutual information values between pairs of nodes.

CLR is designed around the assumption that the em-

pirical distribution provides background information

about the absence of edges. GEne Network Inference

with Ensemble of Trees (GENIE3) (Irrthum et al.,

2010) uses a tree-based method combining with boot-

strap method and feature selection. TIGRESS uses

least angle regression (LARS) (Haury et al., 2012),

which is a sparse regression method, with stability se-

lection. NIMEFI (Ruyssinck et al., 2014) takes an

ensemble approach to combine the results of regres-

sions with feature selection such as support vector re-

gression and the elastic net. PLSNET (Guo et al.,

2016) uses PLS-based feature selection with an en-

semble technique.

3 METHODS

3.1 Approximation of Conditional

Mutual Information

Suppose continuous random variables X,Y ∈ ℜ,Z ∈

ℜ

N−2

. We can compute the conditional mutual in-

formation I(X;Y |Z). The conditional expectation and

standard deviation are written as

(·)

(z) = E[(·)|Z = z], σ

(·)

(z) =

Var[(·)|Z = z].

We write X and Y as

X = m

(Z) + σ

(Z)ε, Y = m

(Z) + σ

(Z)η, (1)

using random variables ε, η.

The entropy function is deﬁned as

H(X) = −

dxp(x)log p(x).

The following relations hold (see Appendix).

H(X + f (Z)|Z) = H(X|Z ), (2)

H( f (Z)X|Z) = H(X |Z) + E

[log f (Z)] . (3)

f is an arbitrary continuous function and E

[(·)] indi-

cates expectation of (·) with respect to the distribution

of Z. Equations (1)-(3) yield I(X;Y |Z) = I(ε; η|Z).

ICAART 2020 - 12th International Conference on Agents and Artiﬁcial Intelligence

298

Furthermore, we ﬁnd I(ε;η|Z) = I(ε;η) − I(ε;η;Z).

Finally,

I(X;Y |Z) = I(ε; η) − I(ε;η; Z), (4)

results. The multivariate mutual information (McGill,

1954) is deﬁned as

I(ε; η;Z) = H(ε, η) + H(ε, Z) + H(η,Z)

− (H(ε) + H(η) + H(Z) + H(ε, η, Z)).

One can see that I(ε; η; Z) corresponds to the inter-

section of the uncertainties of ε, η and Z. Thus, if

we ﬁnd values of ε and η that give I(ε;η; Z) = 0, the

conditional mutual information I(X;Y |Z) is equiva-

lent to the mutual information I(ε; η). This translation

of conditional mutual information into mutual infor-

mation avoids any integral with respect to Z. In other

words, if I(ε; η; Z) = 0 holds, we have:

ε ⊥ η ⇔ X ⊥ Y |Z.

The upper bound of I(ε; η;Z) is

|I(ε; η;Z)| ≤ min{I(ε;Z),I(η; Z),

I(ε; η),I(ε;Z|η), I(η; Z|ε), I(ε; η|Z)}. (5)

Instead of evaluating I(ε; η; Z), we evaluate sufﬁcient

condition

I(ε; Z) or I(η; Z) = 0 ⇒ I(ε;η; Z) = 0. (6)

Note that I(ε;Z) or I(η;Z) = 0 is a sufﬁcient, but not

necessary, condition for I(ε;η; Z) = 0. In particular,

if ε and η follow a Gaussian distribution with corre-

lation ρ which is equivalent to partial correlation be-

tween X and Y , we have

I(X;Y |Z) = −

log



1 − ρ



3.2 Heteroscedastic Kernel Ridge

Regression (HKRR)

We suppose that the conditional distribution of X

given Z can be approximated as a Gaussian distribu-

tion,

p(X|Z = z) =

exp

−

2σ

(z)

(x − m

(z))

2πσ

(z)

. (7)

Once we obtain m

(z),σ

(z) from the dataset D ≡

}

i=1

by Heteroscedastic Kernel Ridge Re-

gression (HKRR) (Cawley et al., 2004), we have

− m

)

. (8)

(z),σ

(z) is inferred by solving the minimization

problem of the negative log-likelihood function of (7)

−log

∏

p(x

) =

∑

− m

))

2σ

)

+ log σ

). (9)

The constant term can be ignored. m

(z),log σ

(z) are

written as

(z) =

∑

(z,z

) + b

logσ

(z) =

∑

(z,z

) + b

The parameters α

,α

and kernel matrix

(·)

(z,z

) = hφ

(·)

(z),φ

(·)

)i, are deﬁned by the ker-

nel function regarding the basis function φ. The

function φ maps the data vector z onto the high-

dimensional feature space F , that is, φ

(·)

: Z →

F . h(·),(∗)i represents the inner product between

(·) and (∗). We can ﬁnd ε by solving the min-

imization problem in (9) and determining the pa-

rameters α

,α

. The minimization prob-

lem is solved numerically with iterative solutions of

subproblems that are deﬁned as linear simultaneous

equations (Cawley et al., 2004; Cawley and Talbota,

2004). In addition, the leave-one-out cross validation

error of the minimization problem is obtained analyt-

ically without retraining using the Sherman-Morrison

formula. Similarly, η is obtained by way of y instead

of x.

3.3 Independence Measure

Using the kernel matrices, {K

}

i j

K(x

),{K

}

i j

= K(y

), we deﬁne the mea-

sure of the mutual dependence between X and Y

J(X,Y ) ≡





−





−



(10)

where I

denotes the identity matrix of size n and

denotes the square matrix of size n, all of whose

elements are 1 (Sun et al., 2007). J(X,Y ) = 0 means

that X and Y are independent and the scale of J(X,Y )

is arbitrary. Though one can use mutual information

instead of J to indicate the dependence between X

and Y , the calculation of J avoids the computationally

costly estimation of density distributions.

3.4 Permutation Test

In general, tests for statistical signiﬁcance are re-

quired when inferring the dependence between vari-

ables as statistical errors in the sample prevent the

Approximate Conditional Independence Test using Residuals

299

measure of dependence from ever reaching zero. We

employ permutation test (Edgington and Onghena,

2007) to test the hypotheses,

: X and Y are independent,

: X and Y are not independent.

In permutation tests, the expected distribution of data

given the null hypothesis is generated by permuta-

tions of the dataset. When examining the degree

of dependence between X and Y , the pseudo-dataset

(i)

}

i=1

following the null hypothesis is gener-

ated by random permutations of x

and y

with the

original dataset {x

}

i=1

. I

(i) denotes the i-th el-

ement of the index set, which is generated by random

permutation of the index set i ∈ {1,. . . , n}. We obtain

the null distribution of J(X ,Y ) empirically by evalu-

ating a number of J(X,Y ) with iteratively generated

pseudo-datasets by permutation. The percentile point

J(X,Y ) of the original dataset against the empirically

determined null distribution is the p-value. In gen-

eral, the permutation test is easy to apply when infer-

ring the mutual dependence between X and Y . How-

ever, the permutation test is difﬁcult to apply when

trying to infer the conditional dependence between

X and Y given Z when the data were compiled from

a small sample. Since Z may be associated with X

or Y or both, an intentional sampling technique such

as grouping is needed to retain the associations be-

tween Z and X and/or Y . Even such intentional re-

sampling techniques are difﬁcult if the dataset was

prepared from a small sample, and datasets used in

biology tend to be compiled from small samples.

3.5 Reliability of p-value

The standard error of independence measure J is esti-

mated by Jackknife method

Jack

n − 1

∑



J − J



, (11)

where J

is independence measure using the data

set of sample size n − 1 removed sample i, and

J =

∑

. We write the p-value in the permutation test

for J = J

(·)

as p(J

(·)

), and deﬁne a reliability of p-

value as

reli

= p(J

(l)

) − p(J

(u)

), (12)

where J

(l)

= max{0, J

− SE

Jack

}, J

(u)

= J

+ SE

Jack

is the value of J calculated from the whole data set.

The domain of p

reli

is [0,1]. The reliability of p-value

decreases with an increase in p

reli

Algorithm 1 : Let D be the n × m matrix describing the

dataset, where n is the sample size and m is the number of

variables/nodes. The vector d

·i

represents the i-th column

of D.

for each pair of nodes i and j do

x ⇐ d

·i

,y ⇐ d

· j

,Z ⇐ {d

·k

}

k\i, j

Infer m

,σ

by HKRR for x and y on Z.

ε and η is obtained by the (8).

Compute J(ε; η).

Generate the null distribution of independence

between ε and η through permutations.

Obtain p-value by comparing J(ε; η) to the null

distribution.

Compute J(ε, Z) and J(η, Z).

Generate the null distributions of independence

between ε and Z and between ε and Z through

permutations.

Obtain p-values by comparing J(ε;Z) and

J(η; Z) against each of the null distributions.

Compute the reliability of p-value by the (12)

and omit the low reliable p-values.

end for

4 ARTIFICIAL GENE NETWORK

INFERENCE

The datasets from the Dream4 challenge (Schaffter

et al., 2011) were used to evaluate the proposed

method. The datasets are generated by simulations

based on ordinary differential equations that imitate

the biochemical reactions that make up a gene regu-

lation network. We employed multifactorial datasets

comprising ﬁve networks that include 100 nodes.

The multifactorial dataset corresponds to steady-state

measurements of all network nodes after a multifacto-

rial perturbation. The multifactorial perturbations are

given by slightly increasing or decreasing the basal

activation of all genes of the network simultaneously

by different random amounts. Thus, the data matrix

D for each network consists of 100 rows that corre-

spond to 100 measurements under perturbation of a

single node and 100 columns that correspond to all

100 nodes of the network. We infer the presence of an

edge between nodes i and j by calculating the approx-

imating conditional mutual information between i and

j given all other nodes except i and j. The data ma-

trix is divided into three parts, x, y and Z, where x and

y are vectors consisting of the i-th and j-th columns

of data matrix D, respectively, and Z is the redeﬁned

data matrix that consists of D excluding the i-th and

j-th columns. The parameters m

(z) and σ

(z) are

inferred by HKRR, setting x as output and Z as in-

ICAART 2020 - 12th International Conference on Agents and Artiﬁcial Intelligence

300

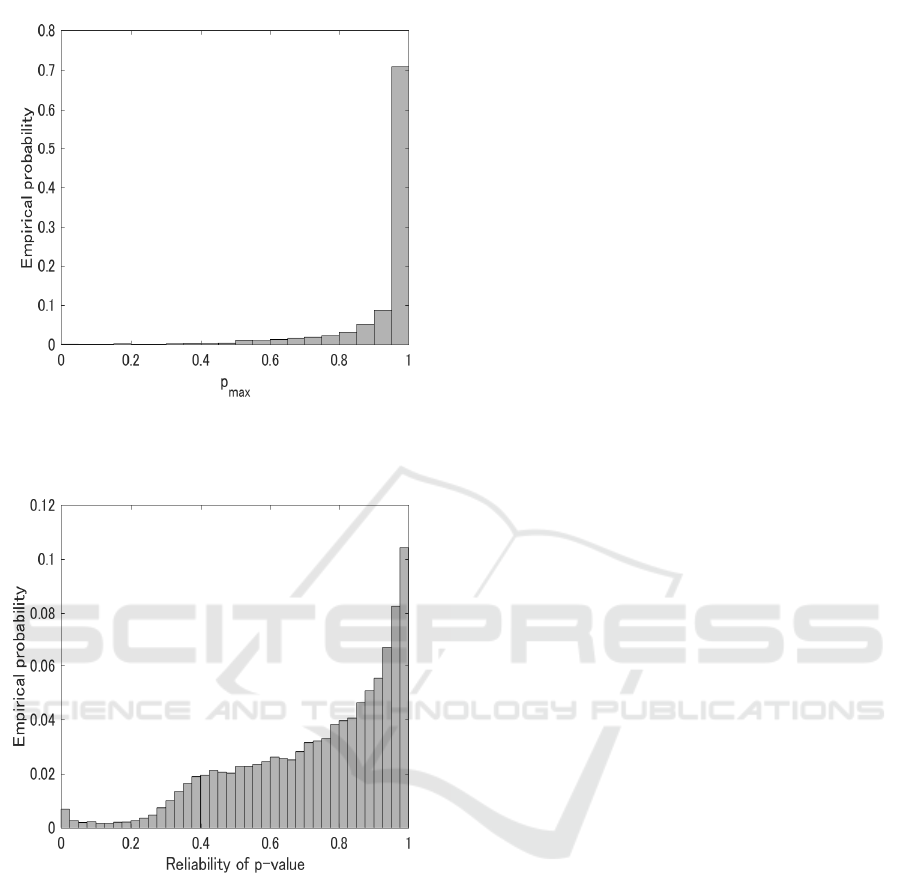
Figure 1: Empirical probability distribution of p

max

for all

inferred edges of ﬁve networks. A total of 24750 were in-

ferred.

Figure 2: Empirical probability distribution of reliability of

p-value for all inferred edges of ﬁve networks. A total of

24750 were inferred.

put. Similarly, by setting y as output, the parameters

(z) and σ

(z) are inferred. ε and η are determined

with (8). Leave-one-out training of sample µ is used

to infer m

(z) and m

(z), from which ε

and η

analytically. The Gaussian kernel function

(·)

(x, x

) = exp



−β

(·)

k x − x



, (13)

is used for kernel functions K

and K

. The

same hyper parameters of HKRR are set for the x

and y input models, and are determined so that the

leave-one-out cross validation error, which is ana-

lytically estimated without retraining (Cawley et al.,

2004), is minimized with a grid search. In the grid

search, we set the hyper parameters as β

= [1.00e-

4, 1.78e-4, 3.16e-4, 5.62e-4, 1.00e-3], β

=[1.00e-

6, 3.16e-6, 1.00e-5], λ

=[5.00e-4, 7.50e-4, 1.00e-3,

1.30e-3, 1.50e-3], and λ

=[0.1, 0.55, 1]. λ

and λ

are weight parameters of the `

norm-regularization

terms for m

(z) and σ

(z), respectively. The Gaus-

sian kernel function is also included in the indepen-

dence measure J, and the scaling parameter is set as

=0.01.

Permutation tests in 50000 trials are applied to

check for the independence of ε and η. Instead of

imposing the condition that I(ε;η; Z) = 0 for ε and η,

the sufﬁcient condition, which is x and Z or y and Z

are independent, is examined in post-processing. The

term p

max

is deﬁned as max[p

, p

], where p

and

are the p-values of the permutation tests for the

independence of x and Z, and of y and Z, respec-

tively. The ratio of p

max

< 0.05 to all results is al-

most 0.0019(Fig.1). Thus, we do not discriminate

between edges that failed to fulﬁll the sufﬁcient con-

dition below. The result p

max

< 0.05 is not equiv-

alent to I(ε; η; Z) 6= 0, as the latter is a sufﬁcient,

but not necessary condition. Even if p

max

< 0.05,

I(ε; η;Z) = 0 may hold. In general, there no guar-

antee that I(ε; η; Z) = 0 when inferring ε and η using

nonlinear regression models. However, we consider

that the measure is sufﬁciently reliable if the gener-

alization error in the data set is small enough, since

most regression models assume that noise is added

to the output independently. We plan to clarify this

hypothesis in the future. We employed top 10% re-

liable p-values for network inference. Thus, the p-

values which have larger p

reli

than the value of 10 per-

centile point of p

reli

were omitted. The each empirical

probability distribution of p

reli

is similar among ﬁve

inferred networks (Fig.2), and that of 10 percentile

point of p

reli

was around 0.4. The point can be seen

as the edge of plateau of distribution, and empirical

probability rapidly decreases with an decrease in p

reli

The proposed method for network inference is sum-

marized as pseudo-code in algorithm1.

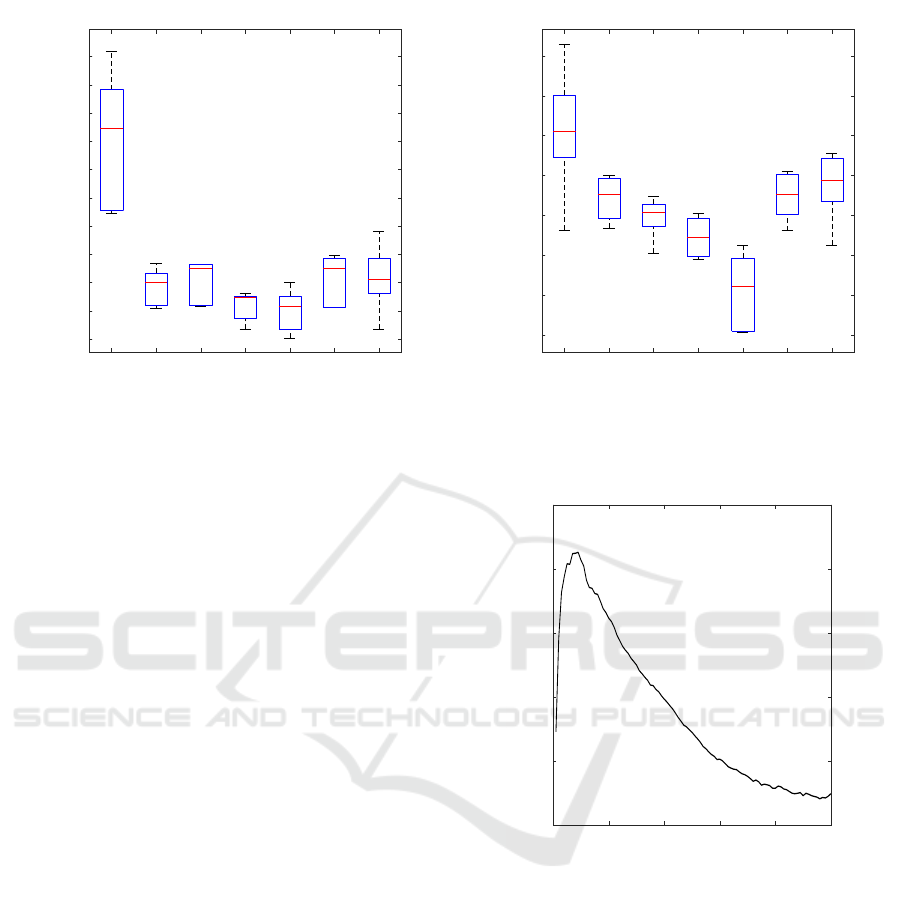
We compared our proposed method against GE-

NIE3(Irrthum et al., 2010), TIGRESS(Haury et al.,

2012), CLR(Faith et al., 2007), ARACNE(Margolin

et al., 2006), NIMEFI(Ruyssinck et al., 2014),

PLSNET(Guo et al., 2016). The proposed method

performs better than the other methods in terms of

both the average area under the receiver operating

characteristic curve (AUROC) and the average area

under precision recall curve (AUPR) (Fig.3), although

the low reliable p-values are omitted in the perfor-

mance evaluation of proposed method. This result

indicates that approximate conditional independence

and omitting low reliable p-value is effective for in-

Approximate Conditional Independence Test using Residuals

301

Prop.(Top10%) GENIE3 TIGRESS CLR ARACNE NIMEFI PLSNET

0.1

0.15

0.2

0.25

0.3

0.35

0.4

0.45

0.5

0.55

0.6

AUPR

(a)

Prop.(Top10%) GENIE3 TIGRESS CLR ARACNE NIMEFI PLSNET

0.6

0.65

0.7

0.75

0.8

0.85

0.9

0.95

AUROC

(b)

Figure 3: Boxplot of (a)AUPR and (b) AUROC of the results for ﬁve inferred networks. The results except proposed method

were taken from (Guo et al., 2016)

ferring the associations of a gene network. Infer-

ring whole network is not always needed. One of the

goals of network inference for biologists is to ﬁnd un-

known associations in biological knowledge. There-

fore, there is an advantage to infer a part of network

more accurately rather than whole of that, although it

is depending on the intended use. Furthermore, merg-

ing parts of network of high reliable p-values inferred

by various estimators would be a promising strategy

to identify whole network structure.

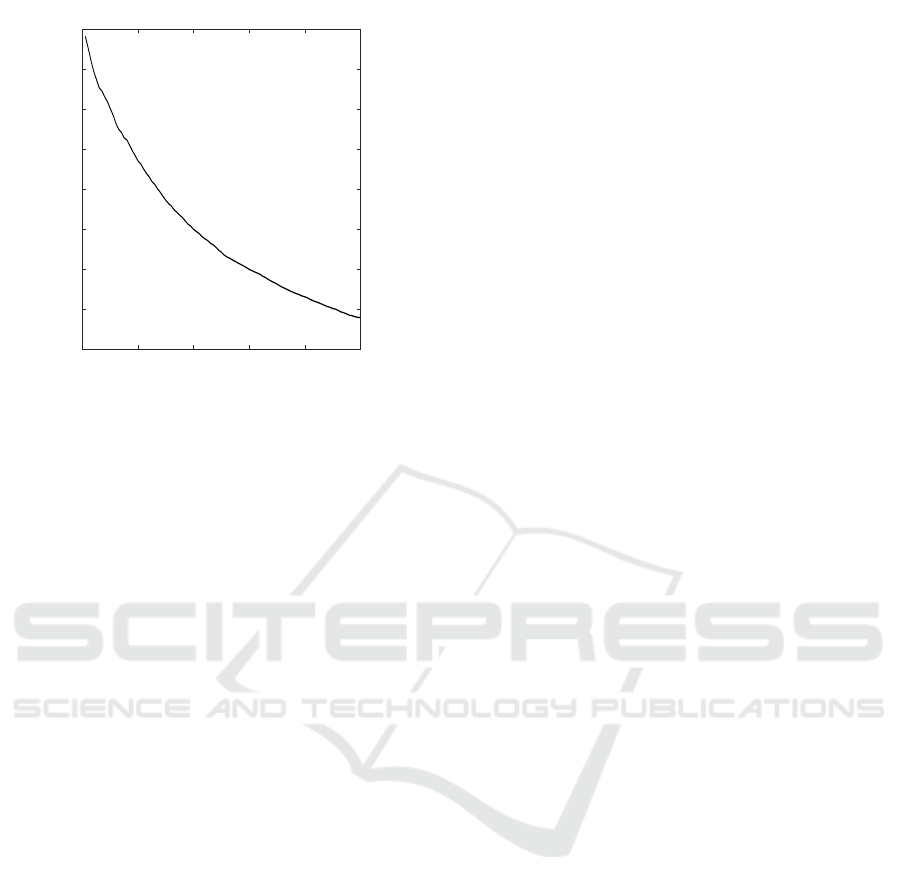
The AUPR almost monotonically decreases with

an increase in unreliable p-values, whereas the AU-

ROC is skewed bell-shaped curve (Fig.4, 5). In gen-

eral, the precision recall (PR) curve is a useful mea-

sure, when dealing with highly skewed datasets in the

class distribution(Davis and Goadrich, 2006). In other

words, the PR curve offers insight about the quality

of inferred association networks that are not dense,

as biological networks tend to be. Given that AUPR

is put more weight than AUROC, the characteristics

of monotonic decrease of AUPR is useful, and the

threshold of p

reli

is determined by the degree to which

accuracy is required.

The advantage of permutation testing is that it re-

turns a p-value. AUROC and AUPR reveal potential

performances of network inference, but the network

structure affects how the threshold for judging the

presence of an edge is determined in practice. The

p-value can be considered as a normalized score de-

ﬁned in [0,1], so the scale of the measure is always

constant. Additionally, the score can be easily in-

terpreted because the probability was under a given

statistical assumption that when conditional or ordi-

nary independence is true, the conditional or ordinal

0 20 40 60 80 100

top x%

0.65

0.7

0.75

0.8

0.85

0.9

AUROC

Figure 4: Average AUROC for inferred networks of reliable

top x% edges.

mutual information would be greater than or equal to

observed result.

5 CONCLUSION

This article has proposed a novel computational

method for approximating conditional mutual infor-

mation based on the distribution of residuals in re-

gression models of the data. The proposed method

translates the problem of conditional independence to

that of determining independence, to enable the use of

permutation testing. The translation of the problem is

an essential feature of the proposed method. The pro-

ICAART 2020 - 12th International Conference on Agents and Artiﬁcial Intelligence

302

0 20 40 60 80 100

top x%

0.15

0.2

0.25

0.3

0.35

0.4

0.45

0.5

0.55

AUPR

Figure 5: Average AUPR for inferred networks of reliable

top x% edges.

posed method can translate a problem to use other es-

timators of residuals ε, η and independence measures

instead of HKRR and J. The score of p-value offered

by the permutation test can be interpreted as the sig-

niﬁcance level, and this threshold is easier to deter-

mine than other scores such as the conditional mutual

information. Additionally, the reliability of p-value is

deﬁned.

The proposed method was applied to inferring

artiﬁcial gene networks from the Dream4 challenge

datasets, and had the better performance in terms of

AUROC and AUPR. Although the proposed method

infers an part of network by omitting low reliable

p-values, there an advantage to ﬁnd unknown asso-

ciations. Furthermore, merging parts of network of

high reliable p-values inferred by various estimators

would be a promising strategy to identify whole net-

work structure.

The proposed method would be basically ex-

tended to the inference of associative networks in case

that the dataset is many-dimensional, that is, X and

Y can be multidimensional. This method may prove

useful, for instance, in the examination of associations

between layers or pathways in transomics datasets.

The HKRR method is employed to infer ε and η in

the method proposed above. However, if p(x|Z) or

p(y|Z) can have a multi-modal distribution for some

ﬁxed Z, HKRR is no longer suitable. The appropriate

method for inferring ε and η depends on the distri-

bution of the data in question, and demands further

study.

ACKNOWLEDGEMENTS

This work was supported by the Creating informa-

tion utilization platform by integrating mathemati-

cal and information sciences, and development to so-

ciety, CREST (JPMJCR1912) from the Japan Sci-

ence and Technology Agency (JST) and by the Japan

Society for the Promotion of Science (JSPS) KAK-

ENHI Grant Number (JP18H04801, JP18H02431)

and Kayamori Foundation of Informational Science

Advancement.

REFERENCES

Cawley, G. and Talbota, N. (2004). Fast exact leave-one-out

cross-validation of sparse least-squares support vector

machines. Neural Networks, 17:1467–1475.

Cawley, G. C., Talbota, N., Foxalla, R. J., Dorlingb, S. R.,

and Mandic, D. P. (2004). Heteroscedastic kernel

ridge regression. Neurocomputing, 57:105–124.

Cover, T. M. and Thomas, J. (2006). Elements of Informa-

tion Theory. Wiley-Interscience New York, NY, USA,

2nd edition.

Daub, C. O., Steuer, R., Selbig, J., and Kloska, S.

(2004). Estimating mutual information using b-

spline functions–an improved similarity measure for

analysing gene expression data. BMC bioinformatics,

5(1):118.

Davis, J. and Goadrich, M. (2006). The relationship be-

tween precision-recall and roc curves. In Proceed-

ings of the 23th international conference on Machine

learning (ICML’06), pages 233–240.

Edgington, E. and Onghena, P. (2007). Randomization

Tests. Chapman and Hall/CRC, 4th edition.

Faith, J., Hayete, B., Thaden, J., Mogno, I., Wierzbowski,

J., Cottarel, G., Kasif, S., Collins, J., and Gardner,

T. (2007). Large-scale mapping and validation of es-

cherichia coli transcriptional regulation from a com-

pendium of expression proﬁles. PLoS Biol., 5(1):e8.

Guo, S., Jiang, Q., Chen, L., and Guo, D. (2016). Gene reg-

ulatory network inference using pls-based methods.

BMC Bioinformatics, 17(545).

Hastie, T., Tibshirani, R., and Friedman, J. (2001). The

Elements of Statistical Learning. Springer New York

Inc, NY, USA.

Haury, A.-C., Mordelet, F., Vera-Licona, P., and Vert, J.-

P. (2012). Tigress: trustful inference of gene regula-

tion using stability selection. BMC systems biology,

6(1):145.

Irrthum, A., Wehenkel, L., Geurts, P., et al. (2010). Inferring

regulatory networks from expression data using tree-

based methods. PloS one, 5(9):e12776.

Margolin, A., Nemenman, I., Basso, K., Wiggins, C.,

Stolovitzky, G., Favera, R., and Califano, A. (2006).

Aracne: An algorithm for the reconstruction of gene

regulatory networks in a mammalian cellular context.

BMC Bioinformatics, 7(57).

Approximate Conditional Independence Test using Residuals

303

McGill, W. J. (1954). Multivariate information transmis-

sion. Psychometrika, 19(2):97–116.

Pearl, J. (2009). Causality:Models, Reasoning and Infer-

ence. Cambridge University Press New York, NY,

USA.

Ruyssinck, J., Geurts, P., Dhaene, T., Demeester, P., Saeys,

Y., et al. (2014). Nimeﬁ: gene regulatory network

inference using multiple ensemble feature importance

algorithms. PLoS One, 9(3):e92709.

Schaffter, T., Marbach, D., and Floreano, D. (2011).

Genenetweaver: in silico benchmark generation and

performance proﬁling of network inference methods.

BIOINFORMATICS, 27(16):2263–2270.

Sun, X., Janzing, D., Sch

olkopf, B., and Fukumizu, K.

(2007). A kernel-based causal learning algorithm. In

Proceedings of the 24th international conference on

Machine learning (ICML’07), pages 855–862.

APPENDIX

The formula for equation (2) is widely known (Cover

and Thomas, 2006).

Theorem 1. When X = f (Z)ε, H(X|Z) = H(ε|Z) +

[log f (Z)].

proof. we have p

X|Z

(x|z) =

f (z)

ε|Z



f (z)



, then,

H(X|Z = z) = H(ε|Z = z) + log f (z). Thus, we ob-

tain

H(X|Z) = E

[H(X|Z = z)] = H(ε|Z) + E

[log f (Z)] .

Similarly, we obtain H(X,Y |Z) = H(ε|Z) +

[log f (Z)g(Z)].

ICAART 2020 - 12th International Conference on Agents and Artiﬁcial Intelligence

304