
Modelling in GeoGebra in the Context of Holistic Approach Realization
in Mathematical Training of Pre-service Specialists
Liudmyla I. Bilousova
1 a
, Liudmyla E. Gryzun
2 b
, Svitlana H. Lytvynova
3 c
and
Valentyna V. Pikalova
4,1 d
1
Kryvyi Rih State Pedagogical University, 54 Gagarin Ave., Kryvyi Rih, 50086, Ukraine
2
Simon Kuznets Kharkiv National University of Economics, 9A Nauky Ave., Kharkiv, 61166, Ukraine
3
Institute for Digitalisation of Education of the National Academy of Educational Sciences of Ukraine, 9 M. Berlynskoho
Str., Kyiv, 04060, Ukraine
4
National Technical University “Kharkiv Polytechnic Institute”, 2 Kyrpychova Str., Kharkiv, 61002, Ukraine
Keywords:
Modeling Activity on GeoGebra, Mathematical Training of Pre-service Specialists, Holistic Education,
Computer Dynamic Model.
Abstract:
In accordance with its aim, the article represents students’ modeling activity (held within inter-university
projects of Kharkiv GeoGebra Institute) which resulted in the complex of GeoGebra models focused on holistic
learning of Mathematics at higher school and university. Proper theoretical background for the complex design
is elaborated and the stages of the students’ modeling activity are covered. The models in the developed
complex are grouped in the three sections. The first group consists of the models which enable to facilitate
mastering basic essential mathematical concepts (objects) by the potential trainees. The second group is
focused on the realization of transdisciplinary connections between Mathematics and other subject domains.
The third group embraces models which provide real-life problems solving based on the models investigation.
All the groups are represented in the article along with specific examples of the models. In order to facilitate
potential trainees’ personal cognitive activity that is expected by holistic education, it was elaborated procedure
of cognitive activity which includes some tips on changing the parameters of the dynamic model, monitoring
the results, investigating, making conclusions etc. Such a procedure is aimed to streamline understanding the
essence of the concept (phenomenon). The didactic support for each model was developed by the students to
involve potential trainees into the solving special problems and real-life tasks which encourage them to obtain
holistic understanding of the basic concepts via special cognitive activity based on work with dynamic models.
The said didactic support is characterized in the paper. The prospects of further research are outlined.
1 INTRODUCTION
The analysis of the evidence of university and pre-
university mathematics training as well as the results
given in recent studies (Bobyliev and Vihrova, 2021;
Elkin et al., 2017; Semenikhina and Drushliak, 2014;
Singh, 1996; Vlasenko et al., 2019), testify the num-
ber of drawbacks of contemporary school mathemat-
ics training which then lead to the difficulties faced
by the university students and raise the problems of
increasing the level of mathematical education both
a
https://orcid.org/0000-0002-2364-1885
b
https://orcid.org/0000-0002-5274-5624
c
https://orcid.org/0000-0002-5450-6635
d
https://orcid.org/0000-0002-0773-2947
at school and university.
According to the (Bevz, 2003; Bilousova et al.,
2019; diSessa et al., 2004), the most common learn-
ing difficulties which brake the process of successful
mastering mathematics are the following. Students
find mathematical concept to be difficult to take in and
to apply them properly to practical tasks. It leads to
inability to achieve basic educational goals by the stu-
dents which results in their loosing interest to Math-
ematics. Finally, it becomes impossible for the stu-
dents to see the beauty of the science and to appreci-
ate its importance for mastering other knowledge do-
mains.
One of the essential problems of mathematical
training that can cause the learning difficulties is the
absence of holistic understanding of mathematics as a
Bilousova, L., Gryzun, L., Lytvynova, S. and Pikalova, V.
Modelling in GeoGebra in the Context of Holistic Approach Realization in Mathematical Training of Pre-service Specialists.
DOI: 10.5220/0010925700003364
In Proceedings of the 1st Symposium on Advances in Educational Technology (AET 2020) - Volume 1, pages 499-510
ISBN: 978-989-758-558-6
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
499

basis and tool for solving interdisciplinary tasks and
real-life problems. Unfortunately, for the most of
students, Mathematics remains too abstract curricu-
lum subject which is really complicated and distracted
from real world. Hence, the students are demotivated
to master it and feel true necessity to its deep under-
standing.
The said problems of mathematical training which
are faced nowadays by the pre-service specialists of
different majors cause the necessity of finding and ap-
plying new approaches to mathematics learning. One
of such approaches seems to be holistic educational
paradigm which aims to provide dynamic, harmo-
nized, and interconnected ways of learning.
According to the research on the holistic ap-
proach, the core concept of holistic education is the
cohesive development of the students’ personality
both at the intellectual and emotional levels (Singh,
1996). In addition, it is underlined that the said cohe-
sive progress should base on the links between real-
life problems and personal experience of a trainee.
Among basic principles of holistic education the
studies (in particular, (Mahmoudi et al., 2012; Miller,
2004, 1991; Miller et al., 2005)) point out some pil-
lars which seem to be essential in the context of the
problems of Mathematics training, mentioned above.
The first principles expects students’ freedom and au-
tonomy. So, within the holistic paradigm any trainee
is considered to be really active participant of the
learning process who is ready to interact with reality
through his own cognitive activity with his own ups
and downs.
Next pillar of the holistic approach is necessity to
establish connections and relationships between the
object of learning and existing knowledge. The more
links trainees have, the stronger memories are formed
in their minds and better understanding of the whole
they obtain.
Similar to the establishing links is the principle of
transdiciplinarity which focuses teaching and learning
on ruining boundaries between subject fields them-
selves as well as between subject areas and reality.
Researchers also point out that holism helps both
the connection facet and transdiciplinarity, because it
seems to be fruitful to learn separate things which in
fact are not separate. However, at the same time it is
necessary to understand how they work together.
The analysis of the holistic education basis reveals
a need to apply efficient learning tools enabled to
provide holistic approach to nowadays teaching and
learning.
One of such tool seems to be computer dynamic
models (CDM). The learning of recent studies on
their didactic facilities testifies that CDM have quite
powerful potential as for revealing transdisciplinary
connections and facilitating their understanding by
trainees. In particular, researchers point out that CDM
are typically based on the mathematical model of a
concept (process, phenomenon, etc.), and enable to
visualize its essence at real time operation, learn dy-
namic changes, and investigate the concept or process
via active cognition. In such a way CDM help to
form and develop students’ techniques of mental ac-
tivity including transdisciplinary ones (Semenikhina
and Drushliak, 2014; Alessi, 2000).
Characterizing advantages and facilities of CDM
using in the context of holistic education, it is im-
portant to emphasize that they encourage students to
learn objects independently and actively. In addition,
they reveal and demonstrate in action the wholeness
of the learnt concepts (phenomenon).
In this context, it is essential to focus on the valu-
able potential of contemporary mathematical com-
puter environments which enable to create the mod-
els of different complexity, visualize changes of the
model behavior and do proper research. Despite the
great variety of the said software on the modern IT
market, we would like to focus on modeling facilities
of free GeoGebra software which provides a trainee
with convenient tools to develop a CDM, and do ef-
fective simulations and investigations with it. In par-
ticular, GeoGebra allows to create geometrical objects
and obtain easily their algebraic interpretation; get in-
teractive and dynamic visualization of the objects of
various essence; manipulate with the model parame-
ters to monitor the changes etc (Pikalova, 2018; Kra-
marenko et al., 2020). In addition, online service Ge-
oGebraTube grants the access to the variety of ex-
isting elaborations provided by the global GeoGebra
community which unites the educators and students
all over the world.
Nowadays, GeoGebra Institutes work in many
countries and make together International GeoGe-
bra Institute (IGI) as a global organization that nour-
ishes and stimulates collaboration between practition-
ers and researchers, seeking to expand the community
of independent GeoGebra users.
GeoGebra Institute, Kharkiv, Ukraine, which has
been realizing its mission since 2010 within IGI, fo-
cuses on:
1) promoting the dissemination and productive use
of software, scientific, educational, methodolog-
ical developments of the international GeoGebra
community in professional activities of mathe-
maticians and other specialists;
2) encouraging students and teachers to conduct re-
search in mathematics, physics, computer science
and information technology;
AET 2020 - Symposium on Advances in Educational Technology
500

3) implementation of the concept of STEM-
education in educational practice;
4) involvement of students and teachers in cooper-
ation with the international GeoGebra commu-
nity via participation in the conferences and other
events initiated by the IGI.
One of the interesting and significant inter-
university projects of Kharkiv GeoGebra Institute was
involving students of various specialties into mod-
eling activity focused on various GeoGebra models
elaboration and learning the modeled objects (pro-
cesses, dependences etc.).
The purpose of the article is to represent stu-
dents’ modeling activity which resulted in the com-
plex of GeoGebra models focused on holistic learning
of Mathematics at higher school and university.
2 THEORETICAL FRAMEWORK
During the research, the set of theoretical, empirical,
and modelling methods were applied.
Characterizing the arrangement of the said stu-
dents’ modeling activity within Kharkiv GeoGebra
Institute, we can describe all necessary stages of the
work.
At the first stage, the core task was formulated
for the students as following: to develop the complex
of GeoGebra models for the maintaining learning of
Mathematics at higher school and university based on
holistic approach.
In addition, there were formulated necessary re-
quirements for the whole complex which determined
its potential functions and enabled to realize exactly
holistic paradigm according to its aim and principles
(covered above).
In accordance with Requirement 1, the students
had to develop different groups of models. The first
group consists of the models which enable to facilitate
mastering basic and complicated mathematical con-
cepts (objects) by the potential trainees. The second
group of the models must be focused on the realiza-
tion of transdisciplinary connections between Math-
ematics and other subject domains. The third group
has to provide real-life problems solving, based on
the models investigation. Such models and simula-
tions should emphasize the meta-role of Mathematics
as well as demonstrate its practical value (rather than
pure abstract science).
Requirement 2 determined all the models to be
dynamic, to visualize immediately the results of the
trainee’s manipulation and encourage them to learn
the modeled concept actively, via their own experi-
ence.
Requirement 3 expected the complex to be cloud-
based, that is, to be available at www.geogebra.org for
the global GeoGebra community. According to recent
studies, cloud-based learning environment for teach-
ing and learning STEM disciplines opens wide hori-
zons for holistic education due to the realized support
for various processes of learning and research activi-
ties; great level of learning resources flexibility; inte-
gration of variety of educational components based on
innovative technologies. On the other hand, it seems
to be powerful motivational factor for the students
evolved into the complex elaboration as their work
makes them participants of the global community.
Thus, at the first stage of the modeling activity,
the students had to understand main features of holis-
tic theory, to realize their core task and the common
requirements to the complex, plan the work and allo-
cate sub-tasks.
Next stage of the work was analytical one which
created necessary theoretical background for develop-
ment of all three groups of dynamic GeoGebra mod-
els.
At this stage of the complex elaboration the
students made deep and comprehensive analysis of
Mathematics to reveal its key concepts and their po-
tential links with the notions of other subject domains.
In order to meet the main pillars of holistic educa-
tional approach (covered earlier) it is necessary to re-
veal key objects of learning in the subject areas, es-
tablish connections between them, and build chains
of proper transdisciplinary links.
Researchers distinguish different types of trans-
disciplinary connections. However, scientists (in par-
ticular, Bevz (Bevz, 2003), diSessa et al. (diSessa
et al., 2004), McDonald and Czerniak (McDonald and
Czerniak, 1994)) recommend to base the connections
classification upon the set of three main grounds: in-
formation content of the subject domain, structure of
learning activity, and organization of educational pro-
cess.
As a result, considering the transdisciplinary con-
nections from the standpoints of holistic education,
the students had to reveal key concepts of subjects,
detect their place in the current curriculum, consider
peculiarities of their mastering and proper cognitive
activity.
These procedures were done through the learn-
ing main content threads of the said curriculum sub-
jects (Ministerstvo osvity i nauky Ukrainy, 2017a,b)
and didactic analysis of each subject domain (covered
in (Gryzun, 2018, 2016)). Main content threads of
Mathematics, Science subjects (Physics, Chemistry,
Biology) and Computer Science enabled us to reveal
some transdisciplinary chains. We would like to point
Modelling in GeoGebra in the Context of Holistic Approach Realization in Mathematical Training of Pre-service Specialists
501

out a paramount role of penetrating content threads
in revealing transdisciplinary concepts and links be-
tween them. According to the Concept of the New
Ukrainian School, there are four penetrating content
threads – “Ecology security and sustainable develop-
ment”, “Civil responsibility”, “Health and security”,
“Financial literacy” – which are seen as a mean of
key competences integration of all curriculum sub-
jects. The penetrating threads are considered to be
socially important meta-topics that focus teaching and
learning on the trainees’ holistic understanding of the
world. They are recommended to be regarded during
the learning environment creation at all the levels of
education (Elkin et al., 2017).
Finally, at the analytical stage of the described
modeling activity, the students obtained the set of
connection chains between the Mathematics and other
subject domains. In particular, there were revealed the
links:
• Mathematics – Computer Science;
• Mathematics – Physics;
• Physics – Mathematics – Biology;
• Mathematics – Economics;
• Mathematics – Building (design) and others.
Subsequent detailed analysis of the qualification
standards, textbooks, and subject areas resulted in
establishing of transdisciplinary links between the
learning elements (LE), representing concepts and
phenomena which are co-explored by several subject
domains. In particular, the effective semantic analysis
was held with the help of specialized software, such
as: TextAnalyst 2.0, Text Miner 12.1 (its Text Parsing
Node), Trope 8.4.
Such a “smart” analysis of the subject areas en-
abled to distinguish the weightiest LEs of the specific
subject area along with their conceptual links. Basing
on the depicted analysis, for the revealed weightiest
LEs of Mathematics it was built a graph, representing
their transdisciplinary links with exact learning ele-
ments (LE1...LEn) of other subject domains (SD), ac-
cording to the chains of connections mentioned ear-
lier.
The general scheme of the graph representing
their transdisciplinary links with exact learning ele-
ments (LE1...LEn) of subject domains (SD) as well as
the example of the graph for selected LEs, represent-
ing the transdisciplinary links for the chain: Physics-
Mathematics-Biology (Used below for the transdisci-
plinary Model “Lens”), are given on the figures 1 and
2.
3 RESULTS AND DISCUSSION
The results of theoretical framework were used by the
students at the design stage of their modelling activ-
ity on the development of the complex of GeoGebra
models, focused on holistic learning of Mathematics
at higher school and university.
The process of the models elaboration provided
by the students (with accordance to the requirements
formulated at the preparation stage) embraces some
phases. At the first phase mathematical model of the
future computer model is built. At this point it is
done:
1) revealing and learning of the transdisciplinary
essence of the proper concept (See theoretical
framework);
2) defining of the mathematical dependencies which
can illustrate and investigate the concept;
3) determination of the fixed model parameters and
changeable ones along with the range and step of
their changes;
4) picking up proper graphic elements which are able
to illustrate dynamic changes;
5) revealing of transdisciplinary tasks and real-life
problems which might be solved by the model;
6) elaboration of didactic support as a scheme of
work upon the ransdisciplinary tasks and real-life
problems directed on the forming holistic image
of the said concept (phenomenon).
At the second phase the mathematical model is
built in the environment of GeoGebra. In particular,
the set of standard GeoGebra tools are used (Points,
Lines, Special Lines, Polygon, Circle and Arc, Mea-
surement, Transformations) as well as the CAS com-
ponents (Calculations and Analysis Tools). For real-
ization of dynamic transformations, the Action Object
Tools and Movement Tools are used (Semenikhina
and Drushliak, 2014; Pikalova, 2018).
In order to make the use of the complex more flex-
ible and available to a wide community of students
and teachers, it was organized it in the form of Ge-
oGebra Book. GeoGebra Book is a cloud service
which enables to gather GeoGebra resources, to en-
hance them didactically, and to share them easily. Due
to this fact, the complex of models is oriented to be
a component of a cloud-based learning environment
available to the global GeoGebra community.
The third phase is devoted to the testing, debug-
ging and improving of the model.
The models in the complex are grouped in the
three sections according to the Requirement 1: the
AET 2020 - Symposium on Advances in Educational Technology
502
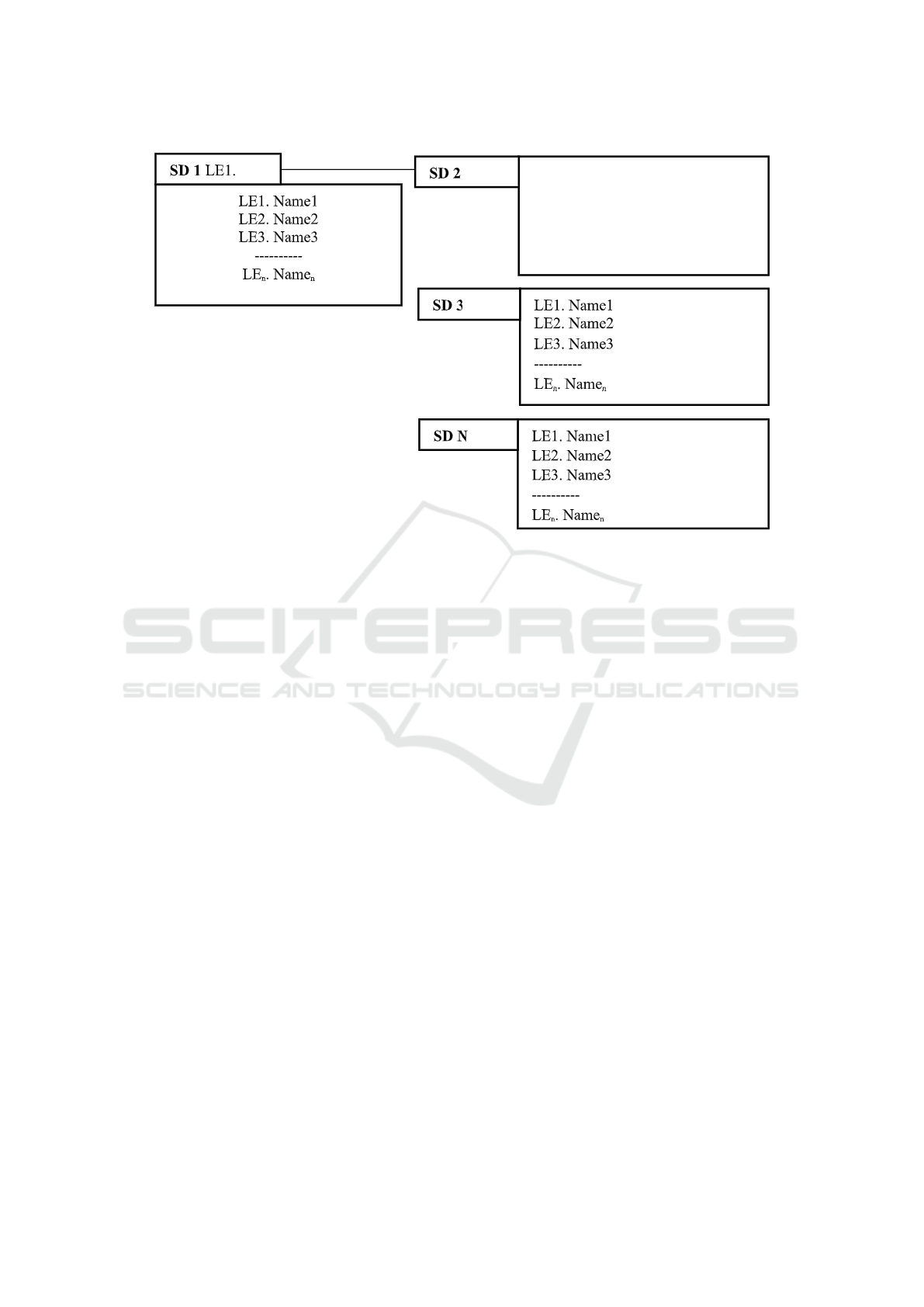
Figure 1: The common scheme of the graph, representing their transdisciplinary links with exact learning elements
(LE1...LEn) of subject domains (SD).
first group consists of the models which enable to fa-
cilitate mastering basic and complicated mathemati-
cal concepts (objects) by the potential trainees; the
second group is focused on the realization of transdis-
ciplinary connections between Mathematics and other
subject domains; the third group embraces models
which provide real-life problems solving based on the
models investigation.
Each of the models is presented in the complex
according to the general scheme.
It includes (see examples below):
• model title;
• chain of the transdisciplinary links which are il-
lustrated by the model;
• model description which explains concept (phe-
nomenon) that is a prototype of the model;
• dynamic model itself with a proper functionality;
• procedure of cognitive activity on the realizing the
essence of the concept (phenomenon);
• didactic support as a set of transdisciplinary tasks
and real-life problems for forming holistic image
of the said concept (phenomenon), and a scheme
of work upon them;
• graph of the revealed transdisciplinary links for
the visualization and remembering this holistic
representation.
As it was mentioned above, holistic education ex-
pects trainees’ personal cognitive activity. In order
to facilitate it, it was elaborated procedure of cogni-
tive activity which includes some tips on changing the
parameters of the dynamic model, monitoring the re-
sults, investigating, making conclusions etc. Such a
procedure is aimed to streamline understanding the
essence of the concept (phenomenon).
The didactic support for each model is developed
to involve potential trainees into the solving special
problems and real-life tasks which encourage them to
obtain holistic understanding of the basic concepts via
special cognitive activity based on work with dynamic
models. All of the tasks focus the trainees on the re-
vealing and realizing transdisciplinary links.
Some of the models with their description and
functionality are included into more than one subject
section. However, didactic support as a set of trans-
disciplinary tasks for each model is specific in each
section and focuses on different transdisciplinary con-
nections.
Below we demonstrate fragmentary some of the
models from various groups of the complex created
by the students within the modeling activity (accord-
ing to general scheme of model presentation depicted
above) and offer recommendations as for their using
to provide holistic learning of Mathematics at high
school and university.
As it was said above, the dynamic models of the
Modelling in GeoGebra in the Context of Holistic Approach Realization in Mathematical Training of Pre-service Specialists
503

Figure 2: The example of the graph for selected LEs, representing the transdisciplinary links for the chain: Physics-
Mathematics-Biology (Used below for the transdisciplinary Model “Lens”).
first group enable to facilitate mastering basic and
complicated mathematical concepts (objects) by the
potential trainees. The models are accompanied by
special didactic support focusing them on investiga-
tion and holistic learning of the modeled concept. A
lot of the models expect the model transformation by
a trainee with the aim of its extension on different
class of problems.
Among the models of this group it is worth
mentioning the models Elementary functions inves-
tigation (figure 3), Triangular properties learning,
Graphical inequalities solution, Calculation of the
area limited by the curve (figure 4), Remarkable
curves investigation, Investigation of the approxima-
tion curve and others.
Example 1. Model “Remarkable curves investiga-
tion. Epicycloids”
Chain of the transdisciplinary links: Geometry-
Algebra-Mechanics.
Model description: According to definition,
epicycloids is a plane curve made by tracing the path
of the fixed point P on the circumference of a circle
(called epicycle) which rolls without slipping around
another fixed circle. R is the radius of the fixed circle,
r is the radius of the rolling circle. The model is built
based on the kinematic definition of epicycloids and
illustrates its different types. Unlike cycloid, epicy-
cloids are not transcendental.
Procedure of cognitive activity with the model (se-
lected tasks of the elaborated didactic support by the
students):
1. Manipulate the model parameters to figure out
how the number of the curve lobes depends on the
ratio n of R and r. Answer the questions:
• What types of epicycloids is obtained at n=1,
n=2, n=3?
• What happens, when n is integer and when n is
rational? Make conclusions.
2. Monitore the model work, and calculate position
of the point P via radiuses (R, r), the radian from
the tangential point to the moving point and the ra-
dian from the starting point to the tangential point.
3. Transform the original model of epicycloids into
the model of hypocycloid, answering the ques-
AET 2020 - Symposium on Advances in Educational Technology
504

Figure 3: Episodes of cognitive activity on the model Elementary functions investigation.
Figure 4: Episodes of manipulation with the model Calculation of the area limited by the curve.
tions and doing proper steps:
• How to calculate R now, when the small circle
“rolls” along inside part the bigger circle?
• How to calculate the speed of the point P which
remain the trace? Why?
• How must animated points P and the center of
smaller circle move now? How are their move-
ment directions related?
4. Use obtained model of hypocycloid, monitor its
work and convince that its number of cusps is also
controlled by the ratio n. Investigate the curve be-
havior, answering the questions:
• How many cusps does the curve have, if n is
integer n?
• How is hypocycloid transformed at n=2?
• What value of n stops the work of the model?
Why? How does the curve look like?
• Investigate the curve behavior at 1<n<2 and
n>2. Make conclusions.
Selected episodes of the students’ cognitive activ-
ity with the dynamic model “Remarkable curves in-
vestigation. Epicycloids” are given on the figure 5.
The models of the second group are concentrated
on the realization of transdisciplinary connections be-
tween Mathematics and other subject domains. In
particular, it contains the models Clock (connections:
algebra, geometry, trigonometry, physics, sociology,
history, philosophy); Mathematical pendulum (con-
nections: mathematics, physics) (figure 6); Number
systems (connections: algebra, computer science, dis-
crete mathematics, history); Binary tree (connections:
discrete mathematics, computer science) (figure 7)
and many others.
Work upon the transdisciplinary models of the
second group is selectively shown in the Example 2
below.
Example 2. Model “Lens”
Chain of the transdisciplinary links: Physics-
Mathematics-Biology.
Model description: The model illustrates princi-
ple of operation of a lens as a simplest optical device
that focuses or disperses a light beam. A lens consists
of a single piece of transparent material (e.g. glass
or plastic). A lens can focus light to form an image
which differs it from prism (See Model “Optical dis-
persion”). A lens has its optical axis, two focuses,
main optical center and plane (you can find their def-
initions in your textbook). Lenses are classified by
the curvature of the two optical surfaces. The model
demonstrates the operation of exactly biconvex lens.
Procedure of cognitive activity with the model (se-
Modelling in GeoGebra in the Context of Holistic Approach Realization in Mathematical Training of Pre-service Specialists
505

Figure 5: Episodes of the students’cognitive activity with the dynamic model “Remarkable curves investigation. Epicycloids”.
Figure 6: Episodes of the students’cognitive activity with the transdisciplinary model Mathematical pendulum.
lected tasks):
1. Operate the model. Change curvature with the
slider. Monitor the focuses positions and image
positions. Find and formulate dependences.
2. Fix the lens curvature and change the object posi-
tion relative to the focus. What is happening with
the image of the object?
3. Fix the object at the distances: d=2F, d>2F, d<2F.
Analyze changes and make conclusions.
4. Analyze changes of the image’s size and position
when the object is between 2F and F, between F
and lens center.
Fragment of didactic support as a set of transdisci-
plinary tasks and real-life problems for forming holis-
tic understanding of the optical device from the stand-
point of Mathematics, Physics, and Biology):
1. Manipulate the model parameters. What is math-
ematical dependence between object distance to
the lens and focus distance? How is it called?
Write the formula of the dependence.
2. What geometrical figures describe the object, its
image, light beams and the phenomena of light
penetration through the lens?
3. What geometrical facts and properties are re-
vealed by the device operation?
4. Which angles are equal at any values of the model
parameters? Why? Which rays are parallel?
Why?
5. Working with the model, detect the parameters
of the model which provide the highest optical
power of the lens.
6. Manipulating the model and using the scheme of
the optical system of a human eye (figure 8), an-
swer the questions: (1) what are the components
of the eye optical system? (2) what is the differ-
ence between real and virtual image? (3) what are
the basics of a human eye functioning from the
standpoint of physics? (4) can you explain eye-
sight disorders (short sight, long sight, etc.) via
physical concepts and phenomena? (5) compare
the principles of human eye operation and work
of a digital camera.
Episodes of transdisciplinary tasks doing and the
model operating are shown on the figure 9.
Graph of the revealed transdisciplinary links for
the visualization and remembering this holistic repre-
sentation presented on figure 2 above.
The third group of the created models embraces
ones that provide real-life problems solving based on
the so called STEM investigation. As it is expected by
the requirements, the models of the third group en-
able simulations which help realize the meta-role of
AET 2020 - Symposium on Advances in Educational Technology
506
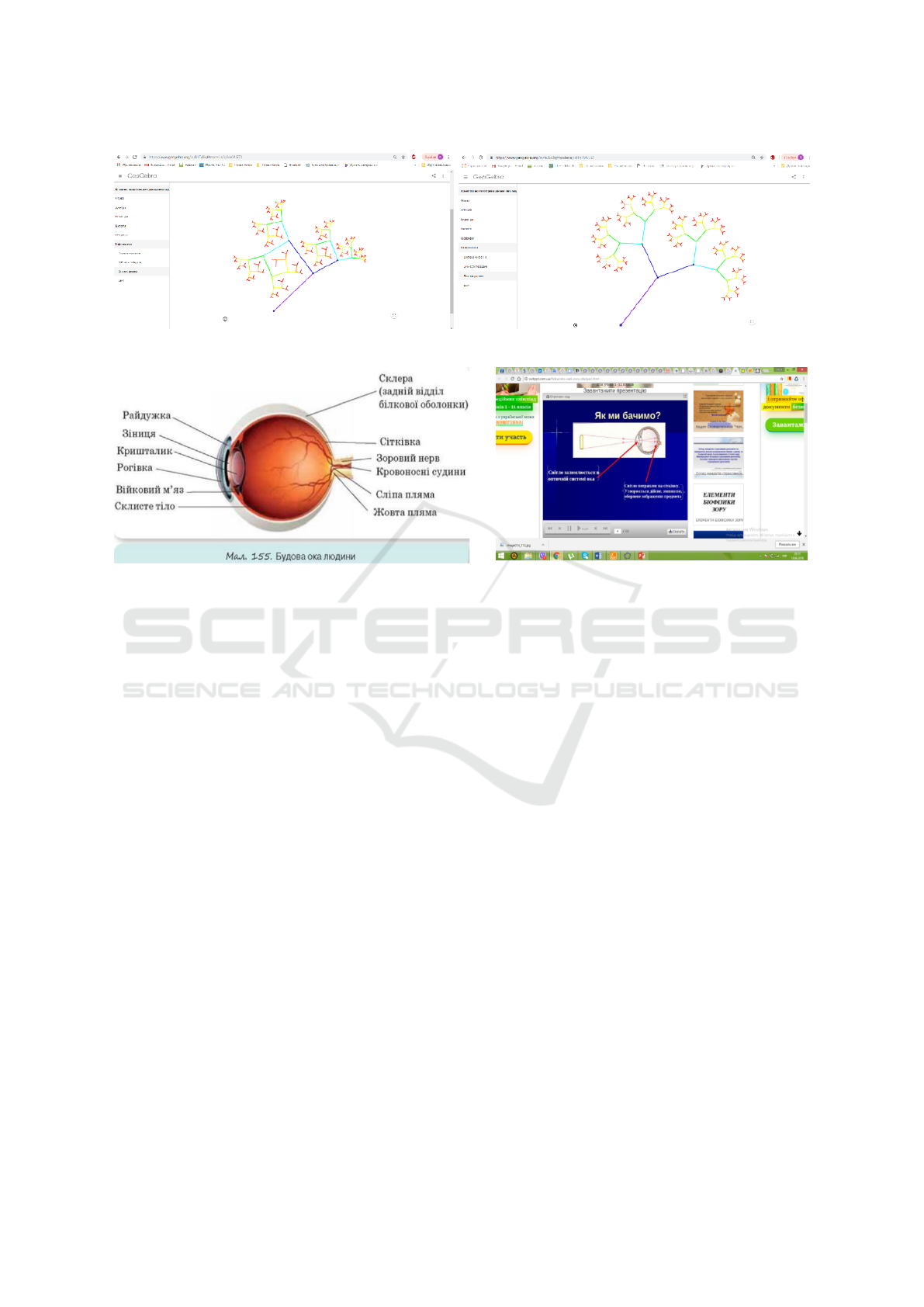
Figure 7: Episodes of the students’cognitive activity with the transdisciplinary model Binary tree.
Figure 8: Scheme of the optical system of a human eye.
Mathematics as well as demonstrate its applied value
for practical daily needs. It includes the models such
as Investigation of shooting path; Lift work; Geomet-
rical transformations in real-life measurements; Re-
markable triangular points; Bridge approximations
and many others.
Selected fragments of the real-life tasks solving
within the dynamic models Investigation of shoot-
ing path and Geometrical transformations in real-life
measurements are given on the figure 10.
Below we are giving the example of STEM
investigation which it is recommended to build,
maintaining the model Fermat-Torricelli points
investigations.
Example 3. Real-life problems solving on the
model Fermat-Torricelli points investigations
Investigation 1. Construct the second Fermat-
Torricelli point by constructing right triangles on the
sides inward. Investigate the properties of the Fermat-
Torricelli point: the sum of the distances from the
point to the vertices of the triangle is minimal, and
all the vertices are visible from it at an angle of 120°.
Investigation 2. Using the obtained dynamic
model, investigate the position of the Fermat-
Torricelli point (with to the triangle), when the tri-
angle has one angle greater than 120°. Determine
whether it will have its properties in this situation.
Determine how the point will behave when there is
an angle of 120°.
Investigation 3. Elaborate the model and try to
figure out how to use the properties of the point to
solve current problems in your city.
1. Imagine that you need to place the emergency
medical center so that it was at a minimum dis-
tance from the three points of the city A, B, C.
Using a digital map of the city as a working geo-
metric field GeoGebra.
2. Match the points of the city to the vertices of
the triangle and determine if there is a Fermat-
Torricelli point for this triangle, find this point for
it.
3. Determine which geographical point on the map
corresponds to the found Ferma-Torricelli point.
Investigate whether it is possible to locate an
emergency center at this point in terms of social,
economic and geographical conditions.
4. If this is not possible, manipulate the model pa-
rameters, change the position of the points A, B,
C and find out their geometric location so that the
built triangle and its Ferma-Torricelli point meet
the current social needs of the city.
Investigation 4. Formulate a mathematical prob-
lem about the use of the properties of the Ferma-
Torricelli point, which can arise when building roads
Modelling in GeoGebra in the Context of Holistic Approach Realization in Mathematical Training of Pre-service Specialists
507
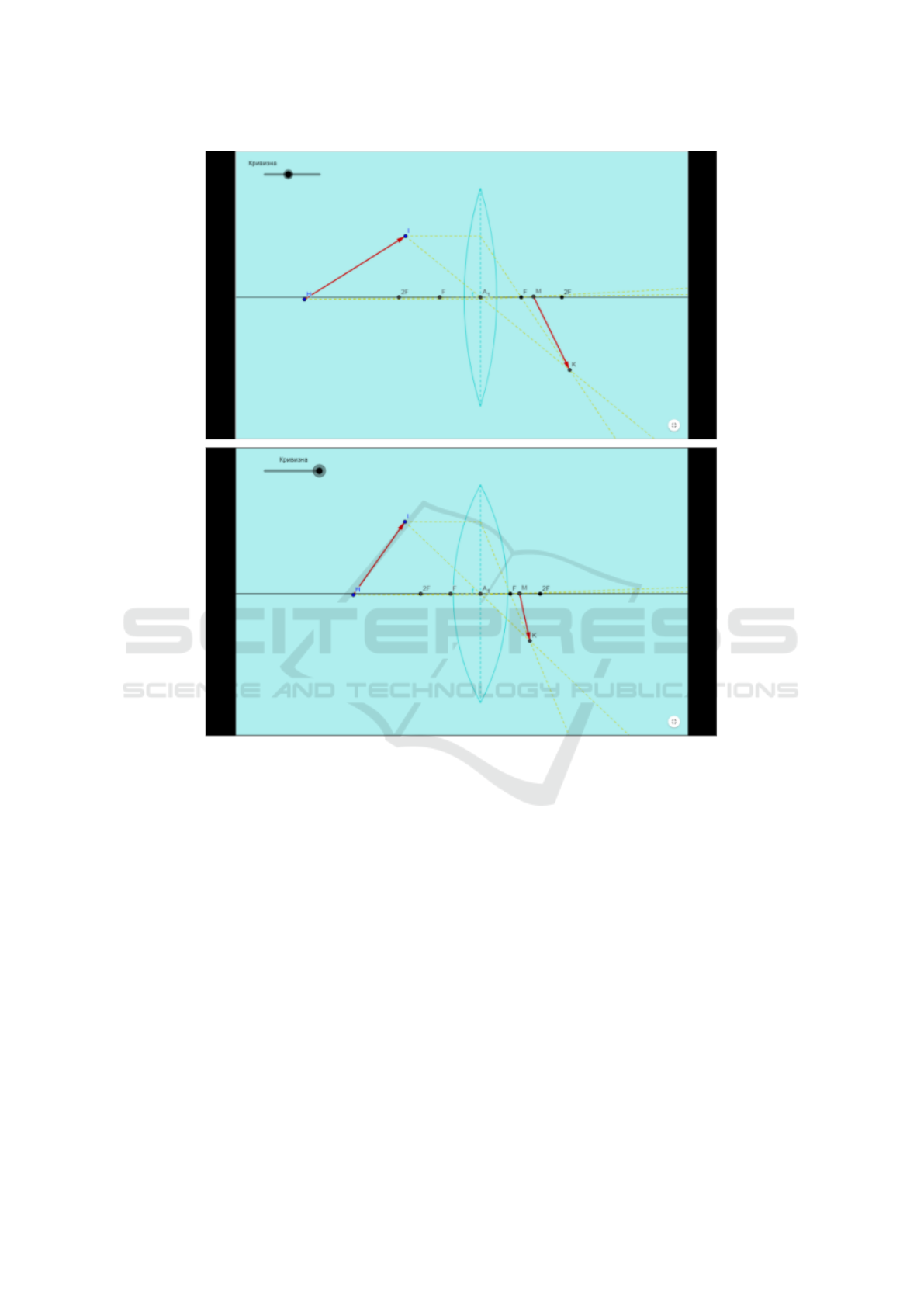
Figure 9: Episodes of transdisciplinary tasks solving, operating the model “Lens”.
between settlements in your region in order to save
resources. Use the dynamic model to solve and inves-
tigate this problem.
Summarizing the presentation of the complex
of GeoGebra dynamic models created by the stu-
dents (pre-service specialists of different specialities)
within the realization of holistic approach to their
mathematical training, we would emphasize that be-
sides models, the students developed special didactic
support as a set of transdisciplinary tasks and real-life
problems for forming holistic image of the said con-
cept (phenomenon).
The prepared didactic support includes the trans-
disciplinary tasks of various types. In particular, there
are tasks on establishing connections between math-
ematical concepts and notions of other subject areas.
The aim of these tasks is to specify and generalize
mentioned connections; to form the system of the no-
tions of different level of generalization and subor-
dination; to illustrate casual relations of phenomena.
This type of the problems are directed on the forming
of the set of potential trainees’ skills of integrative
properties: to understand meta-role of Mathematics
for other domains of knowledge; to explain processes
and phenomena of one domain with the help of con-
cepts of other branch; to make outlook conclusions
based on common concepts, and others.
Besides, the developed didactic support can offer
transdisciplinary tasks for potential trainees on the de-
termination of community of the facts from differ-
ent subject domains. They allow to specify learn-
ing material, to form new mathematical concepts and
explain them from the standpoints of other branches
of science, to use some mathematical facts to illus-
trate other ones. Such tasks are aimed at the forming
students’ skill of facts’ analysis, generalization and
AET 2020 - Symposium on Advances in Educational Technology
508

Figure 10: Selected fragments of the real-life tasks solving within the dynamic models Investigation of shooting path and
Geometrical transformations in real-life measurements.
explanation from the standpoint of general scientific
ideas; skill to integrate generalized facts into the ex-
isting knowledge system; skill to apply generalized
knowledge into practice.
In addition, into the didactic support there are in-
cluded the tasks on the establishing connections be-
tween theoretical knowledge and methods, and their
practical use. Mostly they are real-life problems
which focus on the ruining boundaries between Math-
ematics, other subject domains and reality. They
might help to form the trainees’ ability to see scien-
tific subtext in pure practical tasks, to attract general-
ized knowledge from related areas, and to apply them
to resolving the problem.
Thus, the cloud-based complex of GeoGebra
models (created by the pre-service specialists of dif-
ferent specialities) as for their functionality provides
main principles of the holistic education, such as con-
nections establishing, personal cognitive activity, fo-
cus on the ruining boundaries between subject fields
and reality.
It seems to be relevant to predict positive influence
of the complex application on the forming of potential
trainees’ holistic system of mathematical knowledge.
In addition, we would like to point out that the
complex is a result of modeling activity of the stu-
dents within the realization of holistic approach to
their mathematical training. In this context, our ob-
servations and monitoring all the stages of the stu-
dents’simulation work in the process of the complex
development, allow to predict not only raising the
level of their mathematical knowledge. Our monitor-
ing programs and regular surveys also testify definite
impact on the level of the students’ investigative (en-
quiry) skills. In particular, there was detected pos-
itive dynamic of cognitive, motivational and behav-
ioral components of the said skills. Generalization
and statistical analysis of the obtained empirical re-
sults make prospects of our research.
4 CONCLUSIONS
In accordance with its purpose, the article repre-
sents students’ modeling activity (held within inter-
university projects of Kharkiv GeoGebra Institute)
which resulted in the complex of GeoGebra models
focused on holistic learning of Mathematics at higher
school and university.
Proper theoretical background for the complex de-
sign is elaborated and the stages of the students’ mod-
eling activity are covered. The models in the devel-
oped complex are grouped in the three sections. The
first group consists of the models which enable to fa-
cilitate mastering basic essential mathematical con-
cepts (objects) by the potential trainees. The sec-
ond group is focused on the realization of transdisci-
plinary connections between Mathematics and other
subject domains. The third group embraces models
which provide real-life problems solving based on the
models investigation. All the groups are represented
in the article along with specific examples of the mod-
els.
In order to facilitate potential trainees’ personal
cognitive activity that is expected by holistic educa-
tion, it was elaborated procedure of cognitive activity
which includes some tips on changing the parameters
of the dynamic model, monitoring the results, inves-
tigating, making conclusions etc. Such a procedure is
aimed to streamline understanding the essence of the
concept (phenomenon). The didactic support for each
model was developed by the students to involve po-
tential trainees into the solving special problems and
real-life tasks which encourage them to obtain holistic
understanding of the basic concepts via special cogni-
tive activity based on work with dynamic models. The
said didactic support is characterized in the paper.
The prospects of further research are outlined.
Modelling in GeoGebra in the Context of Holistic Approach Realization in Mathematical Training of Pre-service Specialists
509

REFERENCES
Alessi, S. (2000). Designing educational support in
system-dynamics-based interactive learning environ-
ments. Simulation & Gaming, 31(2):178–196.
Bevz, V. (2003). Mizhpredmetni zviazky yak neobkhidnyi
element predmetnoi systemy navchannia (Transdisci-
plinary connections as a necessary element of the sub-
ject system of learning). Matematyka v shkoli, 6:6–11.
Bilousova, L., Gryzun, L., Zhytienova, N., and Pikalova,
V. (2019). Search algorithms learning based on cog-
nitive visualization. CEUR Workshop Proceedings,
2387:472–478.
Bobyliev, D. Y. and Vihrova, E. V. (2021). Problems and
prospects of distance learning in teaching fundamental
subjects to future mathematics teachers. Journal of
Physics: Conference Series, 1840(1):012002.
diSessa, A. A., Gillespie, N. M., and Esterly, J. B. (2004).
Coherence versus fragmentation in the development
of the concept of force. Cognitive Science, 28(6):843–
900. https://onlinelibrary.wiley.com/doi/abs/10.1207/
s15516709cog2806 1.
Elkin, O., Hrynevych, L., kalashnikova, S., Khobzey,
P., Kobernyk, I., Kovtunets, V., Makarenko, O.,
Malakhova, O., Nanayeva, T., Shiyan, R., and Us-
atenko, H. (2017). The New Ukrainian School:
conceptual principles of secondry school reform.
MESU, Kyiv. https://mon.gov.ua/storage/app/media/
zagalna%20serednya/Book-ENG.pdf.
Gryzun, L. (2016). Integrative technology of academic sub-
jects structuring and its applications to practical di-
dactic issues. Aktualni pytannia humanitarnykh nauk,
16:309–315. http://www.aphn-journal.in.ua/archive/
16 2016/39.pdf.
Gryzun, L. (2018). Integrative approach to the curricu-
lum and content design for the pre-service teachers’
training. PEOPLE: International Journal of Social
Sciences, 4(2):1446–1462. https://grdspublishing.org/
index.php/people/article/view/1572.
Kramarenko, T., Pylypenko, O., and Muzyka, I. (2020).
Application of GeoGebra in Stereometry teaching.
CEUR Workshop Proceedings, 2643:705–718.
Mahmoudi, S., Jafari, E., Nasrabadi, H., and Liaghatdar, M.
(2012). Holistic education: An pproach for 21 cen-
tury. International Education Studies, 5(3):178–186.
McDonald, J. and Czerniak, C. (1994). Develop-
ing interdisciplinary units: Strategies and exam-
ples. School Science and Mathematics, 94(1):5–
10. https://onlinelibrary.wiley.com/doi/abs/10.1111/j.
1949-8594.1994.tb12281.x.
Miller, J. (2004). Educational alternatives: A map
of the territory. Paths of Learning, 20:20–27.
http://www.holisticedinitiative.org/wp-content/
uploads/documents/ron millermap of educational
alternatives.pdf.
Miller, J. P., Karsten, S., Denton, D., Orr, D., and Kates,
I. C., editors (2005). Holistic Learning and Spiritual-
ity in Education: Breaking New Ground. State Uni-
versity of New York Press, Albany.
Miller, R., editor (1991). New Directions in Education: Se-
lections from Holistic Education Review. Holistic Ed-
ucation Press, Brandon.
Ministerstvo osvity i nauky Ukrainy (2017a). Bi-
olohiia 6–9 klasy. navchalna prohrama dlia za-
halnoosvitnikh navchalnykh zakladiv (biology
grades 6–9. curriculum for general educational
institutions). https://mon.gov.ua/storage/app/
media/zagalna\%20serednya/programy-5-9-klas/
onovlennya-12-2017/15.biologiya-6-9.docx.
Ministerstvo osvity i nauky Ukrainy (2017b). Navchalni
prohramy dlia 5-9 klasiv (curriculum for 5-9 grades).
https://mon.gov.ua/ua/osvita/zagalna-serednya-
osvita/navchalniprogrami/navchalni-programi-5-9-
klas.
Pikalova, V. (2018). Tutorial on mastering the dynamic
mathematics package GeoGebra as a tool for im-
plementing STEAM-education: a textbook. KhNPU
imeni H.S. Skovorody, Kharkiv.
Semenikhina, O. V. and Drushliak, M. H. (2014). GeoGebra
5.0 tools and their use in solving solid geometry prob-
lems. Information Technologies and Learning Tools,
44(6):124–133. https://journal.iitta.gov.ua/index.php/
itlt/article/view/1138.
Singh, K. (1996). Education for the global society.
In Learning: The Treasure Within. Report to UN-
ESCO of the International Commission on Educa-
tion for the Twenty-First Century. UNESCO Publish-
ing. https://www.gcedclearinghouse.org/sites/default/
files/resources/%5BENG%5D%20Learning 0.pdf.
Vlasenko, K., Chumak, O., Sitak, I., Lovianova, I., and
Kondratyeva, O. (2019). Training of mathematical
disciplines teachers for higher educational institutions
as a contemporary problem. Universal Journal of Ed-
ucational Research, 7(9):1892–1900.
AET 2020 - Symposium on Advances in Educational Technology
510
