Direct NC Toolpath Generation from 3D Point Cloud Datasets

Muslimin

*, Katerina Mukti

, Hasvienda M. Ridlwan

, M. Sholeh

, Ade Sumpena

, Jiang Zhu

Hayato Yoshioka

, Tomohisa Tanaka

Department of Mechanical Engineering, Politeknik Negeri Jakarta, Jl. Prof. Siwabewssy Kampus UI, Depok, Indonesia

Department of Mechanical Engineering, School of Engineering, Tokyo Institute of Technology

I1-35, 2-12-1, O-okayama, Meguro, Tokyo 152-8552, Japan

Laboratory for Future Interdisciplinary Research of Science and Technology (FIRST), Institute of Innovative Research

(IIR), Tokyo Institute of Technology, 2-12-1 Ookayama, Meguro, Tokyo 152-8550, Japan

Keywords: 3D point cloud data, direct tool path, reverse engineering, G-code

Abstract: In reverse engineering, the measurement of the object's surface is carried out by 3D scanning producing 3D

point cloud data. Scanning performed from various positions will have different data, which will then be

registered to form a product topography. The next process is to reconstruct 3D CAD, which is then converted

into working drawings, used for manufacturing processes such as CNC machining by generating G-Code. The

crucial stage was the 3D CAD reconstruction of the point cloud dataset, which required a complicated

triangulation process and long computation time. In this research, 3D point cloud data is used directly to

generate tool paths for CNC machining without 3D CAD reconstruction. The goal is to shorten the reverse

engineering time with a quality that can still meet the requirements. The stage is to model the tool path of the

tools used in CNC machining relative to feature point cloud sets. This toolpath will be used as the basis for

creating G-code. The toolpath makes it possible to degenerate directly from the verified 3D point cloud

registration data based on the modeling results.

1 INTRODUCTION

In reverse engineering, the measurement of an

object's surface is carried out using a 3D laser scan,

which produces 3D point cloud data sets. Scanning

from various positions will have different data, which

will then be registered to form a product topography.

The next stage is the CAD reconstruction of the data

points (Muslimin et al., 2015). CAD surfaces created

are usually in the form of a parametric computer

representation, such as B-helical, Bezier, non-

uniform rational surfaces, and so on. However, 3D

CAD reconstruction is complicated, time-consuming,

and requires operator expertise since accuracy is the

primary reverse engineering goal. Today's laser

scanners are equipped with 3D CAD reconstruction

software, but they are not compatible enough to

handle data noise, edge sharpness, holes, and so on

(Sun et al., 2002)(Muslimin et al., 2015). On the other

hand, the manufacturing process directly from the

point cloud data set without prior CAD reconstruction

is possibly implemented (Chui et al., 2002)(Makki et

al., 2011)(Liu et al., 2013).

Many manufacturing processes can apply to

realize product duplication directly from the point

cloud data set. The method includes additives using a

3D printer, CNC machines to duplicate molds and

moldings for molded products, forging products, and

permanent mold casting products, and so on. In the

additive manufacturing process using a 3D printer,

the point cloud dataset at x, y, z coordinates are

converted into STL format and can then be directly

processed by a 3D printer. In the CNC machining

An application by developing numerical control

(NC) pathways directly from a point cloud dataset is

proposed in this work. The tool path is restricted by

part material, cutter tools, cutting speeds, and work

features. The NC-tool way directly from the point

cloud data has been developed since the popular 3D

scanner used in the reverse technique (Chui et al.,

2002)(Yau & Hsu, 2009)(D. Zhang, 2009). However,

its effectiveness still needs further development. This

method includes NC tool line generators for 3-axis

milling (Zhang et al., 2010) and 5-axis milling (Marie

et al., 2004).

The tool path planning issues were how to make

more accurate machining and smoother, efficient NC-

138

Muslimin, ., Mukti, K., Ridlwan, H., Sholeh, M., Sumpena, A., Zhu, J., Yoshioka, H. and Tanaka, T.

Direct NC Toolpath Generation from 3D Point Cloud Datasets.

DOI: 10.5220/0010574100003153

In Proceedings of the 9th Annual Southeast Asian International Seminar (ASAIS 2020), pages 138-145

ISBN: 978-989-758-518-0

tool paths to speed up the process and complete the

complex reconstruction process. This research's main

contribution is to propose an innovative method for

NC (numerical control) tool path generation directly

from a registered point cloud data set. The final goal

is to make a point cloud data conversion system into

G-code CNC machines in the reverse engineering

process.

2 LITERATUR REVIEW

Two critical objectives of the NC-tool path are

machining effectivity and accuracy. Machining

effectiveness deals with tool motions, consisting of

two methods: forward and sidestep. The forward step

is for the line portion connecting adjacent CC (cutter

contact) circumstances, and the highest permissible

chordal variation is called machining tolerance. The

machining accuracy deals with the geometry and

tolerance of the machining process's final result

compared to the specified target. Also, it deals with

surface finishing.

There are two approaches to converting the point

cloud dataset into NC toolpath, the direct and indirect

methods. The differences between the direct method

and indirect method in tool path creation from 3D

point cloud data set are as the following (Zhang,

2009):

1) Indirect tool path generation: In this method,

surface CAD model reconstruction is generated

from the point cloud dataset. Some CAD

software such as CATIA, SolidWorks, and

IMAGEWARE support surface remodeling from

3D point cloud data sets; however, it still needs

interaction from the users to get more precise

surface regeneration with advanced experience

in facade modeling.

2) Direct tool path generation: This method is used

directly from the point cloud dataset without

CAD image regeneration. Due to the inadequacy

of an underlying surface representation, there are

two problems:

a) It is challenging to obtain adaptive

advancing steps and track intervals, driving

to lower machining performance because

without a continuous surface.

b) It is laborious to restrain the machining

exactitude when the input is complex

geometry and noisy.

3 DIRECT NC TOOL PATH

GENERATION

In industry, 3-axis CNC machines are employed for

both the coarse and finish machining process.

Regularly, 3-axis machining techniques for complex

surfaces use a ball end mill cutter. The ball end mills

is a zero cutting speed at the bottom of the ball. This

issue can be overcome by using other cutter

geometries such as flat end mills or multi-axis tool

paths such as four axes or five axes CNC machines.

In this research, NC-milling is used because the

object is the prismatic shape. A three-axis tool path is

adopted for computation. The main steps of the

generation of an efficient NC tool path directly from

point cloud datasets registration proposed in this

research are as follows:

1) Orient the point cloud data with a machined

surface into the z-axis and consider the cutting

tool's direction. It is crucial to start the planning

of the tool path from (0,0,0).

2) Classify all main machined surfaces into

complex features and non-complex features.

Complex surfaces include free-form surfaces,

curves, and ruled surfaces.

3) Select the machining method, tool type, and tool

diameter and shape.

4) Establish a cutting step. Assume all process

consists of three stages of machining processes:

rough machining, semi-finishing, and finishing.

a) Rough machining: using 10 mm diameter of

a flat end mill cutting tool.

b) Semi-finishing: employing 5 mm diameter

of a ball end mill.

c) Finishing: Using 3 mm diameter of a ball

end mill.

Rough machining (flat-end mill)

a) Establish cutting range and the distance

between the cutting process using flat-end

mill parameters.

b) Establish space (allowance) for cutting.

c) Consider the forward steps and backward

steps of tools regarding point cloud

conditions. The grid method is applied to

evaluate the forward and backward steps of

tools so that there is no over-cut.

Semi-finishing cutting and Finish Cutting using

a ball-end mill.

a) Select the diameter of the cutter.

b) Establish cutting range and the distance

between the cutting process by using ball-

end mill parameters.

c) Establish space (allowance) for cutting.

Direct NC Toolpath Generation from 3D Point Cloud Datasets

139

d) Consider the forward steps and backward

steps of tools regarding point cloud

conditions. The grid method is used to

evaluate the forward and backward steps of

tools to no over-cutting.

e) Consider interpolation.

3.1 Method of Machining Type and

Tools Selection

In the selecting machining method, it can be

recognized easily by looking at the object's shape. If

the object shape is prismatic, the NC milling process

is chosen. On the other hand, if the object shape is

cylinder NC turning process is applied. The next step

is selecting the tools and parameters of the cutting

process. Single-step machining or multi-steps

machining can be considered depending on the

complexity of an object to be cut.

The selection of a milling cutter, according to the

six steps:

1) Define the operation type

2) Define the material of the workpiece.

3) Select the cutter concept

4) Select the milling cutter

5) Select the insert

6) Define the start values

Considering the feature type in the tools selection

is very important to ensure the machining process

(Lin & Koren, 1996).

3.2 Toolpath Planning Selection

The current tool path generation used has mainly two

steps. The first is to specify the cutter contact point,

often called cutter cutting (CC), on the part surface,

and then the second is to offset that point to yield the

cutter location (CL). The cutter cutting is the location

where the tool touches the part surface. There exist

some tool path generation methods that are popular in

the industry. Some of them are discussed in the next

sections.

Tool path patterns are commonly applied in NC-

path generating: parallel, iso-parametric method, iso-

planar method, isophote, constant scallop method,

and spiral.

The isoparametric method (Zou & Zhao, 2013) is

one of the simplest methods used to create a tool path.

In this method, the cutter contact positions are

specified along with the isoparametric lines on the

part surface. Isoparametric lines are curves of

constant parameter value on the parametric body.

Linear segments usually approximate the

isoparametric track. However, if the linear features

are extensive, it may result in undercuts on the

model's surfaces, which are already machined in the

previous operation.

The other methods commonly used are the

Cartesian method, offset surface method, and sidestep

method. The offset surface process (Chen & Ravani,

1987) generates the tool path by compensating the

part features by the cutter's radius. The center of the

cutter tool traces along the offset surface to machine

the piece, and the tool path is then calculated by

identifying tool passes on the offset surface.

However, self-intersections of tool path can occur

that leads to over cut or cavities of undercut must be

detected or corrected while performing offset surface

algorithm.

3.3 Selection and Definition of NC

Tools Path Parameters

A mill with a large radius will be efficient in

removing a more significant amount of material

volume in common. However, if the mill's radius is

greater than the concave curvature radius, the tool

will interfere and over-cut. Therefore, choosing the

proper parameter of the device is very important to

make the process more efficient.

The most important thing to select tool diameter

is the minimum curvature in workpieces to be

processed. The minimum curvature of the product to

be cut has to be known. The minimum curvature

requirement is more significant than the radius of

tools to execute the cutting process. If the minimum

curvature is lower than the tool's part's radius, it

cannot be cut.

3.3.1 Flat-end Mill Parameters

The flat-end mill is used to remove the maximum

material to be cut and result in a shorter path. This

cutter is useful in face and shoulder cutting

operations. Notations used in defining flat end mill

parameters are CL=cutter location in 𝑂



𝑥



,𝑦



,𝑧





vertex point 𝑝𝑥



,𝑦



,𝑧



, and cutter radius R cutting

allowance = δ.

The material will be cut if the location of material

is within the radius of the cutter (point 𝑝 is inside CC-

region) formulated as bellow:

In this case, it always starts from point 𝑝



0,0,0



Parameters are selected as below:

a) Cutting direction, related to the x-direction.

- For the forward step: 𝑥



𝑥



𝑅

for free

boundary and 𝑥



𝑥



𝑅𝛿

for the net-

shape boundary, where 𝛿is cutting allowance.

ASAIS 2020 - Annual Southeast Asian International Seminar

140

- For the backward step: 𝑥



𝑥



𝑅

for free

boundary and at the end, 𝑥



𝑥



𝑅𝛿 for

net shape boundary.

b) Depth of cut, related to the z-direction

- For free boundary: 𝑧



𝑧



- For net shape boundary: 𝑧



𝑧



𝛿.

- Interval z (subdivision surface) is d (d=depth

of cut, depending on the material).

c) Cutting interval related to the y-direction

- Maximum interval is 2R

- For free boundary: 𝑦



𝑦



- For net shape boundary: 𝑦



𝑦



𝛿 for a

right step and 𝑦



𝑦



𝛿 for a left step.

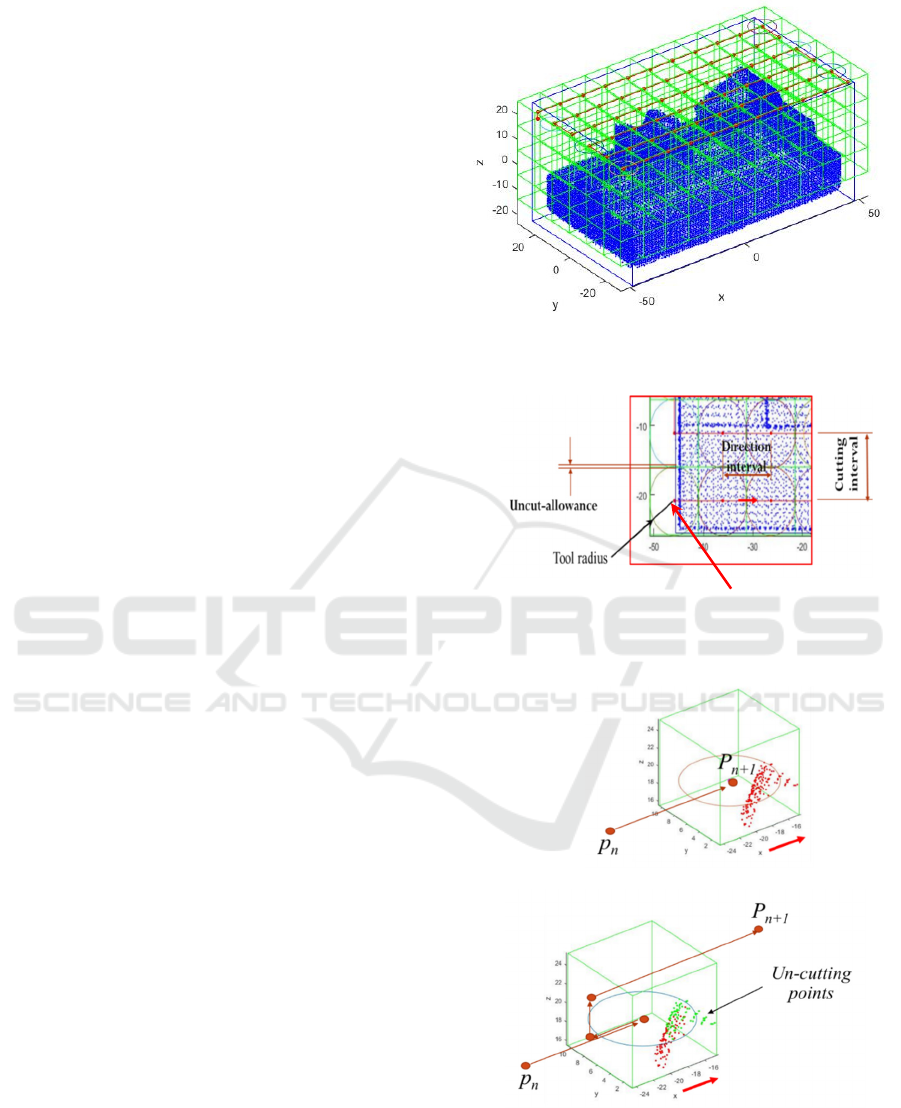
The steps of NC tool path planning are as follows:

1) Define the grid method (see [1][3]) with grid

size equal to the size of cutter diameter minus

half of the allowance (2R – 0.5* δ). See Fig. 1.

2) Start from CL in x minimum of material



𝑥



0.5∗𝛿



, and y minimum of material



𝑦



0.5∗𝛿



, and z maximum - the depth

of cut



𝑧



 𝑡ℎ𝑒 𝑑𝑒𝑝𝑡ℎ 𝑜𝑓 𝑐𝑢𝑡



(see Fig. 2).

3) Move forward to the next grid and check the

condition::

 If the grid is empty, the point is cutter

location

 If the grid consists of points, check the

requirement to move to the other direction,

such as move-in z-direction or y-direction

(see Fig. 3). Figure 3 shows the CL when

the CC is over cut. Therefore, moving the

CL so that there is no overcut. Figure 4

depicts the tool path for one completed

step. There are some grids with the point

cloud so that CL is moving in the up

direction. Figure 5 illustrates the tool path

for one completed step in x- and y-

direction.

4) After finishing one cycle, forward-moving to

x+. If x is the maximum tool, it is then moved

into y+ and then moved backward to x-. If the

tool reaches y foremost tool moves into z-. The

process is iterative until rough cutting is

finished.

Figure 1 Grid System for Rough Cutting by Using Flat-End

Mill

Figure 2 Parameters of Cutting and Starting Point of

Cutting

(a)

(b)

Figure 3 Evaluation of Next Step of Tools (a) CC Cut Point

Cloud (Over-Cut) and (b) the Solution by Moving CC of

the Tools

Starting point

Direct NC Toolpath Generation from 3D Point Cloud Datasets

141

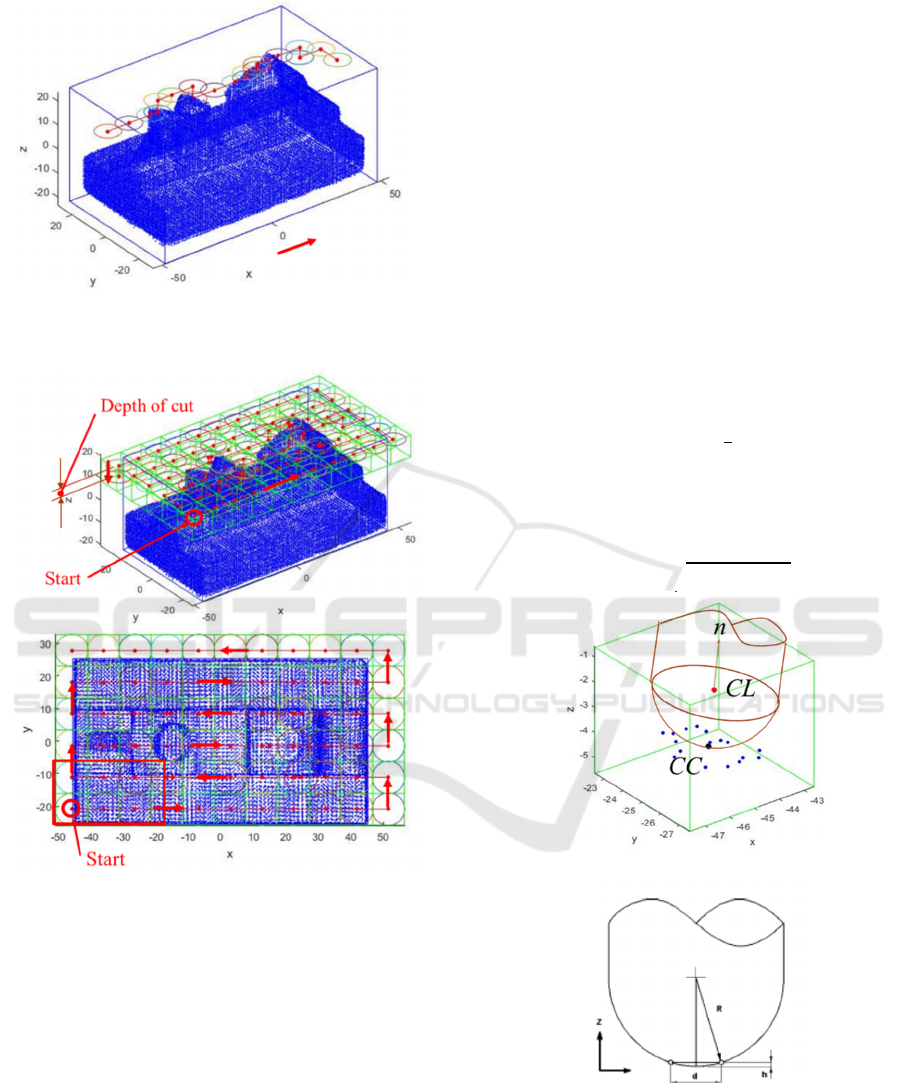
Figure 4 Tool Path for One Cycle. There is some tool cl

moving

Figure 5 Tool Path for One Cycle x and y Direction

3.3.2 Ball-end Mill Parameters

The objective of using the ball-end mill, in this case,

is to pursue the accuracy with certain tolerance and

surface smoothness with certain surface quality

(Ingeniería et al., 2016)(Yin, 2004).

The condition should be considered in the ball-

end parameter selection as the following:

 Assume the vertex point is p (x

, y

, z

) and

the cutter's radius R. The center point of the

cutter's bottom is

𝑟





𝑥



,𝑦



,𝑧





, and

cutting allowance = δ.

 Verify the point p is within the CC region or

not by using the following formula (see Fig.

6.11):

𝑥



𝑥







𝑦



𝑦







𝑅



 Cutting direction, related to x-direction

 In flat surface:

 Interval= 2R

 For concave and convex surface

 Using interpolation

 Depth of cut, related to z-axis

 In net shape: t (t = tolerance)

 Calculate maximum z

of based on the

point in CC region using the following

formula:

𝑧



𝑧







𝑅







𝑥



𝑥











𝑦



𝑦













+ t

Where t is tolerance.

 Cutting interval related to y-axis direction is

using the following formula (see Fig. 2):

𝑑2





2𝑅 ℎ



ℎ

Figure 6 Ball-End Mill Position

(a) Ball and mill parameters

ASAIS 2020 - Annual Southeast Asian International Seminar

142

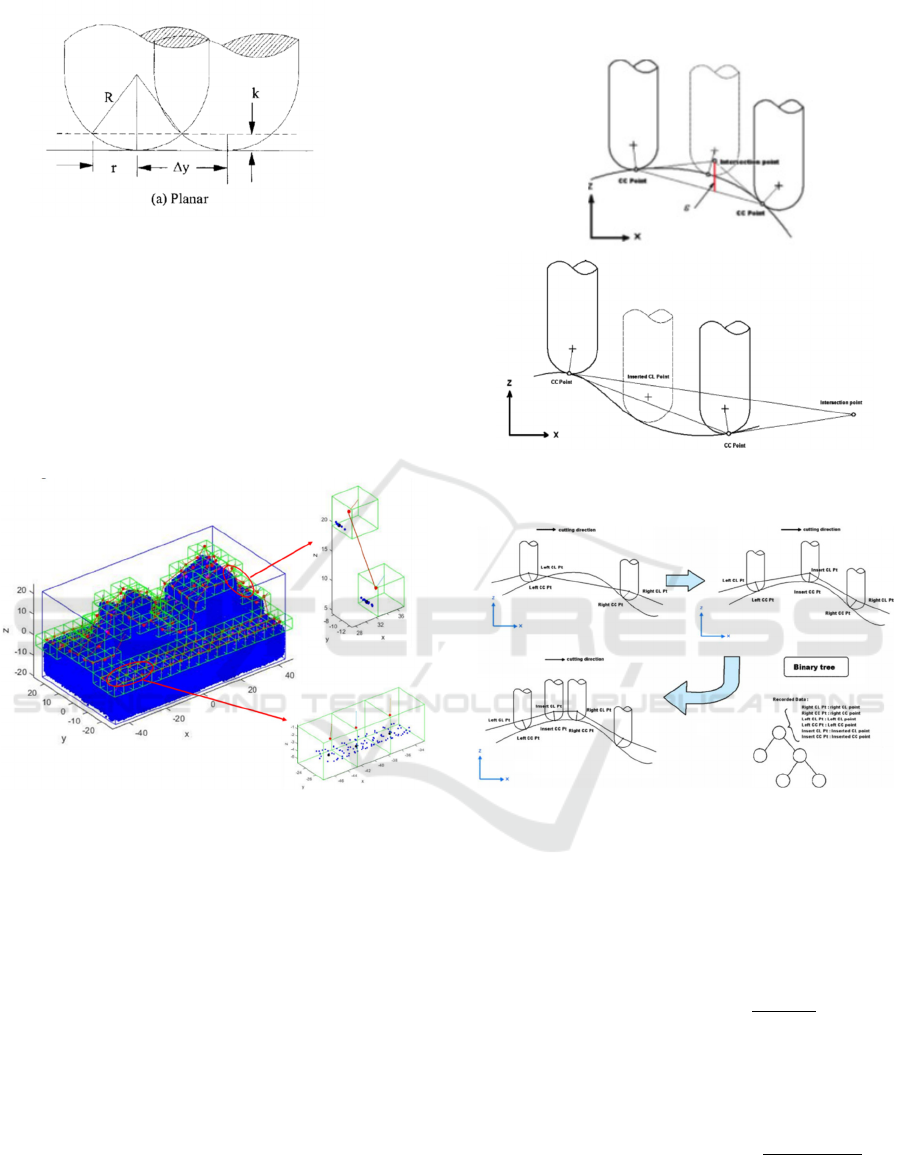
(a) Ball in interval

Figure 7 Ball-End Mill Cutting Interval (Yau & Hsu, 2009)

To define cutter location, it firstly generates a grid

in z-value maximum (for z-direction cutting) (Park,

2003). The second step is to check the tool location

(CC and CL) in each consecutive grid (forward and

backward moving). The principal of semi-finished

and finished process are equal. However, ball

diameter and interval of cutting are different as shown

in Fig. 8.

Figure 8 Ball-End Mill Path Checking

The condition of each grid in which CC and CL

are located is checked. There are two cases of grid CC

and CL condition.

- Case 1: the same z-value for the next grid, so

only check the cutter contact (CC).

- Case 2: different z-value, besides checking the

cutter contact (CC), the interpolation is

applied and paths between grids are checked..

3.3.3 Interpolation

The interpolation method (Yau & Hsu, 2009) is used

to solve the convex and concave curvature condition

in the tool's moving, as displayed in Fig. 9. Figure 10

presents the condition of overcutting in tool moving.

The solving is by generating buffer points (points

from interpolation process) to avoid over-cut. A

binary tree can be used to define the next buffer point

that created.

Figure 9 Overcut Condition in Concave and Convex

Surface (Yau & Hsu, 2009).

Figure 10 Ball-End Mill Overcut Condition and the Solving

by Using Buffer Point (Yau & Hsu, 2009).

Buffer points are generated by using interpolation

method. Figure 11 shows the interpolation method.

The principal of interpolation is using the intersection

line. Buffer point that calculated by interpolation

method are using the following equation:

𝑃



.𝑧𝑃



.𝑧



𝑃



.𝑥𝑃



.𝑥









.



.





.



.



where

𝑃



is the projection of the intersection

point to the CC line.

𝜀𝑃



.𝑧𝑃



.𝑧𝑃



.𝑧𝑃



.𝑧





𝑃



.𝑥𝑃



.𝑥





𝑃



.𝑧𝑃



.𝑧

𝑃



.𝑥𝑃



.𝑥



Direct NC Toolpath Generation from 3D Point Cloud Datasets

143

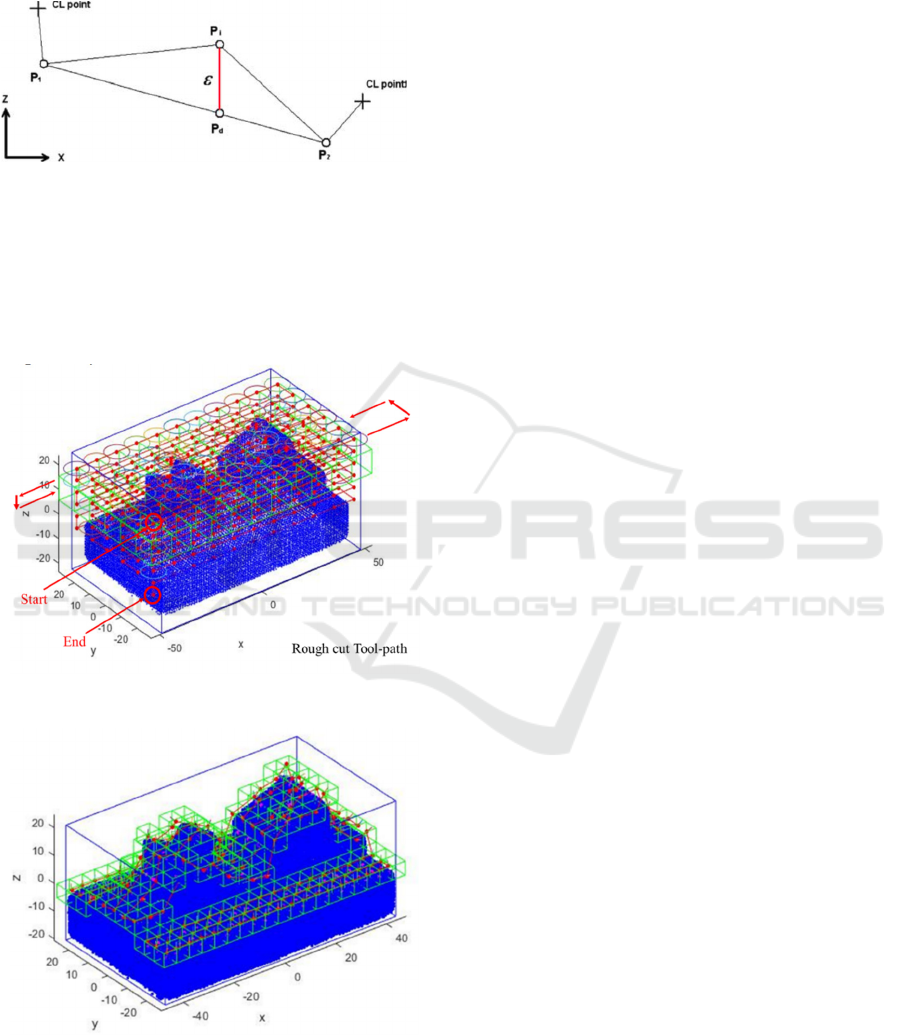
where

𝜀

is step error. If

𝜀

is greater than the

machining tolerance, a different CL (buffer point)

should be interpolated at the intersection point.

Figure 11 the Interpolation Method (Yau & Hsu, 2009).

4 RESULT AND DISCUSSION

The computation CL for rough cutting and semi-

finished cutting is shown in Fig. 12 and Fig. 13,

respectively.

Figure 12 Rough Cutting CL Computation Result

Figure 13 Semi-finished Cutting CL Computation Result

In this research, the method to generate a tool path

from validated point cloud datasets registration is

described. The broader implementation can be useful

in mechanical design, die and mold, and even art and

medical. The machining tools step consists of several

stages: rough cutting, semi-finishing cutting, and

finishing cutting.

As seen in Fig. 12 and Fig. 13, the tool orientation

vectors are correctly oriented towards each point's

normal vector. This section proposes an algorithm for

generating a tool path of a 3-axis or 5-axis directly

from a point cloud dataset. However, some

shortcomings must be considered. As The grid is

created, the grid's size must be set, as shown in Fig.

1. The grid size would influence the machine

accuracy in the actual contour. The point number

filtered out within the grid affects the path precision.

If a rough grid is employed, i.e., in mm order,

numerous points can be filtered out. Consequently,

the tool path is not proper, and the feature surface to

be cut is rough.

The developed method can be applied to generate

tool paths from the subsurface relative to the

corresponding grid point cloud. Based on the point

cloud's isolation in the formed grid, the tool center

point relative to the point cloud data is determined.

The tool path between the tool center points of two

neighboring grids is obtained from the two-nodal

trajectory projection in a 2D triangular lattice. This

path is verified whether it is tangent to another point

or not. If there is a tangent point to the tool path in the

triangle's projection, it is necessary to filter it; if it

does not attain, it will go directly to the next point. 3D

distance between cutter center points in adjacent grids

is not taken into account.

If another feature form (in the form of data cloud

points) exists between two cutter center points in the

adjacent grid, that feature must be considered in

determining the tool path. The accuracy of the cutter

cuts in the two adjacent grids will also be affected. In

addition, special features such as sharp edges, sharp

elbows, sharp edges in the projection profile cannot

be recognized in the proposed algorithm. Thus, for

these cases, some algorithm modifications have to be

made.

5 CONCLUSIONS

This research discusses generating the NC-tool path

directly from point cloud data. Firstly, the machining

process and cutter used are defined. Secondly,

selecting the type of path will be used in this system.

Some parameters can be assigned to control

machining processes such as the dimension of an

object, its position and orientation, surface roughness,

workpiece material, and machining tolerance, and so

ASAIS 2020 - Annual Southeast Asian International Seminar

144

on. The other machining parameters to be considered

in the process are cutting speed, spindle speed, feed

per minute, maximum chip thickness, feed per tooth,

and some tooth of the cutter, feed per revolution, and

depth of cut, remove rate, machining time, power,

pitch and so on. Those parameters will influence the

efficiency machining and surface quality of

machining.

Thirdly, the tool path type is defined. In this case,

the iso-parametric method is selected. Fourthly, the

parameters of the tool are defined. The flat-end cutter

for coarse cutting and ball-end cutter for the semi-

finished and finished surface is confirmed in this case.

Fifthly, a tool path with selected tools parameters is

generated. In this case, the grid method is applied to

evaluate the next tool moving direction. The tool path

for rough cutting and semi-finishing cutting is

generated. By implementation into a real case, it can

be concluded that the proposed method is beneficial

to create point NC-tool path directly from point cloud

data.

REFERENCES

Chen, Y. J., & Ravani, B. (1987). Offset surface generation

and contouring in computer-aided design. Journal of

Mechanical Design, Transactions of the ASME, 109(1),

133–142. https://doi.org/10.1115/1.3258777

Chui, K. L., Yu, K. M., & Lee, T. C. (2002). Direct tool-

path generation from massive point input. Proceedings

of the Institution of Mechanical Engineers, Part B:

Journal of Engineering Manufacture, 216(2), 199–206.

https://doi.org/10.1243/0954405021519843

Ingeniería, F. De, Autónoma, U., Luis, D. S., Manuel, A.,

No, N., López, E. A. M., Lim, T. (2016). IMECE2013-

65483 A new method for the generation of tool paths for

finishing near net shape components. 1–10

Lin, R., & Koren, Y. (1996). Efficient Tool-Path Planning

for Machining Free-Form Surfaces. 118(FEBRUARY)

Liu, Y., Xia, S., & Qian, X. (2013). Direct Numerical

Control ( NC ) Path Generation : From Discrete Points

to Continuous Spline Paths. 12(September 2012), 1–12.

https://doi.org/10.1115/1.4006463

Makki, A., Tournier, C., Lartigue, C., Makki, A., Tournier,

C., Lartigue, C., & Mehdi-, C. (2011). 5-axis Direct

Machining of Rough Clouds of Points To cite this

version : https://doi.org/10.3722/cadaps.2010.591-600

Marie, J., Duc, E., Lartigue, C., & Bourdet, P. (2004). A

new format for 5-axis tool path computation , using

Bspline curves. 36, 1219–1229.

https://doi.org/10.1016/j.cad.2003.12.002

Muslimin, Zhu, J., Yoshioka, H., Tanaka, T., & Saito, Y.

(2015a). Study on plane feature extraction in

registration of laser scanning data sets for reverse

engineering. Journal of Advanced Mechanical Design,

Systems and Manufacturing, 9(5), 1–14.

https://doi.org/10.1299/jamdsm.2015jamdsm0076

Muslimin, Zhu, J., Yoshioka, H., Tanaka, T., & Saito, Y.

(2015b). The utilization of feature extraction in

registration method of laser data sets in reverse

engineering of fidelity and precision part. Proceedings

of the 8th International Conference on Leading Edge

Manufacturing in 21st Century, LEM 2015, (February

2017)

Park, S. C. (2003). Tool-path generation for Z-constant

contour machining. CAD Computer Aided Design,

35(1), 27–36. https://doi.org/10.1016/S0010-

4485(01)00173-7

Sun, Y., Page, D. L., Paik, J. K., Koschan, A., & Abidi, M.

A. (2002). Triangle mesh-based edge detection and its

application to surface segmentation and adaptive

surface smoothing. IEEE International Conference on

Image Processing, 3, 825–828.

https://doi.org/10.1109/icip.2002.1039099

Yau, H., & Hsu, C. (2009). Generating NC tool paths from

random scanned data using point-based models. 897–

907. https://doi.org/10.1007/s00170-008-1542-1

Yin, Z. (2004). Rough and finish tool-path generation for

NC machining of freeform surfaces based on a

multiresolution method. 36, 1231–1239.

https://doi.org/10.1016/j.cad.2004.01.003

Zhang, D. (2009). Adaptive NC Path Generation From

Massive Point Data With. 131(February), 1–13.

https://doi.org/10.1115/1.3010710

Zhang, Z., Savchenko, M., Hagiwara, I., & Ren, B. (2010).

3-Axis NC Tool Path Generation and Machining

Simulation for Subdivision Surface of Complex Models.

10(1), 1–9

Zou, Q., & Zhao, J. (2013). Computer-Aided Design Iso-

parametric tool-path planning for point clouds.

Computer-Aided Design, 45(11), 1459–1468.

https://doi.org/10.1016/j.cad.2013.07.001

Direct NC Toolpath Generation from 3D Point Cloud Datasets

145