Fractal Generating Techniques

Younes S. Alwan

, Khalid Saeed Lateef Al-badri

, Ghazwan S. Alwan

and Marwah Q. Majeed

Electromechanical Engineering Dept., University of Samarra, Samarra City, Saladin, Iraq

Physics Dept., University of Samarra, Samarra City, Saladin, Iraq

Mechanical Engineering Dept., University of Tikrit, Tikrit City, Saladin, Iraq

Civil Engineering Dept., University of Samarra, Samarra City, Saladin, Iraq

Keywords: Fractal, Fractal Generator, Generation Techniques.

Abstract: Globally, researchers have been trying to produce the most comprehensive description of introducing fractals

and utilizing them in different sciences. Their effort lies in elaborating and recruiting the scope of fractals in

science and applications, such as antenna design, computer software programming. Further, the modern world

needs the products to be compact, efficient and economically suitable, where fractals bring such

recommendations. In this review article, we present a briefed description of fractals, types of fractals, merits

of fractals and, most importantly, fractal generator techniques along with their mathematical techniques and

software.

1 INTRODUCTION

In mathematics, a fractal is a complete, iterative-like,

and self-alike mathematical set whose Hausdorff

aspect or direction firmly overrides its topological

dimension. Fractals are available universally in nature

because of their predisposition to seem approximately

identical at different aspects, as appears in the

consecutively trivial amplifications of the Mandelbrot

set. Further, fractals have alike arrangements at

progressively small sizes that is similarly known as

intensifying symmetry or unfolding symmetry

(Mandelbrot, 1983). When this repetition is strictly the

same as the relating generated almost same copy at

every scale, like what appears in the Menger sponge, a

fractal has a self-similar arrangement.

Fractal is an, somehow, irregular or disjointed

geometric shape, which can be sub-partitioned in

parts, where each part is roughly a smaller copy of a

whole fractal object (Paul, 1991). It is a natural

phenomenon or a mathematical expression, which has

a repeating pattern that displays at every scale. If the

replication is the same at every scale, it is called a

self-similar pattern. Fractals can also be nearly the

same at different levels and includes the idea of a

https://orcid.org/0000-0002-9133-4705

https://orcid.org/0000-0003-3678-4954

detailed pattern that repeats itself. As seen in nature,

most physical systems, structures, objects and works

are not east-to-recognize systematic geometric and

are not mathematically calculated shapes of the

standard geometry.

Many patterns of fractals can be generated by

utilizing inspirations from the areas of natural

sciences. An example of such an inspiration is the

diffusion-limited aggregation (DLA) that describes,

apart from other descriptions, the diffusion-

aggregation of zinc ions in an electrolytic solution on

electrodes. Other examples of naturally generated

fractals because of their ultimate structure are the

flowers, vegetables, etc. Fractal would appear when

analyzing ice particles; hence, it shows a dramatic

presentation of fractal growths as monitored by

utilizing a specialized telescopic tool. Further, fractal

shows itself in the structure of many living organs and

bodies of animals. For instance, fractal patterns have

a critical role in fortifying and shaping the shell in

snails, where their shells revolve in an obvious way

of fractal shape. Such observation is noticeable in

almost every aspect of life (Douglas et al., 2003). In

addition, Large-scale objects like galaxies and small-

scale items like atoms are all offering different forms

of fractal generating initiatives. Moreover, movements,

motion, and interpolation mathematical processes in

science exhibit stochastic models that contain fractal

behavior; hence, every single item in the universe can

initiate a fractal behavior at some point.

This reviewing work is mostly dedicated for the

techniques by which fractals are generated, because

fractals have templates and/or functions with a

prototype item. At that point, the prototype grows

within some patterns to build the whole structure of

the fractal body. The paper, however, has been

divided into many divisions to comprehend and

visualize a full panorama of what to discuss about

fractal initiation and how to generate fractals. The

first division talks about an explanation of where the

idea of fractals have come from. In the next division,

merits of utilizing fractals are discussed, whereas the

following section collects many fractal generation

techniques with some supporting explanation.

Moreover in this work, the next section depicts the

mathematical representation of fractal generation.

Before the conclusion and references, the final

section mentions the computer software programs

dedicated for fractals.

2 FRACTALS CONCEPT

There have been tremendous number of researchers

and mathematicians around the globe trying to

elaborate the key philosophy of the fractal spreading

in the universe. The apparent behavior of natural

fractal pattern expose an attitude of the nature to build

living and non-living objects that mimic their own

items; i.e. as if the nature’s printer types the same

generator with different scaling factors to have such

infinite-like patterns; hence, nature would select the

simplest procedure to fill space and size. At that point,

the simplest way would be to accumulate almost-

similar structures in, somehow, different styles to

expose the final product.

Artificial fractals are useful to express and

modulate objects that may contain a base to start

from, such as decorations, computer images, civil

structures, architecture, interpolation, engineering

tools, economics, etc. The most important merit of

artificial fractals is the ability to comprehend current

solution needs and to create the suitable fractal

texture that fits the different desires. On the other

hand, natural fractals follow the needs of nature,

without an exact explanation as mentioned earlier.

However, it still needs further discovery to explain

the origin of fractals and why/how it has reached such

forms, but it is probably not able to explain without

utilizing deeper physical, mathematical theories and

maybe super computers and algorithms.

3 MERITS OF USING FRACTALS

Fractals have grabbed many properties into account,

inspired primarily from nature. Depending on the

field that uses iterative geometric properties, merits

of fractals can be classified into some items as listed

(Douglas et al., 2003).

1. In-fit size structure.

2. Low profile packages

3. Conformal

4. Broadband and/or multiband

5. Fast growing attitude

6. Predictable approach throughput

7. Easiness of programming and modelling

8. Fashion style and artistic design

9. Forecast of many life representations

10. Key to explain prospective and existing

theorems.

According to the aforementioned and other

properties, fractals and similar geometric designs

have become the desirable figures with respect to

researchers, designers, and programmers.

4 AGGREGATION OF SOME

FRACTAL GENERATION

FIGURES

Over ages, mathematicians and scientists have found

and developed fractal shapes depending on the

application they intend to adopt. This section presents

a comprehensive overview of some common fractal

geometries that have been developed or discovered.

These designs have been used in developing modern

and innovative designs of technological and

engineering system structures, such as demographic

mapping, computer software, systems models,

microwave assemblies and antennas.

4.1 Sierpinski Gasket

The first iterations in the construction of the

Sierpinski gasket are shown in Figure 1. The process

of the geometry of such construction is a fractal

beginning with an equilateral triangle, as illustrated in

the first stage of Figure 1. The next iteration in the

construction is to remove a central triangle that is

located at the mid of the original triangle. This newly

removed triangle has vertices at the centers of each

side of the original triangle as shown in Stage 1. This

process repeats itself for the remaining three

triangles, as shown in Stage 2, 3, and 4 for the same

figure. Consequently, the Sierpinski-gasket fractal is

generated by carrying out this consecutive process an

infinite amount of times. Further, Sierpinski gasket is

an example of a generally self-similar fractal. From

an RF engineering viewpoint, a practical clarification

of Figure (1) is that the black triangular areas

characterize a metallic conductor; while the white

triangular areas characterize regions where metal has

been removed (Douglas et al., 2003).

Figure 1: Sierpinski-gasket fractal construction.

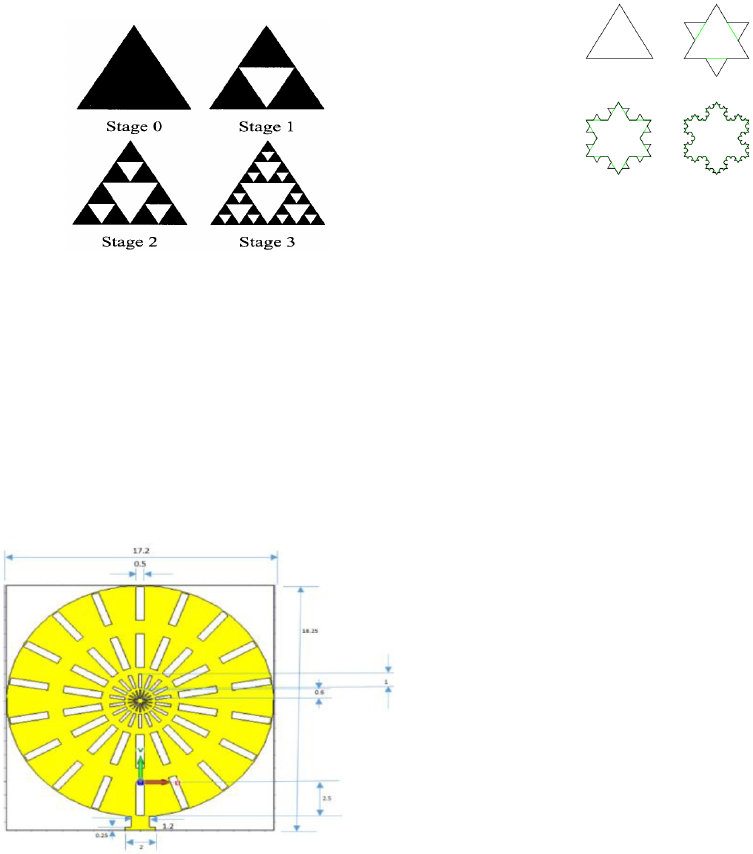
4.2 Fracal by Entrenches

In this design, a new idea of patterning a fractal antenna

comes in a reality, where a circular patch that contains

entrenches was utilized in this process, as shown in

Figure 2. The process of this design takes the manner

of internally enclosed circles of entrenches. Further,

the first far tire has a designated number of slots, where

other tires have the same number as well with smaller

size of slots in each circle.

Figure 2: Fractal of entrenches.

4.3 Koch Snowflake Fracta

This design is another pattern of fractals, and is well

mentioned by many researchers around the world. For

instance, it takes its shape primarily from the

microscopic-scale design of a snowflake unit.

The design starts out as a solid equilateral triangle

like the Sierpinski gasket, as illustrated in Figure 2.

Nevertheless, unlike the Sierpinski gasket that is

formed by downgrading the size of the triangles from

the original structure, the Koch snowflake is

accumulated by adding downgrading triangles into

the structure in an iterative style, as in Figure 3

(Douglas et al., 2003).

Figure 3: Koch snowflake fractal iterations.

4.4 Self-similarity Fractals

It refers to objects that contain smaller copies or

duplicates of itself at arbitrary scales. Figure 4 shows

an example of a natural self-similarity fractal. Such

fractal can further be divided into three items of self-

similarity fractals.

4.4.1 Exact Self-similarity Fractal

The fractal is the same at diverse balances. Such

fractal is the sturdiest kind of the self-similarity type.

4.4.2 Quasi-self-similarity Fractal

The fractal is about to be alike at diverse balances.

This one is a fewer specific system of self-similarity

type. Such fractals comprehend minor duplicates of

the whole fractal in slanted forms.

4.4.3 Statistical Self-similarity

It is the weakest type of self-similarity; hence, this

fractal has computational or statistical measurements

that are preserved across scales. However, most

famous definitions of fractals imply some meaning of

statistical self-similarity (a dimension of a fractal is a

numerical measurement that is kept across scales).

Further, random fractals are kind of fractals that are

computationally or statistically self-similar, but

neither quasi-self-similar nor exactly self-similar

(Nicoletta, 2013).

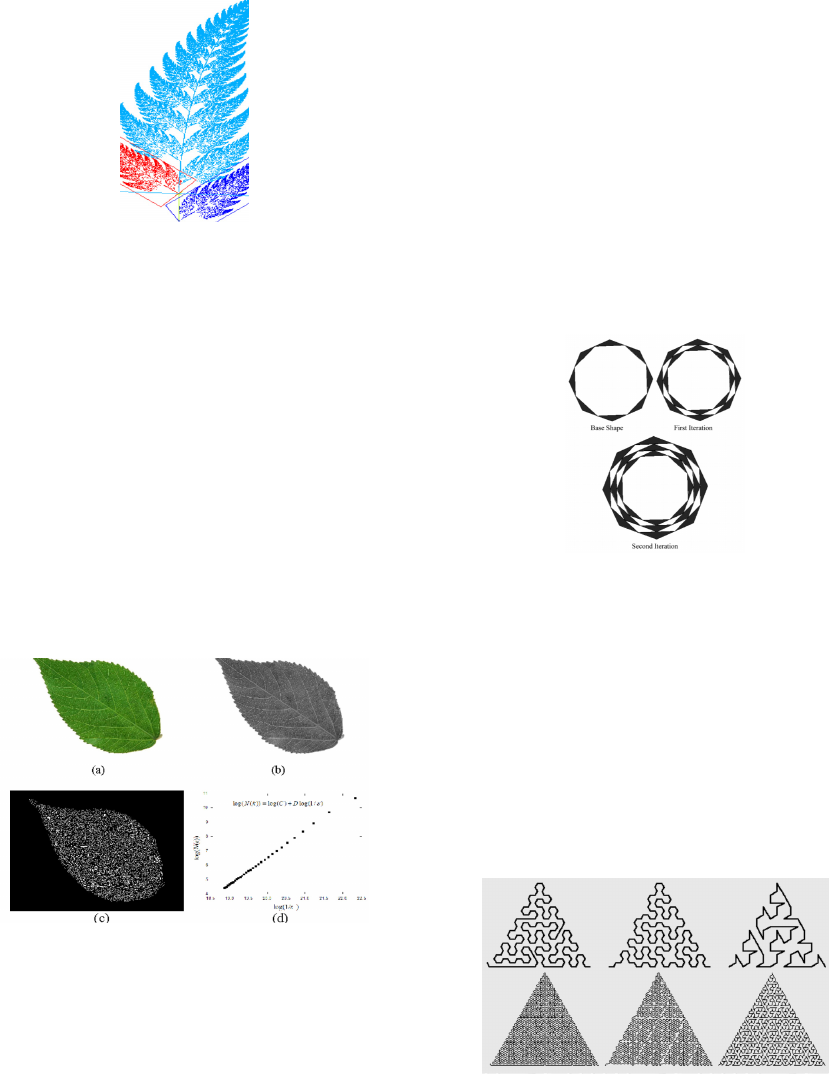
Figure 4: Barnsley fern exhibiting self-similarity fractal

behavior.

4.5 Pixel-covering Method Fractal

It is useful to compute the fractal dimensions of

objects, such as leaves, based on many plant species

acquired from several places for the sake of plant

classification and identification. Therefore, both

contour fractal dimension and the contour & nervure

fractal dimension can distinguish leaves between

different types effectively despite a little deficiencies.

The process works by adding the fractal dimension of

nervure details into the whole classification system

that can determine leaves more robustly than that of

contour and contour & nervure. Figure 5 depicts a

classification process by using pixel-covering method

(Wei et al., 2009).

Figure 5: A classification process by pixel-covering

method.

4.6 Fractals for Geo-chemical

Exploration Data of a Geological

Area

In this type of fractals, multi-fractal method is carried

out to process up to 1:200000 stream sediment geo-

chemical examination data of a geographical area.

Fractal dimension characteristics of a number of

elements connected with minerals are gained based

on (C-A) fractal technique, in addition to diverse geo-

chemical anomaly stages and components mixtures

(Shili Liao et al., 2012).

4.7 Growing-to-the-inside Fractals

This technique in generating fractals was proposed by

some researchers. Abolfazl Azari proposed an

example of such design (Abolfazl, 2011). The design

takes the shape of octagonal arrays formed by placing

elements in an equilateral triangular net. Hence, these

arrays can be viewed as involving of a single item at

the center, bounded by several concentric eight

element circular arrays. Figure 6 depicts the iterations

of the proposed design of such fractal.

Figure 6: The iterations of the proposed fractal by

(Abolfazl, 2011).

4.8 Space Filling Techniques as

Fractals

Space filling techniques can serve as a method of

generating fractals. They take the merit of packing

extra lines and curves as the rank of the technique gets

higher. For instance, the most famous techniques to fill

spaces are Hilbert, Peano, Moore, Dragon, Gosper,

Koch techniques. Figure 7 shows three patterns that fill

spaces in a deterministic mathematical style.

Figure 7: Three curves for filling spaces as fractals

(teachout).

4.9 Three-dimensional Fractals

They exist in nature and mathematics and cover many

aspects of fractalism in nature and artificial

computations. Most natural fractals are, somehow, in

the form of 3D pattern; hence, they mostly change

their way of spreading in more than one plane.

Moreover, some examples of three-dimensional

fractals are DNA, neurons, natural or artificial

surfaces, soil, clouds, etc. Figure 8 exposes an

example of a natural three-dimensional fractal.

Figure 8: A 3-D fractal shape.

4.10 Fractals of Multi-scroll Chaotic

Attractors

Attractors are sets of numerical values of a system

that goes to evolve, though they sometimes look

complicated and random. In fractals, sets of multi-

scroll chaotic attractors are hard to simulate and to be

put in a mathematical model to represent the fractal

structure. However, Lu Chen attractor and the

modified Chua chaotic attractor are examples of

modeling attractors and are applicable to comprehend

the fractal implementation. Figure 9 shows an

example of a multi-scroll chaotic attractor fractal.

Figure 9: Fractal of multi-scroll chaotic attractors.

5 MATHEMATICAL

REPRESENTATION OF

FRACTAL INITIATION

Fractals have wide scopes of mathematical

characterization that fill a specific boundary of

occupation. Further, large number of fractals are

deterministic, i.e. they commonly can be predicted by

utilizing mathematical and logical formulas. In

addition, it is likely to have fractals that are hard or

impossible to obtain a computational formula of

representation. In such a case many naturally built

fractal shapes, such as coral reefs, trees, landscapes,

etc. As indicated by many researchers around the

world, it is not completely known the precise reason

that explains the mathematical patterning of fractals

in nature. The following lists some mathematical

patterns of fractal characterization.

5.1 Fractal Interpolation

Chih-Chin Huang, Shu-Chen Cheng, and Yueh Min

Huang in the refrence (Chih-Chin et al., 2010)

investigated a new algorithm to generate a new

interpolation scheme. Such an algorithm is helpful in

the techniques concerning generating and forecasting

fractal numbers out of a few numbers. Figure 10

shows an example of fractal interpolation of images.

Figure 10: Fractal interpolation of images (Pantelis et al.,

2007).

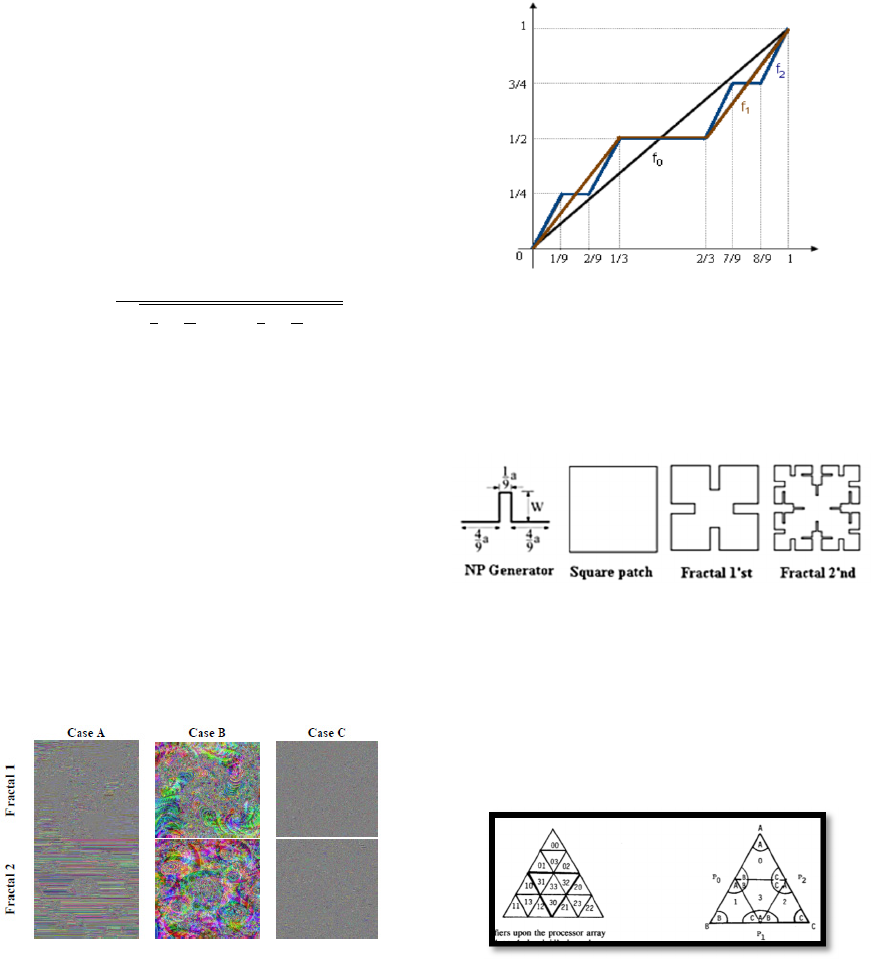
5.2 Iterated Function Systems

Iterated function systems, or (IFS), represent a very

various technique for properly generating a wide-

ranging useful fractal structures. Such iterated

function systems stand on the application of a series

of affine transformations as in figure 11 (Douglas et

al., 2003).

Figure 11: the construction of the standard Koch curve via

an iterated function system (IFS) approach.

5.3 Circulation of Fractals

As an example of such technique is what appears

earlier in this article in the item [Fractal by

entrenches]. When the designer used multi-circles of

entrenches (18 circle per rotation) that have the same

characteristics with different scales.

5.4 Super-formula

Johan Gielies presented this formula. Such a formula

mostly describes the natural fractal phenomenon

(Nicoletta, 2013). The following equation describes

the general formula of this theory.

𝑟𝑓∅











 





∅















 





∅











5.5 Logarithmic Fractals

This technique is mostly useful in the fractals that

relate to natural organs. Figure 5 represents a vital

organ having such technique (Wei et al., 2009).

5.6 Pseudo Random Key-stream

Generator

Pseudo random number generators have played a

critical research point due to the demand on quality-

encoded content that is essential in all of the structure

of the communication networks. Such technique has

many examples and can be found in variety of

research papers as in figure 12.

Figure 12: Example of Pseudo Random Keystream

Generator using Fractals (Sherif et al., 2013).

5.7 Space filling Curvature Formulas

There are many formulas to represent such

curvatures, such as Cantor function, Tietze extension

theorem, Euclidean metric, Lindenmayer system, L-

System, segment division, Weierstrass function, other

deterministic and un-deterministic methods. Figure

13 shows an example of Cantor function that has a

fractal extension in its higher order formulas.

Figure 13: A graph of Iterative Construction of Cantor

function.

5.8 NP Generator Model

It includes iterating a Narrow Pulse within a specific

shape as in figure 14.

Figure 14: A model of NP generator for a square patch

(Mahatthanajatuphat et al., 2007).

5.9 Triangular Sub-divisions

This kind of fractal formation may exist in fractal-

related computer processors and arrays (Wainer,

1988). An example of such generator can be shown in

figure 15.

Figure 15: A sub-divisions method process (Wainer, 1988).

5.10 Multi-scroll Chaotic Attractor

Generator

Many models represent such structures and have an

evolving approach, resembling Lu Chen and the

modified Chua chaotic attractors. Figure 16 shows an

example of a system of fractal processes and

transformation Φ (Bouallegue, 2011).

Figure 16: System of fractal processes and transformation

as an example of Multi-scroll chaotic attractor generator.

5.11 Random Iteration Algorithm

The preliminary set is a single point and at each point

of iteration, only one of the essential affine

transformations is used to compute the following

level (Ankit et al., 2014). Moreover, Hsuan T. Chang

presented a group of decoded images by the random

iteration algorithm as in figure 17 (Hsuan, 2001).

Figure 17: Decoded images of fractals by the random

iteration algorithm: (a) Sierpin´ski triangle, (b) fern, (c)

castle, and (d) snowflake.

5.12 Stochastic Fractal Search (SFS)

Algorithm

Such algorithm is considered to be a development of

Evolutionary Algorithms (EAs), and it uses the

diffusion merit that is seen frequently in random

fractals. The particles in such algorithm discover the

searching space more powerfully and is used

optimization processes (Salimi, 2015).

6 FRACTAL-GENERATING

SOFTWARE

Fractal generation software represents every kind of

software of graphics generating images of fractals.

However, there are numerous programs of fractal

generation obtainable, together open and profitable.

Mobile applications are accessible to play with fractal

designs. Various programmers generate fractal

software for their interest due to the innovation and

due to the challenges in comprehending the related

mathematical problems. Therefore, generating

fractals has directed many large difficulties and

projects for pure mathematics.

Mainly, there are two key approaches of two-

dimensional generation of fractals. First of which is

to conduct a process of iteration to simplify

calculations by recursion generation (Daniel, 2017).

On the other hand, the other chief approach is with

Iterated-Function-Systems (IFS) that consist of an

amount of affine alterations. In method number one,

every pixel within fractal images is assessed based on

a function and, at that time, colored, beforehand the

similar procedure is conducted to the following pixel.

Hence, the previous technique characterizes the

traditional stochastic method, whereas the second

builds a linear model of fractals. Utilizing recursion

have permitted program operators to generate

complicated images over modest direction [19-21].

• Chaotica:

A commercialized fractal art software

and renderer prolonging flam3 as well as

Apophysis function.

• Apophysis:

An open-source fractal flame

software intended for Microsoft Windows and

Macintosh.

• Fractint:

Free software to display numerous

types of fractals. The software was created on

MS-DOS, after that transported to the Atari ST,

Macintosh and Linux.

• Electric Sheep:

An open-source spread screen

saving software, and was established by S.

Draves.

• Kalles Fraktaler:

A free Windows built fractal

zooming program.

• Milkdrop:

A hardware with accelerated music

visualizing plugin intended for Winamp that was

initially advanced by R. Geiss.

• XaoS:

A fractal zooming software with

interaction.

• Fyre:

An open source cross-platform apparatus

intended for creating images centered about

histograms of repeated chaotic functions.

• OpenPlaG: It generates fractal by sketching

modest functions and is PHP based.

• MojoWorld Generator: It was a commercial

fractal landscape initiator intended for Windows.

• Sterling: Freeware fractal generator software

inscribed with C language.

• Picogen: A freeware open source cross platform

terrain initiator written in C++.

• Terragen: A generator of fractal terrain, which

can handle animations in Mac OS X and

Windows.

• Wolfram Mathematica: Dedicated for many

computer science software and for creating

fractal images as well.

• Ultra Fractal: A rendering generator for fractals

in Mac OS X and Windows.

7 CONCLUSION

In this research-reviewing article, the authors give a

summarized idea of collecting what many researchers

have been investigating in the field of fractals. During

decades, the concept of understanding fractals in

nature has led to employ this idea in the industrialized

and artificial forms. Backed from its history, area of

fractals is developing in terms of classification,

benefits, future employment, further understanding

and relation with life origins. It is expected, in

addition, that such field in researching fractals and

utilizing it in modern-life employment would

enhance the efforts in finding new algorithms to

expand the atmosphere that fractals deploy.

Furthermore, there is a fact that utilizing fractals in

the fields of microwave and antenna engineering has

practically occupied the most complicated and

expanded effort by engineers and researchers through

theory, simulation, and prototyping.

For the sake of future direction, fractal generating

techniques will develop further to comprehend the

increasing demands in variety of applications; hence,

the incoming trend is seeking for more compact and

practical designs and concepts.

REFERENCES

Mandelbrot, Benoit B. “The fractal geometry of nature,"

Macmillan, 1983.

Paul Bourke, “An Introduction to Fractals," 1991.

Douglas H. Werner and Suman Gangul, “An Overview of

Fractal Antenna Engineering Research," IEEE

Antennas and Propagation Magazine. Vol. 45, NO. 1,

p.p. 38 – 57, February 2003.

Nicoletta Sala, “Fractal geometry and super formula to

model natural shapes," IJRRAS, Vol.16, Issue 4, p.p. 78

– 92, Oct. 2013.

Wei Jiang, Cui-Cui Ji, and Hua Jun Zhu, “Fractal Study on

Plant Classification and Identification," International

Workshop on Chaos-Fractals Theories and

Applications, Shenyang, China, p.p. 434 – 438, 6-8

Nov. 2009.

Shili Liao, Shouyu Chen, and Xiaohu Deng, “Application

of Fractal Approach to Process Geochemical

Exploration Data of Baiyin Area, Gansu Province,"

Fifth International Workshop on Chaos-fractals

Theories and Applications, Dalian, China, p.p. 303 –

307, 18 – 21 Oct. 2012.

Abolfazl Azari, “A New Super Wideband Fractal

Microstrip Antenna," IEEE Transactions on Antennas

and Propagation, Vol. 59, No. 5, p.p. 1724 – 1727, May

2011. Website: http://teachout1.net/village/copyright.

html/Gary, teachout

Chih-Chin Huanga, Shu-Chen Chengb, and Yueh M.

Huanga, “The Design of a Fractal-based Number

Generator," International Workshop on Chaos-Fractal

Theory and its Applications, Kunming, China, p.p. 435

– 439, Oct. 29 – 31, 2010.

Pantelis Bouboulis, Pantelis Bouboulis, “A general

construction of fractal interpolation Functions on grids

of IRn," European Journal of Applied Mathematics,

18:449-476, August 2007.

Sherif H. AbdElHaleem, Ahmed G. Radwan and Salwa K.

Abd-El-Hafiz, “Design of Pseudo Random Keystream

Generator Using Fractals," IEEE 20th International

Conference on Electronics, Circuits, and Systems

(ICECS), United Arab Emirates, p.p. 887 – 880, Dec.

2013.

Mahatthanajatuphat, Chatree, and Prayoot Akkaraekthalin,

“Fractal Array Antennas with NP Generator Model," In

ISAP, 1202-5. Japan, 2007.

M.Wainer, “Generating Fractal-Like Surfaces on General

Purpose Mesh-Connected Computers," IEEE

Transactions on computers, Vol. 37, No. 7, p.p. 882 –

886, July 1988.

Bouallegue, K. “Generation of Multi-Scroll Chaotic

Attractors from Fractal and Multi-Fractal Processes," In

2011 Fourth International Workshop on Chaos-Fractals

Theories and Applications, p.p. 398 – 402, 2011.

https://doi.org/10.1109/IWCFTA.2011.87.

Ankit Garg, Akshat Agrawal and Ashish Negi, “A Review

on Natural Phenomenon of Fractal Geometry,"

International Journal of Computer Applications (0975 –

8887), p.p. 1 – 7, Vol. 86, No. 4, January 2014.

Hsuan T. Chang, “Relocation, scaling, and quantization

effects on fractal images," Optical Engineering, 40 (6),

p.p. 941 – 951, June 2001.

Salimi, Hamid. “Stochastic Fractal Search: A Powerful

Metaheuristic Algorithm." Knowledge-Based Systems

75 (February 1, 2015): 1 – 18. https://doi.org/10.1016/

j.knosys.2014.07.025.

Daniel Shi_man. "Chapter 8. Fractals". The Nature of Code.

Retrieved 5 March 2017.

Chen, Yan Qui, and Guoan Bi. “3-D IFS Fractals as Real-

Time Graphics Model," Computers & Graphics,

Computer Graphics in China, 21, no. 3 (May 1, 1997):

367 – 70. https://doi.org/10.1016/S0097-8493(97)000

14-9.

Nikiel, Slawomir S. “True-Colour Images and Iterated

Function Systems." Computers & Graphics 22, no. 5

(October 1, 1998): 635-40. https://doi.org/10.1016/S0

097-8493(98)00072-7.

Peitgen, Heinz-Otto; Peter Richter (1986). The Beauty of

Fractals. Springer-Verlag. p. 2. ISBN 978-0883859711.

Retrieved 7 May 2017.