
Various Approaches to the Application of Answer Set Programming in
Order-picking Systems with Intelligent Vehicles
Steffen Schieweck
1,2
, Gabriele Kern-Isberner
1
and Michael ten Hompel
2
1
Chair 1 Computer Science, TU Dortmund, Otto-Hahn-Str. 12, Dortmund, Germany
2
Chair of Materials Handling and Warehousing, TU Dortmund, Joseph-von-Fraunhofer-Str. 2-4, Dortmund, Germany
Keywords:
Answer Set Programming, Multi-agent Systems, Application, Hybrid Systems.
Abstract:
Intelligent, self-driving vehicles on public roads are widely noted in the media nowadays. In warehouse and
production systems, such vehicles have been common for a number of years, even though their intelligence
has only come to awareness in the recent years. Those systems are especially tailored to work in volatile
environments which change (to some degree) every few weeks or months. Thus, programming is required to be
as flexible as possible while still providing high efficiency. Answer set programming is a well known paradigm
which has received remarkable attention in the recent years. In this paper several approaches are presented
and evaluated to apply answer set programming to an order-picking system with intelligent vehicles. The
interconnected planning tasks are the dispatching of vehicles to driving jobs and the assignment of customer
orders to picking stations.
1 INTRODUCTION
The currently established continuous conveying sys-
tems are tailored to work in environments where
steady and well-predictable demand occurs. Intelli-
gent, self-driving vehicles are the answer to a global
market which has become highly unpredictable and
fast-moving. However, the intelligence of those ve-
hicles is restricted by the tasks and solutions the de-
signer and programmer initially envisaged. As a re-
sult, more costly programming has to be conducted
whenever a new task or solution is introduced. An-
swer set programming (ASP) is well known for its
simplicity and efficiency for programming and find-
ing optimal solutions and thus serves an ideal tool
for the systems mentioned above. In this paper we
discuss several approaches to the fusion of intelligent
vehicles for order-picking with ASP and approach the
question if this might be beneficial.
The planning task which is implemented with
ASP has the restriction of not requiring any physical
adaption of the system. Still, we aim for a significant
increase of performance. A combinatorial problem
for such order-picking systems is vehicle dispatching,
meaning the assignment of driving jobs to vehicles.
In the specific context of order-picking systems, the
question arises to which picking station a customer
order is assigned. All of the items of a customer order
must be transported to the same picking station which
have limited capacity. Thus, due to limited capacity
a driving job may not be able to select (see section 3)
which makes the decisions interconnected. Also, they
must be completed at the same time and raise poten-
tial for a holistic optimization of the system, e.g. con-
cerning the utilization of the picking stations.
2 FUNDAMENTALS
In the following we will provide some fundamentals
of the presented work. The concept of answer set pro-
gramming will be introduced briefly (further details
may be found in e.g. (Dovier et al., 2009) and (Geb-
ser, 2013)). After that, cellular transport systems are
described. A (more) formal definition of the planning
task is presented in chapter 3.
2.1 Answer Set Programming
An answer set program P consists of a number of
rules of the form
r : H ← A
1
, ..., A
n
, not B
1
, ..., not B
m
. (1)
where H, A
1
, ..., A
n
, B
1
, ..., B
m
are literals and ”not” is
a so-called default negation operator. H is head(r)
Schieweck S., Kern-Isberner G. and ten Hompel M.
Various Approaches to the Application of Answer Set Programming in Order-picking Systems with Intelligent Vehicles.
DOI: 10.5220/0006489300250034
In Proceedings of the 9th International Joint Conference on Computational Intelligence (IJCCI 2017), pages 25-34
ISBN: 978-989-758-274-5
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
and A
1
, ..., A
n
, not B
1
, ..., not B
m
is body(r), respec-
tively. H holds if pos(r) = A
1
, ..., A
n
is true and
neg(r) = B
1
, ..., B
m
are false or not known. A rule
without body is called a fact and holds without any
precondition. A rule without head is a constraint and
excludes the set defined in body(r) from the answer
set.
An encoding of an answer set program contains
a number of such rules which may (and will) inter-
connect. A valid answer set satisfies all of the given
rules. While the most basic structure of a rule is as
described, rules may look differently to achieve spe-
cific grounding and solving behaviors (Gebser, 2013).
With todays ASP-grounders and -solvers, one may
specify objective functions to select an optimal an-
swer set from the set of valid ones.
A set S of literals is a model (an answer set) of
P , if H ∈ S whenever pos(r) ⊆ S and neg(r) ∩ S =
/
0
for every r ∈ P . S is a stable model of P , if S is
the ⊆-minimal model of P
S
where P
S
is the reduct
of P relative to the set S as defined by (Gelfond and
Lifschitz, 1988; Gelfond and Lifschitz, 1991)
P
S
:= {H ← A
1
, ..., A
n
|
H ← A
1
, ..., A
n
, not B
1
, ..., not B
m
∈ P ,
{B
1
, ..., B
m
} ∩ S =
/
0}
(2)
A rational agent can gain knowledge from P . He con-
siders any literals P
S
true and the remaining literals
false.
2.2 Cellular Transport System
In the domain of facility logistics, cellular transport
systems received considerable attention in the recent
years. They are the embodiment of multi-agent sys-
tems for the purpose of in-house transport of goods
and handling units such as pallets, bins or cartons.
Cellular Transport Systems consist of structural and
functional elements like racks, picking stations and
lifts and a number of conveying units. The trans-
port units are intelligent and self-organizing which
enables them to decide and act autonomously. They
may be manifested by single continuous conveying
units which are able to work upon ”plug-and-play”
by detecting the meta-structure of the conveying sys-
tem and collaborate to achieve conveying objectives
(Mayer, 2009). In this paper, a manifestation in form
of a fleet of intelligent vehicles is considered which
operate in an order-picking system.
The Cellular Conveyor System has been devel-
oped jointly by Fraunhofer-Institute for Material
Flow and Logistics IML and Dematic GmbH. Its
unique feature is the vehicles capability of moving on
the various levels of rack as well as on the ground
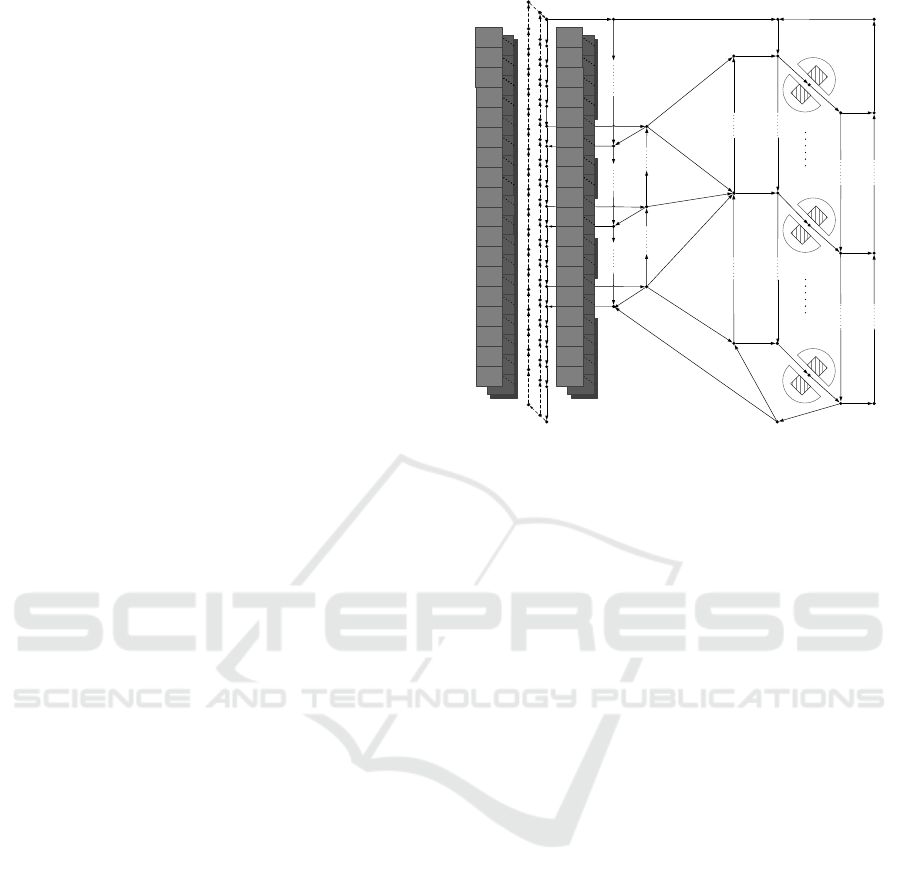
Figure 1: Example of routing graph.
floor. The system consists of one (or multiple) racks,
picking stations, article bins, order bins, vehicles and
lifts which transport the vehicles vertically. The arti-
cle bins are stored in the rack(s). If a specific stock
keeping unit (sku) is ordered, the related article bin
is retrieved by a vehicle and transported to one of
the picking stations. The system is automated by a
large degree. Nonetheless, as in most order-picking
systems, the isolated pick-and-put procedure of skus
from the article bins to the order bins is conducted by
workers (order pickers) who are located at the picking
stations. After picking has been completed the vehi-
cle transports the bin back into the rack and stores it.
The lifts are required to reach the various levels of the
rack. They are located at the beginning and the end of
an aisle. The vehicles move on dedicated virtual paths
which compose to a graph (see Figure 1). The edges
of the graph are unidirectional. Thus, no reservation
procedure for edges is necessary. As an additional
consequence, one of the lifts is dedicated for the up-
bound transport of the vehicles and the other lift for
the downbound transport.
The control architecture of the vehicles consists
of three layers which are connected by UDP-sockets.
The sensor and actuator layer is at the lowest level and
responsible for tasks which are strongly coupled to
the hardware and time-critical (e.g. position control,
safety, sensor data acquisition). The operational layer
is on the mid-level and responsible for tasks like lo-
calization, path planning and collision avoidance. The
autonomous behavior is located at the strategical level
and implemented via software agents. Those agents
are capable of communicating with other agents in the

system (Kamagaew et al., 2011).
Currently, such an external system is responsible
for job management (aka dispatching) (Kamagaew
et al., 2011). Dispatching is conducted using the FIPA
protocol (Foundation for Intelligent Physical Agents
FIPA, 2002). The external system releases a broadcast
to all vehicles once a new order-line arrive. The avail-
able (idle) vehicles bid for the order-line and the high-
est bidder is assigned the offered driving job. Hence,
if the system runs under full utilization (which is de-
sirable for economical reasons), the operation results
in a simple first-come-first-served (FIFO) procedure.
2.3 Related Work
The assignment of driving tasks to vehicles has been
studied intensely in the domain of operations re-
search. The vehicle scheduling problem decides
when, where and how any vehicle in a system shall
act. Routing is included in this problem. The problem
may be tackled online or offline. The offline prob-
lem can theoretically be solved to optimality using
a multiple traveling salesman model which has NP-
complexity. Real-life scenarios require online solv-
ing due to uncertainty of the environment states. This
may be realized with a rolling horizon, in which the
planning is conducted for a limited future timespan
(Le-Anh and de Koster, 2006).
Vehicle dispatching strategies only assign driving
jobs to vehicles. Often, the planning horizon has a
timespan of zero. This results in simple rules from
which the assignment is made. Especially in multi-
agent systems, the choice weather the decision is
made central or distributed is of interest (Vis, 2006).
Existing research dealing with the theoretical
foundations is diverse. Among them are optimiza-
tion models (Yang et al., 2004), heuristics (Bartholdi
and Platzman, 1989), disposition strategies (de Koster
et al., 2004) but also more complex methods such as
fuzzy logic (Benincasa et al., 2003) and ant colony
algorithms (Saidi-Mehrabad et al., 2015) are used.
Cellular transport systems are a rather new field
of research. Therefore, publications are sparse and
mainly engage with the physical design of the sys-
tems (Guizzo, 2008; Kamagaew et al., 2011). To our
knowledge, no publications from other authors exist
which deal with the combination of ASP and cellular
transport systems.
3 TASK DEFINITION
An order-picking system has the purpose of the as-
sembly of customer orders. In a warehouse, a set
M of skus is held in inventory. A customer order
O ⊂ M consists of a number n
P,O
of skus which are
condensed to n
O
≤ n
P,O
order-lines l in which skus
with the same identity compose to one order-line
1
.
The system has a number of picking stations S, stor-
age positions R and vehicles F. The picking sta-
tions have equal capacity c
S
. The incoming customer
orders are stored in a list of orders L. Given the
time t
O
of an order O the orders are sorted such that
t
1
≤ t
2
≤ ... ≤ t
q−1
≤ t
q
.
The vehicles move on a graph G = (V, E) with a
set of nodes V and a set of edges E. V = {V
R
;V
S
;V
W
}
where V
R
are nodes which identify storage locations
in the rack, V
S
are nodes which identify picking sta-
tions where bins need to be delivered to and V
W
are
waypoints without further functionality. The edges
are unidirectional. On G, the vehicles need to travel a
distance d to fulfill the systems purpose.
The planning task is the assignment l
v
= (v, l) of
a vehicle v to an order-line and the related assign-
ment o
s
= (O, S) of an order to a picking station. We
aim to maximize the number of satisfied order-lines
per time N
l
:
z
1
: max N
l
(3)
Also, a balanced utilization u
s
between the picking
stations is favored:
z
2
: min
∑
S
|
u
avg
− u
s
|
(4)
with
u
avg
=
1
S
S
∑
i=1
u
i
(5)
One vehicle can only transport one bin at a time. The
capacity c
S
of a picking station may not be exceeded
by the number of orders O assigned to the same pick-
ing station at a time.
For the planning task, the agents are given a hori-
zon H with size n. Informally speaking, they are
given the opportunity to select an order-line from a
pool which consists of the next n unfulfilled order-
lines of L. Note that, if the same article is part of
multiple orders in H, the vehicle may approach mul-
tiple picking stations between retrieval and storing to
satisfy multiple order-lines with one cycle. Thus, we
define a driving job j which is selected from H. Every
unique storage position is one Pos ∈ H. Every job j
has one pickup node V
p
∈ V
R
, one or multiple deliv-
ery nodes V
d
⊆ V
S
and one storing node V
r
= V
p
. If
1
E.g. if a customer orders 500 business cards, n
O
= 1.

j has multiple delivery nodes it will be referred to as
an eos-job (economy of scale). The latter definition of
the storing node implies that bins are transported back
to the same location from which they were extracted.
Practically speaking, we assume a fixed storage pol-
icy. Finally, we define that all of the order-lines l of
a customer-order O must be transported to the same
picking station
V
d,l
1
= V
d,l
2
= ... = V
d,l
n
∀l
i
∈ O (6)
4 SYSTEM DESIGN
The developed approaches are tailored to work in a
realistic scenario and will be evaluated as such (see
section 5). To cope with the complexity real-life sce-
narios provide, the implemented planning agents op-
erate with limited knowledge.
First, the rating of the order-lines l ∈ H will be
based on the driving distance d
p
⊂ d to the pickup
nodes V
p
. The remaining steps to complete the driv-
ing task are not considered for the rating as they do
not depend on the assignment of the vehicle. Also,
every order-line needs to be completed at some point
of time. As a consequence, those steps have no influ-
ence on the overall system performance. We assume a
strong correlation between driving distance and driv-
ing time. Second, for the assignment of orders to
picking stations only orders are assumed to reserve
capacity
• for which at least one driving job has been
started yet and
• which have unsatisfied order-lines remaining.
The first assumption is trivial, as no order bin is re-
quired at the picking station before the first order-line
has been delivered. The second assumption implies
that any driving job which has already been started
will reach a possibly capacity-critical picking station
before the currently assigned one. Otherwise, the cur-
rently assigned will have to start a new attempt for
delivery as no capacity for its order bin is available.
A new attempt will result in a detour on G such that
other vehicles may reach the picking station and some
time passes until the current vehicle reaches the pick-
ing station again.
For all of the implementations, a blackboard ar-
chitecture has been implemented for the multi-agent
system. The blackboard contains information about
the incoming customer orders (denoted as L). Also,
information about the status of the order-line and the
corresponding order are published on the blackboard.
Depending on the approach, specific agents have read
and write privileges for the blackboard. For example,
an agent may annotate for an order-line to be com-
pleted and add an assignment o
S
.
In this paper three approaches are described and
evaluated:
• distributed planning with hybrid encoding
(section 4.1)
• distributed planning with numbering concept
(section 4.2)
• central planning with hybrid encoding
(section 4.3)
For all of the implementations the ASP grounder and
solver clingo (Gebser et al., 2014) in version 4.5.4 of
the Windows build has been used.
4.1 Distributed Planning
Some versions of the distributed approach with hybrid
encoding have been discussed in (Schieweck et al.,
2016). We will describe the superior version of the
encoding and its operation in the overall system in the
following.
The implementation follows the trend towards dis-
tributed systems by increasing the vehicles auton-
omy and enabling them to take their own decision.
This approach has been selected due to its high anal-
ogy to the current systems architecture, its flexibil-
ity and low expected computing times. As soon as
a vehicle completes a driving task it requests a new
driving job. Assuming full utilization of the system
(which is the most critical state) a number of driv-
ing jobs is available. At that point of time, the vehi-
cle makes the assignments for both l
v
and o
S
, if re-
quired. The vehicles planning agent extracts the rel-
evant information from the blackboard and translates
them to an ASP-instance (see Listing 1). The instance
contains information about the available order-lines
(order pos/3), the current assignments of orders to
picking stations (order pickst/2) and the vehicles
position (veh position/2).
In the encoding the driving jobs (pos/2) are ex-
tracted in line 8. After, we ensure that the vehi-
cle is assigned exactly one driving job in the atom
pos veh/2. In line 10 existing assignments of orders
to picking stations are transferred to the new atom
as order pickst/2 to differ between new and ex-
isting assignments. If a driving job j is selected, at
least one of its corresponding order-lines l must be
assigned to the vehicle (line 11). The selection of the
order-line requires assignment of the related order, if
no assignment exists already (line 12). The assign-
ment is then conducted in lines 13 and 14 with respect
to the capacity restriction c pickst of the picking sta-
tions.

1 instance
2 orde r_ po s (69 , 33 ,43 6 ) . ord er _p os (70 ,3 4 ,322) . o r d e r_ po s ( 7 6 ,36 , 2 41) . or de r_ p o s (82 , 39 ,44 6 ) .
3 orde r_ po s (83 , 39 ,12 4 ) .
4 ord e r _ p ic ks t (3 3 , 2 ) . o r d e r _ p i ck st (34 ,3) . or de r_ pi c k s t (36 ,1) . or d e r _ p i c ks t (39 ,8 ) .
5 veh _ p o s it io n ( 4 ,573) .
6
7 encoding
8 pos ( P ) :- o rd er _ p o s (_ , _ ,P ) .
9 1{ pos _v e h (P , V ) : p o s ( P) }1 : - veh ( V ) .
10 as _o r d e r_ pi c k s t (O , S ) : - o rd er _p i c k s t (O , S ) , pi cks t ( S ) .
11 1{ job _v e h (Ix , V ) : o r d er _p os ( Ix , _ ,P ) } :- p os _ ve h ( P , V ) .
12 as _ or de r ( O ) :- j ob _v e h (Ix , V ) , o rd er _p os ( Ix , O ,_ ) ,
not or de r_ p i c k s t ( O , _ ) .
13 1{ as _ o r de r_ p i c ks t (O , S ) : pic k st ( S) }1 :- a s_ o r d er ( O ) .
14 :- pic k st ( S ) , c _ p ic ks t +1{ a s _o r d e r _ pi c k s t ( O , S ) }.
15
16 dis t (A , B , @d is ta n c e ( A ,B ) ) :- v eh _ po s ( _ , A ) , pos ( B ) .
17 pos _v e h (P , V ,C ) :- p os _v e h (P , V ) , ve h_ p o s i t i o n ( V , A ) , dist ( A ,P , C ) .
18 num Jo b s ( K ) :- K =# cou n t { Ix : jo b _v eh ( Ix , V ) }.
19 nu mO r d e r P ic ks t ( X ) :- pic k st ( S ) , X =# coun t { O : a s_ o r d er _p i c k st ( O ,S ) }.
20 ma x N u mO rd e r P ic k s t ( Y ) : - Y=# max { X : n u m O rd er P i c k s t (X ) }.
21
22 # m in im iz e { C@3 : p o s_ ve h ( P ,V , C ) }.
23 # m ax im iz e { K@1 : n u mJ ob s ( K ) }.
24 # m in im iz e { Y@2 : m a x N um O r d er P i c ks t ( Y ) }.
Listing 1: Excerpt of encoding for distributed planning with exemplary instance (n = 5).
In line 16 to 20 the rating of the driving jobs
is implemented. Note that in line 16 we use the
@-directive to compute the distance of the vehicle to
the various bins with a Dijkstra-Algorithm (Dijkstra,
1959). The Windows build of clingo allows for the in-
clusion of Lua scripts in the ASP-encoding. Thus, hy-
brid programming is implemented. Some tests were
conducted comparing the Dijkstra-algorithm with the
A*-algorithm. For the prevailing structure, Dijkstra
provided lower calculation times. The distance to
the bins position is minimized with highest priority.
Then, the maximum of the number of orders assigned
to all picking stations is minimized, resulting in a lev-
eled utilization. To be able to use eos-jobs properly
the number of order-lines l completed with this single
driving job j is maximized.
4.2 Location Numbering
The proposed approach is an evolution of the one de-
scribed in section 4.1, resulting from first tests and
insights to the aforementioned approach. While in
the previous approaches hybrid programming is used,
we try to eliminate the routing algorithm in the cur-
rent approach. This is due to the high expected
calculation time of the routing algorithm, especially
when it comes to scalability. ASP is tailored for
combinatorial, complex problems. The routing prob-
lem however, has been investigated many times and
existing algorithms are expected to be superior to
the implementation of the routing problem in ASP
2
.
Thus, a different approach has been developed which
makes use of the unidirectional structure of the rout-
ing graph. By testing and implementing we hope to
find a good approximation of the optimal solution.
Also, we hope to gain insights on how costly the rout-
ing algorithm is for the current planning task.
As a matter of fact, every driving job starts and
ends in the rack. All of V
R
are given names such
that simple comparison yields an estimation for the
ranking of the driving jobs with shortest traveling dis-
tance d
p
. An example of the numbering for one rack
is given in Figure 2. As a consequence, the multi-
agent system is extended by a numbering agent which
reassigns the names according to the concept. The
numbering agent also has an ASP-encoding imple-
mented which requires information about the length
of the rack, the number of rack levels and the po-
sition of the rack entries and generates the 2-tuple
t = (id
old
, id
new
).
E2
102
103
E1E3104
203202201 206205204 207
303302301 306305304 307
E2
102
103
E1E3104
203202201 206205204 207
303302301 306305304 307
101101
Figure 2: Example of numbering concept.
2
Again, tests were conducted to indicate this.

1 le ve l_ po s ( N , P / 100 ) :- or d e r _p os (N ,_ , P ) .
2 le ve l_ ve h ( V , P / 100 ) :- ve h_ po s i t i o n ( V , P) .
3 n um Pi ck s t ( Max ) : - Max =# m a x { S: pi ck st _n od e (S , _ ) }.
4
5 % c a s e 1 % c ase 2 % c ase 3
6 po ss ib le P o s 1 ( N ) : - ... po ss ib le P o s 2 ( N ) : - ... po ss ib le P o s 2 ( N ) : - ...
7 se le ct ed B i n 1 ( N ) : - ... se le ct ed B i n 2 ( N ) : - ... se le ct ed B i n 3 ( N ) : - ...
8
9 s el ec t e d B i n ( N ) : - s e l e ct ed Bi n1 ( N ) .
10 s el ec t e d B i n ( N ) : - s e l e ct ed Bi n2 ( N ) .
11 s el ec t e d B i n ( N ) : - s e l e ct ed Bi n3 ( N ) , n o t s e le ct ed Bi n 2 ( _ ) .
12
13 po s _v e h (B , V ) : - s el e c t e d B i n ( N ) , o r d e r_ po s (N ,_ , B ) , v eh _ p o s i t i on (V , _ ) .
Listing 2: Excerpt of encoding for distributed planning with numbering concept.
The vehicles planning agent has an encoding sim-
ilar to Listing 1. Lines 16 and 18 are substituted by
Listing 2. Also, the optimization statement in line 22
is no longer necessary. First, the rack levels of the
order-lines l ∈ H are calculated in lines 1 and 2. The
number of the picking stations is expressed in the
atom numPickst/1 in line 3. Afterwards, the cases
1. the vehicle is not in the rack,
2. the vehicle is in the rack and at least one driving
job j ∈ H starts on the same level in driving direc-
tion of v and
3. the vehicle is in the rack and a driving job j ∈ H
is available.
If case I applies and the capacity restriction
for at least one job of the position is fulfilled
an atom possiblePosI/1 is created. Multiple
possiblePosI/1 may exist for each I. The minimum
number has the lowest traveling distance d
p
and is
transferred to selectedBinI/1. While case 1 ex-
cludes the other cases, 2 and 3 may occur in the
same instance. Then, selectedBin2/1 is assigned
because the bin can be picked up on the way to the
outside of the rack (line 10 and 11). Line 13 is
the interface to the existing encoding and translates
selectedBinI/1 to pos veh/2.
4.3 Central Planning
The distributed approaches fit into the existing trend
towards local decision making of intelligent units.
However, multi-agent systems rarely exist without
any central agents which have the ability to coordi-
nate the overall system (see e.g. section 2.2 with the
current architecture). As described in chapter 2.2 the
existing system contains a central entity for dispatch-
ing. A global optimum for a planning problem is ex-
pected to have an objective value at least as good as
multiple local optima. On the other hand, the search
for a global optimum raises higher complexity. The
following approach has been developed to test the im-
pact of the global optimum and the capability of ASP
to find the optimum with satisfiable computing times.
An exemplary situation in which a central plan-
ning approach is superior to a distributed approach is
depicted in Figure 3. Vehicle 1 requests a new driving
task and has bin a and b available. Bin b induces a
shorter distance and will be selected in the distributed
approach, even though the difference between a and
b is comparatively small. For vehicle 2 bin a remains
for which it has to travel through the whole rack and
use the lifts twice. A central planning approach can
minimize the overall traveling distance for all vehi-
cles. In this case, vehicle 1 is assigned bin a with a
slightly larger traveling distance. As a consequence,
vehicle 2 can reach bin b which induces considerably
less traveling distance.
For the current approach a central dispatching
agent is added to the multi-agent system. Just like
in the previous implementations the agent has a hori-
zon H of order-lines available from which it conducts
the assignments l
v
and o
S
. Once a vehicle completes
a driving job it tries to find a new driving job which is
assigned for itself on the blackboard. If no assignment
2
b
DistributedCentral
1
a
b
2
b
1
a
b
Figure 3: Distributed vs. central planing.

1 :- p o s ( P ) , 2{ po s_ v eh (P , V ) }.
2 sp o s i t i on (V , Pos ) : - oc cu p ie d (V , P o s ) .
3 sp o s i t i on (V , Pos ) : - ve h _ p o s i t io n (V , P o s ) , not oc c u p ie d ( V , _ ).
4 dist ( SPos , TPos , @d i st an ce ( SPos , TP o s ) ) : - spo si ti on (_ , SPos ) , pos ( TPos ) .
5 ve h _d ri ve (V , D ) : - p os _v e h (P , V ) , sp os it io n ( V , S Pos ) , d ist ( SPos ,P ,D ) .
6
7 # m in im iz e { D@3 : v eh _ d r i v e (V , D ) }.
Listing 3: Excerpt of encoding for central planning.
can be found a new planning cycle is initialized
3
. At
that point of time, the planning agent creates a plan
for all of the vehicles v in the system and assigns ex-
actly one j for each v and publishes the result on the
blackboard. The agent requires the additional infor-
mation about the status of each vehicle. The status is
defined by the occupation and if an occupation exists,
the final vehicle position induced by driving job j.
For the comparability of the implementations, n
is redefined. Note that a minimum of F order-lines
must be available in H to allow for one assignment l
v
for each vehicle v. Also, the amount of undesirable,
unassigned order-lines in H shall stay the same. Thus,
the central planning agent has a number of
n
cen
= n + F − 1 (7)
order-lines available.
The central planning agent has a similar encoding
as the distributed agents in Listing 1. The differing
lines are displayed in Listing 3. In line 1 we ensure
that each vehicle receives only one driving job. If a
vehicle is occupied, the atom occupied/2 is added
to the problem instance and the starting point for the
next job is defined with sposition/2 (line 2). If the
vehicle is not occupied, we assume that it does not
move until the next driving job starts (line 3). The
necessary distances are computed in line 4. Again, a
routing algorithm is used. If an assignment is made
the vehicle has to travel the distance D which is noted
in the atom veh drive/2 (line 5). The overall travel-
ing distance to the starting positions is minimized in
line 7.
5 EVALUATION
The approaches which are described in section 4 are
evaluated in the following. First, the experimental de-
sign is described (section 5.1). Second, the results are
described and interpreted (section 5.2).
3
The planning procedure may be started even before.
This is the protocol which has been implemented to the sim-
ulation.
5.1 Experimental Design
For the evaluation a Demo3D simulation model has
been created. The simulation model has the pur-
pose of a development and evaluation environment.
For being able to validate the functionality of the ap-
proaches, their behavior inducted by the encodings
could be tested instantly. Also, an interface between
the simulation environment and the employed ASP-
grounder and -solver clingo 4.5.4 has been created.
Demo3D was selected due to its programming struc-
ture which is close to agent-based systems. Single
entities are assigned proprietary C#-scripts which ex-
change information with messaging protocols. Thus,
the simulation could be implemented similarly to a
real-world application. The level of abstraction of the
simulation is relatively low. Just like the real vehicles,
their digital replications possess proximity sensors
which slow the vehicle down (proximity < 3 m) and
let it come to an halt eventually (proximity < 1 m).
Working towards comparable results not only the
approaches described in section 4 were implemented
but also counterparts with classical (imperative) pro-
gramming as well as the FIFO approach. The qual-
ity of the implementations is in the following quanti-
fied by their improvement compared to the FIFO ap-
proach and indicated by ∆. The experimental design
consists of a basic system from which single parame-
ters are varied. The basic system has one rack with a
capacity of 500 bins, S = 5 picking stations, F = 5 ve-
hicles, uniformly distributed demand among the skus
Table 1: Data of simulated system.
Parameter Value Unit
Vehicle
Speed floor 1 m/s
Speed rack 2 m/s
Acceleration/Deceleration 0,5 m/s
2
Time loading/unloading 4,5 s
Lift
Speed 2 m/s
Acceleration/Deceleration 2 m/s
2
Picking time per order-line 5 s
0,01
0,1
1
10
100
3 4 5 6 7 8 9 10 11 12 13 14 15
Size n of horizon H
11
12
13
14
15
16
17
18
19
20
Driving tasks/
vehicle/hour
0,001
0,01
0,1
1
10
100
1000
1 3 5 7 9 11 13 15 17 19
Computing time
[sec]
Number of vehicles F
16
17
18
19
20
asp_dij asp_num imp_dij imp_num Zasp FIFO
Casp
2 4 6 8 10 12 14 16 18 20
10
0
10
1
10
2
10
3
10
-1
10
-2
10
-3
10
0
10
1
10
2
10
-1
10
-2
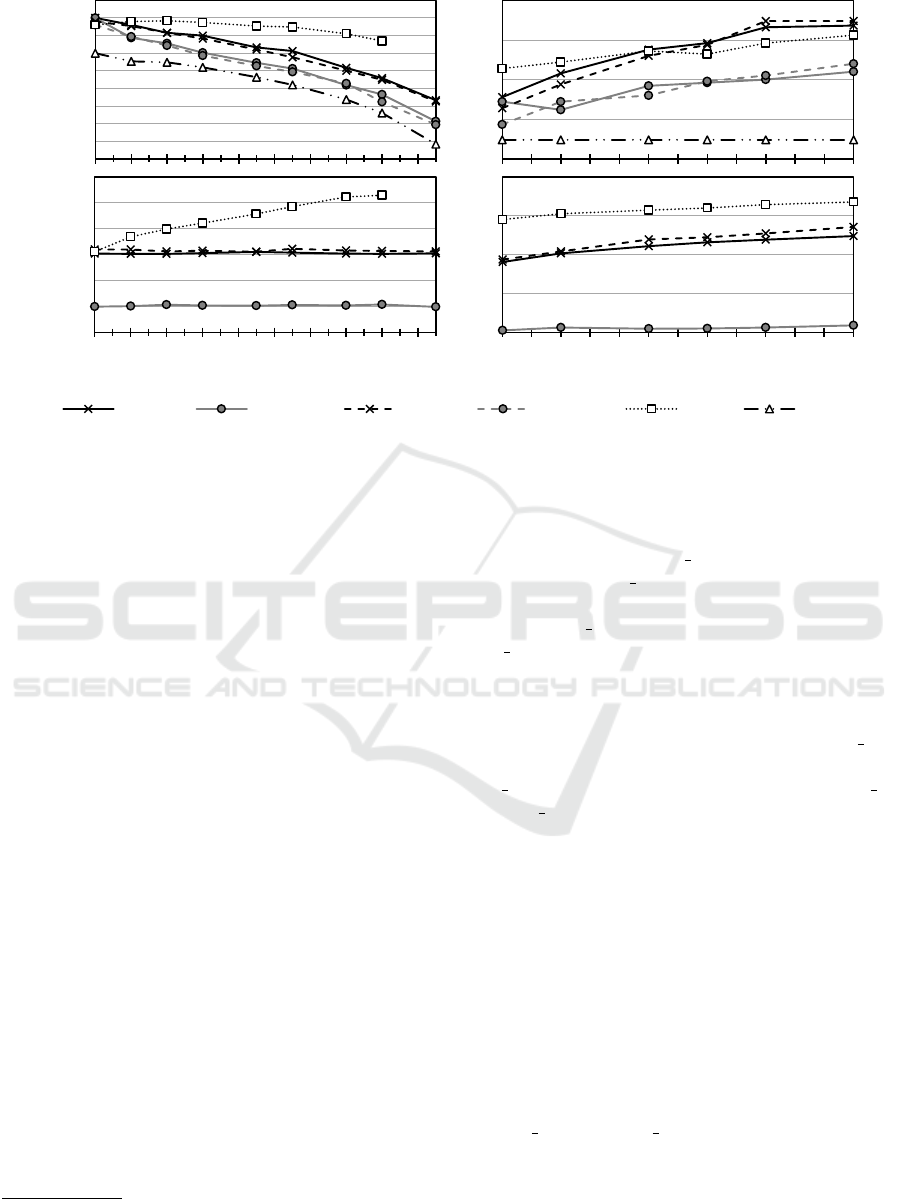
Figure 4: Evaluation of the approaches.
and a horizon with n = 5 order-lines. The parame-
ter variations were tested for five hours of simulation
time each. The central and distributed planning agents
are granted a computing time of 200 seconds to find
the optimal solution
4
. After this time, three options
may occur:
• An optimal answer set has been found and the
computation has been terminated at a time < 200
seconds.
• The solver has not terminated the computation
procedure yet and
– an answer set has been found. The answer set
may or may not be optimal.
– no answer set has been found.
If no answer set has been found the simulation run
was terminated.
5.2 Experimental Results
Some key results of the simulation runs are depicted
in Figure 4. Note that the computing time (bottom)
is presented with a logarithmic y-Axis. We define
the number of driving tasks which have been com-
pleted by one vehicle per hour on average as the per-
formance.
Generally, the performance of a vehicle decreases
with a growing number of vehicles in the system (top
left). This is due to blocking and congestion of the
vehicles on the routing graph. For the variation of the
4
This is the time a vehicle needs approximately for one
driving task.
number of vehicles the highest average performance
was achieved by the central approach (Casp, ∆19%).
The distributed approaches with hybrid programming
achieve ∆13% (ASP, asp dij) and ∆12% (classical
programming, imp dij). With the distributed ap-
proaches with numbering concept an improvement of
7% (ASP, asp num) and 6% (classical programming,
imp num) is achieved. For the distributed approaches
the computing time (bottom left) is constant with in-
creasing vehicle number as the instance of every sin-
gle planning agent is independent of this parame-
ter. No measurable computing times for imp num
and FIFO were recorded. The computing time for
asp num was 0.01 seconds on average. For asp dij
and imp dij the times were on average 1.13 and 1.45
seconds, respectively. The increase is caused by the
routing algorithm. Separate experiments revealed that
the average computing time for the routing on the
graph of the basic system is roughly 0.2 seconds. The
computing time of the central approach increases al-
most exponentially with the number of vehicles. As
a consequence, the experiments with 20 vehicles did
not produce results due to the 200 seconds limit.
With growing size n of the horizon H the perfor-
mance (top right) of the vehicles increases. For all of
the simulation runs, the central (∆13%) and the dis-
tributed, hybrid approaches (∆13% ASP, ∆12% im-
perative) achieve the highest performance followed
by asp num and imp num (∆6% each). Remark-
ably, the performance of Casp increases by a smaller
amount than the other approaches, even though a cen-
tral approach is expected to be superior. The limited
knowledge has an impact in those scenarios. While in

the distributed approaches the planning is conducted
exactly at the time needed, the central planning agent
has to take a wider look into the future. However,
the limitation of the knowledge stays the same due to
rapidly growing complexity of the problem (e.g. in
an state-action encoding with consideration of time
points). Thus, in the central approach a capacity of
a picking station may be considered as occupied by
the time of the planning while in real-life operation
it has been released in due time. The computing time
(bottom right) grows steadily for all of the approaches
which use the routing algorithm. The highest increase
is noted for Casp due to the redefinition of the hori-
zon size n
cen
. For the distributed approaches the in-
crease is roughly constant to the 0.2 seconds which
are required to compute the distance to every l ∈ H.
The computing time of asp num only increases from
0.009 seconds to 0.011 seconds with a horizon size of
3 and 15, respectively.
Generally, a slight decrease of performance oc-
curs from the ASP implementations to their impera-
tive counterparts. At this point, the flexible structure
of the ASP encodings proves to be advantageous. In
the ASP approaches it is possible to prioritize the eos-
jobs such that, if two driving jobs induce the same
distance and utilization, the driving job which com-
pletes the most order-lines will be selected. The im-
perative implementations have a less flexible structure
in which first an order-line is selected and if possible,
more order-lines with the same bin are added:
1. Setup of horizon H.
2. Calculate distances d
p
.
3. Choose minimum distance order-line l
min
.
4. Search eos of l
min
in H with d
p,eos
= d
p,min
.
5. Assign station(s) o
S
with respect to c
S
and u
avg
.
6.(a) If no o
S
could be assigned, eliminate l
min
from
H, clear o
S
∀ l
min
and go to (2).
(b) Else, assign order-line(s) l
v
.
In the case mentioned above weather the order-line
with or without eos-job is selected is random. Also,
one might note that the priority of eos-jobs is third in
the ASP approaches and they are searched for second
in their counterparts. This is due to the fixed sequence
in imperative programs. In this case, all of the poten-
tial l must be found to verify possible c
S
.
Furthermore, the computing time of the ap-
proaches with the numbering concept is remarkably
low. Unfortunately, the performance of the ap-
proaches is low as well, even though an improvement
compared to the FIFO experiments could be achieved.
We find the reason for this in the rating of the stor-
age positions on different levels. While the hybrid
approaches always select the positions which are the
easiest to reach, asp num and imp num prefer the po-
sitions on the lower levels because they have lower
numbers (see Figure 2). As a final note, the comput-
ing times of the imperative counterparts are certainly
induced by some degree by the simulations interface
to the routing algorithm. Generally, we expect a well
programmed imperative code to be faster than a gen-
eral purpose ASP solver. However, especially for sys-
tems which are designed to work in volatile environ-
ments the flexibility and comfort of programming is
key which is remarkably good for ASP. This can be
elucidated with the small length of the encodings in
this paper as well as the small adaptions necessary
between the approaches.
6 CONCLUSION AND OUTLOOK
The presented work combines answer set program-
ming with the innovative field of application of intel-
ligent vehicles in an industrial setup. The approaches
are tailored to work in a real-life environment and are
evaluated as such. The general approach of allow-
ing the planning agents to select driving jobs from a
horizon achieves a considerable improvement of per-
formance without any physical adjustment of the sys-
tem. The approaches to the planning task do not cause
an immense complexity. However, for operational
planning even seconds become valuable. For most
cases, central planning achieved a higher performance
than the distributed approaches. The limited knowl-
edge plays a critical role for the performance, espe-
cially when the planning horizon is large. Answer set
programming as a method promises great capabilities
in systems which are made to work in changing and
volatile environments. This is due to good computing
times and especially easy modeling and high flexibil-
ity.
For future steps we recommend the evaluation of
further planning tasks to be implemented with ASP
and combinations of those. As a final step, the most
promising approaches should be implemented and
tested with existing vehicles.
REFERENCES
Bartholdi, J. J. and Platzman, L. K. (1989). Decentralized
control of automated guided vehicles on a simple loop.
IIE Transactions, 21(1):76–81.
Benincasa, A. X., Morandin, O., and Kato, E. R. R. (2003).
Reactive fuzzy dispatching rule for automated guided
vehicles. In IEEE International Conference on Sys-
tems, Man and Cybernetics, pages 4375–4380.

de Koster, R. B., Le-Anh, T., and van der Meer, J. (2004).
Testing and classifying vehicle dispatching rules in
three real-world settings. Journal of Operations Man-
agement, 22(4):369–386.
Dijkstra, E. W. (1959). A note on two problems in connex-
ion with graphs. Numerische Mathematik, 1(1):269–
271.
Dovier, A., Formisano, A., and Pontelli, E. (2009). An
empirical study of constraint logic programming and
answer set programming solutions of combinatorial
problems. Journal of Experimental & Theoretical Ar-
tificial Intelligence, 21(2):79–121.
Foundation for Intelligent Physical Agents FIPA (2002).
Fipa contract net interaction protocol specification.
Gebser, M. (2013). Answer set solving in practice. Morgan
& Claypool, San Francisco, CA.
Gebser, M., Kaminski, R., Kaufmann, B., and Schaub, T.
(2014). Clingo = asp + control: Extended report.
Gelfond, M. and Lifschitz, V. (1988). The stable model se-
mantics for logic programming. Journal of Symbolic
Logic, 57(1):274–277.
Gelfond, M. and Lifschitz, V. (1991). Classical negation in
logic programs and disjunctive databases. New Gen-
eration Computing, 9(3-4):365–385.
Guizzo, E. (2008). Three engineers, hundreds of robots, one
warehouse. IEEE Spectrum, 45(7):26–34.
Kamagaew, A., Stenzel, J., Nettstrater, A., and ten Hompel,
M. (2011). Concept of cellular transport systems in
facility logistics. In 5th International Conference on
Automation, Robotics and Applications, pages 40–45.
Le-Anh, T. and de Koster, R. B. (2006). A review of de-
sign and control of automated guided vehicle systems.
European Journal of Operational Research, 171(1):1–
23.
Mayer, S. H. (2009). Development of a completely decen-
tralized control system for modular continuous con-
veyor systems. Dissertation, Karlsruhe University,
Karlsruhe.
Saidi-Mehrabad, M., Dehnavi-Arani, S., Evazabadian, F.,
and Mahmoodian, V. (2015). An ant colony algo-
rithm for solving the new integrated model of job shop
scheduling and conflict-free routing of agvs. Comput-
ers & Industrial Engineering, 86:2–13.
Schieweck, S., Kern-Isberner, G., and ten Hompel, M.
(2016). Using answer set programming in an order-
picking system with cellular transport vehicles. In
IEEE International Conference on Industrial Engi-
neering and Engineering Management, pages 1600–
1604.
Vis, I. F. A. (2006). Survey of research in the design and
control of automated guided vehicle systems. Euro-
pean Journal of Operational Research, 170(3):677–
709.
Yang, J., Jaillet, P., and Mahmassani, H. (2004). Real-time
multivehicle truckload pickup and delivery problems.
Transportation Science, 38:135–148.
