
Optimal Energy Management Strategy of Plug-in Hybrid Electric Bus in
Urban Conditions
Nadir Ouddah, Lounis Adouane, Rustem Abdrakhmanov and Elkhatib Kamal
Institut Pascal/IMobS3, UCA/SIGMA - UMR CNRS 6602, Clermont-Ferrand, France
Keywords:
Heavy Hybrid Vehicle, Energy Management Strategy, Optimal Control, Pontryagin’s Minimum Principle.
Abstract:
In this paper, an energy management strategy (EMS) for a specific multi hybrid plug-in electric bus is designed.
This bus is equipped with an internal combustion engine, a hydraulic motor, an electric motor and battery.
Considering the physical characteristics of the studied hybrid electric bus (i.e., the system dynamics and the
power sources limits), an optimal control technique based on Pontryagin’s minimum principle (PMP) is used in
order to ensure that the bus achieve a significant improvement in energy efficiency. Furthermore, information
of traffic conditions obtained from intelligent transportation systems is used to further optimize the energy
management strategy and to accurately control the battery depleting rate. The work proposed in this paper is
conducted on a dedicated high-fidelity model of the hybrid bus, that was developed on MATLAB/TruckMaker
software. The obtained results verify the effectiveness and validity of the developed energy management
strategy.
1 INTRODUCTION
A hybrid vehicle uses, by definition, at least two en-
ergy sources associated with the mechanical transmis-
sion to ensure its propulsion. The advantage of the
hybridization of vehicles is to overcome the two main
drawbacks of internal combustion engines that are the
low energy efficiency and the power irreversibility
which makes the engine unable to retrieve the energy
incurred during braking. Hybridization will therefore
draw on the strengths of different types of engines
by combining the excellent efficiency and reversibil-
ity of electric motors with the high energy density
of fossil fuels which increases the energetic auton-
omy, limits the vehicle weight and reduces refueling
time. The presence of additional power sources in the
HEV introduces additional degrees of freedom in con-
trolling the drivetrain, since at each time the driver’s
power request can be delivered by either one of the
on-board energy sources or their combination. The
additional degrees of freedom can be leveraged to re-
duce fuel consumption and pollutant emissions and
also to optimize other possible cost such as battery
life (Tang et al., 2015). This task is performed by
the energy management strategy which is the high-
est control layer of the drivetrain’s control strategy.
In commercially available HEV, the energy manage-
ment has been traditionally performed using heuristic
controllers in which rules are designed to manage the
on-board energy of the vehicle (Mashadi and Emadi,
2010) (Kamal et al., 2017). Such control strategies
are effective in real-time implementation but they re-
quire a careful calibration of the parameters (Mi et al.,
2011). A significant improvement with respect to
such strategies is achieved with model based opti-
mal control methods. These methods can be divided
into numerical and analytical approaches. In numeri-
cal optimization methods like dynamic programming
(Ximing et al., 2015), the global optimum is found
numerically under the assumption of full knowledge
of the future driving conditions. Unfortunately,the re-
sults obtained through dynamic programming cannot
be implemented directly due to its high computational
demands. To remedy this problem, approximated dy-
namic programming (Johannesson et al., 2007) and
stochastic dynamic programming (Moura et al., 2011)
(Johannesson et al., 2007) had been suggested as pos-
sible solutions. Analytical optimization methods, on
the other hand, use a mathematical problem formula-
tion to find an analytical solution that makes the ob-
tained solution faster than the purely numerical meth-
ods. Within this category, Pontryagin’s minimum
principle based energy management strategy is in-
troduced as an optimal control solution (Teng et al.,
2014). This approach can only generate an optimal
solution if implemented offline since in this case the
304
Ouddah, N., Adouane, L., Abdrakhmanov, R. and Kamal, E.
Optimal Energy Management Strategy of Plug-in Hybrid Electric Bus in Urban Conditions.
DOI: 10.5220/0006436803040311
In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 1, pages 304-311
ISBN: 978-989-758-263-9
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

driving cycle is supposed to be known in advance. For
online implementation Equivalent Fuel Consumption
Minimization (ECMS) methods that lead to subopti-
mal solutions have been proposed for HEVs (Volkan
et al., 2011). ECMS is based on instantaneous op-
timization, and is simple enough to be implemented
in real-time applications. Model predictive control
based methods have been also applied to solve on-
line the energy management problem (Fengjun et al.,
2012). One of the main drawbacks of this approach
is the high computational power required to calcu-
late the optimal power split at each sampling interval.
This paper details the development of energy manage-
ment strategies to optimize the power distribution in
a plug-in hybrid bus actuated by three distinct types
of power (internal combustion engine, electric motor
and hydraulic motor). Among the energy manage-
ment strategies discussed above, Pontryagin’s mini-
mum principle based optimization turns out to be the
most appropriate approach to design an energy man-
agement strategy for the considered hybrid bus since
it can guarantee, under given conditions, near opti-
mality while keeping the methodology simple. Thus,
an adaptation of this optimization approach to a plug-
in multi hybrid bus is proposed in this work and the
obtained optimization algorithm is implemented in an
overall optimization scheme in order to achieve the
most efficient way of bus operation. The key contribu-
tions are firstly in formulating the optimization prob-
lem so as all the sources of power of the studied hy-
brid bus are considered by the optimization algorithm.
Secondly, the general concepts initially presented in
literature are improvedby taking into account the mo-
tors dynamic limits. And finally, an overall optimiza-
tion scheme based on the use of predicted optimal ve-
locity trajectory of the bus is proposed. In fact, since
the route of the bus, roads levels variations and even
traffic lights are well known, prediction of optimal
velocity trajectory for the trip can be carried out by
means of information obtained from intelligent trans-
portation systems (Wu et al., 2014). This available
knowledge of the future driving cycle is exploited, in
this latter contribution, to make the bus more efficient
(even in the presence of exogenous and unpredictable
events such as the traffic jam) and to ensure the de-
sired battery depleting level. The paper is structured
as follows: section 2 describes the studied hybrid bus
architecture and model. Section 3 introduces the pro-
posed energy management strategy. In section 4, sev-
eral simulations results are presented showing the ef-
ficiency of the proposed energy management strategy.
Finally, conclusions and some prospects are given in
the last section.
2 MODELING OF THE HYBRID
BUS
The aim of this section is to illustrate the architecture
and the mathematical model of the studied system,
i.e., BUSINOVA hybrid bus, developed by SAFRA
(cf. Figure 1)
1
. This bus is composed of an electric
motor, a hydraulic motor, an internal combustion en-
gine and battery as the propulsion drivetrain system
of the vehicle. The electric motor is a 103 kW perma-
nent magnet electrical machine from Visedo
r
devel-
oped especially for heavy duty applications. It has six
polepairs and its nominal voltage is 500 V (VISEDO,
2014). The internal combustion engine is produced
by VM Motori
r
. It delivers a maximum torque of
340 N.m at 1400 rpm and its maximum produced
power is 70 kW (VMMotori, 2015). The hydraulic
motor is a Parker
r
V14 series with a displacement
that varies between 22 and 110 cm
3
(Parker, 2014).
Figure 1: BUSINOVA hybrid bus.
2.1 Hybrid Bus Drivetrain Architecture
The model of the studied hybrid bus is based on a
series-parallel power-split hybrid architecture. A sim-
ple block diagram of the power flows on the bus is
shown in Figure 2.
Figure 2: Block diagram of the drivetrain power flows.
(ICE: internal combustion engine, HP: hydraulic pomp,
HM: Hydraulic motor, EM: electric motor).
The electric and hydraulic motors are both directly
connected to the transmission and can ensure simul-
taneously or independently the traction of the bus. On
1
http://www.businova.com
Optimal Energy Management Strategy of Plug-in Hybrid Electric Bus in Urban Conditions
305

the other hand, the internal combustion engine is cou-
pled to a hydraulic pump for drivingthe hydraulic mo-
tor and therefore allowing the engine load shifting.
The rotational speeds of the hydraulic motor and the
electric motor are imposed by the wheels speed in
proportion to the reduction ratios of hydraulic and
electric motors respectively.
Moreover, the rotational speed ω
HM
and the torque
T
HM
of the hydraulic motor are expressed as a func-
tion of the rotational speed and the torque of the in-
ternal combustion engine as follows.
ω
HM
(T
ICE
,D
HM
) =
D
HP
.η
v
HM
.ω
ICE
D
HM
.η
v
HP
(1a)
T
HM
(T
ICE
,D
HM
) =
D
HM
.η
m
HM
.T
ICE
D
HP
.η
m
HP
(1b)
where ω
ICE
, T
ICE
are respectively rotational speed
and torque of the engine, and D
HM
, D
HP
, η
m
HM
, η
m
HP
,
η
v
HM
, η
v
HP
are respectively the displacements, me-
chanical efficiency and volumetric efficiency of the
hydraulic motor (HM) and the hydraulic pump (HP).
2.2 Control Oriented Model
The amount of residual energy of the battery, com-
monly represented by the estimation of the battery
state of charge SOC (Tang et al., 2015) or the bat-
tery state of energy SOE (Mura et al., 2015) is the
main dynamic state in optimal control of HEVs. In
particular, the state equation connects the variation
of the battery’s remaining energy to the control vari-
able of the system. In the formulation of the energy
management problem of the hybrid bus studied in this
paper, the SOE instead of the SOC, is considered as
the dynamic state x(t). There are several advantages
of using the estimated SOE to represent the battery
residual energy. Indeed, the energy loss on the inter-
nal resistance, the electrochemical reactions and the
decrease of the battery voltage are considered in the
SOE estimation (Xingtao et al., 2014). Based on the
previous assumption of using estimated SOE to rep-
resent the battery residual energy, the control oriented
model can be represented by:
˙x(t) = f (x(t), u(t), w(t)) (2)
where
x(t) = SOE(t), u(t) =
T
HM
ω
HM
, w(t) =
T
wheel
ω
wheel
(3)
u(t) is the control input and w(t) is an exogenous in-
put.
The above model can be rewritten as follows.
˙x(t) =
d SOE (t)
dt
= −
P
BAT
E
max
= −
P
EM
ηE
max
(4)
Depending on whether the battery is in discharg-
ing phase (
˙
SOE ≤ 0) or in charging phase (
˙
SOE ≥ 0),
η is defined as follows (Tremblay et al., 2007):
η =
η
BAT
in discharging phase
1/η
BAT
in charging phase
(5)
Equation (4) is obtained from the battery internal re-
sistance model (Tremblay et al., 2007). In this equa-
tion, E
max
is the maximum energy that can be stored
in the battery, η
BAT
is the efficiency of the battery,
P
BAT
is the power delivred by the battery and P
EM
is
the power consumed by the electric motor to produce
torque T
EM
at speed ω
EM
.
3 ENERGY MANAGEMENT
STRATEGY
The following section details the design procedure
of the proposed energy management strategy, which
aims to decide how to split the driver’s demanded
power between the different power sources of the hy-
brid drivetrain. This should allow to optimize the se-
lected criterion without sacrificing the bus drivabil-
ity. The optimal control problem formulation is firstly
presented and then the analytical expression of the
proposed solution is described. These power man-
agement strategy is based on Pontryagin’s minimum
principle.
3.1 Optimal Control Problem
Formulation
Since our primary goal is to minimize the energy con-
sumption of the bus, the energy management prob-
lem is formulated as an optimal control problem.
The objective is to find, at each sample time, the
optimal value of the control input that minimizes a
cost function representing the power consumption of
the drivetrain. This minimization of the cost func-
tion must be done under a certain number of con-
straints. In fact, the drivetrain components dimen-
sioning imposes minimum and maximum limits on
the exchanged powers. These limits form the follow-
ing constraints:
• The internal combustion engine and electric mo-
tor have limited operating ranges. Therefore, pro-
vided or absorbed torques must be comprised be-
tween minimum and maximum limits.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
306

T
min
EM
≤ T
EM
(t) ≤ T
max
EM
(6)
T
min
HM
T
min
ICE
,D
HM
≤ T
HM
≤ T
max
HM
(T
max
ICE
,D
HM
)
(7)
The maximum and minimum torque limits of
the internal combustion engine and electric motor
vary according to the variation of the system’s op-
erating point (torque-speed). Look-up tables are
therefore used to determine their values at each
time.
• The instantaneous power demand of the drivetrain
should always be satisfied, which results in,
ρ
1
T
HM
(T
ICE
,D
HM
) + ρ
2
T
EM
(t) − T
wheel
(t) = 0
(8)
where ρ
1
and ρ
2
are the gearbox’ reduction ratios
of hydraulic and electric motors respectively. The
total torque at the wheels is equal to the sum of
the torques delivered by each of the motors pro-
portionally to the reduction ratios.
Compared with energy management problem for-
mulation for charge sustaining HEV (Mura et al.,
2015), there is no sustainability constraint on the fi-
nal SOE for plug-in HEV allowing the charge de-
pleting operation. Thus, the energy consumed on the
entire cycle does not come exclusively from the fuel
since most of the available electrical energy is sup-
plied from the grid. This implies that the cost func-
tion must take into account all the energy sources used
to ensure the traction of the bus. This is why the
cost function J to be minimized over the time inter-
val [t
i
, t
f
] is defined based on the total electric and
fuel energy consumed by the vehicle as follows.
J=
Z
t f
ti
P
F
(u(t)) + P
BAT
(u(t))dt (9)
where P
F
is the instantaneous power of the fuel (en-
gine power input). As in several other papers dealing
with this topic (Mura et al., 2015), it is expressed in
terms of the fuel flow rate ˙m
f
and the lower heating
value of the fuel (Q
LHV
= 43MJ/kg) using the formu-
lation given in equation (10).
P
F
( u(t)) = ˙m
f
(u(t)) Q
LHV
(10)
The control variables (T
HM
and ω
HM
) are linked
together trough the hydraulic motor dynamics, there-
fore, there can only be one target control value at a
time. In this paper, we have chosen to leave the rota-
tion speed free so that it will be imposed by the wheels
speed. The hydraulic motor torque is thus the only re-
maining control variable that can be used to decide
how to split the driver’s demanded power.
The optimization problem is then to find the hy-
draulic torque that should be provided at every sample
time in order to minimize the total energy consumed
while checking the constraints thus mentioned above
(cf. equations (6) to (8)). To these constraints it is
added a new constraint (11) which aims to limit the
admissible control region in order to take into account
the limits of the hydraulic motor dynamics and conse-
quently taking into account the limits of the internal
combustion engine dynamics.
dT
HM
dt
− ξ ≥ 0 (11)
with ξ is the maximum hydraulic torque variation
measured over a short period of time.
To introduce constraints in the optimization prob-
lem, these are transformed into equality constraints.
The constraint (11) can be rewritten as follows (Wang
and Wah, 1998).
dT
HM
dt
− ξ−
˙
ε
2
= 0 (12)
where ε is a slack variable.
By using equation (8), it is possible to rewrite the
constraints (6) and (7) as a single constraint on the
control variable as follows.
˜
T
min
HM
T
min
HM
,T
max
EM
≤ T
HM
≤
˜
T
max
HM
T
max
HM
,T
min
EM
(13)
with
˜
T
min
HM
= max(ρ
1
.T
min
HM
,T
wheel
− ρ
2
.T
max
EM
) (14)
˜
T
max
HM
= max(ρ
1
.T
max
HM
,T
wheel
− ρ
2
.T
min
EM
) (15)
It means that when the torque applied to the wheel
is too significant to be only produced by the electric
motor, the
˜
T
min
HM
limit imposes a minimum torque on
the hydraulic motor. Additionally,
˜
T
max
HM
limit prevents
the electric motor torque set-point to become less than
T
min
EM
.
Finally, using a 2
nd
order approximation, the con-
straint (13) is written as the equivalent form given by
(16),
−T
2
HM
+ αT
HM
+ β = 0 (16)
with
α=
˜
T
max
HM
−
˜
T
min
HM
(17)
β=
˜
T
max
HM
.
˜
T
min
HM
(18)
Optimal Energy Management Strategy of Plug-in Hybrid Electric Bus in Urban Conditions
307
3.2 Energy Management Algorithm
With the optimization problem fully defined, Pontrya-
gin’s minimum principle can be used to give numer-
ical solution. According to Pontryagin’s minimum
principle, minimizing the cost function given in (9)
is equivalent to minimizing the Hamiltonian function
H of the system at each instant of time.
H (x(t), u(t), λ(t)) = P
F
ρ
1
T
HM
(t),
1
ρ
1
ω
HM
(t)
−
λ(t)
ηE
max
− 1
P
ME
ρ
2
T
EM
(t),
1
ρ
2
ω
EM
(t)
(19)
where λ(t) is the costate (or the Langrange multi-
plier).
For the considered energy management problem,
an extended Hamiltonian function is defined to ac-
count for the constraint (12) and (16). The additional
terms are introduced using a new Lagrange multiply-
ers (i.e., γ(t) et σ(t) respectively).
H (x(t), u(t), λ(t), γ(t) , σ(t)) =
P
F
ρ
1
T
HM
(t),
1
ρ
1
ω
HM
(t)
−
λ(t)
ηE
max
− 1
P
ME
ρ
2
T
EM
(t),
1
ρ
2
ω
EM
(t)
+γ(t)
−T
2
HM
+ αT
HM
+β) + σ(t)
dT
HM
dt
− ξ
2
(20)
The optimal control law which minimize the
Hamiltonian H must satisfy the following necessary
conditions for optimality:
∂H(t)
∂u(t)
=
∂H(t)
∂T
HM
(t)
= 0 (21)
−
∂H(t)
∂x(t)
= −
∂H(t)
∂SOE(t)
=
˙
λ
∗
(t) (22)
∂H (t)
∂λ(t)
= ˙x
∗
(t) (23)
∂H(t)
∂γ(t)
= −T
2
HM
+ αT
HM
+ β = 0 (24)
∂H(t)
∂σ(t)
=
dT
HM
dt
− ξ
2
=
˙
ε (25)
The costate λ is determined by the condition (23).
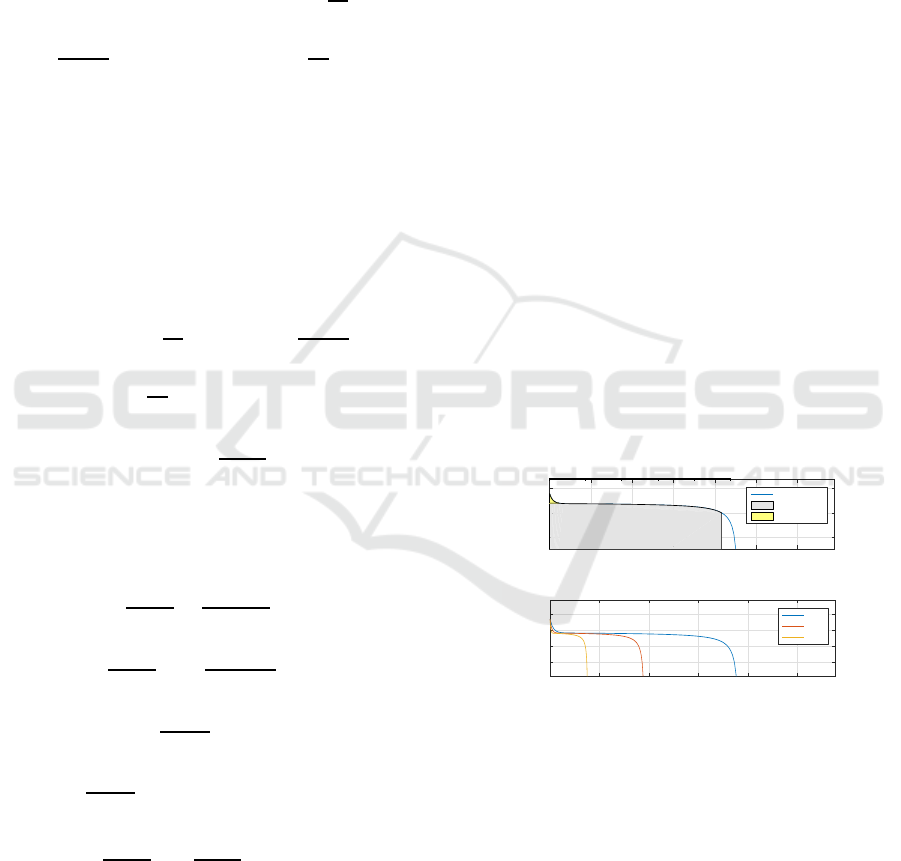
While taking into account the battery discharge
characteristics shown in Figure 4, it is clear that bat-
tery voltage is relatively independent on the battery
state of energy SOE and thus the power consumed by
the electric motor P
EM
(t) is also independent on the
battery SOE (Kirk, 2012) (Lino and Sciarretta, 2007).
Under this assumption, it is straightforward to con-
sider that the costate λ is a constant value during the
entire driving cycle since the derivative of the Hamil-
tonian function H in (23) is null in this case.
The condition (21) determines the optimal control
trajectory T
∗
HM
(t). If this necessary condition is sat-
isfied, then the optimal hydraulic torque T
∗
HM
(t) must
be given by equation (26).
T
∗
HM
(t) = arg min
T
HM
∈U
H(SOE (t),T
HM
(t),λ(t))
(26)
where U is defined as the admissible control set.
After the hydraulic motor torque is obtained, the in-
ternal combustion engine torque and speed are calcu-
lated according to the desired speed and torque of the
hydraulic motor. Thanks to the displacement tuning
capability of the hydraulic motor, the internal com-
bustion engine load can be shifted freely to operate
this latter close to its maximum efficiency curve. Es-
pecially in this case, the speed of the internal combus-
tion engine is not imposed by the wheels speed and it
can be set to a nearly constant value where the engine
is the most efficient. To reach this goal, the displace-
ment of the hydraulic motor is controlled online by
using equation (1a). Thereafter, the engine torque is
calculated as a function of the displacement and the
optimal torque of the hydraulic motor by using equa-
tion (1b).
Time (hours)
0 0.5 1 1.5 2 2.5 3
Voltage (Volts)
400
500
600
Nominal Current Discharge Characteristic at 108.6957 Amperes
Discharge curve
Nominal area
Exponential area
Time (hours)
0 10 20 30 40 50
Voltage (Volts)
450
500
550
600
Fully Charged Voltage: E0 = 581.6883 Volts, Internal Resistance: R = 0.02 Ohms
6.5 A
13 A
32.5 A
SOE
020406080100
Figure 3: Discharge characteristics of the used battery.
The energy management strategy could have
greater potential for power savings if an optimal speed
profile is predicted for each trip of the bus based on
the actual driving conditions. Indeed, buses run on the
same route every day, stop invariably at similar loca-
tions and they could even have some dedicated lanes
of the road in some cities which facilitates driving
conditions prediction compared to other type of vehi-
cles. Therefore, several studies have been conducted
to optimize bus speed profiles (Dib et al., 2014). With
this approach in mind and to further improve the en-
ergy management strategy proposed in this paper, a
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
308
control scheme that uses the information on the op-
timal speed profile is proposed in order to configure
the energy management algorithm developed previ-
ously. Therefore, the optimal speed profile is first de-
termined by using a dedicated speed profile optimiza-
tion algorithm based on a predictive intelligent con-
trol (Gunter et al., 2016). Thereafter, at the beginning
of each new trip of the bus, the obtained optimal speed
profile is utilized to search iteratively, using a shoot-
ing search method (Serrao et al., 2011), the value of
the costate λ that generates the correct final SOE
f
at
the end of the daily duty time of the bus. In fact, for
a given driving cycle there exists only one value of
the costate for which the solution that minimizes the
Hamiltonian H at each sample time is also the one that
satisfies the terminal condition on the final value of
SOE. This corresponds to the global optimal solution
of the problem. The obtained overall energy manage-
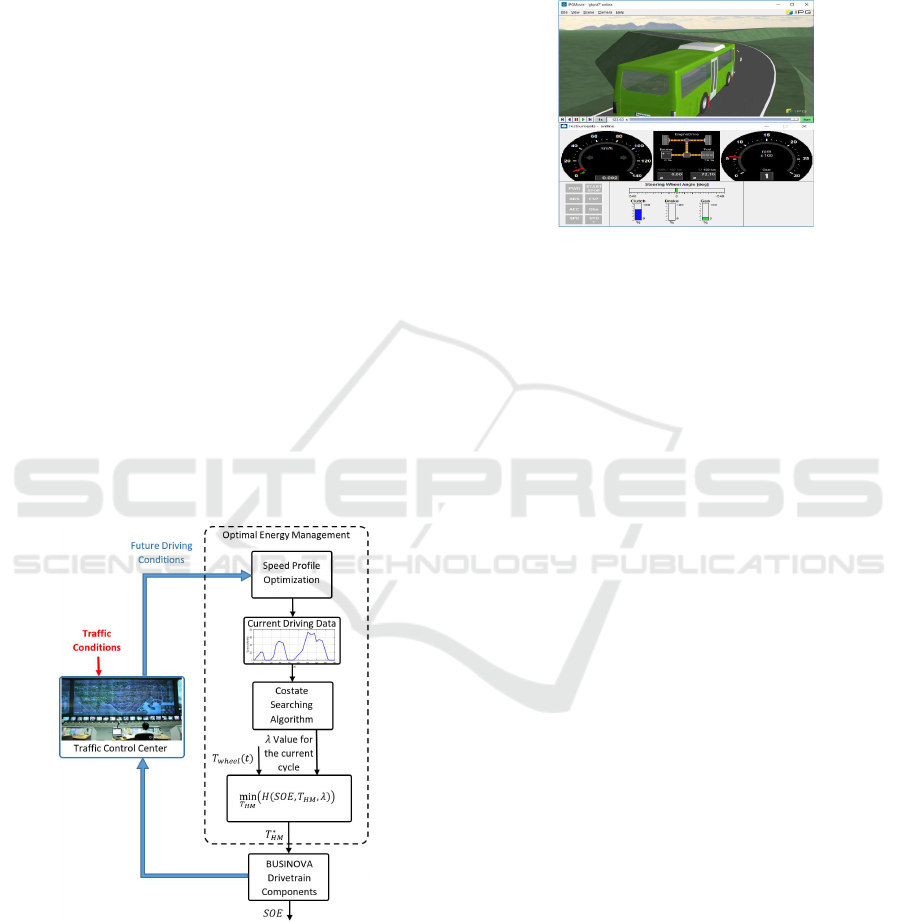
ment scheme is illustrated in Figure 4. As stated be-
fore, the choice of the costate value must be made to
ensure, in each trip of the bus, a charge-depleting rate
which allows to reach desired final SOE
f
at the end
of a full day driving period. In this paper, it is con-
sidered that the initial value of SOE is 90% and the
desired final value of SOE after eight hours of driving
is 17%. The working hypothesis behind this assump-
tion is to use the maximum amount of energy that can
be consumed from the battery in one day driving.
Figure 4: Block diagram of the proposed power manage-
ment strategy.
4 SIMULATION RESULTS
The implementation of the proposed energy manage-
ment strategy is carried out using a dedicated high-
fidelity model of the hybrid bus, that was developed
on Matlab/TruckMaker software (cf. Figure 5), in or-
der to investigate their performance in a test platform
which reproducesaccurately the real operating behav-
ior of the bus.
Figure 5: TruckMaker test platform.
Figure 6 shows the overall simulation results
of the proposed energy management strategy over
an optimized driving cycle which represents differ-
ent usage conditions of the studied hybrid electric
bus including urban and extraurban driving environ-
ments. The video showing this overall demonstra-
tion using TruckMaker is available from this link:
https://goo.gl/8mJT3s.
Figure 6(a) gives an outline of the desired speed
and the actual bus speed when the designed opti-
mization algorithm is applied to calculate the optimal
power split. As one can observe in this figure, the bus
speed follows the reference speed curve with only a
small tracking error. This observed speed tracking er-
ror is due to the important response time of the mo-
tors. The contribution of the fuel energy and the elec-
tric energy to the total power and torque at the wheels
is illustrated in Figure 6(b) and 6(c) respectively. The
SOE profile is also illustrated in Figure 6(d). Accord-
ing to Figure 6 (b), it is shown that the distribution of
the power demand between the electric motor and the
hydraulic motor is correctly assured and the required
power at the wheels is totally satisfied over the entire
driving cycle. The dynamic limits of the motors de-
fined during the synthesis of the energy management
strategy are also respected as can be seen in these fig-
ures. Since the driving cycle is known in prior, the
proposed energy management strategy finds the op-
timal power split which operates the engine around
its maximum efficiency curve to minimize the power
consumption of the drivetrain. The fluctuation range
of the power delivered by the engine is directly related
to the amount of electric energy available for electric
assist and it allows to always satisfy the constraints of
the final SOE of the battery. A battery discharge of
0.45% is observed at the end of the driving cycle sim-
Optimal Energy Management Strategy of Plug-in Hybrid Electric Bus in Urban Conditions
309
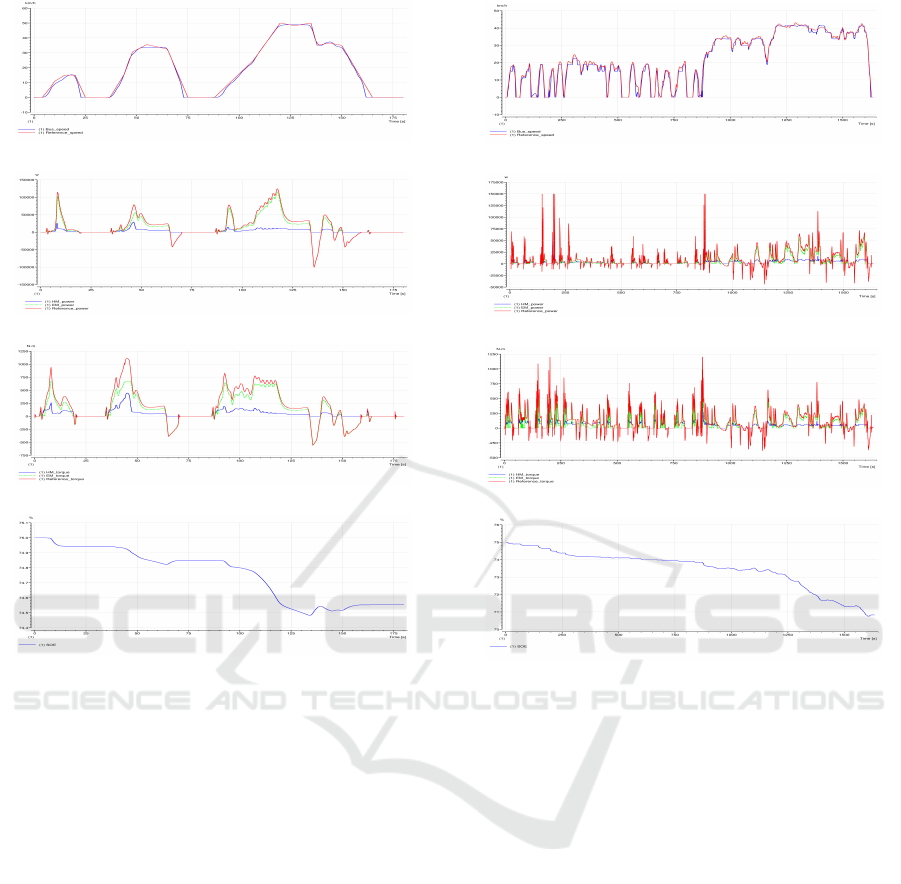
(a)
(b)
(c)
(d)
Figure 6: Simulation results of the proposed energy man-
agement strategy: (a) driving cycle, (b) power distribution
profile, (c) torque distribution profile, (d) SOE profile.
ulated in this test, which corresponds, by extrapola-
tion, to a discharge from 90% to 17% after 8 hours
driving period. Otherwise, the energy management
strategy doesn’t use the engine to charge the battery,
because its efficiency is too low and thus recharg-
ing the battery using fuel energy is not cost-effective.
deepen the analysis under more realistic and ex-
haustivetest conditions, the proposed energy manage-
ment algorithm is evaluated over the FTP-75 (Federal
Test Procedure) normalized driving cycle. This cy-
cle includes acceleration and deceleration phases in
urban and suburban environments. It thus constitutes
an interesting study support for evaluating the perfor-
mance of the energy management strategy in the dif-
ferent phases of operation of the real hybrid bus. The
results obtained from this test are presented in Figure
7.
(a)
(b)
(c)
(d)
Figure 7: Simulation results of the energy management al-
gorithm on the FTP-75 driving cycle: (a) driving cycle, (b)
power distribution profile, (c) torque distribution profile, (d)
SOE profile.
5 CONCLUSION
An optimal energy management strategy, based on
Pontryagin’s minimum principle, is designed in this
paper for a a plug-in multi hybrid bus. The proposed
approach combines the system’s dynamical equations
with the control objectives formulated in the form
of a cost function and constraints to determine at
each instant the optimal value of the control variable
which minimizes the power consumption of the hy-
brid bus. Furthermore, based on the characteristics
of the studied urban bus, which runs generally on the
same routes, the energy management strategy is fur-
ther improved by searching the optimal driving cycle
for each bus trip while using the available traffic infor-
mation. The final battery SOE level is also controlled
by selecting an appropriate value of the costate at each
time the bus starts a new lap. The validation tests re-
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
310

sults show that the proposed optimization approach
can ensure optimal operation for the hybrid bus while
having the advantage of being very simple to imple-
ment in practice thanks to its high computational ef-
ficiency. Nonetheless, to achieve this performance
level, good accuracy for estimating road traffic con-
ditions is required. In future works, additional opti-
mization criterion such as: reduction of battery aging
and pollutant emissions will be added to the already
existing optimal control algorithm. The tradeoff be-
tween the different optimization criteria will be inves-
tigated in order to achieve the most efficient drivetrain
operation.
ACKNOWLEDGEMENTS
This project is supported by the ADEME (Agence
De l’Environnement et de la Matrise de l’Energie) for
the national french program: Investissement d’Avenir,
through BUSINOVA Evolution project.
REFERENCES
Dib, W., Chasse, A., and Moulin, P. (2014). Optimal energy
management for an electric vehicle in eco-driving ap-
plications. In Control Engineering Practice, vol. 29.
IEEE.
Fengjun, Y., Junmin, W., and Kaisheng, H. (2012). Hybrid
electric vehicle model predictive control torque-split
strategy incorporating engine transient characteristics.
In Transactions on Vehicular Technology. IEEE.
Gunter, H., Marcus, S., Uli, W., and Oliver, S. (2016).
Predictive planning of optimal velocity and state of
charge trajectories for hybrid electric vehicles. In
Journal of Control Engineering Practice. Elsevier.
Johannesson, L., Asbogard, M., and Egardt, B. (2007). As-
sessing the potential of predictive control for hybrid
vehicle powertrains using stochastic dynamic pro-
gramming. In Transactions ITSC, vol. 8, no. 1. IEEE.
Kamal, E., Adouane, L., Abdrakhamanov, R., and Ouddah,
N. (2017). Hierarchical and adaptive neuro-fuzzy con-
trol for intelligent energy management in hybrid elec-
tric vehicles. In IFAC World Congress. Elsevier.
Kirk, D. (2012). Optimal Control Theory: An Introduction.
Dover, NY, USA, 2nd edition.
Lino, G. and Sciarretta, A. (2007). Vehicle propulsion sys-
tems. Springer-Verlag Berlin Heidelberg, Berlin, vol.
1 edition.
Mashadi, B. and Emadi, S. (2010). Dual-mode power-split
transmission for hybrid electric vehicles. In Transac-
tions on Vehicular Technology. IEEE.
Mi, C., Masrur, A., and Gao, D. W. (2011). Plug-in hybrid
electric vehicles, in Hybrid Electric Vehicles: Prin-
ciples and Applications With Practical Perspectives.
Wiley, NY, USA, 2nd edition.
Moura, S. J., H. Fathy, D. C., and Stein., J. (2011). A
stochastic optimal control approach for power man-
agement in plug-in hybrid electric vehicles. In Trans-
actions on Control Systems Technology, vol. 19, no. 3.
IEEE.
Mura, R., Utkin, V., and Onori, S. (2015). Energy man-
agement design in hybrid electric vehicles: A novel
optimality and stability framework. In Transactions
On Control Systems Technology, Volume: 23, Issue:
4. IEEE.
Parker (2014). Parker hy30-8223/uk catalogue. In :
https://goo.gl/bExyDj.
Serrao, L., Onori, S., and Rizzoni, G. (2011). A compara-
tive analysis of energy management strategies for hy-
brid electric vehicles. In Journal of Dynamic Systems,
Measurement, and Control, vol. 133, no 3. IEEE.
Tang, L., Rizzoni, G., and Onori, S. (2015). Energy man-
agement strategy for hevs including battery life opti-
mization. In Transactions on Transportation Electri-
fication.
Teng, L., Yuan, Z., De-xing, L., and Feng-chun, S. (2014).
Real-time control for a parallel hybrid electric vehicle
based on pontryagin’s minimum principle. In Confer-
ence and Expo in Transportation Electrification Asia-
Pacific.
Tremblay, O., Dessaint., L., and Dekkiche, A. (2007). A
generic battery model for the dynamic simulation of
hybrid electric vehicles. In Vehicle Power and Propul-
sion Conference. IEEE.
VISEDO (2014). Visedo powerdrum pdr-xxs-3200-t310
technical features. In : https://goo.gl/Bg1q4q.
VMMotori (2015). Vm motori vm-r754eu5-05d/4 technical
features. In : https://goo.gl/7oLVD3.
Volkan, S., Metin, G., and Seta, B. (2011). A novel ecms
and combined cost map approach for high-efficiency
series hybrid electric vehicles. In Transactions on Ve-
hicular Technology, vol. 60, no 8. IEEE.
Wang, T. and Wah, B. (1998). Handling inequality con-
straints in continuous nonlinear global optimization.
In Journal of Integrated Design and Process Science,
vol. 2, no 3. iospress.
Wu, G., Boriboonsomsin, K., and Barth, M. (2014). De-
velopment and evaluation of an intelligent energy-
management strategy for plug-in hybrid electric ve-
hicles. In Transactions on Intelligent Transportation
Systems, vol. 15, no 3. IEEE.
Ximing, W., Hongwen, H., Fengchun, S., and Zhang, J.
(2015). Application study on the dynamic program-
ming algorithm for energy management of plug-in hy-
brid electric vehicles. In vol. 8, no 4. Energies.
Xingtao, L., W. Ji, Z. C., and Zonghai, C. (2014). A method
for state of energy estimation of lithium-ion batteries
at dynamic currents and temperatures. In Journal of
Power Sources, vol. 270. Elsevier.
Optimal Energy Management Strategy of Plug-in Hybrid Electric Bus in Urban Conditions
311
