
Adaptive Neural Control for Bilateral Teleoperation System using
External Force Approach
Outayeb Adel Mohamed, Ferguene Farid and Toumi Redouane
LRPE Laboratory, Automatic and Instrumentation Department, U.S.T.H.B University,
BP n°32, El Alia-Bab Ezzouar, 16111 Algiers, Algeria
Keywords: Bilateral Teleoperation, External Force Control, Adaptive Control, Identification, Neural Network,
Estimation Parameter.
Abstract: The paper deals with external force control approach based on four channel scheme, that is reported in
previous paper (Outayeb et al., 2016). The problem of controlling bilateral teleoperation system under
disturbances due mainly to unknown environment, dynamic robot uncertainties and in presence of noisy
measurement of force sensors is considered. The Control Algorithms are obtained on two control strategies,
the first one consists on a force/Impedance control approach applied to the master robot, whereas the second
one consists on external force control loop combined with position control loop applied to the 3-DOF
nonlinear slave robot. A neural network (NN) compensator and online environment estimation based on
forgetting factor recursive least squares method (FFRLS) are integrated, to eliminate the effects of
uncertainties in dynamic model of the slave robot, as well as, to estimate the unknown time varying
characteristics of the environment under noisy measurements of force sensors. Numerical simulations using
Labview show the efficacy of proposed scheme to guarantee system stability and acceptable transparency
performance.
1 INTRODUCTION
Teleoperation is sometimes associated with
manipulation of environments that are too distant or
inaccessible to man, but also to interact with small
area like human body cavity to improve surgical
performances in terms of less invasive operations and
more confortable positions.
A teleoperation system consists of a teleoperated
robot (slave device) controlled by a local control
station equipped with haptic interface for the
reproduction of the effort applied at the remote site
(master device) via a telecommunication channel.
The two major issues in teleoperation are stability
robustness which may constitute a problem
especially in presence of time delays in the
communication and transparency performance which
mean that operator should feel as he is directly acting
in the remote site (Lawrence, 1993).
There exist various kinds of control schemes for
teleoperation systems. In theory and under ideal
conditions, four-channel and even three-channel
control architectures offer perfect transparency with
linear model of master and slave robots (Lawrence,
1993; Zaad and Salcudean, 1999). However in some
of these structure both position and force signals are
transmitted from one site to another. Therefore,
measurement of force in both sides is inevitable to
ensure full transparency. By consequence mounting
force sensors on robots causes some limitations such
as high expense, increasing noise and soft structure
(Ohnishi et al., 1994; Dehghan et al., 2014).
Unfortunately, an ideal transparent bilateral
teleoperation system cannot be conceived without
compromising stability, which highly depends on the
robustness of the control scheme implemented under
disturbances due mainly to unknown characteristics
of the environment, the dynamics of robots and
delays in communications (Park and Cho, 1999; Ye
et al., 2013; Artigas et al., 2011).
For this reason, in the literature a number of
control schemes have been developed based on
different criteria including the passivity, compliance,
predictive and adaptive control considering either
linear or nonlinear models of manipulators. A
comparative study based on several approaches can
be found in (Arcara and Melchiorri, 2002).
This paper is organized as follows: section 2
Mohamed, O., Farid, F. and Redouane, T.
Adaptive Neural Control for Bilateral Teleoperation System using External Force Approach.
DOI: 10.5220/0006419603090315
In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 2, pages 309-315
ISBN: Not Available
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
309

presents the formulation of dynamical models of
constrained robots used in master and slave sites
respectively, specified in task space. In Section 3, we
demonstrate a control algorithms laws designed for
both master and slave stations. Moreover, neural
compensator is developed in this section, followed by
Section 4 which discusses an online estimation of
environment based on FFRLS algorithm. Finally,
simulation results are shown in Section 5 and
conclusion is drawn in section 6.
2 DYNAMIC MODELS
In this section, we consider a bilaterally controlled
teleoperator system where both the master and the
slave are 3-DOF with revolute joints, that dynamic
models are described as follows.
2.1 Dynamic Model of Slave Robot
Consider a nonlinear teleoperated manipulator
system consisting of 3-DOF with dynamics given by:
,
(1)
Where
is the inertia matrix,
,
is the
vector of Coriolis and centrifugal forces,
is the
gravity term and
is the generalized torque acting
on q. Defining the Jacobian as:
(2)
With
is the Cartesian velocity, and the acceleration
is given by
Substituting (2) and (3) in (1), and applying the
relation between the joint torque
and the
Cartesian force
at the end-effector,
,
the dynamic robot in contact with environment can
be written in Cartesian coordinates as
,
(4)
With
,
(6)
(7)
Where
is the vector of external forces appears at
the end-effector when the robot is in contact,
and
are respectively the forces due to the controlled
torque and friction.
2.2 Dynamic Model of Master Robot
The geometric form of master robot is identical to the
slave robot. Unless it is characterized by known
linear dynamic model which is represented by the
following equation:
(8)
Where
,
and
refers the impedance
characteristic of this robot in the joint
space.Reformulating this end into Cartesian space
and applying the same manner as below, the model
equation is given as :
(9)
Where
is the force applied by the operator on
end-effector master interface.
3 CONTROLLER DESIGN
This section is carried out to present a proposed
control scheme based on the Force/Impedance
controller applied at the master, and the
Force/Position control loop using external force
approach developed to the slave device.
3.1 Master Controller
The block diagram of proposed controller is shown in
(Fig. 1), The force/impedance control is designed to
obtain desired behavior of the manipulator described
by the following relationship between end-effector
motion and applied force exerted by the operator
Where
,
represent the desired inertia and
damping respectively,
is the force recovered from
noisy force sensors measured in the remote site.
Given the manipulator dynamics and in order to
achieve the desired impedance behavior, an inverse
dynamics control law can be proposed as
1
Where the hats denote the available estimates of the
corresponding dynamic terms, this controller is
operational in either free or constrained space, by
taking account the correction of the error occurred in
the positioning of the local robot when the slave
robot is constrained by the environment.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
310
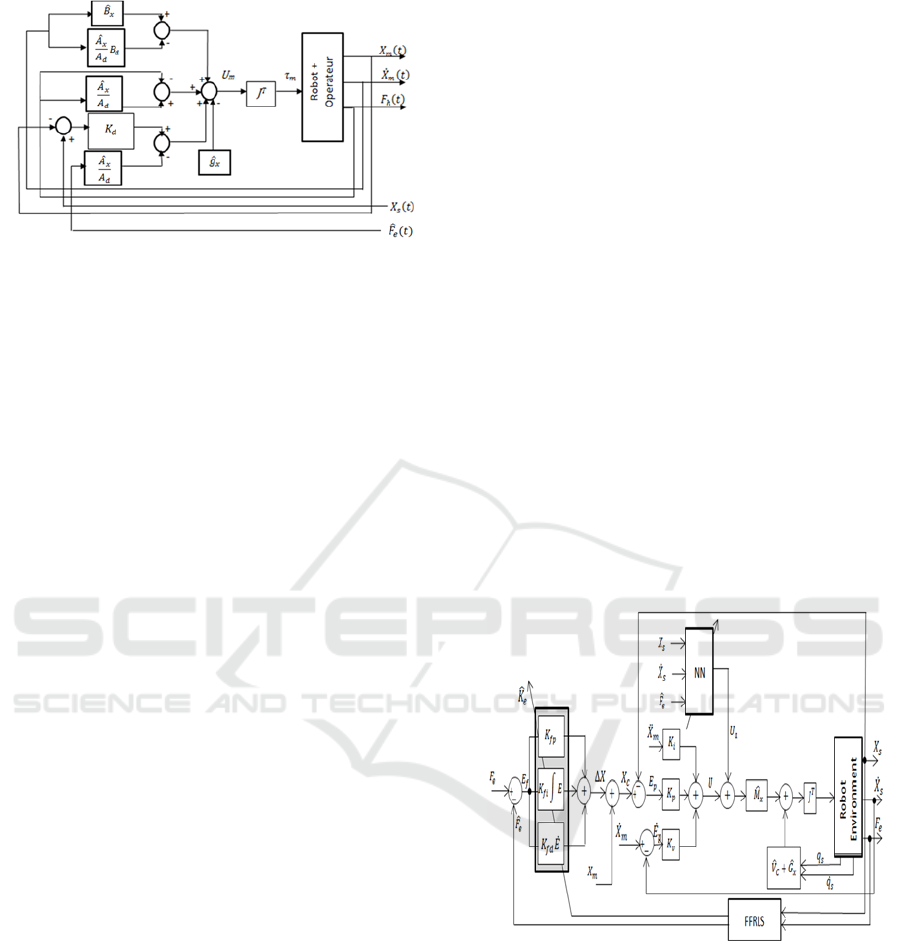
Figure 1: Force/Impedance control structure for the master
interface.
3.2 Slave Controller
An adaptive force/position control scheme is
developed in this section according to the external
force control concept proposed in literature (Schutter
and Van Berussel, 1988), where we take into account
the uncertainty dynamics of slave robot, unknown
location of the object, variable stiffness of the
environment and noisy quality of force sensor. For
this end, we have integrated two complementary
techniques based on a neural compensator and a
FFRLS method described later.
Where the hats denote the available uncertain
estimates of the dynamic terms
,
,
and
is
the signal force recovered from noisy measured
force sensor, by applying the online environment
estimation method that will be discussed in section
4.
By following the external force control approach,
is designed to assure a compliant motion by
feeding the error between desired force
and actual
force
into the force controller, this contact force
acts as correction which will modify the desired
trajectory applied to the position control loop, so:
(13)
With
∆
∆
Where ∆
presents the correction of desired
position
Namely, as (Chiaverini and Sciavesco, 1999) the
dynamic model of the slave represents a highly
nonlinear and strongly coupled system for which the
nonlinear dynamic decoupling approach can be
adopted. The closed loop dynamic equation can be
rewritten as
∆
(14)
∆
∆
∆
∆
With
∆
When ∆ denotes the uncertainty terms.
The Neural compensator output
, described
later, is trained to minimize the uncertainty terms
in14.
let
(15)
Since the control objective is to generate
to
reduce to zero. We propose here to use as the
error signal for training the neural network.
In the ideal case (
0 the output of the neural
compensator is required to be
∆
∆
∆
∆
(16)
The slave controller is schematized by the following
diagram
Figure 2: Adaptive structure of external Force controller
loop combined with FFRLS estimator and NN
compensator for the Slave manipulator.
3.3 Neural Network Compensator
Design
The network model selected in this paper in order to
implement the proposed artificial neural network
compensator is a three layer network structure (see
Fig.3) which is composed of a linear input layer I =
[X
t
X
t
F
t
], a non-linear hidden layer of
sigmoid type expressed by the following equation:
Adaptive Neural Control for Bilateral Teleoperation System using External Force Approach
311

2
1
1
(17)
And an output layer of linear processing unit.
Therefore, the input-output relationship of the
network is
2
1
∑
1
(18)
Where,
are the weights between the input layer
and the hidden layer,
are the weights between
the hidden layer and the output layer,
is the bias of
the j-th neuron in the hidden layer and
is the bias
of the k-th neuron in the output layer.
Figure 3: Structure of Neural Network Compensator
The goal is to generate an auxiliary computed
torque
altering the training signal to be zero as
either
or
, and that is based on the
minimization of a quadratic function , where is
given by:
1
2
(19)
The weight updating law is obtained by using the
back-propagation algorithm of the gradient
(Ferguene and Toumi, 2005). This algorithm
consists of modifying a variable
in the opposite
direction to the derivative function of the error,
yields the gradient of as:
(20)
Where the weight adaptation law with a momentum
term is:
∆
∆
1
(21)
With is the update rate and is the momentum
coefficient. Explicitly, the resulting algorithm can be
derived by making use of (20).
∆
0.5
1
∆
1
(22)
∆
∆
1
∆
0.5
1
∆
1
∆
∆
1
4 ENVIRONMENT DYNAMIC
In this paper, we propose a good online estimation
algorithm that have objective to track and identify the
location and dynamic characteristics of any
constraints in a robot's workspace.
The model considered is not homogeneous in the
sense that it is manifested by a time varying
stiffness
. More specifically, this environment has
the following dynamics:
0.25∗
∗sin
∗
Where
is the position of the object at rest, and
is a
33
constant diagonal stiffness matrix. In
discrete domain, the environment dynamics can be
written as (Ljung, 1987):
,
0
(24)
Where the subscript k denotes the time instant,
,
,…,
is the measurement vector,
the vector of parameters,
the modeling error
and measurement noise,
the penetration at sample
time . , the parameter is the sample time.
4.1 Estimation Method of Unknown
Time Varying Parameter
For abruptly parameter identification, the use of RLS
method with periodic initialization of estimated value
can highly capture the new values of the parameter.
However for real time varying parameter estimation,
it is necessary to apply forgetting factor to RLS
algorithm. The concept of FFRLS algorithm has the
tracking ability as the covariance ceases to exist
gradually to zero with time, Hence this method can
be viewed as giving less weight to older data and
more weight to recent data. Smaller forgetting factors
will improve the tracking ability and can affect the
stability of the algorithm (Vahidi et al., 2005). The
“loss-function” is then defined as :
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
312

,
1
2
(25)
Where is called forgetting factor and01.
Obviously, small values for λ puts greater emphasis
on recent data and can be calculated recursively
using the update equations derived as follows:
1
(26)
1
(27)
With
1
1
(28)
1
(29)
is normally referred to as the covariance
matrix of parameters
. More detailed derivation
can be found in books on parameter estimation such
as (Astrom and Wittenmark, 1994).
5 SIMULATION
To check out the efficiency of the proposed
approach, two geometric identical 3-DOF rotary
manipulators are simulated, a slave robot whose
parameters are taken from the first three links of
Puma 560 arm (Armstrong and Khatib, 1986),
whereas a linear master robot whose parameters are
assumed to be known accurately. Model uncertainties
included a 5 Kg Mechanical tool attached to the third
link, Coulomb friction and viscous friction torques
added to each joint where
0.8
0.5
. For the NN compensator we have
chosen nine input neurons
9
and seven
hidden neurons
10
. The back propagation
algorithm parameters are: 0.001, 0.9.
Weights are initially randomly selected and adjusted
every sampling time in online fashion.
On the assumption of unknown geometric
proprieties of manipulated object and in order to
calculate an online estimation of their stiffness from
poor quality force sensors measurements, we apply a
FFRLS method with
0
0,
0
15000/,
0.975, The gains of controller law and the
desired Impedance are fixed experimentally by
,
40,
800
,
40
⁄
,
40
⁄
,
0.15,
400,
8000
Task space has object with flat surface and variable
stiffness which depends on time with:
∗
∗
∗
(30)
The test bed consists of master and slave robots
situated at positions
,
0.4115,0.150,0.4331
of different sites. Initially, the operator applies
constant force
through 3 directions on the end-
effector interface to move it with respect to the
desired impedance calculated above (10), while the
slave robot starts tracking the trajectory generated by
master interface until it crashes the object situated at
unknown position (supposed in our simulation at
0.45,0.21,0.55
). At this time, the
operator pushes the interface with sinusoidal force as
given by equation (31). The slave robot is being in
constrained space, so it moves with master’s position
and controls the force of interaction on the surface of
the object according to the force applied by the
operator, in this case, the slave robot will dominate a
force action over position action. By consequence,
different positions will generated and transmitted to
the master station in order to move it with respect to
slave robot position. The input signal of force applied
by operator is given by
001
813
82∗sin
6.28∗
35
857
07
(31)
In Figure 4, it’s obviously marked the quality of
recovered signal from noisy force sensors
measurements over 3 directions, and when
interacting with environment characterized by time
varying stiffness.
In Figures (5.1) and (5.2), the responses
illustrates that the whole system is stable and
guarantees equality between the force applied by the
operator and that applied to the environment.
Moreover, it presents a good tracking of both master
and slave trajectory either in free or constrained
space.
Considering fair results obtained compared with
those obtained in previous work. We conclude the
ability to investigate with complex methods
proposed for controlling a local manipulator, to
deals with more complicated problems in
teleoperation system.
Adaptive Neural Control for Bilateral Teleoperation System using External Force Approach
313
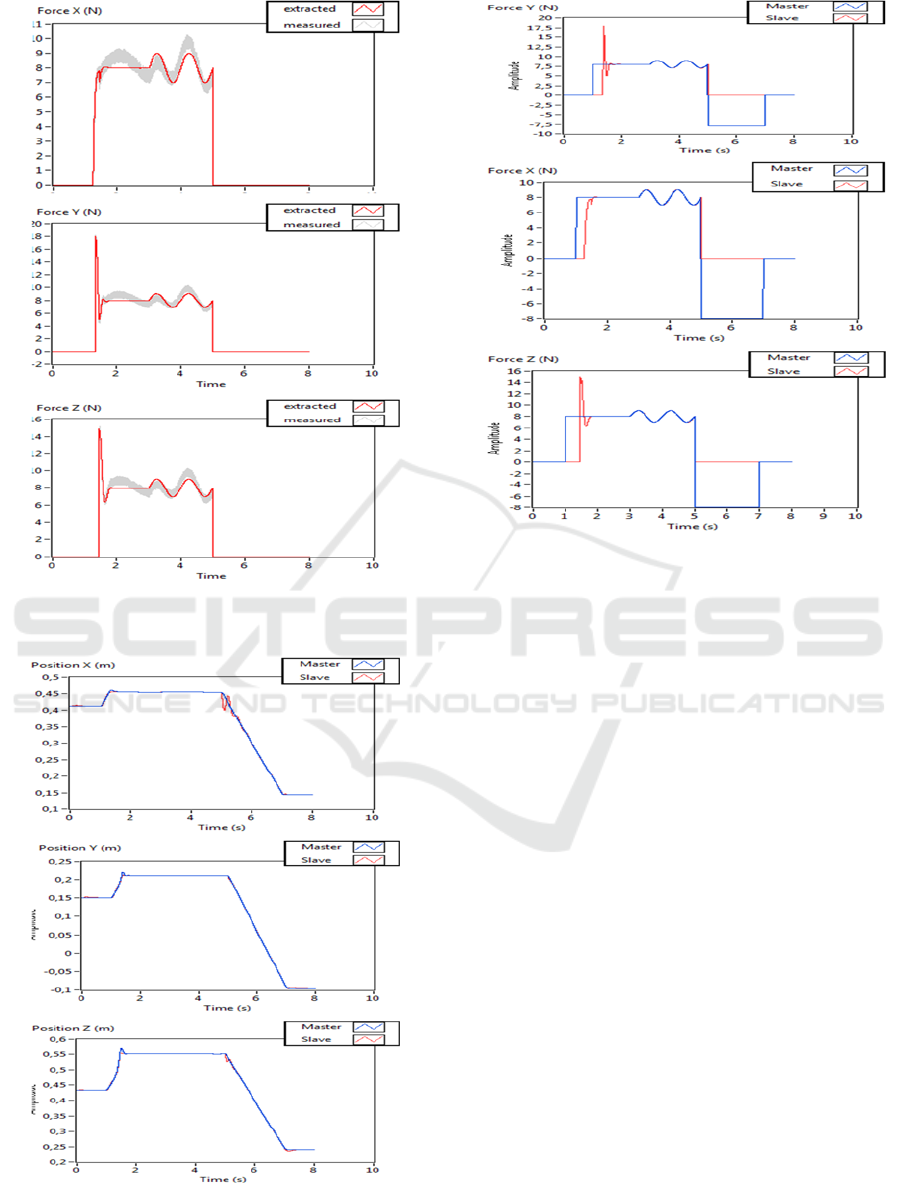
Figure 4: The recovered force signal and noise rejected
along X, Y and Z axis.
Figure 5.1: Position Tracking along X, Y and Z axis for
teleoperation system.
Figure 5.2: Force applied along X, Y and Z axis for
teleoperation system.
6 CONCLUSION
In this work, an adaptive force/position control
algorithm in bilateral teleoperation system is
developed, using an external force control approach,
taking advantage of four channel structure that we
have presented in previous work. Our approach is
based on force/impedance controller at the master
and external force control loop, combined with a
neural compensator and forgetting factor recursive
least square estimator at the slave.
The results of simulations obtained with our
proposed scheme are convincing and similar to those
reported in (Outayeb et al., 2016).
Whole
teleoperator system stability is guaranteed with
acceptable transparency performances, even when
there are the slave robot dynamic uncertainties,
unknown and variable environment stiffness, and
poor measurements of force sensors.
Studies are remained as a proposed future work
going along with designing more robust controller,
by considering a full unknown dynamic of slave
robot and environment.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
314

REFERENCES
Arcara P., Melchiorri C., 2002. Control schemes for
teleoperation with time delay : A comparative study.
Robotics and Autonomous Systems, 38(1):49–64.
Armstrong B., Khatib O., 1986 . The explicit dynamic
model and inertial parameters of the PUMA 560 arm ,
IEEE Int. Conf. on Robotics and Automation, San
Francisco –U.S.A, pp. 510-518.
Artigas J., Ryu J., Preusche C., and Hirzinger G., 2011.
Network representation and passivity of delayed
teleoperation systems, in Proc. IEEE/RSJ Int.Conf.
Intell. Robots Syst., pp.177–183.
Astrom A., and Wittenmark B., 1994. Adaptive Control.
Addison Wesley, second edition.
Chiaverini S., Sciavesco L., 1998. the parallel approach to
force/position control of manipulators in task space
with dominance in force, in Proc,2
nd
IFAC Symp.
Robot Contr. (SYROCO’88), Karlsruhe, D, Oct. pp.
137-143
Dehghan S. A. M., Danesh M., and Sheikholeslam F.,
2014. Adaptive hybrid force/position control of robot
manipulators using an adaptive force estimator in the
presence of parametric uncertainty, Advanced
Robotics,.
Ferguene F., Toumi R., 2005. A Neural Approach to
Force/Position Parallel Control of Robotic
Manipulators Application to the Follow-up of
Trajectory in Unknown Stiffness Environment, in
Proc. International computer systems and information
technology conference Vol. N°1, pp. 247-251 ,
Algiers, Algeria.
Lawrence D.A., 1993. Stability and transparency in
bilateral téléopération. IEEE Trans. on Rob and Aut.
9(5), 624–637.
Ljung L., 1987 . System identification : Theory for the
user , Linkoping University, Sweden, PTR Prentice
Hall.
Ohnishi K., Matsui N., and Hori Y., 1994. Estimation,
identification, and sensorless control in motion control
system , Proc. IEEE, vol. 82, no.8, pp. 1253–1265.
Outayeb A., Ferguene F., Toumi R., 2016 . Bilateral
control of nonlinear teleoperation system using
parallel force/position control approach and online
environment estimation. In: IEEE Int. Conf. On
Methods and Models in automation and robotics
(MMAR’2016), pages 1110–1115, Międzyzdroje,
Poland.
Park J.H., and Cho H.C., 1999. Sliding-mode controller
for bilateral teleoperation with varying time delay. In:
IEEE Int. Conf. on Adv. Intell. Mechatronics. Atlanta,
GA.pp. 311–316.
Schutter J., Van Berussel H., 1988. Compliant robot
motion II. A control approach based on external
control loop , Int. Journal of Robotics Research, Vol.
n°4, pp. 18-33.
Vahidi A., Stefanopoulou A., and Peng H., 2005.
Recursive Least Squares with Forgetting for Online
Estimation of Vehicle Mass and Road Grade: Theory
and Experiments. Vehicle System Dynamics, vol. 43,
no. 1, pp. 31-55.
Ye Y., Pan Y.J., and Hilliard T., 2013. Bilateral
teleoperation with time-varying delay: A
communication channel passification approach,
IEEE/ASME Trans. Mechatronics, vol. 18, no. 4, pp.
1431–1434.
Zaad H.K., Salcudean, S.E., 1999. On the use of local
force feedback for transparent teleoperation. Proc. of
the IEEE Int. Conf. On Robotics and Automation
(ICRA’99), pages 1863–1869, Detroit, Michigan,
USA.
Adaptive Neural Control for Bilateral Teleoperation System using External Force Approach
315
