Short-Term Traffic Prediction under Both Typical and Atypical

Traffic Conditions using a Pattern Transition Model

Traianos-Ioannis Theodorou

1,2

, Athanasios Salamanis

, Dionysios D. Kehagias

, Dimitrios Tzovaras

and Christos Tjortjis

Information Technologies Institute, Centre for Research & Technology Hellas, GR 57001 Thermi-Thessaloniki, Greece

International Hellenic University, GR 57001 Thermi-Thessaloniki, Greece

Keywords: Short-Term Traffic Prediction, Atypical Conditions, Automatic Incident Detection, Support Vector Machines,

K-Nearest Neighbour, Autoregressive Integrated Moving Average.

Abstract: One of the most challenging goals of the modern Intelligent Transportation Systems comprises the accurate

and real-time short-term traffic prediction. The achievement of this goal becomes even more critical when the

presence of atypical traffic conditions is concerned. In this paper, we propose a novel hybrid technique for

short-term traffic prediction under both typical and atypical conditions. An Automatic Incident Detection

(AID) algorithm, based on Support Vector Machines (SVM), is utilized to check for the presence of an

atypical event (e.g. traffic accident). If such an event occurs, the k-Nearest Neighbors (k-NN) non-parametric

regression model is used for traffic prediction. Otherwise, the Autoregressive Integrated Moving Average

(ARIMA) parametric model is activated for the same purpose. In order to evaluate the performance of the

proposed model, we use open real world traffic data from Caltrans Performance Measurement System

(PeMS). We compare the proposed model with the unitary k-NN and ARIMA models, which represent the

most commonly used non-parametric and parametric traffic prediction models. Preliminary results show that

the proposed model achieves larger accuracy under both typical and atypical traffic conditions.

1 INTRODUCTION

Nowadays, the interest in developing Intelligent

Transportation Systems has grown significantly with

respect to the need for providing qualitative

transportation services, either for individuals or fleets

of vehicles. In this context, the ability to accurately

predict traffic in various steps ahead in time is of

paramount importance.

The main reason, for which the traditional traffic

prediction models fail to accurately predict traffic in

real conditions is the presence of atypical conditions.

These may include severe weather conditions, car

accidents, road maintenance works and traffic

congestion, due to special cultural events (e.g.

concerts or sport games). These atypical conditions

often result in steep spikes in the traffic time series

that the standard traffic prediction models fail to

accurately represent, as these models are based on big

traffic data with insignificant abnormalities.

Also, atypical events are difficult to classify

because they vary in type, duration, severity, effect on

the state of the traffic network, etc. On the other hand,

incidents may occur that do not cause observable

effects on traffic. Similarly, the occurrence of spikes

in a traffic time series does not necessarily correspond

to atypical conditions. These cases render the

problem of traffic prediction in atypical conditions as

a non-trivial one.

In this paper, we present a novel pattern transition

model for short-term traffic prediction for typical, as

well as (and more importantly) atypical conditions.

We use an SVM-based automatic incident detection

model to automatically detect the presence of an

atypical situation. When this case occurs, the non-

parametric k-NN regression model is fetched to

calculate the predicted traffic value. Otherwise, the

ARIMA parametric model is activated.

In summary, our main contributions can be outlined

as follows:

1. We propose a novel pattern transition model

for short-term traffic prediction under both

typical and atypical conditions. Our model

automatically recognizes the presence of an

atypical situation and activates the most

Theodorou, T-I., Salamanis, A., Kehagias, D., Tzovaras, D. and Tjortjis, C.

Short-Term Trafﬁc Prediction under Both Typical and Atypical Trafﬁc Conditions using a Pattern Transition Model.

DOI: 10.5220/0006293400790089

In Proceedings of the 3rd International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2017), pages 79-89

ISBN: 978-989-758-242-4

appropriate prediction model, based on the

outcome of an incident detection algorithm.

2. The proposed model incorporates the

incident information for more accurate

prediction.

3. We evaluate the functionality and

performance of our model against real data

that includes both traffic and incident

information.

The rest of the paper is organized as follows.

Section 2 summarizes related work. Section 3

describes the data used for training our prediction

model and for its evaluation, whereas Section 4

provides a detailed description of the implemented

model. Section 5 presents the evaluation framework,

including the process of setting up the various

experiments, the selection of the various datasets, the

metrics used for the evaluation of both the incident

detection and traffic prediction models and also the

experimental results. Finally, Section 6 concludes the

paper, reviewing the main contributions and

suggesting future directions.

2 RELATED WORK

The research problem of short-term traffic prediction

has been extensively studied in the last ten years. The

various relevant techniques can be roughly classified

into the following four major categories: naïve,

parametric, non-parametric and hybrid.

The naïve methods are the most cost-effective

prediction models and are mainly used as benchmark

against more sophisticated methods. They are

characterized by the absence of any advanced

mathematical model. Some of the most common

naïve methods for traffic prediction include the use of

the last observed value, the simple moving average

with a predefined time window T and the cumulative

moving average of all past traffic values.

Parametric models are the ones, which involve the

estimation of predefined parameters using historical

traffic data. These methods mainly originate from

time series analysis. Most of the works in this class

are based on the classic Box & Jenkins

Autoregressive Integrated Moving Average model

(Box and Jenkins, 1971). In their work, Stathopoulos

and Karlaftis presented a multivariate state-space

ARIMA approach for modelling and predicting

traffic flow, showing that different model

specifications are more appropriate for different

periods of the day (Stathopoulos and Karlaftis, 2003).

Moreover, Kamarianakis and Prastacos developed a

Space-Time ARIMA model with robust behavior

(Kamarianakis and Prastacos, 2005) which was

extended by Min and Wynter in an effort to deal with

the supposed stationarity of the process and the

constant relationship between the neighbor road

segments in a traffic network (Min and Wynter,

2011). More recently, an Auto-Regressive Moving

Average with an eXogenous input (ARMAX) model

with an optimal multiple-step-ahead predictor of

traffic demand was proposed by Wu et al. (Wu at al,

2014). In the same class, Mu et al. proposed a method

that utilizes heterogeneous delay embedding (HDE)

to extract an informative feature space for regression

analysis of traffic data (Mu et al., 2012). Additional

similar approaches include the works of (Guo and

Williams, 2010, Kamarianakis et al., 2012, Ghosh et

al., 2009).

The non-parametric models are mainly originated

from the machine learning field and are based on k-

NN regression, Artificial Neural Networks (ANN)

and Support Vector Regression (SVR) techniques.

The k-NN in short-term traffic prediction was

introduced by Smith and Demetsky who claimed that

it performs better than both the historical average and

parametric ARIMA model in terms of robustness

against variable data sets (Smith and Demetsky,

1996). The k-NN non-parametric regression

algorithm was utilized by several other researchers

for building accurate traffic prediction models (De

Fabritiis et al., 2008, Kindzerske and Ni, 2007,

Myung et al., 2012, Zheng and Su, 2014). Regarding

the use of ANNs, Vlahogianni et al. introduced the

auto- and cross-correlated effect of the traffic flow

time series in a neural network model in the form of

external information (Vlahogianni et al., 2003).

Finally, Wu et al. (Wu et al., 2003) and Hu et al. (Hu

et al., 2015) used the SVR algorithm for increasing

the accuracy of prediction.

Noticeable research effort has been given on the

development of hybrid traffic prediction techniques

that try to exploit the strong characteristics of both

parametric and non-parametric approaches. These

include e.g. a model that combines ARIMA and ANN

processes (Zhang, 2003), but also the combination of

Non-linear Autoregressive Moving Average with

exogenous inputs (NARMAX) that involves fuzzy

systems with ANN (Gao and Er, 2005). Similarly,

Quek et al. presented a special case of a fuzzy neural

network for short-term traffic prediction that shows

high adaptation to the input and high prediction

capacity (Quek et al., 2006).

Despite the multitude of proposed models for

short-term traffic prediction, very few of them deal

with the problem of traffic prediction under atypical

traffic conditions, such as rapid weather changes,

VEHITS 2017 - 3rd International Conference on Vehicle Technology and Intelligent Transport Systems

traffic incidents, road maintenance works, and special

events (e.g. concerts or sport events) etc. These

abnormalities lead to traffic conditions that the

traditional traffic predictions models are difficult to

capture. To this end, relevant research efforts are

quite limited. Amongst those, Castro-Neto et al.

proposed the Online Support Vector Regression (OL-

SVR) model for short-term traffic prediction under

both typical and atypical conditions (Castro-Neto et

al., 2009). They compared their model with well-

known models including Gaussian Maximum

Likelihood (GML), Holt exponential smoothing and

ANN and have proved that even if the GML model

shows the best performance in terms of prediction

accuracy under typical traffic conditions, the OL-

SVR model performs even better under non-recurring

atypical traffic conditions. Another example is the use

of three different prediction models, each with a

different configuration of the explanatory traffic

variable (Guo et al., 2010).

In this approach, it is shown empirically that k-

NN in conjunction with the third configuration of the

explanatory variable outperforms the ANN under all

conditions. Also in an extension of the previous work,

it is proven that the k-NN and SVR non-parametric

regression models have similar prediction accuracy

under typical traffic conditions but k-NN outperforms

SVR during atypical ones (Guo et al., 2012). By

enhancing the previous k-NN model with data

smoothing and de-noising components an even better

accuracy can be achieved (Guo et al., 2014). Hybrid

approaches have been also developed, such as the

Online Boosting Non-Parametric Regression

(OBNR), consisting of two parts: (a) a typical non-

parametric regression model for typical conditions,

and (b) a boosting part activated when atypical traffic

conditions occur and deactivated when the traffic

state turns back to normal. Real data experiments

prove that the OBNR model performs better than the

classic non-parametric regression and SVR models

during atypical traffic conditions (Wu et al., 2012).

Finally, an alternative approach was proposed by

Ni et al. which, in addition to traffic, it also uses data

from social networks (Twitter) in order to predict

traffic, prior to major sport game events. By fusing

both tweet rate and semantic features into the typical

prediction model, improved prediction accuracy can

be achieved (Ni et al., 2014).

A closer look on the current literature, does reveal

that in none of the aforementioned models traffic data

with atypical incidents is used for training. On the

contrary, training is based solely on data from typical

Available at: http://pems.dot.ca.gov/

conditions, whereas data from both typical and

atypical conditions is used for testing. Hence, the key

characteristic that distinguishes our work from the

current literature, is that in our model we incorporate

traffic data with atypical condition into the training

process of our proposed model. This is expected to

produce more accurate traffic prediction models.

3 DESCRIPTION OF DATA

The Caltrans Performance Measurement System

(PeMS

), was used for building and evaluating our

model. PeMS is an Archived Data User Service that

collects over ten years of data for historical analysis.

The traffic data is coming from over 39,000 Vehicle

Detection Stations (VDS) scattered on the freeway

system of all major metropolitan areas of the State of

California, USA. They include flow, occupancy and

speed values, as well as meta-information about the

VDS, e.g. the identification numbers of the district

and the freeway, in which the VDS is located, the

coordinates of the VDS, etc. Traffic data is sampled

every 30 seconds and aggregated into 5-minute and

1-hour time intervals. The user can select to acquire

the data either in raw or aggregated format.

Figure 1: PeMS Caltrans map.

PeMS also provides incident data collected by the

California Highway Patrol (CHP). This dataset

contains information about the incidents occurred on

the Caltrans network, such as location of the incident

(latitude, longitude), timestamp, type (e.g. car

accident, road maintenance works etc.), duration (in

minutes), etc. The incidents are reported by network

users to CHP, which maintains logs. The map of the

overall area that provides traffic and incident data in

PeMS is shown in Figure 1.

For the purpose of our research we have used a

small part of the above dataset for training and

evaluating our model. In particular, our dataset

Short-Term Trafﬁc Prediction under Both Typical and Atypical Trafﬁc Conditions using a Pattern Transition Model

includes speed probes recorded in the areas of San

Jose, Oakland, California (district 4 in Figure 1) and

covers a total time period of 123 days, from May 1 to

August 31, 2015. We acquired data in their

aggregated form in 5-minute intervals. Also, the

dataset contains only incident data in the same area

and time period.

4 PATTERN TRANSITION

ALGORITHMS

In this section, we present the pattern transition model

we have developed for traffic prediction under both

typical and atypical conditions. We use a SVM-based

AID model to detect the occurrence of atypical

conditions. On detection of an atypical situation by

the AID, the k-NN non-parametric regression model

is activated. Otherwise, the ARIMA parametric

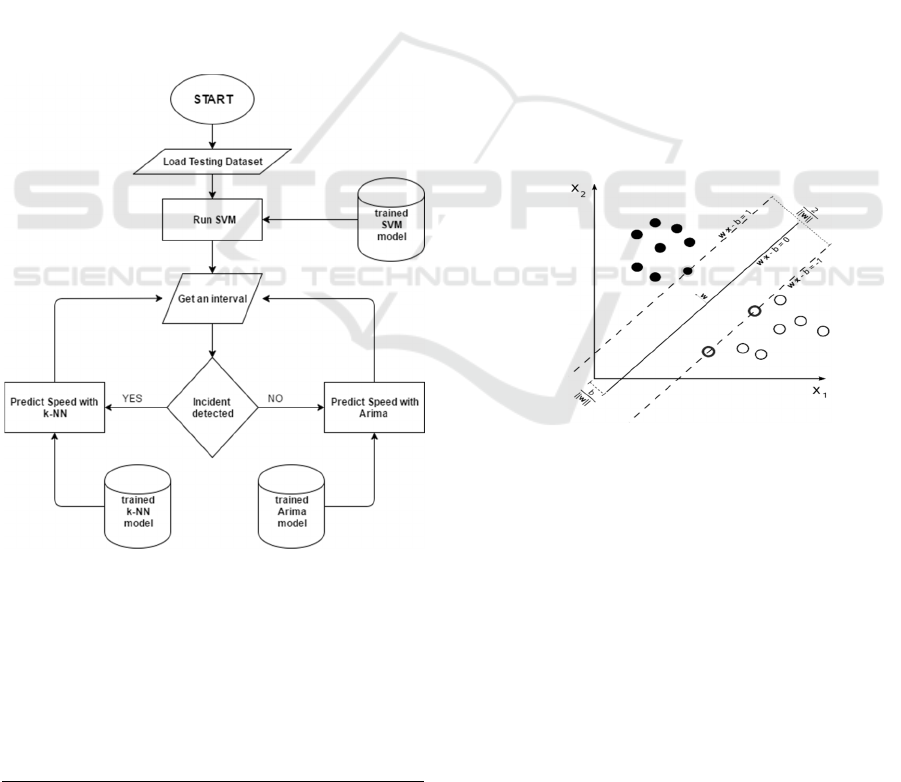
model is used. The flow chart of the Figure 2 shows

the whole process.

Figure 2:Flow Chart of the proposed method.

In the following subsections, we present all

modules that comprise the proposed model.

4.1 Automatic Incident Detection

In order to create our AID model, we used a

supervised machine learning algorithm. Specifically,

https://en.wikipedia.org/wiki/Support_vector_machine

we chose the Support Vector Machines algorithm,

which is fairly robust to irrelevant features (Gakis et

al. 2014). The basic idea of SVM is to generate a

hyperplane that divides the data set into classes. Our

problem is a binary classification one, thus we have

two classes, which represent the presence or absence

of an incident at a specific time interval and road of

the traffic network.

In the linear SVM, we are given a training data set

with n points of the form (x

, y

), …, (x

, y

) where y

indicates the class and takes either 1 or -1 as a value,

and x

is a p-dimensional real vector, called feature

vector. In our case the number of features is five,

hence x

is a 5-dimensional vector. The objective is to

find the maximum-margin hyperplane that divides the

group of points x

for which y

= 1, from the group of

such points that y

= -1, so that the distance between

the hyperplane and the nearest point x

from either

group is maximized. Any hyperplane can be written

as the set of all vectors x that satisfy:

0wx b⋅− =

(1)

where w is the normal vector to the hyperplane and

b/|w| a parameter that defines the offset of the

hyperplane from the origin, along the normal vector

w as shown in Figure 2.

Figure 3: Maximum-margin hyperplane and margins on

linear SVM kernel

In the feature extraction process, we tested both

speed and occupancy values in order to select the best

features. Initially we used only speed values to create

the features, and then we added features derived from

occupancy values. When the occupancy values

were

included to the feature extraction process, the

accuracy of the AID model was reduced and as a

consequence the traffic prediction accuracy. Finally,

different types of data (e.g. weather data) could be

used in the feature extraction process, but this remains

to be examined as future work.

VEHITS 2017 - 3rd International Conference on Vehicle Technology and Intelligent Transport Systems

For this reason, we used only speed in order to

detect the incidents occurred in a highway. Therefore,

we extracted two features based on the speed of the

road of interest and its adjacent roads. In addition to

the current time interval, the speed values of previous

intervals are also taken into account.

The first extracted feature F

is taken as the

difference between the speed of the road of interest

and the average speed of its adjacent roads, in the

direction that the vehicles travel, at current time. This

value was normalized by the speed of the road of

interest at the same time.

,(),

roi t ar j t

roi t

−



(2)

In (2), S represents speed, whereas index ar refers to

the adjacent road, roi refers to the road of interest, k

is the total number of adjacent roads and t is the

current interval.

We also extracted the following three features

(based on F

) for three time intervals prior to the

current one:

,1 (),1

roi t ar j t

roi t

−−

−



(3)

,2 (),2

roi t ar j t

roi t

−−

−



(4)

,3 (),3

roi t ar j t

roi t

−−

−



(5)

The selection of the optimal number of previous

intervals, was made after experimentation with

various numbers.

The selection of the above features is based on the

observation that when an incident occurs on a road,

the average speed of this road and its neighbouring

ones, in the same direction, decreases. However,

taking into account only the values of these features,

results in a biased model, prone to error, as it becomes

capable of detecting low speeds, and especially much

lower than the speed of the adjusted roads. Therefore,

the selection of one more feature was necessary. To

this end, we used as an extra feature the average

absolute deviation of the real speed of the road of

interest at current time with respect to its average

value of all previous intervals up to the current one

(including this).

|()|

()

roi t j roi

roi t k

roi

SmS

−



(6)

where S is the speed of the road of interest, p is the

number of past intervals, over which we calculate the

average value m(S). As a fifth feature, we also tested

the squared deviation from the mean of the speed.

This resulted in reduced classifier’s accuracy. These

are the five feature that comprise the vector space

model for each road of interest. Based on the feature

vectors produced in this way, a different SVM-based

AID model is built for each road of interest.

Finally, we experimented with various values for

the C parameter of the SVM algorithm, using one-out

cross validation, in order to estimate those that fit

better to our case. Using a grid search on C = 2

-5

, 2

-3

…, 2

with step 2, we concluded that the most

appropriate value is C = 1.1.

4.2 Traffic Prediction

For the task of traffic prediction, we used two models:

(a) the ARIMA parametric model and (b) the k-NN

model, in order to predict traffic under typical and

atypical conditions, respectively. Based on the

relevant literature regarding traffic prediction under

atypical conditions (Section 2), the time series models

fail to capture the abnormalities on the values of the

examined traffic variable, that are generated during a

traffic incident. On the other hand, the non-parametric

models and specifically the non-parametric

regression (e.g. k-NN regression) can follow these

abnormalities especially when these models have

been fitted using data from similar past abnormal

conditions.

4.2.1 Autoregressive Integrated Moving

Average

The Auto Regressive Integrated Moving Average

(ARIMA) family of models is the most widely

deployed approach for vehicular traffic prediction

and for time series prediction in general. ARIMA is a

generalisation of the Auto-Regressive Moving

Average (ARMA) model, which is applied strictly to

stationary time series.

An ARIMA (p, d, q) process is expressed as:

Short-Term Trafﬁc Prediction under Both Typical and Atypical Trafﬁc Conditions using a Pattern Transition Model

()

11 1

itit

LLX L

θε

 

 

−⋅−⋅=+⋅

 

 



(7)

where p is the order of the autoregressive model, d is

the degree of differencing and q is the order of the

moving average model. In our case, we used an

ARIMA (3, 1, 0) model with three previous terms and

degree of differencing for reaching stationarity.

The resulted model is show in equation:

'' ' '

,1,12,23,3roi t roi t roi t roi t

SS S S

ϕϕ ϕ

−− −

=⋅ +⋅ +⋅

(8)

where

,,,1roit roit roit

SSS

−

=−

(9)

is the differenced S

’

process, which is wide-sense

stationary. According to Pfeifer and Deutsch, the best

estimate of parameters φ are the maximum likelihood

estimates (Pfeifer and Deutsch, 1980). As without a

priori knowledge of their initial values, these

estimates cannot be exactly computed, a close

approximation via ordinary least squares (OLS) is

used. In particular, for every training sample an

equation of the form of (9), is constructed where φ are

the unknown parameters. This forms a linear

overdetermined system of equations of the form:

=⋅

(10)

The system given by the aforementioned equation can

be re-written by the use of normal equations, as:

()

XXy

⋅= ⋅

(11)

Using the OLS method we take the following

solution.

()

XXy

−

=⋅⋅⋅

(12)

When the model is built (the φ parameters have been

estimated) we use the following equation for

calculating the predicted value:

''''

12132th t t t

SSSS

ϕϕ ϕ

+−−

=⋅+⋅ +⋅

(13)

where, h is the prediction horizon.

4.2.2 k-Nearest Neighbors

For the prediction of the speed values under atypical

conditions we have chosen the k-NN regression

model which appears to be a suitable algorithm for

atypical traffic prediction, using an atypical historical

dataset. k-NN is a non-parametric algorithm that

stores all available cases and predicts the numerical

target based on a similarity measure and an averaging

scheme. The k-NN algorithm has been used in

statistical estimation and pattern recognition tasks,

already since the beginning of 1970’s as a non-

parametric technique.

k-NN prediction is based on the current state

vector (at current time interval t), of the form:

,,,1,2,

,, ,,

roi t roi t roi t roi t roi t p

ySSS S

−− −











(14)

where S is the traffic variable (in our case speed) and

p the number of past intervals. As shown, the current

state vector of a road of interest depends on the values

of speed at the current and previous p time intervals.

In order to make prediction, the k-NN algorithm

creates vectors of the form (14), y

1,t

, y

2,t

, … , y

N,t

for N

other roads of the network. When a prediction for the

road of interest for h intervals ahead in time is

requested, the algorithm compares y

roi,t

, with y

1,t

, y

2,t

… , y

N,t

using a distance metric (usually Euclidean

distance) and keeps the k vectors with the shortest

distances.

Then, it calculates the value S

roi,t+h

using an averaging

scheme on the estimated k neighbors, which in the

simplest form is given by (15).

it h

roi t h



(15)

In our implementation, we used the inverse

distance weighted average as the averaging scheme,

as shown in (16).

iith

roi t h



(16)

where:

()

11 1

iroii

roi t j i t j

−−

== =

−



(17)

VEHITS 2017 - 3rd International Conference on Vehicle Technology and Intelligent Transport Systems

We chose the optimal value for k via one-out cross

validation in our data set, based on the prediction

accuracy results. By this process, we concluded that

the most optimal value of k in our case was 6.

5 EVALUATION

In this section, we present the set-up of the evaluation

framework, including the construction of the traffic

time series and their enrichment with incident

information, the choice of a specific part of the

Caltrans road network as case study and the

separation of the training and test data. Finally, the

preliminary evaluation results are presented.

5.1 Constructing Traffic Time Series

with Incident Information

In order to build and evaluate our model the first step

was to pre-process the initial data (both traffic and

incidents) in order to create traffic time series that will

include incident information. For this reason, we

discretized time into 5-minute intervals and we

aggregated the speed values that belong to each

interval. We used this formulation in order to both fit

our model and to make predictions for a number of

steps ahead in time. In the case of short-term traffic

prediction, the predictions are made for up to 1 hour

ahead in time, i.e. 12 5-minutes intervals.

In the examined area, there are 350 VDS in total,

from which 112 were not taken into account because

they provided only zero values. The traffic data from

the remaining 238 VDS were matched to road

segments of the Caltrans network (based on their

coordinates). This process resulted into 55 road

segments having traffic data. As we described above,

the features of our AID model take into account not

only the speed of the road of interest, but also the

speed of its adjacent roads. For this reason, we kept

only the road segments for which, their spatial

neighbors traffic data exist.

Concerning incident data, there were 4,193

incidents in the area and time period concerned.

These incidents where matched to the aforementioned

55 road segments, for which traffic data is available.

For each day of the total examined period and each of

these 55 road segments, a speed time series was

constructed from speed values occurred in the

specific 5-minute interval of this day and road

segment. In this way 6,765 (55 road segments times

123 days of traffic data for each road segment) speed

were constructed. These time series, in addition to

traffic information, include typical and atypical

intervals, indicated by 0 and 1, respectively. The

value 1 indicates presence of an incident in the

specific time interval and 0 its absence. For instance,

for the road segment with identification number 76 on

May 21, 2015 on time interval 01:10-01:15 the

corresponding value of the speed time series is

‘66.55;0’. This means that the speed was 66.55 mph

and no incident situation was present.

5.2 Case Study: A Part of US101

Highway

One of the main difficulties when trying to predict

traffic under atypical conditions, is that the effect of

abnormalities on traffic time series is not easily

observable and interpretable. For instance, there may

be an incident with specific characteristics (type,

duration, severity, etc.) that caused a steep fall on the

traffic time series of a road network, and another

incident with exactly the same characteristics that

happened on the same road at a different time of the

day and had no effect on the traffic time series. On the

other hand, there may be observable discrepancies

from the typical pattern of the traffic time series that

do not necessarily correspond to the presence of an

incident. These situations may confuse the AID

model. In order to overcome these difficulties, we had

to choose road segments with observable effects on

their traffic time series due to occurring incidents.

5.3 Training Versus Testing Data

The traffic time series of the aforementioned road

segment consist the main data set. From this, the one

that corresponds to 25 August, 2015 was selected as

a test time series, which has both typical and atypical

intervals. This time series was selected because it has

spikes that corresponds to the occurrence of incidents.

The preceding 116 time series formed the training

data set. From this, we created three separated data

sets in order to fit our model and the benchmarking

methods in different traffic conditions. The first data

set includes only the ones without atypical intervals

(incident-free), whereas the second data set includes

those with both typical and atypical (incident).

Finally, the third one contains all time series (total).

We trained the AID and the k-NN models using

the total training data set, whereas for the ARIMA

model the incident-free data set was used. Hence, we

incorporate incident information to the fitting process

of our model, as opposed to the current related work.

Short-Term Trafﬁc Prediction under Both Typical and Atypical Trafﬁc Conditions using a Pattern Transition Model

5.4 Benchmarks and Accuracy Metrics

For the evaluation of the AID model we calculated a

number of metrics using one-out cross validation in

the total training data set. The first metric that we

calculated was the accuracy:

TP TN

Accuracy

TP FP TN FN

+++

(18)

where TP is the true positive, TN the true negative,

FP the false positive and FN the false negative

predicted classes. However, accuracy is not really a

reliable metric for the real performance of a classifier

when the number of samples in different classes vary

greatly (unbalanced target) because it will yield

misleading results. In our case, from the total number

of 288 intervals in the traffic time series, only in 30

or less intervals an incident was occurred. For this

reason, in order to evaluate our model accurately, we

calculated two additional metrics. The first one is

sensitivity, a measurement of the proportion of

positives that are correctly identified, whose formula

is shown below:

Sensitivity

TP FN

(19)

The second additional metric is specificity, which

measures the proportion of negatives that are

correctly identified. Its formula is given by the

following equation:

Specificity

TN FP

(20)

Using the sensitivity and specificity we created the

Receiver Operating Characteristic (ROC) curve,

which illustrates the performance of our classifier.

For benchmarking we used the unitary ARIMA

and k-NN models. These models were initially fitted

using only the incident-free training data set, as

happens in most of the works on traffic prediction

under atypical conditions in current literature, and

then using different combinations of all three datasets

(incident-free, incident and total). We assessed the

resulted accuracies by the means of two metrics: (a)

the Root Mean Square Error (RMSE) and (b) the

Symmetric Mean Absolute Percentage Error

(SMAPE).

RMSE is given by the following formula:

()

RMSE

−



(21)

where n is the number of predictions, A

the actual

values and P

the predicted values.

SMAPE gives a percentage error that has both a

lower and an upper bound of 0% and 100%,

respectively. This makes its values more easily

interpretable. The formula of SMAPE is the

following:

100%

||||

SMAPE

nAP

−

=⋅



(22)

where n is the number of predictions, A

the actual

values and P

the predicted values.

5.5 Experimental results

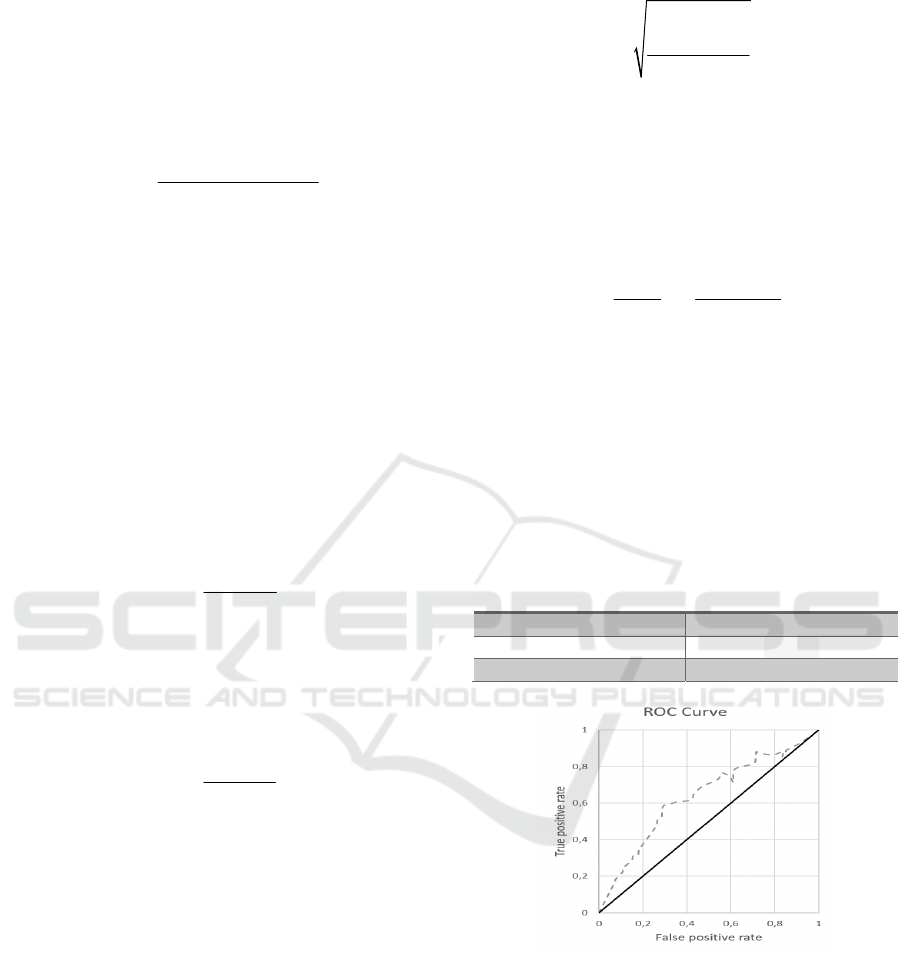
The evaluation results of the AID model are shown in

Table 1. Additionally, the ROC curve of the classifier

is shown in Figure 1.

Table 1: The evaluation results of the AID model.

AID evaluation metrics

Accurac

0.8986

Sensitivit

0.6364

Specificit

0.9091

Figure 4: ROC curve of the proposed AID schema.

We can see that although the proposed model is

quite above the line of no-discrimination (the

diagonal line), it is also quite far from the upper left

corner of the ROC space (best possible classification

prediction). This mainly happens due to the

imbalance of the records of the classification classes

(incident, non-incident) in the examined data set. In

any case, the curve shows that there is enough room

for improvement for the proposed AID model.

VEHITS 2017 - 3rd International Conference on Vehicle Technology and Intelligent Transport Systems

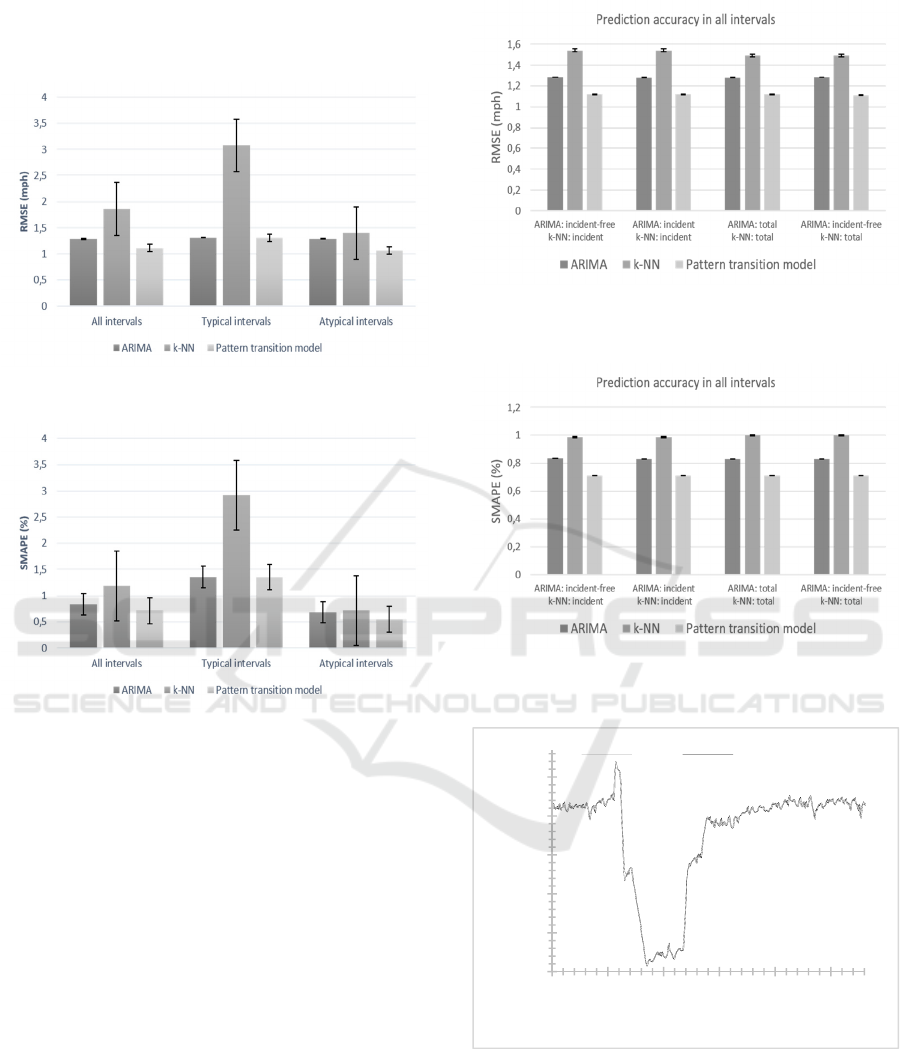
The results of the experiments regarding the

prediction accuracy of our model are shown in Figure

5 and Figure 6.

Figure 5: Prediction accuracy results in RMSE.

Figure 6: Prediction accuracy results in SMAPE.

As shown in the aforementioned figures, in total,

the proposed model outperforms its competitors. In

particular, our model presents almost similar

prediction accuracy with the ARIMA model under

typical conditions, but it exhibits the best

performance under atypical conditions.

As already mentioned, the benchmarking models

were initially trained by incident-free data.

Subsequently, we conducted a series of experiments,

in which the two unitary benchmarking models were

trained using different combinations of the incident-

free, incident and total data sets. In this way, we

incorporated the incident information not only in the

data fitting process of the proposed model, but also in

the fitting process of its competitors. As shown in

Figure 7 and Figure 88, again the proposed model

presents superior accuracy for all intervals.

Figure 7: Prediction accuracy results in RMSE, for different

benchmarking combinations and for all intervals.

Figure 8: Prediction accuracy results in SMAPE, for

different benchmarking combinations and for all intervals.

Figure 9: Real and predicted speed time series.

In Figure 9 is shown both the actual and the predicted

time series of speed. It is obvious that the proposed

model fits the actual values of speed.

In order to evaluate the statistical significance of

the improvement that our model introduces we run a

t-test. To this end, we examine the null hypothesis

0 50 100 150 200 250

Speed (mph)

5-minute inteval

real predicted

Short-Term Trafﬁc Prediction under Both Typical and Atypical Trafﬁc Conditions using a Pattern Transition Model

that the proposed model has equal accuracy with the

ARIMA model. Since there is no indication that the

predicted values have normal distributions, we used

the Wilcoxon signed-rank test. The test showed that

at significance level of 0.05 the null hypothesis could

be rejected for all the aforementioned benchmarking

cases. Therefore, we can claim that the proposed

model presents statistically significantly better

accuracy from the ARIMA model in all cases.

6 CONCLUSIONS

In this paper we introduced a novel hybrid method for

short-term traffic prediction under both typical and

atypical traffic conditions. We introduced a SVM-

based AID model that identifies the presence of

atypical conditions. We use the ARIMA parametric

model or the k-NN non-parametric regression model

if the AID identifies typical or atypical conditions,

respectively. We evaluated our model using real open

data from the Caltrans PeMS and showed that it

outperforms the benchmarking models in terms of

prediction accuracy under both typical and atypical

conditions.

The proposed model can be implemented using

either speed or flow data. In this work, we selected

speed data because speed is a traffic variable that

provides clearly interpretable results regarding the

traffic state of a network and also it can be easily

converted to travel time, which is a useful metric for

many ITS applications like vehicle routing.

Future work involves experimenting with

additional feature extraction techniques for

improving the accuracy of the proposed AID model.

Furthermore, more extensive comparison of the

proposed model against additional prediction models

using larger data sets is essential for further

investigating the conditions under which the

proposed model provides the best performance.

ACKNOWLEDGMENT

This work has been partially supported by the

European Commission through the project

RESOLUTE (ID: 653460), funded by Horizon 2020.

The opinions expressed in this paper are those of the

authors and do not necessarily reflect the views of the

European Commission.

REFERENCES

Abdulhai, B., Porwal H., Recker, W., 1997. Short term

freeway traffic flow prediction using genetically

optimized time delay based neural net-works. Proc.,

Transportation Research Board Annual Meeting,

Washington D. C., USA.

Box, G. E. P. and Jenkins, G. M., 1971. Time series analysis

forecasting and control. Operational Research

Quarterly, 22(2), June, pp.199-201.

Castro-Neto, M., Jeong, Y. S., Jeong, M. K., Han, L. D.,

2009. Online-SVR for short-term traffic flow prediction

under typical and atypical traffic conditions. Expert

Systems with Applications, 36(3), pp.6164-6173.

Clark, S., 2003. Traffic Prediction Using Multivariate

Nonparametric Regression. Journal of Transportation

Engineering, 129(2), pp.161-168.

De Fabritiis, C., Ragona, R., Valenti, G., 2008. Traffic

estimation and prediction based on real time floating car

data. Proc., IEEE 11

International Conference on

Intelligent Transportation Systems, pp.197-203.

Dougherty M. S. and Cobbet M. R., 1997. Short term inter-

urban traffic fore-casts using neural networks.

International Journal of Forecasting, 13(1), March,

pp.21-31.

Gakis E., Kehagias D., Tzovaras D., 2014. Mining Traffic

for Road Incidents Detection. IEEE 17

International

Conference on Intelligent Transportation Systems,

Qingdao, China, pp. 930-935.

Gao, Y. and Er, M., J., 2005. Narmax time series model

prediction: feed-forward and recurrent fuzzy neural

network approaches. Fuzzy Sets and Systems, 150(2),

March, pp.331-350.

Ghosh, B., Basu, B., O’Mahony, M., 2009. Multivariate

short-term traffic flow forecasting using time-series

analysis. IEEE Transactions on Intelligent

Transportation Systems, 10(2), pp.246-254.

Guo, F., Krishnan, R., Polak, J. W., 2012. Short-Term

Traffic Prediction Under Normal and Abnormal Traffic

Conditions on Urban Roads. 91

Transportation

Research Board Annual Meeting, Washington D. C.,

USA.

Guo, F., Krishnan, R., Polak, J. W., 2014. A novel three-

stage framework for short-term travel time prediction

under normal and abnormal traffic conditions. 93

Transportation Research Board Annual Meeting,

Washington D. C., USA.

Guo, F., Polak, J. W., Krishnan, R., 2010. Comparison of

Modelling Approaches for Short-Term Traffic

Prediction under Normal and Abnormal Conditions.

IEEE 13

International Conference on Intelligent

Transportation Systems, Madeira Island, Portugal.

Guo, J. and Williams, B. M., 2010. Real-time short-term

traffic speed level forecasting and uncertainty

quantification using layered Kalman filters.

Transportation Research Record: Journal of

Transportation Research Board, 2175, pp.28-37.

Hu, W., Yan, L., Liu, K., Wang, H., 2015. A Short-term

Traffic Flow Forecasting Method Based on the Hybrid

PSO-SVR. Neural Processing Letters, pp.1-18.

VEHITS 2017 - 3rd International Conference on Vehicle Technology and Intelligent Transport Systems

Innamaa, S., 2000. Short term prediction of traffic situation

using MLP-neural networks. Proc., 7

World Congress

on Intelligent Systems, Turin, Italy, pp.1-8.

Kamarianakis, Y. and Prastacos, P., 2005. Space-time

modelling of traffic flow. Computers & Geosciences,

31(2), pp.119-133.

Kamarianakis, Y., Shen, W., Wynter, L., 2012. Real-time

road traffic forecasting using regime-switching space-

time models and adaptive LASSO. Applied Stochastic

Models in Business Industry, 28(4), pp.297-315.

Kindzerske, M. D. and Ni, D., 2007. Composite nearest

neighbour nonparametric regression to improve traffic

prediction. Transportation Research Record: Journal

of Transportation Research Board. 1993(1), pp.30-35.

Min, W. and Wynter, L., 2011. Real-time traffic prediction

with spatiotemporal correlations. Transportation

Research Part C: Emerging Technologies, 19(4),

August, pp.606-616.

Mu, T., Jiang, J., Wang, Y., 2012. Heterogeneous delay

embedding for travel time and energy cost prediction

via regression analysis. IEEE Transactions on

Intelligent Transportation Systems, 14(1), pp. 214-224.

Myung, J., Kim, D. K., Kho, S. Y., Park, C. H., 2012. Travel

Time Prediction Using k-Nearest Neighbour Method

with Combined Data from Vehicle Detector System and

Automatic Toll Collection System. Transportation

Research Record: Journal of Transportation Research

Board, 2256, pp.51-59.

Ni, M., He, Q., Gao, J., 2014. Using Social Media to Predict

Traffic Flow under Special Event Conditions. 93

Transportation Research Board Annual Meeting,

Washington D. C., USA.

Pfeifer, P. E. and Deutsch, S. J., 1980. A three-stage

iterative procedure for space-time modelling.

Technometrics, 22(1), February, pp.35-47.

Quek, C., Pasqueir, M. and Lim, B. B. S., 2006. Pop-traffic:

a novel fuzzy neural approach to road traffic analysis

and prediction. IEEE Transactions on Intelligent

Transportation Systems, 7(2), June, pp.133-146.

Smith, B. L. and Demetsky, M. J., 1996. Multiple interval

freeway traffic flow prediction. Transportation

Research Record: Journal of Transportation Research

Board, 155(4), pp.136-141.

Stathopoulos, A. and Karlaftis, M. G., 2003. A multivariate

state-space approach for urban traffic flow modelling

and prediction. Transportation Research Part C:

Emerging Technologies, 11(2), April, pp.121-135.

Vlahogianni, E. I., Karlaftis, M. G., Golias, J. C., 2003. A

multivariate neural network predictor for short term

traffic prediction in urban signalized arterial. Proc. 10

IFAC Symposium on Control in Transportation

Systems, Tokyo, Japan, August.

Williams, B. M., Dursavula, P. K., Brown, D. E., 1998.

Urban freeway traffic flow prediction – Application of

seasonal autoregressive integrated moving average and

exponential smoothing models. Transportation

Research Record: Journal of Transportation Research

Board, 1644, pp.132-141.

Wu, C. H., Wei, C. C., Su, D. C., Chang, M. H., Ho, J. M.,

2003. Travel Time Prediction with Support Vector

Regression. IEEE 6

International Conference on

Intelligent Transportation Systems, Shanghai, China.

Wu, T., Xie, K., Xinpin, D., Song, G., 2012. A online

boosting approach for traffic flow forecasting under

abnormal conditions. Proc., 9

International

Conference on Fuzzy Systems and Knowledge

Discovery, Sichuan, China.

Zhang, G. P., 2003. Time series prediction using a hybrid

ARIMA and neural network model. Neurocomputing,

50, January, pp.159-175.

Zheng, Z., Su, D., 2014. Short-term traffic volume

forecasting: A k-nearest neighbour approach enhanced

by constrained linearly sewing principle component

algorithm. Transportation Research Part C: Emerging

Technologies, 43, pp.143-157.

Wu, Cheng-Ju, Schreiter, Thomas, & Horowitz, Roberto

2014. Multiple-clustering ARMAX-based predictor

and its application to freeway traffic flow prediction.

American Control Conference (ACC), 2014 IEEE

Short-Term Trafﬁc Prediction under Both Typical and Atypical Trafﬁc Conditions using a Pattern Transition Model