
Primitive Shape Recognition via Superquadric Representation
using Large Margin Nearest Neighbor Classifier
Ryo Hachiuma, Yuko Ozasa and Hideo Saito
Graduate School of Science and Technology, Keio University, Yokohama, Japan
{ryo-hachiuma, yuko.ozasa, hs}@keio.jp
Keywords:
Superquadrics, 3D Shape Primitives, Primitive Shape Recognition, Large Margin Nearest Neighbor.
Abstract:
It is known that humans recognize objects using combinations and positional relations of primitive shapes.
The first step of such recognition is to recognize 3D primitive shapes. In this paper, we propose a method for
primitive shape recognition using superquadric parameters with a metric learning method, large margin nearest
neighbor (LMNN). Superquadrics can represent various types of primitive shapes using a single equation with
few parameters. These parameters are used as the feature vector of classification. The real objects of primitive
shapes are used in our experiment, and the results show the effectiveness of using LMNN for recognition based
on superquadrics. Compared to the previous methods, which used k-nearest neighbors (76.5%) and Support
Vector Machines (73.5%), our LMNN method has the best performance (79.5%).
1 INTRODUCTION
Nowadays, due to the improvement of sensing tech-
nology, the 3D data of a scene or an object can easily
be captured by a depth sensor, such as Kinect (Zhang,
2012). 3D object recognition is one of the important
tasks in the field of computer vision for understanding
scenes and robot manipulation.
It has been widely studied that how human rec-
ognize objects (Marr D, 1982; Biederman, 1987). It
is said that a small number of fundamental primi-
tives suffice to represent most objects for the purpose
of generic recognition, and we recognize and decide
the attributes of objects using the combinations and
positional relations of these primitives (Biederman,
1987). Therefore, it is important to recognize objects
by these primitives to achieve a recognition system
based on human recognition.
To achieve primitives-based recognition, it is nec-
essary to represent primitives with consistency and
simplicity. One of the most appropriate representa-
tions is superquadrics (Barr, 1981). Superquadrics are
one of the methods for primitive shape representation
that can represent a variety of shapes with few param-
eters.
We focus on primitive shape-based object recog-
nition using superquadric representation. There are
two related works that recognize objects using su-
perquadric representation: k-nearest neighbor (kNN)
(Raja and Jain, 1992) and support vector machines
(SVM) (Xing et al., 2004).
Recently, metric learning has been considered a
high-performance classifying method. In particular,
large margin nearest neighbor (LMNN) is a metric
learning method with a training Mahalanobis distance
metric for kNN classification (Weinberger and Saul,
2009). In this paper, we present a method that recog-
nizes superquadric parameters with LMNN.
Before the low-cost depth sensor Kinect (Zhang,
2012) was developed, it was difficult to evaluate the
results of object recognition using superquadric pa-
rameters with real objects. Raja, N. S. and Jain, A.
K. (Raja and Jain, 1992) used real objects in their
experiments. They captured one snapshot of each
real object, and they recognize one superquadric pa-
rameter per object with Euclidean distance match-
ing. Xing, W.
et.al.
(Xing et al., 2004) used only
ideal parameters and did not use real objects in their
experiments. They classify these ideal parameters
with SVM. In our experiment, we captured hundreds
of shots of real primitive objects with a depth sen-
sor, and we constructed a primitive object dataset us-
ing Kinect(Zhang, 2012). This dataset enables us to
evaluate in detail our method using real objects and
compare our method with previous work (Raja and
Jain, 1992; Xing et al., 2004). No previous stud-
ies have compared the classification results with kNN
and SVM. Our experiments show that the proposed
method with the LMNN classifier has the highest per-
formance in comparison with SVM and kNN classi-
Hachiuma R., Ozasa Y. and Saito H.
Primitive Shape Recognition via Superquadric Representation using Large Margin Nearest Neighbor Classifier.
DOI: 10.5220/0006153203250332
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 325-332
ISBN: 978-989-758-226-4
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
325

fiers.
The novelty of this paper is to use LMNN for
primitive shape recognition based on superquadrics.
There are three contributions of this paper. First, a
3D dataset of real primitive objects is constructed.
Second, the parameters of the superquadrics of real
objects are estimated, and these parameters are used
for the recognition. Third, we compare the results of
three classifiers: kNN, SVM, and LMNN.
The rest of the paper is organized as follows. We
review related work on 3D object recognition and su-
perquadrics in the field of computer vision in Sec-
tion 2. Section 3 describes our methods and our
superquadric parameter estimation and recognition
model. The experimental results and evaluations of
recognition are shown in Section 4. Finally, Section 5
concludes the paper.
2 RELATED WORKS
We present primitive shape-based object recognition,
and superquadrics are used for the primitive shape
representation. In this section, we briefly introduce
several related approaches to primitive shape-based
object recognition. Moreover, as superquadrics have
been used in many different ways in the field of com-
puter vision, we also introduce these research.
2.1 3D Object Recognition based on
Primitive Shapes
Due to the improvement of sensing technology, 3D
object recognition methods have been studied. There
are two major kinds of 3D object recognition meth-
ods. One is based on specific feature extraction and
recognition, while the other is based on the human
recognition system. The former method creates a
histogram of normal vectors or relations of neigh-
bors (Rusu et al., 2009; Tombari et al., 2010; Tang
et al., 2012). These histogram-based approaches have
high performance with specific object recognition or
in cluttered scenes.
In the extensive literature on 3D object recogni-
tion, some studies discuss the human recognition sys-
tem. For example, Nieuwenhuisen, M.
et.al.
pro-
posed a robot grasping method by estimating cylin-
drical parameters of objects (Nieuwenhuisen et al.,
2012). We employed superquadricsto represent prim-
itive shapes, so that not only cylinders but also other
primitives could be represented. Somani, N.
et.al.
present a method for specific object recognition that
considers the physical constraints of the primitives’
orientation (Somani et al., 2014). We do not con-
sider the constraints of orientations. However, as we
used a statistical machine-learning method for object
recognition, our method has the potential to be imple-
mented in genetic object recognition. It is necessary
to segment objects into primitive shapes to achieve
object recognition that is represented in several prim-
itives. Garcia S. (Garcia, 2009) showed that the suit-
able segmentation algorithm for man made objects is
segmentation based on primitive fitting or 3D volu-
metric approaches. In this paper, primitive-based ob-
ject segmentation will be explored.
2.2 Superquadrics in the Field of
Computer Vision
Superquadrics in the field of computer vision has
been investigated since (Pentland, 1986), and the
research of superquadrics is actively developed in
around 1990s. studies on superquadrics in the field
of computer vision were on superquadric parameter
estimation based on depth images (Solina and Bajcsy,
1987). Solina and Bajcsy presented a method for rec-
ognizing pieces of mail using superquadric parame-
ters estimated from range images.
Thus, superquadrics have been used for object
shape approximation (Strand et al., 2010; Solina and
Bajcsy, 1990; Saito and Kimura, 1996), novelty de-
tection (Drews Jr. et al., 2010), object segmentation
(Chevalier et al., 2003; Leonardis et al., 1997), object
grasping (Varadarajan and Vincze, 2011), and colli-
sion detection (Moustakas et al., 2007).
However, only few studies have conducted primi-
tive shape recognition using superquadric representa-
tion (Xing et al., 2004; Raja and Jain, 1992). Raja, N.
S. and Jain, A. K. (Raja and Jain, 1992) experimented
with crafted primitive objects using kNN, while Xing,
W.
et.al.
(Xing et al., 2004) experimented with ideal
superquadric parameters using SVM. In this paper,
we use superquadric parameters for object recogni-
tion, and we employ the classifier LMNN. We exper-
imented with real primitive shapes.
3 PRIMITIVE SHAPE-BASED
RECOGNITION
In this section, we introduce a method to recognize
primitives based on superquadric representation. Our
method in this paper consists of 2 main steps: First,
superquadric parameter is estimated from 3D data
points of the object. Second, we set these estimated
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
326

parameters as a feature vector F
F
F and recognize F
F
F us-
ing LMNN.
3.1 Superquadrics
Superquadrics are an extension of quadric surfaces
those include superellipsoids, supertoroids, and su-
perhyperboloids. Superquadrics have been proposed
for use as primitives for shape representation in the
field of computer graphics (Barr, 1981) and computer
vision (Pentland, 1986). A superquadric surface can
be defined by the 3D vector x.
x(η,ω) =
a
1
cos
ε
1
(η)cos
ε
2
(ω)
a
2
cos
ε
1
(η)sin
ε
2
(ω)
a
3
sin
ε
1
(η)
, (1)
−π/2 ≤ η ≤ π/2, −π ≤ ω ≤π.
The surface of superquadrics is located in the original
coordinate system. In Eq. (1), there are two inde-
pendent variables: η and ω. Parameter η is the angle
that expresses between the x-axis and the projection
of vector x in the x-y plane, and parameter ω is the
angle that expresses between vector x and its projec-
tion to the x-y plane. Eq. (1) can be written in implicit
form as Eq. (2) by eliminating two parameters: η and
ω.
f(x
s
,y
s
,z
s
)=
(
x
s
a
1
2
ε
2
+
y
s
a
2
2
ε
2
)
ε
2
ε
1
+
z
s
a
3
2
ε
1
= 1.
(2)
In Eq. (2), there are five parameters (a
1
,a
2
,a
3
,ε
1
,ε
2
).
Parameters a
1
,a
2
,a
3
are scale parameters that define
the superquadric size in the x, y, and z coordinates,
respectively, and parameters ε
1
and ε
2
are shape rep-
resentation parameters that express squares along the
z axis and the x-y plane, while the index s denotes that
the point belongs to the superquadric-centeredcoordi-
nate. Fig. 1 shows various superquadrics by changing
the shape-representation parameters ε
1
and ε
2
.
As shown in Fig. 1, the superquadric surface is
shaped like a cylinder when ε
1
≪ 1 and ε
2
= 1, is
shaped like a cuboid when ε
1
≪ 1 and ε
2
≪ 1, and is
shaped like a sphere when ε
1
= 1 and ε
2
= 1.
3.1.1 Coordinate Transformation
As explained, the superquadric surface is located in
its original coordinate system, but the input 3D point-
cloud from the depth sensor is located in the world
coordinate system. We want to transform a point
from the world coordinate system to the superquadric-
centered coordinate system with transformation ma-
trix T. A relationship between the world coordinate
Figure 1: The various superquadric shapes according to ε
1
and ε
2
.
system (x
w
,y
w
,z
w
) and the superquadric-centered co-
ordinate system (x
s
,y
s
,z
s
) can be expressed in the fol-
lowing Eq. (3), where the transformation matrix T
can be decomposed in rotation R(θ
x
,θ
y
,θ
z
) and trans-
lation t(t
x
,t
y
,t
z
).
x
s
y
s
z
s
1
= (R|t)
x
w
y
w
z
w
1
. (3)
3.1.2 Superquadric Parameter Estimation
Superquadrics can be expressed in implicit form,
which is called “inside-outside” function. When
f(x
s
,y
s
,z
s
) > 1, the point p(x
s
,y
s
,z
s
) lies outside of
the surface, and if f(x
s
,y
s
,z
s
) = 1, the point lies on
the surface, and if f(x
s
,y
s
,z
s
) < 1, the point lies in-
side the surface. If a point (x
w
,y
w
,z
w
) from the world
coordinate is given, Eq. (2) can be re-written with five
parameters for superquadrics and six for transforma-
tion.
Given a set of N unstructured 3D data points, we
want to estimate 11 parameters that the input 3D data
points will fit or be close to the superquadrics model
surface. As the superquadric surface must satisfy Eq.
(2), we want to minimize Eq. (4) to estimate su-
perquadric parameters.
N
∑
i=0
( f(x
w
i
,y
w
i
,z
w
i
) −1)
2
. (4)
However, 3D data points captured from a depth
sensor have self-occlusion, and tremendous size dif-
ferences of superquadrics can be fit into Eq. (4). It
is known that by multiplying the square root of the
scale parameters
√
a
1
a
2
a
3
to minimize the function
described in Eq. (4), it is possible to estimate the
Primitive Shape Recognition via Superquadric Representation using Large Margin Nearest Neighbor Classifier
327

smallest superquadrics by fitting the following 3D
data points.
n
∑
i=0
(
√
a
1
a
2
a
3
( f(x
w
i
,y
w
i
,z
w
i
) −1))
2
. (5)
Since function
√
a
1
a
2
a
3
( f(x
w
i
,y
w
i
,z
w
i
) − 1) is
a nonlinear function of 11 parameters, it is well
known to solve function in Eq. (5) as a nonlin-
ear least squares problem, in particular by using the
Levenberg-Marquardt algorithm (Press et al., 1986).
Moreover, when ε
1
,ε
2
< 0.1, the inside-outside func-
tion will be numerically unstable, and as shown in
Fig. 1, the superquadric will have concavities when
ε
1
,ε
2
> 2.0. We use the constraints when minimiz-
ing the function in Eq. (5) for the shape parame-
ters: 0.1 < ε
1
,ε
2
< 2.0 and for the scale parameters
: a
1
,a
2
,a
3
> 0.0. However, it is important to decide
the initial parameters because this decision will in-
volve the local minimum. We will explain the setting
of the initial parameters in the next section.
3.1.3 Finding the Initial Parameters
As the function in Eq. (5) is not a convex function,the
initial parameters will determine which local mini-
mum the minimization will converge. It is important
to estimate the rough parameters: translation, rota-
tion, scale, and shape parameters.
First, as it is difficult to roughly estimate the shape
of the object, the initial shape parameters ε
1
and ε
2
are set to 1, which means that the shape of the initial
model is an ellipsoid. Second, the centroid of all 3D
data points can be used to estimate the initial transla-
tion. Third, to compute the initial rotation, we com-
pute the covariance matrix of all n 3D data points.
From this covariance matrix, three pairs of eigenvec-
tors and eigenvalues can be computed. The largest
eigenvector of the covariance matrix always points in
the direction of the largest variance of the data, and
the magnitude of this largest vector equals the corre-
sponding eigenvalue. The second largest eigenvector
is always orthogonalto the largest and points in the di-
rection of the second largest spread of the data which
is the same as the third vector. Therefore, the eigen-
vectors can be used as the initial rotation parameters,
and the eigenvalues can be used as the initial scale
parameters.
3.2 Recognition System
In this paper, we set five superquadric param-
eters (ε
1
,ε
2
,a
1
,a
2
,a
3
) as a feature vector F
F
F =
(ε
1
,ε
2
,a
1
,a
2
,a
3
) that is estimated from the 3D data
points of the object, and we apply the statistical
machine-learning method to recognize objects.
Let {(F
F
F
i
,l
i
)}
L×N
i=1
denote a training set of L×N la-
beled examples with inputs F
F
F ∈ R
5
and discrete class
labels y
i
. L stands for the number of classes, and N
stands for the number of examples per class through
the rest of the paper. LMNN (Weinberger and Saul,
2009) is one of the metric learning methods that trains
a Mahalanobis distance metric for kNN classification.
Let covariance matrix M and the Mahalanobis dis-
tance D
M
(F
F
F
p
,F
F
F
q
) between two inputs, F
F
F
p
and F
F
F
q
,
be defined as follows.
D
M
(F
F
F
p
,F
F
F
q
) =
q
(F
F
F
p
−F
F
F
q
)
T
M(F
F
F
p
−F
F
F
q
) (6)
where p and q denote the target indices, and 0 ≤
{p,q} ≤ L×N.
This metric is optimized with the goal that kNN
always belongs to the same class, while data from
different classes are separated by a large margin. It
means that minimizing the Mahalanobis distance be-
tween a target data F
F
F
i
and data that belongs to the
same class of F
F
F
i
, maximizing the Mahalanobis dis-
tance between F
F
F
i
and data belongs to different classes
of F
F
F
i
. Hence, input data will be able to classify with
accuracy. However, the computation cost will be ex-
traordinarily huge if it computes the Mahalanobis dis-
tance between a target data F
F
F
i
and all data belonging
to the same class. LMNN uses k target neighbors to
reduce the computation cost. Target neighbor is the k
nearest data to the F
F
F
i
with the same class. Moreover,
it uses the idea of a large margin. A margin is a unit
that separates data with different classes. As above,
matrix M is learned as an optimization problem with
Eq. (7).
Minimize
∑
ij
η
ij
D
M
(F
F
F
i
,F
F
F
j
) + c
∑
ijh
(1−δ
ih
)ξ
ijh
subject to:
D
M
(F
F
F
i
,F
F
F
h
) −D
M
(F
F
F
i
,F
F
F
j
) ≥ 1−ξ
ijh
ξ
ijh
≥ 0
M 0.
(7)
where ηij denotes an indicate function η ∈ {0,1}
whether input F
F
F
j
is a target neighbor of input F
F
F
i
or
not, and δ
ih
also denotes an indicate function whether
label l
i
is the same class to l
h
or not. ξ
ijh
are the slack
variables. c is a constant value range of 0 to 1.
The first term in the minimize function is the sum
of the Mahalanobis distance between input F
F
F
i
and k
target neighbors, and the second term is the penalty
term because it returns a positive value when the dis-
tance with the same label is smaller than with the dif-
ferent label.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
328

4 EXPERIMENTS
We conducted two main experiments in order to eval-
uate and analyze the superquadric parameter estima-
tion and effectiveness of LMNN. In Section 4.1, the
superquadric parameters of five kinds of daily ob-
jects are estimated, and the appropriateness of the
estimated parameters are evaluated. In Section 4.2,
recognition using estimated parameters is evaluated.
The proposed LMNN method is compared with the
methods using kNN and SVM.
4.1 Superquadrics Estimation
First, we evaluated the results of the superquadric pa-
rameter estimation. We captured five objects using
Kinect v.1 (Zhang, 2012) as a depth camera in this
paper. Each object was put on the floor, and we cre-
ated the 3D points of the object by extracting the
3D data points of the floor using the RANSAC algo-
rithm (Schnabel et al., 2007), and the isolated points
were extracted using Euclidean clustering (Rusu and
Cousins, 2011). Fig. 2 shows the results of the es-
timation. In this figure, (1a),(2a), ··· ,(5a) shows
the RGB image of the objects captured from Kinect
v.1, and (1b),(2b),···,(5b) shows the estimated su-
perquadric surface.
Each estimated superquadric parameter is in the
list in Fig. 2. We can compare these estimated
parameters and look on Fig. 1 to see which su-
perquadric shape that is correspond to them. For ex-
ample, shape parameters of object (1a) is (ε
1
,ε
2
) =
(0.10,0.18), and it represents a cube in Fig. 1. More-
over, scale parameters of object (1a) (a
1
,a
2
,a
3
) =
(0.12,0.07,0.03) are reasonable because the size of
this object is width = 22.8 cm, length = 11.7 cm,
and height = 5.1 cm, and the ratio of each side is
width:length:height = 4.47:2.29:1.0.
4.2 Recognition with Real Objects
The experiments conducted to check the performance
of the SVM, kNN, and LMNN classifiers for su-
perquadric classification in this section. Five types
of primitive-shaped objects were used for the experi-
ments (L = 5). The objects were cuboid (width = 20
cm, length = 20 cm, and height = 10 cm), large cube
(width = length = height = 25 cm), pyramid (width =
length = 20 cm), cylinder (radius = 10 cm, height =
20 cm), and small cube (width = length = height = 20
cm). These objects are shown in Fig. 3.
We constructed a dataset by capturing 240 data
(N = 240) per object placed on the floor. Each of
Table 1: Classification accuracy (%) with SVM.
SVM
Linear Poly RBF
F
1
45.3 51.2 62.3
F
2
42.5 38.8 52.0
F
3
60.8 64.2 73.5
Table 2: Classification accuracy (%) with kNN and LMNN
(k = 3,5).
kNN LMNN
k=3 k=5 k=3 k=5
F
1
62.2 60.5 60.0 60.2
F
2
68.1 68.1 65.4 65.4
F
3
74.7 76.5 78.9 79.5
these data were taken from different angle and posi-
tions. The 240 data were split into 160 data for train-
ing and 80 for test. To evaluate the effectivenessof the
superquadrics parameter, three different feature sets
(F
F
F
1
,F
F
F
2
, and F
F
F
3
) were selected for our comparison
experiments.
F
F
F
1
= (ε
1
,ε
2
),
F
F
F
2
= (a
1
,a
2
,a
3
),
F
F
F
3
= (ε
1
,ε
2
,a
1
,a
2
,a
3
).
(8)
Linear SVM and non-linear SVM (SVM with
polynomial kernel and RBF kernel) are evaluated in
this paper. Tab(1) shows that the SVM with an RBF
kernel has the best performance for feature vector
F
F
F
1
,F
F
F
2
, and F
F
F
3
, and it shows that feature vector F
F
F
3
has the best performance with kernels, which means
that not only the shape parameters but also the scale
parameters have to be effective for superquadric ob-
ject recognition. Comparing F
F
F
1
and F
F
F
2
, F
F
F
1
has bet-
ter performance than F
F
F
2
. This means that shape pa-
rameters are more valid than scale parameters. Fig.
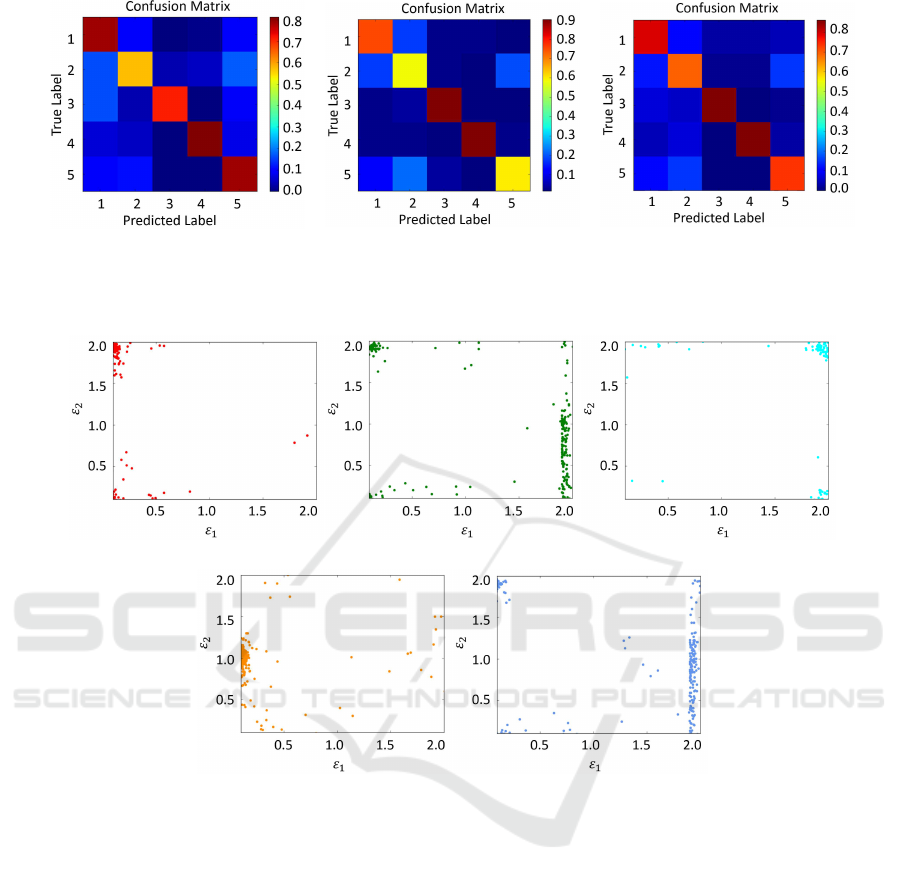
4 (a) shows the confusion matrix of the SVM classi-
fier when the set of C = 100.0,γ = 0.1. C and γ are
parameters of SVM with the RBF kernel, and these
parameters are optimized in our experiment.
Second, the experimental results for the kNN and
the LMNN classifier are shown in Tab. 2 with neigh-
borhood size k = 3. Fig. 4 (b) and (c) show the confu-
sion matrices of the kNN and LMNN classifiers when
k = 3. LMNN has the best performance (79.5%) in
comparison with the kNN (76.5%) and SVM (73.5%)
classifier with feature vector F
F
F
3
.
Fig. 5 shows the scatter plot of estimated pa-
rameters ε
1
and ε
2
for each object shown in Fig. 3.
We will take a closer look at Fig. 5 and Fig. 1.
Fig. 5(4) shows a scatter plot of ε
1
and ε
2
for the
Primitive Shape Recognition via Superquadric Representation using Large Margin Nearest Neighbor Classifier
329

(1a) (2a) (3a) (4a) (5a)
(1b) (2b) (3b) (4b) (5b)
(1)(ε
1
,ε
2
) = (0.10,0.18),(a
1
,a
2
,a
3
) = (0.12,0.07,0.03)
(2)(ε
1
,ε
2
) = (0.10,0.80),(a
1
,a
2
,a
3
) = (0.05,0.05,0.09)
(3)(ε
1
,ε
2
) = (0.10,0.10),(a
1
,a
2
,a
3
) = (0.10,0.02,0.03)
(4)(ε
1
,ε
2
) = (0.12,0.10),(a
1
,a
2
,a
3
) = (0.05,0.05,0.04)
(5)(ε
1
,ε
2
) = (0.10,0.10),(a
1
,a
2
,a
3
) = (0.06,0.11,0.02)
Figure 2: Five objects and the results of the superquadric parameter estimation (a: RGB Image object 3D data points b:
Superquadric surface).
(1) Cuboid (2) Large cube (3) Pyramid
(4) Cylinder
(5) Small cube
Figure 3: Primitive shapes used in the recognition section.
cylinder. Plots are concentrated in the vicinity of
(ε
1
= 0.1,ε
2
= 1), and (ε
1
= 0.1,ε
2
= 1) which also
represents a cylinder in Fig. 1. As the small cube and
large cube are the same shape on a different scale,
they have similar scatter plots. More interestingly,
most of the parameters are distributed in the vicin-
ity of (ε
1
= 2.0,0.1 < ε
2
< 2.0), the parameter repre-
sents an octahedron. For object (3), the pyramid, the
superquadrics cannot represent it(tetrahedron), so the
parameter of the pyramid is scattered in the vicinity of
the octahedron. As we explained in Section 4.1, there
is a double representation of the cube, and the param-
eters of the object (1), the cuboid, are distributed in
(ε
1
= 0.1,ε
2
= 0.1) and (ε
1
= 0.1,ε
2
= 2.0). This
double representation will be a crucial issue for recog-
nition accuracy.
5 CONCLUSIONS AND FUTURE
WORK
We proposed a method for recognizing primitive
shapes that are represented in superquadric parame-
ters using LMNN. The main novelty of this paper is
as follows:
• Applying the metric learning method LMNN for
primitive shape recognition with superquadric pa-
rameters.
The main contributions of this paper are as follows:
• Creating a the 3D primitive dataset captured by an
depth sensor.
• Estimating superquadric parameters for real daily
objects.
• Comparing the classification result for kNN,
SVM, and LMNN.
We evaluated the result of superquadric parame-
ter estimation, and recognition with these parameters.
We evaluated the two main experiments in order to
analyze superquadric parameter estimation and effec-
tiveness of LMNN. The superquadric parameters of
five kinds of daily objects were estimated, and the ap-
propriateness of the estimated parameters were eval-
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
330
(a) Confusion matrix with
SVM.
(b) Confusion matrix with
kNN.
(c) Confusion matrix with
LMNN.
Figure 4: Comparison of the confusion matrices of each classifier.
(1) Cuboid (2) Large cube (3) Pyramid
(4) Cylinder
(5) Small cube
Figure 5: Scatter Plot of (ε
1
,ε
2
) for each object shown in Fig. 3.
uated. The recognition using the estimated parame-
ters was evaluated. The proposed LMNN method was
compared with kNN and SVM, and the results showed
that LMNN had the best performance (79.5%).
In future work, based on the human recognition
system, we plan to segment objects into primitive
shapes so that objects can be represented in combi-
nations. Although there is a method for superquadric-
based segmentation (Leonardis et al., 1997), it is dif-
ficult to capture the dense 3D data of objects in real
environment. Therefore, we have to present a new
method that can segment the sparse 3D data of ob-
jects into primitive shapes.
ACKNOWLEDGEMENTS
This work was partially supported by MEXT/JSPS
Grant-in-Aid for Scientific Research(S) 24220004,
and JST CREST Intelligent Information Process-
ing Systems Creating Co-Experience Knowledge and
Wisdom with Human-Machine Harmonious Collabo-
ration
REFERENCES
Barr, A. H. (1981). Superquadrics and angle-preserving
transformations. IEEE Computer graphics and Ap-
plications, 1(1):11–23.
Biederman, I. (1987). Recognition-by-components: a the-
Primitive Shape Recognition via Superquadric Representation using Large Margin Nearest Neighbor Classifier
331

ory of human image understanding. Psychological re-
view, 94(2):115.
Burges, C. J. (1998). A tutorial on support vector machines
for pattern recognition. Data mining and knowledge
discovery, 2(2):121–167.
Chevalier, L., Jaillet, F., and Baskurt, A. (2003). Segmen-
tation and superquadric modeling of 3d objects. In
WSCG.
Drews Jr., P., Trujillo, P. N., Rocha, R. P., Campos, M.
F. M., and Dias, J. (2010). Novelty detection and
3d shape retrieval using superquadrics and multi-scale
sampling for autonomous mobile robots. In ICRA,
pages 3635–3640.
Garcia, S. (2009). Fitting primitive shapes to point clouds
for robotic grasping. Master of Science Thesis. School
of Computer Science and Communication, Royal In-
stitute of Technology, Stockholm, Sweden.
Leonardis, A., Jaklic, A., and Solina, F. (1997). Su-
perquadrics for segmenting and modeling range data.
IEEE Transactions on Pattern Analysis and Machine
Intelligence, 19(11):1289–1295.
Marr D, V. (1982). A computational investigation into the
human representation and processing of visual infor-
mation.
Moustakas, K., Tzovaras, D., and Strintzis, M. G. (2007).
Sq-map: Efficient layered collision detection and hap-
tic rendering. IEEE Transactions on Visualization and
Computer Graphics, 13(1):80–93.
Nieuwenhuisen, M., St¨uckler, J., Berner, A., Klein, R.,
and Behnke, S. (2012). Shape-primitive based object
recognition and grasping. In Robotics; Proceedings
of ROBOTIK 2012; 7th German Conference on, pages
1–5. VDE.
Pentland, A. P. (1986). Perceptual organization and the
representation of natural form. Artificial Intelligence,
28(3):293–331.
Press, W. H., Flannery, B. P., Teukolsky, S. A., and Vetter-
ling, W. T. (1986). Numerical recipes: the art of sci-
entific computing. Cambridge U. Press, Cambridge,
MA.
Raja, N. S. and Jain, A. K. (1992). Recognizing geons from
superquadrics fitted to range data. Image and vision
computing, 10(3):179–190.
Rusu, R. B., Blodow, N., and Beetz, M. (2009). Fast
point feature histograms (fpfh) for 3d registration. In
Robotics and Automation, 2009. ICRA’09. IEEE In-
ternational Conference on, pages 3212–3217. IEEE.
Rusu, R. B. and Cousins, S. (2011). 3d is here: Point cloud
library (pcl). In Robotics and Automation (ICRA),
2011 IEEE International Conference on, pages 1–4.
IEEE.
Saito, H. and Kimura, M. (1996). Superquadric modeling
of multiple objects from shading images using genetic
algorithms. In Industrial Electronics, Control, and In-
strumentation, 1996., Proceedings of the 1996 IEEE
IECON 22nd International Conference on, volume 3,
pages 1589–1593. IEEE.
Schnabel, R., Wahl, R., and Klein, R. (2007). Efficient
ransac for point-cloud shape detection. In Computer
graphics forum, volume 26, pages 214–226. Wiley
Online Library.
Solina, F. and Bajcsy, R. (1987). Range image interpretation
of mail pieces with superquadrics.
Solina, F. and Bajcsy, R. (1990). Recovery of paramet-
ric models from range images: The case for su-
perquadrics with global deformations. IEEE trans-
actions on pattern analysis and machine intelligence,
12(2):131–147.
Somani, N., Cai, C., Perzylo, A., Rickert, M., and Knoll,
A. (2014). Object recognition using constraints from
primitive shape matching. In International Sympo-
sium on Visual Computing, pages 783–792. Springer.
Strand, M., Xue, Z., Zoellner, M., and Dillmann, R. (2010).
Using superquadrics for the approximation of objects
and its application to grasping. In Information and Au-
tomation (ICIA), 2010 IEEE International Conference
on, pages 48–53. IEEE.
Suykens, J. A. and Vandewalle, J. (1999). Least squares
support vector machine classifiers. Neural processing
letters, 9(3):293–300.
Tang, S., Wang, X., Lv, X., Han, T. X., Keller, J., He,
Z., Skubic, M., and Lao, S. (2012). Histogram of
oriented normal vectors for object recognition with a
depth sensor. In Asian conference on computer vision,
pages 525–538. Springer.
Tombari, F., Salti, S., and Di Stefano, L. (2010). Unique sig-
natures of histograms for local surface description. In
European conference on computer vision, pages 356–
369. Springer.
Varadarajan, K. M. and Vincze, M. (2011). Object part
segmentation and classification in range images for
grasping. In Advanced Robotics (ICAR), 2011 15th
International Conference on, pages 21–27. IEEE.
Weinberger, K. Q. and Saul, L. K. (2009). Distance met-
ric learning for large margin nearest neighbor clas-
sification. Journal of Machine Learning Research,
10(Feb):207–244.
Xing, W., Liu, W., and Yuan, B. (2004). Superquadric-
based geons recognition utilizing support vector ma-
chines. In Signal Processing, 2004. Proceedings.
ICSP’04. 2004 7th International Conference on, vol-
ume 2, pages 1264–1267. IEEE.
Zhang, Z. (2012). Microsoft kinect sensor and its effect.
IEEE multimedia, 19(2):4–10.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
332
