
Sampling Density Criterion for Circular Structured Light 3D Imaging
Deokwoo Lee
1
and Hamid Krim
2
1
Youngsan University, Yangsan, Gyeongnam, South Korea
2
Department of Electrical and Computer Engineering, North Carolina State University, Raleigh, NC, U.S.A.
dwoolee@ysu.ac.kr, ahk@ncsu.edu
Keywords:
3D Reconstruction, Structured Light Pattern, Sampling Theorem, Geometry.
Abstract:
3D reconstruction work has chiefly focused on the accuracy of reconstruction results in computer vision, and
efficient 3D functional camera system has been of interest in the field of mobile camera as well. The optimal
sampling density, referred to as the minimum sampling rate for 3D or high-dimensional signal reconstruction,
is proposed in this paper. There have been many research activities to develop an adaptive sampling theorem
beyond the Shannon-Nyquist Sampling Theorem in the areas of signal processing, but sampling theorem for
3D imaging or reconstruction is an open challenging topic and crucial part of our contribution in this paper.
We hence propose an approach to sampling rate (lower / upper bound) determination to recover 3D objects
(surfaces) represented by a set of circular light patterns, and the criterion for a sampling rate is formulated
using geometric characteristics of the light patterns overlaid on the surface. The proposed method is in a sense
a foundation for a sampling theorem applied to 3D image processing, by establishing a relationship between
frequency components and geometric information of a surface.
1 INTRODUCTION
3D Imaging research has been extensively performed
since a few decades in the areas of computer vision,
image processing and pattern recognition for diverse
applications. In 3D reconstruction, a number of meth-
ods have been proposed for the problem and the pas-
sive (Kolev et al., 2014) and the active ((Geng, 2011),
(Lei et al., 2013)) methods have been widely applied
in practice. Both methods are based on establishing
a geometrical relationship of high dimensional sig-
nal (or 3D object points) and a low dimensional one
(or 2D image projected on the image plane). Readers
also can refer to about recent research of the passive
and the active methods and a hybrid method that com-
bines the passive and the active method for the further
improvement on the quality of the 3D reconstruction
results ((Chan et al., 2008), (Song et al., 2014)). Con-
sider f ∈ R
3
and f
′
∈ R
2
, the problem is to then re-
cover f from given information of f
′
, where f
′
is de-
termined by a transformation P , such that
f
′
= P f, (1)
where P is usually a projection operator (Faugeras
et al., 2001), and the operator yields an approximately
perfect reconstruction of f. In the field of image pro-
cessing and computer vision, the general principle
space in passive methods is triangulation using two
or more 2D image planes generated from a number of
cameras. The relative geometric relationship between
image planes located at different positions and a tar-
get object in 3D domain, and a successful correspon-
dence matching results provide sufficient information
required to recover 3D coordinates of an object sur-
face. The passive methods, however, sometimes fails
high quality reconstruction results because there ex-
ists a inherent limitation and disadvantages due to the
occlusion problem, low textured surface, high com-
putational complexity of the correspondence match-
ing, etc. To alleviate the limitations of the passive
method, active method using structured light patterns
has been employed for 3D reconstruction . The active
method, an alternative to the passive methods, also
solves the reconstruction problems based on the ge-
ometrical relationship between the components (op-
tical center, 3D points on the surface, location of a
light source) by replacing one camera with a light
source generating structured light patterns. It is ob-
vious that data acquisition procedure and efficient use
of data is crucial in reconstruction work in both pas-
sive and active methods. To achieve this efficiency,
reconstruction is closely related to sampling rate rep-
resented as the optimal number of light patterns. This
paper proposes an approach to a sampling theorem
for high dimensional signals and a sampling rate de-
478
Lee D. and Krim H.
Sampling Density Criterion for Circular Structured Light 3D Imaging.
DOI: 10.5220/0006147504780483
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 478-483
ISBN: 978-989-758-227-1
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

termination for structured light 3D imaging applica-
tions. In particular, we determine the lower and the
upper bound criterion of a sampling rate for the re-
construction using structured circular light patterns.
The active method on the basis of circular structured
light patterns provides simple, efficient reconstruc-
tion algorithm, and the active method (Geng, 2011),
in general, achieve accurate reconstruction result in
contrast to the passive method. Once we have one di-
mensional continuous signal, we are interested in the
minimum sampling rate (f
s
) which is represented as
f
s
= 2 f
max
or the maximum sampling interval (T
max
).
Akin to 1D signal, once fully reconstructed, the sur-
face which is a (image) signal of interest, represented
as 3D Euclidean coordinates (triangle meshes com-
posed of vertices and faces), is considered a continu-
ous signal, which yields a natural question about an
optimal number of circular light patterns necessary
for reconstruction of surfaces. The spatial sampling
density (or sampling rate), is defined as the minimum
number of circular patterns to be projected on a sur-
face. The minimum number of circular patterns leads
to the maximum sampling interval between neigh-
boring circular patterns. Determination of the mini-
mum number of the patterns is proposed in this paper.
The sampling rate determination in the field of 3D re-
construction using the structured light pattern has not
gained much attention in contrast to the research for
improving accuracy of reconstruction itself. In this
paper, the sampling rate is ultimately obtained from
the spatial maximum frequency component which is
closely related to geometric characteristics of an ob-
ject surface. This paper proposes the approach to
derivation of the upper and the lower bound of a sam-
pling rate for the surface reconstruction and the sim-
ulations results are also shown to verify the proposed
approaches.
2 SAMPLING RATE
This section details the derivation of the minimum
sampling rate which leads to sufficient representa-
tion of 3D characteristics of a target object surface.
This paper uses curvature information to determine
the minimum sampling rate, and frequency compo-
nents of the surface is derived by establishing a rela-
tionship between curvature and frequency. Intuitively,
required number of circular patterns is determined by
geometric surface shape, for instance, larger number
of the patterns is required for the surface which has
frequent variation of a surface shape. As previously
stated, surface shape deforms a set of concentric cir-
cular patterns. In other words, deformation can be
……
.
j=1 j=2
j=3
j=4
j=5
j=N
i=1
i=2 i=3
............
i=M
i=10
.
.
..........
Figure 1: i and j respectively index the number of points(M)
in each patterns, and the pattern’s position.
represented quantitatively by measuring curvatures of
the patterns projected onto the surface (i.e., original
circle has a constant curvature, but the curvatures are
not constant in deformed circles). These curvatures
can lead to developing a sampling criterion for a sur-
face reconstruction if the relationship between spatial
frequency components and curvature information is
established. This section establishes the relationship
to achieve sampling rate determination. In practice,
given small amount geometric information (i.e., high-
est curvature that is corresponding to a point of high-
est variation in the surface), sampling rate is directly
determined and leads to efficient reconstruction (ap-
proximate geometric reconstruction) system. In this
paper, we assume that we are given the initial num-
ber of circular patterns that are sufficient to represent
3D object (i.e., oversampled) to theoretically derive a
sampling criterion for a surface reconstruction. Once
3D coordinates of a surface are provided, we denote
the surface and the discretely sampled surface (sam-
pled by N concentric circular patterns) by S
w
and S
3
,
represented as
S
w
= {x
w
,y
w
,z
w
}, (2)
S
3
= {x
ij
,y
ij
,z
ij
}, (3)
i = 1,2, ..., M, j = 1,2,.. . ,N,
where where i and j respectively index the number
of points in each patterns, and the pattern’s position
(Fig. 1). Since the present work aims at deriving the
minimum number of the patterns, this paper chiefly
deals with pattern-wise sampling rather than point-
wise sampling under the assumption that M is suffi-
ciently large. Fig. 2, we view j = 1,2, ..., N as a time
index, and the signal of interest is given by
S
3
(t) = {x
i
(t), y
i
(t), z
i
(t)}, (4)
i = 1, 2,.. . ,M, j = 1, 2,.. . ,N.
A sufficiently large N makes S
3
(t) dense and close to
a continuous signal, which we in turn use to introduce
sampling technique using a 1D signal. S
1
(t) is defined
Sampling Density Criterion for Circular Structured Light 3D Imaging
479

d d
Light
Projection
Onto
A Surface
d
1
d
2
1 2
d d
t=1
t=2
t=3
t=N
S
L
domain
S
3
domain
Figure 2: Indices of the location of each curve alternatively
represented as time t to introduce a concept of a frequency
component of a surface.
in the continuous time and S
1
[n] = S
1
(nT) is defined
is the discrete time domain. The Fourier transform of
S
1
(t), S
1
: R → R, is denoted by
S
1
(ω) =
Z
∞
−∞
S
1
(t)e
−jωt
dt, (5)
where ω = 2πf, is a radian frequency. If we assume
that S
1
(t) is bandlimited, has a finite energy (square-
summable or square-intergrable in Lebesgue’s sense)
(Unser, 2000) and is sampled at the points t
n
= nT,
then S
1
(t) can be reconstructed with an appropriate T
as follows :
S
1
(nT) =
∞
∑
n=−∞
S
1
(t)ϕ
2
(t −nT), (6)
S
1
(t) = S
1
(nT) ⋆ ϕ
1
(nT)
=
∞
∑
n=−∞
S
1
(nT)ϕ
1
(t −nT), (7)
(8)
where ’⋆’ denotes the convolution operator, t can be
a time or a index of a sample (e.g., sampled pattern
in Fig. 1, and ϕ
1
(t) and ϕ
2
(t) are orthogonal basis
functions,
< ϕ
1
(k),ϕ
2
(k) >= δ(k −l), (9)
where ’<, >’ is an L
2
inner product operation and δ(t)
is the Dirac delta function. ϕ
1
(t) and ϕ
2
(t) are se-
lected appropriately to solve the reconstruction prob-
lem and are ideal lowpass filters in this paper (i.e.
sinc function) ((Higgins, 2003), (Jerri, 1977), (Mallat,
1989), (Papoulis, 1977), (Unser, 2000)). The recon-
struction process then can be written as
S
1
(t) =
∞
∑
n=−∞
S
1
(nT)sinc(ω
0
(t −nT)), (10)
where sinc(ω
0
(t − nT)) = sin(ω
0
(t − nT))/ω
0
(t −
nT) is a sinc function. Recovery of S
1
(t) from S
1
(nT)
is perfectly conducted by sampling the points from
S
1
(t), or by selecting an appropriate sampling fre-
quency f
s
, where f
s
= 1/T. Akin to determining the
sampling frequency for a 1D signal, our reconstruc-
tion of a surface, S
3
(t) will seek the maximal fre-
quency component f
max
, and this approach can be ap-
plied to any type of signals. We assume that the signal
of interest S
3
(t) is bandlimited or pre-processed by
appropriate filters (Eldar and Pohl, 2009). The sam-
pling rate f
s
provides a sufficient criterion for a ge-
ometric signal recovery, and it is defined in the unit
arc length or pixel. The minimum number of circular
patterns N
s
for the reconstruction is simply obtained
as follows :
N
s
= f
s
×N = 2 f
max
×N, (11)
where N is the initial number of circular patterns pro-
jected onto the surface to extract 3D coordinates, and
N
s
is the minimum number of patterns to reconstruct
the surface. In the experiments with synthetic data,
we initially determine N which can fully reconstruct
(or represent) 3D geometric information of a target
object surface.
2.1 Sampling Rate using the Two-Third
Power Law
Quantifying a surface shape is tantamount to extract-
ing sufficient geometric information (e.g., tangent
vectors, curvatures, etc.) from a surface. To that end,
curvature, the first derivative of a tangent vector, is ge-
ometric information for estimating spatial frequency
components, and the curvature is better to describe
geometric properties of 3D object because it is view-
point invariant. The Two-Third Power Law (Lee and
Krim, 2011), proposed by Paolo Viviani (Lacquaniti
et al., 1983) explains a relationship between an ab-
solute angular velocity and curvature for constrained
movements (Fig. 3). In this method, the constrained
movement of points comprises a curve, from which
we can estimate an angular velocity and curvature of
a curve composed of points. In Fig. 3, r is an Eu-
clidean distance from the reference point to any point
P,
−→
T is a tangent vector, and κ is a curvature based on
an osculating circle where radius is R, and V is an an-
gular velocity which satisfies the following equations
(de’Sperati C and P, 1997):
V(t) = K ·
R(t)
1+ αR(t)
!
1−β
, (12)
V(t) = r(t)ω = 2πr(t) f,
where K depends on the movement duration, called
a velocity gain, α and β are parameters (α, β ∈ R).
Given R(t), and r(t), recall that our purpose here is
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
480

r
T
!
1
( )
dT
s
ds R
! !
!
P
Figure 3: The Two-Thirds Power Law explains a relation-
ship between a geometrical information (i.e. curvature) and
an angular velocity of a curve. Angular velocity is com-
posed of a radius r and an angular frequency ω.
to estimate the maximal frequency component, f
max
,
Eq. (12) is rewritten as follows :
f =
1
2πr(t)
K ·
R(t)
1+ αR(t)
!
1−β
. (13)
Eq. (13) hence yields the maximal frequency compo-
nent and a sampling frequency estimation based on a
Nyquist rate :
f
max
= max
"
1
2πr(t)
K ·
R(t)
1+ αR(t)
!
1−β
#
(14)
f
s
≥ 2f
max
. (15)
Having established the algorithm for a spatial sam-
pling frequency estimation, sampling rate for 3D
object surface is considered. Extended to a 3-
dimensional signal, projected circular patterns on a
surface have two tangential vectors (Fig. 5). Hence,
two curvature components (κ
1ij
and κ
2ij
), the first
derivative of tangential vectors, T
1ij
and T
2ij
are de-
fined at P
ij
with respect to the arc length. For a 3D
signal (i.e., surface), at any point P
ij
, if two orthogo-
nal tangent vectors are selected, then two correspond-
ing curvatures are defined as well.
We can hence acquire the frequency components
corresponding to κ
1ij
and κ
2ij
, respectively, and The
Two-Thirds Power Law for a 3D surface may also be
written as :
ω
1ij
= 2π f
1ij
=
1
r
1ij
·
R
1ij
1+ αR
1ij
!
1−β
, (16)
ω
2ij
= 2π f
2ij
=
1
r
2ij
·
R
2ij
1+ αR
2ij
!
1−β
, (17)
r
1ij
= r
2ij
= r
ij
,
i = 1, 2,.. . ,M, j = 1,2,.. .,N,
!
1 1
, ,
M
N
ij ij ij ij
i j
P x y z
Figure 4: Example of 3D face model(fvinput data).
( 1)thj
1ij
T
!
2ij
T
!
ij
P
th curve(pattern)j
( 1)thj
Figure 5: Vectors defined on a point in a facial curve.
where R
1ij
and R
2ij
are 1/κ
1ij
and 1/κ
2ij
, re-
spectively, and M is the number of points on each
curve and N is the number of curves (patterns) on
the surface. To determine the minimum sampling
rate (2 ×max( f
ij
)) consistent with the Nyquist Rate,
the maximum frequency component, max(f
ij
) is re-
quired, and we define max(f
ij
) as
max( f
ij
) = max[sup( f
1ij
),sup( f
2ij
)]. (18)
Using the relationship between the frequency
component, f
ij
and the corresponding r
ij
, the maxi-
mum frequency is calculated. Prior to measuring the
global maximum f
ij
, local maximum sup( f
1ij
) and
sup( f
2ij
) should be acquired, and each of which sat-
isfies the following,
sup( f
kij
) ≤
1
2π
sup
1
r
kij
·
R
kij
1+ αR
kij
!
1−β
!
, k= 1,2.
(19)
Prior to the measurement of curvatures and r
ij
’s of
all the points of the deformed circular patterns, a nor-
malization of data points is carried out. The normal-
ization yields the determination of the intrinsic char-
acteristics of each curve projection on the surface.
Sampling Density Criterion for Circular Structured Light 3D Imaging
481

2.2 Proposed Sampling Rate
Determination
In case of any dimensional signal, sampling rate can
be determined using curvature information. Using a
Fourier Series, any signal can be represented as a
combination of sinusoidal signal. Based on the princi-
ple of Fourier Series, a signal (or a curve) can ba rep-
resented as α(t) = [t,cosωt],where ω is a frequency
component of a signal. Once α(t) is determined, we
use the following information to estimate a curvature:
α
′
(t) =
dα(t)
dt
= [1, −ωsinωt], (20)
α
′′
(t) =
dα(t)
2
d
2
t
= [0, −ω
2
cosωt]. (21)
For any regular curves, curvature is defined as (Oprea,
2007)
κ =
|α
′
×α
′′
|
|α
′
|
3
, (22)
where α = α(t), × represents the outer product
between two vectors. To achieve the minimum sam-
pling rate, we do not have to measure all curvature
or frequency information. Because a maximal fre-
quency component contributes to the minimum sam-
pling rate. Thus, we represent the target signal as just
α(t) = [t,cosωt] or α(t) = [R(t),z(t)]. If we use cir-
cular patterns each of which has a radius R(t) = t, z(t)
can be represented as a combination of sinusoidal sig-
nals, and ω can be a dominant frequency component,
α(t) = [t,cosωt] is sufficient representation. Curva-
ture can be written as
κ =
|−ωcosωt|
1+ ω
2
sin
2
ωt
3/2
≤
ω
2
1+ ω
2
sin
2
ωt
3/2
. (23)
Then, κ is bounded by 0 ≤ κ ≤ ω
2
and the fre-
quency component can be written as
κ ≤ 4πf
2
,
f ≥
1
2π
√
κ. (24)
Since κ is any curvature value,
f ≥
1
2π
√
κ
max
. (25)
Although this approach is very simple and
straightforward, we only have minimum bound of a
frequency component, which is a drawback of the di-
rect method.
3 SIMULATION RESULTS
Having established representations for colored and
geometric faces, a sampling criterion determines the
minimum number of curves (patterns) to reconstruct
surfaces. Using the algorithms proposed above, the
sampling rate of the surface is shown in Table. I.
7 3D face models are used and they are composed
of vertices and faces. The estimated minimum sam-
pling rate, N
s
, derived from algorithms in the previ-
ous sections, for 5 real face models and 2 synthetic
ones, are shown in Table. I. As shown in Table. I, for
instance, 147 circular patterns are projected onto the
target 3D face and the reconstruction is carried out.
Once reconstructed with 147 patterns, the minimum
number of the patterns is derived based on Eq.s 19
and 25, and try to achieve reasonable reconstruction
result that does not have significant loss of informa-
tion
4 SUMMARY AND CONCLUSION
In this paper, sampling rate determination for 3D re-
construction using structured light patterns has been
discussed. To the best of our knowledge, sampling
rate determination has not been of much interest in the
areas of computer vision and 3D imaging. Although
there have been extensive research about accurate 3D
reconstruction, the efficient reconstruction employing
sampling theorem in 1D signal has been little inves-
tigated. The proposed approach is very efficient and
simple from practical perspectives only by using cur-
vature information defined in facial curves that are
projected light patterns. In practice, there also have
been extensive research about face recognition using
facial curves and our approach also can be used for
efficient 3D face recognition work. Deformation of
a projected light pattern is important key to a recon-
struction and a sampling rate determination in this pa-
per. Although many works about reconstruction have
been done, this is very challenging work to use a cir-
cular pattern and to analyze a relationship of deforma-
tion of a 2D and a 3D image. In aspect of efficiency,
the optimal sampling rate was induced from a cur-
vature estimation. Before determining sampling rate,
we estimated curvatures of set of curveson the 3D ob-
ject. 3D curves are exactly mapped to 2D curves and
these are topologically equivalent to each other. The
highest curvature or the biggest distorted light pattern
on 3D surface is shown as the biggest distorted curve
on 2D image. This implies that values of curvature on
3D are also mapped to the values of curvature on 2D
image. Since a curvature estimation is a method of es-
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
482
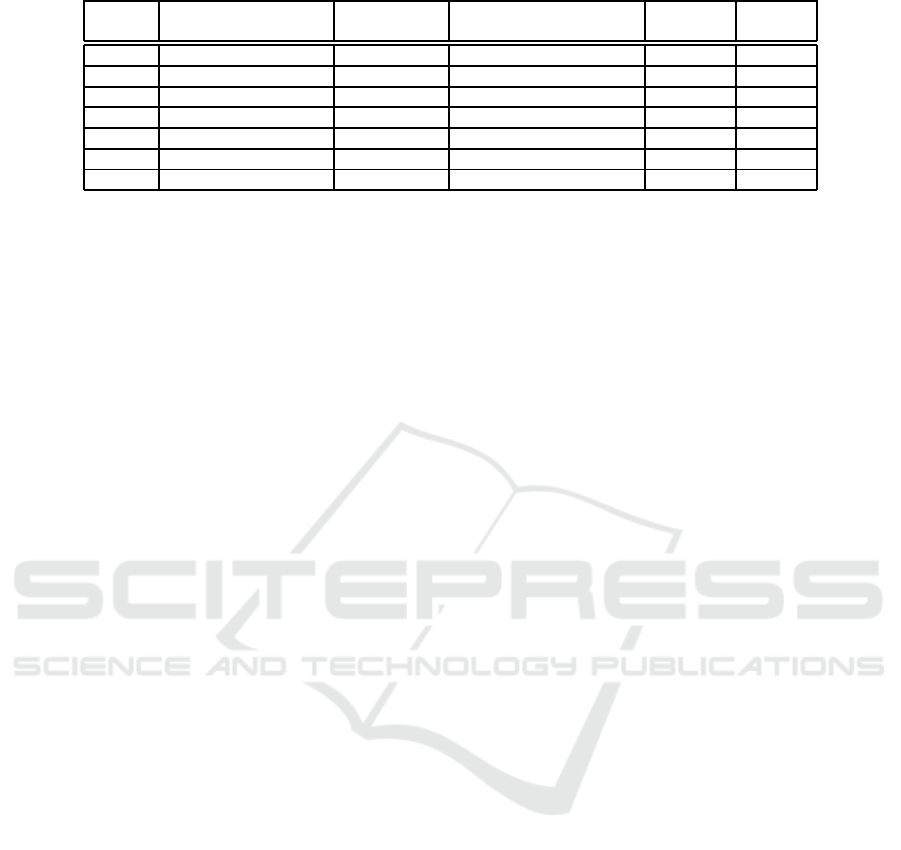
Table 1: Estimated minimum number of patterns.
N f
s
[1/arc length] N
s
(Initial number of patterns) (Sampling rate) (Minimum number of patterns) Size(vertex) Size(face)
Brian 147 0.38 56 15926×3 23526×3
Eric 153 0.40 62 17266×3 23567×3
Greg 142 0.33 47 16257×3 28023×3
Jeff 221 0.49 109 16080×3 18522×3
Weihong 271 0.33 90 15769×3 26959×3
fvgallary 89 0.30 27 5031×3 9999×3
fvinput 93 0.44 41 16092×3 32116×3
timation of curves’ shape, we used average curvature
of each curve in each unit space. So, curvature infor-
mation can tell us the characteristic of curves which is
matched to signal function. Given a maximal curva-
ture variation, we could find the sampling rate and de-
termined the number of light patterns to be projected
for reliable 3D surface reconstruction. In addition,
we have presented an alternative algorithm to deter-
mine the sampling rate of a surface (or defining the
minimum number of light patterns to be projected on
a surface whose maximal curvatures may be known)
subjected to an active light source probing. Such a
rate, in turn plays a key role in the efficient represen-
tation of a surface and its subsequent reconstruction
from these patterns. While our primary application of
interest lies in the area of biometrics and face mod-
eling, the two-thirds-based sampling criterion may
be exploited in many different settings where surface
representation and sampling are of interest (e.g. sur-
face archiving). Although our sampling rate does not
recover the surface perfectly as the Shannon-Nyquist
Sampling Rate does for 1D signals, the sampling cri-
terion we proposed does not show a considerable in-
formation loss to be recognized. In the future, there
are some technical issues to be considered - quantify-
ing the algorithm efficiency (i.e. computational com-
plexity) and the reconstruction accuracy compared to
the previous methods is needed.
REFERENCES
Chan, Y., Delmas, P., Gimel’farb, G., and Valkenburg, R.
(2008). On fusion of active range data and passive
stereo data for 3d scene modelling. In Image and
Vision Computing New Zealand, 23rd International
Conference. IEEE.
de’Sperati C and P, V. (1997). The relationship between cur-
vature and velocity in two-dimensional smooth pur-
suit eye movements. The Journal of Neuroscience,
17(10):3932 – 3945.
Eldar, Y. C. and Pohl, V. (2009). Recovering signals from
lowpass data. CoRR, abs/0907.3576.
Faugeras, O., Luong, Q.-T., and Papadopoulou, T. (2001).
The Geometry of Multiple Images: The Laws That
Govern The Formation of Images of A Scene and Some
of Their Applications. MIT Press, Cambridge, MA,
USA.
Geng, J. (2011). Structured-light 3d surface imaging: atu-
torial. Adv. Opt. Photon., 3(2):128–160.
Higgins, J. (2003). A sampling theorem for irregularly
spaced sample points (corresp.). IEEE Transactions
on Information Theory, 22(5):621 – 622.
Jerri, A. J. (1977). The shannon sampling theorem - its
various extensions and applications: A tutorial review.
Proceedings of the IEEE, 65(11):1565 – 1596.
Kolev, K., Tanskanen, P., Speciale, P., and Pollefeys, M.
(2014). Turning mobile phones into 3d scanners. 2014
IEEE Conference on Computer Vision and Pattern
Recognition (CVPR), 00(undefined):3946–3953.
Lacquaniti, F., Terzuolo, C., and Viviani, P. (1983). The law
relating the kinematic and figural aspects of drawing
movements. Acta Psychologica, 54(13):115 – 130.
Lee, D. and Krim, H. (2011). A sampling theorem for a
2d surface. In Scale Space and Variational Methods
in Computer Vision - Third International Conference,
SSVM 2011, Ein-Gedi, Israel, May 29 - June 2, 2011,
Revised Selected Papers, pages 556–567.
Lei, Y., Bengtson, K., Li, L., and Allebach, J. (2013). De-
sign and decoding of an m-array pattern for low-cost
structured light 3d reconstruction systems. In Im-
age Processing (ICIP), 2013 20th IEEE International
Conference on.
Mallat, S. G. (1989). A theory for multiresolution sig-
nal decomposition: The wavelet representation. IEEE
Trans. Pattern Anal. Mach. Intell., 11(7):674–693.
Oprea, J. (2007). Differential Geometry and Its Applica-
tions. Mathematical Association of America, 2nd edi-
tion.
Papoulis, A. (1977). Signal analysis. Electrical and elec-
tronic engineering series. McGraw-Hill, New York,
San Francisco, Paris.
Song, Y., Glasbey, C. A., Polder, G., and van Heijden, G. W.
(2014). Non-destructive automatic leaf area measure-
ments by combining stereo and time-of-flight images.
IET Computer Vision, 8(5):391–403.
Unser, M. (2000). Sampling—50 Years after Shannon. Pro-
ceedings of the IEEE, 88(4):569–587.
Sampling Density Criterion for Circular Structured Light 3D Imaging
483
