
Coherent Ray-Space Hierarchy Via Ray Hashing and Sorting
Nuno T. Reis, Vasco S. Costa and Jo
˜
ao M. Pereira
INESC-ID / Instituto Superior T
´
ecnico, University of Lisbon, Rua Alves Redol 9, 1000-029 Lisboa, Portugal
Keywords:
Rasterization, Ray-Tracing, Ray-Hashing, Ray-Sorting, Bounding-Cone, Bounding-Sphere, Hierarchies,
GPU, GPGPU.
Abstract:
We present an algorithm for creating an n-level Ray-Space Hierarchy (RSH) of coherent rays that runs on a
GPU. Our algorithm uses a rasterization stage to process the primary rays, then inputs those results in the RSH
stage which processes the secondary rays. The RSH algorithm generates bundles of rays, hashes them and sorts
them. Thus we generate a ray list containing adjacent coherent rays to improve the rendering performance of
the RSH vs a classical approach. Moreover, scene geometry is partitioned into a set of bounding spheres and,
then, intersected with the RSH to further decrease the amount of false ray bundle-primitive intersection tests.
We show that our technique notably reduces the amount of ray-primitive intersection tests, required to render
an image. In particular it performs up to 50% better in this metric than other algorithms in this class.
1 INTRODUCTION
Naive Ray-Tracing (RT), algorithmic complexity is N
x M where N rays are tested against M polygons. Per-
formance is thus low, especially with complex scenes
due to the amount of intersection tests. To optimize
this naive approach, two common scene partition ap-
proaches, Object Hierarchies and Spatial Hierarchies,
are followed to reduce the intersection tests. Our work
instead focuses on Ray Hierarchy optimizations. This
is a less well explored area of the RT domain and one
that is complementary to the Object-Spatial Hierar-
chies. In particular, this paper presents the Coher-
ent Ray-Space Hierarchy (CRSH) algorithm. CRSH
builds upon the Ray-Space Hierarchy (RSH) (Roger
et al., 2007) and Ray-Sorting algorithms (Garanzha
and Loop, 2010). RSH uses a tree where each node
stores a bounding sphere-cone containing a set of
rays. The tree is built via a bottom-up procedure and
traversed in a top-down fashion. Our CRSH algorithm
adds Ray-Sorting to achieve higher efficiency in each
tree node and then expands on this basis with mesh
culling and improved hashing methods.
We hypothesize that improving the coherency of
the rays within each tree node shall lead to tighter
bounding sphere-cones, reducing the amount of inter-
sections. We use hashing, tuned to the type of the ray
(e.g. shadow, reflection and refraction), to improve hi-
erarchy efficiency. Finally we introduce whole mesh
bounding spheres to reduce intersection tests at the hi-
erarchy top level. This shallow spherical BVH allows
us to reduce ray-primitive intersections. We note that
our technique uses a rasterization stage to compute
primary rays, RT is reserved for secondaries.
Our main contributions are:
- a compact ray-space hierarchy (RSH) based on
ray-indexing and ray-sorting to reduce the amount
of ray-primitive intersections.
- improved hashing methods.
- culling meshes from the RSH prior to primitive
traversal.
2 BACKGROUND AND RELATED
WORK
Ray-tracing (Whitted, 1980) is a global illumination
technique for synthesis of realistic images through re-
cursive ray-casting. The ray tracing algorithm casts
primary rays from the eye. When the rays intersect
geometry they can generate extra secondary rays: e.g.
shadow, reflection and refraction rays.
These rays differentiate ray-tracing from the ras-
terization algorithm as they allow realistic reflec-
tions, refractions and shadows without additional
techniques. However at a cost making the ray-tracing
approach compute expensive. There is extensive and
ongoing research around its optimization. Much re-
search involves hierarchies, in the Object or Spatial
T. Reis N., S. Costa V. and M. Pereira J.
Coherent Ray-Space Hierarchy Via Ray Hashing and Sorting.
DOI: 10.5220/0006098001950202
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 195-202
ISBN: 978-989-758-224-0
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
195
domains, to decrease intersection tests in a divide and
conquer fashion.
Object and Spatial Hierarchies help accelerate in-
tersection calculations by culling polygons and ob-
jects far from the rays, hence by reducing the amount
geometry to test.
Ray-Space Hierarchies, use ray bundles or ray
caching to achieve the goal of reducing intersections.
Instead of creating hierarchies based on scene geom-
etry, they are based on the rays being cast in each
frame. Our work is based on this approach and em-
ploys ray bundling and ray hashing (Arvo and Kirk,
1987) (Aila and Karras, 2010).
Roger et al. (Roger et al., 2007)’s RSH algorithm
has five steps. The scene is first rasterized, for the
primary ray trace output, unlike in a traditional ray-
tracer. The first batch of secondary rays is generated
using this information and becomes the basis for the
RSH. The secondaries are bundled into nodes with a
sphere bounding ray origins and a cone bounding ray
directions: this is the bottom-level of the tree. Up-
per levels are created by merging nodes from lower
levels. Once the top-level is reached, the scene ge-
ometry is intersected with the RSH. Hits are stored as
triangle-id/node-id integer pairs. Only these hits will
be tested at the lower levels of the tree, reducing in-
tersection tests within each level. However, since rays
aren’t sorted, even at lower levels of the tree, nodes
will be quite wide requiring too much geometry inter-
sections and increasing the amount of intersections.
We attempt to solve this problem by sorting rays prior
to creating the RSH.
Garanzha and Loop (Garanzha and Loop, 2010)
introduced an algorithm using parallel primitives to
adapt the ray-tracing algorithm to the GPU. Their al-
gorithm sorts generated rays and creates tight-fit frus-
tums on the GPU and then intersects them with the
scene’s Bounding Volume Hierarchy (BVH) tree built
on the CPU. One of the most interesting aspects is the
fast ray sorting step which is done with parallel GPU
primitives. This reduces the overall time of the op-
eration. This approach can be combined with Roger
et al’s (Roger et al., 2007) algorithm to create a more
efficient RSH.
The DACRT (Mora, 2011) algorithm employs
a ray-stream approach that generates a kd-tree on
the fly, while traversing scene geometry, in order to
achieve a low time to first image. Similarly to Roger’s
RSH it also uses conic packets to bundle secondary
rays. However this procedure is limited by the fact
that it can only bundle rays with the exact same origin
within the same cone. In addition it ray-traces pri-
mary rays. This has additional computational over-
head, compared to a rasterization mechanism, hence
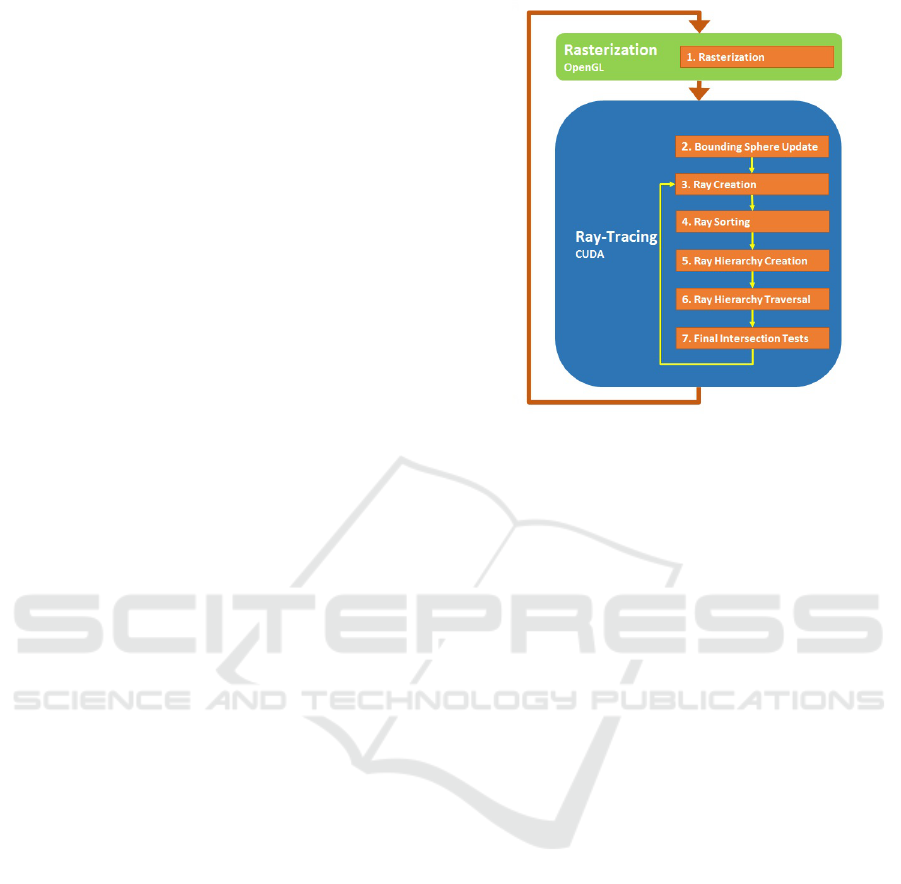
Figure 1: Coherent Ray-Space Hierarchy Overview.
it has worse rendering performance at primaries and
less opportunities for bundling secondaries.
CHC+RT (Mattausch et al., 2015) uses combined
hierarchies in ray space (RSH) and object space
(BVH). It does not use explicit ray bounding prim-
itives. It conservatively culls non-intersecting trian-
gle and screen-space batches. This approach is more
compute intensive on later stages due to the much
simpler RSH, but results in less branch divergence,
making it suitable for GPU implementation. The
BVH is built offline, on the CPU, then transferred
to the GPU. This high quality BVH has fast traver-
sal time, for rapid rendering of static or rigid-body
scenes, but the technique is poorly suited for dynamic
geometry with a high time to first image.
3 OUR ALGORITHM
Our algorithm is performed in seven steps (see Fig-
ure 1). In each frame, steps 1 and 2 are executed just
once while steps 3 through 7 are executed once per ray
batch. Batches can have any combination of shadow,
reflection, or refraction rays.
3.1 Rasterization
Rasterization is the first step to be performed. Al-
though Rasterization solves the rendering problem
conversely vs Ray-Tracing (i.e. projecting primi-
tives to the screen, vs projecting rays backwards to
the primitives), one can complement the other. The
first set of rays, the primary rays, does not convey
the global illumination effects that Ray-Tracing can
GRAPP 2017 - International Conference on Computer Graphics Theory and Applications
196

achieve, e.g. Shadows, Reflections and Refractions.
Hence Rasterization can convey visual results similar
to tracing primary rays, while being much faster and
optimized in graphics hardware. Supplementing the
Rasterization of primary rays with the Ray-Tracing
of secondary rays get us the benefits from both tech-
niques: the efficiency of Rasterization and the global
illumination effects from Ray-Tracing.
In order to combine both techniques, the output
from the fragment shaders used to rasterize the scene
must provide more than just the fragment colors. We
have to create different render targets according to the
information we want to store. In our case, we output
for each fragment its position and normal as well as
its diffuse and specular properties. In terms of imple-
mentation, the fragment shader outputs four different
textures, each containing four 32-bit floats per pixel.
These textures are generated with OpenGL/GLSL and
are then the first level of secondary rays are computed
in CUDA.
3.2 Ray-Tracing
3.2.1 Bounding Sphere Update
Here we update object bounding spheres according
to the transformations (e.g. translate, scale) applied
to the object they contain. Since we only update
the center and radius, there is no need to recalcu-
late the bounding spheres in each frame (transforma-
tions do not invalidate bounding spheres). The min-
imum bounding sphere of the object meshes is pre-
computed with (G
¨
artner, 1999)s algorithm so there is
no impact on render time performance.
3.2.2 Secondary Ray Creation
After the Rasterization step, we generate the sec-
ondary rays. We create an index, for each individual
ray, to speed up ray sorting later on. We use a different
hashing function for each type of ray (see Figures 2,
3). Since each ray has an origin and a direction it
would be straightforward to use these parameters to
create our hash. However for shadow rays it is suf-
ficient to use the light-index, and the ray direction.
This is doable if we invert the origin of the shadow
ray so that it is located at the light source rather than
the originating fragment. To reduce the size of the
hash keys we convert the ray direction into spherical
coordinates (Glassner, 1990) and store both, the light
index and the spherical coordinates, into a 32-bit in-
teger, with the light index having the higher bit-value
such that the shadow rays are sorted a priori according
to the light source.
Figure 2: Shadow Ray Hash.
The Reflection and Refraction rays are also con-
verted to spherical coordinates. However, in this case,
the ray origin is used in the hash, given that these
rays are not coherent with regards to the origin, un-
like shadow rays.
Figure 3: Reflection and Refraction Ray Hash.
Once generation is complete, we have an array
with the generated secondary rays as well as two ar-
rays with the ray keys (ray hashes) and the ray val-
ues (ray position in the ray array) and a final array
with head flags which indicate if there is a ray in the
corresponding position within the key-value arrays,
where we store either a 0 or a 1, indicating if there is
a ray or not, respectively. Using the information from
the head flags array we then run a trimming operator
on the key-value arrays (see Figure 4). This is done
by first applying an inclusive scan operator (Merrill
and Grimshaw, 2009) on the head flags array, which
gives us the number of positions each pair needs to be
shifted to the left. This is done in order to trim the
arrays (Pharr and Fernando, 2005).
Figure 4: Array Trimming.
3.2.3 Secondary Ray Sorting
Here we use a compression-sorting-decompression
scheme, expanding on prior work by Garanzha and
Loops (Garanzha and Loop, 2010). The compression
step exploits the local coherency of rays. Even for
secondary rays, the bounces generated by two adja-
cent rays have a good chance of being coherent. This
can result in the same hash value for both bounces.
Given this information, we compress the ray key-
value pairs into chunks, minimizing the number of
Coherent Ray-Space Hierarchy Via Ray Hashing and Sorting
197
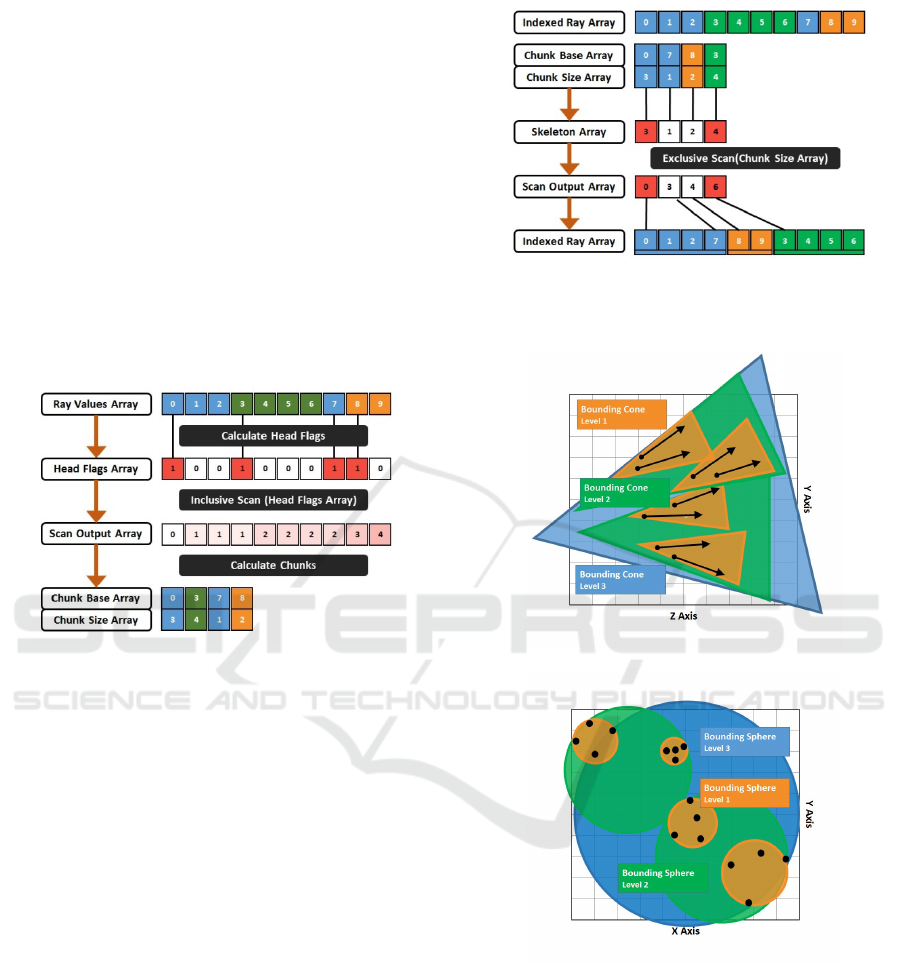
pairs that need to be sorted. To compress the pairs
we utilize a head flags array with the same size as the
key-value pair array, initializing it with 0s in every
position and inserting 1s into positions in which the
key (hash) of the corresponding pair differs from the
previous pair. After populating the head flags array
we apply an inclusive scan operator on it (Merrill and
Grimshaw, 2009). By combining the head flags array
with the scan output array we create the chunk keys,
base and size arrays, which contain the hash, start-
ing index and size of the corresponding chunks (see
Figure 5). The chunk keys are represented in differ-
ent colors at the image below. The chunk base array
represents the original position of the first ray in the
chunk while the chunk size array represents the size
of the chunk, needed for the ray array decompression.
Figure 5: Ray Compression into Chunks.
After ray compression we have an array of chunks
with the information required to reconstruct the initial
rays array. So we can begin the actual sorting. We
radix sort (Merrill and Grimshaw, 2010) the chunks
array according to the chunk keys.
Decompression works by creating a skeleton ar-
ray. This skeleton array is similar to the head flag
arrays we created before except that it contains the
size of the sorted chunks. Next we apply an exclusive
scan operator on the skeleton array. This will give us
the positions of the chunks starting positions on the
sorted key and value arrays. After creating these two
arrays for each position in the scan array we fill the
sorted ray array. We start in the position indicated in
the scan array and finish after filling the number of
rays contained within the corresponding chunk.
3.2.4 Ray Hierarchy Creation
With the sorted rays we can now create the actual hi-
erarchy. Since the rays are now sorted coherently the
hierarchy will be much tighter in its lower levels, giv-
ing us a smaller number of intersection candidates as
we traverse further down the hierarchy. Each node in
the hierarchy is represented by a sphere and a cone
Figure 6: Ray Decompression from Chunks.
(see Figures 7, 8).
Figure 7: Bounding Cone - 2D View.
Figure 8: Bounding Sphere - 2D View.
The sphere contains all the nodes ray origins while
the cone contain the rays themselves (see Figure 9).
This structure is stored with eight floats: the sphere
center and radius (four floats) and the cone direction
and spread angle (four floats). Construction of the
hierarchy is done in a bottom-up fashion. We start
with the leaves, with spheres of radius 0 and a cone
spread angle equal to 0. These leaves correspond to
sorted rays. Parent nodes are created by merging child
nodes. The number of children combined per node is
parametrized.
GRAPP 2017 - International Conference on Computer Graphics Theory and Applications
198
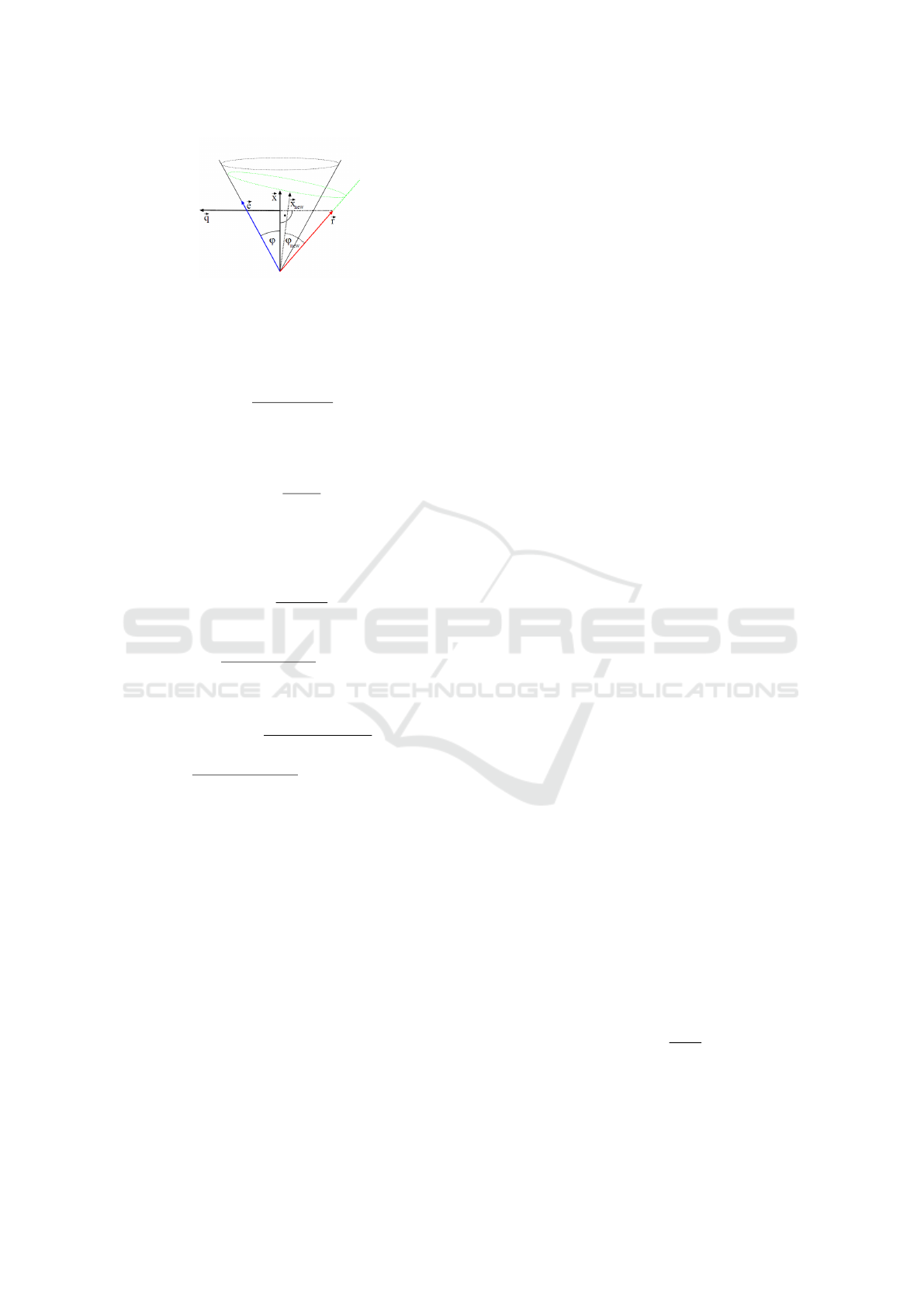
Figure 9: Cone-Ray Union - 2D View. courtesy of (Sz
´
ecsi,
2006).
We use the formulas below to create compact
cones (Sz
´
ecsi, 2006) for the first level nodes.
~q =
(~x ·~r) ·~x −~r
|(~x ·~r) ·~x −~r|
(1)
~e =~x · cos(φ) +~q · sin φ (2)
~x
new
=
~e +~r
|~e +~r|
(3)
cosφ
new
=~x
new
·~r (4)
Otherwise we use these formulas to merge cones:
~x
new
=
~x
1
+ ~x
2
|~x
1
+ ~x
2
|
(5)
cosφ
new
=
arccos(~x
1
+ ~x
2
)
2
+ max(φ
1
,φ
2
) (6)
Finally we merge spheres with this formula:
center
new
=
center
1
+ center
2
2
(7)
radius
new
=
|center
2
− center
1
|
2
+ max(radius
1
,radius
2
)
(8)
Each ray needs to know the corresponding pixel.
Rays are out of order due to sorting. We need a way
to map rays back to screen pixels. Since the hierarchy
is not tied to geometry in the scene it does not matter
for hierarchy creation whether the scene is dynamic
or static. What matters is the number of ray bounces,
so if there are more pixels occupied in the screen, the
hierarchy will have more nodes.
Roger et al. (Roger et al., 2007) also noted that
some nodes might become too large as we travel
higher up into the hierarchy. To mitigate this prob-
lem we decided to limit the number of levels gener-
ated and subsequently the number of levels traversed.
Since rays are sorted before this step, there is much
higher coherency between rays in the lower levels.
If we focus on these rays and ignore the higher lev-
els of the hierarchy we will have better results (as we
shall see in Section 5). There is a possibility that we
might end up having more local intersection tests but
since the nodes in the higher levels of the hierarchy
are quite large, we would most likely end up having
intersections with every single triangle. Thus having
no real gain from calculating intersections on these
higher level nodes to begin with.
3.2.5 Ray Hierarchy Traversal
Once we have an hierarchy tree we can traverse it.
Prior to traversal we compute the bounding spheres
for each object in the scene using Bernd Gartners al-
gorithm (G
¨
artner, 1999).
For the top level of the ray tree we intersect tree
nodes with bounding spheres to further cull intersec-
tions. Finally we traverse the tree in a top-down order,
intersecting each node with geometry. Since parent
nodes fully contain child nodes, triangles rejected on
parent nodes will not be tested again on child nodes.
Let us say we start traversing the tree with the root
node. If a triangle does not intersect the root then this
means that specific triangle will not intersect any of
the children. Since it is the root node, no ray in the
scene will intersect it so we do not have to do any
further intersections with it. We store the intersection
information per level in an array so that child nodes
know the sets of triangles they have to compute inter-
sections against. The intersection tests being run at
this stage are coarse grained. They use the triangle
bounding spheres since we have to do the actual in-
tersection tests in the final stage anyway. Intersection
tests are run in parallel so there is an issue regarding
empty spaces in the textures that contain intersection
information. These arrays need to be trimmed using
the same procedure that was used after ray generation.
These hits are stored as an int32 in which the first 18
bits store the node id and the last 14 bits store the tri-
angle id. This is not a problem for larger scenes as
those are processed in triangle batches. Each hit only
needs to store the maximum number of triangles per
batch.
To calculate the intersection with the node, i.e. the
union of a sphere and a cone, we simplify the prob-
lem by enlarging the triangles bounding sphere (Er-
icson, 2004) and reducing the cones size (see Fig-
ure 10). Cone-sphere intersections were described by
Amanatides (Amanatides, 1984). We use the formula
in Roger et al. (Roger et al., 2007).
result = |C − H| × tan α +
d + r
cosα
> |P − H| (9)
Coherent Ray-Space Hierarchy Via Ray Hashing and Sorting
199
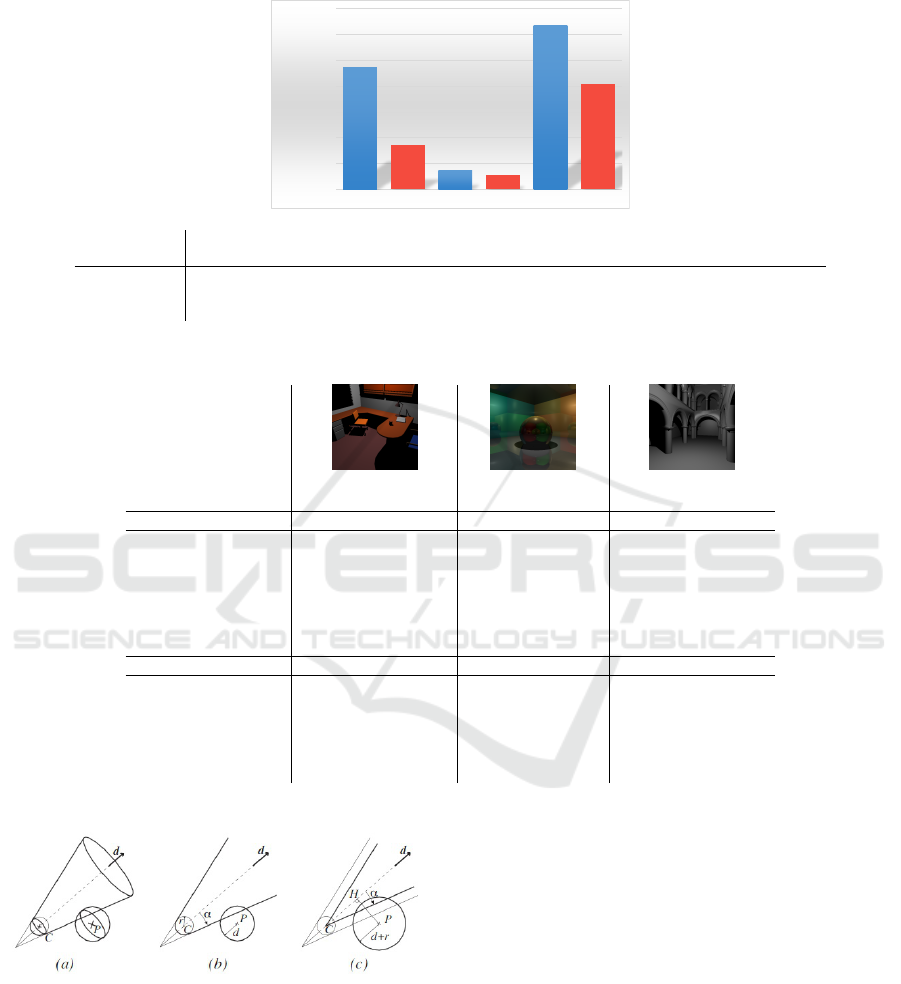
Table 1: OFFICE (251.55 K shadow rays), CORNELL (184.72 K shadow & 524.29 K reflection rays), SPONZA (256.71 K
shadow rays) global rendering performance.
0
100000000
200000000
300000000
400000000
500000000
600000000
700000000
RAH Office Our Office RAH Cornell Our Cornell RAH Sponza Our Sponza
Total Intersections
OFFICE CORNELL SPONZA
ALGORITHM TOTAL # ISECT RELATIVE % TOTAL # ISECT RELATIVE % TOTAL # ISECT RELATIVE %
Brute Force 9133.13 M 100% 606.91 M 100% 17058.58 M 100%
RAH Algorithm 469.68 M 5.14% 72.87 M 12.01% 632.41 M 3.71%
Our Algorithm 170.07 M 1.86% 53.58 M 8.83% 405.62 M 2.38%
Table 2: OFFICE, CORNELL, SPONZA rendering details.
OFFICE CORNELL SPONZA
LEVEL 2 LEVEL 1 LEVEL 2 LEVEL 1 LEVEL 2 LEVEL 1
RAH Algorithm
# SH INTERSECTIONS 142.73 M 202.03 M 3.00 M 5.17 M 266.60 M 261.49 M
# SH MISSES 117.47 M 186.41 M 2.35 M 3.61 M 233.91 M 248.46 M
# SH HITS 25.25 M 15.62 M 0.65 M 1.56 M 32.69 M 13.04 M
# RE INTERSECTIONS 6.49 M 17.80 M
# RE MISSES 4.26 M 14.31 M
# RE HITS 2.23 M 3.49 M
Our Algorithm
# SH INTERSECTIONS 11.56 M 85.57 M 0.75 M 2.38 M 266.60 M 62.67 M
# SH MISSES 0.86 M 76.46 M 0.45 M 0.98 M 258.76 M 53.12 M
# SH HITS 10.70 M 9.12 M 0.30 M 1.40 M 7.83 M 9.55 M
# RE INTERSECTIONS 2.74 M 10.27 M
# RE MISSES 1.45 M 6.98 M
# RE HITS 1.28 M 3.29 M
Figure 10: Cone-Ray Union - 2D View. courtesy of (Roger
et al., 2007).
3.2.6 Final Intersection Tests
After traversing the hierarchy we have an array of
node id and triangle id pairs which represent candi-
dates for the local intersection tests (M
¨
oller, 1997). In
this final step all that remains is to find out which is
the closest intersected triangle for each ray and accu-
mulate shading. Depending on the depth that we want
for the algorithm we might need to output another set
of secondary rays. Since the algorithm is generic, all
that is necessary for this is to output these rays onto
the ray array that we used initially and continue from
the ray-sorting step.
4 TEST METHODOLOGY
We implemented our CRSH algorithm in
OpenGL/C++ and CUDA/C++ and then com-
pared it with our implementation of RAH (Roger
et al., 2007) over the same architecture. We map
our algorithm onto the GPU, fully parallelizing it
GRAPP 2017 - International Conference on Computer Graphics Theory and Applications
200

there. We achieve this mainly by the use of parallel
primitives, like prefix sums (Blelloch, 1990). We
used the CUB (Merrill and Grimshaw, 2009; Merrill
and Grimshaw, 2010) library to perform parallel
radix sorts and prefix sums.
We measure the amount of intersections, includ-
ing misses and hits, to evaluate ray hierarchy algo-
rithms proficiency at reducing the amount of ray-
primitive intersection tests required to render an im-
age. All scenes were rendered at 512 ×512 resolution
using an hierarchy depth of 2 and a node subdivision
of 8 (each upper level node in the hierarchy consists
of the combination of 8 nodes from the level directly
below).
The test information was collected using a
NVIDIA GeForce GTX 770M GPU with 3 GB of
RAM. Our algorithm is completely executed on the
GPU (including hierarchy construction and traversal)
so the CPU has no impact on the test results.
We used three different scenes, OFFICE, COR-
NELL and SPONZA.
The OFFICE scene (36K triangles) is representa-
tive of interior design applications. It is divided into
several sub-meshes; therefore it adapts very well to
our bounding volume scheme. For this scene the em-
phasis was on testing shadow rays.
We selected CORNELL (790 triangles). as it is rep-
resentative of highly reflective scenes. It consists an
object surrounded by six mirrors. On this scene we
focused on testing reflection rays although it also fea-
tures shadow rays in it.
SPONZA (66K triangles), much like OFFICE, is
representative of architectural scenes. For this scene
the emphasis was also on testing shadow rays but for
scenes that do not conform with our bounding volume
scheme. This scene does not adapt well to our scheme
as is not divided into submeshes.
5 RESULTS AND DISCUSSION
5.1 Intersection Results
We hypothesised that our more coherent RSH needs
to compute fewer intersections to render a scene.
We expect more expressive results for shadow rays.
As shadow rays have low divergence classification
should be more coherent than for reflection rays. Ad-
ditionally our hierarchy should be more coherent with
reflection rays than one based on RAH due to the
hashing used. However the incoherence of reflection
rays, vs shadow rays, should lead to a lower quality
hierarchy.
Our initial expectations for Office were to get a
much lower number of intersection tests with our al-
gorithm than with RAH. The scene is a good fit to
our bounding volume scheme and our highly coherent
shadow ray hierarchy. Results (see Table 2) confirm
our initial expectations: we compute 63.79% less in-
tersections than RAH on this scene. 98.14% less than
a brute force approach.
The Cornell scene has reflection rays, which are
more incoherent, so we expected worse results than
with Office. Still we compute 26.47% less intersec-
tions (shadow and reflection rays combined) than the
RAH algorithm and 91.17% less than the brute force
approach.
The final scene, Sponza, is a whole mesh. We did
not employ object subdivision in this scene. Hence
we expected worse results than with Office since we
would only get the benefit of the shadow ray hierarchy
and none from the bounding volume scheme.
We compute 35.86% less intersections than RAH
and 97.62% less than brute force. Since there is no
mesh culling for this scene the results are not as good
as with Office but we still manage to outperform RAH
even without using an integral part of our algorithm.
5.2 Performance Results
These tests were run over the course of 58 frames and
the results for each phase are the average of these 58
frames.
The major time consuming steps are hierarchy
traversal and final intersections. The biggest advan-
tage between our algorithm and the RAH algorithm
resides in the time spent traversing the hierarchy. Our
algorithm is 2.18x faster at traversal than RAH in Of-
fice (see Table 3). This increased time spent travers-
ing the hierarchy means RAH takes about 100% more
time to render each frame than our algorithm.
Table 3: OFFICE, CORNELL, SPONZA render times.
OFFICE CORNELL SPONZA
RAH TIME (MS) TIME (MS) TIME (MS)
RAY CREATION 40.24 125.73 41.22
RAY COMPRESSION 0.00 0.00 0.00
RAY SORTING 0.00 0.00 0.00
RAY DECOMPRESSION 0.00 0.00 0.00
HIERARCHY CREATION 122.17 366.99 126.50
Ours TIME (MS) TIME (MS) TIME (MS)
RAY CREATION 40.43 128.13 41.50
RAY COMPRESSION 16.65 53.92 17.15
RAY SORTING 11.82 50.97 12.70
RAY DECOMPRESSION 99.72 251.95 98.62
HIERARCHY CREATION 130.63 407.09 137.84
Ours vs RAH SPEEDUP SPEEDUP SPEEDUP
HIERARCHY TRAVERSAL 2.18X 1.53X 1.06X
FINAL INTERSECTION TESTS 1.32X 1.02X 1.14X
Much like Office, the Cornell scene takes most of
its time on traversal and calculating the final intersec-
Coherent Ray-Space Hierarchy Via Ray Hashing and Sorting
201

tions. However due to the lower geometric complex-
ity the absolute values aren’t as high. Our algorithm
performs traversal 1.53x faster than RAH in Cornell,
a significant reduction.
Finally for the Sponza scene we see a similar rel-
ative time spent in the traversal of the hierarchy vs
previous scenes. Even though the Sponza scene isn’t
subdivided into separate object meshes, we manage to
slightly outperform RAH at traversal.
6 CONCLUSIONS AND FUTURE
WORK
Our paper described an algorithm to create a Ray-
Space Hierarchy which markedly reduces the inter-
sections, required to ray-trace a scene, due to im-
proved coherency and a shallow BVH.
We achieved our goal of reducing intersections us-
ing a Ray-Space Hierarchy. This technique is orthog-
onal to the use of both Object and Space Hierarchies.
These can be used together to obtain even better re-
sults. Our results show a reduction in computed inter-
sections of 50% for shadow rays and 25% for reflec-
tion rays compared to previous state of the art RSHs.
There is room for improvements: Since the hash
determines how rays are sorted, an hierarchy will
improve if we enhance the ray spatial coherency.
We used spherical bounding volumes and a shallow
BVH. In the future we aim to combine our coher-
ent ray hierarchy with a deeper BVH to further de-
screase ray-primitive intersections e.g. (Bradshaw
and O’Sullivan, 2004).
ACKNOWLEDGEMENTS
This work was supported by national funds through
Fundac¸
˜
ao para a Ci
ˆ
encia e Tecnologia (FCT) with ref-
erence UID/CEC/50021/2013.
REFERENCES
Aila, T. and Karras, T. (2010). Architecture Considera-
tions for Tracing Incoherent Rays. In Proceedings of
the Conference on High Performance Graphics, pages
113–122. Eurographics Association.
Amanatides, J. (1984). Ray Tracing with Cones. SIG-
GRAPH Computer Graphics, 18(3):129–135.
Arvo, J. and Kirk, D. (1987). Fast Ray Tracing by Ray Clas-
sification. SIGGRAPH Computer Graphics, 21(4):55–
64.
Blelloch, G. E. (1990). Prefix Sums and their Applications.
Technical report, Carnegie Mellon University.
Bradshaw, G. and O’Sullivan, C. (2004). Adaptive Medial-
Axis Approximation for Sphere-tree Construction.
ACM Transactions on Graphics (TOG), 23(1):1–26.
Ericson, C. (2004). Real-Time Collision Detection. Series in
Interactive 3-D Technology. Morgan Kaufmann Pub-
lishers Inc.
Garanzha, K. and Loop, C. (2010). Fast Ray Sorting and
Breadth-First Packet Traversal for GPU Ray Tracing.
Computer Graphics Forum, 29(2):289–298.
G
¨
artner, B. (1999). Fast and Robust Smallest Enclosing
Balls. In Proceedings of the 7th Annual European
Symposium on Algorithms, ESA ’99, pages 325–338.
Springer-Verlag.
Glassner, A. S., editor (1990). Graphics Gems. Academic
Press, Inc.
Mattausch, O., Bittner, J., Jaspe, A., Gobbetti, E., Wimmer,
M., and Pajarola, R. (2015). CHC+RT: Coherent Hier-
archical Culling for Ray Tracing. Computer Graphics
Forum, 34(2):537–548.
Merrill, D. and Grimshaw, A. (2009). Parallel Scan for
Stream Architectures. Technical report, University of
Virginia, Department of Computer Science.
Merrill, D. G. and Grimshaw, A. S. (2010). Revisiting Sort-
ing for GPGPU Stream Architectures. In Proceedings
of the 19th International Conference on Parallel Ar-
chitectures and Compilation Techniques, PACT ’10,
pages 545–546. ACM.
M
¨
oller, T. (1997). A Fast Triangle-Triangle Intersection
Test. Journal of Graphic Tools, 2(2):25–30.
Mora, B. (2011). Naive Ray-Tracing: A Divide-And-
Conquer Approach. ACM Transactions on Graphics
(TOG), 30(5):117.
Pharr, M. and Fernando, R. (2005). GPU Gems 2: Pro-
gramming Techniques for High-Performance Graph-
ics and General-Purpose Computation. GPU Gems.
Addison-Wesley Professional.
Roger, D., Assarsson, U., and Holzschuch, N. (2007). Whit-
ted Ray-tracing for Dynamic Scenes Using a Ray-
space Hierarchy on the GPU. In Proceedings of the
18th Eurographics Conference on Rendering Tech-
niques, EGSR ’07, pages 99–110. Eurographics As-
sociation.
Sz
´
ecsi, L. (2006). The Hierarchical Ray Engine. In WSCG
Full Papers Proceedings, pages 249–256. V
´
aclav
Skala-UNION Agency.
Whitted, T. (1980). An Improved Illumination Model for
Shaded Display. Commun. ACM, 23(6):343–349.
GRAPP 2017 - International Conference on Computer Graphics Theory and Applications
202
