Theoretical Notes on Unsupervised Learning in Deep Neural
Networks
Vladimir Golovko
1,2
and Aliaksandr Kroshchanka
1
1
Brest State Technical University, Moskowskaja 267, Brest, Belarus
2
National Research Nuclear University (MEPHI), Moscow, Russia
Keywords: Deep Neural Networks, Deep Learning, Restricted Boltzmann Machine, Data Visualization, Machine
Learning, Cross-entropy.
Abstract: Over the last decade the deep neural networks are the powerful tool in the domain of machine learning. The
important problem is training of deep neural network, because learning of such a network is much
complicated compared to shallow neural networks. This is due to the vanishing gradient problem, poor local
minima and unstable gradient problem. Therefore a lot of deep learning techniques were developed that
permit us to overcome some limitations of conventional training approaches. In this paper we investigate the
unsupervised learning in deep neural networks. We have proved that maximization of the log-likelihood
input data distribution of restricted Boltzmann machine is equivalent to minimizing the cross-entropy and to
special case of minimizing the mean squared error. The main contribution of this paper is a novel view and
new understanding of an unsupervised learning in deep neural networks.
1 INTRODUCTION
Deep neural networks (DNN) currently provide the
best performance to many problems in images,
video, speech recognition, and natural language
processing, etc. (Krizhevsky et al., 2012; Hinton et
al., 2012; Hinton and Salakhutdinov, 2006). In the
general case a deep neural network consists of
multiple layers of neural units and can accomplish a
deep hierarchical representation of their input data.
This kind of neural network has been investigated in
many studies (Hinton et al., 2006; Bengio, 2009;
Bengio et al., 2007.).
This paper deals with an unsupervised learning
technique for restricted Boltzmann machine (RBM),
which can be applied for the training of deep neural
networks. The conventional approach to unsupervi-
sed training the RBM uses an energy-based model
and is based on maximization of the log-likelihood
input data distribution using gradient descent
approach. In this paper we consider the unsupervised
deep learning from another point of view, which
provides a deeper understanding of the nature of
unsupervised learning in deep neural networks. First
of all we use two training criteria, namely square
error and cross-entropy, instead of energy-based
technique. Next, we present the RBM as PCA or
auto-encoder neural network, which consist of three
layers: visible, hidden and visible. Finally, the Gibbs
sampling in order to define mean square error and
cross-entropy loss function is used. As a result we
have proved that maximization of the log-likelihood
input data distribution of restricted Boltzmann
machine is equivalent to minimizing the cross-
entropy and to special case of minimizing the mean
squared error. The rest of the paper is organized as
follows. Section 2 introduces the conventional
approach for restricted Boltzmann machine training
based on an energy model. In Section 3 we propose
the novel techniques for inference of RBM training
rules and finally we give our conclusion.
2 RELATED WORKS
Let us consider the related works in this domain
(Hinton, 2002; Hinton et al., 2006; Erhan et al.,
2010; Mikolov et al., 2011; Bengio et al., 2013).
There are different kinds of deep neural networks:
deep belief neural networks, deep perceptron, deep
convolutional neural networks, deep recurrent neural
networks, deep auto-encoder, deep R-CNN and so
on. It should be noted that the training rules are
identical for different kind of deep neural networks.
Golovko V. and Kroshchanka A.
Theoretical Notes on Unsupervised Learning in Deep Neural Networks.
DOI: 10.5220/0006084300910096
In Proceedings of the 8th International Joint Conference on Computational Intelligence (IJCCI 2016), pages 91-96
ISBN: 978-989-758-201-1
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
91

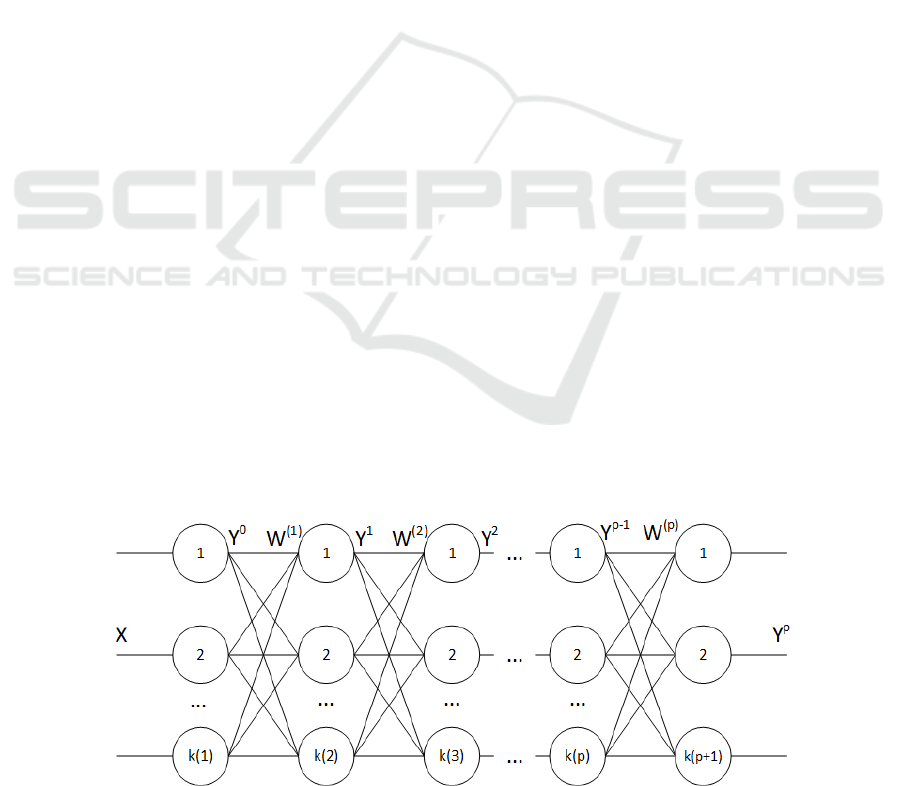
Therefore we will take the many-layered perceptron
as a deep neural network in order to investigate deep
learning rules (Fig.1).
The j-th output unit for k-th layer is given by
)(
k
j
k
j
SFy =
(1)

=
−
+=
1
1
i
k
j
k
i
k
ij
k
j
TyS ω
(2)
where F is the activation function,
k
j
S
is the
weighted sum of the j-th unit,
k
ij
ω
is the weight from
the i-th unit of the (k-1)-th layer to the j-th unit of
the k-th layer, and
k
j
T
is the threshold of the j-th
unit.
For the first layer
ii
xy =
0
(3)
There exist the two main techniques for learning
of deep neural networks: learning with pre-training
using a greedy layer-wise approach and stochastic
gradient descent approach (SGD) with rectified
linear unit (ReLU) transfer function (LeCun et al.,
2015).
The learning with pre-training consists of two
stages (Hinton et al., 2006). The first stage is the
pre-training of neural network using greedy layer-
wise approach. This procedure is started from the
first layer and performed in unsupervised manner.
The second one is fine-tuning all of parameters of
neural network using back-propagation algorithm.
The training with stochastic gradient descent
approach is the online or mini-batch learning using
conventional backpropagation algorithm (Glorot et
al., 2011). The use of ReLU activation function can
help to avoid of vanishing gradient problem, poor
local minima and unstable gradient problem due to
the greater linearity of such kind of activation
function (LeCun et al., 2015).
At present the following paradigm for DNN
learning is used. If training data set is large then
SGD with ReLU is used for deep neural network
learning. Otherwise pre-training and fine-tuning is
applied. So, for instance, for smaller data sets,
unsupervised pre-training helps to prevent
overfitting (LeCun et al., 2015).
The most important stage of deep neural network
training is the pre-training of each layer of the DNN
in unsupervised manner. There exist two main
techniques for DNN pre-training. As a rule the DNN
pre-training is based on either the restricted
Boltzmann machine (RBM) or auto-encoder
approach (Larochelle et al., 2009). In accordance
with the greedy layer-wise training procedure, in the
beginning the first layer of the DNN is trained using
RBM or auto-encoder training rule and its
parameters are fixed. After this the next layer is
trained, and so on. As a result a good initialization of
the neural network is achieved and we can then use
back-propagation algorithm for fine tuning the
parameters of the whole neural network.
Further we will consider the DNN pre-training
technique based on the restricted Boltzmann
machine. In this case the deep neural network can be
represented as a set of restricted Boltzmann
machines. The traditional approach to RBM training
was proposed by G. Hinton and is based on an
energy model. Let's consider the conventional
restricted Boltzmann machine, which consists of two
layers of units: visible and hidden (Fig. 2).
The restricted Boltzmann machine can represent
any discrete distribution if enough hidden units are
used (Bengio, 2009). Often the binary units are used
(Hinton, 2010). The RBM is a stochastic neural
network and the states of visible and hidden units are
defined using a probabilistic version of the sigmoid
activation function.
Figure 1: Deep perceptron.
NCTA 2016 - 8th International Conference on Neural Computation Theory and Applications
92

Figure: 2. Restricted Boltzmann machine.
The key idea of RBM training is to reproduce as
closely as possible the distribution of the input data
using the states of the hidden units. This is
equivalent to maximizing the likelihood of the input
data distribution P(x) by the modification of synaptic
weights using the gradient of the log probability of
the input data. As a result we can obtain the RBM
training rules. In case of CD-k
))()0(()()1(
))()0(()()1(
))()()0()0((
)()1(
kyytTtT
kxxtTtT
kykxyx
tt
jjjj
iiii
jiji
ijij
−+=+
−+=+
−
+=+
α
α
α
ω
ω
(4)
Here α is the learning rate.
Training an RBM is based on presenting a
training sample to the visible units, then using the
CD-k procedure to compute the binary states of the
hidden units p(y|x), sampling the visible units
(reconstructed states) p(x|y), and so on. After
performing these iterations the weights and biases of
the restricted Boltzmann machine are updated. Then
we stack on another hidden layer to train a new
RBM. This approach is applied to all layers of the
deep neural network (greedy layer-wise training).
Finally, supervised fine-tuning of the whole neural
network is performed.
3 A NEW INSIGHT INTO
UNSUPERVISED LEARNING
OF RBM
In this section we will consider the restricted
Boltzmann machine from another point of view,
namely as auto-encoder or the PCA neural network.
We will use two training criteria in order to obtain
RBM learning rule. As a result we have proposed a
new unsupervised learning rule and the novel
techniques to infer the RBM training rules. It is
based on minimization of the reconstruction mean
square error and cross-entropy error function, which
we can obtain using simple iterations of Gibbs
sampling. In contrast to the traditional energy-based
method, which is based on a linear representation of
neural units, the proposed approach permits us to
take into account the nonlinear nature of neural
units.
Let's examine the restricted Boltzmann machine.
We will represent the RBM using three layers
(visible, hidden and visible) (Golovko et al., 2014)
as shown in Fig. 3. As can be seen such a
representation of RBM is equivalent to PCA neural
network, where the hidden and last visible layer is
respectively compression and reconstruction
(inverse) layer.
Let’s consider the Gibbs sampling using
unfolded representation of RBM.
Then Gibbs sampling will consist of the
following procedure. Let x(0) be the input data,
which arrives at the visible layer at time 0. Then the
output of the hidden layer is defined as follows:
)),0(()0(
jj
SFy =
(5)

+=
i
jiijj
TxS )0()0( ω
(6)
Figure 3: Unfolded representation of RBM.
Theoretical Notes on Unsupervised Learning in Deep Neural Networks
93

The inverse layer reconstructs the data from the
hidden layer. As a result we can obtain x(1) at time
1:
)),1(()1(
ii
SFx =
(7)

+=
j
ijiji
TyS )0()1( ω
(8)
After this, x(1) enters the visible layer and we
can obtain the output of the hidden layer the
following way:
)),1(()1(
jj
SFy =
(9)

+=
i
jiijj
TxS )1()1( ω
(10)
Continuing the given process we can obtain on a
step k, that
.)1()(
)),(()(

+−=
=
j
iji
ii
TkykS
kSFkx
ij
ω
(11)
.)()(
)),(()(

+=
=
i
jij
jj
TkxkS
kSFky
ij
ω
(12)
There exist the different ways for RBM training.
It is based on the use of the different learning
criteria. As mentioned before G. Hinton proposed an
energy-based model, which is based on
maximization of the log-likelihood input data
distribution P(x). We suggest using the two loss
functions for RBM learning. The first training
criterion is based on minimization of mean square
error (MSE). The second one involves the
minimization of cross entropy error function. Both
training criteria have the attractive properties and
have been studied in many papers (Golik, 2013;
Glorot and Bengio, 2010). Our main goal here is to
show, that the use of different training criteria leads
to the same learning rules. In the next subsections
we will study these criteria in more detail.
3.1 MSE Training Criterion
Let’s consider the use of mean square error function
for RBM learning. Then the primary goal of training
RBM is to minimize the reconstruction mean
squared error (MSE) in the hidden and visible layers.
The MSE in the hidden layer is proportional to the
difference between the states of the hidden units at
the various time steps. Then in case of CD-k
2
111
))1()((
2
1
)( −−=

===
pypykE
l
j
L
l
m
j
k
p
l
jh
(13)
Similarly, the MSE in the inverse layer is
proportional to the difference between the states of
the inverse units at the various time steps:

== =
−−=
L
l
n
i
k
p
l
i
l
iv
pxpxkE
11 1
2
))1()((
2
1
)(
(14)
where L is the number of training patterns.
In case of CD-k the common reconstruction
mean squared error is defined as the sum of errors:
)()()( kEkEkE
vhs
+=
(15)
Тheorem 1. Maximization of the log-likelihood
input data distribution P(x) in the space of synaptic
weights of the restricted Boltzmann machine is
equivalent to special case of minimizing the
reconstruction mean squared error in the same space,
if we use linear transfer function for neurons.
This theorem states that if we use identity
activation function for RBM units, then the CD-k
training rule for RBM in order to minimizing
reconstruction mean squared error (15) will be
identical to the conventional RBM training rules
Thus the conventional RBM training rules are linear
in terms of MSE minimization. Therefore we shall
call such a machine linear RBM.
Corollary 1. The training rule for a nonlinear
restricted Boltzmann machine in the case of CD-k is
defined as
)))
,
(()1())1()((
)(()())1()(((
)()1(
1
pSFpypxpx
pSFpxpypy
tt
ijii
k
p
jijj
ijij
′
−−−+
′
−−
−=+

=
α
ωω
(16)
))),(())1()(((
)1(
1
pSFpypy
tT
jjj
k
p
j
′
−−−
=+Δ

=
α
(17)
)))(())1()(((
)1(
1
pSFpxpx
tT
iii
k
p
i
′
−−−
=+Δ

=
α
(18)
In this section we have obtained the novel
unsupervised learning rules for restricted Boltzmann
machines, using MSE training criterion. The
traditional energy-based method is based on
maximization of the log-likelihood input data
distribution and leads to the linear representation of
NCTA 2016 - 8th International Conference on Neural Computation Theory and Applications
94

neural units in terms of minimizing the MSE. The
proposed approach, which can be obtained using
simple iterations of Gibbs sampling is based on
minimization of reconstruction mean square error
and leads to nonlinear and linear representation of
neurons. We will call the proposed approach the
reconstruction error-based approach (REBA). For
the first time, the approach described above has been
proposed in (Golovko et al., 2014) for the CD-1 and
in (Golovko et al., 2015; Golovko, 2015) for CD-k.
3.2 Cross-Entropy Training Criterion
The cross-entropy measure (CE) can be used as an
alternative to mean squared error. Let’s consider a
sigmoid neural network and the cross entropy error
function instead of mean square error. The goal of
training RBM is to minimize the cross-entropy in the
hidden and visible layers. In the case of CD-k the
cross-entropy error function in the inverse layer is
defined as

===
















−−−
+−
−
=
L
l
k
p
n
i
l
i
l
i
l
i
l
i
v
pxpx
pxpx
kCE
111
))(1log())1(1(
))(log()1(
)(
(19)
Similarly, the cross-entropy error function in the
hidden layer

===
















−−−
+−
−
=
L
l
k
p
m
j
l
j
l
j
l
j
l
j
h
pypy
pypy
kCE
111
))(1log())1(1(
))(log()1(
)(
(20)
The common cross entropy error function in case
of CD-k is defined as the sum of errors:
)()()( kCEkCEkСE
vhs
+=
(21)
Тheorem 2. Maximization of the log-likelihood
input data distribution P(x) in the space of synaptic
weights restricted Boltzmann machine is equivalent
to minimizing the cross-entropy error function.
Proof. Let’s consider the cross entropy for CD-k.
In this case the cross entropy error function for a
single example is


==
==








−−−
+−
−








−−−
+−
−=
k
p
m
j
jj
jj
k
p
n
i
ii
ii
pypy
pypy
pxpx
pxpx
kCE
11
11
))(1log())1(1(
))(log()1(
))(1log())1(1(
))(log()1(
)(
(22)
Then
()

=
−−−−−=
∂
∂
k
p
jiji
ij
pypxpypx
w
kCE
1
)1()()1()1(
)(
()
()


=
=
=−−−
=−−−
k
p
jiij
k
p
ijij
pypxpxpy
pxpypxpy
1
1
)1()1()()(
)()()()1(
).0()0()()()1()1()()(
...)1()1()2()2()0()0()1()1(
jijijiij
jiijjiij
yxkykxkykxkxky
yxxyyxxy
−=−−−
++−+−
Accordingly, for the thresholds
)0()(
)(
ii
i
xkx
T
kCE
−=
∂
∂
(23)
)0()(
)(
jj
j
yky
T
kCE
−=
∂
∂
(24)
The theorem is proved. As follows from theorem
the RBM learning rules can be obtained in a simpler
way compared to the conventional energy-based
approach. Thus using minimization of the cross-
entropy error function and simple iterations of Gibbs
sampling we have received the conventional linear
RBM learning rules.
The obtained results can be summarized in the
following general theorem.
Theorem 3. Maximization of the log-likelihood
input data distribution P(x) in the space of synaptic
weights restricted Boltzmann machine is equivalent
to minimizing the cross-entropy and to special case
of minimizing the mean squared error:
)min()min())(max(ln
ss
ECExP ==
(25)
Theorem 3 represents a generalization of the
previous results in this paper. It follows from the
theorem that the use of various training criteria leads
to the same learning rules. Therefore the nature of
unsupervised learning of RBM is the same, even if
we use different objective function. The
maximization of the log-likelihood input data
distribution and minimization cross-entropy error
function leads to the linear representation of neural
units in terms of minimizing the MSE. It should be
noted, that applying of training criterion, which is
based on minimization of MSE, we can take into
account also nonlinear representation of neurons.
4 CONCLUSIONS
In this paper we have addressed the key aspects of
Theoretical Notes on Unsupervised Learning in Deep Neural Networks
95

unsupervised learning in deep neural networks. We
described both the traditional energy-based method,
which is based on a linear representation of neural
units, and the proposed approach, which is based on
nonlinear representation of neurons. We have proved
that maximization of the log-likelihood input data
distribution of restricted Boltzmann machine is
equivalent to minimizing the cross-entropy and to
special case of minimizing the mean squared error.
Thus using MSE training criterion we can get both
conventional and novel learning rules.
REFERENCES
Hinton, G., Osindero, S., Teh, Y., 2006. A fast learning
algorithm for deep belief nets. Neural Computation,
18, 1527-1554.
Hinton, G., 2002. Training products of experts by
minimizing contrastive divergence. Neural
Computation, 14, 1771-1800.
Hinton, G., Salakhutdinov, R., 2006. Reducing the
dimensionality of data with neural networks. Science,
313 (5786), 504-507.
Hinton, G. E., 2010. A practical guide to training restricted
Boltzmann machines. (Tech. Rep. 2010-000). Toronto:
Machine Learning Group, University of Toronto.
Krizhevsky, A., Sutskever, L., Hinton, G., 2012. ImageNet
classification with deep convolutional neural networs.
In Proc. Advances in Neural information Processing
Systems, 25, 1090-1098.
LeCun, Y., Bengio, Y., Hinton, G., 2015. Deep learning
Nature, 521 (7553), 436-444.
Mikolov, T, Deoras, A., Povey, D., Burget, L., Cernocky,
J., 2011. Strategies for training large scale neural
network language models. In Automatic Speech
Recognition and Understanding, 195-201.
Hinton, G. at al., 2012. Deep neural network for acoustic
modeling in speech recognition. IEEE Signal
Processing Magazine, 29, 82-97.
Bengio, Y., 2009. Learning deep architectures for AI.
Foundations and Trends in Machine Learning, 2(1), 1-
127.
Bengio, Y., Lamblin, P., Popovici, D., Larochelle, H.,
2007. Greedy layer-wise training of deep networks. In
B. Sch\"olkopf, J. C. Platt, T. Hoffman (Eds.),
Advances in neural information processing systems,
11, pp. 153-160. MA: MIT Press, Cambridge
Erhan, D., Bengio, Y., Courville, A., Manzagol, P.-A.,
Vincent, P., Bengio, S., 2010. Why does unsupervised
pre-training help deep learning? Journal of Machine
Learning Research, 11:625-660.
Larochelle H., Bengio Y., Louradour J., Lamblin P., 2009
Exploring strategies for training deep neural
networks//Journal of Machine Learning Research 1, 1-
40.
Bengio, Y., Courville, A., Vincent, P., 2013.
Representation learning a review and new
percpectives. IEEE Trans. Pattern Anal. Machine
Intell. 35, 1798-1828.
Glorot, X., Bordes, A., & Bengio, Y., 2011. Deep sparse
rectifier networks. In Proceedings of the 14th
International Conference on Artificial Intelligence and
Statistics. JMLR W&CP Volume (Vol. 15, pp. 315-
323).
Golovko, V., Kroshchanka A., Rubanau U., Jankowski S.,
2014. A Learning Technique for Deep Belief Neural
Networks. In book Neural Networks and Artificial
Intelligence, Springer, 2014. – Vol. 440.
Communication in Computer and Information
Science. – P. 136-146.
Golovko, V., Kroshchanka, A., Turchenko, V., Jankowski,
S., Treadwell, D., 2015. A New Technique for
Restricted Boltzmann Machine Learning. Proceedings
of the 8th IEEE International Conference IDAACS-
2015, Warsaw 24-26 September 2015. – Warsaw,
2015 –P.182-186.
Golovko, V., From multilayers perceptrons to deep belief
neural networks: training paradigms and application,
Lections on Neuroinformatics, Golovko, V.A., Ed.,
Moscow: NRNU MEPhI, 2015, pp. 47–84 [in
Russian].
Golik, P. Cross-Entropy vs. Squared Error Training: a
Theoretical and Experimental Comparison / P. Golik,
P. Doetsch, H. Ney // In Interspeech. - Lyon, France,
2013. – P. 1756-1760.
Glorot, X. and Bengio, Y.. 2010. Understanding the
difficulty of training deep feed-forward neural
networks. in Proc. of Int. Conf. on Artificial
Intelligence and Statistics, vol. 9, Chia Laguna Resort,
Italy, 2010, pp. 249–256.
NCTA 2016 - 8th International Conference on Neural Computation Theory and Applications
96