Efﬁcient Distraction Detection in Surveillance Video using

Approximate Counting over Decomposed Micro-streams

Avi Bleiweiss

BShalem Research, Sunnyvale, U.S.A.

Keywords:

Stream Data, Approximate Counting, Sliding Window, Cosine Distance, Surveillance Video, Classiﬁcation.

Abstract:

Mining techniques of inﬁnite data streams often store synoptic information about the most recently observed

data elements. Motivated by space efﬁcient solutions, our work exploits approximate counting over a ﬁxed-size

sliding window to detect distraction events in video. We propose a model that transforms inline the incoming

video sequence to an orthogonal set of thousands of binary micro-streams, and for each of the bit streams we

estimate at every timestamp the count of number-of-ones in a preceding sub-window interval. On window

bound frames, we further extract a compact feature representation of a bag of count-of-1’s occurrences to

facilitate effective query of transitive similarity samples. Despite its simplicity, our prototype demonstrates

robust knowledge discovery to support the intuition of a context-neutral window summary. To evaluate our

system, we use real-world scenarios from a video surveillance online-repository.

1 INTRODUCTION

Instinctive discovery of a context shift in streaming

large volumes of video sequences is a widely studied

problem that has attracted extensive research for the

past dozen years. Change detection is one of principal

interests to diverse real-time application domains, in-

cluding monitoring surveillance feeds, predicting live

weather, tracking stock market ﬂuctuations, and re-

lieving network trafﬁc congestion. Despite its scale

and practical appeal, abnormal event recognition in a

stream remains challenging, as data that arrived be-

fore a change can bias the model towards unsubstan-

tiated characteristics that no longer hold.

Time-varying data streams are of a transient na-

ture and often presented online in a prohibitively

large size. Retaining the entirety of their underpinned

data in an active storage, hence becomes infeasible,

and unless stream elements are processed instantly or

stored, they are disposed of and presumed unaccessi-

ble. Typically, a stream data model allocates a work-

ing space of sufﬁciently limited capacity for placing

summaries or parts of streams, to facilitate fast re-

sponses in processing continuous queries (Leskovec

et al., 2014). One prevalent approach for stream sum-

marization attaches more signiﬁcance to recent ele-

ments relative to those entered at a long time past,

and identiﬁes a sliding window of elements arrived

between the current timestamp and some recent time

formerly. To considerably further reduce the mem-

ory footprint required to keep window summaries,

our work explores the concept of maintaining approx-

imate counts in streaming data (Datar et al., 2002;

Arasu and Manku, 2004; Lee and Ting, 2006). Dis-

tinctly, we chose the primitive counting algorithm,

DGIM (Datar et al., 2002), that maintains a time-

based histogram of active 1’s over a bit stream win-

dow, partitioned into exponentially increasing bucket

sizes. A bucket represents a contiguous time inter-

val and is efﬁciently described by the timestamp of its

most recent end, and the number of ones rendered in

the prescribed period. Bucket creation rules are tai-

lored to trade-off between histogram space require-

ments and the allowable fractional error that tran-

spires in computing approximate counts.

To the best of our knowledge based on published

research to date, our framework is the ﬁrst to incor-

porate anytime query of approximate element counts,

for telling apart a disruptive event in a sustained video

stream. We operate simultaneously on many thou-

sands of factorizable binary micro-streams that are

created inline, and abide by a uniform arrival data-

rate and a consistent time interval between elements.

As each micro-stream temporally links inbound frame

pixels of a spatially identical, two-dimensional co-

ordinate set. At every window frame boundary, we

further coalesce individual micro-stream summaries

into an extremely compact representation of a bag of

Bleiweiss, A.

Efﬁcient Distraction Detection in Surveillance Video using Approximate Counting over Decomposed Micro-streams.

DOI: 10.5220/0006067103270335

In Proceedings of the 8th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2016) - Volume 1: KDIR, pages 327-335

ISBN: 978-989-758-203-5

327

count-of-1’s occurrences. Our work closely leverages

information retrieval (IR) practices, letting window

feature vectors perceived as directions (Baeza-Yates

and Ribeiro-Neto, 1999) that follow efﬁcient cosine

similarity calculations, directly from the well known

Vector Space Model (Salton et al., 1975).

The main contribution of our work is a high-

performance software prototype that devises to keep

an exceptionally compressed rendition of a window

summary. Our learning model is able to make more

informed decisions by classifying distractions over

potentially a cascade of many retained instances of

past windows, as it gains from expanding on the sin-

gle window visibility that reasons similarity in the

time span deﬁned between the current and previous

windows. Furthermore, to conform to real-time query

responses as new video frames arrive, our system is

designed to update bucket properties of all micro-

streams concurrently. Thus efﬁciently subscribing to

the processing step implied by the requisite of satis-

fying DGIM bucket terms, evidently the most inten-

sive compute task in our pipeline. To evaluate our

framework, we use real-world datasets obtained from

the Video Surveillance Online Repository (ViSOR)

(Vezanni and Cucchiara, 2010; ViSOR, 2010).

2 APPROXIMATE COUNTING

In this section, we brieﬂy overview the DGIM algo-

rithm (Datar et al., 2002) as it pertains to a single bi-

nary micro-stream. At its core, the sliding window

model continuously maintains active statistics over

the recently observed N data elements of the stream,

as each element expires after exactly N time steps.

An element is identiﬁed by an absolute frame arrival-

time, and has a timestamp that corresponds to its rela-

tive position in a window. The DGIM method uses an

effective histogram data structure to represent a win-

dow, and provides at anytime a response time of O(1)

for querying the estimated count of ones in the most

recent k bits, for any 1 ≤ k ≤ N. A histogram bucket,

b, is deﬁned by both the timestamp modulo N of its

most recent one arrived, t

, and the count of ones it

contains, denoted henceforth as the bucket size, |b|,

that must be a power-of-2 number. Storage wise, to

retain a bucket we need log

N bits for the timestamp

and log

log

N bits for the size, thus a memory area of

O(logN) bits sufﬁces. On the other hand, there are at

most two buckets of all sizes from log

N down to one,

and no buckets of larger sizes. With O (log N) buckets,

each of O(log N) bits, the total space required for all

the buckets representing a window of size N elements

is therefore O(log

N) bits.

time

timestamp

0 7

bucket size

distribution

8 8 4 2 2 1 1

8 8 4 4 2 1

8 8 4 4 2 1 1

8 8 4 4 2 2 1

8 8 4 4 2 2 1 1

8 8 4 2 1

Figure 1: Satisfying DGIM rules: showing both arrival-time

and timestamp for a window of N = 40 bits. Current time is

60, and at positions 61 through 65, a series of 1’s appear in

the stream. Bucket size adaptation often involves the merger

of two adjacent buckets of the same size into one bucket of

twice the size. The timestamp of the new bucket is the more

recent of the bucket pair.

A guiding principle in constructing the bucket rep-

resentation of a stream window as a series of (t

,|b|)

pairs, states that every position with a one must be

in some bucket, but in no more than a single bucket.

As a new bit element arrives, we follow these steps to

modify the histogram and satisfy the DGIM rules:

• First, we check the earliest bucket. If its times-

tamp reached N + 1, the bucket has expired and

dropped from the list.

• No change is required for a new data element of

0. Otherwise, we create a new bucket with the

current timestamp and a size of one.

• We then traverse the bucket list in a non-

decreasing size order. If there are more than two

buckets of the same size, we merge the earliest

pair of buckets into a single bucket of twice the

size, and its timestamp set to the more recent of

the two buckets.

The last step may unfold into a chain of bucket

merges, limited however to at most log

N unique

bucket sizes. Figure 1 further illustrates bucket size

adaptation in a real-world scenario, as new bits ap-

pear in the stream. Respectively, at time 65, bucket

(25,8) falls out of the window and is thereby dropped.

As three buckets of size one are formed, we combine

the leftmost two, (24,1) and (23,1), and replace them

with bucket (24, 2). This leads to three buckets of

size two, thus merging (22,2) and (20,2) into (22,4).

Consequently, three buckets of size 4 arise and we

unite (15, 4) and (7,4) to create (15,8). Merging

two adjacent buckets of identical size requires con-

stant time and hence, a new data bit can be efﬁciently

processed in O(logN).

At any time step, to produce an estimate of the

count of active ones in the last k bits of the window,

for some 1 ≤ k ≤ N, we locate the bucket with the

KDIR 2016 - 8th International Conference on Knowledge Discovery and Information Retrieval

328

earliest timestamp that includes at least some of the

k most recent bits. The approximate count of ones

becomes the sum of the sizes of all the succeeding

buckets, plus half the size of the earliest bucket. The

absolute error, ε, in this estimate is hence no greater

than 50% of the earliest bucket size. By increasing

the number of buckets, r, for each size (r > 2), we

introduce more buckets of smaller size and the error

is therefore upper bounded by 1/(r − 1). This prop-

erty is essential and implies that choosing sufﬁciently

large r limits the error to any suitable fraction ε > 0.

3 DISTRACTION DETECTION

Before we detail the steps to learn counting features

in a self-sustained time-series, we introduce some no-

tation. The incoming frame-based video is best inter-

preted in our system as a macro-stream represented

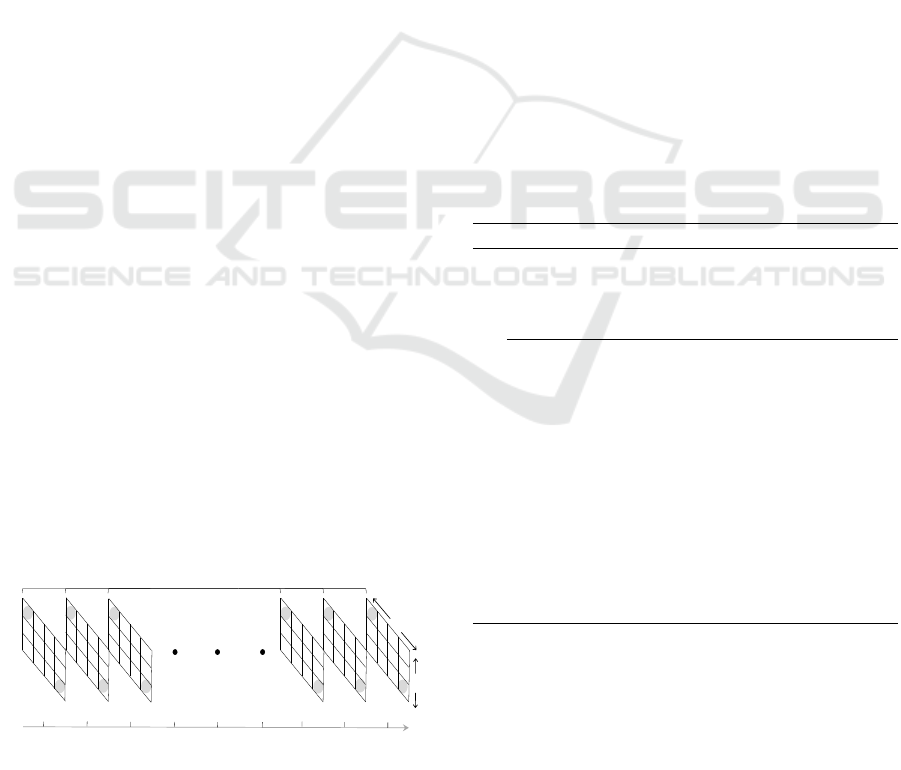
by a matrix S of separable binary micro-streams,

each proceeding along the time course of a respec-

tive frame pixel. Given the uniform frame extent of

width n and height m, the total number of micro-

streams our system maintains and queries simultane-

ously for approximate counts is hence n × m. Spa-

tially, we denote a temporal micro-stream, s

i j

, where

1 ≤ i ≤ m and 1 ≤ j ≤ n (Figure 2). Correspondingly,

we deﬁne a count matrix, C

, we sample at successive

window-bound frames ∈ {N,2N,...,W N}, where W

is the maximum admissible integral number of win-

dows delimited by the length, in frames, of the input

video sequence, as w takes running window indices

∈ {1,2,...,W }. Elements c

i j

of the count matrix, cap-

ture the estimate of count of ones in the k frames

preceding the current window boundary, for each bi-

nary micro-stream, respectively. Incidents of identical

counts in C

, each in the [0,k] range, are summed and

further binned into a compact bag of words vector,

, of a reduced dimensionality |V

| = k + 1. V

of linear O(k) storage and provides for both efﬁcient

similarity computations, and for retaining an extended

past of window summaries.

1 2 3 N N+1 N+2

Sliding Windows

Frames





    





    

Figure 2: Sliding window visualization of the incoming bi-

nary converted macro-stream, highlighting the time course

expansion of bits for micro-streams s

and s

Our process for analyzing distraction events in a

macro-stream, commences with the extraction of win-

dow bound features, as outlined in Algorithm 1. Ev-

ery video frame that enters our pipeline is ﬁrst bi-

nary converted from a gray-scale or color format by

constructing the frame intensity histogram and apply-

ing pixel-level thresholding. A newly arrived frame is

timestamped modulo N, and is thereafter interpreted

as an m by n array of new bits, each corresponding to

the spatially matching micro-stream, s

i j

. At its out-

set, the baseline of a new frame launches a concur-

rent bucket update for maintaining the DGIM rules,

and affects the entire collection of micro-streams, s

i j

We determine a window boundary, after an initial la-

tency of N frames and for every N frames that fol-

low, by testing timestamp modulo N for zero. At win-

dow markers, we query the estimated count of ones

for the past k frames from each micro-stream, s

i j

, and

respectively ﬁll the cells, c

i j

, of our window speciﬁc

count matrix, C

, simultaneously. Lastly, we perform

a reduction operation on the current count matrix that

leads to our compressed window feature vector, V

The number of active past windows, W, for retaining

window feature vectors, prescribes a ﬁxed time inter-

val to learn distractions from, and is either derived

directly, or set as a not-to-exceed system level param-

eter for an inﬁnite video sequence.

Algorithm 1: Window Feature Extraction.

1: input: frame f , window N, frames-of-interest k

2: output: window feature vector V ←

3: timestamp ← index( f ) mod N

4: for i = 1 to m do

5: for j = 1 to n do

6: update-bucket(s

i j

,threshold( f

i j

))

7: if not(timestamp) then

8: c

i j

← query(s

i j

,k)

9: end if

10: end for

11: end for

12: if not(timestamp) then

13: V ← bag-of-counts(C)

14: end if

15: return V

For detecting distraction, we match features of

the sampled windows at integral multiples of N

frames, by computing a single-term form of simi-

larity between the pair of the current and previous

window representations. Our window properties are

inherently directional and are distributed in a non-

Euclidean space, hence we chose cosine similarity

(Salton et al., 1975; Baeza-Yates and Ribeiro-Neto,

Efﬁcient Distraction Detection in Surveillance Video using Approximate Counting over Decomposed Micro-streams

329

1999) as the distance metric that measures the angle

between the two window-bound feature vectors

sim

·V

w−1

k V

w−1

, (1)

where w is the running index of the current window,

such that w ≥ 2. In addition to the window feature

vector, V

, we also retain the point similarity measure,

sim

, that requires O(1) storage space, per window.

In its basic embodiment, our system alerts a distrac-

tion event on a window edge, as the point similarity

value computed exceeds a globally speciﬁed thresh-

old parameter, τ. Conversely, by maintaining a series

of distances for formerly evaluated window pairings,

we ﬁt discretized similarity samples of multiple past

windows onto a curve. We could then use a more gen-

eralized version of the dynamic time warping algo-

rithm (Efrat et al., 2007), for matching a pair of par-

tially overlapping similarity curves, each comprised

of an identical distance sample-count.

4 EVALUATION

To evaluate our system in practice, we have imple-

mented a software prototype that realizes the con-

cept of maintaining stream statistics over sliding win-

dows, for effective distraction detection. A distraction

marks an abrupt shift in a stable context that typiﬁes

the input stream, and may last up to a few seconds.

We use OpenCV to capture real-world surveillance

video and feed each frame to our processing pipeline,

designed with the objective to keep up with incoming

frame rate. For conciseness, we use the compact nota-

tion λ(N,k) to describe our parametrically driven im-

plementation, and seek to analyze the impact of vary-

ing model parameters on our system performance.

4.1 Experimental Setup

One indispensable resource for practitioners in the

ﬁeld of analyzing surveillance video is the pub-

licly accessible, Video Surveillance Online Reposi-

tory (ViSOR) (ViSOR, 2010). ViSOR is highly exten-

sive and offers over a dozen of surveillance datasets

acquired by tracking both indoor and outdoor en-

vironments for many hours, and captured by either

static or dynamic settings of single and multi camera

installations. The video sequence footage produced is

available in either a compressed or an uncompressed

format, and may optionally contain companion anno-

tation meta-data (Vezanni and Cucchiara, 2010) for

use as a ground-truth reference. In our experiments,

we employed three surveillance streams from the Vi-

SOR dataset of the Unimore university that surveyed

the near outdoors of several campus buildings. The

properties of the sequences, we henceforth denote as

visor i, where i ∈ {1,2,3}, are further listed in Ta-

ble 1. Our experimental videos are natively MPEG-

1 compressed, they share a uniform frame resolu-

tion that translates to 98,304 micro-streams for each,

and frames are presented in a single-component gray-

scale format. The ﬁled length of the videos varies

from over two to about seventeen thousand frames,

and facilitates a reasonable sampling rate for learning

window bound features.

Table 1: Properties of the three ViSOR surveillance se-

quences we use in our experiments. They track the near

outdoors of a conﬁned Unimore campus area by deploying

a multi camera setup.

visor 1 visor 2 visor 3

Width 384 384 384

Height 256 256 256

Frames 2631 8661 17078

FPS 25 25 25

(a) visor 1 (1:40). (b) visor 2 (3:00). (c) visor 3 (5:06).

Figure 3: Distraction snapshots of people entering the ﬁeld-

of-view of the static camera, shown for each of the ViSOR

sequences (in minutes into the video from start).

Our experimental videos track a fairly benign and

mostly static background (Table 1), as one or several

persons walk or rush their way and occasionally enter

and thereafter exit the camera ﬁeld-of-view, to estab-

lish a scene distraction (Figure 3). ViSOR test streams

are supplemented by concept data that is rather ab-

stract, and to serve a useful ground-truth in our evalu-

ation required us to manually assemble pertinent tim-

ing information. We have thus extended the ViSOR

meta-data by hand annotating occurrences of distrac-

tion, linking each record to a scene in-and-out time-

interval. Intervals are inherently non-overlapping and

their endpoints assigned absolute frame timestamps.

From our ViSOR videos, we singled out 14, 7, and 44

events of interest, respectively, along with their dis-

tinct intervals (see APPENDIX).

Our experiments ascribe a discrete value set to

each of our model parameters, N and k, listed in Ta-

KDIR 2016 - 8th International Conference on Knowledge Discovery and Information Retrieval

330

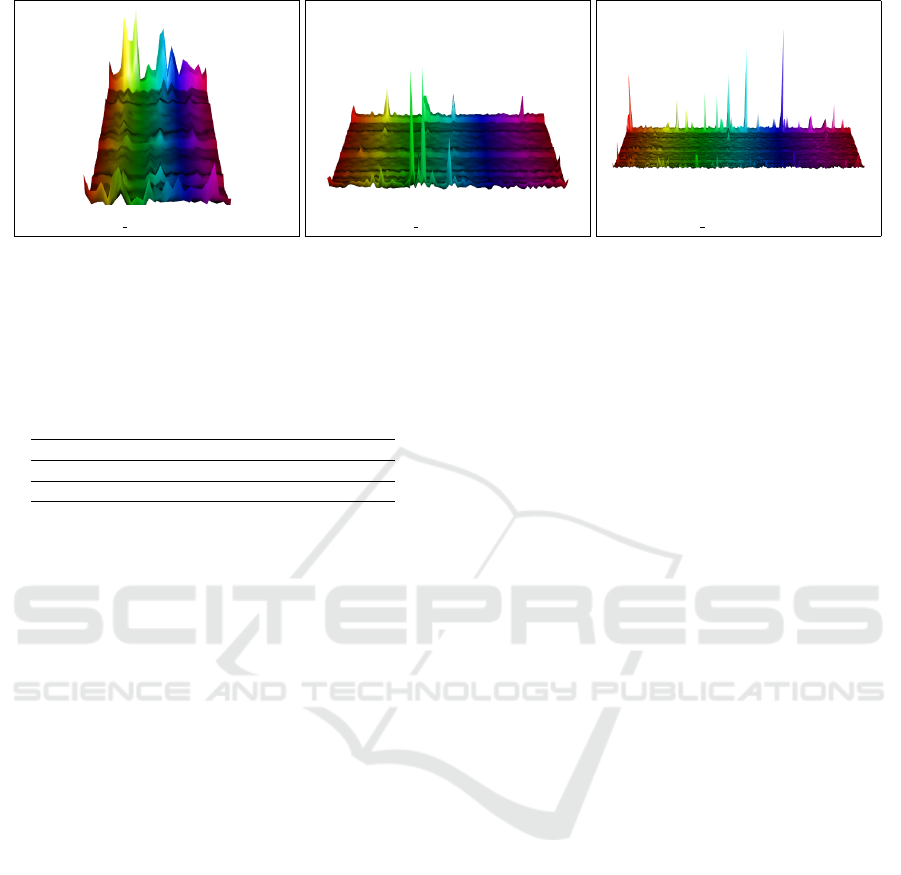
(a) visor 1: W = 26 windows. (b) visor 2: W = 86 windows. (c) visor 3: W = 170 windows.

Figure 4: Visualization of temporally distributed, window-bound feature vectors, V

, extracted for stream counting parameters

N = 100 and k = 50. Presented as a height ﬁeld over a two-dimensional grid, (W,k + 1), and shown for each of our ViSOR

experimental sequences.

Table 2: Experimental parameter selection of window size,

N, in frames, and k, the number of past frames, or prior bits

in the context of a micro-stream, to query an approximate

count of ones.

Window (N) Query (k)

100 10 20 50

200 20 50 100

500 50 100 250

ble 2. For each window length choice, N, there are

three query period selections, k, that range propor-

tionally between 10 to 50 percent of the window size.

Ultimately, we seek the proper design trade-offs in

choosing both intra and inter window parameter pair-

ings, to improve the system success rate for detect-

ing distraction. For the current implementation, we

present results pertained to our point based similar-

ity approach, however, extending to similarity curve

matching (Efrat et al., 2007) is outside the scope of

this study and is deferred to future work.

4.2 Experimental Results

In a system of similar goals as ours, exercising overly

conservative and more cautious practices is often de-

vised for signaling a distraction event in a stream.

The percentage of false positives we encounter is di-

rectly related to the choice of our similarity threshold

value, τ, thus subscribing to more unintentional event

triggers with a lower τ. To properly adapt to action

choices taken upon alert, we made similarity thresh-

old setting a user tunable. On the other hand, attend-

ing to false negatives and sustain a reduced miss rate

is of a taller order in our design. False negatives are

primarily impacted by the error bound to the approx-

imate count of ones we solicit from a micro-stream,

and is inversely proportional to the number of occur-

rences set for the same bucket size, r. For our ex-

periments, we conﬁgured the construction of the time

histograms with r = 2, to yield a worst-case counting

error, and report next results that score both the iden-

tifying and misinterpreting distraction events in our

ViSOR samples.

First, we validated the temporal evolution of our

approximate count features in a macro-stream. A sur-

face visualization of the extracted window vectors,

, is shown for each of the three ViSOR sequences,

with W = {26,86,170} progressive windows, respec-

tively, as model parameters, (N, k), are assigned uni-

formly to (100,50) (Figure 4). The height ﬁeld is ren-

dered over a two-dimensional regular grid, (W,k + 1),

and cells depict each a scaled count value, aligned

with elements of the unnormalized feature vectors.

Rather than explore post-threshold results that are

notably less informative, we present unsolicited point

similarities. Given the non-negative elements of our

bag-of-counts window features, V

, the cosine simi-

larity term produces a value bound to the [0,1] range.

To improve clarity of our reporting, we resort to the

more intuitive metric of cosine distance instead, that

attributes greater distraction, or dissimilarity, to a

higher value. For every ViSOR surveillance video,

Table 3 outlines a curve of point dissimilarities, each

for a pair of window feature vectors, (V

w−1

), as a

function of an ascending window id, and factored by

our test choices of model parameters, (N,k). Along

with Table 4 that provides a complementary matrix

form for summarizing the number of identiﬁed in-

cidents obtained from each stream, as a function of

our model parameter choices. Predicted distraction

instances are further correlated with our hand anno-

tated, ground-truth interval data. Every interval rep-

resents a double-edged incident, with distractions oc-

curring upon entry to and exit from the camera ﬁeld-

of-view, respectively. An interval either overlaps two

or more windows, a form that ﬁts well our current-

to-previous count matching model, or may entirely be

conﬁned to a single window and occasionally give rise

to missing events. To properly account for precedence

of false negatives, we chose the F1-score metric to

assess our system-level distraction detection, as out-

Efﬁcient Distraction Detection in Surveillance Video using Approximate Counting over Decomposed Micro-streams

331

Table 3: Curve outline of point dissimilarities, each for a pair of window feature vectors, (V

w−1

), as a function of an

increasing window id. Factored by each of our experimental choices of model parameters, (N, k), and shown for each ViSOR

surveillance video.

visor 1

5 10 15 20 25

0.00 0.01 0.02 0.03 0.04 0.05

Window Id

Dissimilarity

5 10 15 20 25

0.00 0.02 0.04 0.06

Window Id

Dissimilarity

5 10 15 20 25

0.000 0.005 0.010 0.015

Window Id

Dissimilarity

2 4 6 8 10 12

0.00 0.02 0.04 0.06 0.08

Window Id

Dissimilarity

2 4 6 8 10 12

0.000 0.004 0.008

Window Id

Dissimilarity

2 4 6 8 10 12

0.000 0.004 0.008

Window Id

Dissimilarity

0.04 0.05 0.06 0.07 0.08

Window Id

Dissimilarity

1 2 3 4

0.000 0.010 0.020 0.030

Window Id

Dissimilarity

1 2 3 4

0.010 0.015 0.020 0.025 0.030

Window Id

Dissimilarity

1 2 3 4

visor 2

0.0000 0.0010 0.0020

Window Id

Dissimilarity

1 13 26 39 52 65 78

0.000 0.001 0.002 0.003 0.004

Window Id

Dissimilarity

1 13 26 39 52 65 78

0.0000 0.0010 0.0020

Window Id

Dissimilarity

1 13 26 39 52 65 78

0.0000 0.0005 0.0010 0.0015

Window Id

Dissimilarity

1 6 12 19 26 33 40

0e+00 2e−04 4e−04 6e−04

Window Id

Dissimilarity

1 6 12 19 26 33 40

0.0000 0.0005 0.0010 0.0015

Window Id

Dissimilarity

1 6 12 19 26 33 40

0.000 0.004 0.008 0.012

Window Id

Dissimilarity

1 3 5 7 9 11 14

0.000 0.004 0.008 0.012

Window Id

Dissimilarity

1 3 5 7 9 11 14

0.000 0.004 0.008 0.012

Window Id

Dissimilarity

1 3 5 7 9 11 14

visor 3

0.000 0.010 0.020

Window Id

Dissimilarity

1 24 50 76 106 140

0.00 0.05 0.10 0.15

Window Id

Dissimilarity

1 24 50 76 106 140

0.000 0.004 0.008 0.012

Window Id

Dissimilarity

1 24 50 76 106 140

0.00 0.02 0.04 0.06

Window Id

Dissimilarity

1 12 25 38 51 64 77

0.0000 0.0010 0.0020 0.0030

Window Id

Dissimilarity

1 12 25 38 51 64 77

0.000 0.002 0.004

Window Id

Dissimilarity

1 12 25 38 51 64 77

0.00 0.05 0.10 0.15

Window Id

Dissimilarity

1 5 9 13 18 23 28 33

0.00 0.05 0.10 0.15

Window Id

Dissimilarity

1 5 9 13 18 23 28 33

0.00 0.02 0.04 0.06 0.08 0.10

Window Id

Dissimilarity

1 5 9 13 18 23 28 33

(100,10) (100,20) (100,50) (200,20) (200,50) (200,100) (500,50) (500,100) (500,250)

Table 4: Distraction occurrence prediction shown as 3x3

matrices for our N by k choices (Table 2), for each of the

ViSOR sequences.

N visor 1 visor 2 visor 3

100 15 13 15 24 24 18 67 54 34

200 7 8 9 18 20 16 51 47 48

500 3 2 2 9 10 8 18 13 16

lined in Table 5 for each of the ViSOR videos. For ref-

erence, Table 6 provides confusion matrices for each

of our videos, as we set false positives uniformly to

zero since they incur little impact on system perfor-

mance. Evidently, the end-to-end F1-score improves

as the stream length increases, and not surprisingly,

both a narrower N for denser sampling of window fea-

tures, and a smaller k for the more recent frames used

to query counts, ameliorate our anomaly hit rate.

Table 5: F1-score measure for system-level distraction de-

tection, for each of the ViSOR video sequences.

visor 1 visor 2 visor 3

0.69 0.73 0.86

Table 6: Confusion matrices of two-class classiﬁcation for

stream counting parameters N = 100 and k = 10, for each

of the ViSOR video sequences.

visor 1

Real

15 13

0 12

Predicted

visor 2

Real

14 10

0 73

Predicted

visor 3

Real

67 21

0 83

Predicted

Our system provides for comparing performance

of our pixel-based time histogram with a more base-

line approach of a frame-based intensity histogram.

For this experiment, we retained a window-worth of

intensity histograms that we construct every frame

right before performing binary thresholding. We con-

sidered 256 bins and computed the mean of the his-

tograms over a window of N frames to extract a win-

dow feature vector of cardinality |V

| = 256. Notably

for the baseline method, we observed an appreciable

increase of false negatives by about 43% on average

across our ViSOR videos. Incurring this higher miss

rate owes primarily to a suboptimal baseline repre-

sentation that severely compromises the stream data.

Rather, our approach decomposes a video into many

thousands of signals processed individually, to closely

preserve the integrity of the original macro-stream

and thus facilitates more robust discovery of distrac-

tion patterns. Computationally, our method with time

complexity O(mnlogN) naturally entails more load

when executed serially, however, a parallel GPU con-

cept that assigns a thread to each of the micro-streams

is capable of a markedly O(logN) lower bound.

Table 7: Average frame rate (FPS) and average micro-

stream processing (uSP) time in microseconds as a func-

tion of modiﬁed model parameters, (N, k), for each of our

experimental ViSOR video streams.

visor 1 visor 2 visor 3

N k FPS uSP FPS uSP FPS uSP

100 10 12.57 0.72 16.51 0.55 11.48 0.79

20 11.23 0.81 18.31 0.49 12.06 0.75

50 10.86 0.83 19.34 0.47 12.73 0.71

200 20 10.85 0.83 14.98 0.60 11.23 0.81

50 10.17 0.89 18.04 0.50 11.01 0.82

100 10.38 0.87 18.47 0.49 11.49 0.79

500 50 10.40 0.87 14.16 0.64 10.00 0.90

100 9.31 0.97 17.56 0.51 9.17 0.99

250 9.30 0.97 17.60 0.51 9.18 0.98

In Table 7, we provide computational runtime of

our implementation, listing for each of the experimen-

tal ViSOR videos the average of both the frame rate

KDIR 2016 - 8th International Conference on Knowledge Discovery and Information Retrieval

332

Table 8: A distraction event in the visor 3 video that arises as a result of a moving white vehicle (outlined in red) that traverses

the camera ﬁeld-of-view from right to left in about a second and totals 25 frames of exposure. The event interval starts at

about frame number 5322 and shown are samples captured on three-frame successions.

5325 5328 5331 5334 5337

frame number

(FPS) and micro-stream processing (uSP) time, mea-

sured in microseconds, as we alter our model param-

eters, (N, k). There is a clear monotonic decrease in

performance as we increase the window size, N, at a

rate that is close to the ratio log N

i−1

/log N

, where i

associates with the current window-size setting. How-

ever, the runtime depends rather weakly on the model

parameter k, as both the check for bucket expira-

tion and the query of approximate counting are pro-

cessed efﬁciently. We demonstrate the highest perfor-

mance on visor 2, and this is mainly attributed to its

fairly sparse and temporally low distraction density of

1250 frames-per-event (FPE) on average, compared

to an FPE of 188 and 38 for visor

1 and visor 3, re-

spectively. Noteworthy in this report is the observed

quadratic impact of the surveillance camera resolu-

tion on our running time. To further address high def-

inition video, our implementation is capable of task-

ing groups of micro-streams concurrently and sustain

a required real-time response for notifying distraction

occurrences as they continuously develop.

Distraction events in our ViSOR test sequences

are mostly typiﬁed by the motion of humans (Figure

3). However, they also occasionally manifest them-

selves by vehicle passing that transpires in the some-

what far background of the monitored area. Figure 8

depicts such a scenario in the visor 3 video where a

white vehicle moves across the camera ﬁeld-of-view

right-to-left and thereof constitutes a valid distraction

instance. This event starts at around frame number

5322 and lasts about a second for a total exposure of

25 frames, with samples shown for every third frame.

Vehicular based events either occur autonomously or

may coincide with a human triggered event. Semanti-

cally, our system interprets both event types equally

and makes no attempt to distinguish between them

in processing a distraction alert. We avoided hand-

annotating vehicular episodes in the meta-data of our

experimental videos, and unless a human distraction

occurrence overlaps with a vehicular one, the event is

presumed false positive.

5 RELATED WORK

Over the past decade, a wide range of diverse schemes

were proposed for automating abnormal event de-

tection in surveillance videos. Among some of the

many algorithms considered in published literature

are techniques that incorporate optical ﬂow, including

a Markov Random Field model that divides the video

into a graphically linked grid of spatio-temporal lo-

cal regions to facilitate probabilistic motion patterns

(Jaechul and Grauman, 2009), and the more recent

research that analyzes compressed domains by con-

sulting codec-dependent meta-data to provide more

accurate object boundaries (Li et al., 2014). To ad-

dress complex events, Chen et. al (2015) proposed

a hypergraph based semi-supervised learning method

that blends motion features with semantic concepts.

Compared to techniques that deploy ordinary graphs,

they report better average precision and recall for de-

tecting multiple moving targets. More data driven is

the spectral clustering method that utilizes an eigen-

vector selection to discover natural grouping patterns

(Xiang and Gong, 2008). Whereas a device speciﬁc

work by Shimada et. al (2015), embodies a stream

originated by a light-ﬁeld camera to create and up-

date a light-ray background model that changes dy-

namically, and demonstrates advantage over a single-

view camera. At a higher level of abstraction, Lee

and Nevatia (2014) sought after a tool that uses shape

based approach to validate whether an identiﬁed ab-

normal event was triggered by a human or not.

Most of the techniques discussed for detecting

change in an inﬁnite stream tend to build explicit and

often oversubscribed models to associate with many

normal events, thus making a distraction hard to de-

ﬁne. Our work rather compares a current event with

the rest of the events observed (Zhong et al., 2004),

and furthermore, by rendering the video as a col-

lection of opaque bit streams, it makes no prior be-

havioral assumptions and neither subscribes to visual

context dependencies.

Efﬁcient Distraction Detection in Surveillance Video using Approximate Counting over Decomposed Micro-streams

333

6 CONCLUSIONS

We have demonstrated the apparent potential in tailor-

ing approximate counting to effectively detect distrac-

tions in unbound surveillance videos, with little hu-

man counseling. Our highly compact bag-of-counts

representation is scalable and provides learning of

many windows that outline a deeper past, to facilitate

the expansion of the more conventional, point similar-

ity approach. Running on an unoptimized prototype

version, the obtained sustainable throughput of about

half the input frame-rate on average, consistently on

all of our experimental videos and the full extent of

model parameter settings, provides for real-time ap-

plication compliance.

A natural progression of our work is to reduce the

absolute counting error by introducing more smaller

buckets for constructing the time-based histogram

over a window, and improve overall detection rate.

Rather than a step function that characterizes window

transitions in the current implementation, the use of a

tapered sliding window offers overlapping windows,

as frames gradually enter and exit the window, to fur-

ther assist and lower distraction misses.

ACKNOWLEDGEMENTS

We would like to thank the anonymous reviewers for

their insightful suggestions and feedback.

REFERENCES

Arasu, A. and Manku, G. S. (2004). Approximate counts

and quantiles over sliding windows. In Principles

of Database Systems (PODS), pages 286–296, Paris,

France.

Baeza-Yates, R. and Ribeiro-Neto, B., editors (1999). Mod-

ern Information Retrieval. ACM Press Series/Addison

Wesley, Essex, UK.

Chen, X. J., Zhan, Y. Z., Ke, J., and Chen, X. B. (2015).

Complex video event detection via pairwise fusion of

trajectory and multi-label hypergraphs. Multimedia

Tools and Applications, pages 1–22.

Datar, M., Gionis, A., Indyk, P., and Motwani, R. (2002).

Maintaining stream statistics over sliding windows.

SIAM Journal of Computing, 31(6):1794–1813.

Efrat, A., Fan, Q., and Venkatasubramanian, S. (2007).

Curve matching, time warping, and light ﬁelds: New

algorithms for computing similarity between curves.

Mathematical Imaging and Vision, 27(3):203–216.

Jaechul, K. and Grauman, K. (2009). Observe locally, in-

fer globally: A space-time MRF for detecting abnor-

mal activities with incremental updates. In Computer

Vision and Pattern Recognition (CVPR), pages 2921–

2928, Miami, FL.

Lee, L. K. and Ting, H. F. (2006). Maintaining signiﬁcant

stream statistics over sliding windows. In Discrete Al-

gorithm (SODA), pages 724–732, Miami, FL.

Lee, S. C. and Nevatia, R. (2014). Hierarchical abnormal

event detection by real time and semi-real time multi-

tasking video surveillance system. Machine Vision

and Applications, 25(1):133–143.

Leskovec, J., Rajaraman, A., and Ullman, J. D., editors

(2014). Mining of Massive Datasets. Cambridge Uni-

versity Press, New York, NY.

Li, H., Zhang, Y., Yang, M., Men, Y., and Chao, H. (2014).

A rapid abnormal event detection method for surveil-

lance video based on a novel feature in compressed

domain of HEVC. In Multimedia and Expo (ICME),

pages 1–6, Chengdu, China.

Salton, G., Wong, A., and Yang, C. S. (1975). A vector

space model for automatic indexing. Communications

of the ACM, 18(11):613–620.

Shimada, A., Nagahara, H., and Taniguchi, R. I. (2015).

Change detection on light ﬁeld for active video

surveillance. In Advanced Video and Signal Based

Surveillance (AVSS), pages 1–6, Karlsruhe, Germany.

Vezanni, R. and Cucchiara, R. (2010). Video surveil-

lance online repository (ViSOR): an integrated frame-

work. Journal of Multimedia Tools and Applications,

50(2):359–380.

ViSOR (2010). Video surveillance online repository.

http://www.openvisor.org .

Xiang, T. and Gong, S. (2008). Video behavior proﬁling

for anomaly detection. Pattern Analysis and Machine

Intelligence, 30(5):893–908.

Zhong, H., Shi, J., and Visontai, M. (2004). Detecting un-

usual activity in video. In Computer Vision and Pat-

tern Recognition (CVPR), pages 819–826, Washing-

ton, DC.

APPENDIX

Our meta-data for hand annotated time intervals that

capture distraction instances from each of our ViSOR

sequences are listed in Table 9.

KDIR 2016 - 8th International Conference on Knowledge Discovery and Information Retrieval

334

Table 9: Hand annotated, in-and-out time intervals that capture distraction events from each of our ViSOR sequences. Interval

endpoints and duration are shown in a minutes:seconds format, as intervals extend to either wholly or partially cover one up

to four windows.

visor 1

event in out duration

1 0:02 0:03 0:01

2 0:18 0:20 0:02

3 0:27 0:28 0:01

4 0:29 0:30 0:01

5 0:40 0:42 0:02

6 0:45 0:47 0:02

7 0:49 0:50 0:01

8 0:51 0:55 0:04

9 0:58 1:02 0:04

10 1:04 1:07 0:03

11 1:17 1:18 0:01

12 1:33 1:35 0:02

13 1:36 1:37 0:01

14 1:40 1:41 0:01

visor 2

event in out duration

1 0:04 0:05 0:01

2 0:55 1:00 0:05

3 1:03 1:06 0:03

4 2:01 2:03 0:02

5 2:10 2:12 0:02

6 2:17 2:20 0:03

7 2:54 3:02 0:08

visor 3

event in out duration

1 0:02 0:03 0:01

2 0:07 0:09 0:02

3 0:17 0:20 0:03

4 0:55 1:01 0:06

5 1:29 1:30 0:01

6 1:51 1:53 0:02

7 1:59 2:06 0:07

8 2:16 2:19 0:03

9 2:29 2:35 0:06

10 3:00 3:03 0:03

11 3:18 3:21 0:03

12 3:48 3:51 0:03

13 3:57 3:59 0:02

14 4:10 4:13 0:03

15 4:27 4:31 0:04

16 4:32 4:34 0:02

17 4:42 4:46 0:04

18 4:49 4:51 0:02

19 4:59 5:02 0:03

20 5:05 5:14 0:09

21 5:38 5:40 0:02

22 5:44 5:47 0:03

23 5:54 5:56 0:02

24 5:59 6:02 0:03

25 6:20 6:23 0:03

26 6:38 6:45 0:07

27 6:49 6:52 0:03

28 7:01 7:04 0:03

29 7:08 7:11 0:03

30 7:24 7:25 0:01

31 7:28 7:31 0:03

32 7:44 7:45 0:01

33 7:47 7:50 0:03

34 7:57 8:00 0:03

35 8:04 8:05 0:01

36 8:07 8:10 0:02

37 8:22 8:24 0:02

38 9:16 9:21 0:05

39 9:53 10:03 0:10

40 10:08 10:11 0:03

41 10:26 10:31 0:05

42 10:54 10:57 0:03

43 10:58 11:00 0:02

44 11:13 11:16 0:03

Efﬁcient Distraction Detection in Surveillance Video using Approximate Counting over Decomposed Micro-streams

335