Bijective Fuzzy Relations
A Graded Approach
Martina Da
ˇ
nkov
´
a
Institute for Research and Applications of Fuzzy Modeling, CE IT4Innovations, University of Ostrava,
30. dubna 22, Ostrava, Czech Republic
Keywords:
Fuzzy Relations, Fuzzy Functions, Partial Fuzzy Functions, Bijective Mappings, Fuzzy Class Theory.
Abstract:
Bijectivity is one of crucial mathematical notions. In this paper, we will present a fuzzy bijective mapping as
a fuzzy relation that has several special properties. These properties come with degrees and so the bijectivity
is also a graded property. We will focus on properties of this type of relations and show graded versions of
theorems on fuzzy bijections that are known from traditional Fuzzy Set Theory.
1 INTRODUCTION
In this work, we will present a gradual version of
results on fuzzy bijective functions from (Demirci,
2000; Demirci, 2001). The presented results
lay foundations for developing a theory of partial
fuzzy functions and partial bijective fuzzy relations
over a simple system of fuzzy partial propositional
logic (B
ˇ
ehounek and Nov
´
ak, 2015). There we deal
with membership functions that admit undefined truth
degrees.
A basis for the notion of fuzzy bijective function
is the notion of fuzzy function. This notion took
many forms by their definitions; e.g., it is any map-
ping that assigns a fuzzy set to a fuzzy set or fuzzy set
to a point (Nov
´
ak et al., 1999); it is a fuzzy relation
that meets two properties, namely, extensionality and
functionality for a partial fuzzy function, and if it is
in addition total then it is called a perfect fuzzy func-
tion (Demirci, 1999; Demirci, 2001; Demirci and Re-
casens, 2004; Perfiljeva I., 2014); etc. Overviews to-
gether with applications can be found in the following
exemplary sources (Klawonn, 2000; Demirci, 2001;
B
ˇ
elohl
´
avek, 2002).
As noted in (Demirci, 2000), not all notions of
fuzzy function do coincide with the classical notion
for crisp functions. We will avoid this problem and
all the subsequent definitions will be consistent with
the classical notion whenever applied on crisp inputs.
We follow up (Da
ˇ
nkov
´
a, 2010a) where the graded
property of extensionality has been studied and
(Da
ˇ
nkov
´
a, 2010b; Da
ˇ
nkov
´
a, 2011) where the graded
property of functionality has been explored and used
to make an implicative model of fuzzy IF–THEN
rules. In (Da
ˇ
nkov
´
a, 2010b), the framework was
that of Fuzzy Class Theory (B
ˇ
ehounek and Cintula,
2005). It enables formulation of notions in the stan-
dard mathematical notation whereas the background
machinery provides the non-classical interpretation.
Since this framework might be difficult to read for
fuzzy mathematicians, we choose the common alge-
braic one for this paper and, in addition, review results
presented in (Da
ˇ
nkov
´
a, 2010b).
2 BASIC NOTIONS
In the following, we will work with algebraic struc-
tures used as basic structures for fuzzy logic of left-
continuous t-norms, the so called monoidal t-norm
based logic.
Definition 1. An MTL-algebra L is a bounded resid-
uated lattice
L = hL, ∨, ∧, ∗, →, 0, 1i (1)
with four binary operations and two constants such
that
• L = hL, ∨, ∧, 0, 1i is a lattice with the largest el-
ement 1 and the least element 0 w.r.t. the lattice
ordering ≤,
• L = hL, ∗, 1i is a commutative semigroup with the
unit element 1, i.e., ∗ is commutative, associative,
and 1 ∗ x = x for all x ∈ L,
• ∗ and → form an adjoint pair, i.e.,
z ≤ (x → y) iff x ∗ z ≤ y for all x, y, z ∈ L,
42
Da
ˇ
nková, M.
Bijective Fuzzy Relations - A Graded Approach.
DOI: 10.5220/0006053300420050
In Proceedings of the 8th International Joint Conference on Computational Intelligence (IJCCI 2016) - Volume 2: FCTA, pages 42-50
ISBN: 978-989-758-201-1
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

• satisfying the pre-linearity equation:
(x → y) ∨ (y → x) = 1.
In the sequel, let us assume L be an MTL-algebra
of the form (1). We will call the operation ∗ product
and → residuum. Moreover, we define the operations
called bi-residuum and powers w.r.t. the product ∗:
x ↔ y =
df
(x → y) ∧ (y → x)
ϕ
n
=
df
ϕ ∗ . . . ∗ ϕ
| {z }
n-times
To reduce the number of parenthesis used in mathe-
matical expressions we set that ∗ has the highest pri-
ority and → the lowest priority out of all operations
that are at the disposal.
Throughout the whole text, we will deal with
fuzzy relations whose membership functions are de-
fined on non-empty sets and take values from the sup-
port of L , and will denote this fact by
⊂
∼
. In the se-
quel, let X ,Y 6=
/
0, R, S
⊂
∼
X × Y , ≈
1
⊂
∼
X × X and
≈
2
⊂
∼
Y × Y are fuzzy relations such that all infima
and suprema needed for the definition of the truth-
value of any expression exist in L.
Which variables belong to which sets is always
clear from the context. Therefore it is not necessary
to specify membership of variables in sets in expres-
sions, including infima and suprema; e.g., we write
W
x,y
R(x, y) instead of
W
x∈X,y∈Y
R(x, y). And for the
sake of brevity we use Rxy instead of R(x, y).
Let us define the following graded properties of
fuzzy relations:
• Reflexivity:
Refl(R) ≡
df
^
x
Rxx
• Symmetry:
Sym(R) ≡
df
^
x,y
(Rxy → Ryx)
• Transitivity:
Trans(R) ≡
df
^
x,y,z
[(Rxy ∗ Ryz) → Rxz]
• Similarity:
Sim(R) ≡
df
Refl(R)∗Sym(R)∗ Trans(R)
• Subsethood:
R ⊆ S ≡
df
^
x,y
(R(x, y) → S(x, y))
• Strong set-similarity:
R
∼
=
S ≡
df
^
x,y
(R(x, y) ↔ S(x, y))
• Set-similarity:
R ≈ S ≡
df
(R ⊆ S) ∗ (S ⊆ R)
• Totality:
Tot(R) ≡
df
^
x
_
y
Rxy
• Surjectivity:
Sur(R) ≡
df
^
y
_
x
Rxy
• Injectivity:
Inj
≈
1,2
(R) ≡
df
^
x,x
0
,y,y
0
[((y ≈
2
y
0
) ∗ Rxy ∗ Rx
0
y
0
) → (x ≈
1
x
0
)]
In the sequel, we will freely use the class notation
that has been formally developed in (B
ˇ
ehounek and
Cintula, 2005). It means that for a fuzzy set A
⊂
∼
X
{x | Ax} respresents A
y ∈ {x | Ax} stands for Ay
and for a fuzzy relation R
⊂
∼
X ×Y
{xy | Rxy} respresents R
x
0
y
0
∈ {xy | Rxy} stands for Rx
0
y
0
and analogously we proceed for an arbitrary expres-
sion ϕ.
Let us introduce the following relational opera-
tions:
R
T
=
df
{yx | Rxy} inverse
R ∩ S =
df
{xy | Rxy ∗ Sxy} strong intersection
R t S =
df
{xy | Rxy ∨ Sxy} union
R u S =
df
{xy | Rxy ∧ Sxy} intersection
We will additionally deal with relational composi-
tions, defined using a class notation. A systematic
study can be find in (B
ˇ
elohl
´
avek, 2002). We will use
three basic relational compositions:
• sup-T composition:
R ◦ S =
df
{xy |
_
z
(Rxz ∗ Szy)}
• BK-subproduct:
R  S =
df
{xy |
^
z
(Rxz → Szy)}
• BK-superproduct:
R  S =
df
{xy |
^
z
(Szy → Rxz)}
Bijective Fuzzy Relations - A Graded Approach
43

The crisp identity = and crisp inclusion v of
fuzzy relation are defined standardly:
R = S if Rxy = Sxy, for all x, y;
R v S if Rxy ≤ Sxy, for all x, y.
Let the following fuzzy relations be of the appro-
priate types; then we can summarize properties of
sup-T-composition (B
ˇ
elohl
´
avek, 2002):
1. Transposition: (R ◦ S)
T
= S
T
◦ R
T
2. Monotony: (R
1
⊆ R
2
) ≤ (R
1
◦ S ⊆ R
2
◦ S)
3. Union:

[
R∈A
R

◦ S =
[
R∈A
(R ◦ S)
4. Intersection:

\
R∈A
R

◦ S v
\
R∈A
(R ◦ S)
5. Associativity: (R ◦ S) ◦ T = R ◦ (S ◦ T )
Properties of BK-products:
1. Transposition: (R  S)
T
= S
T
 R
T
2. Monotony of :
(R
1
⊆ R
2
) ≤ (R
2
 S ⊆ R
1
 S)
(S
1
⊆ S
2
) ≤ (R  S
1
⊆ R  S
2
)
3. Monotony of :
(R
1
⊆ R
2
) ≤ (R
1
 S ⊆ R
2
 S)
(S
1
⊆ S
2
) ≤ (R  S
2
⊆ R  S
1
)
4. Intersection:
\
R∈A
(R  S) =

[
R∈A
R

 S
\
S∈A
(R  S) = R 
\
S∈A
S
5. Union:
[
R∈A
(R  S) v

\
R∈A
R

 S
[
S∈A
(R  S) v R 
[
S∈A
S
Converse inclusions have crisp counter-examples.
6. Residuation: R  (S  T ) = (R ◦ S)  T
7. Exchange: R  (S  T ) = (R  S)  T
2.1 Graded Theorems and Their
Reading
Let us observe the above definitions of relational
properties. For example the totality of R may attain
any degree from L and whenever it attains the de-
gree 1, i.e. Tot(R) = 1, it is total in the classical sense
and we have the correspondence with the classical no-
tion of totality: for all x ∈ X there exists y ∈ Y such
that Rxy = 1. For an arbitrary property ϕ introduced
in this paper, it is valid that if ϕ = 1 then ϕ is identical
to the correspondent classical property.
Statements that will be presented in this paper are
called gradual or graded theorems. It means that in-
stead of a classical theorem of fuzzy mathematics
If (ϕ
1
= 1) and . . . and (ϕ
k
= 1) then (ψ = 1) (2)
we search for a more informative and general (non-
equivalent) form of this statement, the so called
graded theorem:
ϕ
n
1
1
∗ . . . ∗ ϕ
n
k
k
≤ ψ. (3)
By the properties of →, it is equivalent to
(ϕ
n
1
1
∗ . . . ∗ ϕ
n
k
k
→ ψ) = 1 (4)
where ∗ interprets strong conjunction and ϕ
1
, . . . , ϕ
k
,
ψ represent the formalization of premises and the con-
clusion in a form that enjoys degrees of truths. Part of
the analysis is finding out how many times the an-
tecedents ϕ
1
, . . . , ϕ
k
need be used to provide a lower
bound for the degree of the consequent ψ; the result
is encoded in the degrees n
1
, . . . , n
k
.
Graded theorems seem to be difficult for non-
experienced readers; therefore, some translations will
be added as a guideline. The proposed reading of
graded theorems is analogous to the classical case (as
when using classical mathematical logic) and it is dis-
tinguished by a special typeface; for the chosen op-
erations of L, we set:
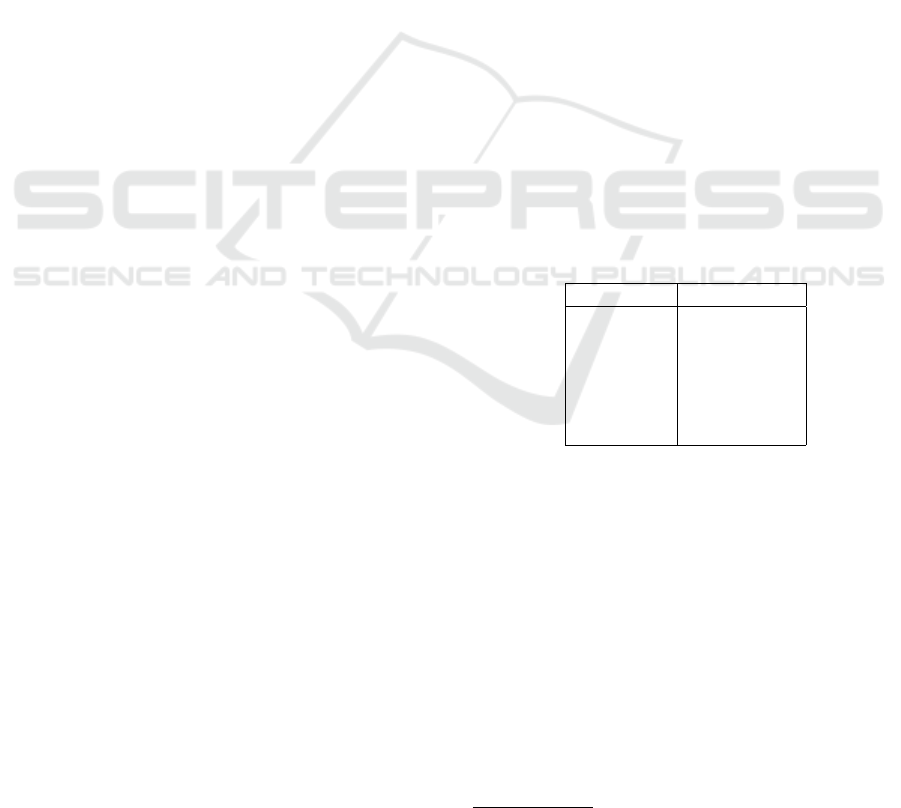
Expression Reading
ϕ → ψ IF ϕ THEN ψ
ϕ ↔ ψ ϕ IFF ψ
ϕ ∧ ψ ϕ AND ψ
ϕ ∨ ψ ϕ OR ψ
ϕ ∗ ψ ϕ and ψ
ϕ = 1 ϕ is TRUE
Hence, (4) can be read as
“It is TRUE that IF ϕ
n
1
1
and . . . and ϕ
n
k
k
THEN ψ.”
Explicitly using degrees, we have that
If ϕ
n
1
1
= d
1
and . . . and ϕ
n
k
k
= d
k
then
ψ ≥ d
1
∗ . . . ∗ d
k
.
1
As an example of a classical theorem (2), we can as-
sume R, S
⊂
∼
X ×X and consider only two antecedents:
let ϕ
1
be “R is a subset of S”, which means that
Rxy ≤ Sxy for all x, y ∈ X; let ϕ
2
be interpreted as
“R is reflexive”, which means Rxx = 1 for all x ∈ X;
and let the consequent ψ be “S is reflexive”. We can
prove the following classical theorem:
If R is a subset of S and R is reflexive then S is
reflexive.
1
Compare with (2).
FCTA 2016 - 8th International Conference on Fuzzy Computation Theory and Applications
44

It can be shown that there is also a graded theorem
(B
ˇ
ehounek et al., 2008) for this statement:
(R ⊆ S) ∗ Refl(R) ≤ Refl(S)
that can be read analogously to the above classical
theorem:
“It is TRUE that IF R ⊆ S and Refl(R) THEN
Refl(S).”
In this case, we have incorporated also additional hid-
den degrees for both properties: if R is reflexive to
a degree r and the degree of subsethood is equal to
d then S is reflexive as much as R is reflexive and
R is a subset of S, which is expressed in degrees as
r ∗ d ≤ Refl(S).
The main difference between classical and graded
theorems is now obvious: having a classical theo-
rem, we use the language of classical mathematical
logic to read the proved theorems, while in the case
of graded theorems, we may read proved inequali-
ties of the form (3) directly using the generalized lan-
guage proposed in the above table. Let us quote from
(Da
ˇ
nkov
´
a, 2007a):
“We write classically, but we think in grades.”
3 EXTENSIONALITY AND ITS
PROPERTIES
The extensionality of a fuzzy relation F
⊂
∼
X ×Y w.r.t.
≈
1
⊂
∼
X
2
, ≈
2
⊂
∼
Y
2
is defined as follows:
Ext
≈
1,2
(F) ≡
df
^
x,x
0
,y,y
0
[(x ≈
1
x
0
) ∗ (y ≈
2
y
0
) ∗ Fxy → Fx
0
y
0
].
The extensionality is one of the most important prop-
erties of fuzzy mathematics. It is used in fuzzy con-
trol, fuzzy logic, fuzzy relational calculus etc., see
(H
´
ajek, 1998; B
ˇ
elohl
´
avek, 2002; Perfilieva, 2001;
Da
ˇ
nkov
´
a, 2007b).
This notion generalizes the classical one that is of
the following form: we say that F is extensional w.r.t.
≈
1
, ≈
2
if
(x ≈
1
x
0
) ∗ (y ≈
2
y
0
) ∗ Fxy ≤ Fx
0
y
0
,
for all x, x
0
∈ X, y, y
0
∈ Y.
Let us recall that
V
,
W
represent generalized uni-
versal and existential quantifiers, respectively; there-
fore, the generalization is natural. Moreover, let us
emphasize that we do not place any requirements on
≈
1
, ≈
2
. We would like to keep requirements as week
as possible. The reason is that some applications may
not be satisfied with use of similarities, but for exam-
ple proximities (i.e., reflexive and symmetric fuzzy
relations) would be enough, such as in case of Region
Connected Calculus (Batyrshin et al., 2008)
3.1 Extensionality of Set Operations
and Relational Compositions
Let us summarize some properties of extensionality
(Da
ˇ
nkov
´
a, 2010c).
Proposition 2. For arbitrary F, E
⊂
∼
X × Y , the fol-
lowing inequalities are valid:
Ext
≈
1,2
(F)∗Ext
≈
1,2
(E) ≤ Ext
≈
2
1,2
(F ∩ E), (5)
Ext
≈
1,2
(F)∗Ext
≈
1,2
(E) ≤ Ext
≈
2
1,2
(F ∪ E), (6)
Ext
≈
1,2
(F)∧Ext
≈
1,2
(E) ≤ Ext
≈
1,2
(F u E). (7)
Readings of the above results:
It is TRUE that (5) – “IF F and E are extensional
THEN their strong intersection is extensional.”
(6) – “IF F and E are extensional THEN their strong
union is extensional.”
(7) – “IF F and E are extensional THEN their intersec-
tion is extensional.”
In the following, the extensionality of supersets as
well as similar sets will be studied.
Proposition 3. For arbitrary F, E
⊂
∼
X ×Y we have:
(F ⊆ E)
2
≤ [Ext
≈
1,2
(F) → Ext
≈
1,2
(E)], (8)
(F ≈ E)
2
≤ [Ext
≈
1,2
(F) ↔ Ext
≈
1,2
(E)]. (9)
Observe that (8) and (9) express the extension-
ality of a higher order for Ext
≈
1,2
w.r.t. ⊆
2
and ≈
2
,
respectively. It means, extensionality when the vari-
ables are fuzzy relations instead of ordinary elements
of X,Y and both (8) and (9) are valid for arbitrary
F, E
⊂
∼
X ×Y .
Readings of the results:
(8) – “IF F is a subset of E (we need this requirement
twice) and F is extensional THEN E is extensional.”
(9) – “IF F and E are similar sets (we need this re-
quirement twice) THEN F is extensional IFF E is ex-
tensional.”
The inequalities (8) and (9) together with proper-
ties of relational compositions produces a long list of
consequences.
Corollary 4. Let
C
1
≡
df
(E
1
⊆ E
2
)
2
,
C
2
≡
df
(F
1
⊆ F
2
)
2
,
C
3
≡
df
(E
1
≈ E
2
)
2
,
C
4
≡
df
(F
1
≈ F
2
)
2
.
Bijective Fuzzy Relations - A Graded Approach
45

Then the following inequalities are valid for arbi-
trary F, F
1
, F
2
⊂
∼
X ×Y and E, E
1
, E
2
⊂
∼
Y × Z:
C
1
≤ [Ext
≈
1,2
(F ◦ E
2
) → Ext
≈
1,2
(F ◦ E
1
)],
C
1
≤ [Ext
≈
1,2
(F  E
1
) → Ext
≈
1,2
(F  E
2
)],
C
1
≤ [Ext
≈
1,2
(F  E
2
) → Ext
≈
1,2
(F  E
1
)],
C
2
≤ [Ext
≈
1,2
(F
2
 E) → Ext
≈
1,2
(F
1
 E)],
C
2
≤ [Ext
≈
1,2
(F
1
 E) → Ext
≈
1,2
(F
2
 E)],
C
3
≤ [Ext
≈
1,2
(F ◦ E
2
) ↔ Ext
≈
1,2
(F ◦ E
1
)],
C
3
≤ [Ext
≈
1,2
(F  E
2
) ↔ Ext
≈
1,2
(F  E
1
)],
C
3
≤ [Ext
≈
1,2
(F  E
1
) ↔ Ext
≈
1,2
(F  E
2
)],
C
4
≤ [Ext
≈
1,2
(F
2
 E) ↔ Ext
≈
1,2
(F
1
 E)],
C
4
≤ [Ext
≈
1,2
(F
1
 E) ↔ Ext
≈
1,2
(F
2
 E)].
Intersection:
Ext
≈
1,2

\
F∈A
F

◦ E

≤ Ext
≈
1,2

\
F∈A
(F ◦ E)

,
Ext
≈
1,2

[
F∈A
(F  E)

≤ Ext
≈
1,2

\
F∈A
F

 E

,
Ext
≈
1,2

[
E∈A
(F  E)

≤ Ext
≈
1,2

F 
[
E∈A
E

.
Union:
Ext
≈
1,2

[
F∈A
F

◦ E

= Ext
≈
1,2

[
F∈A
(F ◦ E)

,
Ext
≈
1,2

\
F∈A
(F  E)

= Ext
≈
1,2

[
F∈A
F

 E

,
Ext
≈
1,2

\
E∈A
(F  E)

= Ext
≈
1,2

F 
\
E∈A
E

.
4 FUNCTIONALITY AND ITS
PROPERTIES
In this section, we will introduce a property of fuzzy
relation called functionality that is a direct generaliza-
tion of the related crisp notion.
Let the functionality property be given as follows:
Func
≈
1,2
(F) ≡
df
^
x,x
0
,y,y
0
[(x ≈
1
x
0
) ∗ Fxy ∗ Fx
0
y
0
→ (y ≈
2
y
0
)].
It generalizes the following classical notion of func-
tionality of F (Demirci, 1999): we say that F is func-
tional w.r.t. ≈
2
if
F(x, y) ∗ F(x, y
0
) ≤ y ≈
2
y
0
, for all x ∈ X, y, y
0
∈ Y .
Taking a closer look at the latter expression, we
uncover the hidden crisp equality related to the vari-
able x. Our setting determines distinguishability on
the input space by ≈
1
. Therefore we have incorpo-
rated this fact by modifying the left side of the above
inequality. Finally, we replace the universal quantifier
with its graded generalization (as infimum) and obtain
our definition.
Example 5. Let L be an arbitrary MTL-algebra,
f : X → Y be an arbitrary function and d ∈ L. The
following relation is functional to the degree 1 w.r.t.
the crisp equality =, =:
F
1
(x, y) =
(
d for y = f (x),
0 otherwise.
Example 6. Let X = Y = [0, 1] and L be the standard
MV-algebra, i.e., L = [0, 1],
x ∗ y =
df
0 ∨ (x + y − 1)
x → y =
df
1 ∧ (1 − x + y).
Let ∼ be a similarity on L defined as:
x ∼ y =
df
0 ∨ (1 − 3 · |x − y|).
Then we find out that:
1. F
2
(x, y) = (y ∼ sin(x)) is functional to the degree 1
w.r.t. ∼, ∼.
2. F
3
(x, y) = (y ∼ f (x)), where
f (x) =

1.7x
2
, x ∈ [0, 0.5],
cos(0.9x) − 0.5, otherwise,
is functional to the degree 1 w.r.t. =, ∼.
3. F
4
(x, y) = F
2
∨ F
3
is functional to the degree 0
w.r.t. ∼, ∼. Take x = x
0
= 1 and y = 0.1, y
0
= 0.8;
then F(x, y) ⊗ F(x
0
, y
0
) = 1, but y ∼ y
0
= 0.
4.1 Functionality of Relational
Operations and Compositions
Let us summarize some properties of functionality
(Da
ˇ
nkov
´
a, 2010c).
Proposition 7. The following inequalities are valid
for arbitrary F, E
⊂
∼
X ×Y :
Func
≈
1,2
(F)∗Func
≈
2,3
(E) ≤ Func
≈
1,3
(F ◦ E),
Func
≈
1,2
(F)∗Func
≈
1,2
(E) ≤ Func
≈
2
1,2
(F ∩ E),
Func
≈
1,2
(F)∧Func
≈
1,2
(E) ≤ Func
≈
1,2
(F u E).
We can also prove the following properties of re-
lations analogous to those of the classical notions.
FCTA 2016 - 8th International Conference on Fuzzy Computation Theory and Applications
46

Proposition 8. It can be proved that
(E ⊆ F)
2
≤ [Func
≈
1,2
(F) → Func
≈
1,2
(E)],
(F ≈ E)
2
≤ [Func
≈
1,2
(F) ↔ Func
≈
1,2
(E)],
are valid for arbitrary F, E
⊂
∼
X ×Y .
We can generate a long list of corollaries the rela-
tional compositions analogous to Corollary 4. Since
the list of corollaries is identical to that of Corollary 4
(only replacing Ext with Func), we do not feel the
need to repeat it.
5 FUZZY FUNCTIONS
Let us start with the graded notion of partial fuzzy
function:
Function
≈
1,2
(F) ≡
df
Ext
≈
1,2
(F)∧Func
≈
1,2
(F),
which joins extensionality and functionality using ∧.
Hence, the degree of being a partial fuzzy function is
computed as the minimum of the degrees of these two
properties. Extensionality means we can substitute
the original inputs by indistinguishable ones. The
functionality tells us that the images of indistinguish-
able elements are indistinguishable. Therefore, we
must still track what is indistinguishable, i.e., how
we choose ≈
1,2
. These relations represent the gran-
ularity of X and Y , respectively, which means that
they should be the coarsest relations in our system en-
abling the distinguishability of elements.
Let us fix for this section that F, F
f
, F
f
F
⊂
∼
X ×Y ,
≈
1
⊂
∼
X
2
, ≈
2
⊂
∼
Y
2
and f , f
F
, f
F
f
: X 7→ Y .
5.1 Fuzzy Functions and Their Crisp
Counterparts
In classical mathematics, crisp functions can be ex-
pressed as functional relations and vice-versa. This
relation is given by y = f (x) for f : X 7→ X. In fuzzy
mathematics we deal with ≈
1
, ≈
2
that do not need to
be similarity or equality relations and moreover, we
have to consider the graded compatibility property
w.r.t. ≈
1,2
(generalization of (B
ˇ
elohl
´
avek, 2002)) de-
fined as
Comp
≈
1
,≈
2
( f ) ≡
df
^
x,y
(x ≈
1
y) → ( f (x) ≈
2
f (y)).
For any function f , the condition Comp
=,=
( f )
is trivially valid (to the degree 1). Similarly, by
definition, Comp
=,≈
2
( f ) =
V
x
( f (x) ≈
2
f (x)); thus,
provided that ≈
2
is reflexive, Comp
=,≈
2
( f ) = 1 for
each f .
Let us first explore how the relation between com-
patibility and functionality/extensionality looks like
for a specially chosen relation F
f
(x, y) =
df
y ≈
2
f (x).
Lemma 9. Let
F
f
(x, y) =
df
y ≈
2
f (x),
C ≡
df
Sym(≈
2
)∗(Trans(≈
2
))
2
.
Then:
Tot( f ) ≤ Tot(F
f
),
C ≤ [Comp
≈
1
,≈
2
( f ) → Func
≈
1
,≈
2
(F
f
)],
C ≤ [Comp
≈
1
,≈
2
( f ) → Ext
≈
1
,≈
2
(F
f
)].
Theorem 10. Let F
f
and C be as in Lemma 9, and
moreover let
Definition(F, f ) ≡
df
^
x
[F(x, f (x)) ↔
_
y
F(x, y)],
C
0
≡
df
Refl(≈
2
)∗Definition(F
f
, f
F
f
) ∗ Tot( f ).
Then the following estimations are valid:
C ≤ Comp
≈
1
,≈
2
( f ) → Function
≈
1
,≈
2
(F
f
), (10)
C
0
≤ f
F
f
≈ f . (11)
Reading of the results: “It is TRUE that
(10) – IF ≈
2
is symmetric and transitive (we need
the transitivity twice) and f is compatible, THEN
y ≈
2
f (x) is fuzzy function.”
(11) – IF ≈
2
is reflexive and f is total and f
F
f
is such
that for an arbitrary x: [ f
F
f
(x) ≈
2
f (x) IFF there ex-
ists y: y ≈
2
f (x)], THEN f
F
f
is similar to f .”
The reverse problem can be formulated as follows:
consider a fuzzy relation F and let us find a crisp func-
tion f
F
such that it is compatible with (≈
1
, ≈
2
) and its
extension to fuzzy relation F
f
F
is similar to F.
Theorem 11. Let
D ≡
df
Tot(F)∗ Definition(F, f
F
),
D
0
≡
df
D ∗ Refl(≈
1
)∗Sym(≈
2
).
Then it can be proved that
D
2
≤ Func
≈
1,2
(F) → Comp
≈
1,2
( f
F
), (12)
D
0
≤ Function
≈
1,2
(F) → (F
f
F
≈ F). (13)
Reading of the results: “It is TRUE that
(12) – IF F is functional and total (we need total-
ity twice) and f
F
is such that for an arbitrary x:
[F(x, f
F
(x) IFF there exists y: F(x, y)] (also needed
twice) THEN f
F
is the compatible function.”
(13) – IF F is a total fuzzy function and f
F
is as above
and ≈
1
is reflexive and ≈
2
is symmetric THEN F
f
F
is
indistinguishable from F.”
Bijective Fuzzy Relations - A Graded Approach
47

6 FUZZY BIJECTIONS
Traditionally, bijectivity refers to a mapping while
here we are dealing with fuzzy relations generally.
Let us look how the classical notion can be general-
ize to fuzzy relations and whether we get analogical
results.
Let a, b ∈ N
+
, R
⊂
∼
X ×Y and ≈
1
⊂
∼
X
2
, ≈
2
⊂
∼
Y
2
for this section.
We define (a, b)-bijection as a property of a fuzzy
relation R w.r.t. ≈
1,2
as follows:
Bij
a,b
≈
1,2
(R) ≡
df
(Inj
≈
1,2
(R))
a
∗ (Sur(R))
b
.
The coefficients a, b refer to the numbers of times the
respective properties are used in the above definition.
E.g., (2, 1)-bijection is defined as:
Inj
≈
1,2
(R)∗Inj
≈
1,2
(R)∗Sur(R).
It means that a relation R that is injective (to a
degree m) and surjective (to a degree n) is (2, 1)-
bijective (to the degree m ∗ m ∗ n).
Let us summarize the well known results on the
particular properties important for fuzzy bijections.
Proposition 12. Let Prop be one of the properties
{Tot, Sur, Func, Inj}; then the following expressions
are valid:
Tot(R) = Sur(R
T
)
Func
≈
1,2
(R) = Inj
≈
1,2
(R
T
)
(R
1
≈ R
2
) ∗ Tot(R
1
) ≤ Tot(R
2
)
(R
1
≈ R
2
) ∗ Sur(R
1
) ≤ Sur(R
2
)
(R
1
≈ R
2
)
2
∗ Func
≈
1,2
(R
1
) ≤ Func
≈
1,2
(R
2
)
(R
1
≈ R
2
)
2
∗ Inj
≈
1,2
(R
1
) ≤ Inj
≈
1,2
(R
2
)
Prop(R) ∗ Prop(S) ≤ Prop(R ◦ S)
for an arbitrary R, R
1
, R
2
⊂
∼
X ×Y , S
⊂
∼
Y × Z.
Guidelines for the proof of this proposition can be
found in (B
ˇ
elohl
´
avek, 2002).
From the above proposition we easily deduce the
following identity.
Theorem 13.
(Tot(R))
b
∗ (Func
≈
1,2
(R))
a
= Bij
a,b
≈
1,2
(R
T
)
The next theorem shows relationships between
compositions of a fuzzy bijection R and R
T
and the
indistinguishability relations ≈
1
and ≈
2
.
Theorem 14.
Refl(≈
1
)∗(Sur(R))
2
∗ Function
≈
1,2
(R) ≤
[(R
T
◦ R) ≈ ≈
2
] (14)
Refl(≈
2
)∗(Sur(R
T
))
2
∗ Function
≈
1,2
(R
T
) ≤
[(R ◦ R
T
) ≈ ≈
1
] (15)
Refl(≈
1
)∗Refl(≈
2
)∗(Tot(R))
2
∗
Function
≈
1,2
(R) ≤
(Bij
1,2
≈
1,2
(R) →
[[(R ◦ R
T
) ≈ ≈
1
] ∧ [(R
T
◦ R) ≈ ≈
2
]]) (16)
The proof of this theorem is too long to fit the page
number limitation, therefore it is omitted and left for
a full journal paper that is already in preparation.
Reading of the results: “It is TRUE that
(14) – IF ≈
1
is reflexive and R is a surjective (needed
twice) fuzzy function THEN (R
T
◦ R) ≈ ≈
2
.”
(15) – IF ≈
2
is reflexive and R
T
is a surjective (needed
twice) fuzzy function THEN (R ◦ R
T
) ≈ ≈
1
.”
(16) – IF ≈
1
is reflexive and ≈
2
is reflexive and R
is a total (needed twice) fuzzy function THEN IF R
is (1, 2)-bijective (because we need surjectivity twice
and injectivity only once) THEN (R
T
◦ R) ≈ ≈
2
AND
(R ◦ R
T
) ≈ ≈
1
.”
Interesting is the fact that we have to require from
≈
1
and ≈
2
only reflexivity to prove the above inequal-
ities. And of course, that there is a need for hav-
ing powers of surjectivity and totality. It is obviously
a non-trivial generalization of the following classical
theorem (Demirci, 2000).
Theorem 15. Let ≈
1
, ≈
2
be similarities, i.e., reflex-
ive, symmetric and transitive fuzzy relations.
If R is a bijective total fuzzy function w.r.t. ≈
1,2
then (R
T
◦ R) ≈ ≈
2
and (R ◦ R
T
) ≈ ≈
1
.
Example 16. Let X ,Y be non-empty sets of elements
with ≈
1
⊂
∼
X, ≈
2
⊂
∼
Y , F be the set of all functions
f : X 7→ Y and R be the set of all fuzzy relations
F, F
0
⊂
∼
X × Y . Moreover, let ∼
1
⊂
∼
F and ∼
2
⊂
∼
R
defined as:
f ∼
1
f
0
≡
df
^
x∈X
( f (x) ≈
2
f
0
(x)),
F ∼
2
F
0
≡
df
^
x∈X,y∈Y
(F(x, y) ↔ F
0
(x, y)).
Define a mapping M : F 7→ R by the following as-
signment:
M[ f , F](x, y) =
df
F(x, y) = (y ≈
2
f (x)).
In other words, M is a crisp function from F to R
assigning a fuzzy relation F to a crisp function f .
It can be proved that M is injective provided that
≈
2
is symmetric and transitive. Generally, we can
show that
Sym(≈
2
)∗Trans(≈
2
) ≤ Inj
∼
1,2
(M),
FCTA 2016 - 8th International Conference on Fuzzy Computation Theory and Applications
48

which means that as much ≈
2
is symmetric and tran-
sitive, at least that much R is injective.
To show surjectivity we incorporate (13):
D ∗ Tot(F) ∗Function
≈
1,2
(F) ≤ (F
f
F
∼
2
F),
where
D ≡
df
Refl(≈
1
)∗Sym(≈
2
)∗Definition(F, f
F
).
We would like to have = instead of ∼
2
and that will
work only with crisp properties on the left of the in-
equality. Thus M is surjective (to degree 1) provided
that F is a total fuzzy function, ≈
1
is reflexive, ≈
2
is
symmetric and f
F
is such that y = f
F
(x) if and only if
F(x, f
F
(x)) =
W
y∈Y
F(x, y).
All these properties led us to the following conclu-
sion: Let ≈
1
be reflexive and ≈
2
be symmetric. Then
M is (1, 1)-bijection to the degree that is bounded
from below by degrees of symmetry (a) and transitiv-
ity (b) of ≈
2
. Hence M is a (1, 1)-bijection at least to
degree a ∗b between F and a subset of R of total fuzzy
functions.
7 CONCLUSIONS
In this contribution, we have reviewed the results on
extensionality and functionality properties in the al-
gebraic framework. Also the well known representa-
tion theorem for fuzzy functions has been presented
in the graded form. Moreover, we have introduced
the graded notion of a bijective relation and showed
graded theorems that generalize the known results of
fuzzy mathematics. It appeared that we can relax a
lot of requirements on relations describing indistin-
guishability of elements of the respective universes.
The main advantage of the presented approach is that
it incorporates the whole scale for degrees of truth.
An evaluation of the degrees of the antecedents of a
graded theorem provides the additional information
about the estimation of the degree of the consequent.
We have shown that graded theorems bring a new
light into the already well established classical theory
of fuzzy functions and fuzzy bijective relations and
generally, to fuzzy mathematics. An intended class of
applications of the introduced theory of fuzzy func-
tions and fuzzy bijective relations is connected with
fuzzy rules, especially, the implicative model of fuzzy
rules (Da
ˇ
nkov
´
a, 2011;
ˇ
St
ˇ
epni
ˇ
cka M., 2013). It is due
to the fact that this model is closely connected with
fuzzy functions; and by Theorem 14, fuzzy functions
are closely related to bijections. Moreover, this re-
search is a basis for developing a theory of partial
fuzzy functions and partial bijective fuzzy relations
over a simple system of fuzzy partial propositional
logic, i.e., a fuzzy propositional logic which admits
undefined truth degrees (B
ˇ
ehounek and Nov
´
ak, 2015).
It is a topic for future research to find some interest-
ing examples that actively work with degrees and use
the presented graded theorems.
ACKNOWLEDGEMENTS
The work was supported by grant No. 16–191705
“Fuzzy partial logic” of GA
ˇ
CR and project LQ1602
“IT4I XS” of M
ˇ
SMT
ˇ
CR.
REFERENCES
Batyrshin, I., Sudkamp, T., Schockaert, S., Cock, M. D.,
Cornelis, C., and Kerre, E. E. (2008). Special sec-
tion: Perception based data mining and decision sup-
port systems fuzzy region connection calculus: An in-
terpretation based on closeness. International Journal
of Approximate Reasoning, 48(1):332 – 347.
B
ˇ
ehounek, L., Bodenhofer, U., and Cintula, P. (2008). Rela-
tions in Fuzzy Class Theory: Initial steps. Fuzzy Sets
and Systems, 159(14):1729–1772.
B
ˇ
ehounek, L. and Cintula, P. (2005). Fuzzy class theory.
Fuzzy Sets and Systems, 154(1):34–55.
B
ˇ
ehounek, L. and Nov
´
ak, V. (2015). Towards fuzzy partial
logic. In Proceedings of the IEEE 45th International
Symposium on Multiple-Valued Logics (ISMVL 2015),
pages 139–144. IEEE.
B
ˇ
elohl
´
avek, R. (2002). Fuzzy Relational Systems: Founda-
tions and Principles, volume 20 of IFSR International
Series on Systems Science and Engineering. Kluwer
Academic/Plenum Press, New York.
Da
ˇ
nkov
´
a, M. (2007a). On approximate reasoning with
graded rules. Fuzzy Sets and Systems, 158(6):652
– 673. The Logic of Soft ComputingThe Logic of
Soft Computing {IV} and Fourth Workshop of the
{ERCIM} working group on soft computing.
Da
ˇ
nkov
´
a, M. (2007b). On approximate reasoning with
graded rules. Fuzzy Sets and Systems, 158:652–673.
Da
ˇ
nkov
´
a, M. (2010a). Approximation of extensional fuzzy
relations over a residuated lattice. Fuzzy Sets and Sys-
tems, 161(14):1973 – 1991. Theme: Fuzzy and Un-
certainty Logics.
Da
ˇ
nkov
´
a, M. (2010b). Representation theorem for fuzzy
functions – graded form. In Abstracts of Interna-
tional Conference on Fuzzy Computation, pages 56–
64, SciTePress - Science and Technology Publica-
tions.
Da
ˇ
nkov
´
a, M. (2010c). Representation theorem for fuzzy
functions – graded form. In INTERNATIONAL CON-
FERENCE ON FUZZY COMPUTATION 2010, pages
56 – 64, Portugal. SciTePress - Science and Technol-
ogy Publications.
Bijective Fuzzy Relations - A Graded Approach
49

Da
ˇ
nkov
´
a, M. (2011). Generalized implicative model of a
fuzzy rule base and its properties. In Cognitive 2011,
pages 116 – 121. IARIA.
Demirci, M. (1999). Fuzzy functions and their fundamental
properties. Fuzzy Sets and Systems, 106(2):239 – 246.
Demirci, M. (2000). Fuzzy functions and their applications.
Journal of Mathematical Analysis and Applications,
252(1):495 – 517.
Demirci, M. (2001). Gradation of being fuzzy function.
Fuzzy Sets and Systems, 119(3):383 – 392.
Demirci, M. and Recasens, J. (2004). Fuzzy groups, fuzzy
functions and fuzzy equivalence relations. Fuzzy Sets
and Systems, 144(3):441 – 458.
H
´
ajek, P. (1998). Metamathematics of Fuzzy Logic, vol-
ume 4 of Trends in Logic. Kluwer, Dordercht.
Klawonn, F. (2000). Fuzzy points, fuzzy relations and fuzzy
functions. In Nov
´
ak, V. and Perfilieva, I., editors, Dis-
covering the World with Fuzzy Logic, pages 431–453.
Physica-Verlag, Heidelberg.
Nov
´
ak, V., Perfilieva, I., and Mo
ˇ
cko
ˇ
r, J. (1999). Mathemat-
ical Principles of Fuzzy Logic. Kluwer, Dordrecht.
Perfilieva, I. (2001). Logical approximation. Soft Comput-
ing, 2:73–78.
Perfiljeva I.,
ˇ
Sostak. A. (2014). Fuzzy function and the gen-
eralized extension principle. In FCTA 2014, pages 169
– 174, Lisboa, Portugal. SCITEPRESS.
ˇ
St
ˇ
epni
ˇ
cka M., D. B. B. (2013). Implication-based mod-
els of monotone fuzzy rule bases. FUZZY SET SYST,
232(1):134 – 155.
FCTA 2016 - 8th International Conference on Fuzzy Computation Theory and Applications
50