Verifying and Mapping the Mereotopology of Upper-level Ontologies
Lydia Silva Mu
˜
noz
1
and Michael Gr
¨
uninger
2
1
Computer Science, University of Toronto, 40 St. George Street , M5S 2E4, Toronto, Ontario, Canada
2
Mechanical and Industrial Engineering, University of Toronto,
5 King’s College Road, M5S 3G8, Toronto, Ontario, Canada
Keywords:
DOLCE, DOLCE-CORE, SUMO, Ontology Mapping, Ontology Verification, Upper-level Ontology, Mereo-
logy, Topology, Mereotopology.
Abstract:
Upper-level ontologies provide an account of the most basic, domain-independent, existing entities, such as
time, space, objects, and processes. Ontology verification is the process by which a theory is checked to rule
out unintended models, and possibly characterize missing intended ones. In this paper, we verify the core
characterization of mereotopology of the Suggested Upper Merged Ontology (SUMO), and the mereology of
the Descriptive Ontology for Linguistic and Cognitive Engineering (DOLCE), while relating their axioma-
tizations via ontology mapping. As a result, we propose the correction and addition of some axioms to the
analyzed theories which eliminate unintended models and characterize missing ones. In addition, we show
by formal means which is the relation existing between the axiomatization of mereology in both upper-level
ontologies, and make available a modular representation in first-order logic of the SUMO characterization of
mereotopology.
1 INTRODUCTION
Automatic applications appealing to ontologies for in-
teroperation are unambiguously integrated only when
the models of their shared features are equivalent.
However, ontologies admitting unintended models
ambiguously characterize their vocabularies, which
can generate misunderstandings that hinder interop-
erability.
Upper-level ontologies, also called foundational
ontologies, provide an account of the most basic,
domain independent, existing entities, such as time,
space, objects and processes. As ontologies are cru-
cial for the Semantic Web, upper level ontologies are
essential for the ontology engineering cycle in activ-
ities such as ontology building and integration. Up-
per level ontologies can be used as the foundational
substratum on which new ontologies are developed,
because they provide some fundamental ontological
distinctions, which can help the designer in her task
of conceptual analysis, (Guarino, 1998). They can
be used as a backbone on top of which more specific
concepts can be characterized while reusing their root
vocabulary and their general knowledge. In ontology
integration, they can be used as oracles for meaning
clarification (Euzenat and Shvaiko, 2013).
Various upper level ontologies have been devel-
oped in languages with higher or equivalent expres-
sivity to first-order logic, such as SUMO (Niles
and Pease, 2001) and DOLCE (Gangemi et al.,
2002)(Borgo and Masolo, 2009), and translations of
them, with loss, to lightweight language OWL
1
, made
available. Therefore, semantic mappings connect-
ing their axiomatizations are necessary to facilitate
interoperability among applications that commit to
the characterizations provided by different upper level
ontologies. Those mappings need to be formal, which
guarantees their interpretability by automatic agents,
and also need to be represented in an expressive lan-
guage such as standard first-order logic.
2
Ontology verification (Gr
¨
uninger et al., 2010) is
the process by which a theory is checked to rule out
unintended models, and possibly characterize miss-
ing intended ones. Therefore, ontology verification
1
https://www.w3.org/2001/sw/wiki/OWL
2
The expressive power of first-order logic makes its use
necessary for the representation of mappings that charac-
terize features that are not representable in lightweight lan-
guages, such as Description Logics. In addition, checking
the correctness of those mappings results facilitated by the
fact that first-order theorem proving in standard first-order
logic is a mature field, and, although semi-decidable, first-
order reasoning on small modules results in an acceptable
trade-off among expressivity and efficiency.
Muñoz, L. and Grüninger, M.
Verifying and Mapping the Mereotopology of Upper-Level Ontologies.
DOI: 10.5220/0006052100310042
In Proceedings of the 8th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2016) - Volume 2: KEOD, pages 31-42
ISBN: 978-989-758-203-5
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
31

reduces semantic ambiguity. Since foundational on-
tologies are expected to be broadly reused, their veri-
fication results necessary.
In this paper, we verify the subtheory of core
mereotopological concepts of the SUMO founda-
tional ontology and the mereology of the DOLCE-
CORE, the fragment of DOLCE focused on entities
that exist on time. In addition, we formally relate
their respective axiomatizations via first-order logic
mappings. As a result, we propose the correction, and
addition, of some axioms which rule out unintended
models or characterize missing ones. As an additional
outcome of our work, we have produced a modu-
lar representation stated in standard first-order logic
of the complete SUMO subtheory of mereotopology.
We have used automatic theorem prover Prover9 and
model finder Mace4 (McCune, 2010) for the auto-
matic tasks involved in the work described in this pa-
per.
2 ONTOLOGY MAPPING
Ontology mapping, also called ontology matching,
and ontology alignment, is concerned with the ex-
plicit representation of the existing semantic corre-
spondences among the axiomatizations of different
ontologies
3
via bridge axioms (Euzenat and Shvaiko,
2013), which are called translations definitions in the
context of first-order logic.
Building a map between two first-order logic on-
tologies T
1
and T
2
that interprets the first into the sec-
ond involves translating every symbol of theory T
1
into the language of T
2
, translating every sentence of
T
1
into the language of T
2
, and checking the ability
of T
2
to entail every axiom of T
1
. The following def-
inition formalizes the notion of relative interpretation
between first-order logic theories.
Definition 1. A map π interprets a theory T
1
into a
theory T
2
iff for every sentence α in the language of
T
1
, T
1
|= α ⇒ T
2
|= α
π
; being α
π
the syntactic transla-
tion of α into the language of T
2
.
The following theorem that follows fom (Ender-
ton, 1972), introduces a fundamental relation between
the models of a theory and the models of the theories
that it interprets. Given such a relation, in order to
demonstrate that a given theory T
2
can represent every
feature that another theory T
1
represents, it suffices to
3
We assume that an ontology is a set of sentences called
axioms closed under logical entailment that state the prop-
erties that characterize the behaviour of a set of symbols
representing constants, relations and functions, called the
signature of the ontology.
demonstrate that theory T
2
is able to interpret theory
T
1
.
Theorem 1. If a theory T
1
is interpreted by a theory
T
2
by means of a given map π, there is another map δ
that sends every model of T
2
into a model of T
1
.
3 ONTOLOGY VERIFICATION
An ontology admits unintended models when it is
possible to find features of its underlying conceptu-
alization which are not characterized by its axiom-
atization. Ontology Verification in first-order logic
(Gr
¨
uninger et al., 2010) is based on the fact that theo-
ries with different vocabularies unambiguously char-
acterize the same concepts only if their sets of mod-
els are equivalent. Verifying an ontology T ideally
consists of classifying the actual models M of T by
means of a representation theorem,
4
which relates the
models of T with the models M
intended
of an alterna-
tive axiomatization of T built with well understood
theories. Such a representation theorem must be ei-
ther proved or disproved. The following definition
from (Pearce and Valverde, 2012) relates the notion
of ontology mapping with the fundamentals of ontol-
ogy verification:
Definition 2. Two theories T
1
and T
2
are synony-
mous iff there exist two sets of translation definitions
∆ and Π, respectively from T
1
to T
2
and from T
2
to T
1
,
such that T
1
∪ Π is logically equivalent to T
2
∪ ∆.
Given Definition 2, from Theorem 1 follows that
the models of synonymous theories are equivalent,
and therefore ontology mapping can be used for clas-
sifying the sets of models of two ontologies as equiv-
alent.
4 DOLCE
The Descriptive Ontology for Linguistic and Cogni-
tive Engineering DOLCE (Gangemi et al., 2002) (Ma-
solo et al., 2003) is a freely available upper ontol-
ogy that is part of the WonderWeb project
5
, which
is aimed to provide the infrastructure required for a
large-scale deployment of ontologies intended to be
4
A representation theorem is a theorem that formally
classifies a given class of structures as equivalent to another
class of structures whose properties are better understood.
The stated equivalence makes possible the extrapolation of
those properties to the classified structures, facilitating their
understanding.
5
http://wonderweb.semanticweb.org
KEOD 2016 - 8th International Conference on Knowledge Engineering and Ontology Development
32

Figure 1: Top categories of DOLCE-CORE.
the foundation for the Semantic Web. DOLCE has a
cognitive approach, i.e., it presents the world as it is
grasped by humans, based on human knowledge and
culture, in opposition to ontological realism (Grenon
and Smith, 2004), which intends to present the world
as it is, independently of the bias of human percep-
tion. The development of DOLCE has followed the
principles of the OntoClean methodology (Guarino
and Welty, 2002). The first version of DOLCE had
a representation in Modal Logic, a translation with
loss into standard first-order logic, a translation with
further loss into OWL, and also an alignment with
WordNet (Gangemi et al., 2003). A new version of
the fragment of the original ontology that focuses on
entities that exist on time, called temporal particulars,
was presented in (Borgo and Masolo, 2009), called
DOLCE-CORE, whose main categories are shown in
Figure 1. We will circumscribe our work to the ax-
iomatization of DOLCE-CORE.
At the top of DOLCE-CORE the category of
temporal-particulars PT is partitioned into six basic
categories: objects O, events E, individual qualities
Q, regions R, concepts C, and arbitrary sums AS. Cat-
egories ED (endurant) and PD (perdurant) of DOLCE
were, respectively, renamed O (ob ject) and E (event)
in DOLCE-CORE. The axiomatization of mereology
in DOLCE-CORE is as follows,
6
where predicate P
represents parthood, and (1)-(3) respectively stand for
the reflexivity, transitivity, and antisymmetry of rela-
tion P. Overlap of parts and mereological sum repre-
senting binary fusion of parts are respectively defined
in (4) and (5), while (7)-(11) characterize the dissec-
6
Axioms (9), (10), (14), and (15) are the instantia-
tion of DOLCE higher-order axiom schemas for the sub-
categories of main categories Q and R which are rele-
vant for our work. A complete version of DOLCE-CORE
mereology represented in first-order logic is available at
colore.oor.net/ontologies/dolce-core/mereology.in
tivity of P across categories, and (12)-(17) close the
sum of parts inside each category.
(∀x)P(x, x) (1)
(∀x, y)P(x, y) ∧ P(y, z) → P(x, z) (2)
(∀x, y)P(x, y) ∧ P(y, x) → (x = y) (3)
(∀x, y)Ov(x, y) ≡ (∃z)(P(z, x) ∧ P(z, y)) (4)
(∀x, y, z)SUM(z, x, y) ≡
(∀v)Ov(v, z) ↔ Ov(v, x)∨Ov(v, y)
(5)
(∀x, y)¬P(x, y) → (∃z)P(z, x)∧¬Ov(z, y) (6)
(∀x, y)O(y) ∧ P(x, y) → O(x) (7)
(∀x, y)E(y) ∧ P(x, y) → E(x) (8)
(∀x, y)T (y) ∧ P(x, y) → T (x) (9)
(∀x, y)T Q(y) ∧ P(x, y) → T Q(x) (10)
(∀x, y)C(y) ∧ P(x, y) → C(x) (11)
(∀x, y, z)O(x) ∧ O(y) ∧ SUM(z, x, y) → O(z) (12)
(∀x, y, z)E(x) ∧ E(y) ∧ SU M(z, x, y) → E(z) (13)
(∀x, y, z)T (x) ∧ T (y) ∧ SU M(z, x, y) → T (z) (14)
(∀x, y, z)T Q(x) ∧ T Q(y) ∧ SU M(z, x, y) → T Q(z)
(15)
(∀x, y, z)C(x) ∧C(y) ∧ SUM(z, x, y) → C(z) (16)
(∀x, y, z)AS(x) ∧ AS(y) ∧ SUM(z, x, y) → AS(z) (17)
Due to the ontological commitment represented
by axiom (6), the mereology characterized in
DOLCE-CORE is an extensional mereology
7
accord-
ing to (Casati and Varzi, 1999) (Varzi, 2007).
5 SUMO
SUMO (Niles and Pease, 2001) is a freely available
upper level ontology whose top categories are shown
in Figure 2. Like DOLCE, SUMO has a cognitive
bias. In addition to the main ontology, which contains
about 4000 axioms, SUMO has been extended with
a mid-level ontology and a number of domain spe-
cific ontologies, all of which account for 20,000 terms
and 70,000 axioms. SUMO has been translated into
OWL and WordNet (Niles and Pease, 2003). The rep-
resentation language of SUMO is SUO-KIF
8
, a very
expressive dialect of KIF
9
with many-sorted features,
whose syntax permits higher-order constructions such
as predicates that have other predicates, or formulas,
as their arguments, and the existence of predicates
7
It can be proved that in an extensional mereology non-
atomic entities whose proper parts are the same, are identi-
cal, i.e., every entity is exhaustively defined by its parts.
8
http://suo.ieee.org/SUO/KIF/suo-kif.html
9
http://logic.stanford.edu/kif/kif.html
Verifying and Mapping the Mereotopology of Upper-Level Ontologies
33

Figure 2: Top categories of SUMO.
and functions of variable arity (Benzm
¨
uller and Pease,
2012).
We have translated (with loss) into standard first-
order logic, and modularized, the subset of SUMO
that characterizes the notion of mereotopology, which
resulted in the hierarchy of subtheories shown in Fig-
ure 3, where each theory conservatively extends
10
its
related theories below. Due to space limitations, we
only address in this work the study of modules PART,
SUM, PRODUCT, DECOMPOSITION, TOPOL-
OGY, and MEREOTOPOLOGY. The first-order logic
axiomatization of all the modules shown in Figure 3
can be found at colore.oor.net/ontologies/sumo/modules.
Differently from DOLCE-CORE, which defines
parthood by means of unique relation P across ev-
ery category representing entities that exist on time
and space, SUMO adopts various partial orderings to
address the part-whole relationship in different cate-
gories. Regarding entities that are in space and time,
classified as Physical in SUMO, relations part and
subProcess respectively characterize part-whole rela-
tions for members of Object and Process, while rela-
tion temporalPart represents part-whole for members
of TimePosition, which extends to points and intervals
of time.
5.1 Module PART
Module PART represents the relation among a whole
and its parts by characterizing relation part as a par-
tial order, and defines the overlapping of parts, partial
overlapping, and relation properPart. Given the ax-
iomatization of part, relation properPart results to be
10
A theory T
0
is a conservative extension of a theory T if
every theorem of T is a theorem of T
0
, and every theorem
of T
0
in the signature of T is also a theorem of T .
Figure 3: Modular decomposition of the SUMO axiomati-
zation of concepts related to mereotopology. Arrows point
to conservative extensions
10
among modules. Signature
members are shown in the module that first introduces them.
a strict partial order.
Definition 3. Module PART is the subtheory com-
posed by axioms (18) to (24).
(∀x, y)part(x, y) → Ob ject(x) ∧ Ob ject(y) (18)
(∀x)Ob ject(x) → part(x, x) (19)
(∀x, y)part(x, y) ∧ part(y, x) → (x = y) (20)
(∀x, y, z)part(x, y) ∧ part(y, z) → part(x, z) (21)
(∀x, y)overlapsSpatially(x, y) ↔
(∃z(part(z, x)∧ part(z, y)))
(22)
(∀x, y)overlapsPartially(x, y) ↔ ¬part(x, y)
∧¬part(y, x) ∧ (∃z)part(z, x)∧ part(z, y)
(23)
(∀x, y)properPart(x, y) ↔ part(x, y) ∧ ¬part(y, x) (24)
5.2 Module SUM
The mereological sum of two parts to conform a
whole is represented in module SUM by function
symbol MereologicalSumFn.
KEOD 2016 - 8th International Conference on Knowledge Engineering and Ontology Development
34

Figure 4: With the original characterization of mereological
sum, every two objects in every model of SUMO must be
in relation part, such as objects O
1
and O
2
in (a). Models
corresponding to (b) and (c) with overlapping objects with-
out being one part of the other, or with disjoint objects, are
not admitted by SUMO submodule SUM.
Definition 4. Module SUM is the subtheory that ex-
tends module PART by means of axioms (25) and (26).
(∀x, y, z)Ob ject(x) ∧ Ob ject(y) →
((z = MereologicalSumFn(x, y)) →
(∀p)(part(p, z) ↔ (part(p, x) ∨ part(p, y)))
(25)
(∀x, y)Ob ject(x) ∧ Ob ject(y) →
Ob ject(MereologicalSumFn(x, y))
(26)
Given two objects, the existence of their mereo-
logical sum is vacuously guaranteed in this theory due
to the use of a function symbol to represent such an
operation.
We have found that due to the reflexivity property
of relation part, there exists always a part p of the ob-
ject indicated by variable z in axiom (25), which is z
itself, for which (part(p, x) ∨ part(p, y) holds. There-
fore, the following is a theorem of SUMO:
11
(∀x, y, z)Ob ject(x) ∧ Ob ject(y)∧
(z = MereologicalSumFn(x, y)) →
(part(z, x) ∨ part(z, y)
(27)
Also due to the reflexivity of relation part and ax-
iom (25), both arguments x and y must be a part of
their mereological sum z, and the following is also a
theorem of SUMO:
11
(∀x, y, z)Ob ject(x) ∧ Ob ject(y)∧
(z = MereologicalSumFn(x, y)) →
(part(x, z) ∧ part(y, z)
(28)
Given theorems (27) and (28), and due to the anti-
symmetry of relation part, it holds that z must be x or
y, this fact entails the inconvenient consequence that
every pair of objects in the universe of every interpre-
tation of SUMO must be in relation part, which shows
that SUMO misses intended models where there exist
objects that are disjoint, or that overlap without being
one part of the other, as depicted in parts (b) and (c) of
Figure 4. The following proposition proves our claim:
11
Proof available at: colore.oor.net/ontologies/sumo/
mereotopology/proofs.
Proposition 1. SUM |= (∀x, y)Ob ject(x) ∧ Ob ject(y) →
(part(x, y) ∨ part(y, x).
Proof. By using Prover9, we have produced a proof
for this proposition.
11
In order to characterize those missing models
that Proposition 1 identifies, we propose the sub-
stitution of axiom (25) by sentence (29) in module
SUM, which corresponds to the representation of the
sumpremum, or join of lattices (Davey and Priestley,
2002), where the partial order is given by the relation
part. We call EXTENDED SUM to the resulting the-
ory, and prove that it does not rule out intended mod-
els where objects exist that overlap or are disjoint, and
also that the characterization of mereological sum sat-
isfies the commutative and idempotence laws.
(∀x, y, z)Ob ject(x) ∧ Ob ject(y) →
((z = MereologicalSumFn(x, y) →
(∀p)(part(z, p) ↔ part(x, p) ∧ part(y, p)))
(29)
Proposition 2. Let EXT ENDED SU M be the theory
that results from substituting axiom (25) in module
SUM by axiom (29). Then,
(a) EXTENDED SUM 6|= (∀x, y)Ob ject(x) ∧ Ob ject(y)
→ (part(x, y) ∨ part(y, x)
(b) EXTENDED SUM |= (∀x, y, z)Ob ject(x)∧Ob ject(y)
∧ Ob ject(z) ∧ (MereologicalSumFn(x, y) = z) →
(MereologicalSumFn(y, x) = z)
(c) EXTENDED SUM |= (∀x, y, z)part(x, y) → (Mereolo
gicalSumFn(x, y) = y)
Proof. (a): Let S
1
be the theory that results
from adding sentence (∃x, y)Ob ject(x) ∧ Ob ject(y) ∧
¬(part(x, y) ∧ ¬part(y, x) to module EX T ENDED SUM.
By using Mace4, we have created a model of S
1
.
11
(b);(c): By using Prover9 we have demonstrated
that sentences (∀x, y, z)Ob ject(x) ∧ Ob ject(y) ∧
Ob ject(z) ∧ (MereologicalSumFn(x, y) = z) →
(MereologicalSumFn(y, x) = z) and (∀x, y, z)part(x, y) →
(MereologicalSumFn(x, y) = y) are theorems of theory
EXT ENDED SUM.
11
5.3 Module PRODUCT
Given two objects, its mereological product intu-
itively corresponds to the intersection of both objects.
SUMO represents the notion of mereological product
by means of function symbol MereologicalProductFn.
Definition 5. Module PRODUCT is the subtheory
that extends module PART by means of axioms (30)
and (31).
(∀x, y, z)Ob ject(x) ∧ Ob ject(y) →
((z = MereologicalProductFn(x, y)) →
(∀p)(part(p, z) ↔ part(p, x)∧ part(p, y)))
(30)
Verifying and Mapping the Mereotopology of Upper-Level Ontologies
35

(∀x, y)Ob ject(x) ∧ Ob ject(y) →
Ob ject(MereologicalProductFn(x, y))
(31)
Given two objects, the existence of their mereo-
logical product is vacuously guaranteed in SUMO due
to the use of a function symbol to represent such an
operation.
The characterization of mereological product in
SUMO corresponds to the in f imum or meet of the cor-
responding arguments on the lattice that relation part
defines. We have found that from the characteriza-
tion of mereological product of SUMO follows that
every pair of objects (x, y) must overlap, which indi-
cates that SUMO misses those intended models where
there exist objects that do not overlap. The following
proposition proves our claim:
Proposition 3. PRODUCT |= (∀x, y)Ob ject(x) ∧
Ob ject(y) → (overlapsSpatially(x, y)).
Proof. By using Prover9, we have produced a proof
for this proposition.
11
In order to make possible the admission of those
missing models that Proposition 3 identifies, we pro-
pose substitutig axiom (30) by sentence (32), and call
EXTENDED PRODUCT to the resulting theory:
(∀x, y, z)overlapsSpatially(x, y) →
((z = MereologicalProductFn(x, y)) →
(∀p)(part(p, z) ↔ part(p, x)∧ part(p, y)))
(32)
Proposition 4. Let EXTENDED PRODUCT
be the theory that results from substitut-
ing axiom (30) in module PRODUCT by ax-
iom (32). Then, EXT ENDED PRODUCT 6|=
(∀x, y)Ob ject(x) ∧ Ob ject(y) → overlapsSpatially(x, y).
Proof. Let P
1
be the theory that results
from adding sentence (∃x, y)Ob ject(x) ∧
Ob ject(y) ∧ (¬(overlapsSpatially(x, y)) to module
EXT ENDED PRODUCT . By using Mace4, we have
created a model of theory P
1
.
11
5.4 Module DECOMPOSITION
The remainder between a whole and its proper parts
is represented by function symbol MereologicalDif-
ferenceFn in module DECOMPOSITION:
Definition 6. Module DECOMPOSITION is the sub-
theory that extends module PART by means of axioms
(33) and (34).
(∀x, y, z)Ob ject(x) ∧ Ob ject(y) →
((z = MereologicalDi f f erenceFn(x, y)) →
(∀p)properPart(p, z) ↔
properPart(p, x) ∧ ¬properPart(p, y))
(33)
(∀x, y)Ob ject(x) ∧ Ob ject(y) →
Ob ject(MereologicalDi f f erenceFn(x, y))
(34)
Because the mereological difference, or remain-
der, between a whole and one of its parts is rep-
resented in SUMO by a function symbol, its exis-
tence is vacuously guaranteed in every case at the ex-
penses of having spurious evaluations of the symbol
MereologicalDi f f erenceFn. However, regarding the
supplementation principles (35) to (38), respectively
named in (Varzi, 2007) as weak company, strong com-
pany, supplementation, and strong supplementation,
Proposition 5 shows that those principles are not the-
orems of SUMO. These principles contribute to clas-
sify the degree of ontological commitment of the on-
tology with the existence of the remainder between a
whole and one of its proper parts.
Proposition 5. Axioms (35), (36), (37), and (38) are
not theorems of theory PART ∪ DECOMPOSIT ION.
(∀x, y)properPart(x, y) →
∃z(properPart(z, y) ∧ −(z = x))
(35)
(∀x, y)properPart(x, y) →
(∃z)(properPart(z, y) ∧ ¬part(z, x))
(36)
(∀x, y)properPart(x, y) →
(∃z)(Part(z, y) ∧ ¬overlapsSpatially(z, x))
(37)
(∀x, y)¬part(y, x) →
(∃z)(Part(z, y) ∧ ¬overlapsSpatially(z, x))
(38)
Proof. Let P
1
be the union of theories PART and DE-
COMPOSITION with the respective negation of ax-
ioms (35), (36), (37), and (38). By using Mace4, we
have built a model of P
1
.
11
We have found that the characterization of sym-
bol MereologicalDifferenceFn given by (33) and (34)
introduces unintended models where the remainder
overlaps with the subtrahend:
Proposition 6. DECOMPOSIT ION |= (∀x, y, z)
Ob ject(x) ∧ Ob ject(y) ∧ (z = MereologicalDi f f erenceFn
(x, y)) ∧ properPart(y, x) → properPart(y, z)).
Proof. Let us assume that Ob ject(x) ∧ Ob ject(y) ∧
z = MereologicalDi f f erenceFn(x, y) holds, and let p
be such that (p = y) in (33), then, it results
properPart(y, Mereological Di f f erenceFn(x, y))
In order to eliminate such a class of unintended
models, we propose the addition of definitions (39)
to (42), and the substitution of axiom (33) by sen-
tence (43) in module DECOMPOSITION, and call
EXTENDED DECOMPOSITION to the resulting the-
ory. We following demonstrate that this theory does
KEOD 2016 - 8th International Conference on Knowledge Engineering and Ontology Development
36

not admit the unintended models that Proposition 6
identifies
(∀x, y)weak dis joint(x, y) ↔
(∀z)(part(z, x)∧ part(z, y) → N(z))
(39)
(∀x)N(x) ↔ (∀z)part(x, z)
(40)
(∀x)U(x) ↔ (∀z)part(z, x)
(41)
(∀x, z)comp(x, z) ↔
(∀y)(part(y, z) ↔ weak dis joint(y, x))
(42)
(∀x, y, z)Ob ject(x) ∧ Ob ject(y) →
((MereologicalDi f f erenceFn(x, y) = z) →
(∀p)(part(p, z) ↔
part(p, x) ∧ weak dis joint(p, y)))
(43)
Proposition 7. EXT ENDED DECOMPOSIT ION 6|=
(∀x, y, z)Ob ject(x) ∧ Ob ject(y) ∧ (z = MereologicalDi f f e
renceFn(x, y)) ∧ properPart(y, x) → properPart(y, z)).
Proof. Let D
1
be the theory that results
from adding sentence (∃x, y, z)Ob ject(x) ∧
Ob ject(y) ∧ (z = MereologicalDi f f erenceFn(x, y)) ∧
properPart(y, x) ∧ ¬properPart(y, z)) to module
EXT ENDED DECOMPOSIT ION. By using Mace4,
we have created a model of theory D
1
.
11
Finally, We prove that the resulting mereology af-
ter all our proposed changes is satisfiable.
Proposition 8. The theory PART ∪
EXTENDED SUM ∪ EXTENDED PRODUCT ∪
EXTENDED DECOMPOSITION is satisfiable.
Proof. By using Mace4 we have constructed a model
for the proposed union of theories.
11
5.5 Module TOPOLOGY
Since mereology can only represent the relation of
parts with their respective wholes, predicate con-
nected is characterized in this module to represent
a more general symmetric and reflexive spatial rela-
tionship among objects which are not necessarily in a
part-whole relation.
Definition 7. Module TOPOLOGY is the subtheory
composed by axioms (44) to (46).
(∀x)Ob ject(x) → connected(x, x) (44)
(∀x, y)connected(x, y) → Ob ject(x) ∧ Ob ject(y) (45)
(∀x, y)connected(x, y) → connected(y, x) (46)
5.6 Module MEREOTOPOLOGY
This module is intended to characterize the relation-
ship between the notions of mereology and topology.
In it, both predicates, meetsSpatially, which repre-
sents external connection among objects, and over-
lapsSpatially, are declared disjoint specializations of
predicate connected. However, the axiomatization of
this theory is logically equivalent to conservative def-
initions (47) and (48). The module MEREOTOPOL-
OGY is therefore a definitional extension of modules
TOPOLOGY and PART.
Definition 8. Module MEREOTOPOLOGY is the the-
ory that extends modules TOPOLOGY and PART by
means of definitions (47) and (48).
(∀x, y)overlapsSpatially(x, y) ↔
connected(x, y)∧(∃z) part(z, x)∧ part(z, y)
(47)
(∀x, y)meetsSpatially(x, y) ↔
connected(x, y)∧¬(∃z) part(z, x)∧ part(z, y)
(48)
We have found that the monotony of relation con-
nected with respect to parthood was not characterized
in SUMO, which introduces unintended models as the
one represented in Figure 5 where all parts share one
point, but only shaded ones result to be connected.
Figure 5: Model of SUMO where the monotony of rela-
tion connected with respect to parthood was not characte-
rized. Even though connected(z, x), part(x, y), part(y, u),
and part(u, v) hold, connected(z, y) and connected(z, v) do
not hold, while connected(z, u) does hold.
Proposition 9. MEREOTOPOLOGY 6|= (∀x, y)
part(x, y) → ∀z(connected(z, x) → connected(z, y))
Proof. Let M
1
= be the theory that re-
sults from adding sentence (∃x, y)(part(x, y) ∧
(∃z)(connected(z, x) ∧ ¬(connected(z, y)) to module
MEREOTOPOLOGY, using Mace4 we have built a
model of M
1
.
11
In order to rule out those unintended models that
proposition 9 identifies, we propose the addition of
axiom (49) to this module and call EXTENDED
MEREOTOPOLOGY to the resulting theory.
(∀x, y)part(x, y) →
∀z(connected(z, x) → connected(z, y))
(49)
Verifying and Mapping the Mereotopology of Upper-Level Ontologies
37

Table 1: Mapping of SUMO and DOLCE main categories.
(∀x)Ob ject(x) ≡ O(x) (50)
(∀x)Process(x) ≡ E(x) (51)
(∀x)TimePosition(x) ≡ T (x) (52)
(∀x)Region(x) ≡ S(x) (53)
Table 2: Translations DOLCE PART-T into SUMO TIME.
(∀x)T (x) ≡ TimePosition(x) (54)
(∀x, y)P(x, y) ≡ temporalPart(x, y) (55)
(∀x, y)Ov(x, y) ↔ (TimeInterval(x)
∧TimeInterval(y)
∧overlapsTemporally(x, y)) ∨
(TimePoint(x) ∧ TimeInterval(y)
∧temporalPart(x, y)) ∨
(TimeInterval(x) ∧ TimePoint(y)
∧temporalPart(y, x)) ∨
(TimePoint(x) ∧ TimePoint(y) ∧ x = y)))
(56)
6 MAPPING SUMO AND DOLCE
In order to relate SUMO and DOLCE we assume
that the changes that we have proposed in section
5 for eliminating unintended models and character-
izing missing intended ones have been performed
in SUMO. There is no axiomatization in DOLCE-
CORE, neither in DOLCE, that corresponds to the no-
tion of topology, therefore our mappings are circum-
scribed to the axiomatization of mereology in both
theories.
Analyzing the axiomatizations of SUMO and
DOLCE-CORE, we have found that the concept of
time, as a region where objects exists and events oc-
cur, is represented in SUMO by category TimePosi-
tion, and in DOLCE-CORE by category T . By exam-
ining the predicates that characterize the participation
of objects in events in both ontologies, and also by the
type of relation that the main categories of SUMO and
DOLCE-CORE have with time and space, we have
built the translation definitions of Table 1 for the main
categories shown in Figures 1 and 2.
6.1 Mapping Time
The subtheory SUMO TIME, whose modular struc-
ture is shown in Figure 7, characterizes the behaviour
of time in SUMO. This theory, which was verified
in (Silva Mu
˜
noz and Gr
¨
uninger, 2016), includes 3
Table 3: Translations TIME MEREOLOGY into DOLCE
PART-T.
(∀x)TimeInterval(x) ≡ T (x) (57)
(∀x, y)temporalPart(x, y) ≡ P(x, y)
∧T (x) ∧ T (y)
(58)
(∀x, y)overlapsTemporally(x, y) ≡ Ov(x, y)
∧T (x) ∧ T (y)
(59)
submodules
12
TIME POINT, TIME MEREOLOGY,
and TIME INTERVAL, such that each module is a
conservative extension of each connected subtheory
below it in Figure 7. These 3 subtheories respec-
tively characterize a linear ordering between instants
of time, a part-whole relation among intervals of time,
and an account of Allen’s interval relations starts, fin-
ishes, during, earlier, and meetsTemporally (Hayes,
1996). Finally, theory SUMO TIME characterizes a
part-whole relationship that includes intervals and in-
stants of time.
On the other hand, DOLCE-CORE characterizes
parthood by unique predicate P across every category,
including T . By means of the following definition and
theorem we classify the relationship that exists among
DOLCE PART-T and SUMO TIME:
Definition 9. SUMO TIME is the theory given by the
axioms in colore.oor.net/ontologies/sumo/modules/
sumo-time, TIME MEREOLOGY is the theory given
by SUMO axioms (60) to (65), and DOLCE PART-T
is the theory given by axioms (1)-(4) and (9).
(∀x)TimeInterval(x) → temporalPart(x, x).
(60)
(∀x, y)temporalPart(x, y)∧
temporalPart(y, x) → (x = y).
(61)
(∀x, y, z)temporalPart(x, y)∧
temporalPart(y, z) → temporalPart(x, z).
(62)
(∀x, y)overlapsTemporally(x, y) →
TimeInterval(x) ∧ TimeInterval(y)
(63)
(∀x)TimeInterval(x) →
overlapsTemporally(x, x)).
(64)
(∀x, y)TimeInterval(x) ∧ TimeInterval(y) →
(overlapsTemporally(x, y) ↔
((∃z)(TimeInterval(z)∧
temporalPart(z, x)∧temporalPart(z, y))))
(65)
Theorem 2. Theory SUMO TIME interprets theory
DOLCE PART-T.
12
Available at colore.oor.net/ontologies/sumo/modules
KEOD 2016 - 8th International Conference on Knowledge Engineering and Ontology Development
38

Table 4: Translations DOLCE PART-E into SUMO SUB-
PROCESS.
(∀x)E(x) ≡ Process(x) (66)
(∀x, y)P(x, y) ≡ subProcess(x, y) (67)
(∀x, y)Ov(x, y) ≡ (∃z)(subProcess(z, x)∧
subProcess(z, y))
(68)
Table 5: Translations SUMO SUBPROCESS into DOLCE
PART-E.
(∀x)Process(x) ≡ E(x) (69)
(∀x, y)subProcess(x, y) ≡ E(x) ∧ E(y) ∧ P(x, y) (70)
Proof. Let us call ∆ to the set of translations defini-
tions shown in Table 2. Using Prover9 we have shown
that SUMO TIME ∪ ∆ |= DOLCE PART-T.
Theorem 3. Theory DOLCE PART-T interprets the-
ory TIME MEREOLOGY.
Proof. Let us call ∆ to the set of translations defi-
nitions shown in Table 3. Using Prover9 we have
shown that DOLCE PART-T ∪ ∆ |= TIME MEREO-
LOGY.
6.2 Mapping Events
Regarding the representation of events in SUMO and
DOLCE, by means of the following definition and
theorem we classify the relationship that their respec-
tive part-whole axiomatizations have as synonymy.
Definition 10. SUMO SUBPROCESS is the theory
given by axioms (71)-(74), and DOLCE PART-E is
the theory given by axioms (1)-(3) and (8).
(∀x, y)subProcess(x, y) → Process(x) ∧ Process(y) (71)
(∀x)Process(x) → subProcess(x, x) (72)
(∀x, y)subProcess(x, y)∧subProcess(y, z) →
subProcess(x, z)
(73)
(∀x, y)subProcess(x, y)∧subProcess(y, x) → (x = y) (74)
Theorem 4. SUMO SUBPROCESS is synonymous
with DOLCE PART-E.
Proof. Let ∆ be the set of translations definitions
shown in Table 4. Using Prover9 we have shown that
SUMO SUBPROCESS ∪ ∆ |= DOLCE PART-E. Let Γ
be the set of translations definitions shown in Table 5.
Using Prover9 we have shown that DOLCE PART-E
∪ Γ |= SUMO SUBPROCESS.
13
.
13
Proof available at: colore.oor.net/ontologies/sumo/
mereotopology/proofs
Table 6: Translations DOLCE PART-O into SUMO PART.
(∀x, y)P(x, y) ≡ part(x, y)) (75)
(∀x, y)Ov(x, y) ≡ overlapsSpatially(x, y))
(76)
Table 7: Translations SUMO PART into DOLCE PART-O.
(∀x, y)part(x, y) ≡ O(x) ∧ O(y) ∧ P(x, y) (77)
(∀x, y)properPart(x, y) ≡ O(x) ∧ O(y)∧
P(x, y) ∧ ¬P(y, x)
(78)
(∀x, y)overlapsSpatially(x, y) ≡
O(x) ∧ O(y) ∧ Ov(x, y))
(79)
(∀x, y)overlapsPartially(x, y) ≡
Ov(x, y) ∧ ¬P(x, y))) ∧ ¬P(y, x))))
(80)
We have verified theories DOLCE PART-E, and
SUMO SUBPROCESS by demonstrating their syn-
onymy with already verified theory colore.oor.net/
ontologies/mereology/m mereology.clif.
6.3 Mapping Objects
Regarding the representation of objects in SUMO and
DOLCE-CORE, by means of the following definition
and theorem we classify the relationship among their
respective part-whole axiomatizations as synonymy.
Definition 11. SUMO PART is the theory given by
axioms (18)-(24), and DOLCE PART-T is the theory
given by axioms (1)-(4) and (7).
Theorem 5. SUMO PART is synonymous with
DOLCE PART-O.
Proof. Let us call ∆ to the set of translations defini-
tions shown in Table 6. Using Prover9 we have shown
that SUMO PART ∪ ∆ |= DOLCE PART-O.
13
Let us call Π to the set of translations definitions
shown in Table 7. Using Prover9 we have shown that
DOLCE PART-O ∪ Π |= SUMO PART.
13
We have verified theories DOLCE PART-O, and
SUMO PART by demonstrating their synonymy
with already verified theory colore.oor.net/ontologies/
mereology/m mereology.clif.
6.4 Mapping SUM
We observe that theories DOLCE SUM, and SUMO
SUM axiomatize the same intended conceptualization
regarding fusion of parts, and they are respective ex-
tensions of synonymous and verified theories DOLCE
PART-O and SUMO PART. Based on that, we verify
theories DOLCE SUM, and SUMO SUM by defining
Verifying and Mapping the Mereotopology of Upper-Level Ontologies
39

Figure 6: Objects x, y, z, t, which do not hold SUM(z, x, y)
but hold MereologicalSumFn(x, y) = z. Arrows represent
relation part of theory SUMO SUM, and relation P of the-
ory DOLCE SUM.
Table 8: Translations DOLCE SUM into SUMO SUM.
(∀x, y, z)SUM(z, x, y) ≡ Ob ject(x) ∧ Ob ject(y)∧
(MereologicalSumFn(x, y) = z)
(81)
mappings among their signatures, then, finding which
axioms of each ontology are not theorems of the other.
By analyzing the obtained results, we identify missing
axioms and corresponding unintended models. Based
on such a verification we have identified the changes
proposed in section 5 to the SUMO ontology.
Definition 12. DOLCE SUM is the theory given by
axioms (1)-(5), (7), and (12).
The axiomatization of SUMO SUM is weaker
than the axiomatization of DOLCE SUM. In fact, let
us consider objects x, y, z, t of Figure 6, such that
properPart(x, z), properPart(y, z), and properPart(t, z)
hold, while none of overlapsSpatially(x, y),
overlapsSpatially(t, y), or overlapsSpatially(x, t)
hold. In parts (a), (b), and (c) of the bottom of
Figure 6 parthood is indicated with arrows from
the part to the whole. According to the charac-
terization of mereological sum on SUMO SUM
(MereologicalSumFn(x, y) = z) hold. However, Parts
(b) and (c) of Figure 6 depict alternative additional
conditions that the characterization of mereological
sum on module DOLCE SUM has. In DOLCE,
any other object t which overlaps with the sum z
must overlap with at least one of the addends x or y,
therefore SUM(z, x, y) does not hold in DOLCE. The
following theorem formalizes our claim.
Theorem 6. SUMO SUM can not interpret DOLCE
SUM.
Proof. Let us call ∆ to the translations shown in Table
6, and Π to the translation shown in Table 8, and let S
1
be the theory that results from adding sentence (82) to
Table 9: Characterization of predicate MSum in SUMO.
(∀x, y, z)MSum(z, x, y) → (∀w)(part(z, w) ↔
(part(x, w) ∧ part(y, w))))
(83)
(∀x, y, z)MSum(z, x, y) →
Ob ject(x) ∧ Ob ject(y) ∧ Ob ject(z)
(84)
(∀x, y)Ob ject(x) ∧ Ob ject(y) →
∃z(Ob ject(z) ∧ MSum(z, x, y))
(85)
(∀x, y, z, t)MSum(z, x, y) ∧ MSum(t, x, y) →
(z = t)
(86)
Table 10: Translation SUMO SUM into DOLCE SUM.
(∀x, y, z)MSum(z, x, y) ≡
Ob ject(x) ∧ Ob ject(y) ∧ SUM(z, x, y)
(87)
theory SUM. Using Mace4, we have built a model of
S
1
∪ ∆ ∪ Π.
13
(∃x, y, z)SUM(z, x, y)∧
¬(∀w)(Ov(w, z) ↔ Ov(w, x) ∨ Ov(w, y))
(82)
In order to translate the symbol
MereologicalSumFn of theory SUM into the lan-
guage of DOLCE-CORE, we have represented the
graph
14
of function MereologicalSumFn by means
of predicate MSum, as shown in Table 9.
Theorem 7. DOLCE SUM can not interpret SUMO
SUM.
Proof. Let us call ∆ to the translations shown in Ta-
ble 1, Π to the translations in Table 7, and ϒ to the
translation in Table 10, and let DOLCE SUM
1
be
the theory that results from adding sentence (88) to
DOLCE SUM. Using Mace4, we have built a model
of DOLCE SUM
1
∪ ∆ ∪ Π ∪ ϒ.
13
(∃x, y)Ob ject(x) ∧ Ob ject(y)∧
(∀z)(¬Ob ject(z) ∨ ¬MSum(z, x, y)) (88)
Figure 7 shows conservative extensions by means
of thin black arrows and relative interpretations (map-
pings), by thick gray arrows from interpreted to in-
terpreting theories. Because every theorem of a
14
A n-ary function f from A
n
to B is representable by a
relation ρ with arity (n+1), called the graph of f, such that:
(a) Every tuple of ρ is a tuple h ¯x, f ( ¯x)i with ¯x ∈ A
n
and
f ( ¯x) ∈ range( f ).
(b) If f ( ¯x) = b and f (¯z) = c, then b = c.
KEOD 2016 - 8th International Conference on Knowledge Engineering and Ontology Development
40

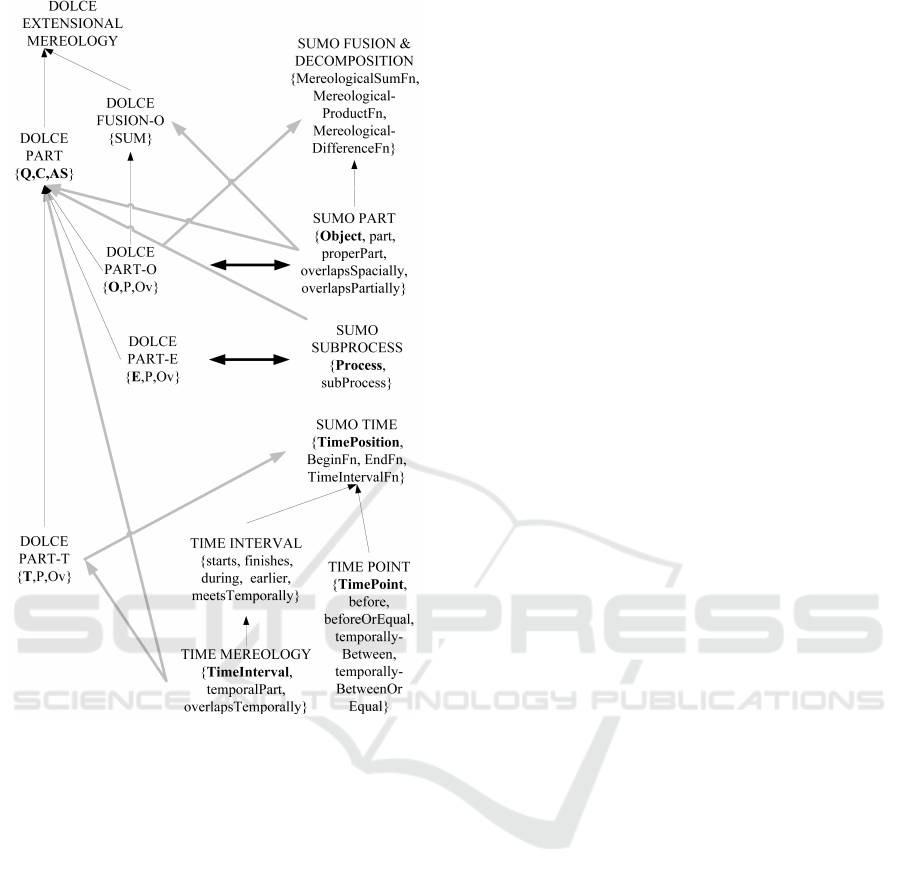
Figure 7: Mappings between modules of DOLCE-CORE
and SUMO. Black thin arrows point to conservative exten-
sions, thick grey arrows are directed from interpreted theo-
ries to interpreting theories, and thick black arrows connect
synonymous theories. Signature members are situated in
the subtheories that introduce them.
theory is also a theorem of its conservative exten-
sions, each conservative extension is capable of in-
terpreting every theory that the modules that it ex-
tends interpret. In particular, module DOLCE PART,
shown in Figure 7, is the theory resulting from the
union of DOLCE PART-T, DOLCE PART-E, and
DOLCE PART-O, plus axioms (10), (11), while mod-
ule DOLCE EXTENSIONAL MEREOLOGY is the
union of DOLCE PART, DOLCE SUM, and ax-
ioms (6), (13), (14), (15), (16), and (17). As in-
dicated by oriented grey arrows, the axiomatization
of part-whole relations in categories Object, Process,
and TimeInterval of SUMO are mappable to DOLCE
minimal axiomatization of mereology represented by
module DOLCE PART. Although not represented in
Figure 7, it holds that because DOLCE EXTEN-
SIONAL MEREOLOGY extends DOLCE PART, it
also interprets SUMO PART, SUMO SUBPROCESS,
and TIME MEREOLOGY. In turn, SUMO SUM in-
terprets DOLCE PART-O. The strongest subtheories
of SUMO and DOLCE-CORE that are synonymous,
and therefore have equivalent models, are the pairs in-
dicated by double black arrows, i.e, DOLCE-PART-O
with SUMO PART and DOLCE-PART-E with SUMO
SUBPROCESS.
7 CONCLUSIONS
We have verified the representation of mereology of
the DOLCE-CORE and the core axiomatization of
mereotopology of SUMO. In the process, we have
identified a series of unintended and missing mod-
els on the analysed subtheories, and have isolated the
strongest subtheories of each ontology in which they
both agree to the extent of having equivalent models.
As a result, we have proposed a set of corrections and
some axioms to be added to the analyzed theories. We
have built a series of formal maps stated in standard
first-order logic which unambiguously relate the ax-
iomatizations of both upper-level ontologies. Finally,
we have produced a modular representation in stan-
dard first-order logic of the complete SUMO subthe-
ory of mereotopology originally stated in higher order
language SUO-KIF.
REFERENCES
Benzm
¨
uller, C. and Pease, A. (2012). Higher-order aspects
and context in SUMO. J. Web Sem., 12:104–117.
Borgo, S. and Masolo, C. (2009). Handbook on Ontologies,
chapter Foundational Choices in DOLCE, pages 361–
381. Springer Berlin Heidelberg, Berlin, Heidelberg.
Casati, R. and Varzi, A. (1999). Parts and Places: The
Structures of Spatial Representation. A Bradford
book. MIT Press.
Davey, B. and Priestley, H. (2002). Introduction to Lat-
tices and Order. Cambridge mathematical text books.
Cambridge University Press.
Enderton (1972). A Mathematical Introduction to Logic.
Academic Press.
Euzenat, J. and Shvaiko, P. (2013). Ontology matching.
Springer-Verlag, Heidelberg (DE), 2nd edition.
Gangemi, A., Guarino, N., Masolo, C., and Oltramari, A.
(2003). Sweetening WORDNET with DOLCE. AI
Magazine, 24(3):13–24.
Gangemi, A., Guarino, N., Masolo, C., Oltramari, A.,
and Schneider, L. (2002). Sweetening ontologies
with dolce. In Proceedings of the 13th Interna-
tional Conference on Knowledge Engineering and
Verifying and Mapping the Mereotopology of Upper-Level Ontologies
41

Knowledge Management. Ontologies and the Seman-
tic Web, EKAW ’02, pages 166–181, London, UK,
UK. Springer-Verlag.
Grenon, P. and Smith, B. (2004). Snap and span: To-
wards dynamic spatial ontology. Spatial Cognition
and Computation, 4(1):69–103.
Gr
¨
uninger, M., Hahmann, T., Hashemi, A., and Ong, D.
(2010). Ontology verification with repositories. In
Formal Ontology in Information Systems, Proceed-
ings of the Sixth International Conference, FOIS
2010, Toronto, Canada, May 11-14, 2010, pages 317–
330.
Guarino, N. (1998). Formal ontology and information sys-
tems. In Formal Ontology in Information Systems
- Proceedings of FOIS 1998, Trento, Italy, 6-8 June
1998. Amsterdam, IOS Press, pp. 3-15., pages 3–15.
IOS Press.
Guarino, N. and Welty, C. (2002). Evaluating ontological
decisions with ontoclean. Commun. ACM, 45(2):61–
65.
Hayes, P. (1996). Catalog of temporal theories. Technical
Report Technical Report UIUC-BI-AI-96-01, Univer-
sity of Illinois Urbana-Champagne.
Masolo, C., Borgo, S., Gangemi, A., Guarino, N., and
Oltramari, A. (2003). WonderWeb deliverable D18
ontology library (final). Technical report, IST Project
2001-33052 WonderWeb: Ontology Infrastructure for
the Semantic Web.
McCune, W. (2005–2010). Prover9 and mace4.
http://www.cs.unm.edu/∼mccune/prover9/.
Niles, I. and Pease, A. (2001). Towards a standard upper
ontology. In FOIS ’01: Proceedings of the interna-
tional conference on Formal Ontology in Information
Systems, pages 2–9, New York, NY, USA. ACM.
Niles, I. and Pease, A. (2003). Linking lexicons and on-
tologies: Mapping WordNet to the suggested upper
merged ontology. In Proceedings of the 2003 Inter-
national Conference on Information and Knowledge
Engineering (IKE ’03), Las Vegas, Nevada.
Pearce, D. and Valverde, A. (2012). Synonymous theories
and knowledge representations in answer set program-
ming. J. Comput. Syst. Sci., 78(1):86–104.
Silva Mu
˜
noz, L. and Gr
¨
uninger, M. (2016). Mapping and
Verification of the Time Ontology in SUMO. In For-
mal Ontology in Information Systems - Proceedings
of the 9th International Conference, FOIS, July 6-9,
2016, Annecy, France.
Varzi, C. A. (2007). Handbook of Spatial Logics, chapter
Spatial Reasoning and Ontology: Parts, Wholes, and
Locations, pages 945–1038. Springer Netherlands,
Dordrecht.
KEOD 2016 - 8th International Conference on Knowledge Engineering and Ontology Development
42