Skip Search Approach for Mining Probabilistic Frequent Itemsets

from Uncertain Data

Takahiko Shintani, Tadashi Ohmori and Hideyuki Fujita

Graduate School of Informatics and Engineering, The University of Electro-Communications, Tokyo, Japan

Keywords:

Frequent Itemset, Probabilistic Data, Uncertain Data.

Abstract:

Due to wider applications of data mining, data uncertainty came to be considered. In this paper, we study

mining probabilistic frequent itemsets from uncertain data under the Possible World Semantics. For each tuple

has existential probability in probabilistic data, the support of an itemset is a probability mass function (pmf).

In this paper, we propose skip search approach to reduce evaluating support pmf for redundant itemsets. Our

skip search approach starts evaluating support pmf from the average length of candidate itemsets. When an

evaluated itemset is not probabilistic frequent, all its superset of itemsets are deleted from candidate itemsets

and its subset of itemset is selected as a candidate itemset to evaluate next. When an evaluated itemset is

probabilistic frequent, its superset of itemset is selected as a candidate itemset to evaluate next. Furthermore,

our approach evaluates the support pmf by difference calculus using evaluated itemsets. Thus, our approach

can reduce the number of candidate itemsets to evaluate their support pmf and the cost of evaluating support

pmf. Finally, we show the effectiveness of our approach through experiments.

1 INTRODUCTION

One of important problems in data mining is

a discovery of frequent itemsets within a large

database(Agrawal and R.Srikant, 1994; Han et al.,

2000). Due to wide applications in frequent item-

set mining, data uncertainty came to be consid-

ered(Aggarwal and Yu, 2009). For example, data col-

lected by sensor device are noisy. The locations of

users obtained through GPS systems are not precise.

The user activities that were estimated from the ac-

celeraion sensor data are underspeciﬁed. The uncer-

tain data is the probabilistic database which each item

and/or transaction has a probability value, called at-

tribute uncertainty model and tuple uncertainty model

respectively. On the probabilistic database, frequent

itemsets are probabilistic. The support of an itemset

is a random variable. Several algorithms for mining

frequent itemsets from uncertain data have been pro-

posed. In (Chuim et al., 2007; Leung et al., 2007;

Leung et al., 2008; Aggarwal et al., 2009; Wang

et al., 2013; MacKinnon et al., 2014; Cuzzocrea

et al., 2015), the frequent itemsets are detected by

their expected support count. However, it is reported

that many important itemsets are missed by using ex-

pected support(Zhang et al., 2008).

By using the Possible Worlds Semantics (PWS),

we can interpretprobabilistic databases(Dalvi and Su-

ciu, 2004). A possible world means the case where

a set of transactions occurs. We can ﬁnd frequent

itemsets under PWS by counting their support counts

from every possible world. Since the enormous num-

ber of possible worlds have to be considered, this is

impractical. The approximate algorithms for ﬁnding

frequent itemsets from the attribute uncertain model

and tuple uncertain model were proposed(Wang et al.,

2012; Leung and Tanbeer, 2013), but these algo-

rithms cannot ﬁnd exact solutions. In (Zhang et al.,

2008), the algorithm for ﬁnding exact solutions of fre-

quent items were proposed, but this algorithm can-

not handle itemsets. The algorithms for ﬁnding exact

solution of probabilistic frequent itemsets were pro-

posed in (Bernecker et al., 2009; Sun et al., 2010).

The bottom-up manner algorithm ﬁnds frequent item-

sets in ascending order of length like Apriori algo-

rithm(Agrawal and R.Srikant, 1994). This algorithm

can prune candidate itemsets by Apriori down-closed

property. The dynamic programing (DP)(Bernecker

et al., 2009) and divide-and-conquer (DC)(Sun et al.,

2010) for evaluating the support probability were pro-

posed. DP and DC evaluate the support probabil-

ity from scratch, so its cost is high. In (Sun et al.,

2010), the top-down manner algorithm, TODIS, was

proposed. TODIS can evaluate the support probabil-

174

Shintani, T., Ohmori, T. and Fujita, H.

Skip Search Approach for Mining Probabilistic Frequent Itemsets from Uncertain Data.

DOI: 10.5220/0006035401740180

In Proceedings of the 8th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2016) - Volume 1: KDIR, pages 174-180

ISBN: 978-989-758-203-5

Table 1: Example of PDB.

TID Transaction Existential Prob.

{a, e, f, g} 0.7

{a, b, e, g} 1.0

{b, c, h, i, j} 0.5

{b, d, f, h, j} 0.8

ity function by inheriting a superset of the itemset, but

it involves evaluating many redundant itemsets.

In this paper, we study mining probabilistic fre-

quent itemsets from uncertain data in the tuple un-

certainty model under PWS by extending our previ-

ous study(Tateshima et al., 2015). We propose skip

search approach to avoid evaluating redundant item-

sets which becomes probabilistic infrequent. Our skip

search approach starts to evaluate the support prob-

ability from the average length of itemsets. When

the evaluated itemset is not probabilistic frequent, it’s

super-itemset is evaluated next. When the evaluated

itemset is probabilistic frequent, its sub-itemset is

evaluated next. Moreover, our skip search approach

evaluates the support probability function efﬁciently

by difference calculus. We show the effectiveness of

our skip search approach by experiments.

This paper is organized as follows. In the next sec-

tion, we explain the problem of mining probabilistic

frequent itemsets. In section 3, we propose our skip

search approach. Performance evaluations are given

in section 4. Section 5 concludes this paper.

2 MINING PROBABILISTIC

FREQUENT ITEMSETS

First, we introduce basic concepts of frequent item-

sets on exact databases. Let L = {i

, i

, . . . , i

} be a

set of literals, called items. Let D = {t

, . . . ,t

} be

a set of transactions, where each transaction t is a set

of items such that t ⊆ I . A transaction has an asso-

ciated unique identiﬁer called TID. A set of items

X ⊆ I is called an itemset. Itemset X is a sub-itemset

of itemset Y if and only if X is a subset of Y. Y is

called a super-itemset of X. We say each transaction

t contains an itemset X, if X ⊆ t. The itemset X has

support s in D if s transactions contain X, here we

denote s = sup(X).

In the tuple uncertainty model, each transaction

has an existential probability p

. Here 0 < p

≤ 1.

Existential probability indicates the probability of the

transaction occurs. Example of probabilistic database

(PDB) in tuple uncertainty model is shown in Table

1. Table 1 consists of ten items with four transac-

tions. For example, T

denotes that the probability of

Table 2: Possible worlds for Table 1.

W Occurred transactions Prob. P(W)

0.03

, T

0.07

, T

0.03

, T

0.12

, T

0.07

, T

0.28

, T

0.12

, T

0.28

a transaction {a, e, f, g} occurs is 0.7.

We can interpret PDB by using PWS. Table 2

shows all possible worlds for PDB in Table 1. Here,

the probability of a possible world W

is denoted as

P(W

), the sum of them is 1(=

∑

P(W

)). For exam-

ple,W

denotes the case where T

and T

occur,T

and

do not occur. The probability of W

is calculated

as follows: P(W

) = p

∗ p

∗(1− p

)∗(1− p

) =

0.7∗ 1.0∗ (1 − 0.5) ∗ (1− 0.8) = 0.07.

Since there are many possible worlds and each

possible world has a probability, the support of an

itemset becomes a random variable. We denote f

(k)

as the probability mass function(pmf) of an itemset X

at sup(X) = k(k ≥ 0). For example, itemset {b, h} is

contained in T

and T

. When both T

and T

occur,

sup({b, h}) becomes 2. The possible worlds where

both T

and T

occur are W

and W

, f

{b,h}

(2) =

P(W

) + P(W

) = 0.4. When either T

or T

oc-

curs, sup({b, h}) becomes 1. The possible worlds

where either T

or T

occurs are W

and W

{b,h}

(1) = P(W

) + P(W

) = 0.5.

When neither T

nor T

occurs, sup({b, h}) becomes

0. The possible worlds where neither T

nor T

occurs

are W

and W

, f

{b,h}

(0) = P(W

) + P(W

) = 0.1.

In PDB, we deﬁne that an itemset X is probabilis-

tic frequent if the following equation is satisﬁed.

Pr(sup(X) ≥ minsup) ≥ minprob (1)

Here, Pr(sup(X) ≥ minsup) is the sum of the prob-

ability that sup(X) is minsup or more. minsup

and minprob are user-speciﬁed minimum thresholds

of the support and the probability. For example,

Pr(sup({b, h}) = f

{b,h}

(2) + f

{b,h}

(1) = 0.9 when

minsup = 1. If minprob = 0.7, {b, h} is probability

frequent.

The problem of mining probabilistic frequent

itemsets is to ﬁnd all itemsets that satisfy equation 1

on the assumption that we are given minsup, minprob

and PDB.

In (Sun et al., 2010), the bottom-up manner al-

gorithm, a-Apriori, was proposed. The p-Apriori

ﬁnds probabilistic frequent itemsets in ascending or-

der of length like Apriori. In the ﬁrst pass (pass

Skip Search Approach for Mining Probabilistic Frequent Itemsets from Uncertain Data

175

1), the support pmf(spmf) for each item are eval-

uated. All the items which satisfy equation 1 are

picked out. These items are called probabilistic fre-

quent 1-itemsets. Here after, k-itemset is deﬁned

a set of k items. The second pass, the 2-itemsets

are generated using probabilistic frequent 1-itemsets,

which are called candidate 2-itemsets. Then spmf

for each candidate 2-itemsets are evaluated, the prob-

abilistic frequent 2-itemsets which satisfy equation

1 are determined. In k-th pass, the candidate k-

itemsets are generated by using probabilistic frequent

(k − 1)-itemsets, spmf for each candidates are evalu-

ated, and the probabilistic frequent k-itemsets are de-

termined. The candidate generation is same as Apri-

ori. This iteration terminates when the probabilistic

frequent itemset becomes empty. The dynamic pro-

graming(DP) algorithm(Bernecker et al., 2009) and

divide-and-conquer(DC) algorithm(Sun et al., 2010)

for evaluating spmf have been proposed. These algo-

rithms do not examine possible worlds. By examin-

ing all transactions in PDB for each candidateitemset,

DC evaluated spmf. The DC divides D into D

and

, spmf of X is evaluated by the convolution of f

X,1

and f

X,2

(k) =

∑

i=0

X,1

(i) ∗ f

X,2

(k− i) (2)

Here, f

X, j

(here, j = 1 or 2) is the pmf of sup(X)

in D

X, j

. The p-Apriori reduces the number of can-

didate itemsets by pruning with the Apriori down-

closed property. However, all transactions in PDB

have to be examined to evaluate spmf for each item-

set.

Next, we explain the top-down manner algorithm,

TODIS(Sun et al., 2010). The TODIS evaluates spmf

of itemsets efﬁciently by inheriting spmf from their

super-itemsets. Since TODIS starts spmf evaluations

from the longest itemset, all potentially probabilis-

tic frequent itemsets have to be identiﬁed on ahead.

These itemsets are called candidate itemsets. It can-

not be probabilistic frequent that an itemset does not

satisfy minsup without considering existential proba-

bility. By ordinary frequent itemset mining algorithm

such as Apriori, TODIS generates all candidate item-

sets which satisfy minsup without considering exis-

tential probability. Hereafter, an itemset which satisfy

minsup without considering existential probability is

called a count frequent itemset. For each candidate

itemset, TODIS also generates id-list, which is uti-

lized to evaluate spmf. An id-list of itemset X is a set

of TIDs which contains X. We denote id-list of item-

set X as L

. Then, TODIS evaluates spmf of every

candidate itemsets in a top-down manner. First, the

spmf of the longest candidate itemsets is evaluated by

DC algorithm. Afterward, the spmf of candidate item-

sets are evaluated in descending order of their length.

The spmf of a candidate itemset is evaluated by inher-

iting spmf of its super-itemset. Here, we show evalu-

ating the spmf of a candidate itemset X. The spmf of

an itemset Z is denoted as f

. Assume that an itemset

Y is a super-itemset of X, and f

is known. f

is eval-

uated from transactions L

. Since X is a sub-itemset

of Y, L

⊇ L

. f

can be evaluated from transactions

in L

and L

\ L

. Let T

, . . . , T

n−1

be a set of trans-

actions in L

\ L

. f

can be evaluated by convolving

, . . . , T

n−1

to f

. Here, let p

be probability that T

occurs, q

(= 1− p

) be probability that T

does not oc-

cur. Let f

(k) be f

at sup(Z) = k. Let f

(k) be spmf

that convolved f

from T

to T

. If any transactions

does not occur, k = 0. f

(0) is calculated as

(0) = f

n−1

(0) = f

(0) ∗ Π

n−1

m=0

(3)

If k ≥ 1, f

i+1

(k) is the sum of the case that T

i+1

occurs

at f

(k− 1) and T

i+1

does not occur at f

(k). f

i+1

(k)

is calculated as

i+1

(k) = f

(k− 1) ∗ p

i+1

+ f

(k) ∗ q

i+1

(4)

(k) is the spmf of sup(X) = k that convolved f

(k)

from T

to T

n−1

, so we can calculate f

(k) by repeat-

ing Equation 4 from i = 0 to n− 1. Thus, f

is evalu-

ated by inheriting f

using Equation 3 and 4. The top-

down manner algorithm efﬁciently evaluates spmf of

an itemset by inheriting the spmf of its super-itemsets.

However, the spmf of all candidate itemsets has to be

evaluated. Even if the evaluated candidate itemset is

not probabilistic frequent, this algorithm cannot avoid

to evaluate of spmf for its super-itemsets. Because all

super-itemsets have already been evaluated.

3 SKIP SEARCH APPROACH

In this section, we describe the way to evaluating

spmf by inheriting the spmf of sub-itemsets. Then,

we explain the skip search approach for avoiding to

evaluate spmf for redundant candidate itemsets.

3.1 Evaluating Spmf by Inheriting

Sub-itemset

TODIS evaluates spmf of candidate itemsets in de-

scending order, so all candidate itemsets can be eval-

uated spmf by inheriting spmf of its super-itemset.

When the order to evaluate spmf is not one way, it

is not enough. We can evaluate spmf of a candi-

date itemset by deconvolving spmf of its sub-itemset.

Here, we propose the way to evaluate spmf by inher-

iting spmf of sub-itemset. Assume that an itemset Y

KDIR 2016 - 8th International Conference on Knowledge Discovery and Information Retrieval

176

is a sub-itemset of a candidate itemset X, and f

known. f

is evaluated from transactions in L

. Since

X is a super-itemset of Y, L

⊆ L

. Let T

, . . . , T

n−1

be a set of transactions in L

\ L

. The spmf of X can

be evaluated by deconvolving T

, . . . , T

n−1

to the spmf

of Y. Here, let p

be the probability that T

occurs,

(= 1− p

) be the probability that T

does not occur.

Let f

(k) be the spmf of X at sup(X) = k. Let f

(k)

be the spmf of sup(Y) = k that deconvolved f

from

to T

. If any transactions does not occur, k = 0.

(0) is calculated as

(0) = f

(0) ∗ q

(5)

(0) is calculated as

(0) =

(0)

(6)

We can calculate f

i+1

(0) by deconvolving f

(0) with

i+1

(0) =

(0)

i+1

(7)

(0) can be calculated by deconvolving f

(0) from

to T

n−1

(0) = f

n−1

(0) = f

(0) ∗ Π

n−1

m=0

(8)

If k ≥ 1, k transactionsoccur. When f

is deconvolved

with T

, f

(k) is calculated as

(k) = f

(k) ∗ q

+ f

(k− 1) ∗ p

(9)

Thus,

(k) =

(k) − f

(k− 1) ∗ p

(10)

When f

is deconvolved with T

, . . . , T

, f

(k) is cal-

culated as

(k) = f

i+1

(k) ∗ q

i+1

+ f

i+1

(k− 1) ∗ p

i+1

(11)

Thus,

i+1

(k) =

(k) − f

i+1

(k− 1) ∗ p

i+1

(12)

(k) can be calculated by deconvolving f

(k) from

to T

n−1

, so we can calculate f

(k) by repeating

Equation 8 to 12 from i = 0 to n− 1.

This difference calculus by inheriting sub-itemset

can be applied to p-Apriori. When pass k ≥ 2, spmf

of candidate itemsets can be evaluated by inheriting

their sub-itemsets. Since p-Apriori ﬁnds probabilis-

tic frequent itemsets in ascending order of the length

of itemsets, all sub-itemsets have already been evalu-

ated. We can evaluate spmf of a candidate k-itemset

by inheriting its sub-itemsets.

3.2 Order to Evaluate Spmf of

Candidate Itemsets

The skip search approach evaluates spmf in a bidi-

rectional way so that we can avoid to evaluate spmf

of probabilistic infrequent itemsets by Apriori down-

closed property. Assume that the spmf of candidate

itemset X was evaluated. If X is not probabilistic

frequent, we can omit to evaluate spmf of all super-

itemset of X. Because an itemset whose sub-itemsets

are not probabilistic frequent cannot be probabilistic

frequent. Since our skip search approach starts evalu-

ating spmf from the average length of candidate item-

sets, it’s super-itemsets that have not been evaluated

spmf are remaining. When X is probabilistic infre-

quent, a sub-itemset of X in candidate itemsets is se-

lected as a candidate itemset to evaluate spmf next.

The spmf of this itemset is evaluated by difference

calculus in section 3.1. When X is probabilistic fre-

quent, spmf of all sub-itemsets of X in candidate item-

sets are evaluated. A super-itemset of X in candidate

itemsets is selected as the candidate itemset to eval-

uate spmf next, since it has a potential to be proba-

bilistic frequent. The spmf of this itemset is evaluated

same as TODIS. Hereby, our skip search approach can

omit evaluations for redundant candidate itemsets.

Here, we show the procedure to select a candidate

itemset evaluating spmf next.

An itemset X in candidate itemsets is selected at

random. Here, the length of X is close to the aver-

age length of candidate itemsets. Then, the spmf

of X is evaluated.

If X is probabilistic frequent:

An itemset Y which is super-itemset of X in

candidate itemsets is selected. The length of

Y is close to the median length of X and the

longest super-itemset of X.

If X is not probabilistic frequent:

An itemset Y

′

which is sub-itemset of X in can-

didate itemsets is selected. The length of Y

′

close to the median length of X and the shortest

unevaluated sub-itemset of X.

If all sub-itemset and super-itemset have been al-

ready evaluated:

An itemset is selected at random.

3.3 Procedure of Skip Search Approach

Here, we describe the procedure of skip search ap-

proach.

Step1. Set of candidate itemsets C , that of evaluat-

ing itemsets E and that of probabilistic frequent

itemsets F are initialized to the empty set.

Skip Search Approach for Mining Probabilistic Frequent Itemsets from Uncertain Data

177

Step2. All count frequent itemsets are inserted to C ,

and their id-lists are generated.

Step3. A candidate itemset c ∈ C is selected from

candidate itemset set at random.

Step4. f

is evaluated from L

. If a super-itemsets

or sub-itemsets of c exists in E , f

is evaluated by

inheriting it. Then, c is deleted from C .

• If c is probabilistic frequent, c is inserted into

F . When any sub-itemset c

′

of c has not been

evaluated yet, f

′

is evaluated, inserted into F

and deleted from C . A super-itemset of c in C

is selected as the candidate itemsets evaluating

spmf next.

• If c is not probabilistic frequent, all super-

itemset of c are deleted from C . A sub-itemset

of c in C is selected as the candidate itemsets

evaluating spmf next.

• If super-itemset and sub-itemset do not exist in

C , a candidate itemset in C is selected from

candidate itemset set at random.

Step5. If the candidate itemset evaluating spmf next

is empty, this procedure terminates. Otherwise,

step4 is repeated.

In skip search approach, candidate itemsets which

are selected at random cannot be evaluated by inherit-

ing their super/sub-itemsets. The spmf of these item-

sets are evaluated by algorithm DP or DC, it is costly.

To solve this problem, we propose another approach,

“skip search approach from maximal”. A maximal

candidate itemsets(Bayardo, 1998) is selected in Step

3. In Step 4, candidate itemsets which are sub-itemset

of selected maximal candidate itemset are evaluated.

This procedure can avoid using DC in Step 4. The

spmf of maximal candidate itemsets have to be evalu-

ated by DC, and most of these itemsets are not prob-

abilistic frequent. However, the cost of evaluating

them by DP or DC is relatively small. Because the

support of these itemset is small. Example of the or-

der to evaluate spmf in skip search approach from

maximal is shown in Figure 1. First, a maximal

candidate itemset {a, b, c, d, e} is selected and eval-

uated. Then a candidate itemset {a, c, d} which is

a sub-itemset of {a, b, c, d, e} is selected and eval-

uated. Since {a, c, d} is not probabilistic frequent,

{a, b, c, d} and {a, c, d, e} which are super-itemsets of

{a, c, d} are deleted. We can omit to evaluate spmf

of {a, b, c, d} and {a, c, d, e}. Next, {a, d} which is

a sub-itemset of {a, c, d} is selected and evaluated.

{a, d} is probabilistic frequent, so spmf of all its sub-

itemsets, {a} and { d}, are evaluated. Then, {a, d, e}

which is a super-itemset of {a, d} is selected as a can-

didate itemset to evaluate next. When all sub-itemsets

Figure 1: Example of the order to evaluate spmf in skip

search approach from maximal.

of {a, b, c, d, e} were evaluated, other maximal candi-

date itemset, for example {d, e, f}, is selected as a

candidate itemset to evaluate next.

This enhance is effective when all candidate item-

sets and their id-lists cannot ﬁt in memory. Since the

information of a maximal candidate itemset and its

sub-itemsets is required in Step 4, we can reduce the

size of memory usage.

4 PERFORMANCE EVALUATION

We evaluated the performance of skip search ap-

proaches by comparing with the top-down manner

algorithm, TODIS, and the bottom-up manner algo-

rithm, p-Apriori. In experiments, p-Apriori evaluates

spmf by ihneriting sub-itemsets described in section

3.1, that is more efﬁcient than using DC. This algo-

rithm is denoted as “p-Apriori w diffcalc” in experi-

mantal results. In skip search approaches and TODIS,

the count frequent itemsets are found by Apriori algo-

rithm. In experimental results, the naive skip search

approach is denoted as “skip”. The skip search ap-

proach described in section 3.3 is denoted as “skip f

max”.

To evaluate the performance of our approach,

synthetic data emulating retail transactions are used,

where the generation procedure is based on the

method described in (Agrawal and R.Srikant, 1994).

The average length of a transaction is 40, the average

length of a frequent itemset is 10, and the dataset size

N is 500k. For each transaction, we set the existential

probability with a Gaussian distribution.

Figure 2 shows the execution time varying

minsup. Here, minprob was set to 0.3. When minsup

is small, the difference between the execution time of

skip search approaches and TODIS. Since the aver-

age length of probabilistic frequent itemsets becomes

long for small minsup, the number of candidate item-

sets which skip search approaches can omit to evalu-

KDIR 2016 - 8th International Conference on Knowledge Discovery and Information Retrieval

178

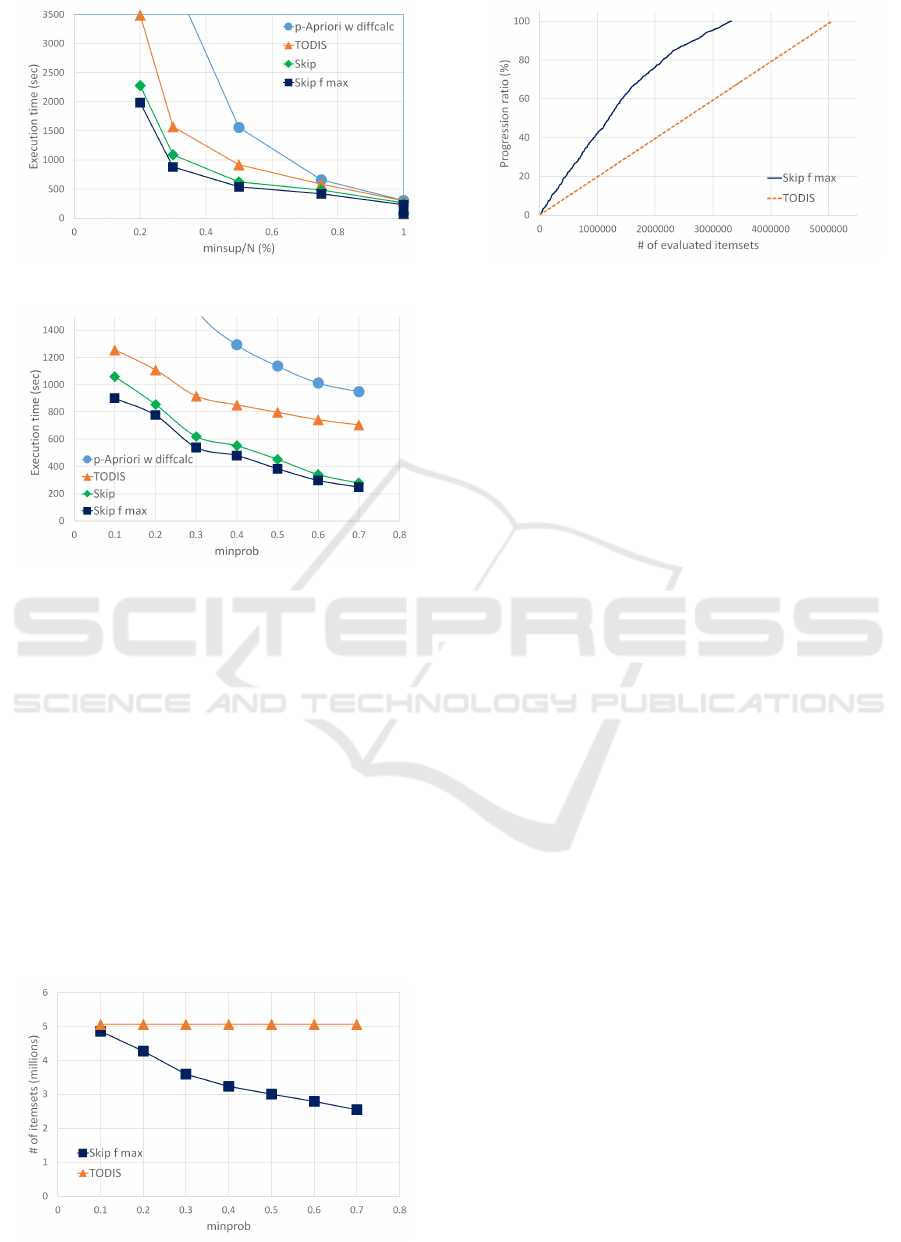
Figure 2: Execution time varying minsup.

Figure 3: Execution time varying minprob.

ate spmf increases.

Figure 3 shows the execution time varying

minprob. Here, minsup was set to 0.003. Our skip

search approaches signiﬁcantly outperform other al-

gorithms. As the minimum probability decreases, the

difference of the execution time between skip search

approaches and TODIS shrinks. In this experiment,

minsup is ﬁxed, so the number of candidate itemsets

is constant (Figure 4). When minprob is small, the

ratio of the number of omitted candidate itemsets be-

comes small. Thus, the difference of the execution

time becomes small. The difference of the execu-

tion time between skip and skip f max becomes small

for large minprob. The number of probabilistic fre-

quent itemsets becomes smaller asminprob increases.

Since the number of probabilistic infrequent itemsets

Figure 4: Number of evaluated itemsets varying minprob.

Figure 5: Progression ratio.

is large, the difference between skip and skip f max

becomes small.

Figure 5 shows the progression ratio of skip f max

and TODIS. The horizontal axis is the number of

itemsets which have been evaluated their spmf, the

vertical axis is the progression ratio. The progres-

sion ratio means the ratio of itemsets either proba-

bilistic frequent or not havebeen conﬁrmed. Here, the

minimum support threshold and the minimum proba-

bility threshold are set to 0.003 and 0.3 respectively.

TODIS evaluates the spmf of candidate itemsets one

by one in descending order, so its progression ratio

becomes linear. In skip f max, its progression ratio

becomes linear when an evaluated candidate itemset

is probabilistic frequent. However, when an evalu-

ated candidate itemset is not probabilistic frequent, its

super-itemsets are deleted at a time, so the gradient of

progression ratio signiﬁcantly increases.

5 CONCLUSIONS

In this paper, we proposed skip search approach for

mining probabilistic frequent itemsets under the Pos-

sible Worlds Semantics. By starting spmf evalua-

tion from the average length of candidate itemsets

for each maximal itemset and its sub-itemsets, our

skip search approach can omit to evaluate redundant

itemsets which become probabilistic infrequent. It

can evaluate spmf efﬁciently by inheriting spmf from

its sub/super-itemsets. Performance evaluations show

our skip search approach from maximal can attain

good performance.

ACKNOWLEDGEMENTS

This work was supported by JSPS KAKENHI Grant

Number JP25280022 and JP26330129.

This work was supported by CREST, Japan Sci-

ence and Technology Agency.

Skip Search Approach for Mining Probabilistic Frequent Itemsets from Uncertain Data

179

REFERENCES

Aggarwal, C., Li, Y., and Wang, J. (2009). Frequent pattern

mining with uncertain data. In 15th ACM SIGKDD In-

ternational Conference on Knowledge Discovery and

Data Mining.

Aggarwal, C. and Yu, P. (2009). A survey of uncertain data

algorithms and applications. In IEEE Transactions on

Knowledge and Data Enginerring.

Agrawal, R. and R.Srikant (1994). Fast algorithm for min-

ing association rules. In 20th International Confer-

ence on Very Large Data Bases.

Bayardo, R. (1998). Efﬁciently mining long patterns from

databases. In 1998 ACM SIGMOD International Con-

ference on Management of Data.

Bernecker, T., Kriegel, H., Renz, M., Verhein, F., and Zue-

ﬂe, A. (2009). Probabilistic frequent itemset mining in

uncertain databases. In 15th ACM SIGKDD Interna-

tional Conference on Knowledge Discovery and Data

Mining.

Chuim, C., Kao, B., and Hung, E. (2007). Mining fre-

quent itemsets from uncertain data. In 11th Paciﬁc-

Asia Conference on Knowledge Discovery and Data

Mining.

Cuzzocrea, A., Leung, C., and MacKinnon, R. (2015). Ap-

procimation to expected support of frequent itemsets

in mining probabilistic sets of uncertain data. In 19th

Annual Conference in Knowledge-Based and Intelli-

gent Information and Engineering Systems.

Dalvi, N. and Suciu, D. (2004). Efﬁcient query evaluation

on probabilistic databases. In 13th International Con-

ference on Very Large Data Bases.

Han, J., Pei, J., and Y.Yin (2000). Mining frequent patterns

without candidate generation. In 2000 ACM SIGMOD

International Conference on Management of Data.

Leung, C., Carmichael, C., and Hao, B. (2007). Efﬁcient

mining of frequent patterns from uncertain data. In

Workshops of 7th IEEE International Conference on

Data Mining.

Leung, C., Mateo, M., and Brajczuk, D. (2008). A tree-

based approach for frequent pattern mining from un-

certain data. In 12th Paciﬁc-Asia Conference on

Knowledge Discovery and Data Mining.

Leung, C. and Tanbeer, S. (2013). Puf-tree: a compact tree

structure for frequent pattern mining of uncertain data.

In 17th Paciﬁc-Asia Conference on Knowledge Dis-

covery and Data Mining.

MacKinnon, R., Strauss, T., and Leung, C. (2014). Disc:

efﬁcient uncertain frequent pattern mining with tight-

ened upper bound. In Workshops of 14th IEEE Inter-

national Conference on Data Mining.

Sun, L., Cheng, R., Cheung, D., and Cheng, J. (2010).

Mining uncertain data with probabilistic gurantees.

In 16th ACM SIGKDD International Conference on

Knowledge Discovery and Data Mining.

Tateshima, H., Shintani, T., Ohmori, T., and Fujita, H.

(2015). Skip search approach for mining frequent

itemsets from uncerdain dataset. In DBSJ Japanese

Journal.

Wang, L., Cheung, D., and Cheung, R. (2012). Efﬁ-

cient mining of frequent item sets on large uncertain

databases. In IEEE Transactions on Data Engineer-

ing.

Wang, L., Feng, L., and Wu, M. (2013). At-mine: an ef-

ﬁcient algorithm of frequent itemset mininf on uncer-

tain dataset. In Journal of Computers.

Zhang, Q., Li, F., and Yi, K. (2008). Finding frequent items

in probabilistic data. In 14th ACM SIGKDD Interna-

tional Conference on Knowledge Discovery and Data

Mining.

KDIR 2016 - 8th International Conference on Knowledge Discovery and Information Retrieval

180