Automatic 3D Point Set Reconstruction from Stereo Laparoscopic
Images using Deep Neural Networks
B
´
alint Antal
Faculty of Informatics, University of Debrecen, Debrecen, Hungary
Keywords:
Endoscope, Laparoscope, Heart, 3D Reconstruction, Depth Map, Deep Neural Networks, Machine Learning.
Abstract:
In this paper, an automatic approach to predict 3D coordinates from stereo laparoscopic images is presented.
The approach maps a vector of pixel intensities to 3D coordinates through training a six layer deep neural
network. The architectural aspects of the approach is presented and in detail and the method is evaluated on a
publicly available dataset with promising results.
1 INTRODUCTION
Minimally invasive surgery (MIS) became a wide-
spread technique to have surgical access to the ab-
domen of patients without casing major damages in
the skin or tissues. Since MIS supporting techniques
like laparascopy or endscopy provide a restricted ac-
cess to the surgeon, computer-aided visualisation sys-
tems are developed. One of the major research ar-
eas in the 3d reconstruction of stereo endoscope im-
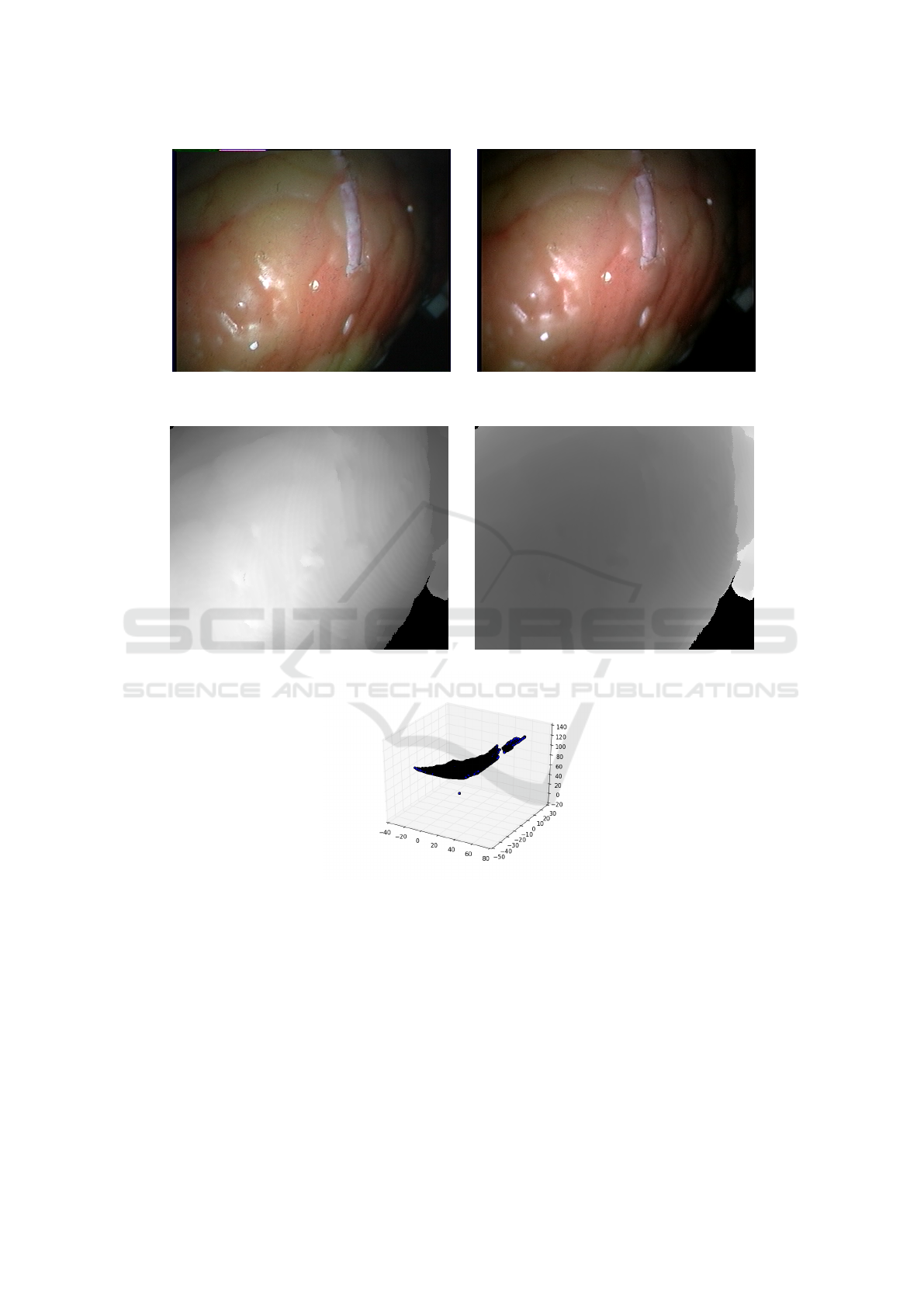
ages. See Figure 1 for an example stereo cardiac la-
paroscopy image pair.
The images are acquired from two distinct view-
points, assisting surgeons to have a sense of depth
during surgery. The usual 3d reconstruction approach
consists of several steps (Maier-Hein et al., 2013), in-
volving the establishment of stereo correspondence
between the pixels of the two viewpoints, which is a
computationally expensive approach and also requires
prior knowledge regarding the endoscope used in the
procedure, limiting its reusability. Figure 2 shows
an example stereo image pair from the (Pratt et al.,
2010) (Stoyanov et al., 2010), alongside the recon-
structed disparsity map, distance map and 3d point
cloud. In this paper, an automatic approach for the
3d reconstruction of stereo endoscopic images will be
presented. The approach is based on deep neural net-
works (DNN) (LeCun et al., 2015) and aims to predict
3d coordinates without the costly procedure of stereo
correspondence. We have evaluated our approach on
a publicly available database where it performed well
compared to a stereo correspondence approach.
The proposed approach only takes the pixel inten-
sity values for the left and right images, and learns
their 3D depth map during training. Figure 3 shows
the flow chart of the proposed approach.
The rest of the paper is organized as follows: sec-
tion 2 describes the proposed approach in details. We
provide our experimental methodology in section 3.
Section 4 contains the results of our experiments and
finally, we draw conclusion in section 5.
2 3D RECONSTRUCTION OF
STEREO ENDOSCOPIC
IMAGES USING DEEP NEURAL
NETWORKS
In this section, the proposed approach is described in
details. Section 2.1 presents an overview on DNNs.
Section 2.2 proposes the architecture of our approach,
while we describe the optimization aspects of the pro-
posed method in section 2.3.
2.1 Deep Neural Networks
Deep Neural Networks (DNNs) are biologically in-
spired machine learning techniques which does not
rely on engineering domain-specific features for each
separate problem but involves a mapping of the input
data (e.g. images) to a target vector using a sequence
of non-linear transformations (LeCun et al., 2015). In
particular, DNNs consists of several layers of high-
level representations on the input data. Each layer
consists of several nodes, which contains weights, bi-
116
Antal, B.
Automatic 3D Point Set Reconstruction from Stereo Laparoscopic Images using Deep Neural Networks.
DOI: 10.5220/0006008001160121
In Proceedings of the 6th International Joint Conference on Pervasive and Embedded Computing and Communication Systems (PECCS 2016), pages 116-121
ISBN: 978-989-758-195-3
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

(a) Left image (b) Right image
Figure 1: An example stereo laparoscopy image pair (Pratt et al., 2010) (Stoyanov et al., 2010).
(a) Disparsity map (b) Distance map
(c) Reconstructed 3D point cloud
Figure 2: Disparsity map, distance map and 3D point cloud extracted from the images shown in Figure 1.
ases and activations in the following form:
out (x) = ( f (W ·x + b)), (1)
where x is an input vector, f is a non-linear activa-
tion function. W is a weight matrix of shape N ×M,
N and M are the output and input dimensions of the
preceding and succeeding layers, respectively, b is a
bias vector. Each DNN has an input layer, an output
layer and several hidden layers of this form. DNN
has proven to be very successful in a wide variety of
machine learning related tasks.
2.2 Architecture of the Proposed DNN
The proposed DNN consists of six layers (see Figure
4).
The input layer takes a six element
vector of the following form: x
i, j
=
(L
i, j
(0), L
i, j
(1), L
i, j
(2), R
i, j
(0), R
i, j
(1), R
i, j
(2)),
where L
i, j
(C) and R
i, j
(C) are the pixel intensites at
the i, j position in channel C = {0, 1, 2} of the left and
right images, respectively. The output layer produces
Automatic 3D Point Set Reconstruction from Stereo Laparoscopic Images using Deep Neural Networks
117

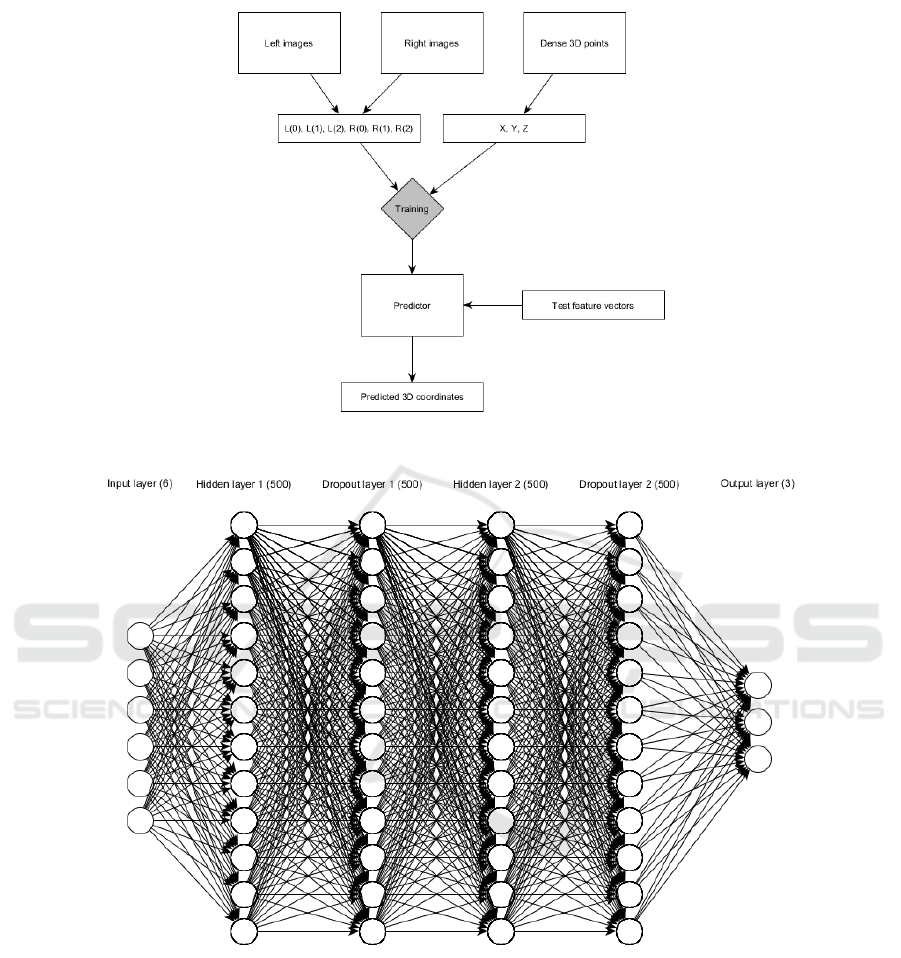
Figure 3: Flow chart of the proposed approach.
Figure 4: Architecture of the proposed DNN.
three outputs, namely the X , Y , Z coordinates of the
input points. Two fully connected dense layers serves
as hidden layers in our architecture with 500 neurons
each. A high-dimensional upscaling of the input
features like this are effective in learning complex
mappings. To avoid overfitting, a dropout layer
after each dense layers were also included, which
introduces random noise into the outputs of each
layer (Srivastava et al., 2014). We have used Rectified
Linear Units as activiations, (Nair and Hinton, 2010)
(Glorot et al., 2011) which is of the form:
f (x) = max (0, x). (2)
2.3 Optimization
We have used an adaptive per-dimension learning rate
version of the stochastic gradient descent (SGD) ap-
proach called Adadelta, which is less sensitive to hy-
perparameter settings than SGD (Zeiler, 2012). Each
W weight matrix and b vector were initialized us-
SPCS 2016 - International Conference on Signal Processing and Communication Systems
118

174
176
178
180
182
184
186
188
190
192
194
0 2 4 6 8 10 12 14 16 18 20
Loss
Epoch
Training loss
Figure 5: Training losses per epoch.
ing the normalized initialization (Glorot and Bengio,
2010):
U





−
√
6
√
n
j
+ n
j+1
,
√
6
√
n
j
+ n
j+1





, (3)
where U is the uniform distribution, n
j
and
n
j+1
are the sizes of the previous and next layers, respec-
tively. To avoid overfitting, we have also applied
Tikhonov regularization for each weight matrix (Ho-
erl and Kennard, 1970). As an energy function, we
have used mean squared error:
MSE =
∑
N

(x −x
0
)
2
+ (y −y
0
)
2
(z −z
0
)
2

N
, (4)
where x, y and z are the ground truth coordinates and
x
0
, y
0
and z
0
are the DNNs predictions, and N is the
number of training vectors, respectively.
3 METHODOLOGY
We have used a laparascpic cardiac dataset to evalu-
ate our approach (Pratt et al., 2010) (Stoyanov et al.,
2010). The dataset consists a pair of videos showing
heart movement. The video consist of 2427 frames,
each of them having a spatial resolution of 360 ×288
and in a standard RGB format. The ground truth is
a depth map containing X , Y , Z coordinates for each
point. We have used a training set of 20 images and
tested our approach on the remaining 2407 frames.
For training, we have allowed 20 epochs to establish
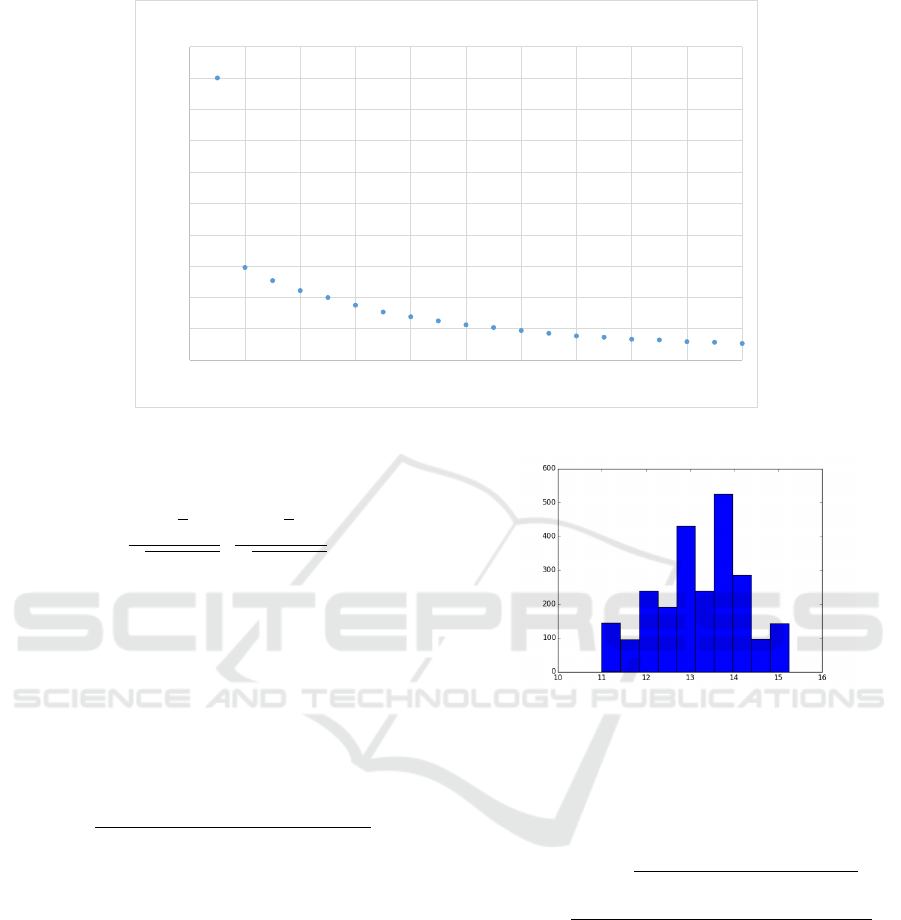
Figure 6: Histogram of root mean squared error losses on
the test data.
the optimal parameters for the DNN. After training,
we have applied pixel-wise classification of the im-
ages of the test set.We have calculated the root mean
squared errors for each image:
RMSE =
∑
N

q
(x −x
0
)
2
+ (y −y
0
)
2
(z −z
0
)
2

N
,
(5)
We have used Theano (Bergstra et al., 2010)
(Bastien et al., 2012) and Keras (Chollet, 2015) for
implementation.
4 RESULTS AND DISCUSSION
First, to show the validity of the DNN architecture
and the training hyperparameters, we have measured
the training loss at each epoch. As it can be seen in
Figure 5, the training loss decreased in each epoch
showing but the curve started to flatten at later epochs.
Automatic 3D Point Set Reconstruction from Stereo Laparoscopic Images using Deep Neural Networks
119

(a) Point cloud from ground truth (b) Point cloud predicted by the proposed method
Figure 7: Comparison of point clouds extracted from the ground truth and by our approach.
We have also calculated the loss on the test in-
stances. In average, the RMSE per image was 13.18.
As it can be seen from Figure 6, there was quite a
big fluctuation in losses (around 11-15). However, the
ground truth was incomplete for some of the images,
which might have affected the ability to properly eval-
uate each individual instances.
However, in some extreme cases (see Figure 7),
the reconstruction by the proposed approach was just
partially successful. To correct issues like this, an ap-
proach which also incorporates on contextual infor-
mation could be used in the future.
5 CONCLUSIONS
Minimally invasive surgical techniques are very im-
portant in clinical settings, however, they require
computational support to allow surgeons to effec-
tively use these techniques in practice. In this paper,
an approach based on deep neural networks has been
introduced, which is unlike the state-of-the-art ap-
proaches, only relies on the input pixels of the stereo
image pair. The approach has been evaluated on a
publicly available dataset and compared well to the
results obtained by a state-of-the-art technique.
ACKNOWLEDGMENTS
This work was supported in part by the project VKSZ
14-1-2015-0072, SCOPIA: Development of diagnos-
tic tools based on endoscope technology supported by
the European Union, co-financed by the European So-
cial Fund.
REFERENCES
Bastien, F., Lamblin, P., Pascanu, R., Bergstra, J., Good-
fellow, I. J., Bergeron, A., Bouchard, N., and Ben-
gio, Y. (2012). Theano: new features and speed im-
provements. Deep Learning and Unsupervised Fea-
ture Learning NIPS 2012 Workshop.
Bergstra, J., Breuleux, O., Bastien, F., Lamblin, P., Pascanu,
R., Desjardins, G., Turian, J., Warde-Farley, D., and
Bengio, Y. (2010). Theano: a CPU and GPU math
expression compiler. In Proceedings of the Python for
Scientific Computing Conference (SciPy). Oral Pre-
sentation.
Chollet, F. (2015). Keras. https://github.com/fchollet/keras.
Glorot, X. and Bengio, Y. (2010). Understanding the diffi-
culty of training deep feedforward neural networks. In
International conference on artificial intelligence and
statistics, pages 249–256.
Glorot, X., Bordes, A., and Bengio, Y. (2011). Deep sparse
rectifier neural networks. In International Conference
on Artificial Intelligence and Statistics, pages 315–
323.
Hoerl, A. E. and Kennard, R. W. (1970). Ridge regression:
Biased estimation for nonorthogonal problems. Tech-
nometrics, 12(1):55–67.
LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep learn-
ing. Nature, 521(7553):436–444.
Maier-Hein, L., Mountney, P., Bartoli, A., Elhawary, H., El-
son, D., Groch, A., Kolb, A., Rodrigues, M., Sorger,
J., Speidel, S., et al. (2013). Optical techniques for
3d surface reconstruction in computer-assisted laparo-
scopic surgery. Medical image analysis, 17(8):974–
996.
Nair, V. and Hinton, G. E. (2010). Rectified linear units
improve restricted boltzmann machines. In Proceed-
ings of the 27th International Conference on Machine
Learning (ICML-10), pages 807–814.
Pratt, P., Stoyanov, D., Visentini-Scarzanella, M., and Yang,
G.-Z. (2010). Dynamic guidance for robotic surgery
using image-constrained biomechanical models. In
Medical Image Computing and Computer-Assisted
Intervention–MICCAI 2010, pages 77–85. Springer.
Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I.,
and Salakhutdinov, R. (2014). Dropout: A simple way
SPCS 2016 - International Conference on Signal Processing and Communication Systems
120

to prevent neural networks from overfitting. The Jour-
nal of Machine Learning Research, 15(1):1929–1958.
Stoyanov, D., Scarzanella, M. V., Pratt, P., and Yang, G.-Z.
(2010). Real-time stereo reconstruction in robotically
assisted minimally invasive surgery. In Medical Im-
age Computing and Computer-Assisted Intervention–
MICCAI 2010, pages 275–282. Springer.
Zeiler, M. D. (2012). ADADELTA: an adaptive learning
rate method. CoRR, abs/1212.5701.
Automatic 3D Point Set Reconstruction from Stereo Laparoscopic Images using Deep Neural Networks
121